Directed Kinetic Self-Assembly of Mounds on Patterned GaAs (001): Tunable Arrangement, Pattern Amplification and Self-Limiting Growth
Abstract
:1. Introduction
2. Results and Discussion
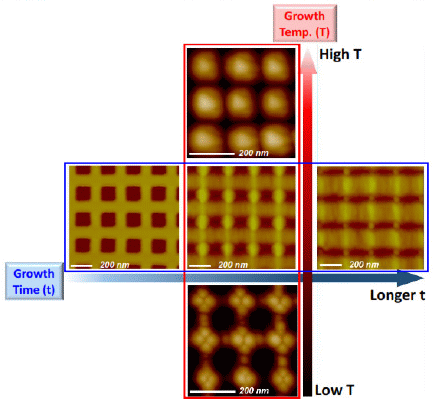
2.1. Directed Self-Assembly and Pattern Amplification
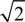 × a/
× a/ 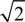 )R45 unit cell with a basis of 5 mounds at (0,0), (A/3, B/3), (2A/3, B/3), (A/3, 2B/3), (2A/3, 2B/3), where A and B are the unit vectors of the lattice, i.e., A = (a/
)R45 unit cell with a basis of 5 mounds at (0,0), (A/3, B/3), (2A/3, B/3), (A/3, 2B/3), (2A/3, 2B/3), where A and B are the unit vectors of the lattice, i.e., A = (a/ 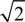 , −a/
, −a/ 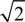 ) and B = (a/
) and B = (a/ 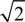 , a/
, a/ 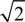 ). These observations are consistent with the results of our kMC simulations [18], which predict an increase in the “natural” mound size with temperature for growth on unpatterned surfaces.
). These observations are consistent with the results of our kMC simulations [18], which predict an increase in the “natural” mound size with temperature for growth on unpatterned surfaces.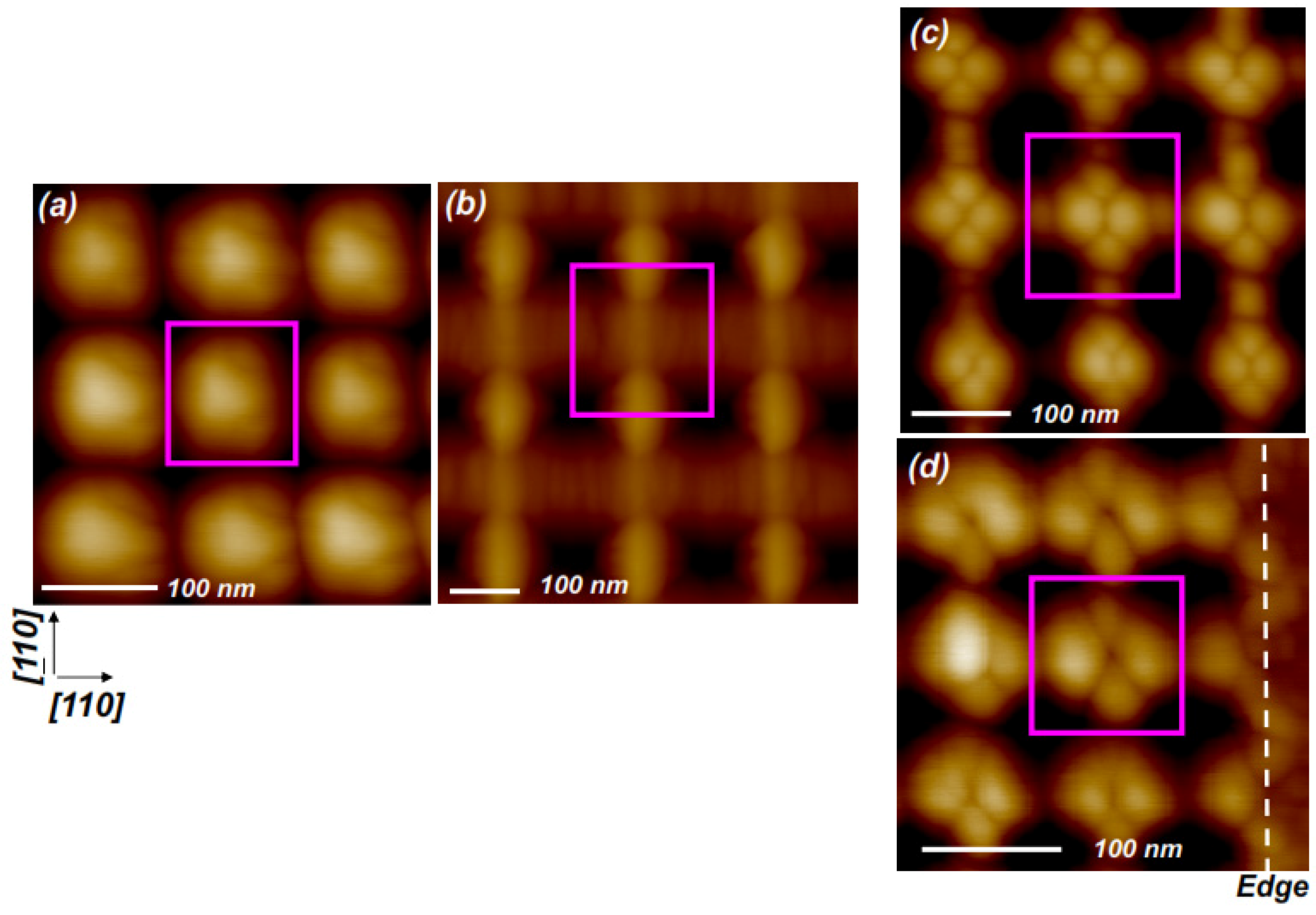
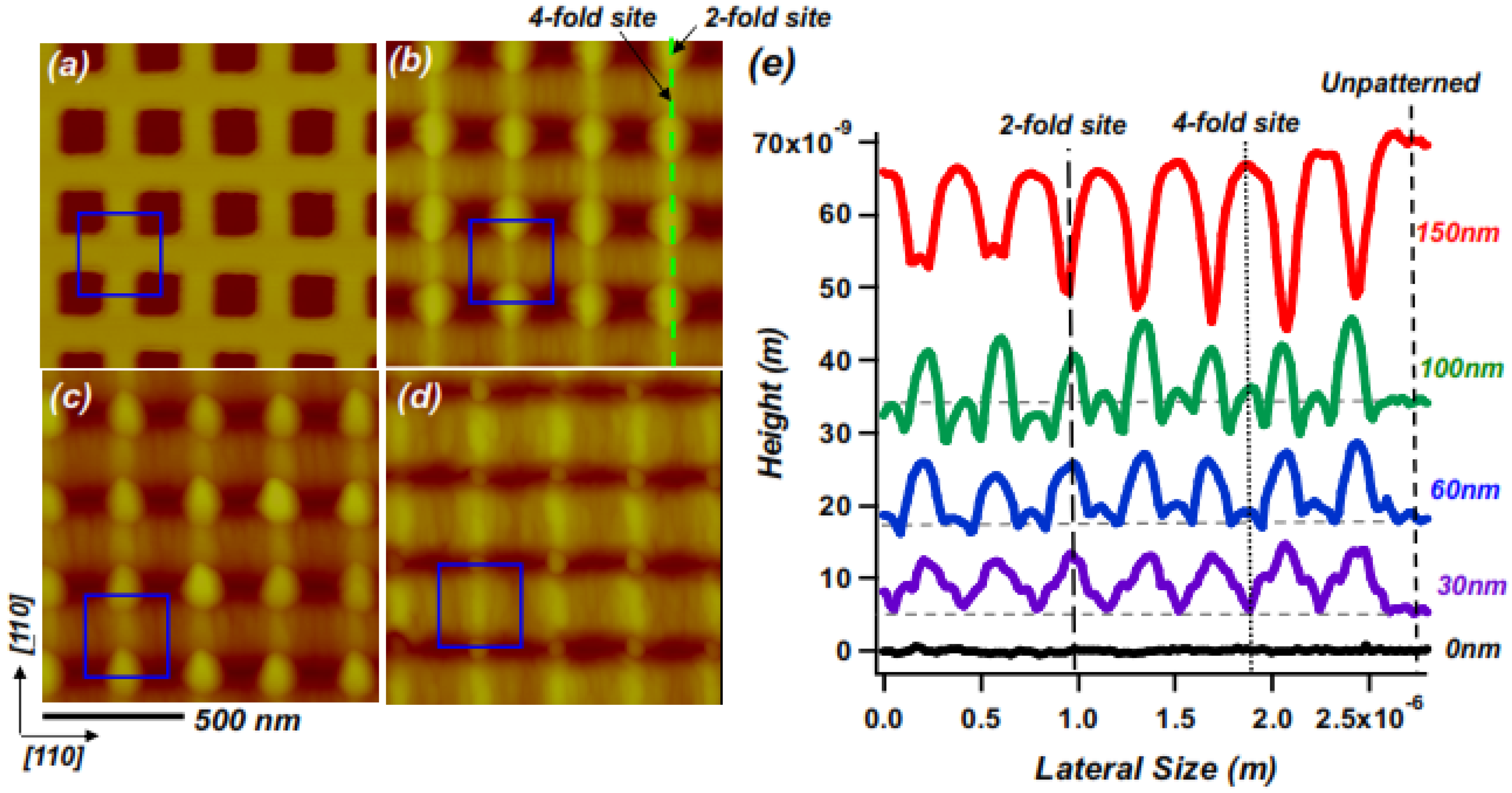
2.2. Self-Limiting Behavior
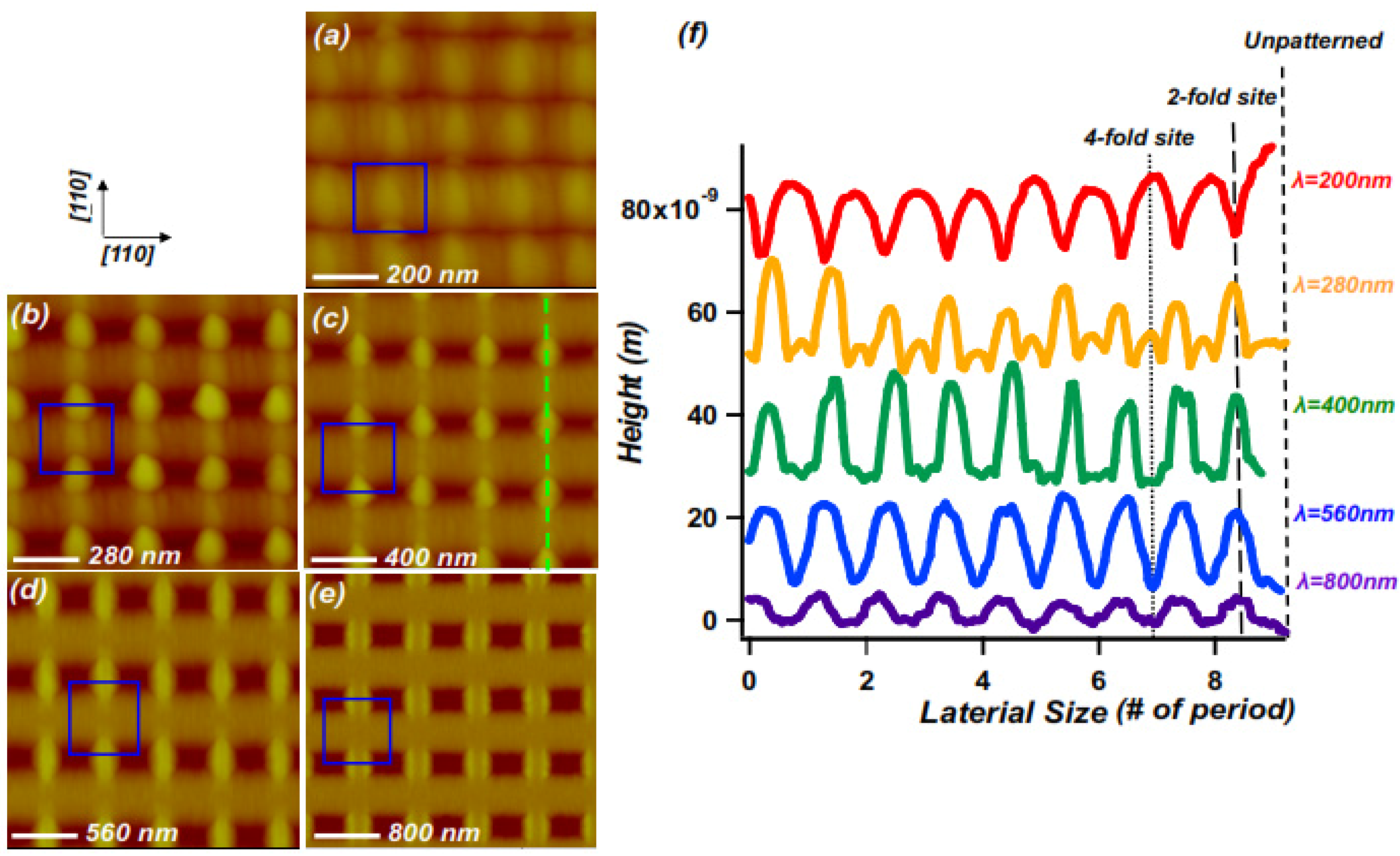
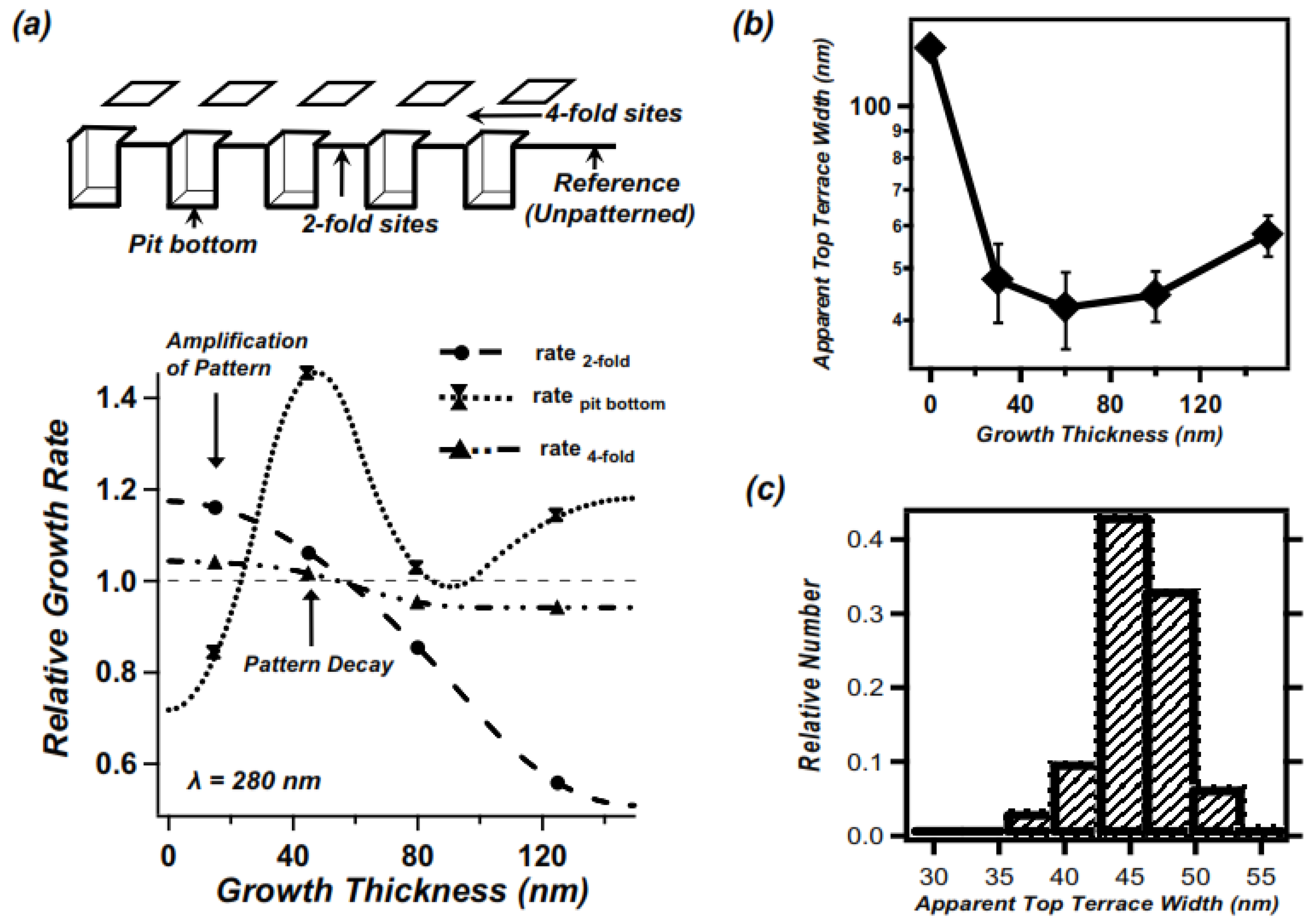
3. Experimental Section
4. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Mann, S. Self-assembly and transformation of hybrid nano-objects and nanostructures under equilibrium and non-equilibrium conditions. Nat. Mater. 2009, 8, 781–792. [Google Scholar] [CrossRef]
- Grzelczak, M.; Vermant, J.; Furst, E.M.; Liz-Marzán, L.M. Directed self-assembly of nanoparticles. ACS Nano 2010, 4, 3591–3605. [Google Scholar] [CrossRef]
- N’Diaye, A.T.; Bleikamp, S.; Feibelman, P.J.; Michely, T. Two-Dimensional Ir Cluster Lattice on a Graphene Moiré on Ir(111). Phys. Rev. Lett. 2006, 215501:1–215501:4. [Google Scholar]
- Gray, J.L.; Hull, R.; Lam, C.-H.; Sutter, P.; Meabs, J.; Floro, J.A. Beyond the heteroepitaxial quantum dot: Self-assembling complex nanostructures controlled by strain and growth kinetics. Phys. Rev. B 2005, 72, 155323:1–155323:11. [Google Scholar]
- Gherasimova, M.; Hull, R.; Reuter, M.C.; Ross, F.M. Pattern level assembly of Ge quantum dots on Si with focused ion beam templating. Appl. Phys. Lett. 2008, 93, 023106:1–023106:3. [Google Scholar]
- Mehta, M.; Reuter, D.; Melnikov, A.; Wieck, A.D.; Remhof, A. An intentionally positioned (In, Ga) As quantum dot in a micron sized light emitting diode. Appl. Phys. Lett. 2007, 91, 123108:1–123108:3. [Google Scholar]
- Martin, A.J.; Saucer, T.W.; Rodriguez, G.V.; Sih, V.; Millunchick, J.M. Lateral patterning of multilayer InAs/GaAs (001) quantum dot structures by in vacuo focused ion beam. Nanotechnology 2012, 23, 135401:1–135401:7. [Google Scholar]
- Hu, H.; Gao, H.J.; Liu, F. Theory of directed nucleation of strained islands on patterned substrates. Phys. Rev. Lett. 2008, 101, 216102:1–216102:4. [Google Scholar]
- Galatsis, K.; Wang, K.L.; Ozkan, M.; Ozkan, C.S.; Huang, Y.; Chang, J.P.; Monbouquette, H.G.; Chen, Y.; Nealey, P.; Botros, Y. Patterning and templating for nanoelectronics. Adv. Mater. 2010, 22, 769–778. [Google Scholar] [CrossRef]
- Vastola, G.; Grydlik, M.; Brehm, M.; Fromherz, T.; Bauer, G.; Boioli, F.; Miglio, L.; Montalenti, F. How pit facet inclination drives heteroepitaxial island positioning on patterned substrates. Phys. Rev. B 2011, 84, 155415:1–155415:7. [Google Scholar]
- Grydlik, M.; Langer, G.; Fromherz, T.; Schäffler, F.; Brehm, M. Recipes for the fabrication of strictly ordered Ge islands on pit-patterned Si (001) substrates. Nanoscale Res. Lett. 2012, 7, 105601:1–105601:6. [Google Scholar]
- Zhong, Z.; Schmidt, O.G.; Bauer, G. Increase of island density via formation of secondary ordered islands on pit-patterned Si (001) substrates. Appl. Phys. Lett. 2005, 87, 133111:1–133111:3. [Google Scholar]
- Politi, P.; Villain, J. Ehrlich-Schwoebel instability in molecular-beam epitaxy: A minimal model. Phys. Rev. B 1996, 54, 5114–5129. [Google Scholar] [CrossRef]
- Ehrlich, G.; Hudda, F.G. Atomic View of Surface Self-Diffusion: Tungsten on Tungsten. J. Chem. Phys. 1966, 44, 1039–1049. [Google Scholar] [CrossRef]
- Schwoebel, R.L.; Shipsey, E.J. Step Motion on Crystal Surfaces. J. Appl. Phys. 1966, 37, 3682–3686. [Google Scholar] [CrossRef]
- Johnson, M.D.; Orme, C.; Hunt, A.W.; Graff, D.; Sudijono, J.; Sander, L.M.; Orr, B.G. Stable and unstable growth in molecular beam epitaxy. Phys. Rev. Lett. 1994, 72, 116–119. [Google Scholar] [CrossRef]
- Tadayyon-Eslami, T.; Kan, H.-C.; Calhoun, L.C.; Phaneuf, R.J. Temperature-driven change in the unstable growth mode on patterned GaAs (001). Phys. Rev. Lett. 2006, 97, 126101:1–126101:4. [Google Scholar]
- Lin, C.-F.; Hammouda, A.B.H.; Kan, H.-C.; Bartelt, N.C.; Phaneuf, R.J. Directing self-assembly of nanostructures kinetically: Patterning and the Ehrlich-Schwoebel barrier. Phys. Rev. B 2012, 85, 085421:1–085421:8. [Google Scholar]
- Braun, O.M.; Kivshar, Y. S. The Frenkel-Kontorova model: Concepts, methods, and applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Bak, P. Commensurate phases, incommensurate phases and the devil’s staircase. Rep. Prog. Phys. 1982, 45, 587–629. [Google Scholar] [CrossRef]
- See supplemental material [Figure S3] for additional examples of the result of growth at 300 °C on larger period templates.
- Shitara, T.; Vvedensky, D.D.; Wilby, M.R.; Jhang, J.; Neave, J.H.; Joyce, B.A. Misorientation dependence of epitaxial growth on vicinal GaAs (001). Phys. Rev. B 1992, 46, 6825–6833. [Google Scholar] [CrossRef]
- See supplemental material [Figure S1] for mound heights vs. grown thickness measured on two different reference levels, which both showed self-limiting behavior.
- Kan, H.-C.; Shah, S.; Tadayyon-Eslami, T.; Phaneuf, R.J. Transient evolution of surface roughness on patterned GaAs(001) during homoepitaxial growth. Phys. Rev. Lett. 2004, 92, 146101:1–146101:4. [Google Scholar]
- Kan, H.-C.; Ankam, R.; Shah, S.; Micholsky, K.M.; Tadayyon-Eslami, T.; Calhoun, L.C.; Phaneuf, R.J. Evolution of patterned GaAs (001) during homoepitaxial growth: Size versus spacing. Phys. Rev. B 2006, 73, 195410:1–195410:4. [Google Scholar]
- Shah, S.; Garrett, T.J.; Limpaphayom, K.; Tadayyon-Eslami, T.; Kan, H.-C.; Phaneuf, R.J. Patterning-based investigation of the length-scale dependence of the surface evolution during multilayer epitaxial growth. Appl. Phys. Lett. 2003, 83, 4330–4332. [Google Scholar] [CrossRef]
- Lin, C.-F.; Kan, H.-C.; Kanakaraju, S.; Richardson, C.J.; Phaneuf, R.J. Evidence for a large, thermal-activated characteristic length scale in unstable homoepitaxial growth on GaAs (001). J. Cryst. Growth 2013, 381, 83–86. [Google Scholar] [CrossRef]
- Elkinani, I.; Villain, J. Growth roughness and instabilities due to the Schwoebel effect: A one-dimensional model. J. Phys. I France 1994, 4, 949–973. [Google Scholar]
- See supplemental material [Figure S2] for mound sidewall orientations vs. grown thickness.
- Kratzer, P.; Scheffler, M. Reaction-limited island nucleation in molecular beam epitaxy of compound semiconductors. Phys. Rev. Lett. 2002, 88, 036102:1–036102:4. [Google Scholar]
- Morgan, C.G.; Kratzer, P.; Scheffler, M. Arsenic dimer dynamics during MBE growth: theoretical evidence for a novel chemisorption state of As2 molecules on GaAs surfaces. Phys. Rev. Lett. 1999, 82, 4886–4889. [Google Scholar] [CrossRef]
- Giesen, M.; Icking-Konert, G.S.; Ibach, H. Interlayer mass transport and quantum confinement of electronic states. Phys. Rev. Lett. 1999, 82, 3101–3104. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lin, C.-F.; Kan, H.-C.; Kanakaraju, S.; Richardson, C.; Phaneuf, R. Directed Kinetic Self-Assembly of Mounds on Patterned GaAs (001): Tunable Arrangement, Pattern Amplification and Self-Limiting Growth. Nanomaterials 2014, 4, 344-354. https://doi.org/10.3390/nano4020344
Lin C-F, Kan H-C, Kanakaraju S, Richardson C, Phaneuf R. Directed Kinetic Self-Assembly of Mounds on Patterned GaAs (001): Tunable Arrangement, Pattern Amplification and Self-Limiting Growth. Nanomaterials. 2014; 4(2):344-354. https://doi.org/10.3390/nano4020344
Chicago/Turabian StyleLin, Chuan-Fu, Hung-Chih Kan, Subramaniam Kanakaraju, Christopher Richardson, and Raymond Phaneuf. 2014. "Directed Kinetic Self-Assembly of Mounds on Patterned GaAs (001): Tunable Arrangement, Pattern Amplification and Self-Limiting Growth" Nanomaterials 4, no. 2: 344-354. https://doi.org/10.3390/nano4020344