A Thermal, Mechanical, and Materials Framework for a Shape Memory Alloy Heat Engine for Thermal Management
Abstract
:1. Introduction
2. SMA Stirling Engine
2.1. Efficiency
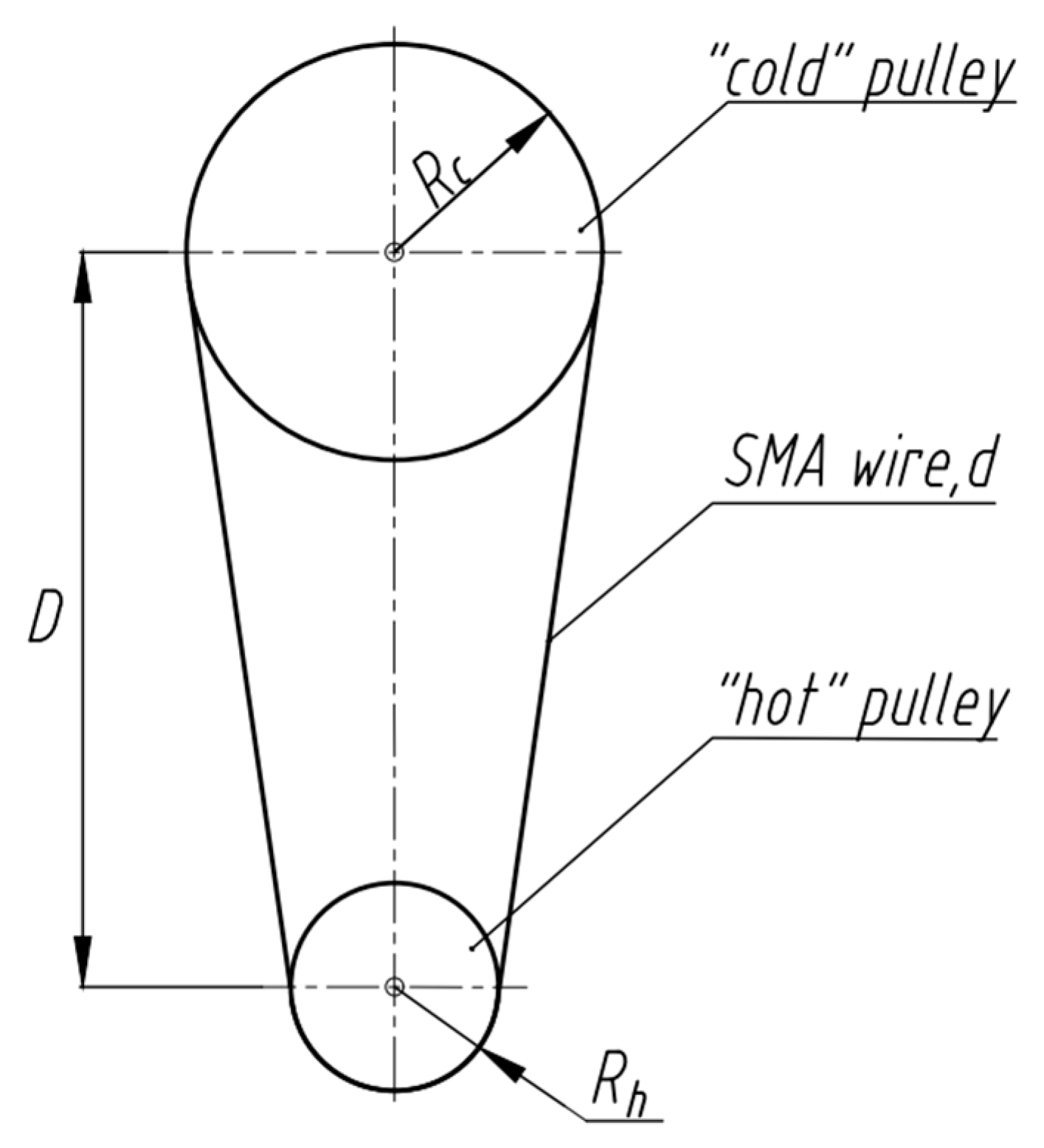
2.2. Configuration
3. Analyses
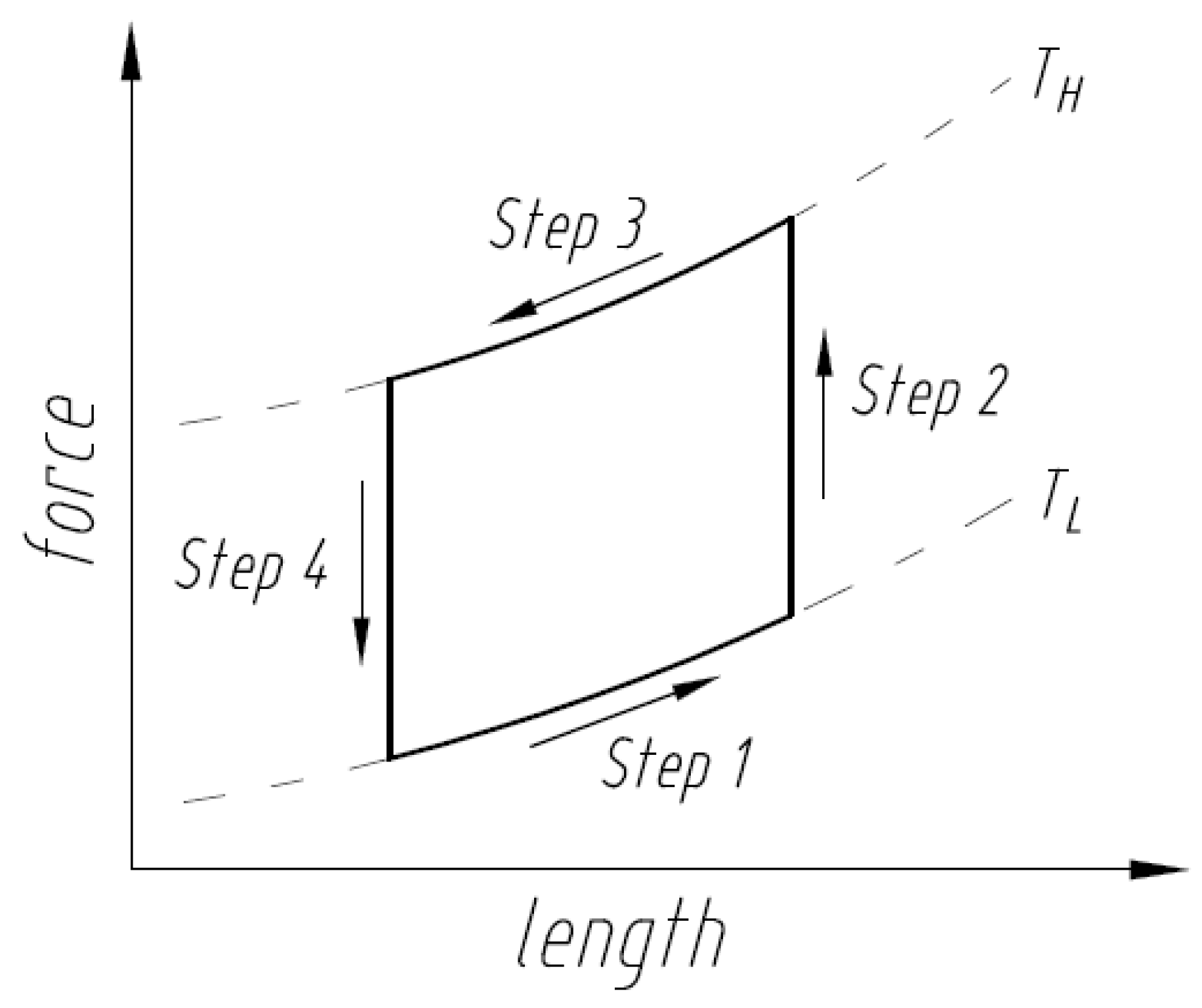
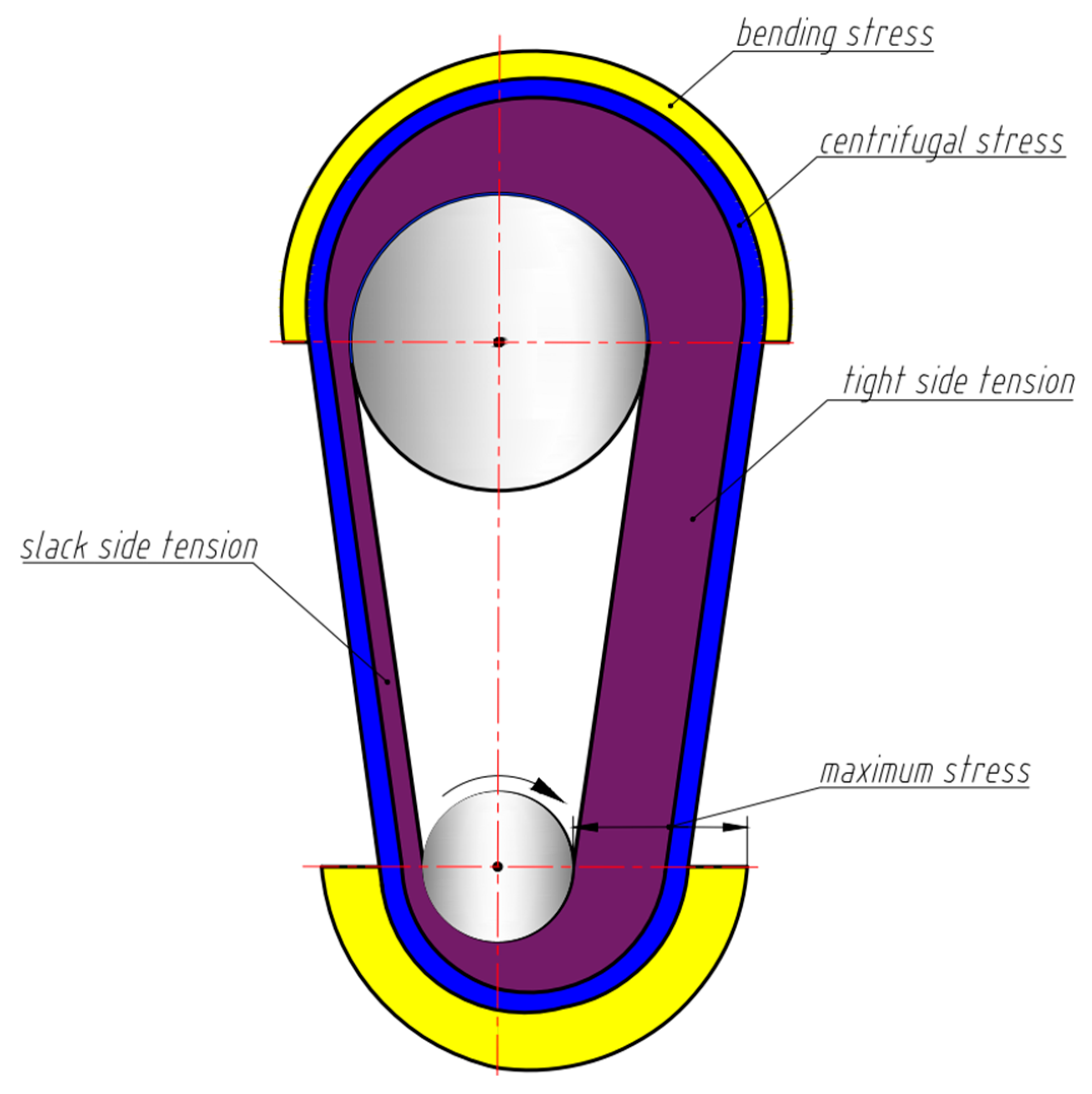
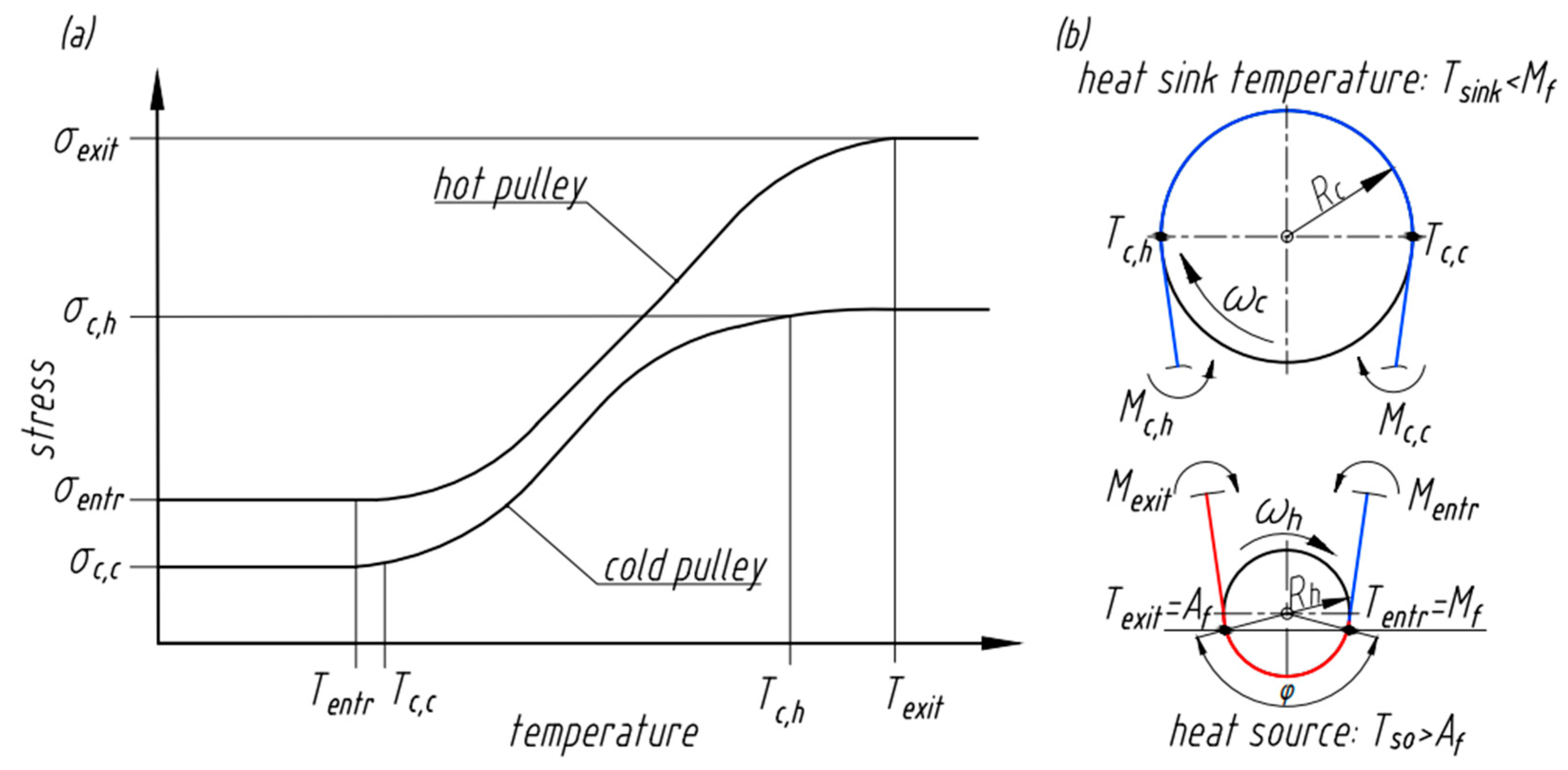
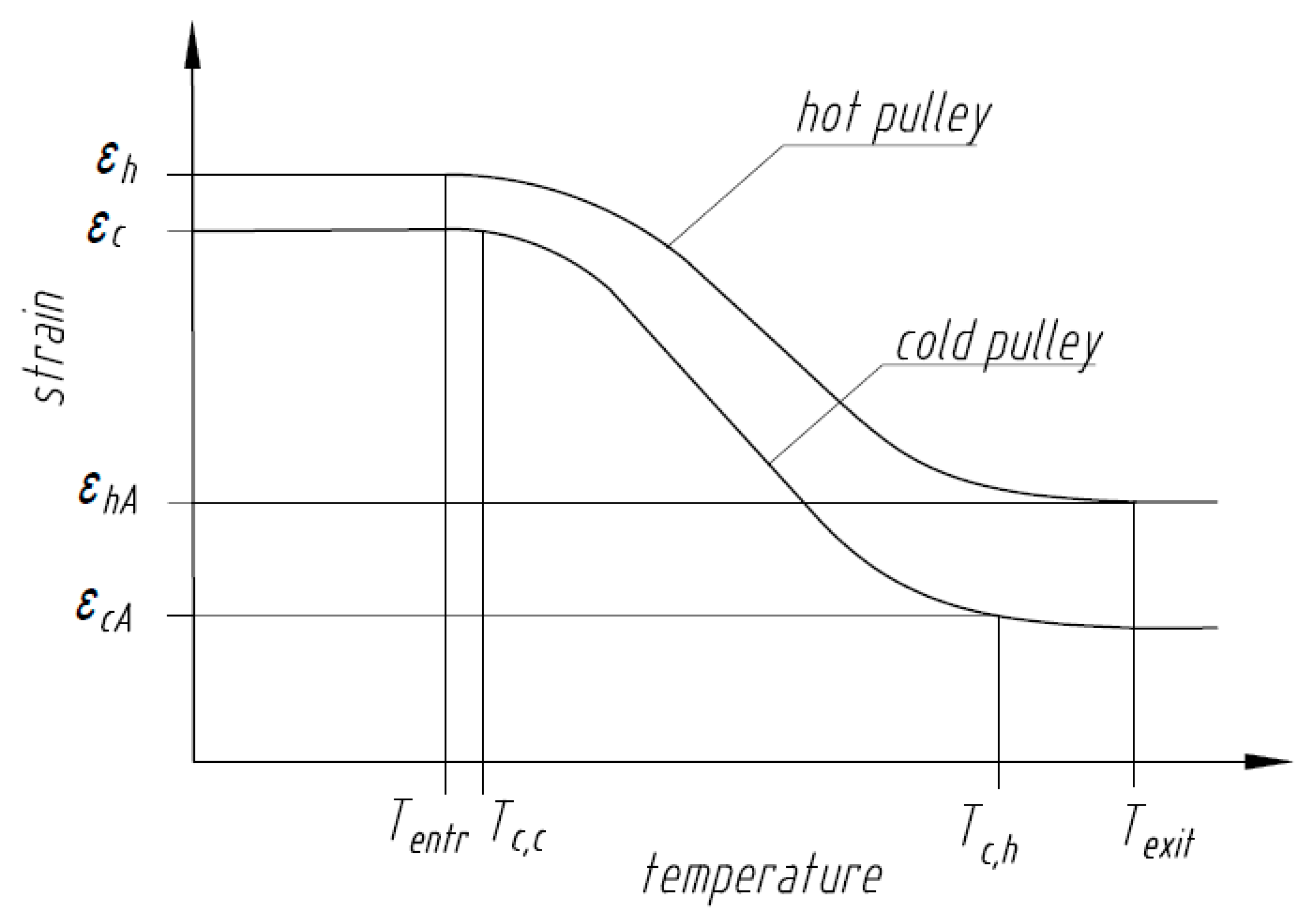
3.1. Mechanical and Thermal Analyses
3.2. Material Thermodynamics
3.3. Material Nano- and Microstructure
4. Implementation
5. Conclusions
- Mechanical aspects in the framework were built on force balances in the SMA element and on the resulting stress distribution. The role of element geometry was assessed in affecting engine output torque and speed from the analysis of the SMA Stirling engine.
- Thermal aspects were addressed by considering the heat transfer rate between the SMA element and both the heat source and the heat sink. The effect of temperature of the heat source relative to the phase transformation temperatures of the SMA was also evaluated.
- The total enthalpy of the transformation was considered from chemical, elastic, and frictional contributions. Each of these terms was connected with the material nano- and microstructure through alloy selection and thermomechanical processing, making recommendations vis-á-vis the size and distribution of precipitates, variant interfaces through texture, cycling and training, defects, nucleation sites (bulk vs. surface), and multi-step transformations (e.g., a trigonal R-phase transformation). Specific cases of tailoring P-phase and H-phase nano-precipitates in NiTiPt and NiTiHf high temperature shape memory alloys (for heat recovery applications) affecting nano- and compound twinning and, subsequently, the enthalpy of the transformation by recourse to ultra fine and nano crystalline grain structures and additionally introducing a inhomogeneous transformation in ultra fine grained materials for adequate starting torque in order for the engine to run without external force, are presented.
- The above aspects were extended to consider a figure of merit for the performance of an SMA heat engine in two modes of operation. The first is where torque is the defining criterion, and the second is where speed is. The importance of separately using both an enthalpy term and a hysteresis term in the proposed FOM is emphasized through competition between the net enthalpy change and the elastic enthalpy change.
- For an SMA heat engine functioning where maximum torque is the criterion, a high FOM is a desirable choice. In contrast to torque, for an SMA heat engine functioning where maximum speed is the criterion, a recommendation on minimizing the FOM is made.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bhattacharya, K. Microstructure of Martensite: Why It Forms and How It Gives Rise to the Shape-Memory Effect; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Ma, J.; Karaman, I.; Noebe, R.D. High temperature shape memory alloys. Int. Mater. Rev. 2010, 55, 257. [Google Scholar] [CrossRef]
- Miranda, D. 2020 NASA Technology Taxonomy. 2020. Available online: https://www.nasa.gov/offices/oct/taxonomy/index.html (accessed on 1 June 2023).
- Browne, A.L.; Keefe, A.C.; Alexander, P.W.; Mankame, N.; Usoro, P.; Johnson, N.L.; Aase, J.; Sarosi, P.; McKnight, G.P.; Herrera, G.; et al. Lightweight thermal energy recovery system based on shape memory alloys: A DOE ARPA-E initiative. In Proceedings of the SPIE 8343 Industrial and Commercial Applications of Smart Structures Technologies 2012, San Diego, CA, USA, 11–15 March 2012. [Google Scholar]
- Abubakar, R.A.; Wang, F.; Wang, L. A review on Nitinol shape memory alloy heat engines. Smart Mater. Struct. 2020, 30, 13001. [Google Scholar] [CrossRef]
- Benafan, O.; Notardonato, W.U.; Meneghelli, B.J.; Vaidyanathan, R. Design and development of a shape memory alloy activated heat pipe-based thermal switch. Smart Mater. Struct. 2013, 22, 105017. [Google Scholar] [CrossRef]
- Krishnan, V.; Bewerse, C.; Notardonato, W.; Vaidyanathan, R. A thermal conduction switch based on low hysteresis NiTiFe shape memory alloy helical springs. Adv. Cryog. Eng. 2008, 54, 3. [Google Scholar]
- Lemanski, J.; Krishnan, V.; Manjeri, R.M.; Notardonato, W.; Vaidyanathan, R. A low hysteresis NiTiFe shape memory alloy based thermal conduction switch. Adv. Cryog. Eng. 2006, 52A, 3. [Google Scholar]
- Krishnan, V.B.; Singh, J.D.; Woodruff, T.R.; Notardonato, W.U.; Vaidyanathan, R. A shape memory alloy based cryogenic thermal conduction switch. Adv. Cryog. Eng. 2004, 50A, 26. [Google Scholar]
- Vaidyanathan, R.; Krishnan, V.; Notardonato, W.U. Shape-Memory Thermal Conduction Switch 5. U.S. Patent No 7752866, 13 July 2010. [Google Scholar]
- Liu, Y. The work production of shape memory alloy. Smart Mater. Struct. 2004, 13, 552. [Google Scholar] [CrossRef]
- Salzbrenner, R. Shape memory heat engines. J. Mater. Sci. 1984, 19, 1827. [Google Scholar] [CrossRef]
- Jiang, W. Analysis and Design of Machine Elements; Wiley Online Library: Hoboken, NJ, USA, 2019. [Google Scholar]
- Tanaka, M. Shape memory alloy engine. In Proceedings of the 27th Intersociety Energy Conversion Engineering Conference, San Diego, CA, USA, 3–7 August 1992. [Google Scholar]
- Duerig, T.W.; Melton, K.; Stöckel, D. Engineering Aspects of Shape Memory Alloys; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Salzbrenner, R.; Cohen, M. On the thermodynamics of thermoelastic martensitic transformations. Acta Metall. 1979, 27, 739. [Google Scholar] [CrossRef]
- ASTM F2082/F2082M-16; Standard Test Method for Determination of Transformation Temperature of Nickel-Titanium Shape Memory Alloys by Bend and Free Recovery. ASTM International: Conshohocken, PA, USA, 2016. [CrossRef]
- Nicholson, D.; Benafan, O.; Padula, S.; Clausen, B.; Vaidyanathan, R. Loading path and control mode effects during thermomechanical cycling of polycrystalline shape memory NiTi. Shape Mem. Superelasticity 2018, 4, 143. [Google Scholar] [CrossRef]
- Nicholson, D.; Padula, S.A.; Benafan, O.; Vaidyanathan, R. Texture evolution during isothermal, isostrain, and isobaric loading of polycrystalline shape memory NiTi. Appl. Phys. Lett. 2017, 110, 251903. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Clausen, B.; Padula II, S.; Noebe, R.; Vaidyanathan, R. On elastic moduli and elastic anisotropy in polycrystalline martensitic NiTi. Acta Mater. 2011, 59, 5055. [Google Scholar] [CrossRef]
- Olson, G.; Cohen, M. Thermoelastic behavior in martensitic transformations. Scr. Metall. 1975, 9, 1247. [Google Scholar] [CrossRef]
- Olson, G.; Cohen, M. A perspective on martensitic nucleation. Annu. Rev. Mater. Sci. 1981, 11, 1–32. [Google Scholar] [CrossRef]
- Nicholson, D.E.; Padula, S.A., II.; Noebe, R.D.; Benafan, O.; Vaidyanathan, R. Thermomechanical Behavior of NiTiPdPt High Temperature Shape Memory Alloy Springs. Smart Mater. Struct. 2014, 23, 125009. [Google Scholar] [CrossRef]
- Dhakal, B.; Nicholson, D.E.; Saleeb, A.F.; Padula, S.A.; Vaidyanathan, R. Three-dimensional deformation response of a NiTi shape memory helical-coil actuator during thermomechanical cycling: Experimentally validated numerical model. Smart Mater. Struct. 2016, 25, 95056. [Google Scholar] [CrossRef]
- Paul, P.P.; Paranjape, H.M.; Amin-Ahmadi, B.; Pagan, D.C.; Chumlyakov, Y.I.; Brinson, L.C. Heterogeneity and inelasticity of deformation in a notched martensitic NiTi shape memory alloy specimen. Acta Mater. 2020, 194, 49. [Google Scholar] [CrossRef]
- Gao, W.; Yi, X.; Sun, B.; Meng, X.; Cai, W.; Zhao, L. Microstructural evolution of martensite during deformation in Zr50Cu50 shape memory alloy. Acta Mater. 2017, 132, 405. [Google Scholar] [CrossRef]
- Molnarova, O.; Tyc, O.; Heller, L.; Seiner, H.; Šittner, P. Evolution of martensitic microstructures in nanocrystalline NiTi wires deformed in tension. Acta Mater. 2021, 218, 117166. [Google Scholar] [CrossRef]
- Waitz, T. The self-accommodated morphology of martensite in nanocrystalline NiTi shape memory alloys. Acta Mater. 2005, 53, 2273. [Google Scholar] [CrossRef]
- Plietsch, R.; Ehrlich, K. Strength differential effect in pseudoelastic NiTi shape memory alloys. Acta Mater. 1997, 45, 2417. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Kocich, R.; Tardif, S.; Dolbnya, I.P.; Kunčická, L.; Micha, J.-S.; Liogas, K.; Magdysyuk, O.V.; Szurman, I. Grain structure engineering of NiTi shape memory alloys by intensive plastic deformation. ACS Appl. Mater. Interfaces 2022, 14, 31396. [Google Scholar] [CrossRef] [PubMed]
- Manjeri, R.M.; Qiu, S.; Mara, N.; Misra, A.; Vaidyanathan, R. Superelastic response of [111] and [101] oriented NiTi micropillars. J. Appl. Phys. 2010, 108, 23501. [Google Scholar] [CrossRef]
- Saburi, T.; Nenno, S. The shape memory effect and related phenomena. In Solid to Solid Phase Transformations; Aaronson, H.I., Loughin, D.E., Sekerka, R.F., Wayman, C.M., Eds.; Met. Soc. AIME: Warrendale, PA, USA, 1981; p. 1455. [Google Scholar]
- Rathod, C.; Clausen, B.; Bourke, M.; Vaidyanathan, R. Neutron diffraction investigation of hysteresis reduction and increase in linearity in the stress-strain response of superelastic NiTi. Appl. Phys. Lett. 2006, 88, 201919. [Google Scholar] [CrossRef] [Green Version]
- Evirgen, A.; Karaman, I.; Pons, J.; Santamarta, R.; Noebe, R. Role of nano-precipitation on the microstructure and shape memory characteristics of a new Ni50.3Ti34.7Zr15 shape memory alloy. Mater. Sci. Eng. A 2016, 655, 193. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.Z.; Liu, L.H.; Yang, C.; Luo, X.; Song, C.H.; Wang, Z.; Wang, J.; Su, Y.D.; Ding, Y.F.; Zhang, L.C.; et al. Simultaneous enhancement of mechanical and shape memory properties by heat-treatment homogenization of Ti2Ni precipitates in TiNi shape memory alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2022, 101, 205–216. [Google Scholar] [CrossRef]
- Lu, H.Z.; Ma, H.W.; Cai, W.S.; Luo, X.; Wang, Z.; Song, C.H.; Yin, S.; Yang, C. Stable tensile recovery strain induced by a Ni4Ti3 nanoprecipitate in a Ni50.4Ti49.6 shape memory alloy fabricated via selective laser melting. Acta Mater. 2021, 219, 117261. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Hamilton, R.; Canadinc, D.; Zhang, X.Y.; Gall, K.; Karaman, I.; Chumlyakov, Y.; Maier, H.J. Detwinning in NiTi Alloys. Metall. Mater. Trans. A 2003, 34, 5. [Google Scholar] [CrossRef]
- Gao, Y.; Zhou, N.; Yang, F.; Cui, Y.; Kovarik, L.; Hatcher, N.; Noebe, R.; Mills, M.; Wang, Y. P-phase precipitation and its effect on martensitic transformation in (Ni, Pt) Ti shape memory alloys. Acta Mater. 2012, 60, 1514. [Google Scholar] [CrossRef]
- Yu, T.; Gao, Y.; Casalena, L.; Anderson, P.; Mills, M.; Wang, Y. H-phase precipitation and its effects on martensitic transformation in NiTi-Hf high-temperature shape memory alloys. Acta Mater. 2021, 208, 116651. [Google Scholar] [CrossRef]
- Sharar, D.J.; Donovan, B.F.; Warzoha, R.J.; Wilson, A.A.; Leff, A.C.; Hanrahan, B.M. Solid-state thermal energy storage using reversible martensitic transformations. Appl. Phys. Lett. 2019, 114, 143902. [Google Scholar] [CrossRef] [Green Version]
- Manjeri, R. Low Temperature and Reduced Length Scale Behavior of Shape Memory and Superelastic NiTi and NiTiFe Alloys. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2009. [Google Scholar]
- Rathod, C.R. Diffraction Studies of Deformation in Shape Memory Alloys and Selected Engineering Components. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2005. [Google Scholar]
- Young, M.; Wagner, M.-X.; Frenzel, J.; Schmahl, W.W.; Eggeler, G. Phase volume fractions and strain measurements in an ultrafine-grained NiTi shape-memory alloy during tensile loading. Acta Mater. 2010, 58, 2344. [Google Scholar] [CrossRef] [Green Version]
- Sawaguchi, T.A.; Kausträter, G.; Yawny, A.; Wagner, M.; Eggeler, G. Crack initiation and propagation in 50.9 at. pct Ni-Ti pseudoelastic shape-memory wires in bending-rotation fatigue. Metall. Mater. Trans. A 2003, 34, 2847–2860. [Google Scholar] [CrossRef]
- Benafan, O.; Brown, J.; Calkins, F.T.; Kumar, P.; Stebner, A.P.; Turner, T.L.; Vaidyanathan, R.; Webster, J.; Young, M.L. Shape-memory alloy actuator design: CASMART collaborative best practices and case studies. Int. J. Mech. Mater. Des. 2014, 10, 1–42. [Google Scholar] [CrossRef]
- Benafan, O.; Moholt, M.R.; Bass, M.; Mabe, J.H.; Nicholson, D.E.; Calkins, F.T. Recent advancements in rotary shape memory alloy actuators for aeronautics. Shape Mem. Superelasticity 2019, 5, 415. [Google Scholar] [CrossRef]
- Benafan, O.; Noebe, R.D.; Padula, S.A., II.; Brown, D.W.; Vogel, S.; Vaidyanathan, R. Thermomechanical cycling of a NiTi shape memory alloy-macroscopic response and microstructural evolution. Int. J. Plast. 2014, 56, 99. [Google Scholar] [CrossRef]
- Manchiraju, D.; Gaydosh, O.B.; Noebe, R.; Vaidyanathan, R.; Anderson, P.M. Thermal cycling and isothermal deformation response of polycrystalline NiTi: Simulations vs. experiment. Acta Mater. 2011, 59, 5238. [Google Scholar] [CrossRef] [Green Version]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikhareva, M.; Vaidyanathan, R. A Thermal, Mechanical, and Materials Framework for a Shape Memory Alloy Heat Engine for Thermal Management. Nanomaterials 2023, 13, 2159. https://doi.org/10.3390/nano13152159
Chikhareva M, Vaidyanathan R. A Thermal, Mechanical, and Materials Framework for a Shape Memory Alloy Heat Engine for Thermal Management. Nanomaterials. 2023; 13(15):2159. https://doi.org/10.3390/nano13152159
Chicago/Turabian StyleChikhareva, Maria, and Raj Vaidyanathan. 2023. "A Thermal, Mechanical, and Materials Framework for a Shape Memory Alloy Heat Engine for Thermal Management" Nanomaterials 13, no. 15: 2159. https://doi.org/10.3390/nano13152159



