Why Do Bi-Factor Models Outperform Higher-Order g Factor Models? A Network Perspective
Abstract
:1. Introduction
Here, we add that, in such a case, a bi-factor model may outperform a higher-order g factor model because the latter is nested within the bi-factor model (Yung et al. 1999), and therefore can only fit worse than the bi-factor model (though perhaps not significantly so). Essentially, this network explanation aligns with Murray and Johnson (2013)’s argument that when fitted models differ from the true model, and these fitted models concern nested models, the most complex of these models will have a higher likelihood of fitting the data. In more technical terms, the more complex model has a higher so-called “fit propensity” (Falk and Muthukrishna 2021).[In a network model, it is] in principle possible to decompose the variance in any of the network’s variables into the following variance components: (1) a general component, (2) a unique component, and (3) components that are neither general nor unique (denoting variance that is shared with some but not all variables). A bi-factor model can then provide a satisfactory statistical summary of these data.(Kan et al. 2020, p. 4)
2. The WAIS–IV; Factor-Analytical versus Psychometric Network Perspectives
2.1. Factor-Analytical Approaches
2.2. A Network Approach
3. Present Study
- If Explanation 1—the bi-factor model represents the true data-generating mechanism—is correct (and Explanations 2 and 3 are not), then:
- Fit statistics will show excellent exact fit and therefore (near) perfect approximate and incremental fit for the bi-factor model;
- A comparison between the bi-factor and higher-order g factor model will reject the latter for being too simplistic, while
- A comparison among three models—the bi-factor, higher-order g factor, and non-nested network model—will judge the latter to be less adequate than the true bi-factor model, so that
- the true bi-factor model is expected to outperform both the nested higher-order g factor model and the non-nested network model.
- If Explanation 2—fit indices are inherently biased in favor of bi-factor models and against higher-order factor models—is correct, then:
- Exact, approximate, and incremental fit statistics may or may not show good or excellent fit for the higher-order g factor model if that is the true model, and, thus, for the bi-factor model, while;
- in a comparison between the true higher-order g factor model and the untrue bi-factor model, the relative fit indices are expected to show an increased preference for the untrue bi-factor model (e.g., higher than the nominal significance level when performing a loglikelihood ratio test).
- If Explanation 3—a non-nested network model underlies the empirical data—is correct (and Explanations 1 and 2 are not), then:
- Fit statistics will show excellent exact, approximate, and incremental fit for this true network model;
- Fit statistics for the bi-factor model may show acceptable fit (and possibly for the higher-order g factor model as well), but (near) perfect fit is unlikely;
- A comparison between the untrue bi-factor model and the untrue higher-order g factor model would reject the latter in favor of the former, because the bi-factor has more fit propensity than the nested higher-order g factor model, whereas;
- A comparison among the three models—the bi-factor, higher-order g factor, and true, nonnested network model—should show a preference for the true (i.e., network) model, such that
- the bi-factor model is expected to outperform the higher-order g factor model, but not the true network model.
4. Method
4.1. Data Generation
4.2. Model Fit Criteria
4.3. Analysis
4.4. Software
5. Results
5.1. Performance of Fit Indices
5.2. Checking the Validity and Plausibility of Remaining Explanations
5.3. Conclusions
6. Discussion
6.1. Limitations
6.2. Strengths
6.3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| BD | SI | DS | MA | VO | AR | SS | VP | IN | CD | LN | FW | CO | CA | PC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BD | 1.00 | 0.42 | 0.43 | 0.48 | 0.44 | 0.49 | 0.35 | 0.60 | 0.43 | 0.38 | 0.42 | 0.55 | 0.39 | 0.32 | 0.43 |
| SI | 0.44 | 1.00 | 0.42 | 0.43 | 0.71 | 0.48 | 0.35 | 0.38 | 0.60 | 0.38 | 0.42 | 0.48 | 0.66 | 0.31 | 0.35 |
| DS | 0.47 | 0.46 | 1.00 | 0.44 | 0.45 | 0.56 | 0.36 | 0.39 | 0.43 | 0.38 | 0.70 | 0.49 | 0.39 | 0.32 | 0.35 |
| MA | 0.50 | 0.41 | 0.44 | 1.00 | 0.45 | 0.50 | 0.36 | 0.46 | 0.44 | 0.39 | 0.43 | 0.52 | 0.40 | 0.32 | 0.38 |
| VO | 0.47 | 0.71 | 0.48 | 0.43 | 1.00 | 0.51 | 0.37 | 0.40 | 0.63 | 0.40 | 0.44 | 0.51 | 0.69 | 0.33 | 0.37 |
| AR | 0.43 | 0.42 | 0.59 | 0.40 | 0.44 | 1.00 | 0.41 | 0.44 | 0.49 | 0.44 | 0.51 | 0.56 | 0.45 | 0.37 | 0.40 |
| SS | 0.39 | 0.38 | 0.41 | 0.36 | 0.40 | 0.37 | 1.00 | 0.32 | 0.36 | 0.63 | 0.35 | 0.41 | 0.33 | 0.49 | 0.29 |
| VP | 0.51 | 0.42 | 0.44 | 0.47 | 0.44 | 0.41 | 0.37 | 1.00 | 0.39 | 0.35 | 0.38 | 0.53 | 0.35 | 0.29 | 0.43 |
| IN | 0.40 | 0.61 | 0.42 | 0.37 | 0.64 | 0.38 | 0.35 | 0.38 | 1.00 | 0.38 | 0.42 | 0.49 | 0.58 | 0.32 | 0.35 |
| CD | 0.40 | 0.39 | 0.41 | 0.37 | 0.41 | 0.38 | 0.62 | 0.38 | 0.35 | 1.00 | 0.38 | 0.44 | 0.35 | 0.46 | 0.31 |
| LN | 0.46 | 0.44 | 0.63 | 0.42 | 0.47 | 0.57 | 0.39 | 0.43 | 0.40 | 0.40 | 1.00 | 0.48 | 0.39 | 0.31 | 0.35 |
| FW | 0.57 | 0.46 | 0.49 | 0.53 | 0.49 | 0.45 | 0.41 | 0.53 | 0.42 | 0.42 | 0.48 | 1.00 | 0.45 | 0.36 | 0.44 |
| CO | 0.43 | 0.65 | 0.44 | 0.40 | 0.69 | 0.40 | 0.37 | 0.40 | 0.59 | 0.38 | 0.43 | 0.45 | 1.00 | 0.29 | 0.32 |
| CA | 0.31 | 0.30 | 0.32 | 0.29 | 0.32 | 0.29 | 0.48 | 0.29 | 0.27 | 0.49 | 0.31 | 0.32 | 0.29 | 1.00 | 0.26 |
| PC | 0.43 | 0.35 | 0.37 | 0.40 | 0.37 | 0.34 | 0.31 | 0.40 | 0.32 | 0.32 | 0.36 | 0.45 | 0.34 | 0.24 | 1.00 |
| BD | SI | DS | MA | VO | AR | SS | VP | IN | CD | LN | FW | CO | CA | PC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BD | 1.00 | ||||||||||||||
| SI | 0.42 | 1.00 | |||||||||||||
| DS | 0.35 | 0.34 | 1.00 | ||||||||||||
| MA | 0.48 | 0.30 | 0.33 | 1.00 | |||||||||||
| VO | 0.38 | 0.72 | 0.36 | 0.30 | 1.00 | ||||||||||
| AR | 0.40 | 0.39 | 0.56 | 0.37 | 0.41 | 1.00 | |||||||||
| SS | 0.34 | 0.30 | 0.31 | 0.30 | 0.32 | 0.31 | 1.00 | ||||||||
| VP | 0.59 | 0.34 | 0.37 | 0.46 | 0.32 | 0.39 | 0.29 | 1.00 | |||||||
| IN | 0.37 | 0.59 | 0.37 | 0.30 | 0.63 | 0.50 | 0.31 | 0.33 | 1.00 | ||||||
| CD | 0.38 | 0.37 | 0.43 | 0.40 | 0.42 | 0.42 | 0.63 | 0.34 | 0.37 | 1.00 | |||||
| LN | 0.34 | 0.34 | 0.70 | 0.31 | 0.36 | 0.47 | 0.26 | 0.34 | 0.35 | 0.36 | 1.00 | ||||
| FW | 0.55 | 0.41 | 0.48 | 0.53 | 0.41 | 0.60 | 0.32 | 0.54 | 0.43 | 0.41 | 0.49 | 1.00 | |||
| CO | 0.38 | 0.66 | 0.39 | 0.31 | 0.69 | 0.43 | 0.29 | 0.34 | 0.60 | 0.37 | 0.42 | 0.46 | 1.00 | ||
| CA | 0.39 | 0.25 | 0.25 | 0.27 | 0.26 | 0.26 | 0.49 | 0.28 | 0.25 | 0.46 | 0.22 | 0.29 | 0.24 | 1.00 | |
| PC | 0.46 | 0.38 | 0.28 | 0.30 | 0.35 | 0.31 | 0.38 | 0.43 | 0.38 | 0.35 | 0.26 | 0.36 | 0.34 | 0.30 | 1.00 |
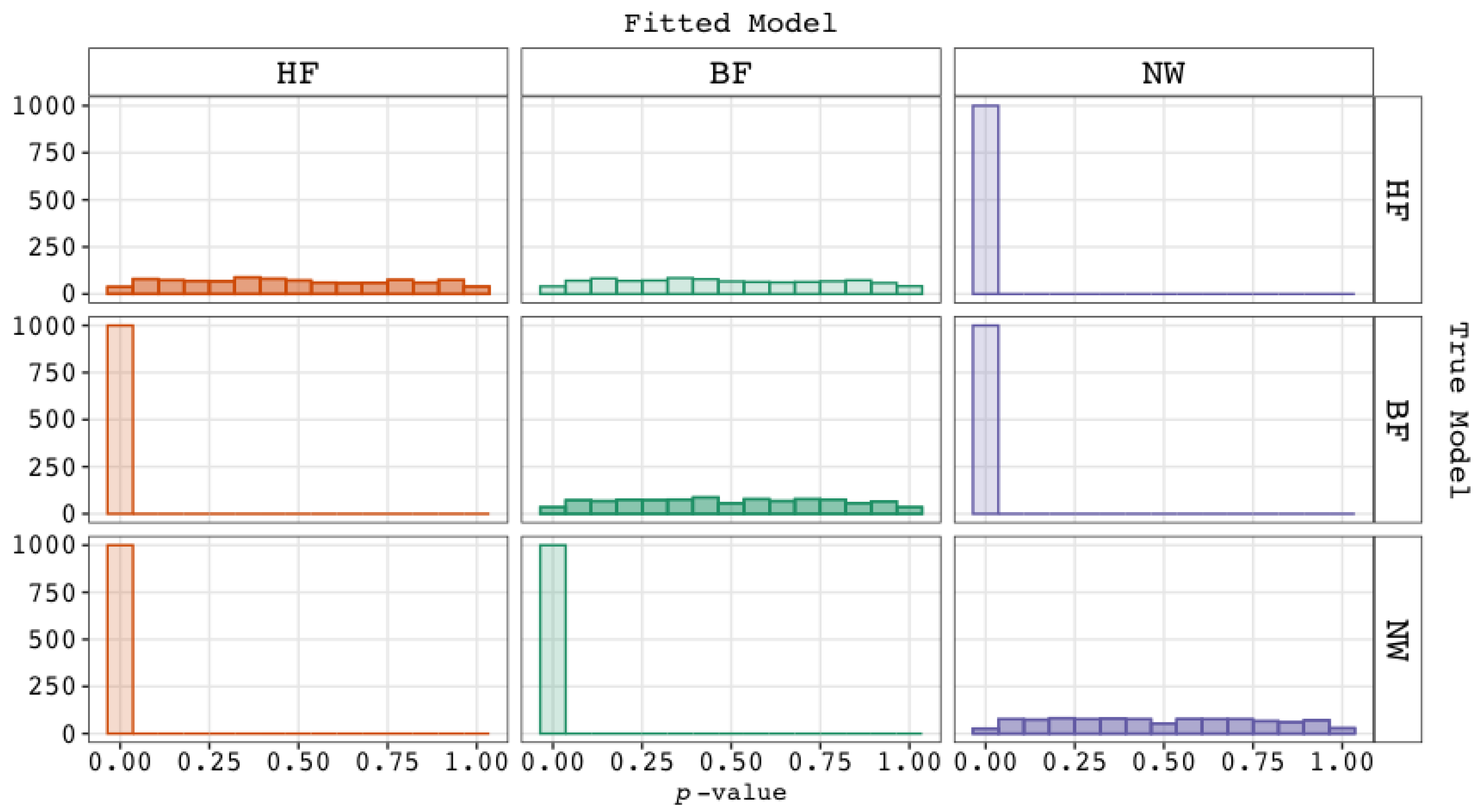
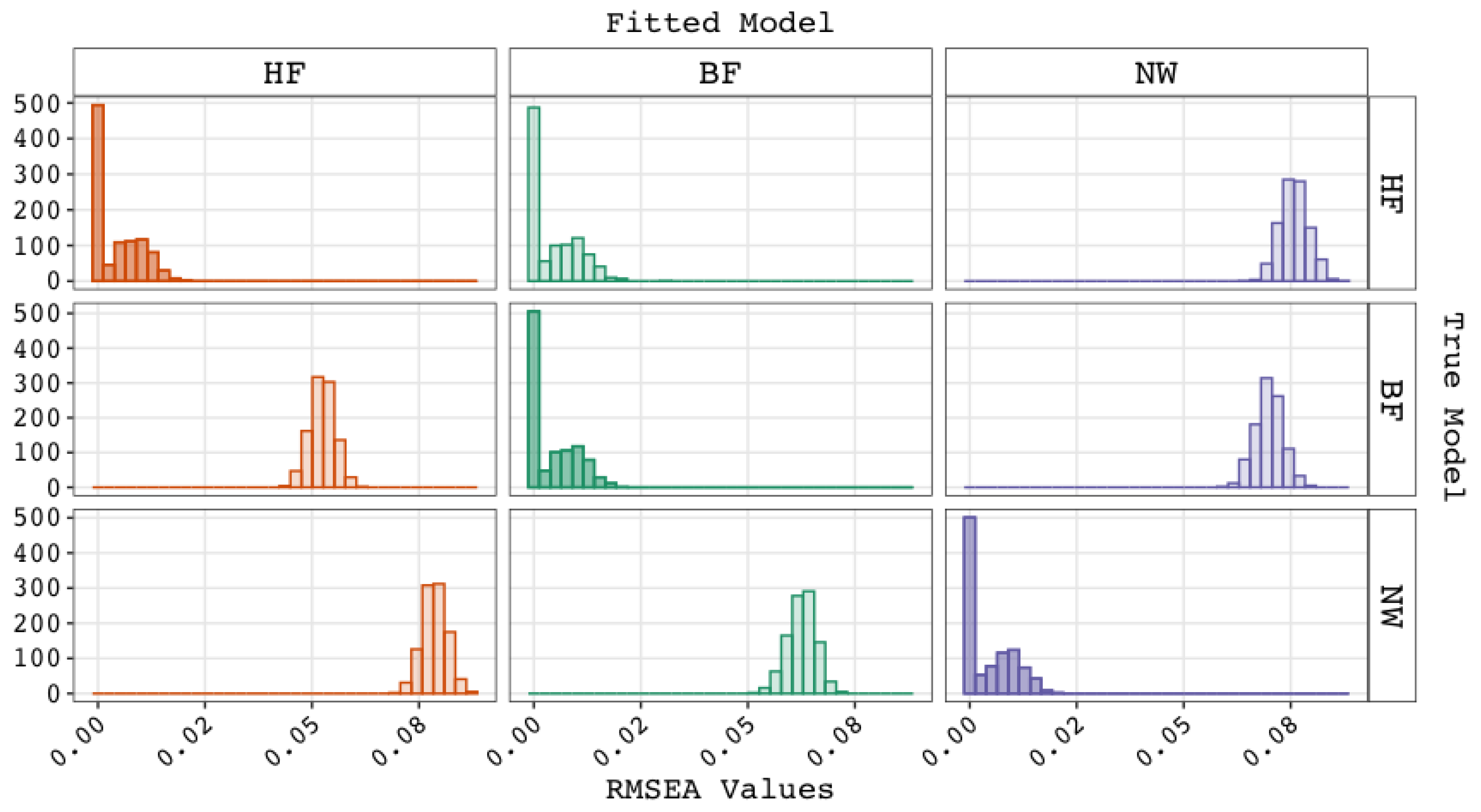
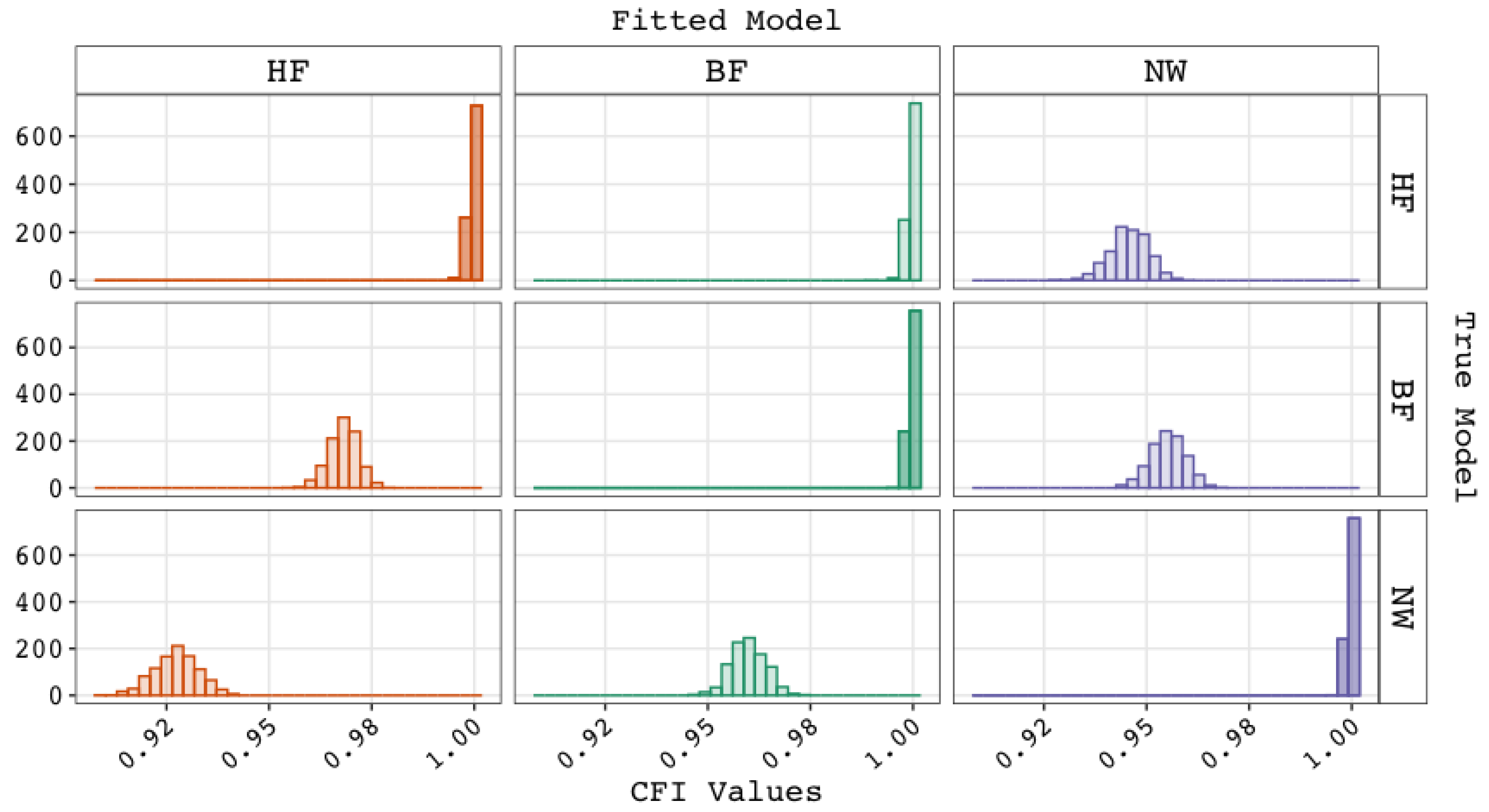
Appendix B. Performance of Fit Indices
Appendix B.1. Expectations
Appendix B.2. Results



| 1 | When the WAIS–IV higher-order g factor model is respecified as a bi-factor model, the standardized loading on g′ of, for instance, subtest SI () would be equal to the standardized factor loading of V on g () multiplied by the standardized factor loading of SI on V () in the higher-order g factor model: . The standardized bi-factor loading on variable V′ () would also be equal to a constant multiplied by the standardized factor loading of SI on V, namely . If we define the ratio (proportion) of the factor loadings on the g′ and V′ as , then it holds that this ratio is equal to the ratio of the factor loadings on the g′ and V′ for the subtests VO, IN, and CO. Thus, the proportionality constraints in the variance decomposition would include . Similarly, , , and Instead of freely estimating factor loadings, 15 loadings and 4 proportions are being estimated, giving an additional 11 degrees of freedom. |
| 2 | This possibility does not exist in most standard statistical software programs. As far as we know, a direct comparison is only possible in R (R Core Team 2022) using package OpenMx (Boker et al. 2011) or psychonetrics (Epskamp 2021). |
| 3 | We note that this network model lacks the rich history that the factor models have and that the use of the term “confirmatory” here is somewhat ambiguous; one might consider the method that was applied as an example of the exploratory mode of confirmatory techniques (Raykov and Marcoulides 2012). On the other hand, the confirmatory factor models of intelligence also originate from prior exploratory factor analyses conducted on other data sets and could also be viewed as cross-validations. Importantly, the different routes taken toward the parameter values do not affect the validity of the simulations or our argumentation. The essence of our simulation study is that, in order to evaluate the fit statistics of the network model effectively, the data generation should produce parameter estimates that are empirically plausible. This evaluates the fit statistics of the network model possible; hence, the provided fit statistics are not biased and, provided Explanation 3 is valid, the evaluation of the plausibility of this explanation is also unbiased. Furthermore, the fact that the configuration of the network model can be replicated across different samples strengthens the generalizability of our findings. |
References
- Beaujean, A. Alexander. 2015. John Carroll’s Views on Intelligence: Bi-Factor vs. Higher-Order Models. Journal of Intelligence 3: 121–36. [Google Scholar] [CrossRef]
- Boker, Steven, Michael Neale, Hermine Maes, Michael Wilde, Michael Spiegel, Timothy Brick, Jeffrey Spies, Ryne Estabrook, Sarah Kenny, Timothy Bates, and et al. 2011. OpenMx: An Open Source Extended Structural Equation Modeling Framework. Psychometrika 76: 306–17. [Google Scholar] [CrossRef]
- Bonifay, Wes, Sean P. Lane, and Steven P. Reise. 2017. Three Concerns with Applying a Bifactor Model as a Structure of Psychopathology. Clinical Psychological Science 5: 184–86. [Google Scholar] [CrossRef]
- Bornovalova, Marina A., Alexandria M. Choate, Haya Fatimah, Karl J. Petersen, and Brenton M. Wiernik. 2020. Appropriate use of bifactor analysis in psychopathology research: Appreciating benefits and limitations. Biological Psychiatry 88: 18–27. [Google Scholar] [CrossRef] [PubMed]
- Borsboom, Denny. 2022. Possible Futures for Network Psychometrics. Psychometrika 87: 253–65. [Google Scholar] [CrossRef]
- Borsboom, Denny, Marie K. Deserno, Mijke Rhemtulla, Sacha Epskamp, Eiko I. Fried, Richard J. McNally, Donald J. Robinaugh, Marco Perugini, Jonas Dalege, Giulio Costantini, and et al. 2021. Network Analysis of Multivariate Data in Psychological Science. Nature Reviews Methods Primers 1: 58. [Google Scholar] [CrossRef]
- Bulut, Okan, Damien C. Cormier, Alexandra M. Aquilina, and Hatice C. Bulut. 2021. Age and Sex Invariance of the Woodcock-Johnson IV Tests of Cognitive Abilities: Evidence from Psychometric Network Modeling. Journal of Intelligence 9: 35. [Google Scholar] [CrossRef]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. New York: Cambridge University Press. [Google Scholar] [CrossRef]
- Cucina, Jeffrey, and Kevin Byle. 2017. The Bifactor Model Fits Better Than the Higher-Order Model in More Than 90% of Comparisons for Mental Abilities Test Batteries. Journal of Intelligence 5: 27. [Google Scholar] [CrossRef]
- Decker, Scott L. 2020. Don’t Use a Bifactor Model Unless You Believe the True Structure Is Bifactor. Journal of Psychoeducational Assessment 39: 39–49. [Google Scholar] [CrossRef]
- Dolan, Conor V., and Denny Borsboom. 2023. Interpretational issues with the bifactor model: A commentary on ‘defining the p-factor: An empirical test of five leading theories’ by southward, cheavens, and coccaro. Psychological Medicine 53: 2744–47. [Google Scholar] [CrossRef]
- Eid, Michael, Stefan Krumm, Tobias Koch, and Julian Schulze. 2018. Bifactor models for predicting criteria by general and specific factors: Problems of nonidentifiability and alternative solutions. Journal of Intelligence 6: 42. [Google Scholar] [CrossRef]
- Epskamp, Sacha. 2021. Psychonetrics: Structural Equation Modeling and Confirmatory Network Analysis, R package version 0.10; Available online: https://cran.r-project.org/web/packages/psychonetrics/index.html (accessed on 21 January 2024).
- Epskamp, Sacha, Giulio Costantini, Jonas Haslbeck, Adela Isvoranu, Angelique O. J. Cramer, Lourens J. Waldorp, Verena D. Schmittmann, and Denny Borsboom. 2021. qgraph: Graph Plotting Methods, Psychometric Data Visualization and Graphical Model Estimation. R package version 1.9.8. Available online: https://cran.r-project.org/web/packages/qgraph/index.html (accessed on 21 January 2024).
- Epskamp, Sacha, Gunter Maris, Lourens J. Waldorp, and Denny Borsboom. 2018. Network Psychometrics. In The Wiley Handbook of Psychometric Testing. Chichester: John Wiley & Sons, Ltd., pp. 953–86. [Google Scholar] [CrossRef]
- Epskamp, Sacha, Mijke Rhemtulla, and Denny Borsboom. 2017. Generalized Network Psychometrics: Combining Network and Latent Variable Models. Psychometrika 82: 904–27. [Google Scholar] [CrossRef] [PubMed]
- Falk, Carl F., and Michael Muthukrishna. 2021. Parsimony in Model Selection: Tools for Assessing Fit Propensity. Psychological Methods 28: 123–36. [Google Scholar] [CrossRef] [PubMed]
- Gignac, Gilles E. 2005. Revisiting the factor structure of the WAIS-R: Insights through nested factor modeling. Assessment 12: 320–29. [Google Scholar] [CrossRef] [PubMed]
- Gignac, Gilles E. 2006. The WAIS-III as a Nested Factors Model. Journal of Individual Differences 27: 73–86. [Google Scholar] [CrossRef]
- Gignac, Gilles E., and Marley W. Watkins. 2013. Bifactor Modeling and the Estimation of Model-Based Reliability in the WAIS-IV. Multivariate Behavioral Research 48: 639–62. [Google Scholar] [CrossRef] [PubMed]
- Golay, Philippe, and Thierry Lecerf. 2011. Orthogonal higher order structure and confirmatory factor analysis of the French Wechsler Adult Intelligence Scale (WAIS-III). Psychological Assessment 23: 143–52. [Google Scholar] [CrossRef] [PubMed]
- Greene, Ashley L., Nicholas R. Eaton, Kaiqiao Li, Miriam K. Forbes, Robert F. Krueger, Kristian E. Markon, Irwin D. Waldman, David C. Cicero, Christopher C. Conway, Anna R. Docherty, and et al. 2019. Are fit indices used to test psychopathology structure biased? A simulation study. Journal of Abnormal Psychology 128: 740–64. [Google Scholar] [CrossRef]
- Hofman, Abe, Rogier Kievit, Claire Stevenson, Dylan Molenaar, Ingmar Visser, and Han van der Maas. 2018. The Dynamics of the Development of Mathematics Skills: A Comparison of Theories of Developing Intelligence. Available online: https://osf.io/xa2ft (accessed on 21 January 2024).
- Holzinger, Karl J., and Frances Swineford. 1937. The Bi-factor method. Psychometrika 2: 41–54. [Google Scholar] [CrossRef]
- Hood, Steven Brian. 2008. Latent Variable Realism in Psychometrics. Ph.D. thesis, Indiana University, Bloomington, IN, USA. [Google Scholar]
- Jensen, Arthur Robert. 1998. The g Factor: The Science of Mental Ability (Human Evolution, Behavior, and Intelligence). Westport: Praeger. [Google Scholar]
- Kan, Kees-Jan, Han L. J. van der Maas, and Stephen Z. Levine. 2019. Extending psychometric network analysis: Empirical evidence against g in favor of mutualism? Intelligence 73: 52–62. [Google Scholar] [CrossRef]
- Kan, Kees-Jan, Hannelies de Jonge, Han L. J. van der Maas, Stephen Z. Levine, and Sacha Epskamp. 2020. How to Compare Psychometric Factor and Network Models. Journal of Intelligence 8: 35. [Google Scholar] [CrossRef]
- Kievit, Rogier A., Ulman Lindenberger, Ian M. Goodyer, Peter B. Jones, Peter Fonagy, Edward T. Bullmore, and Raymond J. Dolan. 2017. Mutualistic coupling between vocabulary and reasoning supports cognitive development during late adolescence and early adulthood. Psychological Science 28: 1419–31. [Google Scholar] [CrossRef] [PubMed]
- Kossakowski, Jolanda J., Sacha Epskamp, Jacobien M. Kieffer, Claudia D. van Borkulo, Mijke Rhemtulla, and Denny Borsboom. 2016. The application of a network approach to health-related quality of life (hrqol): Introducing a new method for assessing hrqol in healthy adults and cancer patients. Quality of Life Research 25: 781–92. [Google Scholar] [CrossRef] [PubMed]
- MacCallum, Robert C., Duane T. Wegener, Bert N. Uchino, and Leandre R. Fabrigar. 1993. The problem of equivalent models in applications of covariance structure analysis. Psychological Bulletin 114: 185–99. [Google Scholar] [CrossRef] [PubMed]
- Major, Jason T., Wendy Johnson, and Ian J. Deary. 2012. Comparing models of intelligence in project talent: The vpr model fits better than the chc and extended gf–gc models. Intelligence 40: 543–59. [Google Scholar] [CrossRef]
- Mansolf, Maxwell, and Steven P. Reise. 2017. When and Why the Second-order and Bifactor Models are Distinguishable. Intelligence 61: 120–29. [Google Scholar] [CrossRef]
- McGrew, Kevin S., W. Joel Schneider, Scott L. Decker, and Okan Bulut. 2023. A psychometric network analysis of chc intelligence measures: Implications for research, theory, and interpretation of broad chc scores “beyond g”. Journal of Intelligence 11: 19. [Google Scholar] [CrossRef]
- Mellenbergh, Gideon J. 1989. Item bias and item response theory. International journal of Educational Research 13: 127–43. [Google Scholar] [CrossRef]
- Morgan, Grant B., Kari J. Hodge, Kevin E. Wells, and Marley W. Watkins. 2015. Are Fit Indices Biased in Favor of Bi-Factor Models in Cognitive Ability Research?: A Comparison of Fit in Correlated Factors, Higher-Order, and Bi-Factor Models via Monte Carlo Simulations. Journal of Intelligence 3: 2–20. [Google Scholar] [CrossRef]
- Murray, Aja L., and Wendy Johnson. 2013. The limitations of model fit in comparing the bi-factor versus higher-order models of human cognitive ability structure. Intelligence 41: 407–22. [Google Scholar] [CrossRef]
- Niileksela, Christopher R., Matthew R. Reynolds, and Alan S. Kaufman. 2013. An alternative Cattell-Horn-Carroll (CHC) factor structure of the WAIS-IV: Age invariance of an alternative model for ages 70–90. Psychological Assessment 25: 391–404. [Google Scholar] [CrossRef] [PubMed]
- Petermann, Franz. 2012. Wechsler Adult Intelligence Scale–Fourth Edition (WAIS-IV) Manual 1: Grundlagen, Testauswertung und Interpretation. Frankfurt: Pearson Assessment. [Google Scholar]
- Raykov, Tenko, and George A. Marcoulides. 2012. A First Course in Structural Equation Modeling. London: Routledge. [Google Scholar]
- R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- RStudio Team. 2022. RStudio: Integrated Development Environment for R. Boston: RStudio, PBC. [Google Scholar]
- Savi, Alexander O., Maarten Marsman, and Han L. J. van der Maas. 2021. Evolving Networks of Human Intelligence. Intelligence 88: 101567. [Google Scholar] [CrossRef]
- Schermelleh-Engel, Karin, Helfried Moosbrugger, and Hans Müller. 2003. Evaluating the Fit of Structural Equation Models: Tests of Significance and Descriptive Goodness-of-Fit Measures. Methods of Psychological Research 8: 23–74. [Google Scholar]
- Schmank, Christopher J., Sara Anne Goring, Kristof Kovacs, and Andrew R. A. Conway. 2019. Psychometric network analysis of the Hungarian WAIS. Journal of Intelligence 7: 21. [Google Scholar] [CrossRef]
- Schmid, John, and John M. Leiman. 1957. The development of hierarchical factor solutions. Psychometrika 22: 53–61. [Google Scholar] [CrossRef]
- Schrank, Fredrick A., and Barbara J. Wendling. 2018. The Woodcock–Johnson IV: Tests of Cognitive Abilities, Tests of Oral Language, Tests of Achievement. New York: The Guilford Press. [Google Scholar]
- Spearman, Charles. 1904. “General Intelligence” Objectively Determined and Measured. American Journal of Psychology 15: 201–93. [Google Scholar] [CrossRef]
- Thurstone, Louis Leon. 1935. The Vectors of Mind: Multiple-Factor Analysis for the Isolation of Primary Traits. Chicago: University of Chicago Press. [Google Scholar]
- Van Bork, Riet, Sacha Epskamp, Mijke Rhemtulla, Denny Borsboom, and Han L. J. van der Maas. 2017. What is the p-factor of psychopathology? Some risks of general factor modeling. Theory & Psychology 27: 759–73. [Google Scholar] [CrossRef]
- Van der Maas, Han, Kees-Jan Kan, Maarten Marsman, and Claire E. Stevenson. 2017. Network Models for Cognitive Development and Intelligence. Journal of Intelligence 5: 16. [Google Scholar] [CrossRef]
- Van der Maas, Han L. J., Conor V. Dolan, Raoul P. P. P. Grasman, Jelte M. Wicherts, Hilde M. Huizenga, and Maartje E. J. Raijmakers. 2006. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review 113: 842–61. [Google Scholar] [CrossRef]
- Van der Maas, Han L. J., Kees-Jan Kan, and Denny Borsboom. 2014. Intelligence Is What the Intelligence Test Measures. Seriously. Journal of Intelligence 2: 12–15. [Google Scholar] [CrossRef]
- Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with S, 4th ed. New York: Springer. ISBN 0-387-95457-0. [Google Scholar]
- Wechsler, David. 2008. Wechsler Adult Intelligence Scale–Fourth Edition (WAIS–IV). San Antonio: NCS Pearson. [Google Scholar]
- Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, Alex Hayes, Lionel Henry, Jim Hester, and et al. 2019. Welcome to the tidyverse. Journal of Open Source Software 4: 1686. [Google Scholar] [CrossRef]
- Yung, Yiu-Fai, David Thissen, and Lori D. McLeod. 1999. On the relationship between the higher-order factor model and the hierarchical factor model. Psychometrika 64: 113–28. [Google Scholar] [CrossRef]
- Zhang, Bo, Tianjun Sun, Mengyang Cao, and Fritz Drasgow. 2020. Using Bifactor Models to Examine the Predictive Validity of Hierarchical Constructs: Pros, Cons, and Solutions. Organizational Research Methods 24: 530–71. [Google Scholar] [CrossRef]
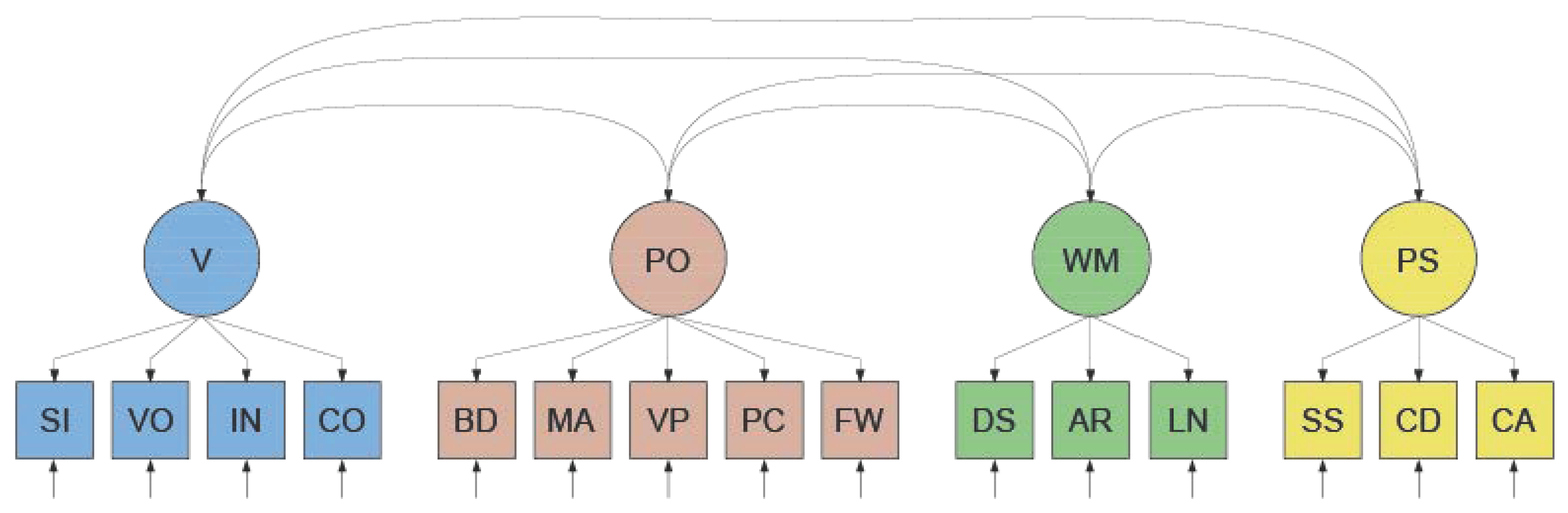
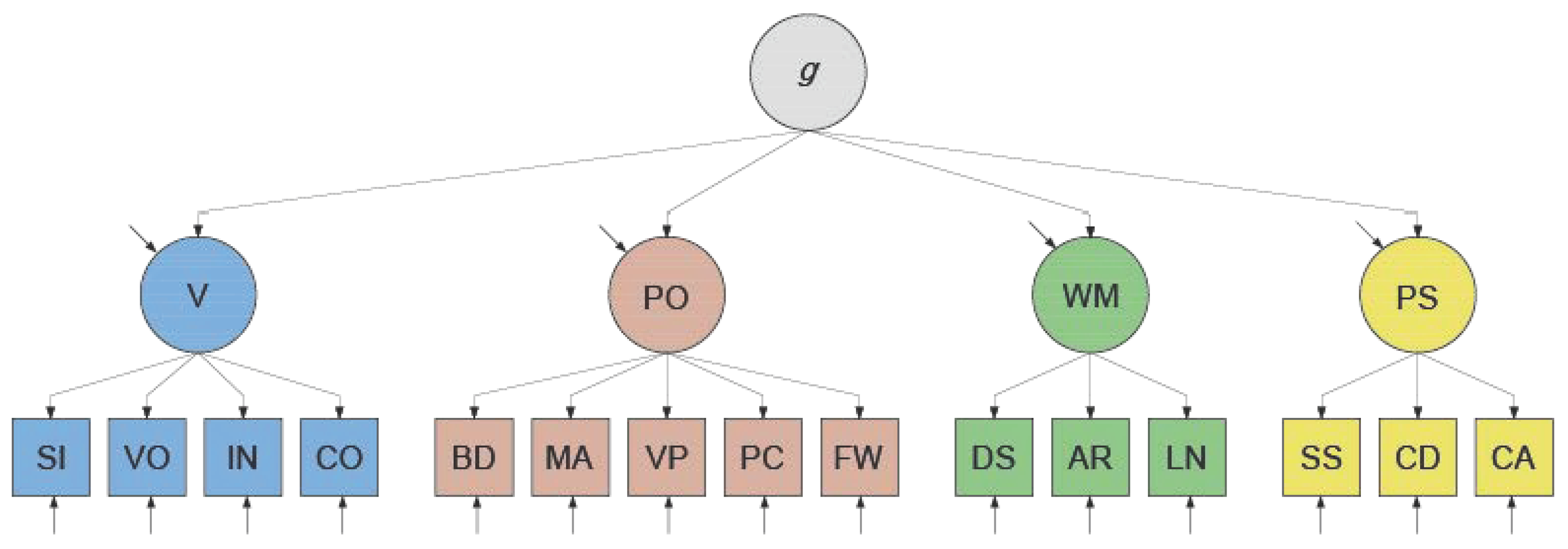
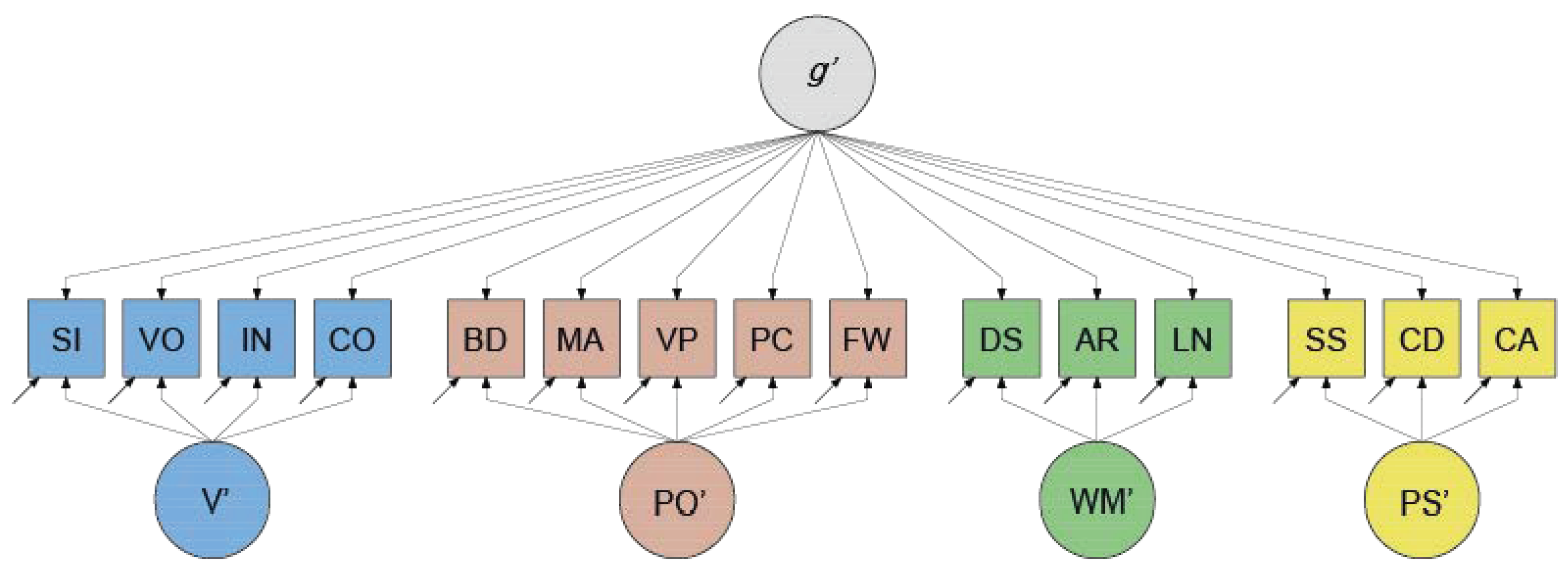
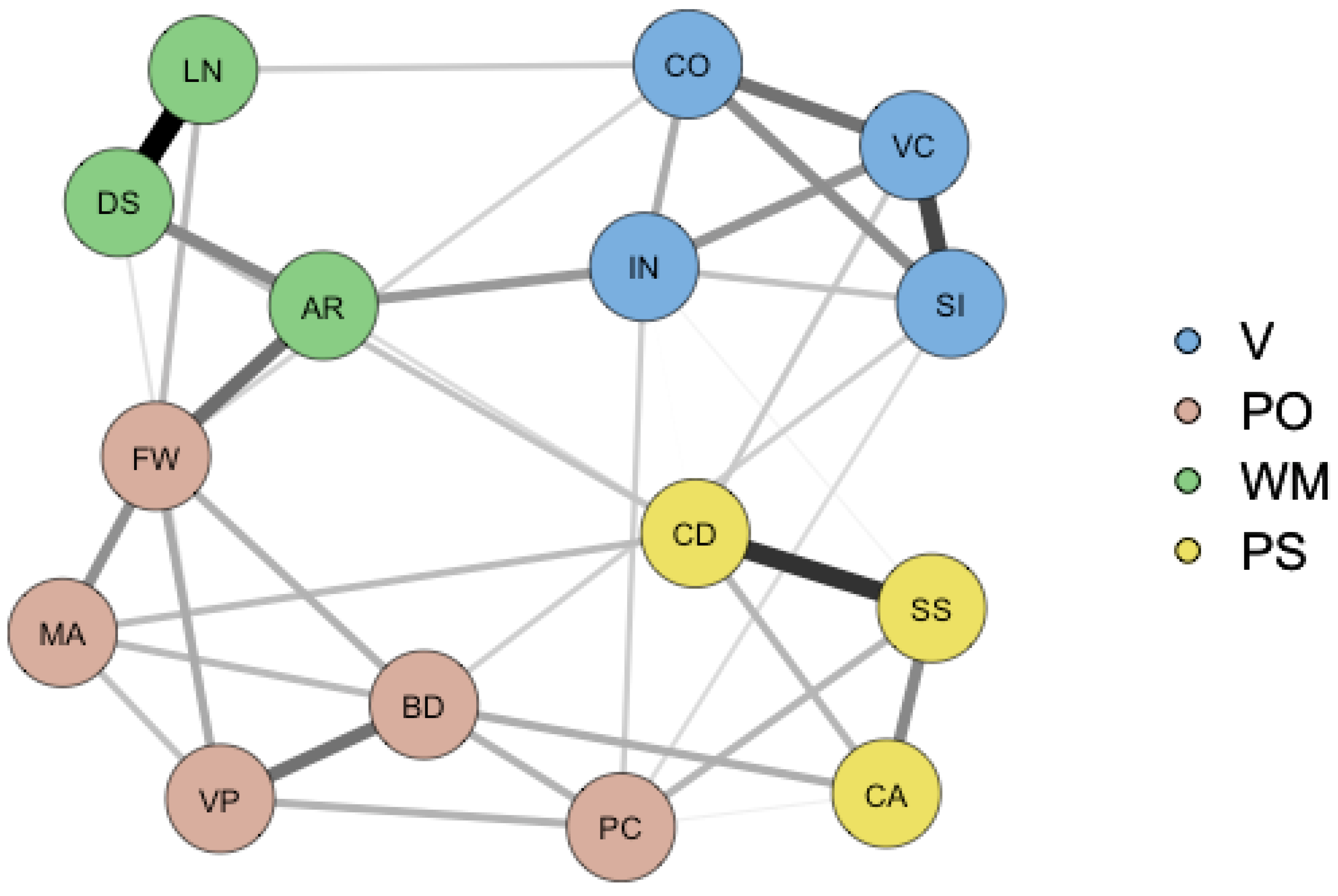

| Category | Subtest | Task Description |
|---|---|---|
| Verbal Ability (V) | Similarities (SI) | Explain the similarity between two words or ideas. |
| Vocabulary (VO) | Identify pictures of objects or provide definitions of words. | |
| Information (IN) | Answer common knowledge questions. | |
| Comprehension (CO) | Respond to questions regarding social settings or popular notions. | |
| Perceptual Organization (PO) | Block Design (BD) | Pattern-based puzzle solving based on a presented model (Timed). |
| Matrix Reasoning (MA) | Choose the best-fitting puzzle for an arrangement of pictures. | |
| Visual Puzzles (VP) | Select three puzzle pieces that might complete the illustrated problem. | |
| Picture Completion (PC) | Choose the missing image component. | |
| Figure Weights (FW) | Solve equations with objects instead of numbers. | |
| Working Memory (WM) | Digit Span (DS) | Listen to numerical sequences and repeat them in a certain order. |
| Arithmetic (AR) | Solving mathematical word problems spoken orally (Timed). | |
| Letter–Number Sequencing (LN) | Recall a sequence of numbers or letters in a given order. | |
| Processing Speed (PS) | Symbol Search (SS) | Determine if a symbol corresponds to any of the symbols in a given sequence. |
| Coding (CD) | Utilize a key to transcribe a code of digits (Timed). | |
| Cancellation (CA) | Cancel out objects of a given collection according to the instructions (Timed). |
| Study | Battery | Higher-Order Factor Model | Comparison | Bi-Factor Model | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CFI | TLI | NFI | RMSEA | AIC | df | ∆df | CFI | TLI | NFI | RMSEA | AIC | df | |||||
| Gignac and Watkins (2013) | WAIS–IV | 0.945 | 0.933 | 0.918 | 0.068 | 314.75 | 246.75 *** | 86 | 99.47 *** | 11 | 0.975 | 0.965 | 0.951 | 0.049 | 237.28 | 147.28 *** | 75 |
| Gignac and Watkins (2013) | WAIS–IV | 0.959 | 0.950 | 0.944 | 0.064 | 366.51 | 298.51 *** | 86 | 101.30 *** | 11 | 0.967 | 0.967 | 0.963 | 0.052 | 287.21 | 197.21 *** | 75 |
| Gignac and Watkins (2013) | WAIS–IV | 0.943 | 0.930 | 0.920 | 0.075 | 347.28 | 279.28 *** | 86 | 118.85 *** | 11 | 0.975 | 0.965 | 0.954 | 0.053 | 250.43 | 16.43 *** | 75 |
| Gignac and Watkins (2013) | WAIS–IV | 0.948 | 0.937 | 0.927 | 0.074 | 341.93 | 273.93 *** | 86 | 78.98 *** | 11 | 0.967 | 0.954 | 0.948 | 0.063 | 284.95 | 194.95 *** | 75 |
| Gignac (2005) | WAIS-R | 0.970 | 0.959 | 0.967 | 0.068 | 443.97 | 391.97 *** | 40 | 229.69 *** | 7 | 0.989 | 0.982 | 0.986 | 0.046 | 228.28 | 162.28 *** | 33 |
| Gignac (2006) | WAIS–III | 0.968 | 0.959 | 0.965 | 0.064 | 723.38 | 663.38 *** | 61 | 215.13 *** | 10 | 0.979 | 0.968 | 0.976 | 0.056 | 528.25 | 448.25 *** | 51 |
| Golay and Lecerf (2011) | WAIS–III | 0.965 | 0.956 | 0.957 | 0.059 | 359.50 | 301.50 *** | 62 | 178.50 *** | 9 | 0.990 | 0.985 | 0.983 | 0.035 | 199.00 | 123.00 *** | 53 |
| Niileksela et al. (2013) | WAIS–IV | 0.964 | 0.967 | 0.942 | 0.067 | 193.62 | 179.62 *** | 71 | 10.76 † | 5 | 0.966 | 0.966 | 0.945 | 0.062 | 192.86 | 168.86 *** | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, K.-J.; Psychogyiopoulos, A.; Groot, L.J.; de Jonge, H.; ten Hove, D. Why Do Bi-Factor Models Outperform Higher-Order g Factor Models? A Network Perspective. J. Intell. 2024, 12, 18. https://doi.org/10.3390/jintelligence12020018
Kan K-J, Psychogyiopoulos A, Groot LJ, de Jonge H, ten Hove D. Why Do Bi-Factor Models Outperform Higher-Order g Factor Models? A Network Perspective. Journal of Intelligence. 2024; 12(2):18. https://doi.org/10.3390/jintelligence12020018
Chicago/Turabian StyleKan, Kees-Jan, Anastasios Psychogyiopoulos, Lennert J. Groot, Hannelies de Jonge, and Debby ten Hove. 2024. "Why Do Bi-Factor Models Outperform Higher-Order g Factor Models? A Network Perspective" Journal of Intelligence 12, no. 2: 18. https://doi.org/10.3390/jintelligence12020018





