An Open-Source Toolbox for PEM Fuel Cell Simulation
Abstract
:1. Introduction
2. Mathematical Model
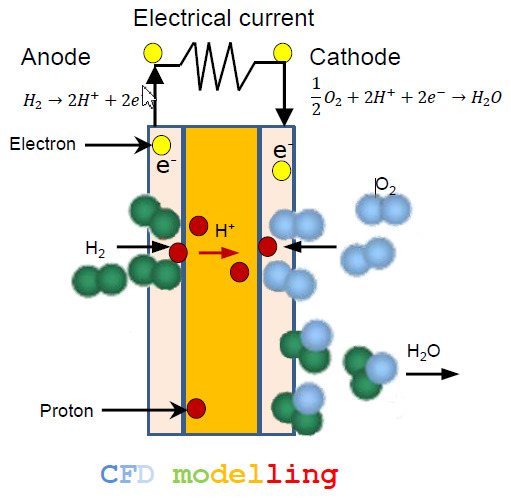
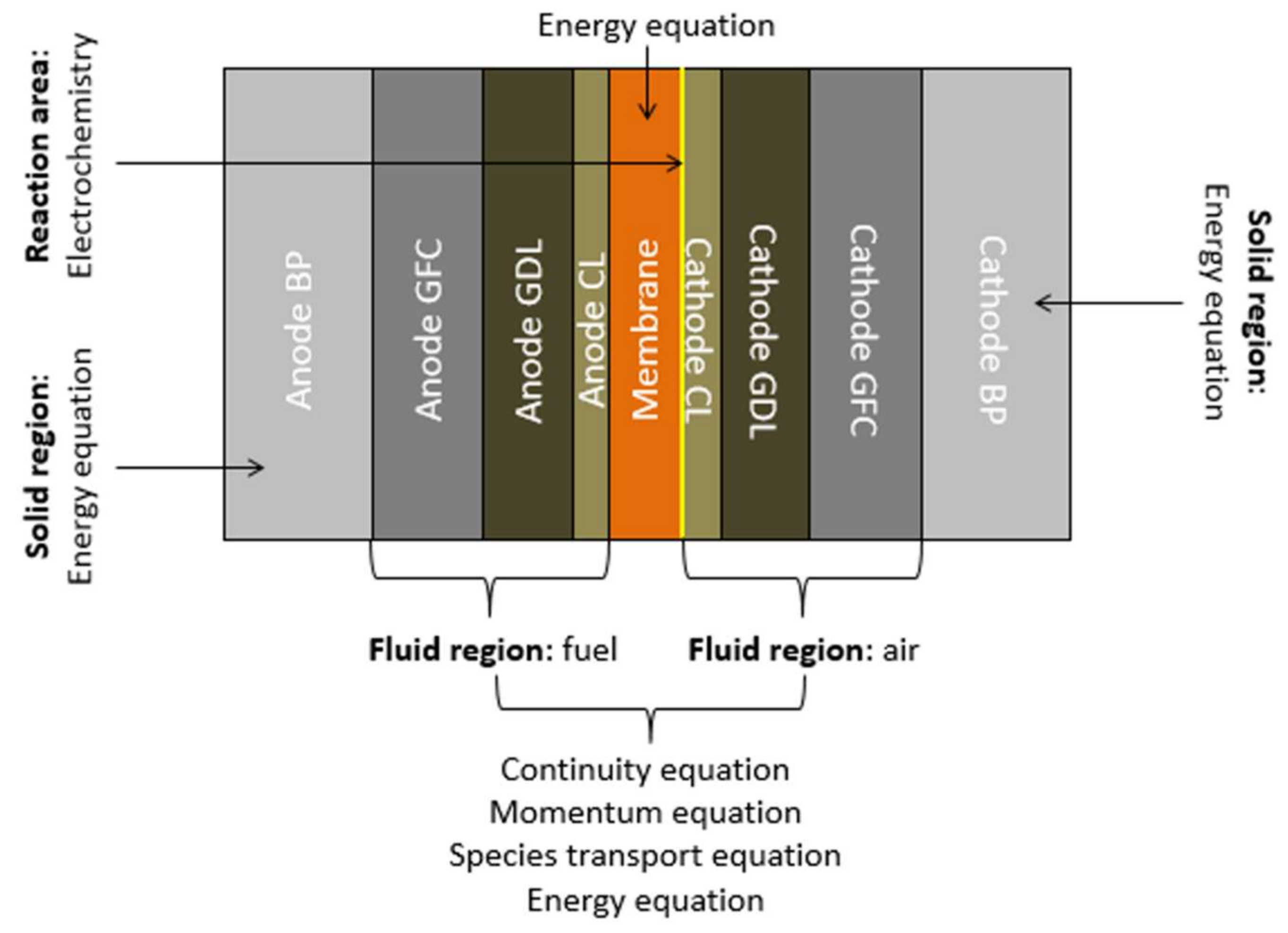
2.1. Cell Geometry and Transport Processes
2.2. Assumptions
2.3. Governing Equations
2.4. Boundary Conditions
3. Numerical Implementation
3.1. Computational Procedure
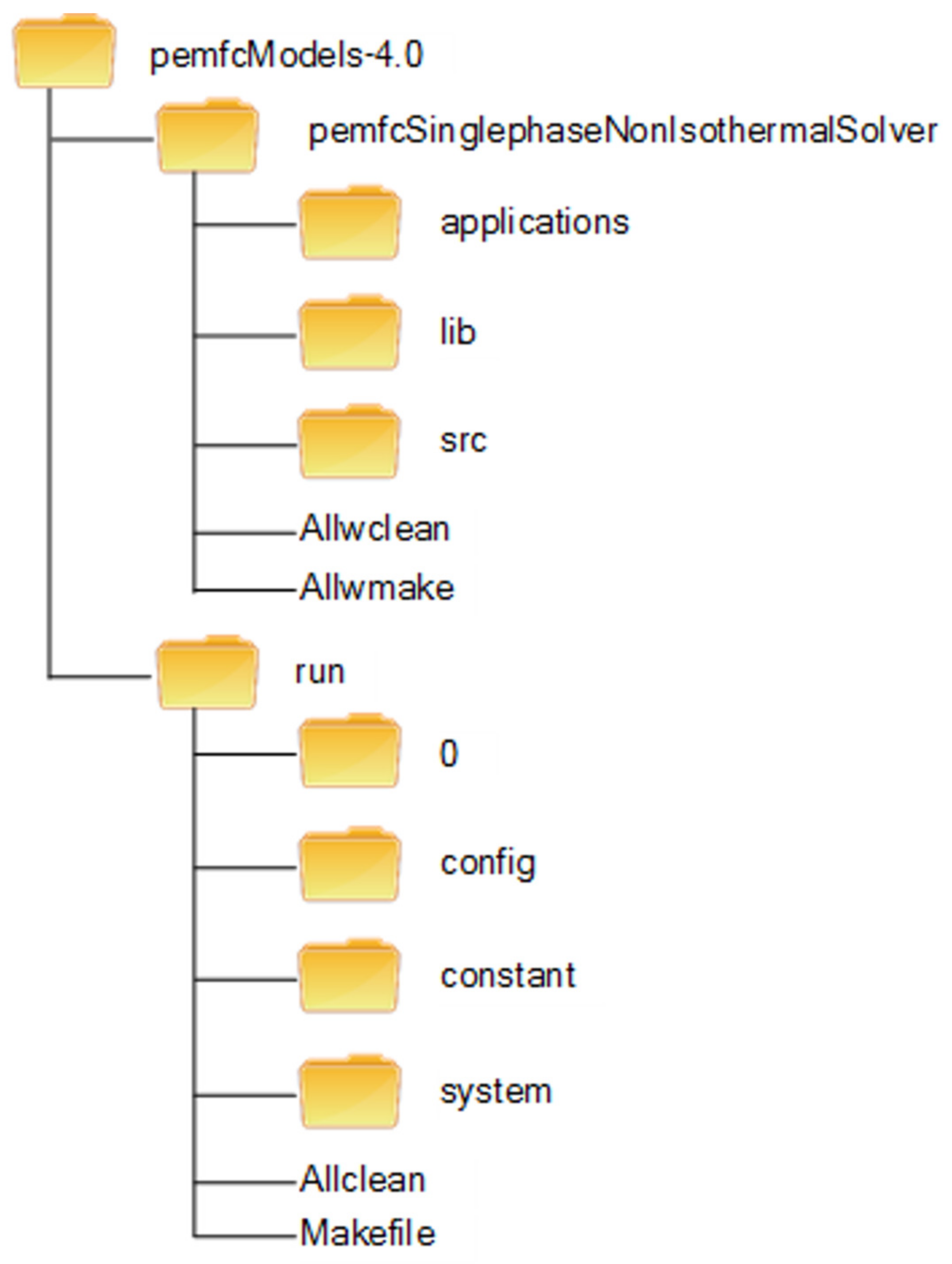
3.2. Toolbox Structure
3.2.1. PemfcSinglephaseNonIsothermalSolver
3.2.2. Run
4. Model Verification
4.1. Mesh Independence Study
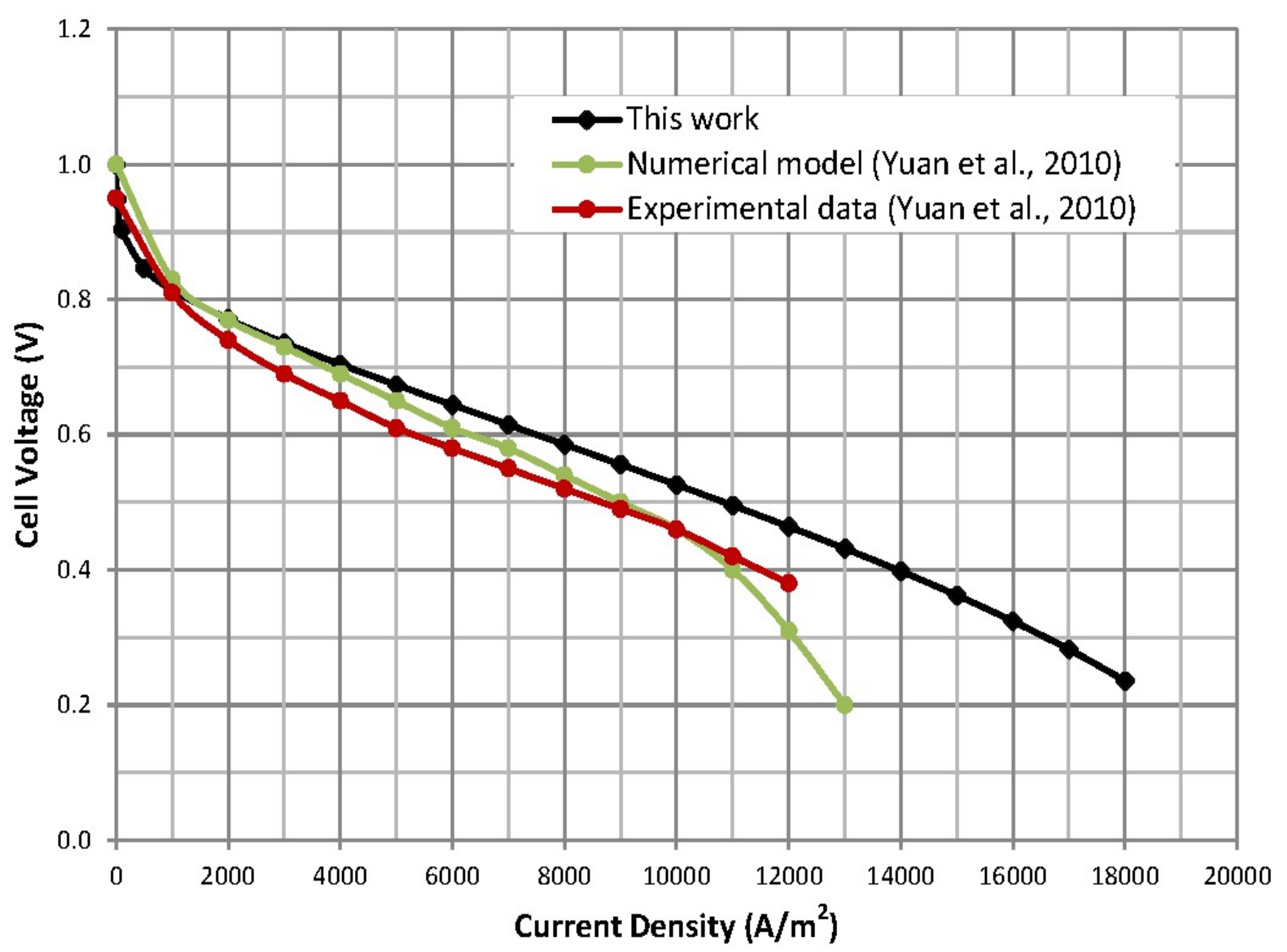
4.2. Comparison with Literature Model Results and Experimental Data
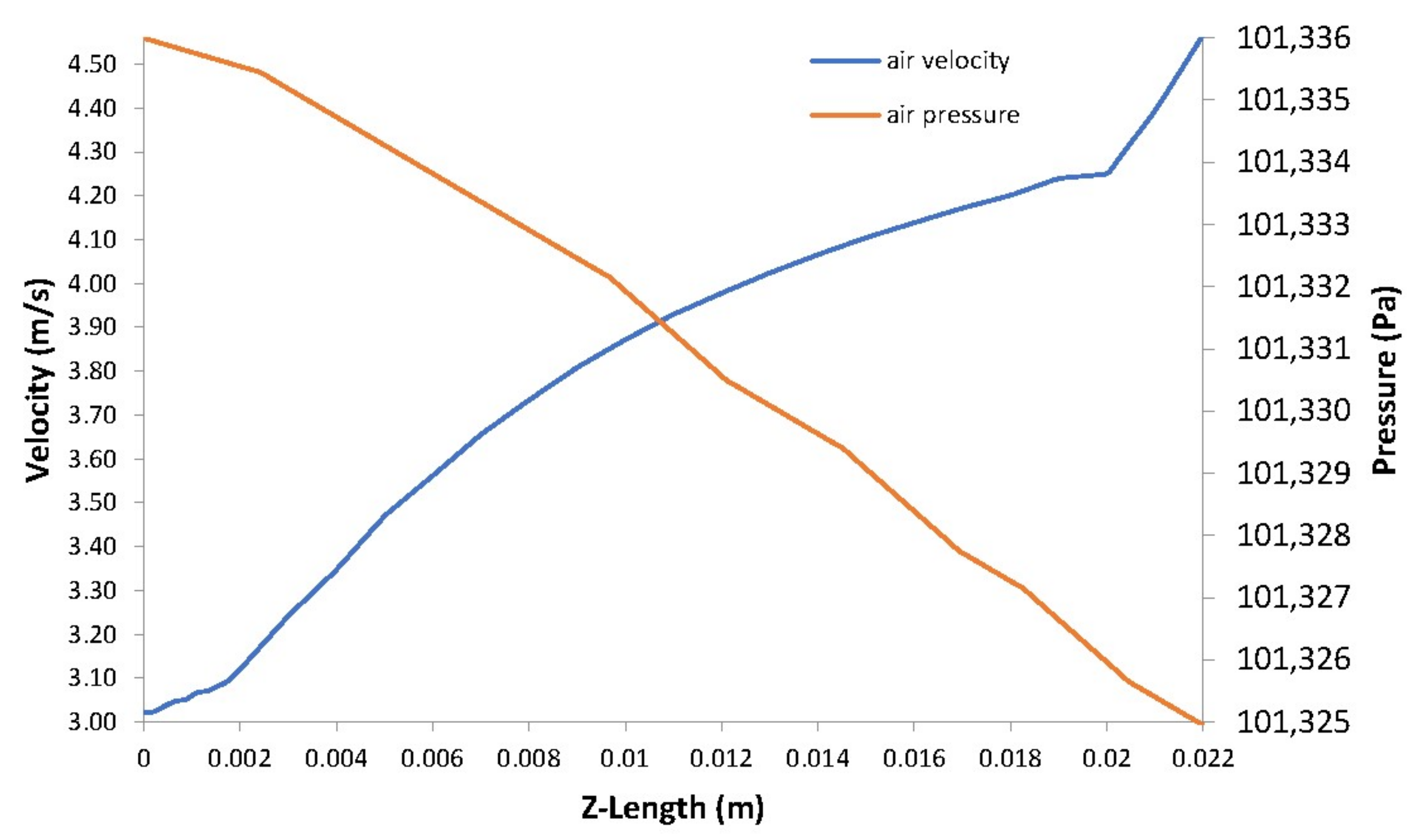
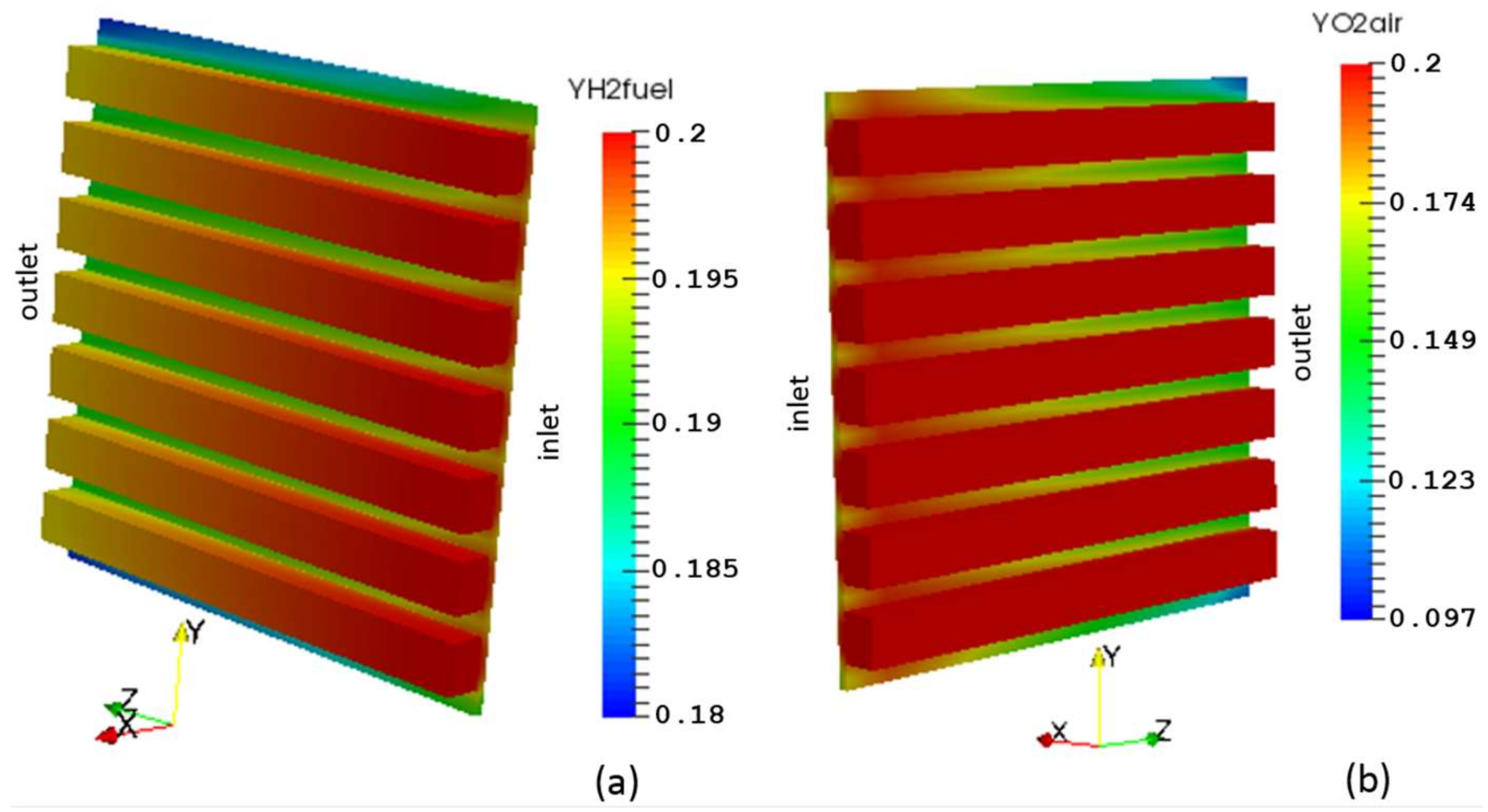
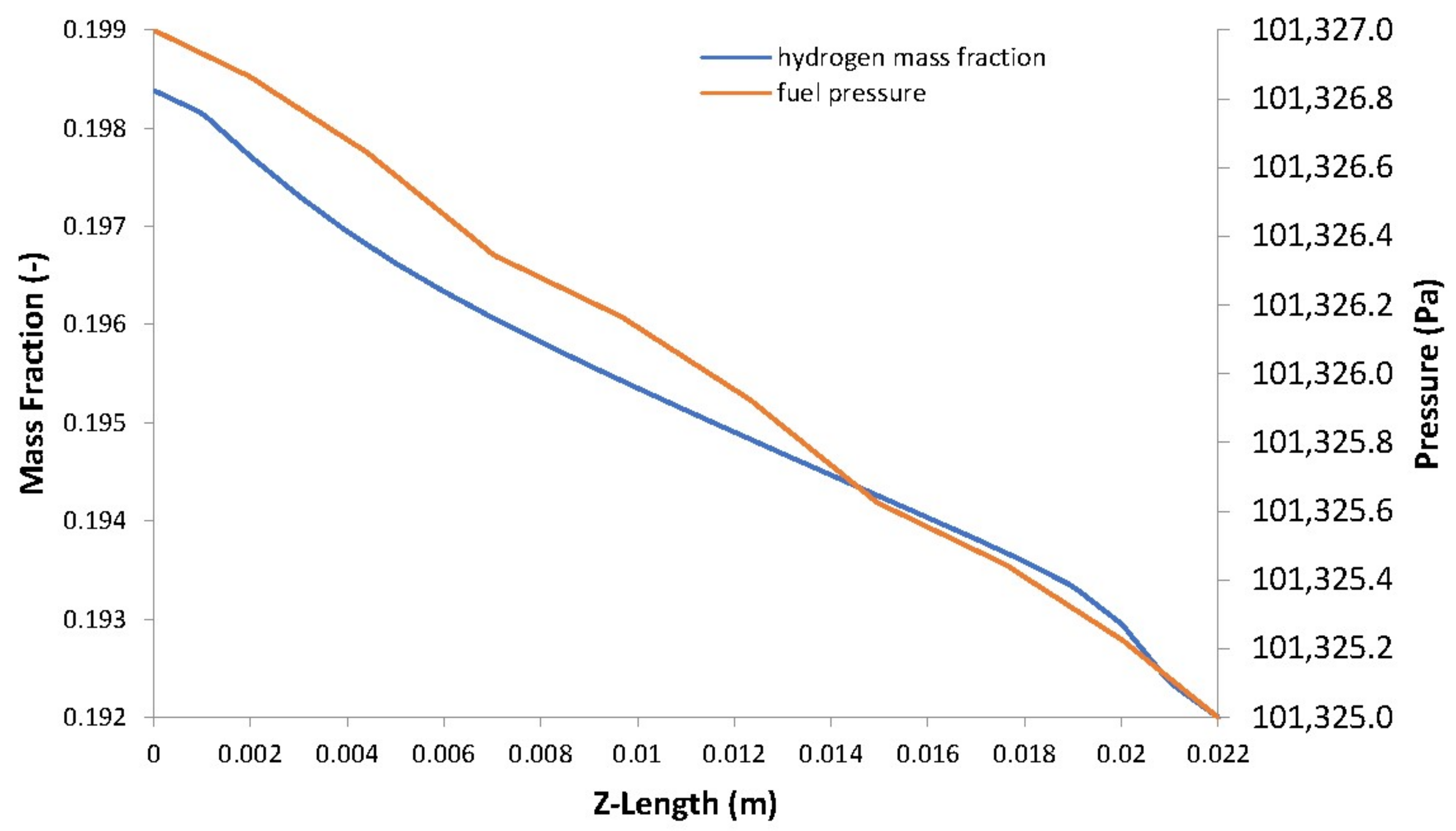
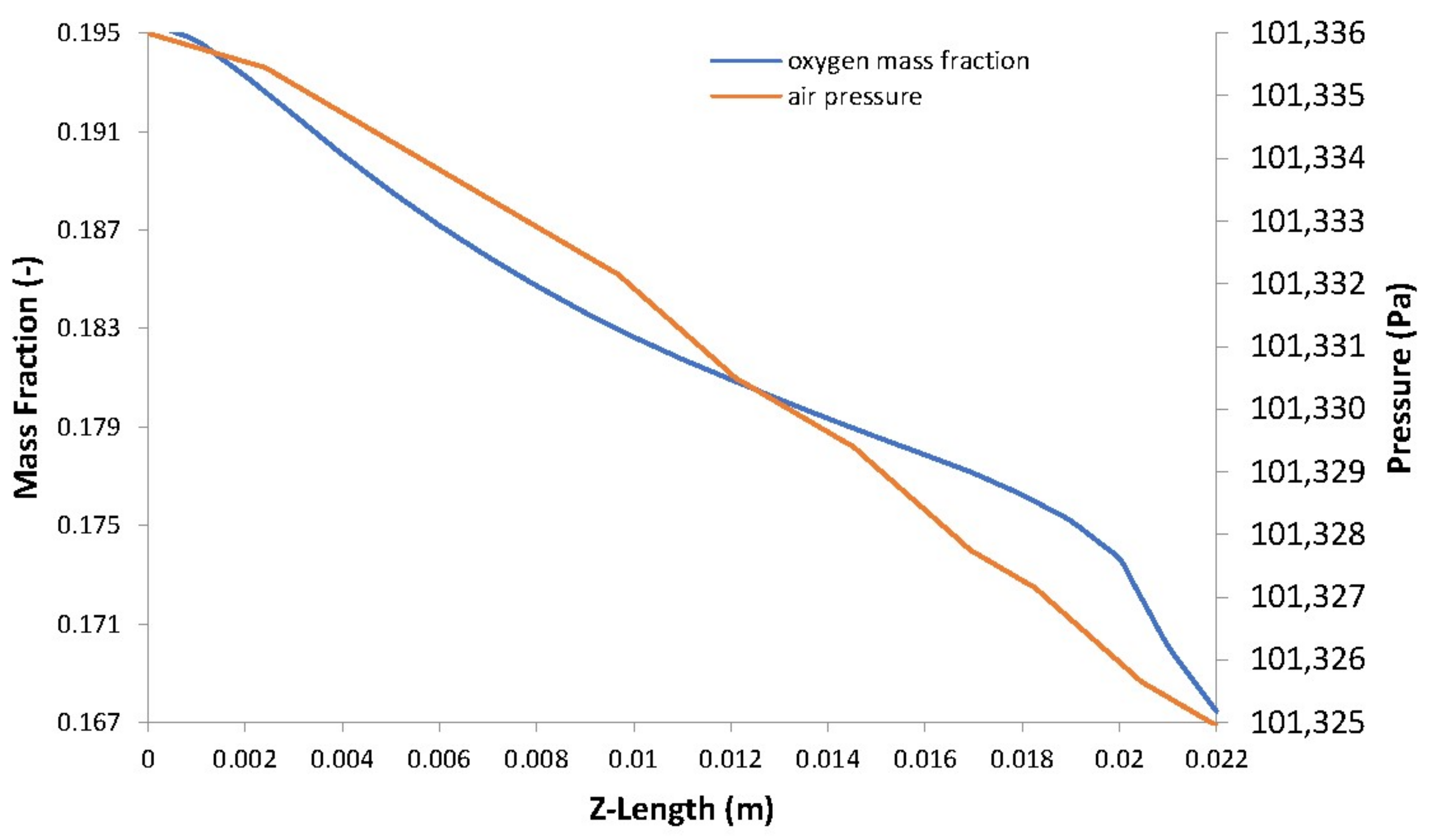
5. Case Study Results and Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| A | area, m2 |
| C | concentration, mol m−3 |
| cp | specific heat capacity, J kg−1 K−1 |
| d | diameter, m |
| D | diffusivity, m2 s−1 |
| E | potential, V |
| F | Faraday’s constant, 96,485 C mol−1 e− |
| ΔG | Gibbs free energy, kJ mol−1 |
| H | latent heat, J kg−1 |
| ΔH | enthalpy of formation, J mol−1 |
| I | current density, A m−2 |
| I0 | exchange current density, A m−2 |
| k | thermal conductivity, W m−1 K−1 |
| K | permeability, m2 |
| M | molar mass, kg kmol−1 |
| ni | number of electron of species i |
| p | pressure, Pa |
| R | universal gas constant, 8.314 J mol−1 K−1 |
| RΩ | area specific resistance, Ω m2 |
| ∆S | entropy of formation, J mol−1 K−1 |
| T | temperature, K |
| velocity vector, m s−1 | |
| v | diffusion volume, m3 |
| V | voltage, V |
| y | mass fraction |
| x | mole fraction |
| z | number of electron transferred |
| Greek letters | |
| α | charge transfer coefficient |
| δ | thickness, m |
| ε | porosity |
| η | overpotential, V |
| μ | dynamic viscosity, Pa s |
| ξ | stoichiometric ratio |
| ρ | density, kg m−3 |
| σe | electrical conductivity, S m−1 |
| σi | ionic conductivity, S m−1 |
| τ | tortuosity |
| Subscripts and superscripts | |
| act | activation |
| c | cathode |
| ch | channel |
| con | concentration |
| E | energy |
| eff | effective |
| H2 | hydrogen |
| H2O | water |
| i | species i |
| j | species j |
| knud | Knudsen |
| L | limiting |
| M | momentum |
| MEA | membrane electrode assembly |
| MEM | membrane |
| mix | mixture |
| N2 | nitrogen |
| O2 | oxygen |
| ohm | ohmic |
| p | pore |
| ref | reference |
| sat | saturation |
| WV | water vapor |
References
- Kone, J.P.; Zhang, X.; Yan, Y.; Hu, G.; Ahmadi, G. Three-dimensional multiphase flow computational fluid dynamics models for proton exchange membrane fuel cell: A theoretical development. J. Comput. Multiph. Flows 2017, 9, 3–25. [Google Scholar] [CrossRef]
- Wu, H.W. A review of recent development: Transport and performance modeling of pem fuel cells. Appl. Energy 2016, 165, 81–106. [Google Scholar] [CrossRef]
- Ferreira, R.B.; Falcao, D.S.; Oliveira, V.B.; Pinto, A. Numerical simulations of two-phase flow in proton exchange membrane fuel cells using the volume of fluid method—A review. J. Power Sources 2015, 277, 329–342. [Google Scholar] [CrossRef]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.B.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A critical review of modeling transport phenomena in polymer-electrolyte fuel cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Wilberforce, T.; El-Hassan, Z.; Khatib, F.N.; Al Makky, A.; Mooney, J.; Barouaji, A.; Carton, J.G.; Olabi, A.G. Development of bi-polar plate design of pem fuel cell using cfd techniques. Int. J. Hydrogen Energy 2017, 42, 25663–25685. [Google Scholar] [CrossRef]
- Zhao, D.D.; Dou, M.F.; Zhou, D.M.; Gao, F. Study of the modeling parameter effects on the polarization characteristics of the pem fuel cell. Int. J. Hydrogen Energy 2016, 41, 22316–22327. [Google Scholar] [CrossRef]
- Laoun, B.; Naceur, M.W.; Khellaf, A.; Kannan, A.M. Global sensitivity analysis of proton exchange membrane fuel cell model. Int. J. Hydrogen Energy 2016, 41, 9521–9528. [Google Scholar] [CrossRef]
- Khazaee, I.; Sabadbafan, H. Effect of humidity content and direction of the flow of reactant gases on water management in the 4-serpentine and 1-serpentine flow channel in a pem (proton exchange membrane) fuel cell. Energy 2016, 101, 252–265. [Google Scholar] [CrossRef]
- Xing, L.; Cai, Q.; Xu, C.X.; Liu, C.B.; Scott, K.; Yan, Y.S. Numerical study of the effect of relative humidity and stoichiometric flow ratio on pem (proton exchange membrane) fuel cell performance with various channel lengths: An anode partial flooding modelling. Energy 2016, 106, 631–645. [Google Scholar] [CrossRef]
- Sezgin, B.; Caglayan, D.G.; Devrim, Y.; Steenberg, T.; Eroglu, I. Modeling and sensitivity analysis of high temperature pem fuel cells by using comsol multiphysics. Int. J. Hydrogen Energy 2016, 41, 10001–10009. [Google Scholar] [CrossRef]
- Ozen, D.N.; Timurkutluk, B.; Altinisik, K. Effects of operation temperature and reactant gas humidity levels on performance of pem fuel cells. Renew. Sustain. Energy Rev. 2016, 59, 1298–1306. [Google Scholar] [CrossRef]
- Osanloo, B.; Mohammadi-Ahmar, A.; Solati, A. A numerical analysis on the effect of different architectures of membrane, cl and gdl layers on the power and reactant transportation in the square tubular pemfc. Int. J. Hydrogen Energy 2016, 41, 10844–10853. [Google Scholar] [CrossRef]
- Khazaee, I.; Sabadbafan, H. Numerical study of changing the geometry of the flow field of a pem fuel cell. Heat Mass Transf. 2016, 52, 993–1003. [Google Scholar] [CrossRef]
- Velisala, V.; Srinivasulu, G.N. Numerical simulation and experimental comparison of single, double and triple serpentine flow channel configuration on performance of a pem fuel cell. Arab. J. Sci. Eng. 2018, 43, 1225–1234. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wang, S.X.; Wang, G.Z.; Yue, L.K. Numerical study of a new cathode flow-field design with a sub-channel for a parallel flow-field polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 2359–2368. [Google Scholar] [CrossRef]
- Ashrafi, M.; Shams, M. The effects of flow-field orientation on water management in pem fuel cells with serpentine channels. Appl. Energy 2017, 208, 1083–1096. [Google Scholar] [CrossRef]
- Zehtabiyan-Rezaie, N.; Arefian, A.; Kermani, M.J.; Noughabi, A.K.; Abdollahzadeh, M. Effect of flow field with converging and diverging channels on proton exchange membrane fuel cell performance. Energy Convers. Manag. 2017, 152, 31–44. [Google Scholar] [CrossRef]
- Barreras, F.; Lozano, A.; Valino, L.; Mustafa, R.; Marin, C. Fluid dynamics performance of different bipolar plates—Part I. Velocity and pressure fields. J. Power Sources 2008, 175, 841–850. [Google Scholar] [CrossRef]
- Lozano, A.; Valino, L.; Barreras, F.; Mustata, R. Fluid dynamics performance of different bipolar plates—Part II. Flow through the diffusion layer. J. Power Sources 2008, 179, 711–722. [Google Scholar] [CrossRef]
- Mustata, R.; Valino, L.; Barreras, F.; Gil, M.I.; Lozano, A. Study of the distribution of air flow in a proton exchange membrane fuel cell stack. J. Power Sources 2009, 192, 185–189. [Google Scholar] [CrossRef]
- Valino, L.; Mustata, R.; Gil, M.I.; Martin, J. Effect of the relative position of oxygen-hydrogen plate channels and inlets on a pemfc. Int. J. Hydrogen Energy 2010, 35, 11425–11436. [Google Scholar] [CrossRef]
- Imbrioscia, G.M.; Fasoli, H.J. Simulation and study of proposed modifications over straight-parallel flow field design. Int. J. Hydrogen Energy 2014, 39, 8861–8867. [Google Scholar] [CrossRef]
- Valino, L.; Mustata, R.; Duenas, L. Consistent modeling of a single pem fuel cell using onsager’s principle. Int. J. Hydrogen Energy 2014, 39, 4030–4036. [Google Scholar] [CrossRef]
- Beale, S.B.; Choi, H.-W.; Pharoah, J.G.; Roth, H.K.; Jasak, H.; Jeon, D.H. Open-source computational model of a solid oxide fuel cell. Comput. Phys. Commun. 2016, 200, 15–26. [Google Scholar] [CrossRef]
- Kone, J.P.; Zhang, X.; Yan, Y.; Hu, G.; Ahmadi, G. CFD Modeling and Simulation of Pem Fuel Cell Using Openfoam. In Proceedings of the Applied Energy Symposium and Forum, REM2017: Renewable Energy Integration with Mini/Microgrid, Tianjin, China, 18–20 October 2017. [Google Scholar]
- Barbir, F. Pem Fuel Cells: Theory and Practice; Elsevier Academic: Amsterdam, The Netherlands; London, UK, 2005; p. 15. 433p. [Google Scholar]
- Sivertsen, B.R.; Djilali, N. Cfd-based modelling of proton exchange membrane fuel cells. J. Power Sources 2005, 141, 65–78. [Google Scholar] [CrossRef]
- Ju, H.; Meng, H.; Wang, C.Y. A single-phase, non-isothermal model for pem fuel cells. Int. J. Heat Mass Transf. 2005, 48, 1303–1315. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Fairbanks, D.F.; Wilke, C.R. Diffusion coefficients in multicomponent gas mixtures. Ind. Eng. Chem. 1950, 42, 471–475. [Google Scholar] [CrossRef]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E.; Rorrer, G.L. Fundamentals of Momentum, Heat, and Mass Transfer, 5th ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Geankoplis, C.J. Transport Processes and Unit Operations, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer electrolyte fuel-cell model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- O’Hayre, R.P.; Cha, S.-W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wang, Y.; Chen, K.S.; Cho, S.C. Pem Fuel Cells:hermal and Water Management Fundamentals; Momentum Press: New York, NY, USA, 2013. [Google Scholar]
- Liu, Z. Fuel Cell Performance; Nova Science Publishers: New York, NY, USA, 2012; p. 10. 284p. [Google Scholar]
- Chang, R.; Goldsby, K.A. General Chemistry: The Essential Concepts; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Yuan, W.; Tang, Y.; Pan, M.Q.; Li, Z.T.; Tang, B. Model prediction of effects of operating parameters on proton exchange membrane fuel cell performance. Renew. Energy 2010, 35, 656–666. [Google Scholar] [CrossRef]
- Todd, B.; Young, J.B. Thermodynamic and transport properties of gases for use in solid oxide fuel cell modelling. J. Power Sources 2002, 110, 186–200. [Google Scholar] [CrossRef]
- Yaws, C.L. Yaws’ Critical Property Data for Chemical Engineers and Chemists; Knovel: New York, NY, USA, 2012. [Google Scholar]
- Parthasarathy, A.; Dave, B.; Srinivasan, S.; Appleby, A.J.; Martin, C.R. The platinum microelectrode nafion interface—An electrochemical impedance spectroscopic analysis of oxygen reduction kinetics and nafion characteristics. J. Electrochem. Soc. 1992, 139, 1634–1641. [Google Scholar] [CrossRef]
- Yaws, C.L. Yaws’ Handbook of Thermodynamic Properties for Hydrocarbons and Chemicals; Knovel: New York, NY, USA, 2009. [Google Scholar]
- Fuller, E.N.; Schettle, P.D.; Giddings, J.C. A new method for prediction of binary gas-phase diffusion coeffecients. Ind. Eng. Chem. 1966, 58, 19–27. [Google Scholar]
- Fuller, E.N.; Ensley, K.; Giddings, J.C. Diffusion of halogenated hydrocarbons in helium. Effect of structure on collision cross sections. J. Phys. Chem. 1969, 73, 3679–3685. [Google Scholar] [CrossRef]






| BP | GFC | GDL | CL | Membrane | |
|---|---|---|---|---|---|
| x-width (mm) | 3 | 1.5 | 0.41 | 0.0037 | 0.127 |
| y-height (mm) | 22 | 2 | 22 | 22 | 22 |
| z-length (mm) | 22 | 22 | 22 | 22 | 22 |
| Description | Symbol | Expression | Source |
|---|---|---|---|
| Gas density | ρ | - | |
| Mole fraction | xi | - | |
| Specific heat capacity | cp | - | |
| Thermal conductivity | k | [29] | |
| Diffusivity of gas species i | Di-mix | [30] | |
| Effective global diffusivity | [31] | ||
| Effective species diffusivity | [31] | ||
| Effective Knudsen diffusivity | [31] | ||
| Knudsen diffusion coefficient | Di-Knud | [32] | |
| Nernst potential | ENernst | - | |
| Area specific resistance | RΩ | [33] | |
| Membrane ionic conductivity | σi | [33] | |
| Membrane water content | λ | [33] | |
| Water vapor activity | a | [33] | |
| Saturation pressure | [33] | ||
| Activation overpotential | ηact | [26] | |
| Ohmic overpotential | ηohm | [26] | |
| Concentration overpotential | ηcon | [34] | |
| Concentration constant | c | [34] | |
| Limiting current density | IL | [26] | |
| Cathode exchange current density | I0,C | [35] | |
| Species mass flux | [26] |
| Equations | Anode Inlet | Anode Outlet | Cathode Inlet | Cathode Outlet | Walls |
|---|---|---|---|---|---|
| Momentum | Ufuel = 1.1055 m s−1 | pfuel = 101,325 Pa | Uair = 3.082 m s−1 | pair = 101,325 Pa | U = 0 |
| Species transport | . | ||||
| Energy | T = 353 K | T = 353 K |
| Parameter or Property | Symbol | Value | Unit | Source |
|---|---|---|---|---|
| Density of air | ρair | 0.914 | kg m−3 | Calculated [37] |
| Density of fuel | ρfuel | 0.2404 | kg m−3 | Calculated [37] |
| Density of membrane | ρMEM | 1980 | kg m−3 | [38] |
| Density of BP | ρBP | 1880 | kg m−3 | [38] |
| Isobaric heat capacity of air | cp,air | 1108.85 | J kg−1 K−1 | Calculated [39] |
| Isobaric heat capacity of fuel | cp,fuel | 2062.74 | J kg−1 K−1 | Calculated [39] |
| Isobaric heat capacity of GDL | cp,GDL | 710 | J kg−1 K−1 | [38] |
| Isobaric heat capacity of CL | cp,CL | 710 | J kg−1 K−1 | [38] |
| Isobaric heat capacity of membrane | cp,MEM | 2000 | J kg−1 K−1 | [38] |
| Isobaric heat capacity of BP | cp,BP | 875 | J kg−1 K−1 | [38] |
| Thermal conductivity of air | kair | 0.02867 | W m−1 K−1 | Calculated [29,39] |
| Thermal conductivity of fuel | kfuel | 0.08396 | W m−1 K−1 | Calculated [29,39] |
| Thermal conductivity of GDL | kGDL | 1.6 | W m−1 K−1 | [38] |
| Thermal conductivity of CL | kCL | 8 | W m−1 K−1 | [38] |
| Thermal conductivity of membrane | kMEM | 0.67 | W m−1 K−1 | [38] |
| Thermal conductivity of BP | kBP | 10.7 | W m−1 K−1 | [38] |
| Electronic conductivity of GDL | σe,GDL | 5000 | S m−1 | [38] |
| Electronic conductivity of CL | σe,CL | 1000 | S m−1 | [38] |
| Electronic conductivity of BP | σe,BP | 8.3 × 104 | S m−1 | [38] |
| Dynamic viscosity of air | μair | 1.5158 × 10−5 | Pa s | Calculated [29,39,40] |
| Dynamic viscosity of fuel | μfuel | 1.5 × 10−5 | Pa s | Calculated [29,39,40] |
| Parameter or Property | Symbol | Value | Unit | Source |
|---|---|---|---|---|
| Cathode charge transfer coefficient | αc | 1.0 | - | - |
| Cathode activation energy | Eact,c | 73,220.0 | J mol−1 | [41] |
| Reference exchange current density | 0.0139 | A m−2 | [41] | |
| Enthalpy of formation of water vapor | −241.826 × 103 | J mol−1 | [42] | |
| Standard entropy of hydrogen | 130.68 | J mol−1 K−1 | [42] | |
| Standard entropy of oxygen | 205.152 | J mol−1 K−1 | [42] | |
| Standard entropy of nitrogen | 191.609 | J mol−1 K−1 | [42] | |
| Standard entropy of water vapor | 188.835 | J mol−1 K−1 | [42] |
| Variable | Symbol | Value | Unit | Source |
|---|---|---|---|---|
| Cell voltage | V | 0.6 | V | - |
| Cell temperature | Tcell | 353 | K | - |
| Air pressure | pair | 101,325 | Pa | - |
| Fuel pressure | pfuel | 101,325 | Pa | - |
| Air velocity | Uair | 3.082 | m s−1 | Calculated [36] |
| Fuel velocity | Ufuel | 1.1055 | m s−1 | Calculated [36] |
| Permeability of porous electrodes | K | 1.0 × 10−11 | m2 | - |
| O2 fixed diffusivity in air mixture | 2.939 × 10−5 | m2 s−1 | Calculated [30,43,44] | |
| Effective O2 fixed diffusivity in air in GDL | 9.732 × 10−6 | m2 s−1 | Calculated [30,31,32,43,44] | |
| Effective O2 fixed diffusivity in air in CL | 7.785 × 10−6 | m2 s−1 | Calculated [30,31,32,43,44] | |
| H2 fixed diffusivity in fuel mixture | 0.122 × 10−3 | m2 s−1 | Calculated [30,43,44] | |
| Effective H2 fixed diffusivity in fuel in GDL | 4.031 × 10−5 | m2 s−1 | Calculated [30,31,32,43,44] | |
| Effective H2 fixed diffusivity in fuel in CL | 1.252 × 10−5 | m2 s−1 | Calculated [30,31,32,43,44] | |
| Mass fraction of O2 | 0.2 | - | - | |
| Mass fraction of air H2O | 0.15 | - | - | |
| Mass fraction of N2 | 0.65 | - | - | |
| Mass fraction of H2 | 0.2 | - | - | |
| Mass fraction of fuel H2O | 0.8 | - | - |
| Mesh 1 | Mesh 2 | Mesh 3 | |
|---|---|---|---|
| Total number of cells | 134,552 | 224,432 | 351,000 |
| Global temperature (K) | Tmin = 353.01 | Tmin = 353.01 | Tmin = 353.01 |
| Tave = 356.05 | Tave = 356.1 | Tave = 356.1 | |
| Tmax = 357.4 | Tmax = 357.5 | Tmax = 357.5 |
| Parameter or Property | This Work | Yuan et al. [38] | |
|---|---|---|---|
| Cell geometry | Number of channels in each electrode | 7 | 1 |
| Channel width (mm) | 1.5 | 1 | |
| Channel height (mm) | 2 | 1 | |
| Channel length (mm) | 22 | 30 | |
| GDL thickness (mm) | 0.41 | 0.2 | |
| CL thickness (mm) | 0.0037 | 0.02 | |
| Membrane thickness (mm) | 0.127 | 0.05 | |
| BP thickness (mm) | 3 | 2 | |
| GDL porosity | 0.5 | 0.55 | |
| CL porosity | 0.4 | 0.475 | |
| Properties | Density of membrane (kg m−3) | 1980 | 1980 |
| Density of BP (kg m−3) | 1880 | 1880 | |
| Heat capacity of GDL (J kg−1 K−1) | 710 | 710 | |
| Heat capacity of CL (J kg−1 K−1) | 710 | 710 | |
| Heat capacity of membrane (J kg−1 K−1) | 2000 | 2000 | |
| Heat capacity BP (J kg−1 K−1) | 875 | 875 | |
| Thermal conductivity of GDL (W m−1 K−1) | 1.6 | 1.6 | |
| Thermal conductivity of CL (W m−1 K−1) | 8 | 8 | |
| Thermal conductivity of membrane (W m−1 K−1) | 0.67 | 0.67 | |
| Thermal conductivity of BP (W m−1 K−1) | 10.7 | 10.7 | |
| Electronic conductivity of GDL (S m−1) | 5000 | 5000 | |
| Electronic conductivity of CL (S m−1) | 1000 | 1000 | |
| Electronic conductivity BP (S m−1) | 8.3 × 104 | 8.3 × 104 | |
| Charge transfer coefficient | 1.0 | 1.25 | |
| Operating conditions | Temperature (K) | 353 | 300 |
| Pressure (Pa) | 101,325 | 100,000 | |
| stoichiometric flow ration | 1.5/2.0 | 1.5/2.0 | |
| Flow configuration | co-flow | co-flow | |
| Phase | single-phase | multiphase | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kone, J.-P.; Zhang, X.; Yan, Y.; Adegbite, S. An Open-Source Toolbox for PEM Fuel Cell Simulation. Computation 2018, 6, 38. https://doi.org/10.3390/computation6020038
Kone J-P, Zhang X, Yan Y, Adegbite S. An Open-Source Toolbox for PEM Fuel Cell Simulation. Computation. 2018; 6(2):38. https://doi.org/10.3390/computation6020038
Chicago/Turabian StyleKone, Jean-Paul, Xinyu Zhang, Yuying Yan, and Stephen Adegbite. 2018. "An Open-Source Toolbox for PEM Fuel Cell Simulation" Computation 6, no. 2: 38. https://doi.org/10.3390/computation6020038