Abstract
Topochemical and electronic structure relationships are shown upon going from ANCl to A2N2Se (A = Zr, Ce) through metathesis. The chalcogen Se (divalent) displacing halogen Cl (monovalent) modifies the arrangements of A–N monolayers within ANCl (…Cl|{AN}|Cl… sequences) to double layers in A2N2Se (…Se|{A2N2}|Se… sequences). The investigation carried out in the framework of the quantum density functional theory DFT points to peculiar features pertaining to the dominant effect of the A–N covalent bond stronger than ionic A–Cl and ionocovalent A–Se, as identified from analyses of bonding from overlap integral, charge transfer, electron localization function mapping. Electronic density of states shows semi-conducting behavior due to the tetravalent character of A. The resulting overall pseudo-binary compounds are expressed formally with full ionization as {AN}Cl and {A2N2}Se.
1. Introduction
In solid state chemistry the huge number of natural and synthesized compounds makes it necessary to draw schemes enabling the scientist to better understand the trends between electronically and structurally related chemical systems. For an illustration, several transition metal T based oxides have the TO6 octahedron as a building-block and the arrangement of TO6 octahedra in a family of compounds is of paramount importance to establish evolutions in structural and physical properties. This was recently shown for the family of oxides—IrO2, CaIrO3, Ca2IrO4, and Ca4IrO6—considered as the sequential operation of increasing amounts of CaO on IrO2 leading to general formulation: (CaO)nIrO2 (n = 0, 1, 2, 4). Then, CaO acts as a ‘chemical scissor’ with the effects of drastically modifying the arrangement of IrO6 octahedra from three-dimensional (3D) in IrO2 rutile characterized by files of edge and corner connecting octahedra to 2D-like in CaIrO3 with planes of edge connected octahedra, then to 1D chains of IrO6 octahedra in Ca2IrO4, and finally to 0D with isolated octahedra. Ab initio computations helped in rationalizing the consequences on the physical and magnetic properties arising for the isolated octahedra [1]. Similarly, a parallel with the Ruddlesden–Popper type phases can be drawn: CaO(CaMnO3)n where calcium monoxide (CaO) is inserted within perovskite-like motifs (CaMnO3) leading to the family Ca2MnO4, Ca3Mn2O7 … [2].
Present work focuses on the redistribution of valence electrons over the chemical constituents in a family of compounds, inducing atomic rearrangement, differentiating electronic structures, and exhibiting original bonding characteristics. Specifically, considering A metals in tetravalent states, namely Zr and Ce here, ZrIVNCl [3] and CeIVNCl [4] are known to crystallize in layered-like structures (2D), trigonal for the first and tetragonal for the latter (cf. Figure 1) while isoelectronic ZrIVO2 and CeIVO2 are three-dimensional (3D) with fluorite-type CaF2 structure. These binary and ternary compounds are valence-isoelectronic:
2 O (2s2, 2p4) ≡ N (2s2, 2p3) + Cl (3s2, 3p5) –the symbol ≡ indicating equivalence–.
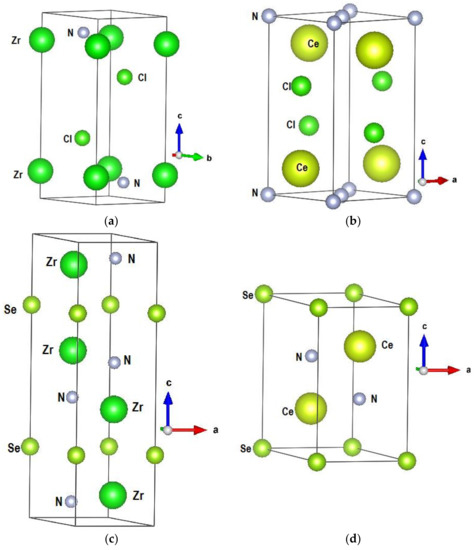
Figure 1.
Sketches of the crystal structures of the A tetravalent cation ternaries: (a) ZrNCl, (b) CeNCl, (c) Zr2N2Se, and (d) Ce2N2Se.
The difference of size: rCl = 0.80 Å versus rN = 0.56 Å on one hand and of electronegativities between N and Cl (χCl = 3.16 versus χN = 3.04) on the other hand result into dA–N~2.3 Å < dA-Cl~3.21 Å underlying differentiated chemical bonds. Furthermore, this could explain the origin of the 2D-like structure. Interestingly, such 2D like arrangements occur within the A2N2Se family with A = Zr [5], Ce [6]. These ternaries can be considered as derived from equiatomic ANCl. This statement relies on topochemical metathesis reaction involving anionic species exchange, through which
(the reaction occurs in vacuo, at T~700 °C, during 24 h) [7,8].
2ANCl + K2Se → A2N2Se + 2KCl
The common characteristics between AO2, ANCl, and A2N2Se is their expression as per one tetravalent A, i.e., formally A4+(O2)4−, A4+(NCl)4− and A4+(½{N2Se})4−. However, a more elaborate insight will be provided with an alternative manner of expressing them in accordance with the structures specificities where A–N bond prevails over A-Cl and A–Se. Consequently, the chemical formula are written as {AN}Cl and {A2N2}Se, hence accounting for the formation of “AN” and “A2N2” within a layered structure. Eventually, as it is shown hereafter, the two ternary compounds will be assimilated to complex binary compounds.
The first argument in favor of this statement is found in the sketches of the crystal structure presented in Figure 1. Also Table 1 provides the crystallographic data. In spite of their different space groups, all ternary compounds show layered-like edifices with succession of A–N substructures monoloayered in ANCl and two-layered within A2N2Se ternaries (A = Zr, Ce) with {A2N2} motifs.

Table 1.
Experimental and (calculated) crystal parameters of β-ZrNCl, CeNCl, Zr2N2Se and Ce2N2Se.
While no discussion of the preparative solid state chemistry features is developed in the present context in as far as they are well detailed elsewhere [7,8], focus is made on the characteristics pertaining to the changing electronic structure and chemical bonding, highlighted through computation results based on the well-established quantum mechanical density functional theory DFT [9,10].
2. Computational Framework
Within DFT, we used VASP code [11,12] to geometry optimize atomic positions and lattice parameters to minimize the inter-atomic forces, close to zero, at which point the charge transfers can be obtained accurately as well as the electron localization mapping.
For this purpose, we used the accurate projector augmented wave (PAW) method [12,13] with potentials built within the generalized gradient approximation (GGA) for an account of the effects of exchange and correlation [14]. With our computational scheme, the conjugate-gradient algorithm [15] was used to relax the atom positions of the different chemical systems into their ground state structure. The structural parameters were considered to be fully relaxed when forces on the atoms were less than 0.02 eV/Å and all stress components were less than 0.003 eV/Å3. The tetrahedron method with Blöchl corrections [16] was applied for both geometry relaxation and total energy calculations. Brillouin-zone (BZ) integrals were approximated using the special k-point sampling of Monkhorst and Pack [17]. The calculations were converged at an energy cut-off of 500 eV for all compounds. The k-point integration is carried out with a starting mesh of 6 × 6 × 6 up to 10 × 10 × 10 for best convergence and relaxation to zero strains. Calculations are scalar relativistic necessary for compounds with Z > 50 i.e., like Ce with Z = 58.
From the calculations which assume starting neutral atomic constituents at the different lattice sites, we analyze the charge density results through the approach of atoms in molecules and crystals (AIM) introduced by Bader [18] consisting of dividing molecules into atoms based on the distribution of electronic charge density. As a matter of fact, the charge density reaches a minimum between atoms in chemical systems, so this is a natural region to separate atoms from each other. Such an analysis can be useful when trends between similar chemical systems are examined as shown herein. In spite of the f character of cerium the calculations not requiring the use of GGA + U schemes for better results.
Properties related with electron localization are obtained from real space analysis of electron localization function (ELF) according to Becke and Edgecomb [19] as initially devised for Hartree–Fock calculations then adapted to DFT methods as based on the kinetic energy in which the Pauli exclusion principle is included: ELF = (1+ χσ2)−1 with 0 ≤ ELF ≤ 1, i.e., ELF is a normalized function. In this expression the ratio χσ = Dσ/Dσ0, where Dσ = τσ − ¼(∇ρσ)2/ρσ and Dσ0 = 3/5 (6π2)2/3ρσ5/3 correspond respectively to a measure of Pauli repulsion (Dσ) of the actual system and to the free electron gas repulsion (Dσ0) and τσ is the kinetic energy density. In this paper, we use ELF planes along selected orientations of the cell to show differentiated electron localizations with color maps: blue areas for no localization, red for full localization, and green for free electron like localization.
Full analysis of the electron band structure with site projected partial density of states PDOS was carried out with the full potential scalar relativistic augmented spherical wave ASW method [20,21]. ASW method implements the qualitative analysis of the chemical bonding based on the overlap integral Sij (i and j designating two chemical species) with the crystal orbital overlap population (COOP) following Hoffmann [22]. In the minimal ASW basis set, we have chosen the outermost shells to represent the valence states using partial waves up to lmax + 1 = 4 for Ce; lmax + 1 = 3 for Zr, Cl, and Se; and lmax + 1 = 2 for N. Low energy lying Cl 3s were considered as core states, not accounted for in the valence basis set. The completeness of the valence basis set is checked for charge convergence. The self-consistent field calculations are run to a convergence of ΔQ = 10−8 for the charge density and the accuracy of the method is in the range of about 10−7 eV regarding energy differences.
3. Geometry Optimization and Energy Dependent Results
The starting step of geometry optimization was carried out to minimize the inter-atomic forces -close to zero at which point the charge transfers can be obtained accurately as well as the description of the electron localization. Furthermore, the energy–volume equation of states will be established for the 2:2:1 compounds (A2N2Se) to evaluate further their bonding peculiarities.
Table 1a–d show the starting experimental and calculated atomic positions and structure parameters of the compounds under study. A fairly good agreement with experiment can be observed—except for ZrNCl where z(Zr) is calculated larger but without change of the trends. The agreement also stands for the relevant the inter-atomic distances with the systematic trend of dA–N < dA–Cl and dA–Se, in line with the 2D-like arrangements of the structures as shown in Figure 1. From the calculated total energies the cohesive energies Ecoh. were extracted. Exemplarily applying to the A2N2Se compounds per formula unit (FU)
where E(A), E(N2), and E(Se) are the energies of the constituents (A = Zr, Ce) calculated in the same conditions as the corresponding compound
Ecoh. = E(A2N2Se) − 2E(A) − E(N2) − E(Se)
Ecoh. (Zr2N2Se) = E(Zr2N2Se) − 2E(A) − E(N2) −E(Se) = −45.12 − (−17.06) − (−16.14) − (−5.22) = −6.7 eV/FU or −1.34 eV/atom.
Ecoh. (Ce2N2Se) = E(Ce2N2Se) − 2E(A) − E(N2) − E(Se) = −40.36 − (−11.54) − (−16.14) − (−5.22) = −7.46 eV/FU or −1.49 eV/atom.
Both compounds are found largely cohesive with negative magnitude of Ecoh. and a slightly higher cohesion within the cerium compound likely related with the differences in crystal structures.
3.1. Charge Transfer
From the converged calculations at large BZ integration the resulting calculated charge density is analyzed based on Bader AIM theory [18]. For the sake of establishing trends with corresponding binary oxides, ZrO2 and CeO2 were also calculated. In the PAW method Zr and Ce were considered with 12 explicit electrons in the calculations, i.e., Zr (4s2, 4p6, 5s2, and 4d2) and Ce (5s2, 5p6, 5d1, 4f1, 6s2). At self-consistent energy convergence, trend of charge transfer is from A to anionic substructures with magnitudes decreasing in the sequence
and larger magnitudes in the case or Zr as can be seen from the values at ±ΔQ line at Table 2. These trends can be correlated with the relatively decreasing ionic character with presence of increasing amounts of nitrogen bringing covalence into the ionic compound throughout the series AO2 → ANCl → A2N2Se.
AO2 → ANCl → A2N2Se

Table 2.
Bader charges “Q” from AIM theory. ±ΔQcmplx is relative to charge change in complex {AN} or {A2N2} entities.
Alternatively one can also check the charge transfer by considering the ternaries with the assumption of {AN}+Cl− and {A2N2}2+Se2− regarded as chemical complexes. The trend of charge transfer is then given at line ±ΔQcmplx.
and
{ZrN}+0.66Cl−0.66; {Zr2N2}+1.14Se−1.14
{CeN}+0.76Cl−0.76; {Ce2N2}+1.06Se−1.06.
Clearly, the formal expression of charges −1 on Cl and −2 on Se is not observed from the Bader charges; such chemical scheme being only obtained in aqueous solutions ex. Na+1aq.Cl−1aq. for rocksalt known as largely ionic, and hardly ever in the solid state. Another argument pertains to the position of Se as a late chalcogen with much less electronegativity χ(Se) = 2.55 versus χ(O) = 3.44.
By expressing the A2N2Se compounds as per A atom, one gets for ½{A2N2} ½Se: ΔQZrcmplx. = ±0.57 and ΔQCecmplx. = ±0.53. Then the same observation of increasing covalence brought by increasing amount of N is observed equally.
Such observations are further argued upon from the point of view of the electron localization function (ELF) [19].
3.2. Electron Localization Function ELF
ELF mapping is expected to illustrate further the different chemical behaviors of A–N on one hand and Cl and Se on the other hand. The slice projections along the c vertical axis are shown in Figure 2. Blue, green, and red contours represent zero, free electron-like, and strong localizations respectively. Four adjacent cells are represented. In ANCl (panels a, b) the succession of {ZrN}, {CeN}, and [Cl]-like planes is highlighted showing the strong A–N bonding differentiated from weaker bonding with blue zones separating them. In panels (c) and (d) reporting ELF slices of A2N2Se, features of double complex motifs are observed with {A2N2} motifs clearly separated from surrounding Se by blue areas along c-axis. Other projections orthogonal to the c axis are shown, illustrating furthermore the A–N bonding.
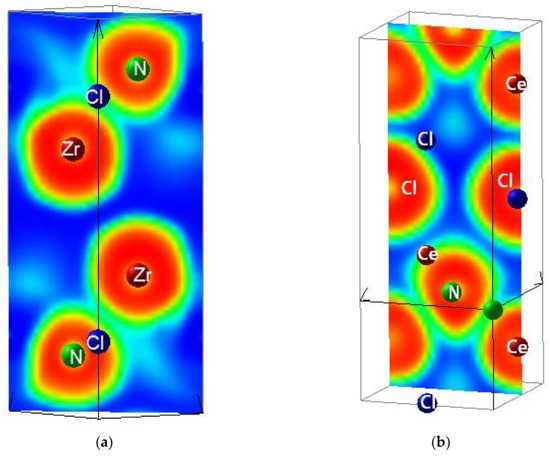
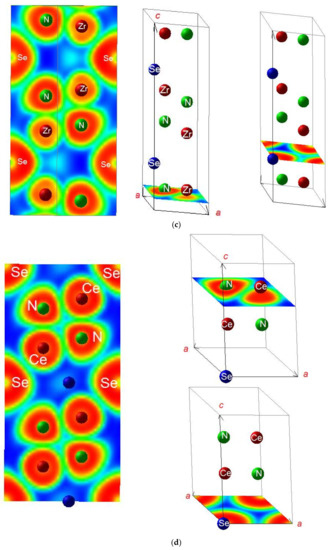
Figure 2.
Sketches of the crystal structures of the A tetravalent cation ternaries: (a) ZrNCl; (b) CeNCl; (c) Zr2N2Se; and (d) Ce2N2Se.
The A–N versus A–Se bonding is further discussed and illustrated in following section based on the overlap integral population analysis together with the site projected electronic density of states PDOS.
4. Electronic Structure and Chemical Bonding
4.1. Electronic Density of States
Using scalar relativistic calculations within the full potential ASW method introduced above we obtained the site projected (partial) density of states PDOS in four panels for the title compounds ZrNCl, CeNCl, Zr2N2Se, and Ce2N2Se shown at Figure 3. The energy reference along the x-axis is with respect to the top of the valence band VB (at EV) in so far that a small gap is observed at the top of the VB, separating it from the conduction band CB, suggesting a semi-conducting behavior.
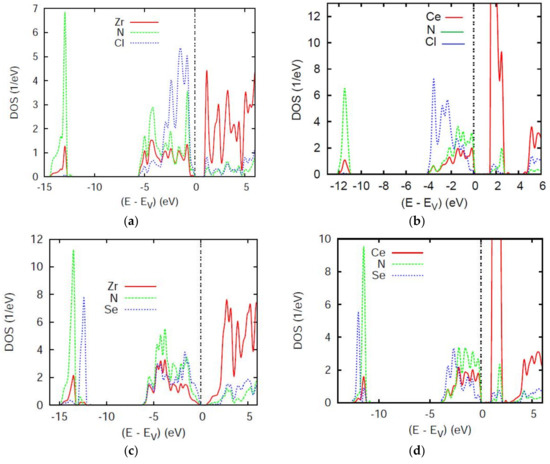
Figure 3.
Site projected density of states PDOS of (a) ZrNCl, (b) CeNCl, (c) Zr2N2Se, and (d) Ce2N2Se.
Focusing firstly on the two equiatomic ternaries ZrNCl and CeNCl, (Figure 3a,b) similarities can be observed for the presence of two PDOS blocks, the low energy lying ones pertaining to s states of N and A separated from the p block found below EV within 5 eV range for ZrNCl and 4 eV range for CeNCl. The CB contains empty Ce 4f and Zr 4d, the latter being much broader, extending over 5 eV while Ce 4f has 1 eV width. This is a well-known feature of the broader transition metal nd bands (especially 4d more than 3d) versus rare earth nf bands (n = 4, 5). Other differences are observed regarding the mixing. For the latter the band gap of ~1.8 eV in CeNCl is almost half this magnitude in ZrNCl at the top of the VB. Focusing on the lower part of the VB, i.e., at ~−12 eV, mixing between A(s) and N(2s) is from the similar shape of the PDOS with however a larger magnitude of N(2s) due the larger electronegativity of N versus A, illustrated by similar PDOS shapes with however much higher intensity of N(2s) PDOS. The largest magnitude of bonding occurs in the p block at the top of VB where N and Cl states mix with A metal itinerant states mainly of d nature. Note that the differentiation of bonding is clearer in CeNCl versus ZrNCl with more similarity between Ce and N states than between Ce and Cl, whereas less differentiating features are observed in ZrNCl. This likely arises from the different crystal structures of the two compounds—i.e., tetragonal versus trigonal (cf. Table 1).
In the Se-based ternaries Figure 3c,d the gap trends are the same as above with even smaller magnitudes due to the less ionic character brought by Se. Here too the different structures (cf. Figure 1; Table 1) can bring differences in the DOS and PDOS positions. For example, Se-s PDOS are inverted in position and show much more isolation (less mixing with valence states) in Zr2N2Se than in Ce2N2Se. Also the p block is 2 eV broader in Zr compound and the gap magnitude is reduced due to the breadth of the Zr 4d band especially showing in the CB. The similar PDOS shapes particularly in the p block at the top of VB, point to chemical bonding which can be qualitatively approached based on the overlap integral Sij (i and j designating two chemical species.
4.2. Chemical Bonding
The quantum mixing between A (Zr, Ce) on one hand and N/Cl/Se on the other hand can be further assessed using the COOP criterion of chemical bonding based on the overlap matrix elements Sij [20]. In the plots positive, negative and zero intensities correspond to bonding, antibonding and non-bonding interactions.
Figure 4a,b show the bonding properties for pair interactions in the equiatomic ternary compounds ZrNCl and CeNCl. The COOPs are, in short hand notation, the overlap integral–weighted DOS also expressed in eV−1 units along the y-axis. For ZrNCl, the whole valence band is of bonding character for both Zr–N and Zr–Cl which however start showing negative COOP at the top of VB, oppositely to CeNCl which exhibits largely antibonding Ce–Cl in the major part of VB. The different natures of Zr (transition metal with broad 4d band) versus Ce (rare earth with localized 4f states within the CB) can be a first observation explaining the observed difference. Nevertheless, the A–N bonding prevails over Zr–Cl.
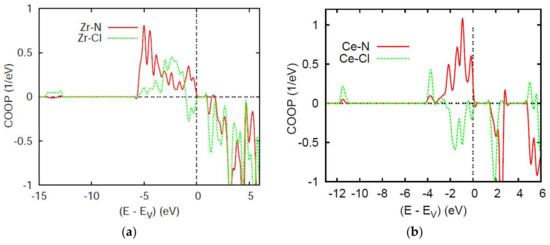
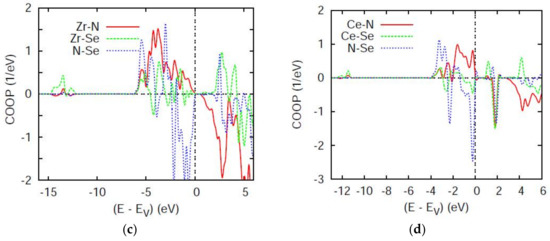
Figure 4.
Chemical bonding based on overlap integrals between two chemical species using the COOP criterion. (a) ZrNCl, (b) CeNCl, (c) Zr2N2Se, and (d) Ce2N2Se.
In Figure 4c,d showing the COOP of A2N2Se the intensities along the y-axis are twice larger in Zr2N2Se which contains 2 formula units (FU) per cell versus Ce2N2Se with 1 FU/cell. The A–N COOP are systematically larger and positive (bonding) throughout the VB than A–Se which furthermore show much larger antibonding negative COOP than in Zr2N2Se. Also one can notice the larger extension of the bonding region in the Zr compound, also observed in the corresponding DOS panel in Figure 3 as well as non-negligible Zr–Se s-like bonding at the bottom of VB. Lastly, the N–Se interaction is half bonding–half antibonding and does not contribute to the stability.
5. A2N2Se: Mechanical Properties from the Energy-Volume Equations of States EOS
The rather significant differences between Zr2N2Se and Ce2N2Se electronic structures call for further investigations regarding the consequences of their specific bonding properties. The strength of bonding and its nature can influence the mechanical properties of a material as its resistance to volume compressibility.
For the purpose of deeper assessment the equilibrium zero-pressure parameters were derived from the energy–volume E(V) equation-of-state (EOS) with calculations around minima found from geometry optimization. The resulting values are plotted in Figure 5. The fit of the curves with a Birch EOS [23]
provides E0, V0, B0, and B’, respectively. The equilibrium energy, the volume, the bulk modulus and its pressure derivative are given in the insert. The fit curves reproduce the trends of the geometry optimization for the volume with a magnitude closer to experiment for the Zr compound. The surprising result is the large difference of magnitudes of bulk modules: B0(Zr2N2Se) = 166 GPa almost twice as large as B0(Ce2N2Se) = 87 GPa. The latter magnitude places the compound in the range of intermetallic compounds [24] softer than typical oxides and ceramics while Zr2N2Se is within hardness range of oxides. Normally the larger the volume, the larger the compressibility; such a statement would make Zr2N2Se softer than Ce2N2Se. However, the opposite is observed. Then the bonding nature of the VB for both Zr–N and Zr–Se (Figure 4c) due to the chemical nature of Zr should be made responsible of the result.
E(V) = E0(V0) + [9/8]V0B0[([(V0)/V])2/3 − 1]2 + [9/16]B0(B’ − 4)V0[([(V0)/V])2/3 − 1]3
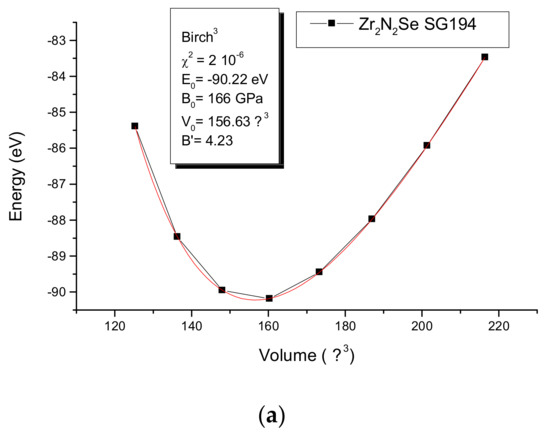
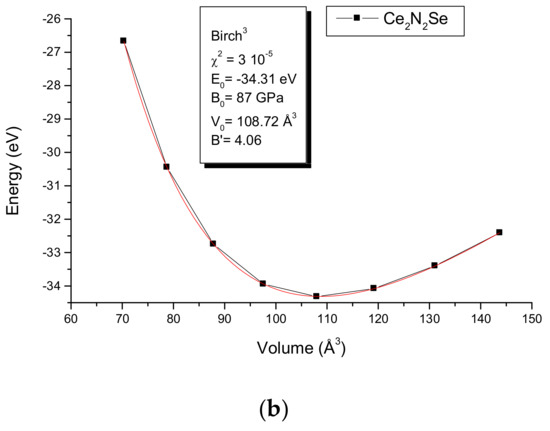
Figure 5.
Energy-volume equation of states EOS and Birch EOS fit values in the inserts for Zr2N2Se and Ce2N2Se.
6. Conclusions
The combined study of ternary nitride chlorides ANCl and nitride selenides A2N2X (A = Zr, Ce) based on quantum DFT investigations has been carried out herein to assess the topochemical metathesis of reaction consisting in the displacement of Cl by Se. The crystal chemistry observables were quantitatively illustrated by DFT results providing charge transfer, electron localization, electron density of states and bonding properties all allowing to consider the behavior of the ternaries as pseudo binaries: {AN}Cl and {A2N2}Se. Due to A–N bonds, generally shorter than A–Se, {AN} motifs are viewed as ‘building-blocks’ of the layered-like structural arrangements along the c-vertical axis forming respectively monolayers within ANCl and bilayers in A2N2Se. The strong bonding of both Zr–N and Zr–Se, opposed to strong Ce–N and weak Ce–Se bonds respectively leading to harder Zr2N2Se than Ce2N2Se.
Acknowledgments
I acknowledge computational facilities provided by the MCIA—clusters at the University of Bordeaux. Parts of the calculations were carried out on the Linux workstations of LGU. I am grateful to Volker EYERT, University of Augsburg and Materials Design Co. (Paris, France, Page: 11) for providing the full potential ASW code.
Conflicts of Interest
The author declares no conflict of interest.
References
- Matar, S.F.; Etourneau, J. (CaO)nIrO2 (n = 1, 2, 4) family: Chemical scissors effects of CaO on structural characteristics correlated to physical properties. Ab initio study. J. Solid State Chem. 2017, 255, 82–88. [Google Scholar] [CrossRef]
- Matar, S.F.; Eyert, V.; Villesuzanne, A.; Whangbo, M.-H. First-principles study of the electronic and magnetic structures of the tetragonal and orthorhombic phases of Ca3Mn2O7. Phys. Rev. B 2007, 76, 054403. [Google Scholar] [CrossRef]
- Juza, R.; Friedrichsen, H. Die Kristallstruktur von β-ZrNCl und β-ZrNBr. Z. Anorg. Allg. Chem. 1964, 332, 173–178. [Google Scholar]
- Ehrlich, G.M.; Badding, M.E.; Brese, N.E.; Trail, S.S.; DiSalvo, F.J. New cerium nitride chlorides: Ce6Cl12N2 and CeNCl. J. Alloys Compd. 1994, 206, 95–101. [Google Scholar] [CrossRef]
- Lissner, F.; Hack, B.; Lerch, M.; Schleid, T. Zr2N2Se: The First Zirconium(IV) Nitride Selenide by the Oxi- dation of Zirconium(III) Nitride with Selenium. Z. Anorg. Allg. Chem. 2012, 638, 1407–1410. [Google Scholar] [CrossRef]
- Yongkwan, D.; DiSalvo, F.J. Ce2SeN2: Ternary selenide nitride containing tetravalent Ce in the Ce2SO2 structure type. Solid State Sci. 2011, 13, 19–22. [Google Scholar]
- Boldyrev, V.V. Topochemistry and topochemical reactions. React. Solids 1990, 8, 231–246. [Google Scholar] [CrossRef]
- Stoltz, C.; Ramesha, K.; Sirchio, S.A.; Gönen, Z.S.; Eichhorn, B.W.; Salamanca-Riba, L.; Gopalakrishnan, J. Topochemical Anion Metathesis Routes to the Zr2N2S Phases and the Na2S and ACl Derivatives (A: Na, K, Rb). J. Am. Chem. Soc. 2003, 125, 4285–4292. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, B864. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultra-soft pseudo-potentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Blöchl, P.E.; Jepsen, O.; Anderson, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Bader, R. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Eyert, V. Basic Notions and Applications of the Augmented Spherical Wave Method. Int. J. Quantum Chem. 2000, 77, 1007–10031. [Google Scholar] [CrossRef]
- Eyert, V. The Augmented Spherical Wave Method—A Comprehensive Treatment; Lecture Notes in Physics; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Hoffmann, R. How Chemistry and Physics Meet in the Solid State. Angew. Chem. Int. Ed. 1987, 26, 846–878. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Matar, S.F.; Chevalier, B.; Pöttgen, R. Intermediate cerium valence intermetallics Ce4RuMg, Ce23Ru7Mg4, CeRu2Mg5, and Ce2Ru4Mg17: Electronic structures and chemical bonding from DFT. Intermetallics 2012, 31, 88–93. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).