A Content-Based Image Retrieval Scheme Using an Encrypted Difference Histogram in Cloud Computing
Abstract
:1. Introduction
- (1)
- A specially designed image encryption method is proposed to support the feature extraction directly from the ciphertext domain.
- (2)
- In EDH-CBIR, users only need to complete the work of image encryption, the feature extraction and index establishment will be completed by cloud server, which will largely reduce the user’s work.
- (3)
- This paper takes the statistical characteristics of difference histogram into account, and considers two difference calculation methods. The retrieval accuracy and security in the two situations are tested and analyzed, respectively.
2. Related Work
3. System and Security Model
- System model.The proposed system includes three entities: image owner, cloud server and users. The specific tasks of the three entities and the communication between them are shown in Figure 1.Image owner side. The image owner holds an original image database , where is the ith image in image database and n is the total image number in the image database. Firstly, the image owner generates the secret keys to encrypt the original image, and the encrypted image database can be represented as . After that, the image owner outsources the encrypted image database to the cloud server.Cloud server side. After receiving the encrypted images, the cloud server extracts image features from the encrypted images and establishes the index. On receiving a search request from user, the cloud server extracts features from the trapdoor, and searches the most similar features in index. The k images with the most similar features are returned to the user.User side. To search the wanted images, the users encrypt the query image as image owner does. The encrypted query image is uploaded as the trapdoor to the cloud server. User decrypts the similar images returned by the cloud server with secret keys.
- Security model.As a typical SSE scheme, the proposed scheme mainly considers semi-honest security model, i.e., honest-but-curious (HBC) security model.In the HBC model, the cloud server will complete the specified tasks, but may take interest in the content of the encrypted image by acquiring and analyzing historical search records. The image owner and the image users are trustworthy believed, meaning that the image owner and image users will not reveal any privacy information to the cloud server during the communication. Furthermore, if image and image return the same similar image set, it is not difficult to infer that the image is similar to image . Hence, the information leakage caused by this way will not be discussed.
4. The Proposed Scheme
4.1. Image Encryption
- Difference matrix computation.Difference histogram is used as the image feature. To extract the feature directly from the encrypted image, the image owner calculates the difference matrix of plaintext image. The difference matrix calculation is divided into the following three steps:
- (1)
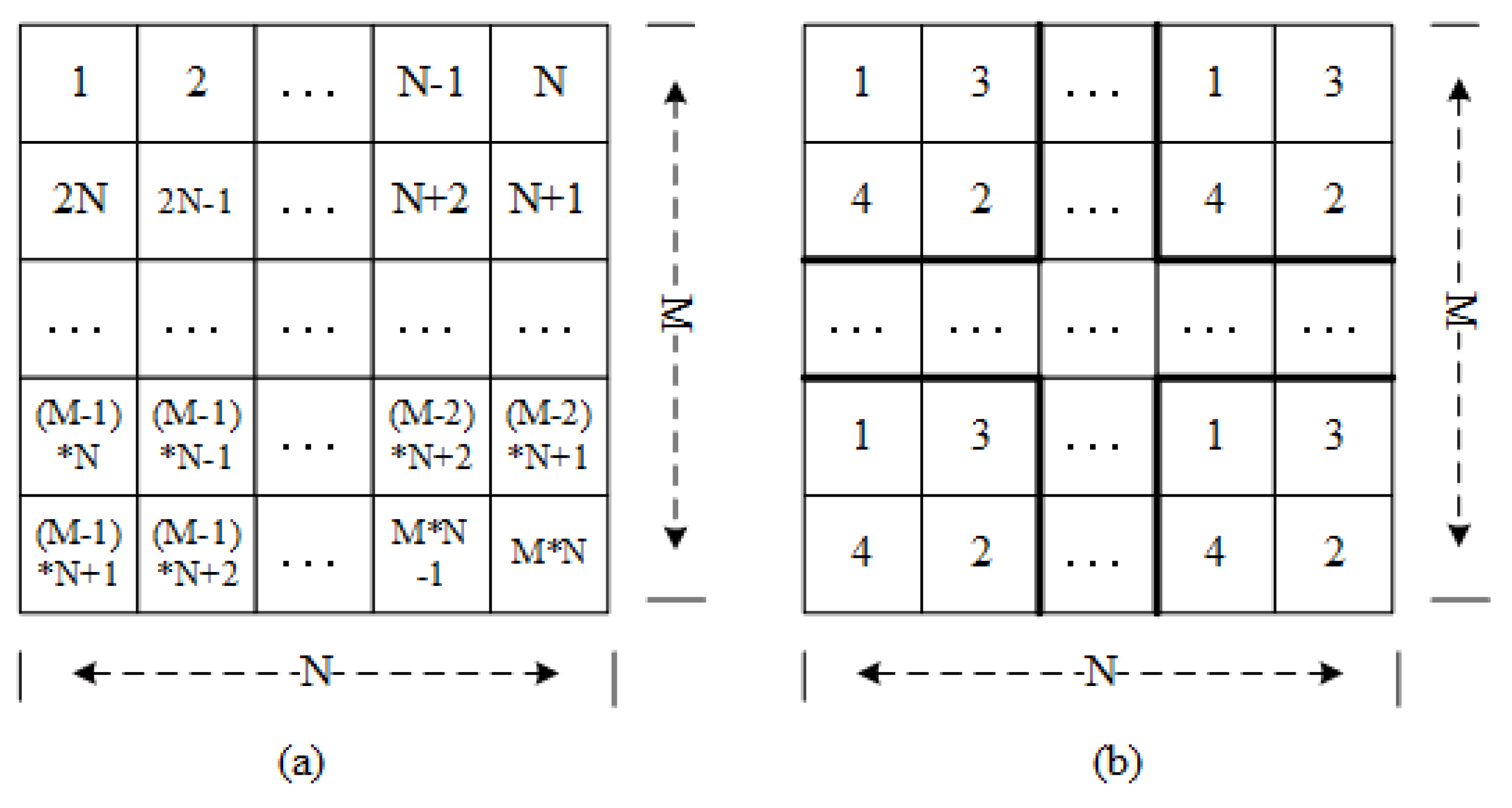
- One-dimensional matrix. Assuming that the image size in the image database is . We select the appropriate conversion method to convert the image pixel matrix into a one-dimensional array , in which the length of is and the . Here, two conversion methods are mainly considered: orderly scanning and disorderly block scanning, and the schematic diagram is shown in Figure 2.For the order scanning method, the pixel values are obtained by orderly scanning the pixel matrix. The scanned sequence is shown in Figure 2a. For the disorderly block scanning method, we firstly divide the image into blocks. Then, the pixel values is obtained by disorderly scanning the block pixel matrix. Note: we arrange image blocks by line priority here. The Figure 2b gives a disorder block scanning example with the block size of .The obtained pixels by two scanning methods are stored sequentially, so that the pixel matrix can be transformed into a one-dimensional array. According to the above scanning methods, we can obtain two kinds of arrays: order array and disorder array. The pixels in two kinds of array are represented as , and the associated pixel values in RGB components are represented as .
- (2)
- Difference value calculation. We acquire one-dimensional difference arrays by subtracting adjacent value in the . The is represented as . The formula of computation as follows:
- (3)
- Difference matrix acquisition. The difference matrix can be gained by inverse conversion of the difference array . The transformation method is the inverse operation of the initial conversion method. The difference position of difference matrix can be represented as , and the corresponding difference value can be represented .
- Difference matrix encryption.After difference matrix computation, we obtain two types of difference matrices: order difference matrix (ODM) and disorder difference matrix (DDM). The difference value in the difference matrix shows the changing trend of the pixel, and the difference position shows the roughness of difference matrix . To prevent the leakage of privacy, we encrypt the difference matrix by value replacement and position scrambling for ODM and DDM. Since the encryption methods are the same, we simply abbreviate as the differential matrix (DM) encryption.
- −
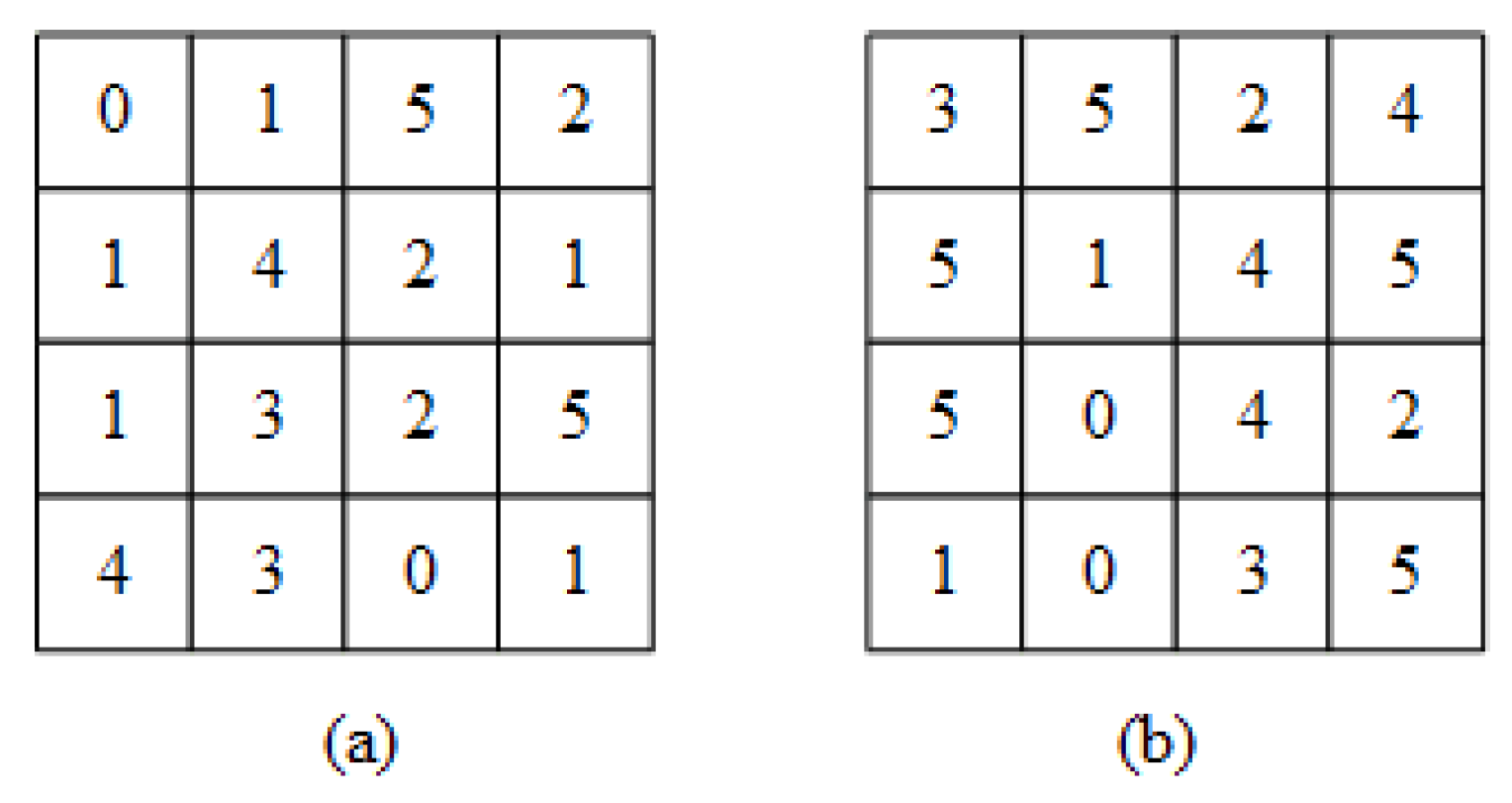
- Value replacement. The image owner firstly generates three random permutations , , of the range by a pseudo-random permutation generator, where the parameter is the minimum difference value and is the maximum difference value in the image database. After that, image owner replaces the original difference value by the value in the random sequence. Denote , , and as the three components of difference values in , and , , are the corresponding encryption results. For , do:A simple example is given to visualize the difference value replacement method. A sequence example is shown in Table 1. We give an original difference matrix in Figure 3a, and replace the original difference values with the values in the random sequence (Table 1), the results are shown in Figure 3b. Note: simple instance does not consider color space and it is just used as instantiated objects.
- ‒
- Position scrambling. is the encryption results of value replacement. The image owner generates three random permutations , , of the rang and three random permutations , , of the rang by a pseudo-random permutation generator. Denote , , as the three components of difference value position p. For , do:Give an example: we assume that a difference in the R component of the difference matrix in position , i.e., . The first value in the random sequence is assumed to be 92, and the first value in the random sequence is assumed to be 88, i.e., . According to the Formula (3), , i.e., the position of first difference position becomes . Operating on all pixel locations, we can get the encrypted image C.
4.2. Feature Extraction and Index Construction
4.3. Image Retrieval
5. Security Analysis
5.1. Security under COA Model
- Security of the encrypted image. Simulator S simulates a image set . The simulator S knows the image number and the image size of the image database, so it can simulate a hypothetical image database similar to real image database . EDH-CBIR contains the encrypted order difference histogram-based CBIR scheme (EODH-CBIR) and the encrypted disorder difference histogram-based CBIR scheme (EDDH-CBIR). The security of the two schemes is analyzed.
- ‒
- EODH-CBIR. To simulate an image in EODH-CBIR, the simulator S needs to solve a permutation to get the order difference matrix, and needs to solve permutations for value replacement, and for pixel scrambling of three components. is defined as the security strength and the of order difference as , which can be expressed as:
- ‒
- EDDH-CBIR. To simulate an image in EDDH-CBIR, the simulator S needs to solve 3* permutations to get disorder difference matrix , permutations for value replacement, and for pixels scrambling of three components. We define the security strength of disorder difference as , which can be expressed as:
- Security of the image feature. The proposed scheme extracts the difference histogram from the encrypted image directly as the image feature. Simulator S simulates an image set . The simulator S can extract simulated features of . The security strength of the image feature is mainly determined by the difference value displacement. Therefore, the security strength of order difference image features can be represented as , and the security strength of disorder difference image features can be represented as .
- Security of the trapdoor. Simulator S simulates a query image . The simulator S knows the size of the query image, so it can simulate a query image with the same pixel number as real query image . The user encrypts the query image as the image owner dose, so it has the same security strength as image encryption. Specific analysis is no longer expounded.
5.2. Security under the KBP Model
6. Experimental Results
6.1. Effectiveness of Image Encryption
6.2. Retrieval Accuracy
6.3. Efficiency
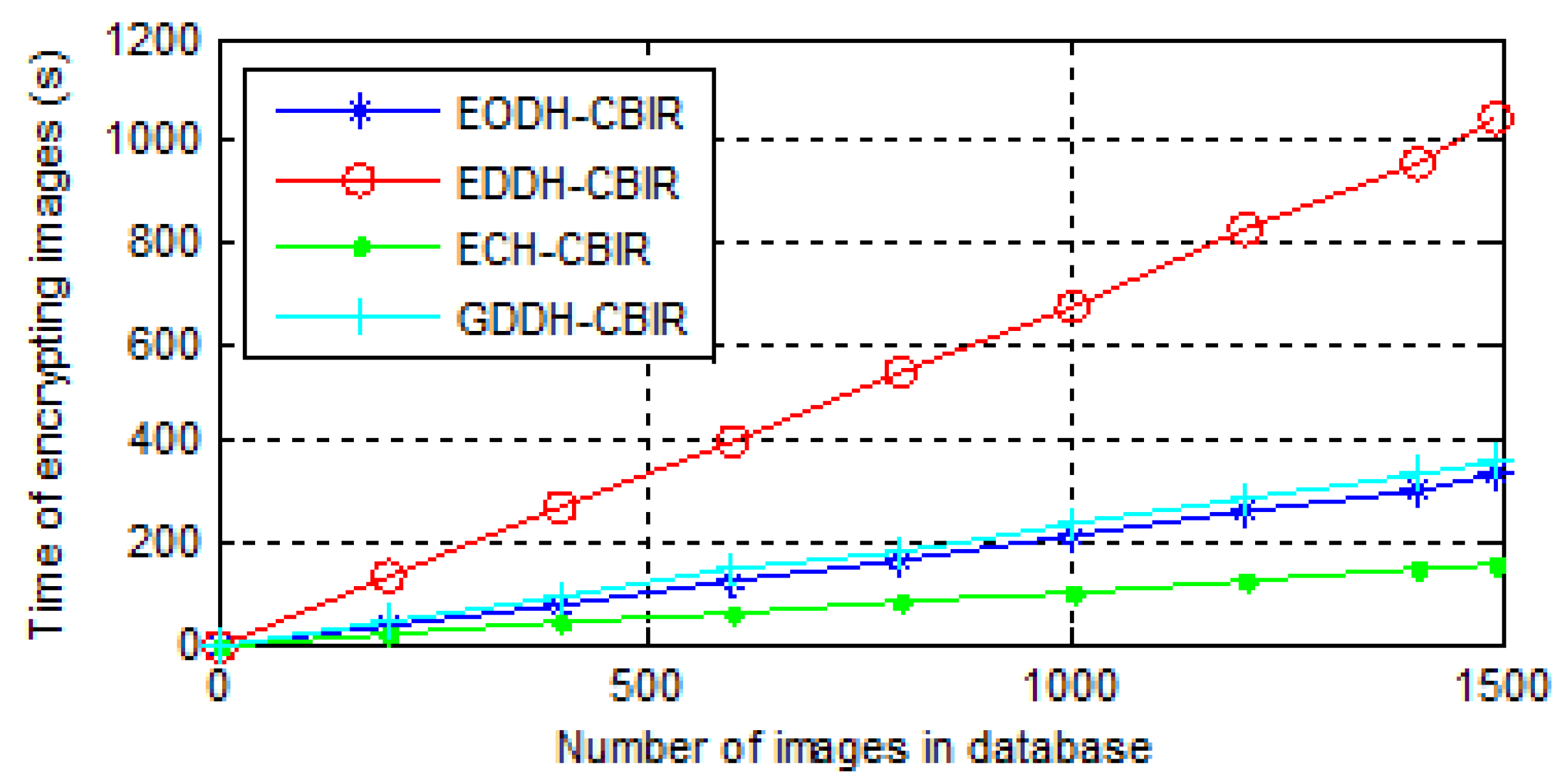
- The time consumption of image encryption. The encryption process of ECH-CBIR includes value replacement and position scrambling. The encryption processes of EODH-CBIR and GDDH-CBIR include the difference matrix calculation, difference value replacement, and pixel scrambling. EDDH-CBIR includes the block difference matrix calculation, the difference value replacement, and pixel permutation. The time consumptions of image encryptions of all above schemes are shown in Figure 10.
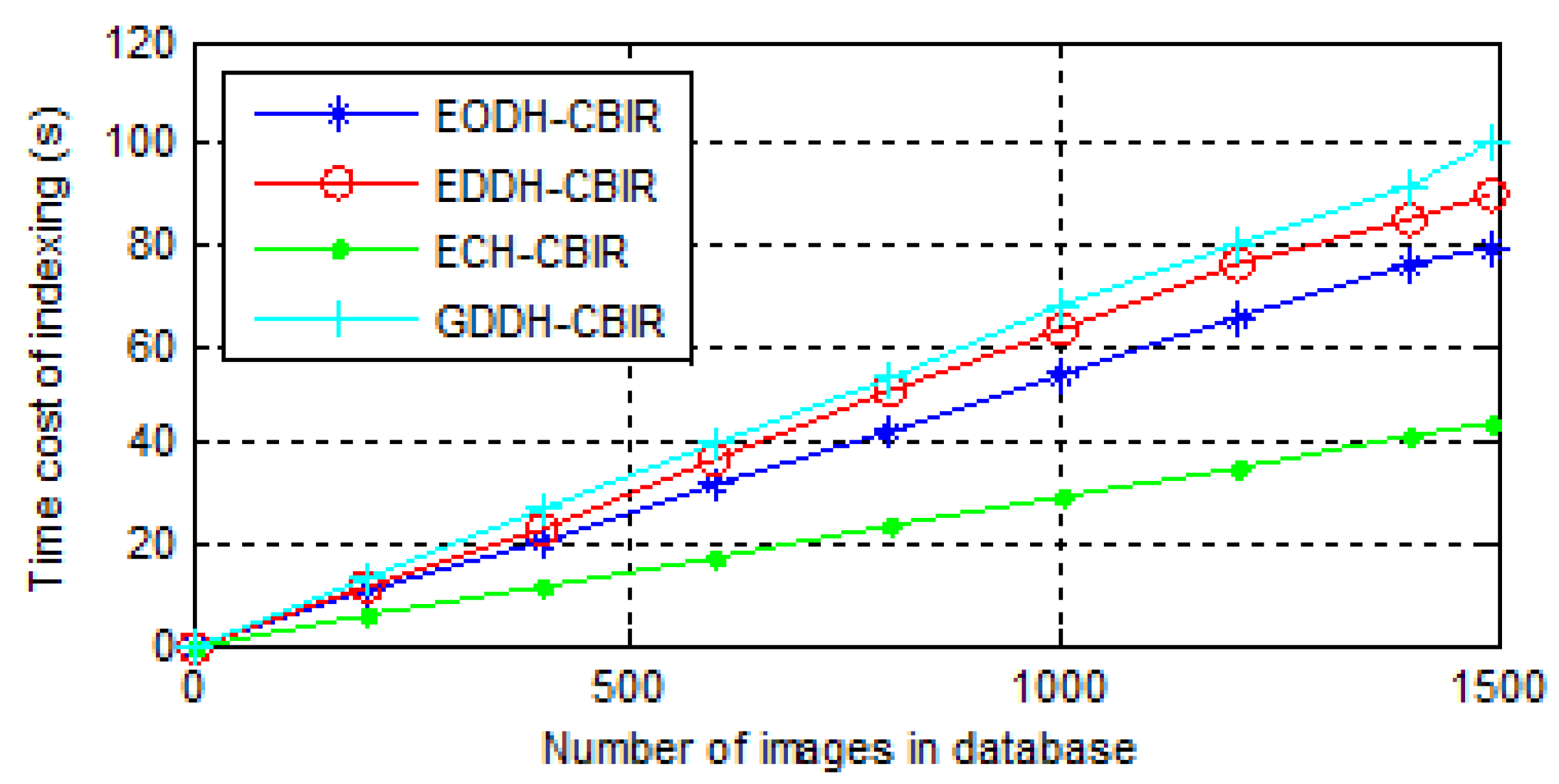
- The time consumption of index construction. A linear index is built for all the schemes so as to observe them more intuitively. Time consumption actually includes feature extraction and indexing, and results of three scheme are shown in Figure 11.
- The time consumption of image retrieval. When the cloud server receives the user’s trapdoor, it searches the index for the k most similar images. The index designed in this paper is a linear one, so the retrieval time is only related to the length of feature vectors. The time consumption of mentioned schemes are shown in Figure 12.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smeulders, A.W.M.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early. IEEE Trans. Pattern Anal. Mach. Intel. 2000, 22, 1349–1380. [Google Scholar] [CrossRef]
- Yong, R.; Huang, T.S.; Chang, S.F. Image Retrieval: Current Techniques, Promising Directions, and Open Issues. J. Vis. Commun. & Image Represent. 1999, 10, 39–62. [Google Scholar]
- Rui, Y.; Huang, T.S.; Ortega, M.; Mehrotra, S. Relevance feedback: A power tool for interactive content-based image retrieval. IEEE Trans. Circuits and Syst. Video Technol. 1998, 8, 644–655. [Google Scholar]
- Liu, Y.; Zhang, D.; Lu, G.; Ma, W.Y. A survey of content-based image retrieval with high-level semantics. Pattern Recognit. 2007, 40, 262–282. [Google Scholar] [CrossRef]
- Akgül, C.B.; Rubin, D.L.; Napel, S.; Beaulieu, C.F.; Greenspan, H.; Acar, B. Content-Based Image Retrieval in Radiology: Current Status and Future Directions. J. Digit. Imaging 2011, 24, 208–222. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Wang, X.; Sun, X.; Wang, Q. A Secure and Dynamic Multi-keyword Ranked Search Scheme over Encrypted Cloud Data. IEEE Trans. on Parallel & Distrib. Syst. 2016, 27, 340–352. [Google Scholar]
- Dong, B.; Liu, R.; Wang, W.H. PraDa: Privacy-preserving Data-Deduplication-as-a-Service. In Proceedings of the 23rd ACM International Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 1559–1568. [Google Scholar]
- Lindell, Y.; Pinkas, B. Secure Multiparty Computation for Privacy-Preserving Data Mining. J. Priv. Confid. 2013, 25, 761–766. [Google Scholar]
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable symmetric encryption: improved definitions and efficient constructions. In Proceedings of the ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 79–88. [Google Scholar]
- Kuzu, M.; Islam, M.S.; Kantarcioglu, M. Efficient Similarity Search over Encrypted Data. In Proceedings of the IEEE International Conference on Data Engineering, Arlington, VA, USA, 1–5 April 2012; pp. 1156–1167. [Google Scholar]
- Hahn, F.; Kerschbaum, F. Searchable Encryption with Secure and Efficient Updates. In Proceedings of the ACM Sigsac Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 310–320. [Google Scholar]
- Yuan, X.; Wang, X.; Wang, C.; Squicciarini, A.; Ren, K. Enabling Privacy-Preserving Image-Centric Social Discovery. In Proceedings of the IEEE International Conference on Distributed Computing Systems, Hsinchu, Taiwan, 30 June–3 July 2014; pp. 198–207. [Google Scholar]
- Weng, L.; Amsaleg, L.; Morton, A.; Marchand-Maillet, S. A Privacy-Preserving Framework for Large-Scale Content-Based Information Retrieval. IEEE Trans. Inf. Forensics & Secur. 2014, 10, 152–167. [Google Scholar]
- Lu, W.; Swaminathan, A.; Varna, A.L.; Wu, M. Enabling search over encrypted multimedia databases. In Media Forensics and Security I; SPIE: Bellingham, WA, USA, 2009; p. 725418. [Google Scholar]
- Lu, W.; Varna, A.L.; Swaminathan, A.; Wu, M. Secure image retrieval through feature protection. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1533–1536. [Google Scholar]
- Lu, W.; Varna, A.L.; Wu, M. Confidentiality-Preserving Image Search: A Comparative Study Between Homomorphic Encryption and Distance-Preserving Randomization. IEEE Access 2014, 2, 125–141. [Google Scholar]
- Xia, Z.; Zhu, Y.; Sun, X.; Qin, Z.; Ren, K. Towards Privacy-preserving Content-based Image Retrieval in Cloud Computing. IEEE Trans. Cloud Comput. 2015. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, X.; Yu, J.; Li, F. Markov Process Based Retrieval for Encrypted JPEG Images. In Proceedings of the International Conference on Availability, Reliability and Security, Toulouse, France, 24–28 August 2015; pp. 417–421. [Google Scholar]
- Xu, D.; Xie, H.; Yan, C. Triple-Bit Quantization with Asymmetric Distance for Image Content Security. Mach. Vis. Appl. 2017, 28, 1–9. [Google Scholar] [CrossRef]
- Bellafqira, R.; Coatrieux, G.; Bouslimi, D.; Quellec, G. Content-based image retrieval in homomorphic encryption domain. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 25–28 August 2015; pp. 2944–2947. [Google Scholar]
- Bellafqira, R.; Coatrieux, G.; Bouslimi, D.; Quellec, G.; Bellafqira, R.; Coatrieux, G.; Bouslimi, D.; Quellec, G.; Quellec, G.; Bellafqira, R. An end to end secure CBIR over encrypted medical database. In Proceedings of the International Conference of the IEEE Engineering in Medicine & Biology Society, Oralndo, FL, USA, 16–20 August 2016; p. 2537. [Google Scholar]
- Ferreira, B.; Rodrigues, J.; Leitao, J.; Domingos, H. Practical Privacy-Preserving Content-Based Retrieval in Cloud Image Repositories. IEEE Trans. Cloud Comput. 2017, PP, 1. [Google Scholar]
- Canetti, R. Universally composable security: a new paradigm for cryptographic protocols. In Proceedings of the IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 8–11 October 2001; p. 136. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Hamming Embedding and Weak Geometric Consistency for Large Scale Image Search. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 304–317. [Google Scholar]







| Original difference value | valmin | … | 0 | 1 | 2 | 3 | 4 | 5 | … | valmax |
| Random sequence | valmax | … | 3 | 5 | 4 | 0 | 1 | 2 | … | valmin |
| Image Identity | Feature Vector |
|---|---|
| ... | ... |
| ... | ... |
| Block size | 50×50 | 100×100 | 200×200 | 500×500 |
| mAP (%) | 50.761 | 51.436 | 49.075 | 48.013 |
| Schemes | EODH-CBIR | EDDH-CBIR | ECH-CBIR | GDDH-CBIR | ODH-CBIR | DDH-CBIR |
|---|---|---|---|---|---|---|
| mAP (%) | 49.923 | 51.436 | 47.865 | 45.787 | 49.923 | 51.436 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Shen, J.; Xia, Z.; Sun, X. A Content-Based Image Retrieval Scheme Using an Encrypted Difference Histogram in Cloud Computing. Information 2017, 8, 96. https://doi.org/10.3390/info8030096
Liu D, Shen J, Xia Z, Sun X. A Content-Based Image Retrieval Scheme Using an Encrypted Difference Histogram in Cloud Computing. Information. 2017; 8(3):96. https://doi.org/10.3390/info8030096
Chicago/Turabian StyleLiu, Dandan, Jian Shen, Zhihua Xia, and Xingming Sun. 2017. "A Content-Based Image Retrieval Scheme Using an Encrypted Difference Histogram in Cloud Computing" Information 8, no. 3: 96. https://doi.org/10.3390/info8030096





