Stabilization of Discrete-Time Markovian Jump Systems by a Partially Mode-Unmatched Fault-Tolerant Controller
Abstract
:1. Introduction
2. Problem Formulation
3. Main Results
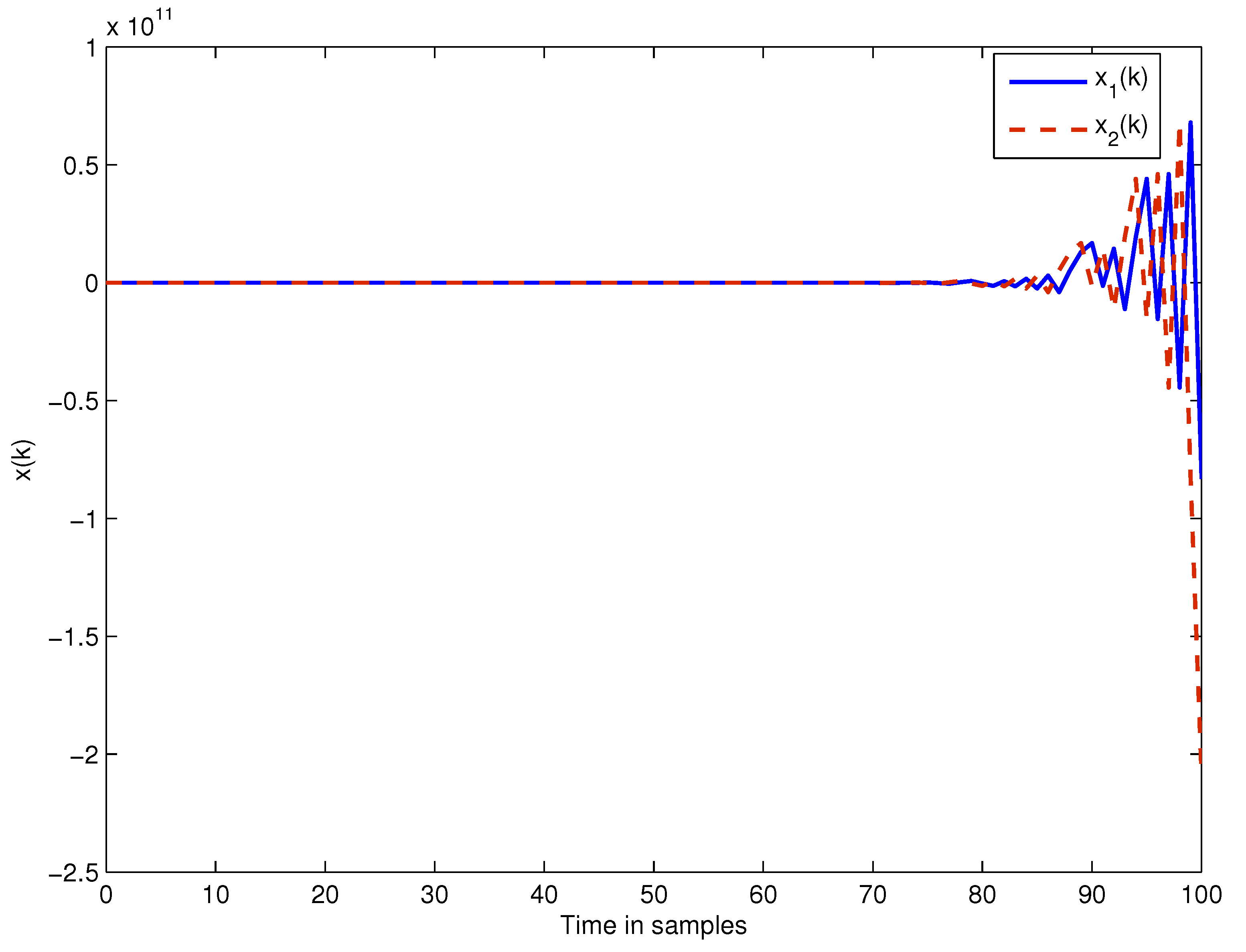
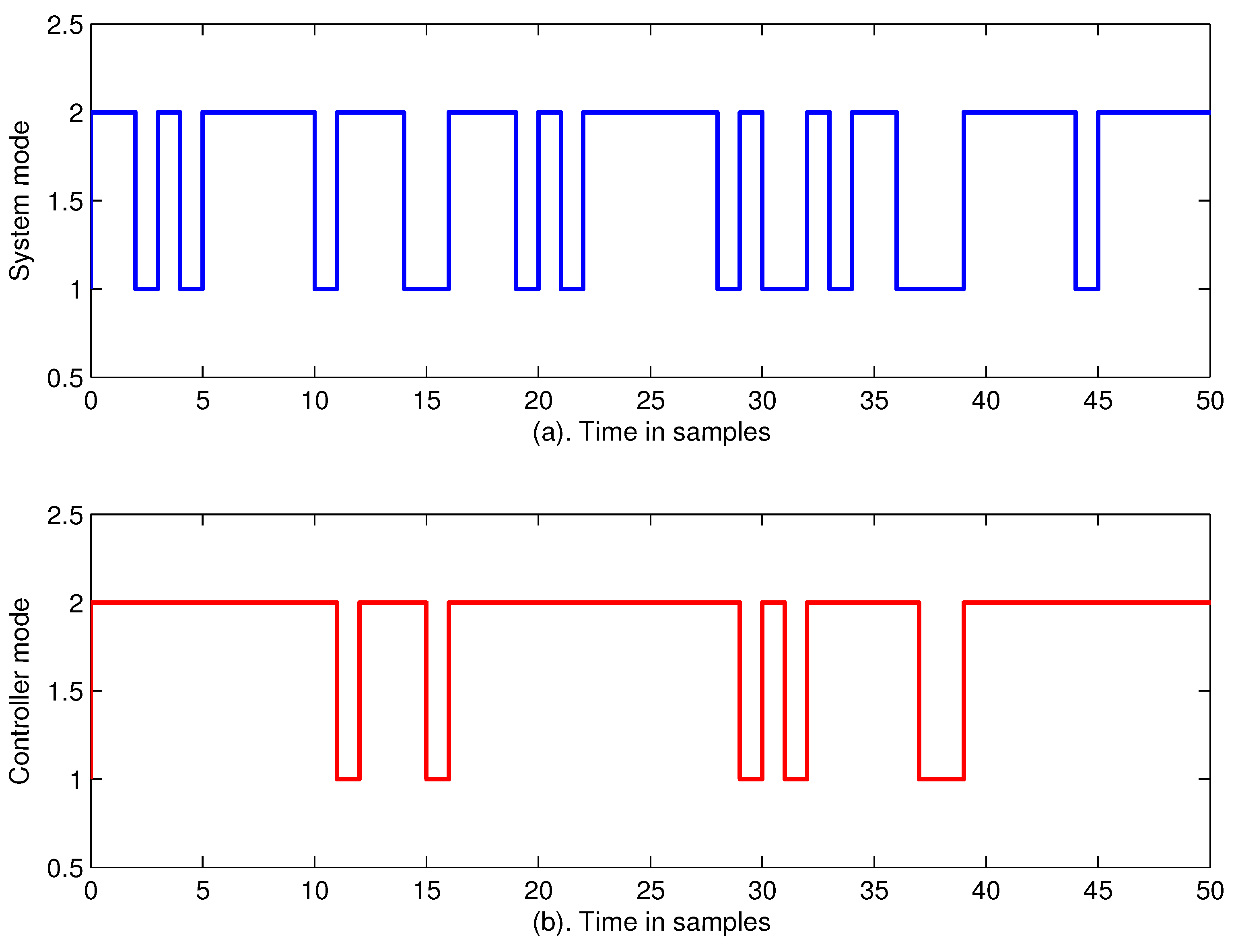
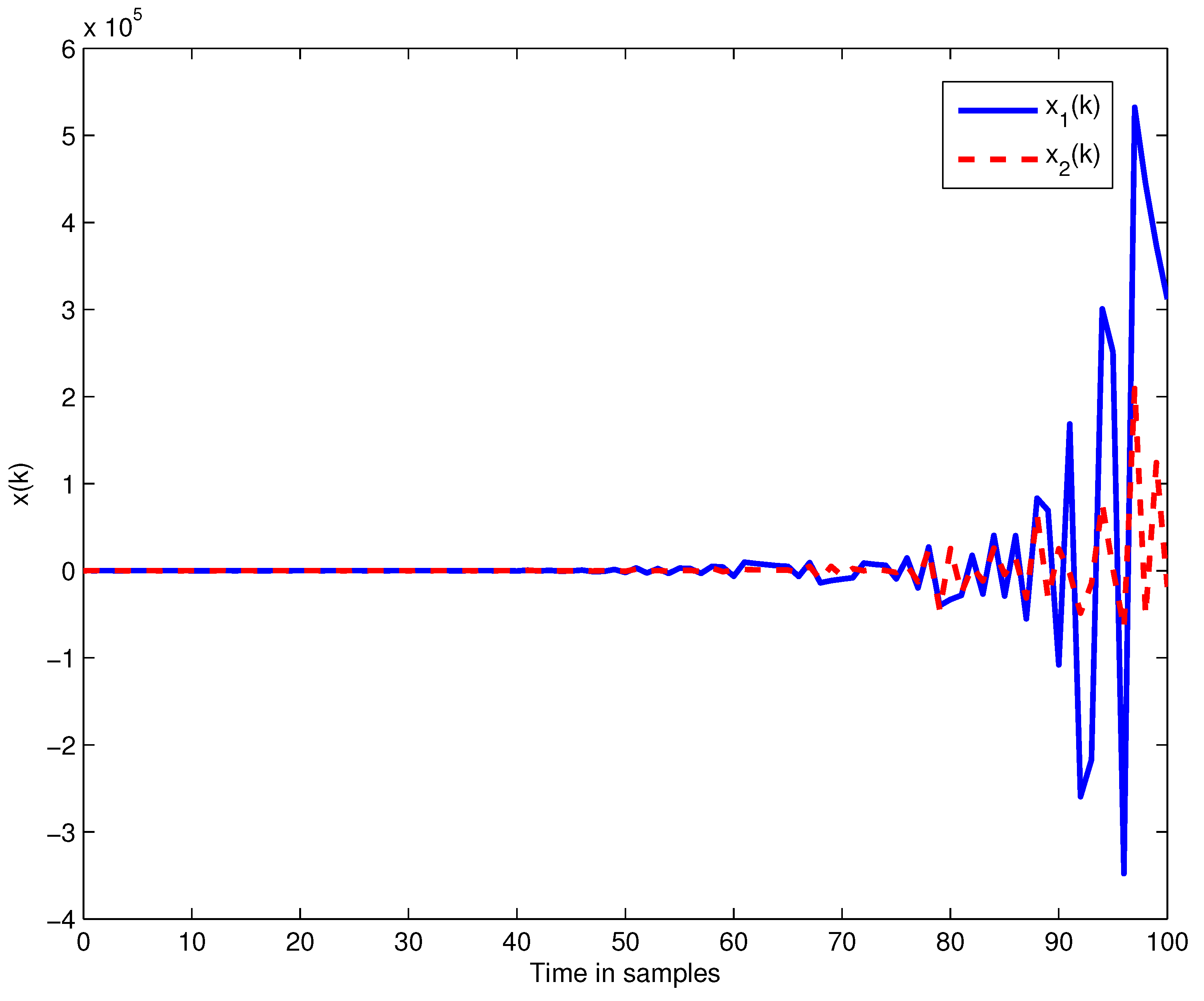
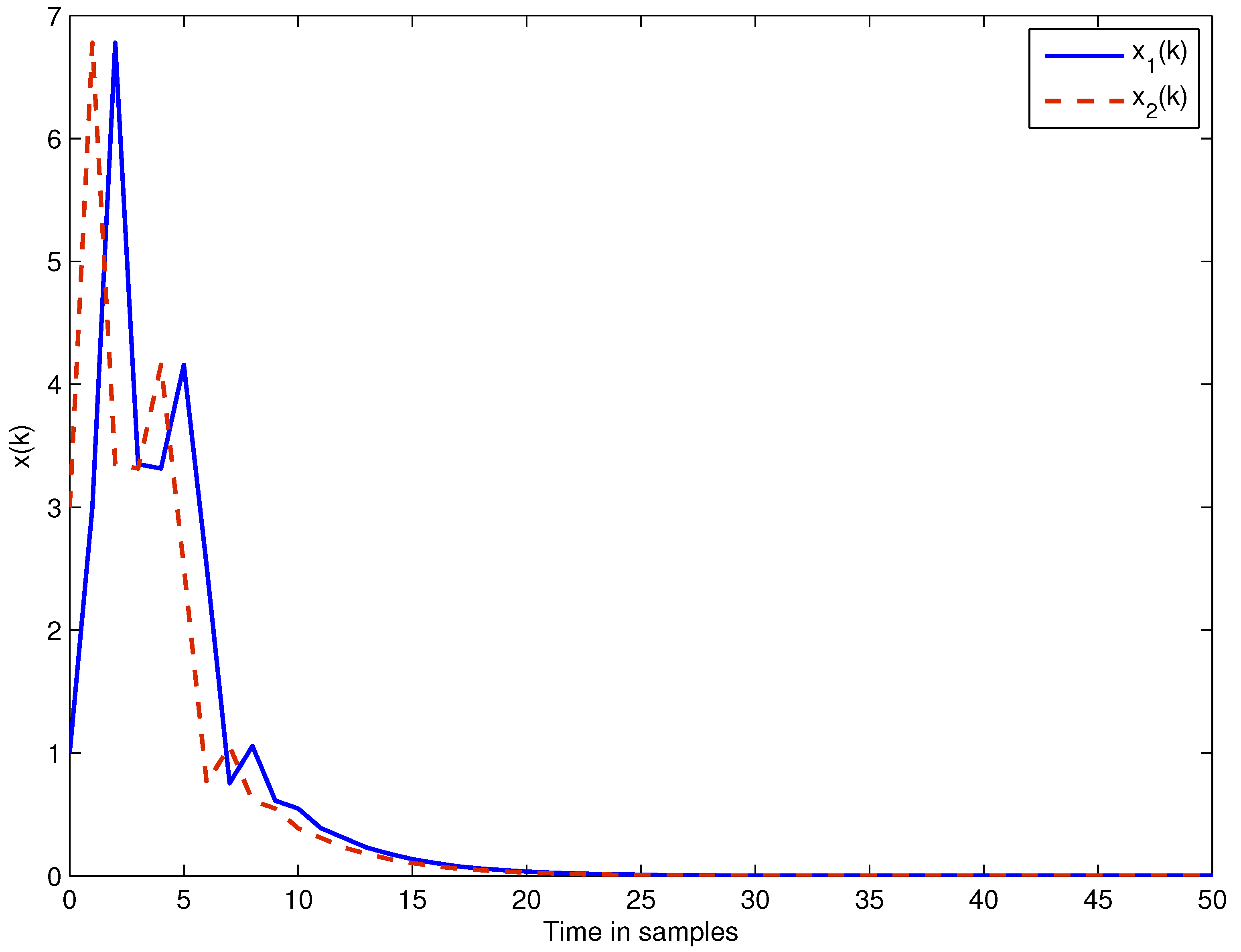
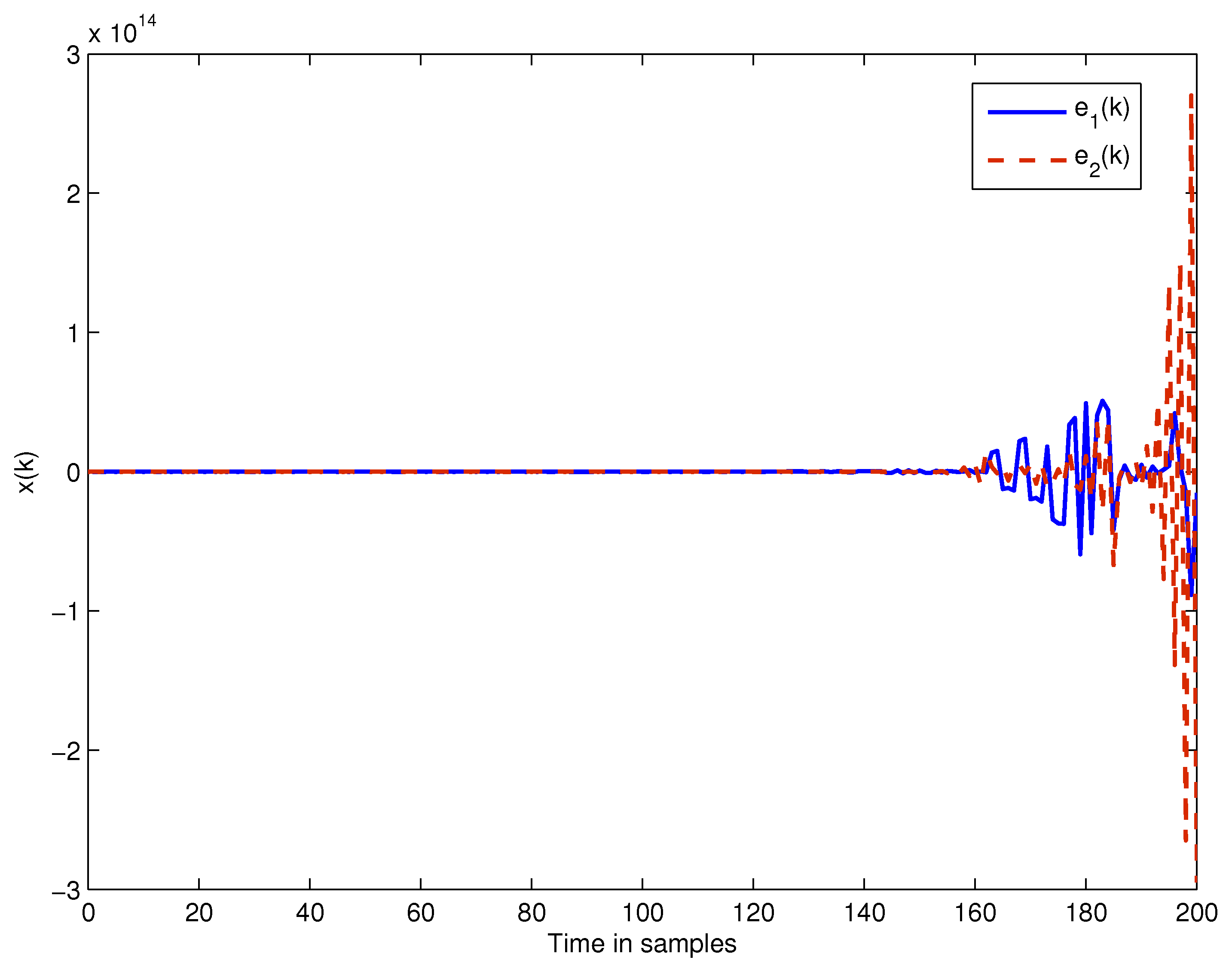
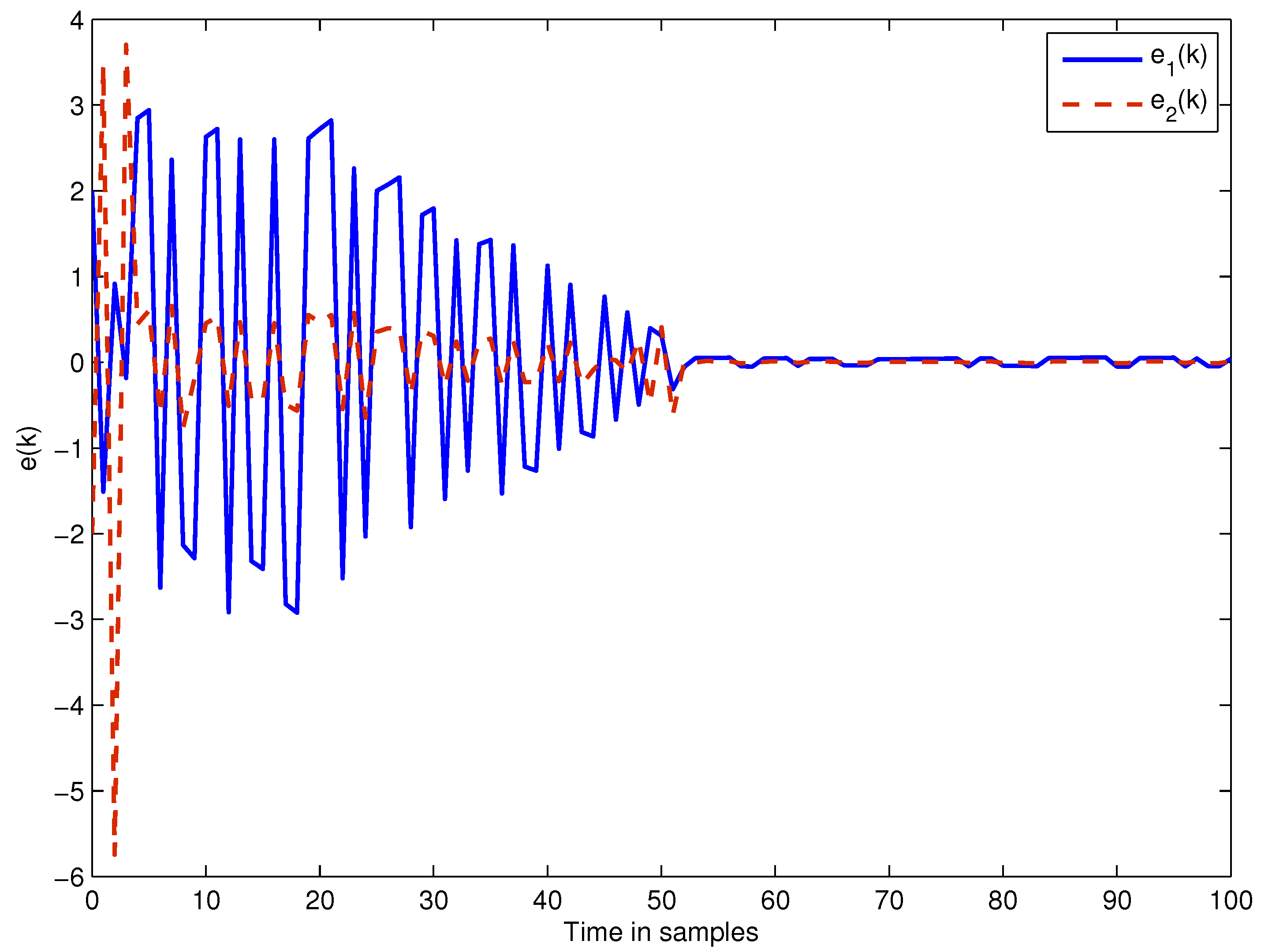
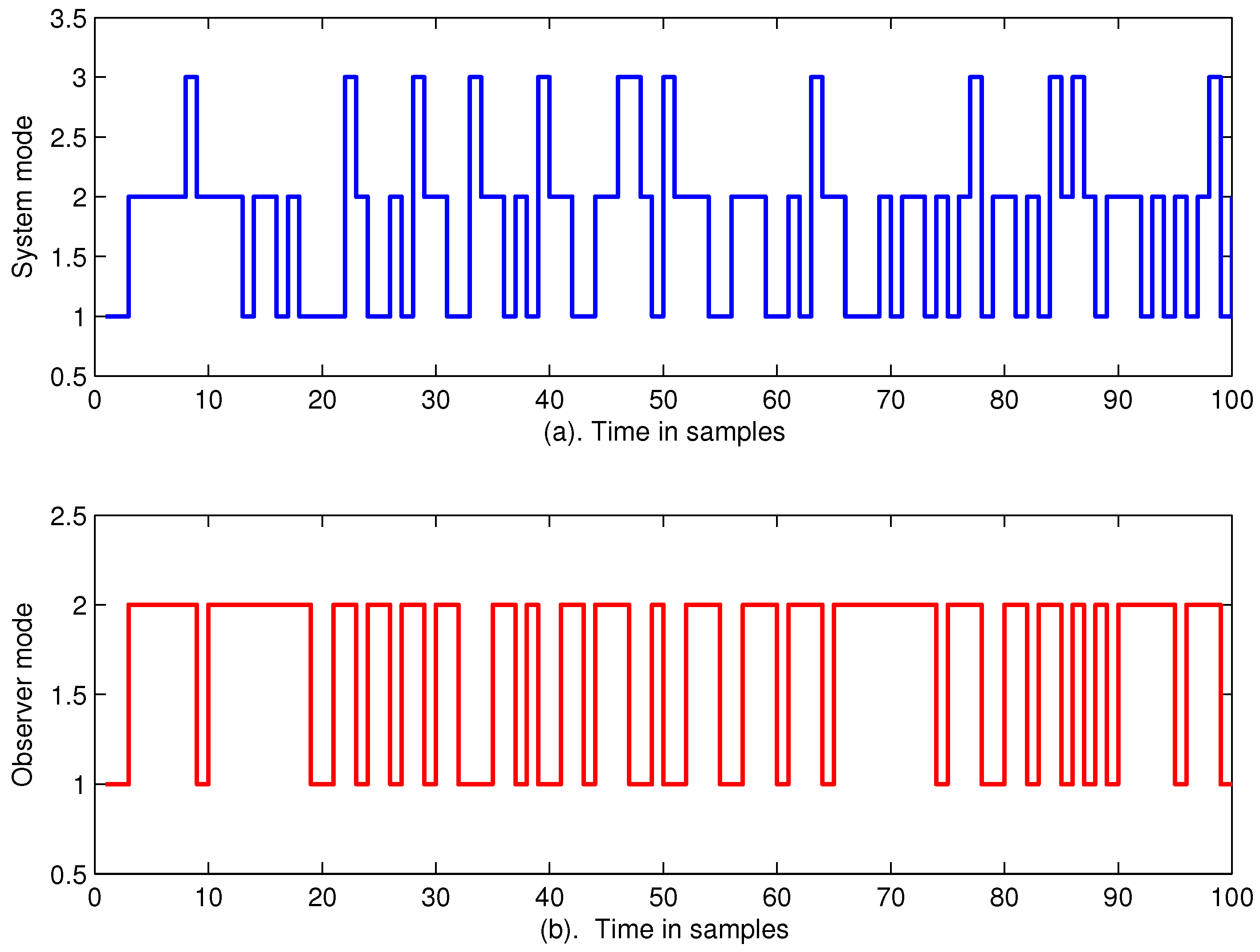
4. Numerical Examples
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiong, J.L.; Lam, J.; Shu, Z.; Mao, X.R. Stability analysis of continuous-time switched systems with a random switching signal. IEEE Trans. Autom. Control 2014, 59, 180–186. [Google Scholar] [CrossRef] [Green Version]
- Lakshmanan, S.; Rihan, F.A.; Rakkiyappan, R. Stability analysis of the differential genetic regulatory networks model with time-varying delays and Markovian jumping parameters. Nonlinear Anal. 2014, 14, 1–15. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Lakshmanan, S.; Sivasamy, R. Leakage-delay-dependent stability analysis of Markovian jumping linear systems with time-varying delays and nonlinear perturbations. Appl. Math. Model. 2016, 40, 5026–5043. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H. Stability analysis of continuous-time Markovian jump time-delay systems with time-varying transition rates. J. Frankl. Inst. 2016, 353, 2418–2430. [Google Scholar] [CrossRef]
- Li, Z.C.; Fei, Z.Y.; Jung, H.Y. New results on stability analysis and stabilization of time-delay continuous Markovian jump systems with partially known rates matrix. Int. J. Robust Nonlinear Control 2016, 26, 1873–1887. [Google Scholar] [CrossRef]
- Wei, Y.L.; Park, J.H.; Karimi, H.R.; Tian, Y.C.; Jung, H.Y. Improved stability and stabilization results for stochastic synchronization of continuous-time semi-Markovian jump neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2017, PP. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.P.; Boukas, E.K.; Chinniah, Y. Stability and stabilization of discrete-time singular Markov jump systems with time-varying delay. Int. J. Robust Nonlinear Control 2010, 20, 531–543. [Google Scholar] [CrossRef]
- Wang, G.L. Robust stabilization of singular Markovian jump systems with uncertain switching. Int. J. Control Autom. Syst. 2013, 11, 188–193. [Google Scholar] [CrossRef]
- Bo, H.Y.; Wang, G.L. General observer-based controller design for singular markovian jump systems. Int. J. Innov. Comput. Inf. Control 2014, 10, 1897–1913. [Google Scholar]
- Qiu, Q.; Liu, W.; Hu, L. Stabilization of stochastic differential equations with Markovian switching by feedback control based on discrete-time state observation with a time delay. Stat. Probab. Lett. 2016, 115, 16–26. [Google Scholar] [CrossRef]
- Liu, X.H.; Xi, H.S. On exponential stability of neutral delay Markovian jump systems with nonlinear perturbations and partially unknown transition rates. Int. J. Control Autom. Syst. 2014, 12, 1–11. [Google Scholar] [CrossRef]
- Chen, W.M.; Xu, S.Y.; Zhang, B.Y.; Qi, Z.D. Stability and stabilisation of neutral stochastic delay Markovian jump systems. IET Control Theory Appl. 2016, 10, 1798–1807. [Google Scholar] [CrossRef]
- Feng, Z.G.; Zheng, W.X. On reachable set estimation of delay Markovian jump systems with partially known transition probabilities. J. Frankl. Inst. 2016, 353, 3835–3856. [Google Scholar] [CrossRef]
- Shen, M.Q.; Yan, S.; Zhang, G.M.; Park, J.H. Finite-time H∞ static output control of Markov jump systems with an auxiliary approach. Appl. Math. Comput. 2016, 273, 553–561. [Google Scholar]
- Chen, J.; Lin, C.; Chen, B.; Wang, Q.G. Output feedback control for singular Markovian jump systems with uncertain transition rates. IET Control Theory Appl. 2016, 10, 2142–2147. [Google Scholar] [CrossRef]
- Chen, W.H.; Guan, Z.H.; Yu, P. Delay-dependent stability and H∞ control of uncertain discrete-time Markovian jump systems with mode-dependent time delays. Syst. Control Lett. 2004, 52, 361–376. [Google Scholar] [CrossRef]
- Qiu, J.; Wei, Y.; Karimi, H.R. New approach to delay-dependent H∞ control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions. J. Frankl. Inst. 2015, 352, 189–215. [Google Scholar] [CrossRef]
- Kwon, N.K.; Park, L.S.; Park, P.G. H∞ control for singular Markovian jump systems with incomplete knowledge of transition probabilities. Appl. Math. Comput. 2017, 295, 126–135. [Google Scholar]
- Zhai, D.; Lu, A.Y.; Liu, M.; Zhang, Q.L. H∞ control for Markovian jump systems with partially unknown transition rates via an adaptive method. J. Math. Anal. Appl. 2017, 446, 886–907. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, J.; Karimi, H.R. A new design of H∞ filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 2013, 93, 2392–2407. [Google Scholar] [CrossRef]
- Luan, X.L.; Zhao, S.Y.; Shi, P.; Liu, F. H∞ filtering for discrete-time Markov jump systems with unknown transition probabilities. Int. J. Adapt. Control Signal Process. 2014, 28, 138–148. [Google Scholar] [CrossRef]
- Sakthivel, R.; Sathishkumar, M.; Mathiyalagan, K.; Anthoni, S.M. Robust reliable dissipative filtering for Markovian jump nonlinear systems with uncertainties. Int. J. Adapt. Control Signal Process. 2016, 31, 39–53. [Google Scholar] [CrossRef]
- Zhou, W.N.; Lu, H.Q.; Duan, C.M.; Li, M.H. Delay-dependent robust control for singular discrete-time Markovian jump systems with time-varying delay. Int. J. Robust Nonlinear Control 2010, 20, 1112–1128. [Google Scholar] [CrossRef]
- Yang, H.J.; Li, H.B.; Sun, F.C.; Yuan, Y. Robust control for Markovian jump delta operator systems with actuator saturation. Eur. J. Control 2014, 20, 207–215. [Google Scholar] [CrossRef]
- Benbrahim, M.; Kabbaj, M.N.; Benjelloun, K. Robust control under constraints of linear systems with Markovian jumps. Int. J. Control Autom. Syst. 2016, 14, 1447–1454. [Google Scholar] [CrossRef]
- Kao, Y.G.; Xie, J.; Zhang, L.; Jung, H.Y. A sliding mode approach to robust stabilization of Markovian jump linear time-delay systems with generally incomplete transition rates. Nonlinear Anal. Hybrid Syst. 2015, 17, 70–80. [Google Scholar] [CrossRef]
- Hou, N.; Dong, H.L.; Wang, Z.D.; Ren, W.J.; Alsaadi, F.E. Non-fragile state estimation for discrete Markovian jumping neural networks. Neurocomputing 2016, 179, 238–245. [Google Scholar] [CrossRef]
- Zhang, L.; Boukas, E.K.; Baron, L.; Karimi, H.R. Fault detection for discrete-time Markov jump linear systems with partially known transition probabilities. Int. J. Control 2010, 83, 1564–1572. [Google Scholar] [CrossRef]
- Wu, Z.G.; Shi, P.; Su, H.; Chu, J. Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled data. IEEE Trans. Cybern. 2013, 43, 1796–1806. [Google Scholar] [CrossRef] [PubMed]
- Dai, A.N.; Zhou, W.N.; Xu, Y.H.; Xiao, C.E. Adaptive exponential synchronization in mean square for Markovian jumping neutral-type coupled neural networks with time-varying delays by pinning control. Neurocomputing 2016, 173, 809–818. [Google Scholar] [CrossRef]
- Chen, L.H.; Huang, X.L.; Fu, S.S. Fault-tolerant control for Markovian jump delay systems with an adaptive observer approach. Circuits Syst. Signal Process. 2016, 35, 4290–4306. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.Z.; Cheng, M.; Li, S.H. Fault-tolerant control of dual three-phase permanent-magnet synchronous machine drives under open-phase faults. IEEE Trans. Power Electron. 2017, 32, 2052–2063. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, B.; Chowdhury, F.N.; Shi, S. Active fault-tolerant control for near space vehicles based on reference model adaptive sliding mode scheme. Int. J. Adapt. Control Signal Process. 2014, 27, 765–777. [Google Scholar] [CrossRef]
- Huang, J.; Shi, Y.; Zhang, X. Active fault tolerant control systems by the semi-Markov model approach. Int. J. Adapt. Control Signal Process. 2014, 29, 833–847. [Google Scholar] [CrossRef]
- Zhou, Q.; Yao, D.Y.; Yao, J.H.; Wu, C.G. Robust control of uncertain semi-Markovian jump systems using sliding mode control method. Appl. Math. Comput. 2016, 286, 72–87. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Palm, R. Robust control by adaptive non-singular terminal sliding mode. Eng. Appl. Artif. Intell. 2017, 59, 205–217. [Google Scholar]
- Rathinasamy, S.; Karimi, H.R.; Joby, M.; Santra, S. Resilient sampled-data control for Markovian jump systems with adaptive fault-tolerant mechanism. IEEE Circuits Syst. Soc. 2017, PP. [Google Scholar] [CrossRef]
- Zhang, X.D.; Parisini, T.; Polycarpou, M.M. Adaptive fault-tolerant control of nonlinear uncertain systems: An information-based diagnostic approach. IEEE Trans. Autom. Control 2004, 49, 1259–1274. [Google Scholar] [CrossRef]
- Shi, F.M.; Patton, R.J. Fault estimation and active fault tolerant control for linear parameter varying descriptor systems. Int. J. Robust Nonlinear Control 2015, 25, 689–706. [Google Scholar] [CrossRef]
- Liu, M.; Cao, X.; Shi, P. Fault estimation and tolerant control for fuzzy stochastic systems. IEEE Trans. Fuzzy Syst. 2013, 21, 221–229. [Google Scholar] [CrossRef]
- Li, H.Y.; Gao, H.J.; Shi, P.; Zhao, X.D. Fault-tolerant control of Markovian jump stochastic systems via the augmented sliding mode observer approach. Automatica 2014, 50, 1825–1834. [Google Scholar] [CrossRef]
- Chen, L.H.; Huang, X.L.; Fu, S.S. Observer-based sensor fault-tolerant control for semi-Markovian jump systems. Nonlinear Anal. Hybrid Syst. 2016, 22, 161–177. [Google Scholar] [CrossRef]
- Zhang, L.X.; Boukas, E.K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 2009, 45, 463–468. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Boukas, E.K.; Shi, P.; Zhang, J.H. Stability and stabilization of continuous-time singular hybrid systems. Automatica 2009, 45, 1504–1509. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Wu, M.; Zhang, J. Stabilization for Markovian jump systems with partial information on transition probability based on free-coonection weighting matrices. Automatica 2011, 47, 79–84. [Google Scholar] [CrossRef]
- Wang, G.L.; Zhang, Q.L.; Yang, C.Y.; Su, C.L. Stability and stabilization of continuous-time stochastic Markovian jump systems with random switching signals. J. Frankl. Inst. 2016, 353, 1339–1357. [Google Scholar] [CrossRef]
- Wang, G.L. Mode-independent control of singular Markovian jump systems: A stochastic optimization viewpoint. Appl. Math. Comput. 2016, 286, 527–538. [Google Scholar] [CrossRef]
- Wang, G.L.; Xu, S.Y.; Zou, Y. Stabilisation of hybrid stochastic systems by disordered controllers. IET Control Theory Appl. 2014, 8, 1154–1162. [Google Scholar] [CrossRef]
- Wang, G.L. H∞ control of singular Markovian jump systems with operation modes disordering in controllers. Neurocomputing 2014, 142, 275–281. [Google Scholar] [CrossRef]
- Sevilla, F.R.S.; Jaimoukha, I.M.; Chaudhuri, B.; Korba, P. A semidefinite relaxation procedure for fault-tolerant observer design. IEEE Trans. Autom. Control 2015, 60, 3332–3337. [Google Scholar] [CrossRef]
- Samuelson, D.D. The Review of Economic Statistics; Harvard University Press: Cambirdge, UK, 1939. [Google Scholar]
- Ackley, G. Macroeconomic Theory; Macmillan: New York, NY, USA, 1969. [Google Scholar]
- Blair, W.P., Jr.; Sworder, D.D. Feedback control of a class of linear discrete systems with jump parameters and quadratic cost criteria. Int. J. Control 2015, 21, 833–841. [Google Scholar] [CrossRef]
| Mode i | Terminology | Description | ||
|---|---|---|---|---|
| 1 | Norm | (or ) in mid-range | 1 | 0.3 |
| 2 | Slump | in high range (or in low) | −0.8 | 0.9 |
| Fault 1 | Fault 2 | Fault 3 | Fault 4 | |
|---|---|---|---|---|
| (0, 0) | (0, 1) | (1, 0) | (1, 1) | |
| s | s | u | s | |
| s | s | s | s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, G. Stabilization of Discrete-Time Markovian Jump Systems by a Partially Mode-Unmatched Fault-Tolerant Controller. Information 2017, 8, 90. https://doi.org/10.3390/info8030090
Liu M, Wang G. Stabilization of Discrete-Time Markovian Jump Systems by a Partially Mode-Unmatched Fault-Tolerant Controller. Information. 2017; 8(3):90. https://doi.org/10.3390/info8030090
Chicago/Turabian StyleLiu, Mo, and Guoliang Wang. 2017. "Stabilization of Discrete-Time Markovian Jump Systems by a Partially Mode-Unmatched Fault-Tolerant Controller" Information 8, no. 3: 90. https://doi.org/10.3390/info8030090




