Fuzzy Color Clustering for Melanoma Diagnosis in Dermoscopy Images
Abstract
:1. Introduction
2. Methodology
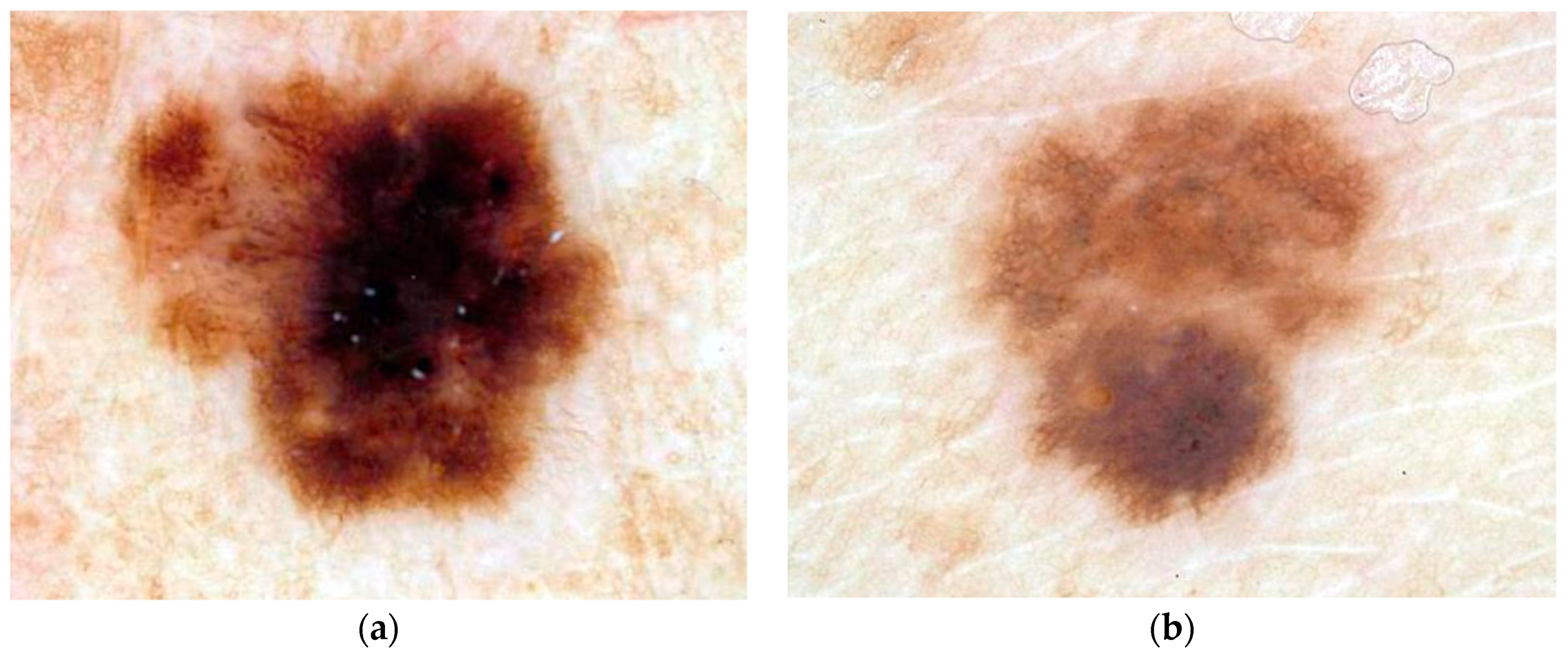
2.1. Dermoscopy Image Data
2.2. Diagnostic Assessment
2.3. Skin Lesion Border Determination
2.4. Relative Color
2.5. Surrounding Skin Color Determination
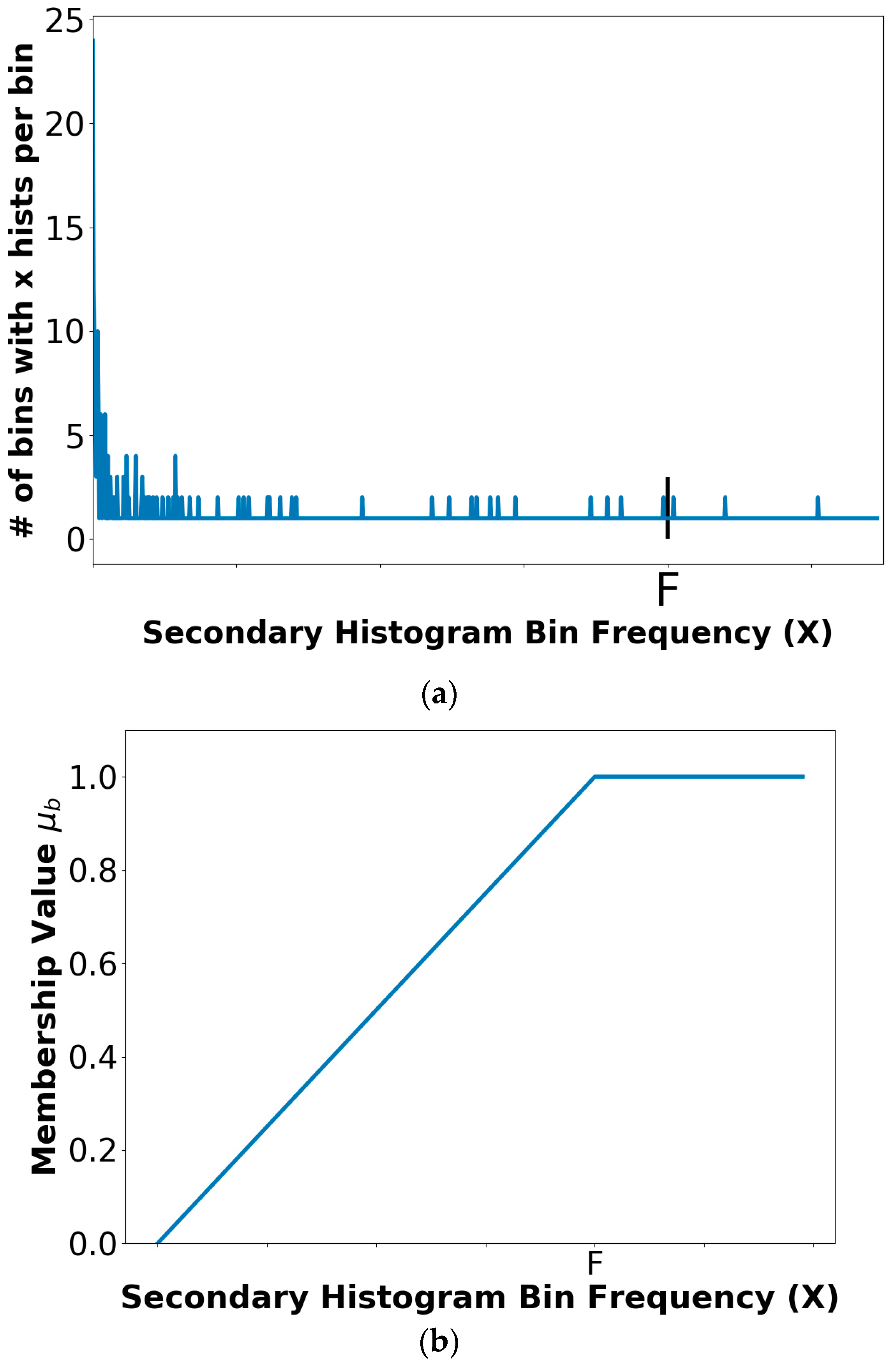
2.6. Color Histogram Bin Determination
2.7. Color Histogram Analysis Technique
2.7.1. Fuzzy Set Description for Trapezoidal Membership Function
2.7.2. Color Feature Determination
2.7.3. Threshold Determination Procedure
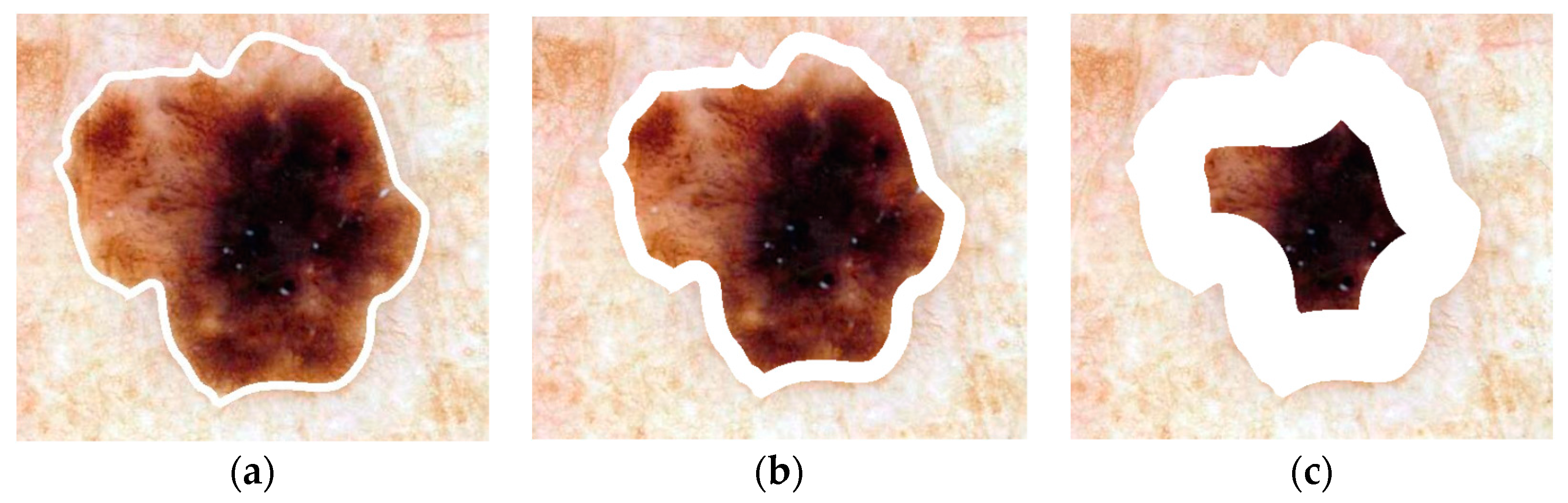
2.8. Lesion Region Analysis
- (1)
- start with the lesion border
- (2)
- compute the distance transform using 8-connected distance to get pixel distance from the lesion boundary inside of the skin lesion
- (3)
- starting with a distance of 0 (lesion boundary), determine the lesion boundary region with distance less than or equal to the current distance
- (4)
- compute the area of the resulting lesion boundary region
- (5)
- retain the lesion boundary region if its area is greater than the boundary area percentage
- (6)
- otherwise, increment the distance by 1 and repeat Steps (2)–(6)
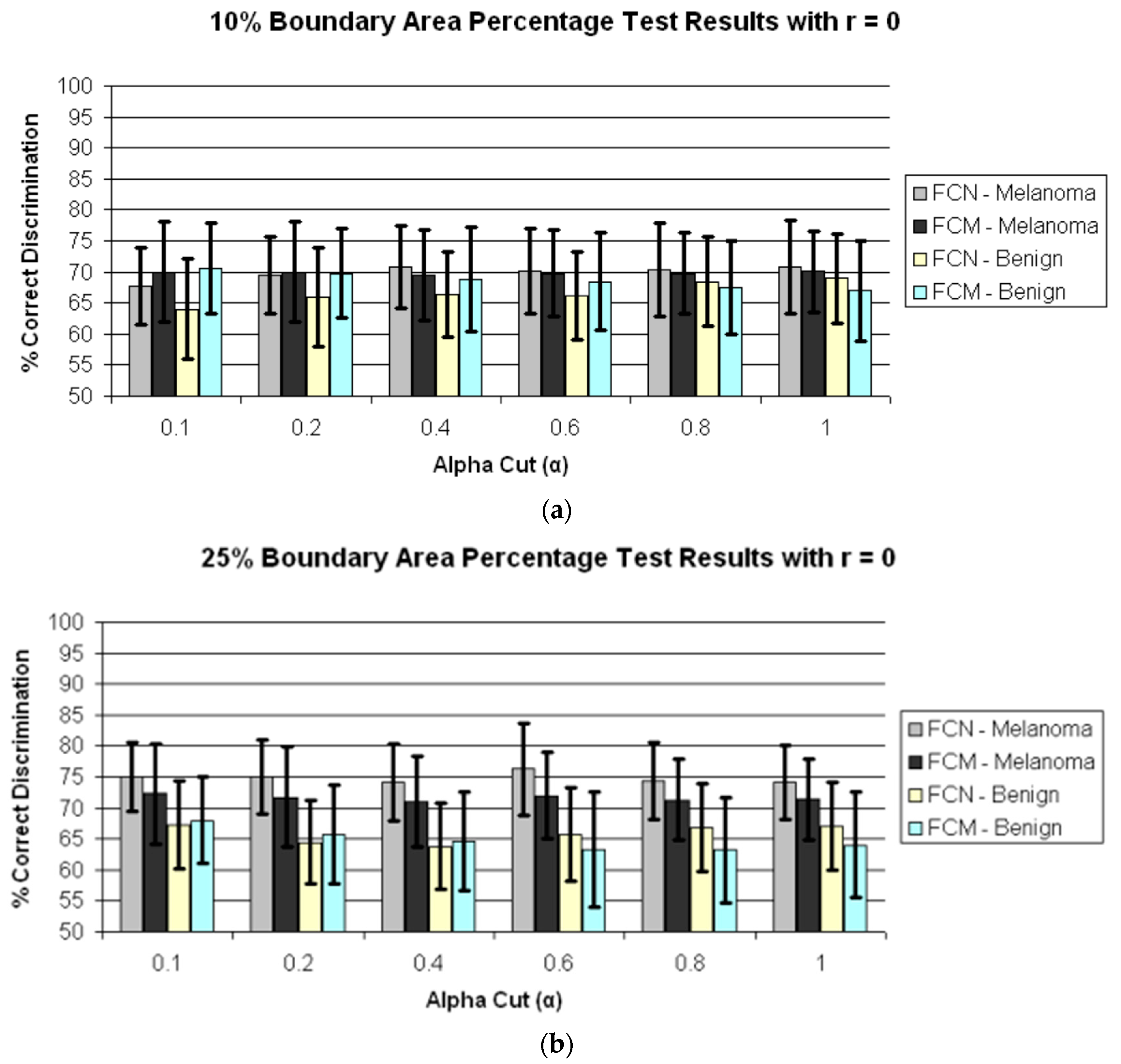
3. Experiments Performed
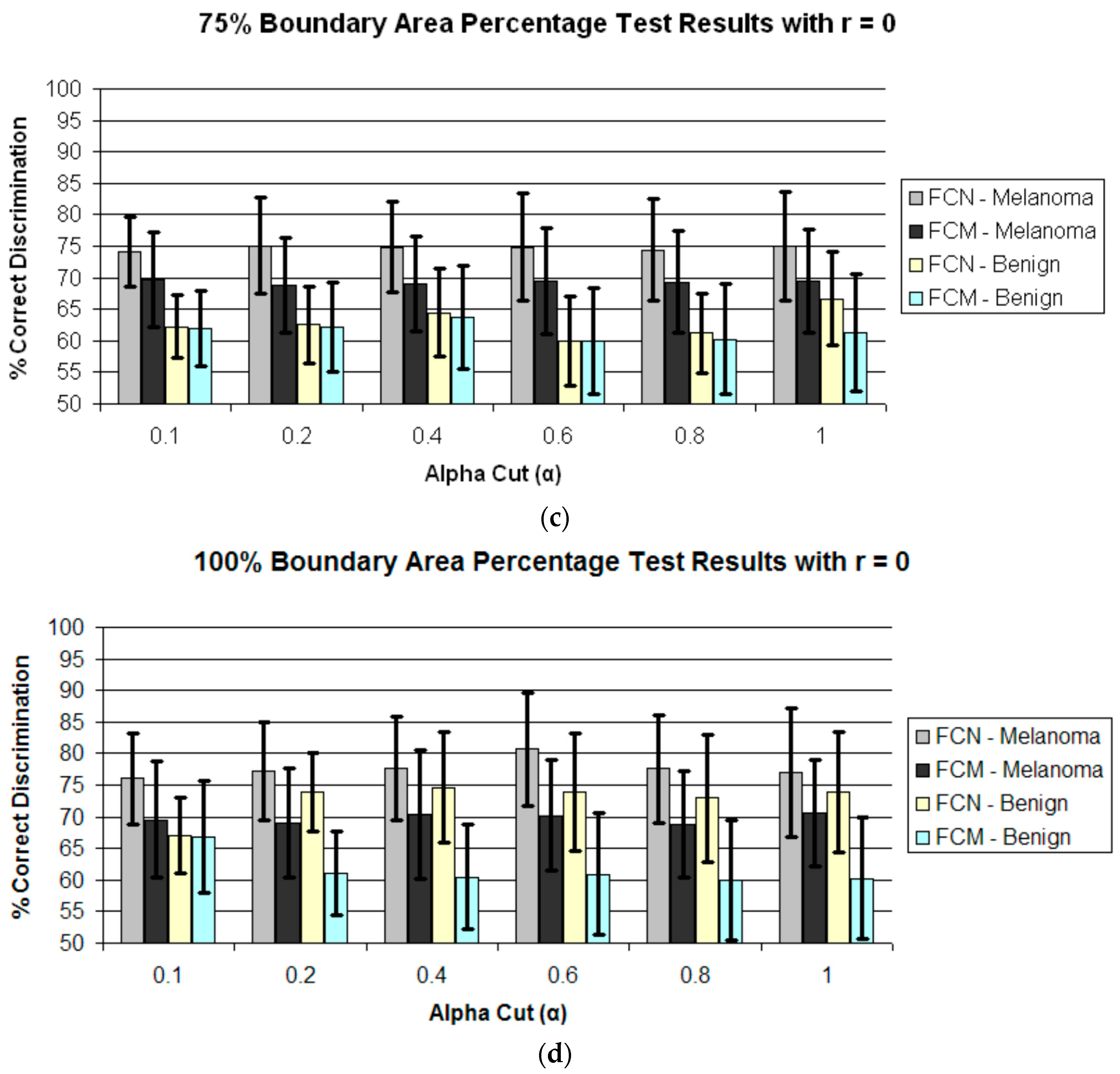
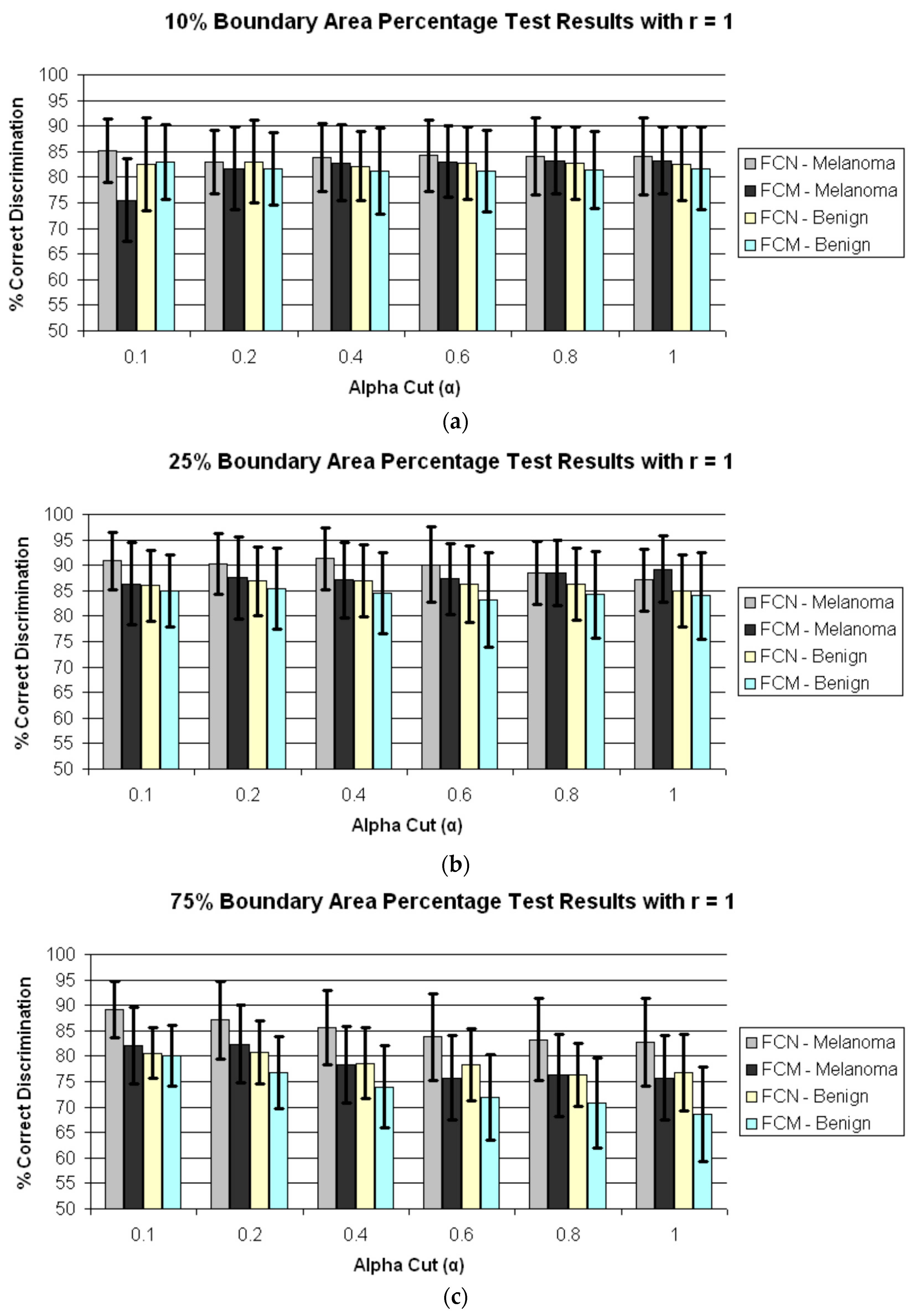
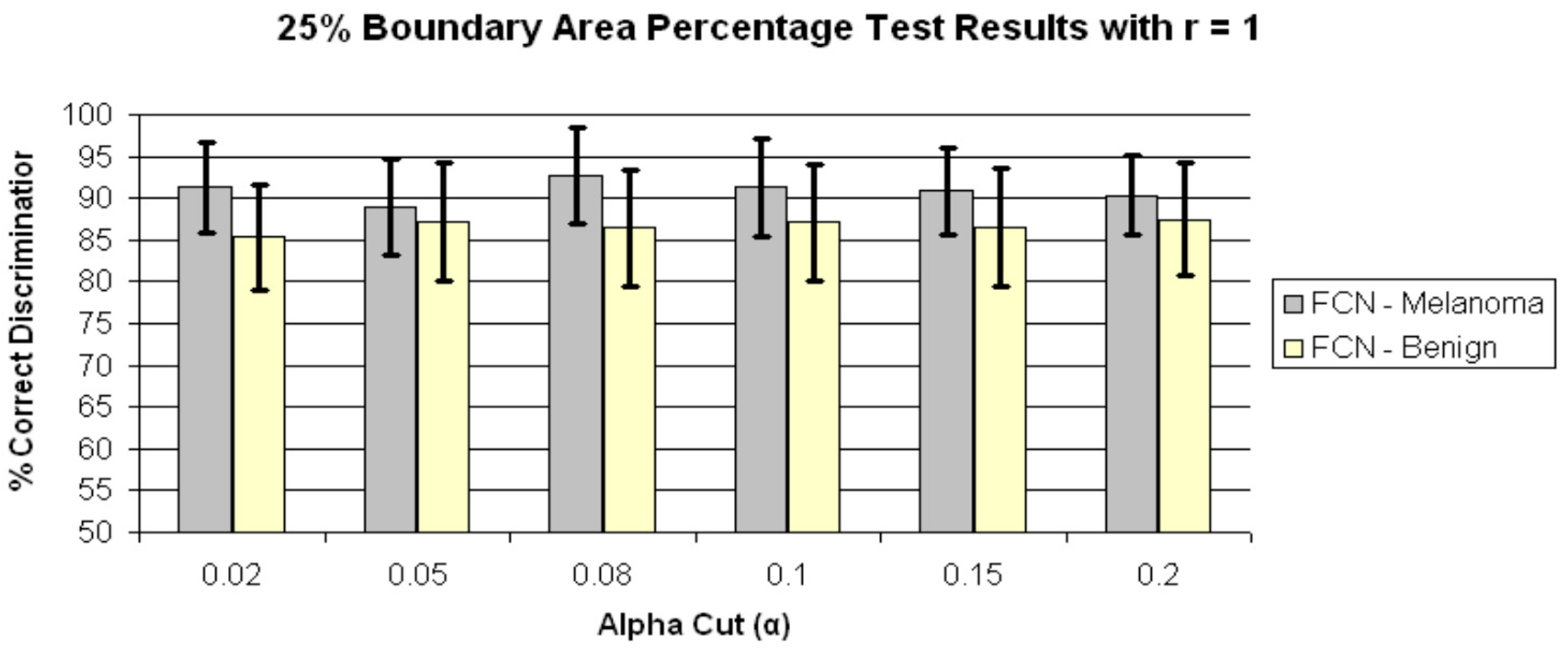
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Marghoob, A.A.; Scope, A. The complexity of diagnosing melanoma. J. Investig. Dermatol. 2009, 129, 11–13. [Google Scholar] [CrossRef] [PubMed]
- Stoecker, W.V.; Stolz, W. Dermoscopy and the diagnostic challenge of amelanotic and hypomelanotic melanoma. Arch. Dermatol. 2008, 144, 1207–1210. [Google Scholar] [CrossRef] [PubMed]
- Menzies, S.W.; Moloney, F.J.; Byth, K.; Avramidis, M.; Argenziano, G.; Zalaudek, I.; Braun, R.P.; Malvehy, J.; Puig, S.; Rabinovitz, H.S.; et al. Dermoscopic evaluation of nodular melanoma. JAMA Dermatol. 2013, 149, 699–709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soon, S.L.; Solomon, A.R., Jr.; Papadopoulos, D.; Murray, D.R.; McAlpine, B.; Washington, C.V. Acral lentiginous melanoma mimicking benign disease: The Emory experience. J. Am. Acad. Dermatol. 2003, 48, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Kittler, H.; Pehamberger, H.; Wolff, K.; Binder, M. Diagnostic accuracy of dermoscopy. Lancet Oncol. 2002, 3, 159–165. [Google Scholar] [CrossRef]
- Vestergaard, M.E.; Macaskill, P.; Holt, P.E.; Menzies, S.W. Dermoscopy compared with naked eye examination for the diagnosis of primary melanoma: A meta-analysis of studies performed in a clinical setting. Br. J. Dermatol. 2008, 159, 669–676. [Google Scholar] [CrossRef] [PubMed]
- Ferris, L.K.; Harkes, J.A.; Gilbert, B.; Winger, D.G.; Golubets, K.; Akilov, O.; Satyanarayanan, M. Computer-aided classification of melanocytic lesions using dermoscopic images. J. Am. Acad. Dermatol. 2015, 73, 769–776. [Google Scholar] [CrossRef] [PubMed]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Carrera, C.; Marchetti, M.A.; Dusza, S.W.; Argenziano, G.; Braun, R.P.; Halpern, A.C.; Jaimes, N.; Kittler, H.J.; Malvehy, J.; Menzies, S.W. Validity and Reliability of Dermoscopic Criteria Used to Differentiate Nevi From Melanoma: A Web-Based International Dermoscopy Society Study. JAMA Dermatol. 2016, 152, 798–806. [Google Scholar] [CrossRef] [PubMed]
- Argenziano, G.; Puig, S.; Zalaudek, I.; Sera, F.; Corona, R.; Alsina, M.; Barbato, F.; Carrera, C.; Ferrara, G.; Guilabert, A.; et al. Dermoscopy improves accuracy of primary care physicians to triage lesions suggestive of skin cancer. J. Clin. Oncol. 2006, 24, 1877–1882. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2016. CA Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2017. CA Cancer J. Clin. 2017, 67, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, S.; Marchetti, M.A.; Navarrete-Dechent, C.; Dusza, S.W.; Kose, K.; Marghoob, A.A. The role of color and morphologic characteristics in dermoscopic diagnosis. JAMA Dermatol. 2016, 152, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Friedman, R.J.; Rigel, D.S.; Kopf, A.W. Early detection of malignant melanoma: The role of physician examination and self-examination of the skin. CA Cancer J. Clin. 1985, 35, 130–151. [Google Scholar] [CrossRef] [PubMed]
- Rubegni, P.; Feci, L.; Nami, N.; Burroni, M.; Taddeucci, P.; Miracco, C.; Munezero Butorano, M.A.; Fimiani, M.; Cevenini, G. Computer-assisted melanoma diagnosis: A new integrated system. Melanoma Res. 2015, 25, 537–542. [Google Scholar] [CrossRef] [PubMed]
- Andreassi, L.; Perotti, R.; Rubegni, P.; Burroni, M.; Cevenini, G.; Biagioli, M.; Taddeucci, P.; Dell’Eva, G.; Barbini, P. Digital dermoscopy analysis for the differentiation of atypical nevi and early melanoma: A new quantitative semiology. Arch. Dermatol. 1999, 135, 1459–1465. [Google Scholar] [CrossRef] [PubMed]
- Landau, M.; Matz, H.; Ethel, T.; Dvir, M.; Brenner, S. Computerized system to enhance the clinical diagnosis of pigmented cutaneous malignancies. Int. J. Dermatol. 1999, 38, 443–446. [Google Scholar] [CrossRef] [PubMed]
- Umbaugh, S.E.; Moss, R.H.; Stoecker, W.V. Automatic color segmentation of images with application to detection of variegated coloring in skin tumors. IEEE Eng. Med. Biol. Mag. 1989, 8, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Green, A.; Martin, N.; Pfitzner, J.; O’Rourke, M.; Knight, N. Computer image analysis in the diagnosis of melanoma. J. Am. Acad. Dermatol. 1994, 31, 958–964. [Google Scholar] [CrossRef]
- Seidenari, S.; Burroni, M.; Dell’Eva, G.; Pepe, P.; Belletti, B. Computerized evaluation of pigmented skin lesion images recorded by a videomicroscope: Comparison between polarizing mode observation and oil/slide mode observation. Skin Res. Technol. 1995, 1, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Aitken, J.F.; Pfitzner, J.; Battistutta, D.; O’Rourke, P.K.; Green, A.C.; Martin, N.G. Reliability of computer image analysis of pigmented skin lesions of Australian adolescents. Cancer 1996, 78, 252–257. [Google Scholar] [CrossRef]
- Ercal, F.; Chawla, A.; Stoecker, W.V.; Lee, H.C.; Moss, R.H. Neural network diagnosis of malignant melanoma from color images. IEEE Trans. Biomed. Eng. 1994, 41, 837–845. [Google Scholar] [CrossRef] [PubMed]
- Ganster, H.; Pinz, A.; Röhrer, R.; Wildling, E.; Binder, M.; Kittler, H. Automated melanoma recognition. IEEE Trans. Med. Imaging 2001, 20, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Heckbert, P. Color image quantization for frame buffer display. In Proceedings of the 9th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’82, Boston, MA, USA, 26–30 July 1982; Volume 16, pp. 297–307. [Google Scholar]
- Faziloglu, Y.; Stanley, R.J.; Moss, R.H.; Stoecker, W.V.; McLean, R.P. Colour histogram analysis for melanoma discrimination in clinical images. Skin Res. Technol. 2003, 9, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Stanley, R.J.; Moss, R.H.; Stoecker, W.V. Colour analysis of skin lesion regions for melanoma discrimination in clinical images. Skin Res. Technol. 2003, 9, 94–104. [Google Scholar] [CrossRef] [PubMed]
- Stanley, R.J.; Stoecker, W.V.; Moss, R.H. A relative color approach to color discrimination for malignant melanoma detection in dermoscopy images. Skin Res. Technol. 2007, 13, 62–72. [Google Scholar] [CrossRef] [PubMed]
- Stanley, R.J.; Moss, R.H.; Stoecker, W.V.; Aggarwal, C. A fuzzy-based histogram analysis technique for skin lesion discrimination in dermatology clinical images. Comput. Med. Imaging Graph. 2003, 27, 387–396. [Google Scholar] [CrossRef]
- Barata, C.; Ruela, M.; Francisco, M.; Mendonça, T.; Marques, J.S. Two systems for the detection of melanomas in dermoscopy images using texture and color features. IEEE Syst. J. 2014, 8, 965–979. [Google Scholar] [CrossRef]
- Stoecker, W.V. Computer Applications in Dermatology; Igaku-Shoin: New York, NY, USA, 1993; ISBN-13 978-0896402386. [Google Scholar]
- Nie, D. Classification of melanoma and clark nevus skin lesions based on medical image processing techniques. In Proceedings of the 3rd International Conference on Computer Research and Development (ICCRD), Shanghai, China, 11–13 March 2011; pp. 31–34. [Google Scholar] [CrossRef]
- Argenziano, G.; Soyer, H.P.; De Giorgi, V.; Piccolo, D.; Carli, P.; Delfino, M.; Ferrari, A.; Hofmann-Wellenhof, R.; Massi, D.; Mazzocchetti, G.; et al. Interactive Atlas of Dermoscopy (Book and CD-ROM); Edra Medical Publishing and New Media: Milan, Italy, 2000; ISBN 88-86457-30-8. [Google Scholar]
- McLean, R.P. Tumor Classification Based on Relative Color Analysis of Melanoma and Non-Melanoma Tumor Images. Master’s Thesis, University of Missouri, Rolla, MO, USA, 1994. [Google Scholar]
- Stoecker, W.V.; Li, W.W.; Moss, R.H. Automatic detection of asymmetry in skin tumors. Comput. Med. Imaging Graph. 1992, 16, 191–197. [Google Scholar] [CrossRef]
- Hance, G.A.; Umbaugh, S.E.; Moss, R.H.; Stoecker, W.V. Unsupervised color image segmentation: With application to skin tumor borders. IEEE Eng. Med. Biol. Mag. 1996, 15, 104–111. [Google Scholar] [CrossRef]
- Klir, G.J.; Folger, T.A. Fuzzy Sets, Uncertainty, and Information; Prentice Hall: Englewood Cliffs, NJ, USA, 1988; ISBN-13 978-0133459845. [Google Scholar]
- Stanley, R.J.; Stoecker, W.V.; Moss, R.H.; Rabinovitz, H.S.; Cognetta, A.B., Jr.; Argenziano, G.; Soyer, H.P. A basis function feature-based approach for skin lesion discrimination in dermatology dermoscopy images. Skin Res. Technol. 2008, 14, 425–435. [Google Scholar] [CrossRef]
- Dalal, A.; Moss, R.H.; Stanley, R.J.; Stoecker, W.V.; Gupta, K.; Calcara, D.A.; Xu, J.; Shrestha, B.; Drugge, R.; Malters, J.M.; et al. Concentric decile segmentation of white and hypopigmented areas in dermoscopy images of skin lesions allows discrimination of malignant melanoma. Comput. Med. Imaging Graph. 2011, 35, 148–154. [Google Scholar] [CrossRef] [PubMed]
- Rader, R.K.; Payne, K.S.; Guntupalli, U.; Rabinovitz, H.S.; Oliviero, M.C.; Drugge, R.J.; Malters, J.J.; Stoecker, W.V. The pink rim sign: Location of pink as an indicator of melanoma in dermoscopic images. J. Skin Cancer. 2014, 2014, 719740. [Google Scholar] [CrossRef] [PubMed]
- Braun, R.P.; Gaide, O.; Oliviero, M.; Kopf, A.W.; French, L.E.; Saurat, J.H.; Rabinovitz, H.S. The significance of multiple blue-gray dots (granularity) for the dermoscopic diagnosis of melanoma. Br. J. Dermatol. 2007, 157, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Stoecker, W.V.; Wronkiewiecz, M.; Chowdhury, R.; Stanley, R.J.; Xu, J.; Bangert, A.; Shrestha, B.; Calcara, D.A.; Rabinovitz, H.S.; Oliviero, M.; et al. Detection of granularity in dermoscopy images of malignant melanoma using color and texture features. Comput. Med. Imaging Graph. 2011, 35, 144–147. [Google Scholar] [CrossRef] [PubMed]

| Computer-Assisted Skin Lesion Diagnosis | ||
|---|---|---|
| Actual Skin Lesion Diagnosis | Benign | Melanoma |
| Benign | True negative (tn) | False positive (fp) |
| Melanoma | False negative (fn) | True positive (tp) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almubarak, H.A.; Stanley, R.J.; Stoecker, W.V.; Moss, R.H. Fuzzy Color Clustering for Melanoma Diagnosis in Dermoscopy Images. Information 2017, 8, 89. https://doi.org/10.3390/info8030089
Almubarak HA, Stanley RJ, Stoecker WV, Moss RH. Fuzzy Color Clustering for Melanoma Diagnosis in Dermoscopy Images. Information. 2017; 8(3):89. https://doi.org/10.3390/info8030089
Chicago/Turabian StyleAlmubarak, Haidar A., R. Joe Stanley, William V. Stoecker, and Randy H. Moss. 2017. "Fuzzy Color Clustering for Melanoma Diagnosis in Dermoscopy Images" Information 8, no. 3: 89. https://doi.org/10.3390/info8030089





