Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Multi-Objective Optimization Problems
Abstract
:1. Introduction
2. Literature Review
3. Multi-Objective Optimization
4. MABBO Algorithm
4.1. Migrationoperator for MOPs
| Algorithm 1 Migration for MOPs (MigrationDo(H, )) |
| For i = 1 to NP // NP is the size of population If rand < Use to probabilistically decide whether to immigrate to If then For Select the emigrating island with probability If then For j = 1 to Nd // Nd is the dimension size End for End if End for End if End if End for |
4.2. Mutation Operator for MOPs
| Algorithm 2 Mutation for MOPs (Mutation Do(H, )) |
| For i = 1 to NP // NP is the size of population Select mutating habitat with probability If is selected, then For j = 1 to Nd // Nd is the dimension size End for End if End for |
4.3. Adaptive BBO for MOPs
4.4. The Redefinition of the Fitness Function
4.5. Main Procedureof Improved MABBO for MOPs
| Algorithm 3 The main procedure of MABBO for MOPs |
|
5. Simulation and Analysis
5.1. Metrics to Assess Performance
5.1.1. Generational Distance (GD)
5.1.2. Spacing Metric (SP)
5.1.3. Coverage Rate (CR)
5.1.4. Error Rate (ER)
5.1.5. Convergence Index (γ)
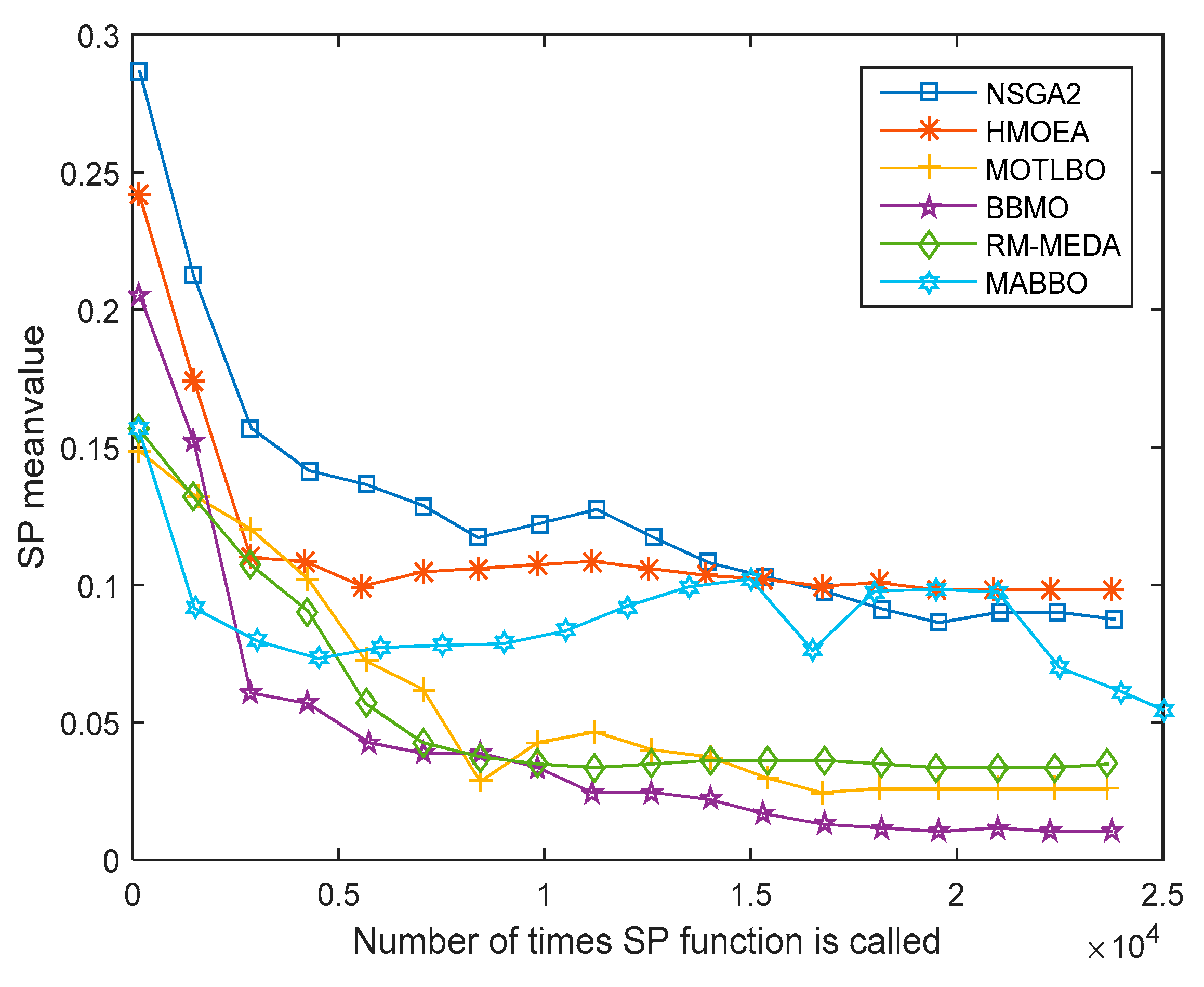
5.2. SimulationComparison and Discussion
5.2.1. MABBO Self Performance Comparison
5.2.2. The Comparison with other MOEAs
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Boussaïd, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. (BBO/DE) With Differential Evolution for Optimal Power Allocation in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2011, 60, 2347–2353. [Google Scholar] [CrossRef]
- Zubair, A.; Malhotra, D.; Muhuri, P.K.; Lohani, Q.D. Hybrid Biogeography-Based Optimization for solving Vendor Managed Inventory System. In Proceedings of the IEEE Congress on Evolutionary Computation 2017, San Sebastián, Spain, 5–8 June 2017; pp. 2598–2605. [Google Scholar]
- Zhang, M.; Zhang, B.; Zheng, Y. Bio-Inspired Meta-Heuristics for Emergency Transportation Problems. Algorithms 2014, 7, 15–31. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R.; Kaveh, M. Improved migration models of biogeography-based optimization for sonar dataset classification by using neural network. Appl. Acoust. 2017, 118, 15–29. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.D. Multi-objective optimization algorithm based on biogeography with chaos. Int. J. Hybrid. Inf. Technol. 2014, 7, 225–234. [Google Scholar] [CrossRef]
- Bi, X.J.; Wang, J.; Li, B. Multi-objective optimization based on hybrid biogeography-based optimization. Syst. Eng. Electron. 2014, 36, 179–186. [Google Scholar]
- Vincenzi, L.; Savoia, M. Coupling response surface and differential evolution for parameter identification problems. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 376–393. [Google Scholar] [CrossRef]
- Trivedi, A.; Srinivasan, D.; Biswas, S.; Reindl, T. Hybridizing genetic algorithm with differential evolution for solving the unit commitment scheduling problem. Swarm Evol. Comput. 2015, 23, 50–64. [Google Scholar] [CrossRef]
- Simon, D.; Mehmet, E.; Dawei, D.; Rick, R. Markov Models for Biogeography-Based Optimization. IEEE Trans. Syst., Man Cybern B Cybern. 2011, 41, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Simon, D. A probabilistic analysis of a simplified biogeography-based optimization algorithm. Evol. Comput. 2011, 19, 167–188. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Simon, D. Analysis of migration models of biogeography-based optimization using Markov theory. Eng. Appl. Artif. Intell. 2011, 24, 1052–1060. [Google Scholar] [CrossRef]
- Boussaïd, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. Two-stage update biogeography-based optimization using differential evolution algorithm (DBBO). Comput. Oper. Res. 2011, 38, 1188–1198. [Google Scholar] [CrossRef]
- Jiang, W.; Shi, Y.; Zhao, W.; Wang, X. Parameters Identification of Fluxgate Magnetic Core Adopting the Biogeography-Based Optimization Algorithm. Sensors 2016, 16, 979. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Cai, Z.; Ling, C.X. DE/BBO: A hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Comput. 2010, 15, 645–665. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D. Blended biogeography-based optimization for constrained optimization. Eng. Appl. Artif. Intell. 2011, 24, 517–525. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Zhou, J.; Yin, M. A perturb biogeography based optimization with mutation for global numerical optimization. Appl. Math. Comput. 2011, 218, 598–609. [Google Scholar] [CrossRef]
- Ergezer, M.; Simon, D.; Du, D. Oppositional biogeography-based optimization. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1009–1014. [Google Scholar] [CrossRef]
- Tan, L.; Guo, L. Quantum and biogeography based optimization for a class of combinatorial optimization. In Proceedings of the first ACM/SIGEVO Summit on Genetic and Evolutionary Computation—GEC2009, Shanghai, China, 12–14 June 2009; ACM: New York, NY, USA, 2009; Volume 2, p. 969. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z.; Ling, C.X.; Li, H. A real-coded biogeography-based optimization with mutation. Appl. Math. Comput. 2010, 216, 2749–2758. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Hybrid Differential Evolution with Biogeography-Based Optimization for Solution of Economic Load Dispatch. IEEE Trans. Power Syst. 2010, 2, 1955–1964. [Google Scholar] [CrossRef]
- Majumdar, K.; Das, P.; Roy, P.K.; Banerjee, S. Solving OPF Problems using Biogeography Based and Grey Wolf Optimization Techniques. Int. J. Energy Optim. Eng. 2017, 6, 55–77. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.; Liang, S.; Wang, A.; Zhang, Y. Beam pattern design of circular antenna array via efficient biogeography-based optimization. AEU-Int. J. Electron. Commun. 2017, 79, 275–285. [Google Scholar] [CrossRef]
- Liu, F.; Nakamura, K.; Payne, R. Abnormal Breast Detection via Combination of Particle Swarm Optimization and Biogeography-Based Optimization. In Proceedings of the 2nd International Conference on Mechatronics Engineering and Information Technology, ICMEIT 2017, Dalian, China, 13–14 May 2017. [Google Scholar]
- Johal, N.K.; Singh, S.; Kundra, H. A hybrid FPAB/BBO Algorithm for Satellite Image Classification. Int. J. Comput. Appl. 2010, 6, 31–36. [Google Scholar] [CrossRef]
- Song, Y.; Liu, M.; Wang, Z. Biogeography-Based Optimization for the Traveling Salesman Problems. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization, Huangshan, China, 28–31 May 2010; pp. 295–299. [Google Scholar] [CrossRef]
- Mo, H.; Xu, L. Biogeography Migration Algorithm for Traveling Salesman Problems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 405–414. [Google Scholar]
- Silva, M.A.C.; Coelho, L.S.; Freire, R.Z. Biogeography-based Optimization approach based on Predator-Prey concepts applied to path planning of 3-DOF robot manipulator. In Proceedings of the 2010 IEEE 15th Conference on Emerging Technologies & Factory Automation (ETFA 2010), Bilbao, Spain, 13–16 September 2010; pp. 1–8. [Google Scholar]
- Lohokare, M.R.; Pattnaik, S.S.; Devi, S.; Panigrahi, B.K.; Das, S.; Jadhav, D.G. Discrete Variables Function Optimization Using Accelerated Biogeography-Based Optimization; Springer: Berlin/Heidelberg, Germany, 2010; pp. 322–329. [Google Scholar]
- Boussaid, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. Hybridizing biogeography-based optimization with differential evolution for optimal power allocation in wireless sensor networks. IEEE Trans. Veh. Technol. 2011, 60, 2347–2353. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y. An effective hybrid biogeography-based optimization algorithm for parameter estimation of chaotic systems. Expert. Syst. Appl. 2011, 38, 15103–15109. [Google Scholar] [CrossRef]
- Ovreiu, M.; Simon, D. Biogeography-based optimization of neuro-fuzzy system parameters for diagnosis of cardiac disease. In Proceedings of the 12th annual conference on Genetic and evolutionary computation—GECCO2010, Portland, OR, USA, 7–11 July 2010; ACM: New York, NY, USA; p. 1235. [Google Scholar] [CrossRef]
- Yin, M.; Li, X. Full Length Research Paper A hybrid bio-geography based optimization for permutation flow shop scheduling. Sci. Res. Essays 2011, 6, 2078–2100. [Google Scholar]
- Reddy, S.S.; Kumari, M.S.; Sydulu, M. Congestion management in deregulated power system by optimal choice and allocation of FACTS controllers using multi-objective genetic algorithm. In Proceedings of the 2010 IEEE PES T&D, New Orleans, LA, USA, 19–22 April 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Reddy, S.S.; Abhyankar, A.R.; Bijwe, P.R. Reactive power price clearing using multi-objective optimization. Energy 2011, 36, 3579–3589. [Google Scholar] [CrossRef]
- Reddy, S.S. Multi-objective based congestion management using generation rescheduling and load shedding. IEEE Trans. Power Syst. 2017, 32, 852–863. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R. Multi-Objective Optimal Power Flow Using Efficient Evolutionary Algorithm. Int. J. Emerg. Electr. Power Syst. 2017, 18. [Google Scholar] [CrossRef]
- Silva, M.A.C.; Coelho, L.S.; Lebensztajn, L. Multi objective biogeography-based optimization based on predator-prey approach. IEEE Trans. Magn. 2012, 48, 951–954. [Google Scholar] [CrossRef]
- Goudos, S.K.; Plets, D.; Liu, N.; Martens, L.; Joseph, W. A multi-objective approach to indoor wireless heterogeneous networks planning based on biogeography-based optimization. Comput. Netw. 2015, 91, 564–576. [Google Scholar] [CrossRef]
- Ma, H.P.; Su, S.F.; Simon, D.; Fei, M.R. Ensemble multi-objective biogeography-based optimization withapplication to automated warehouse scheduling. Eng. Appl. Artif. Intell. 2015, 44, 79–90. [Google Scholar] [CrossRef]
- Reihanian, A.; Feizi-Derakhshi, M.-R.; Aghdasi, H.S. Community detection in social networks with node attributes based on multi-objective biogeography based optimization. Eng. Appl. Artif. Intell. 2017, 62, 51–67. [Google Scholar] [CrossRef]
- Guo, W.A.; Wang, L.; Wu, Q.D. Numerical comparisons of migration models for Multi-objective Biogeography-Based Optimization. Inf. Sci. 2016, 328, 302–320. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Z.; You, P.; Fei, M. Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging. Energy 2017, 135, 101–111. [Google Scholar] [CrossRef]
- Gachhayat, S.K.; Dash, S.K. Non-Convex Multi Objective Economic Dispatch Using Ramp Rate Biogeography Based Optimization. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2017, 11, 545–549. [Google Scholar]
- Zheng, Y.-J.; Wang, Y.; Ling, H.-F.; Xue, Y.; Chen, S.-Y. Integrated civilian–military pre-positioning of emergency supplies: A multi-objective optimization approach. Appl. Soft Comput. 2017, 58, 732–741. [Google Scholar] [CrossRef]
- Veldhuizen, D.A.V.; Lamont, G.B. Evolutionary computation and convergence to a pareto front. In Late Breaking Papers at the Genetic Programming; Koza, J.R., Ed.; Stanford Bookstore: Stanford, CA, USA, 1998; pp. 221–228. [Google Scholar]
- Schott, J.R. Fault tolerant design using single and multi-criteria genetic algorithm optimization. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Zhou, A.M.; Jin, Y.C. RM-MEDA: A regularity model-based multi-objective estimation of distribution algorithm. IEEE Trans. Evol. Comput. 2008, 12, 41–63. [Google Scholar] [CrossRef]
- Zou, F.; Wang, L.; Hei, X. Multi-objective optimization using teaching-learning-based optimization algorithm. Eng. Appl. Artif. Intel. 2013, 26, 1291–1300. [Google Scholar] [CrossRef]
- Tang, L.X.; Wang, X.P. A hybrid multi-objective evolutionary algorithm for multiobjective optimization problems. IEEE Trans. Evol. Comput. 2013, 17, 20–45. [Google Scholar] [CrossRef]
- Ma, H.; Ruan, X.; Pan, Z. Handling multiple objectives with biogeography-based optimization. Int. J. Autom. Comput. 2012, 9, 30–36. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Multi-Objective Optimization Test Problems. In Proceedings of the CEC 2002, Honolulu, HI, USA, 12–17 May 2002; pp. 825–830. [Google Scholar]
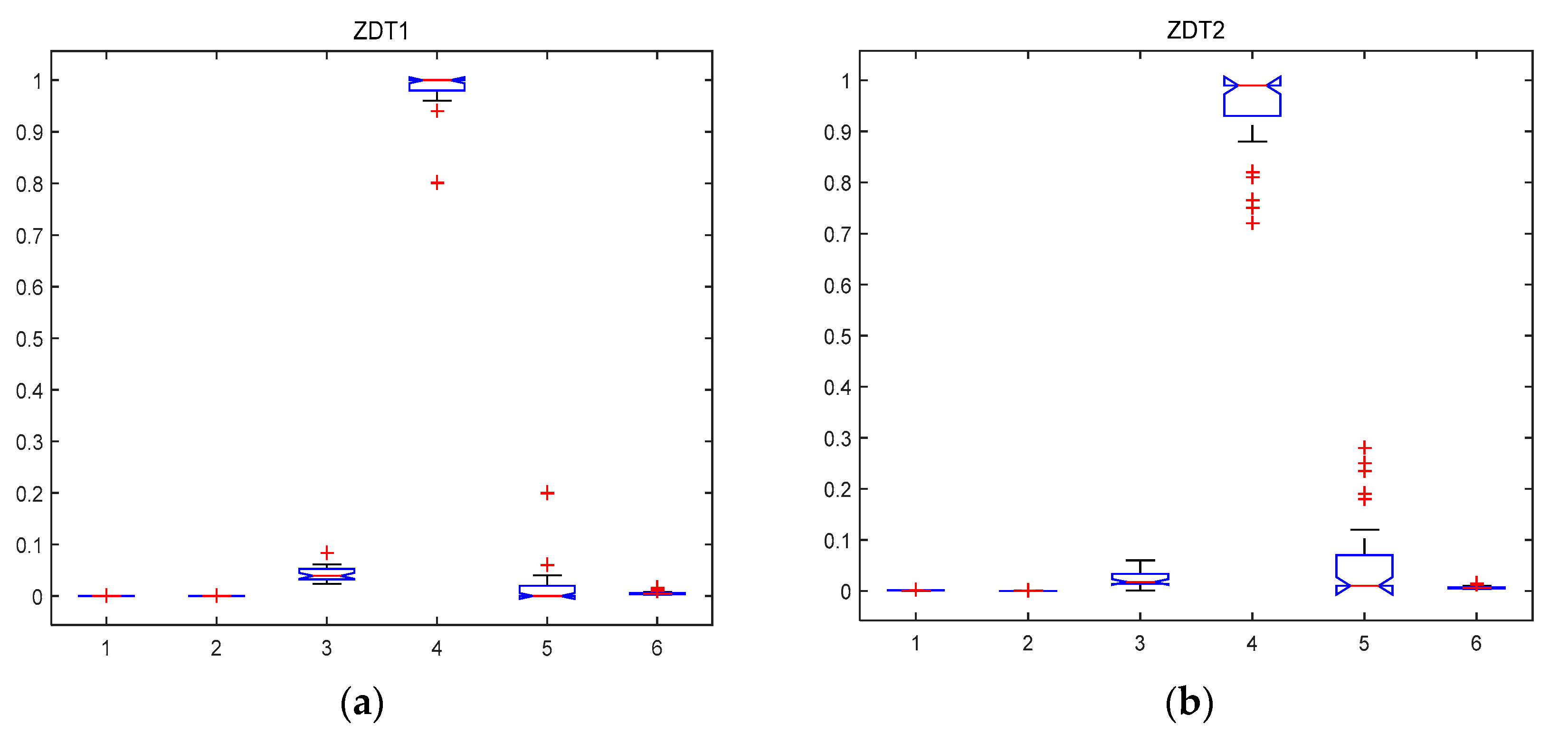
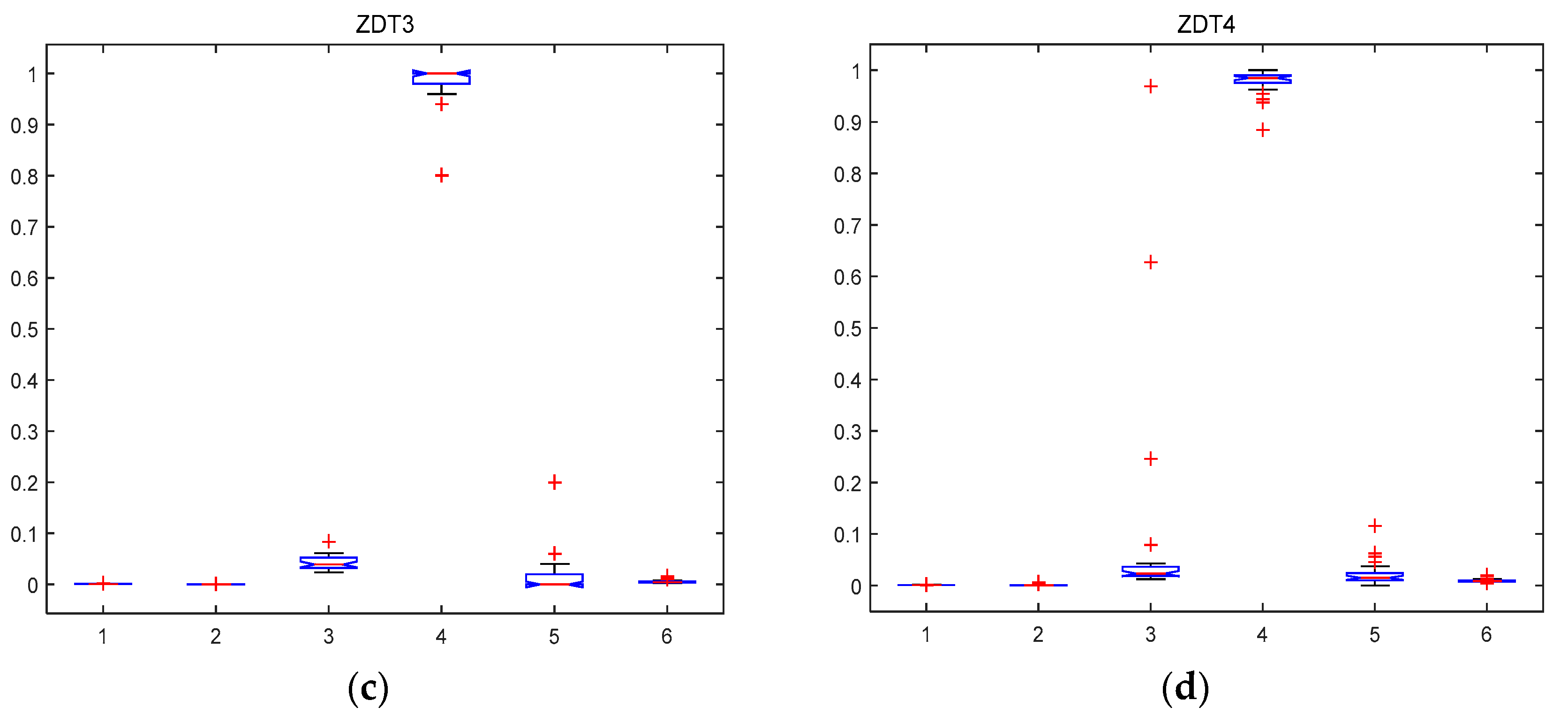
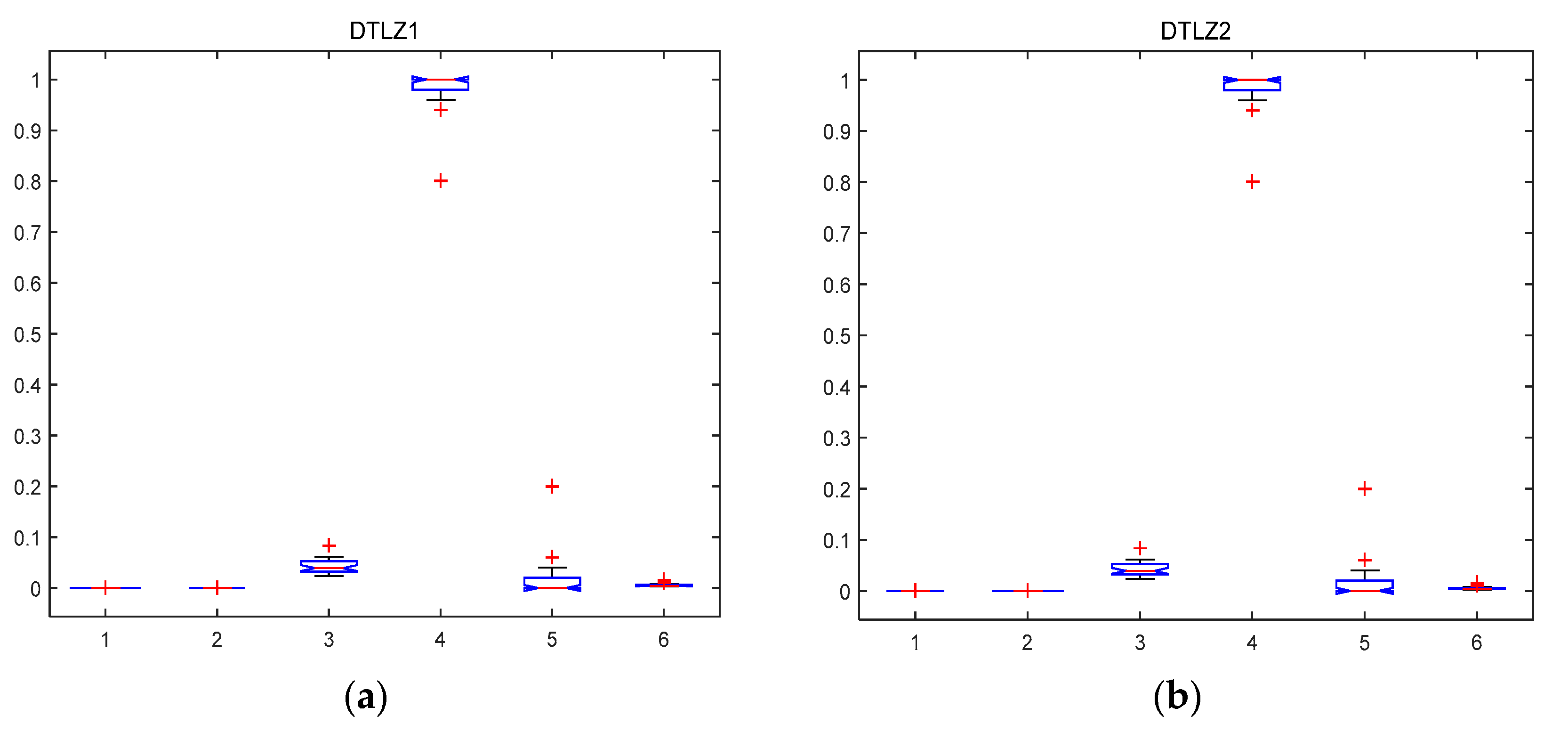
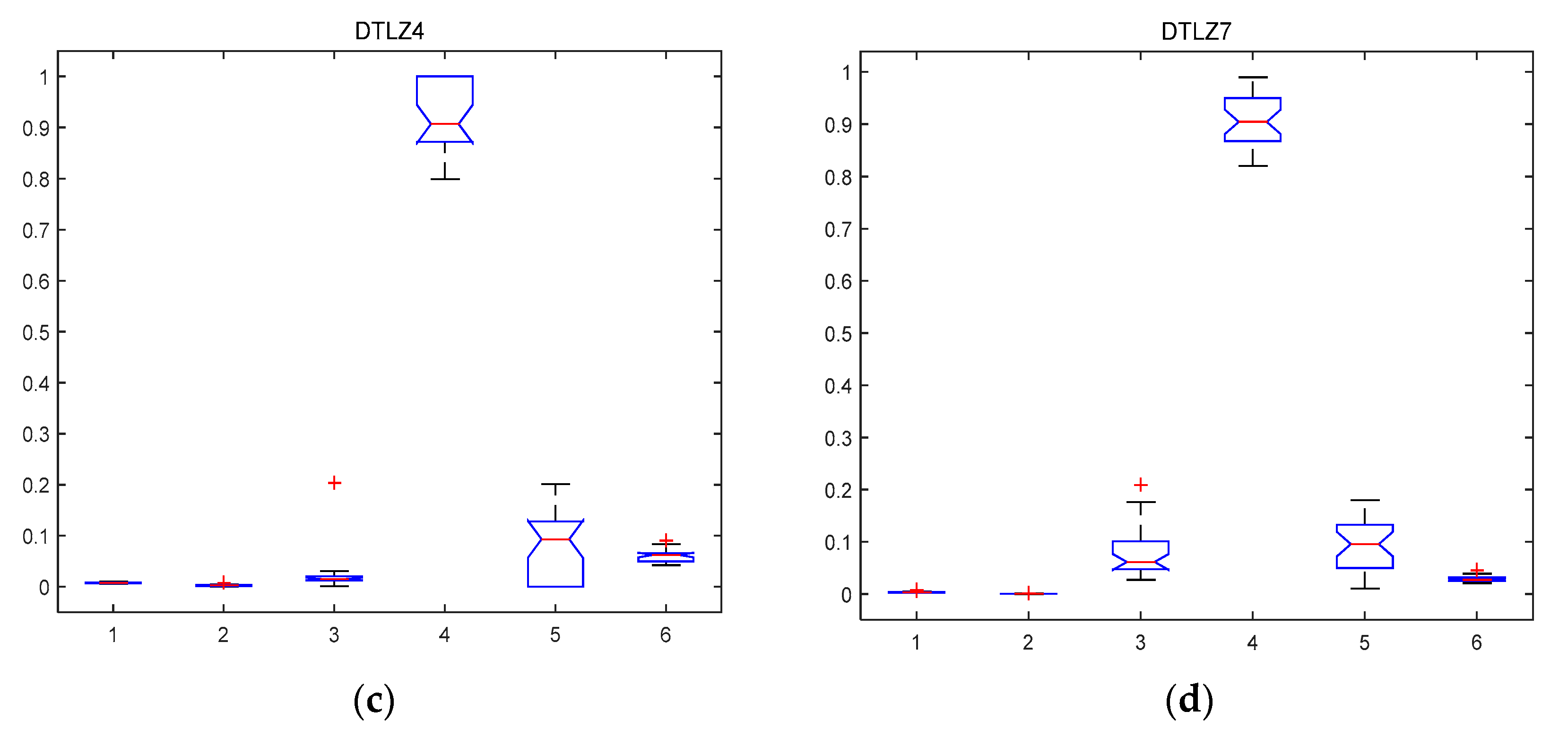

| Function | ZDT1 | ZDT2 | ZDT3 | ZDT4 | DTLZ1 | DTLZ2 | DTLZ4 | DTLZ7 |
|---|---|---|---|---|---|---|---|---|
| Popsize | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| NumVar | 30 | 30 | 10 | 10 | 10 | 10 | 10 | 22 |
| Pmodify | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 |
| Pmutation | 0.05 | 0.005 | 0.005 | 0.005 | 0.2 | 0.005 | 0.005 | 0.05 |
| Elitismkeep | 15 | 15 | 15 | 15 | 10 | 15 | 10 | 10 |
| k1 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| k2 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 |
| k3 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| k4 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| Generation | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| PerLoop | 100 | 100 | 100 | 100 | 10 | 10 | 10 | 10 |
| Algorithm | ZDT1 | ZDT2 | ZDT3 | ZDT4 | ||||
|---|---|---|---|---|---|---|---|---|
| GD | SP | GD | SP | GD | SP | GD | SP | |
| MABBO | 8.44 × 10−4 | 2.33 × 10−2 | 1.28 × 10−3 | 4.37 × 10−2 | 7.22 × 10−4 | 4.29 × 10−2 | 9.64 × 10−4 | 8.47 × 10−2 |
| (2.91 × 10−5) | (1.56 × 10−2) | (4.18 × 10−5) | (7.43 × 10−2) | (2.49 × 10−5) | (1.34 × 10−2) | (5.55 × 10−4) | (2.03 × 10−1) | |
| NSGA-II | 2.93 × 10−3 | 7.79 × 10−3 | 1.85 × 10−3 | 7.41 × 10−3 | 1.78 × 10−3 | 8.42 × 100 | 6.34 × 10−3 | 9.73 × 10−3 |
| (4.74 × 10−4) | (7.40 × 10−3) | (2.99 × 10−3) | (6.57 × 10−3) | (4.75 × 10−3) | (1.75 × 10−3) | (3.96 × 10−3) | (5.32 × 10−3) | |
| BBMO | 2.53 × 10−2 | 2.74 × 10−2 | 3.26 × 10−2 | 7.88 × 10−1 | 7.23 × 10−2 | 4.93 × 10−3 | 3.33 × 10−2 | 4.16 × 10−2 |
| (2.98 × 10−3) | (5.53 × 10−3) | (2.72 × 10−2) | (3.83 × 10−1) | (1.41 × 10−2) | (1.65 × 10−3) | (6.51 × 10−3) | (1.31 × 10−2) | |
| RM-MEDA | 2.87 × 10−3 | 1.10 × 10−2 | 4.76 × 10−3 | 3.88 × 10−3 | 2.17 × 10−3 | 1.19 × 10−2 | 1.54 × 10−3 | 7.25 × 10−3 |
| (8.47 × 10−3) | (1.18 × 10−3) | (1.58 × 10−3) | (1.56 × 10−3) | (9.01 × 10−3) | (2.80 × 10−3) | (1.69 × 10−3) | (1.86 × 10−3) | |
| MOTLBO | 1.59 × 10−3 | 4.01 × 10−3 | 9.34 × 10−4 | 7.38 × 10−3 | 2.04 × 10−3 | 3.37 × 10−3 | 1.42 × 10−3 | 2.49 × 10−3 |
| (3.27 × 10−3) | (3.68 × 10−3) | (1.06 × 10−3) | (6.96 × 10−3) | (8.47 × 10−4) | (3.08 × 10−3) | (2.49 × 10−3) | (2.74 × 10−4) | |
| HMOEA | 3.74 × 10−4 | 5.75 × 10−1 | 3.06 × 10−4 | 7.23 × 10−1 | 6.75 × 10−4 | 3.53 × 10−1 | 1.14 × 10−3 | 3.91 × 10−1 |
| (8.24 × 10−4) | (2.50 × 10−2) | (2.52 × 10−4) | (7.54 × 10−2) | (3.84 × 10−4) | (6.45 × 10−3) | (8.23 × 10−4) | (9.23 × 10−2) | |
| Algorithm | DTLZ1 | DTLZ2 | DTLZ4 | DTLZ7 | ||||
|---|---|---|---|---|---|---|---|---|
| GD | SP | GD | SP | GD | SP | GD | SP | |
| MABBO | 5.84 × 10−3 | 2.96 × 10−2 | 4.41 × 10−3 | 6.13 × 10−2 | 7.57 × 10−3 | 2.81 × 10−2 | 3.41 × 10−3 | 7.96 × 10−2 |
| (1.09 × 10−4) | (9.33 × 10−3) | (1.22 × 10−4) | (2.21 × 10−2) | (2.69 × 10−3) | (4.80 × 10−2) | (3.99 × 10−4) | (4.74 × 10−2) | |
| NSGA-2 | 6.74 × 10−2 | 3.68 × 10−1 | 5.31 × 10−2 | 8.51 × 10−2 | 5.44 × 10−2 | 2.09 × 10−2 | 7.15 × 10−2 | 6.63 × 10−2 |
| (2.25 × 10−1) | (1.66E × 100 | (1.72 × 10−3) | (5.76 × 10−2) | (6.09 × 10−2) | (5.14 × 10−2) | (3.43 × 10−2) | (2.19 × 10−2) | |
| BBMO | 6.34 × 10−2 | 3.85 × 10−1 | 4.81 × 10−2 | 1.12 × 10−2 | 2.45 × 10−1 | 1.75 × 10−1 | 1.42 × 10−1 | 2.22 × 10−1 |
| (1.17 × 10−1) | (2.28 × 10−1) | (5.22 × 10−2) | (3.95 × 10−2) | (3.75 × 10−2) | (2.75 × 10−2) | (2.75 × 10−2) | (1.07 × 10−1) | |
| RM-MEDA | 3.76 × 10−2 | 7.65 × 10−2 | 3.54 × 10−2 | 3.98 × 10−2 | 7.73 × 10−2 | 9.13 × 10−2 | 1.18 × 10−2 | 2.75 × 10−2 |
| (9.45 × 10−2) | (4.53 × 10−1) | (9.20 × 10−2) | (5.92 × 10−2) | (5.76 × 10−2) | (2.53 × 10−2) | (4.28 × 10−2) | (1.95 × 10−2) | |
| MOTLBO | 7.83 × 10−2 | 8.34 × 10−2 | 1.06 × 10−2 | 2.46 × 10−2 | 3.74 × 10−2 | 3.30 × 10−2 | 2.21 × 10−2 | 3.34 × 10−2 |
| (5.97 × 10−1) | (8.13 × 10−2) | (4.92 × 10−3) | (3.66 × 10−3) | (4.99 × 10−2) | (3.06 × 10−2) | (5.54 × 10−3) | (7.92 × 10−2) | |
| HMOEA | 3.37 × 10−2 | 3.04 × 10−1 | 2.41 × 10−3 | 1.23 × 10−1 | 2.23 × 10−2 | 1.23 × 10−1 | 4.84 × 10−3 | 5.38 × 10−1 |
| (7.15 × 10−2) | (2.13 × 10−1) | (6.78 × 10−3) | (2.86 × 10−2) | (1.78 × 10−2) | (3.38 × 10−2) | (9.02 × 10−3) | (5.44 × 10−2) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Yang, Z.; Huang, M. Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Multi-Objective Optimization Problems. Information 2017, 8, 83. https://doi.org/10.3390/info8030083
Feng S, Yang Z, Huang M. Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Multi-Objective Optimization Problems. Information. 2017; 8(3):83. https://doi.org/10.3390/info8030083
Chicago/Turabian StyleFeng, Siling, Ziqiang Yang, and Mengxing Huang. 2017. "Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Multi-Objective Optimization Problems" Information 8, no. 3: 83. https://doi.org/10.3390/info8030083





