A Novel STDM Watermarking Using Visual Saliency-Based JND Model
Abstract
:1. Introduction
2. Perceptual Spread Transform Dither Modulation
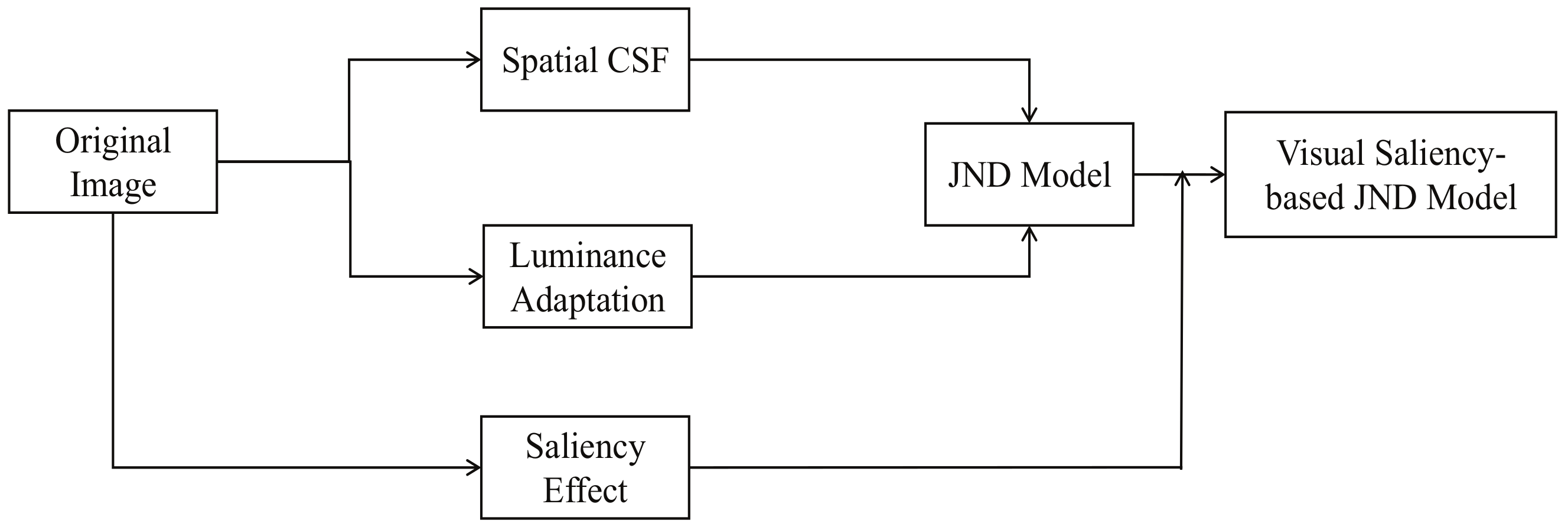
3. Visual Saliency-Based JND Model
3.1. Spatial CSF Effect
3.2. Luminance Adaptation Effect
3.3. Visual Saliency Effect
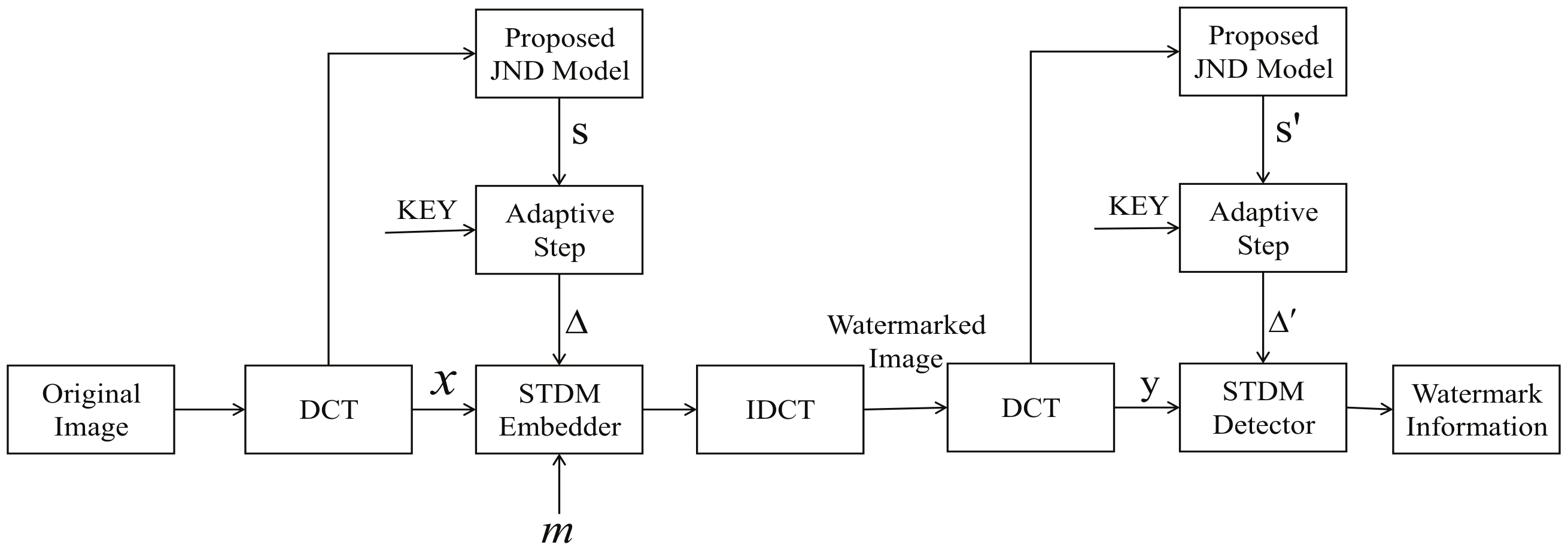
4. STDM Watermarking Using Visual Saliency-Based JND Model
4.1. Watermark Embedding Procedure
- Calculate the saliency value of each pixel in the carrier image, according to Equations (13)–(17), and binarize the gray scale image according to the threshold to obtain a region of “saliency” area and “non-saliency” area of the image.
- Divide the carrier image into eight by eight blocks and perform a DCT transform to determine the DCT coefficients. The coefficients are scanned by zig-zag arrangement. Then select the four to ten DCT coefficients (in zig-zag-scanned order after the eight by eight block DCT on each image) to form a single vector which denoted as the host vector x.
- The JND coefficients are calculated according to Equation (4). According to step (1), the JND coefficients belonging to the “saliency” or the “non-saliency” areas are multiplied by the different modulation factors to obtain the coefficients and form the visual redundancy vector s.
- Following Equation (18), we can get the perceptual slack vector s. Then the host vector x and the perceptual slack vector s are projected onto the given projection vector u, which is set as the , to generate the projections and . Then we can obtain the quantization step size via , which can be multiplied by the embedding strength in practice.
- One bit of the watermark “m” is embedded in the host projection .
- Finally, the modified coefficients are transformed to obtain the watermarked image.
4.2. Watermark Detection Procedure
- Calculate the saliency value of each pixel in the carrier image, according to Equations (13)–(17), and binarize the gray scale image according to the threshold to obtain a region of “saliency” area and “non-saliency” area of the image.
- Divide the carrier image into eight by eight blocks and perform DCT transform to determine the DCT coefficients. The coefficients are scanned by zig-zag arrangement. Then select the four to ten DCT coefficients (in zig-zag-scanned order after the eight by eight block DCT on each image) to form a single vector which denoted as the host vector y .
- The JND coefficients are calculated according to Equation (4). According to step (1), the JND coefficients belonging to the “saliency” or the “non-saliency” area are multiplied by the different modulation factors to obtain the coefficients and form the visual redundancy vector .
- The host vector x and the perceptual slack vector are projected onto the given projection vector u, which is set as the to generate the projections and . Then we can obtain the quantization step size via , which can be multiplied by the embedding strength in practice.
- Use the STDM detector to extract the watermark message according to Equation (3).
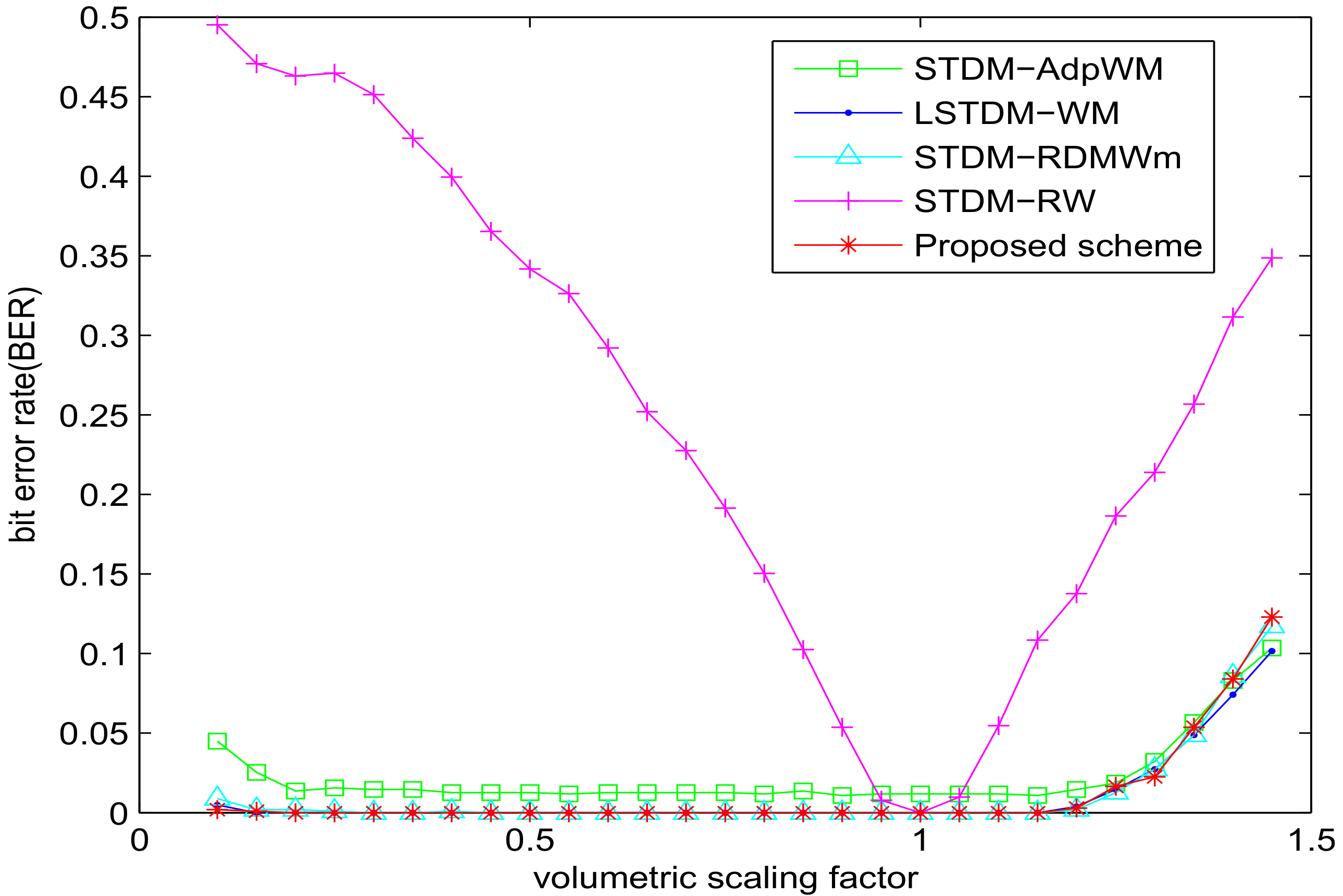
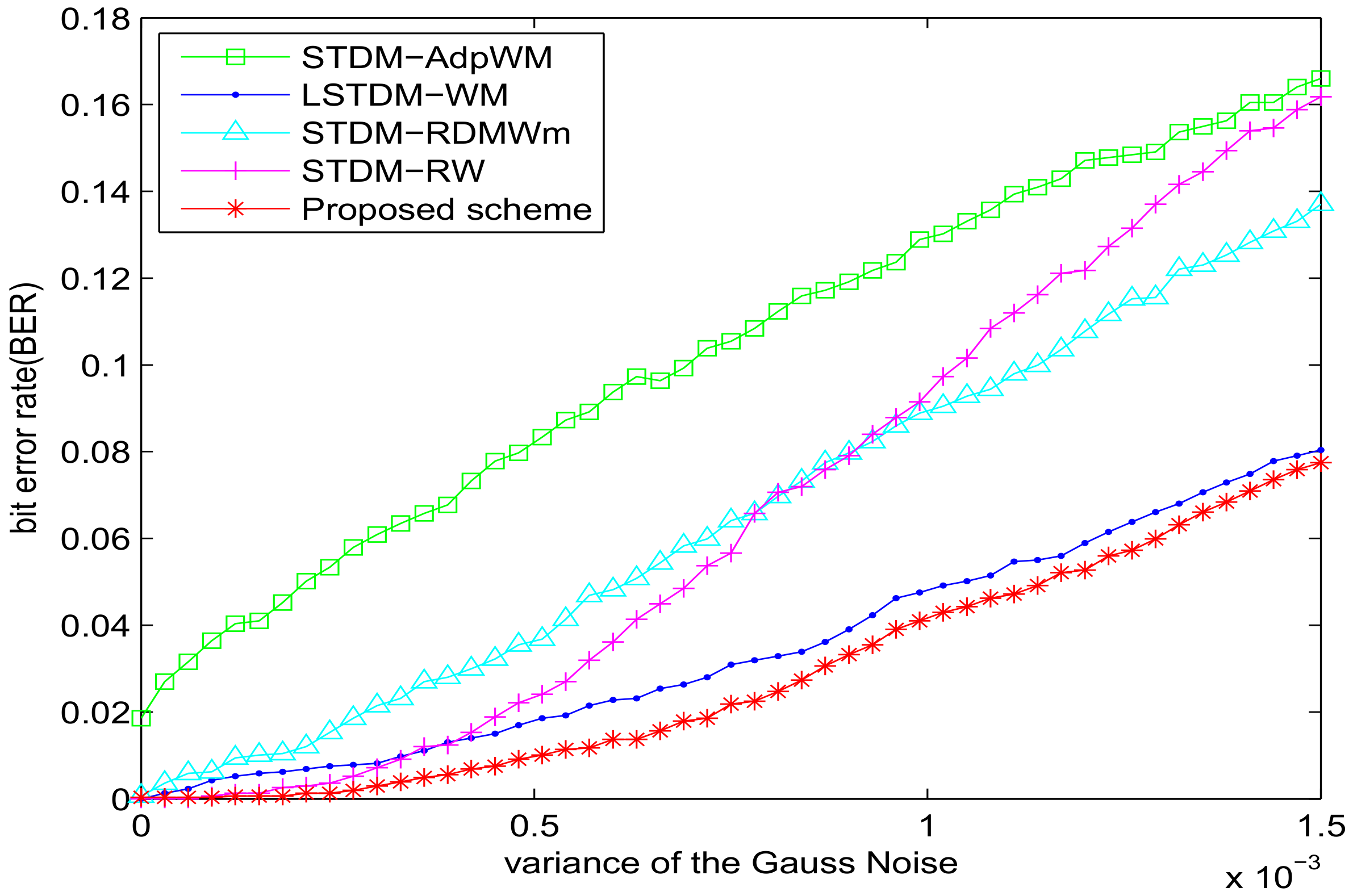
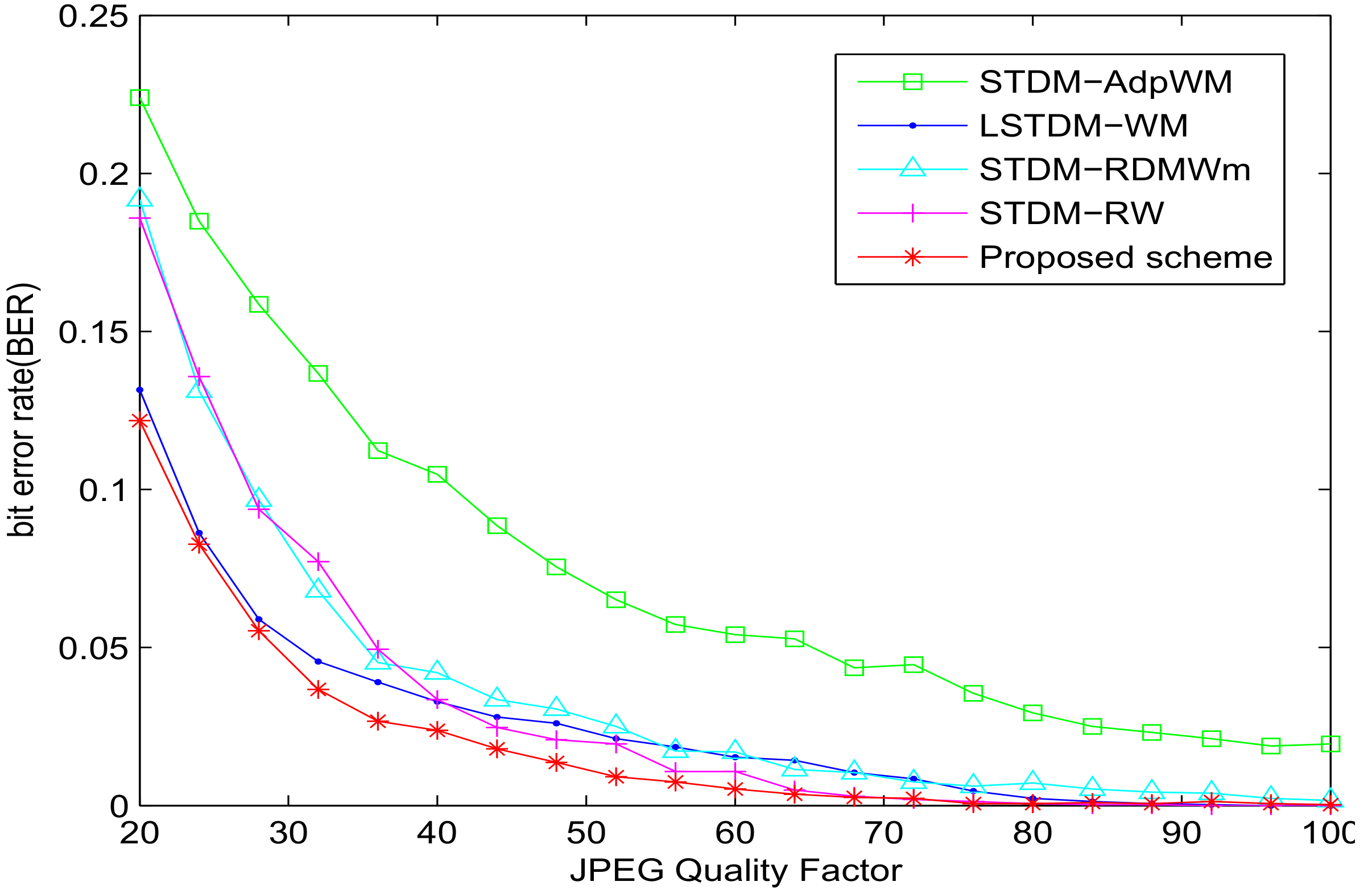
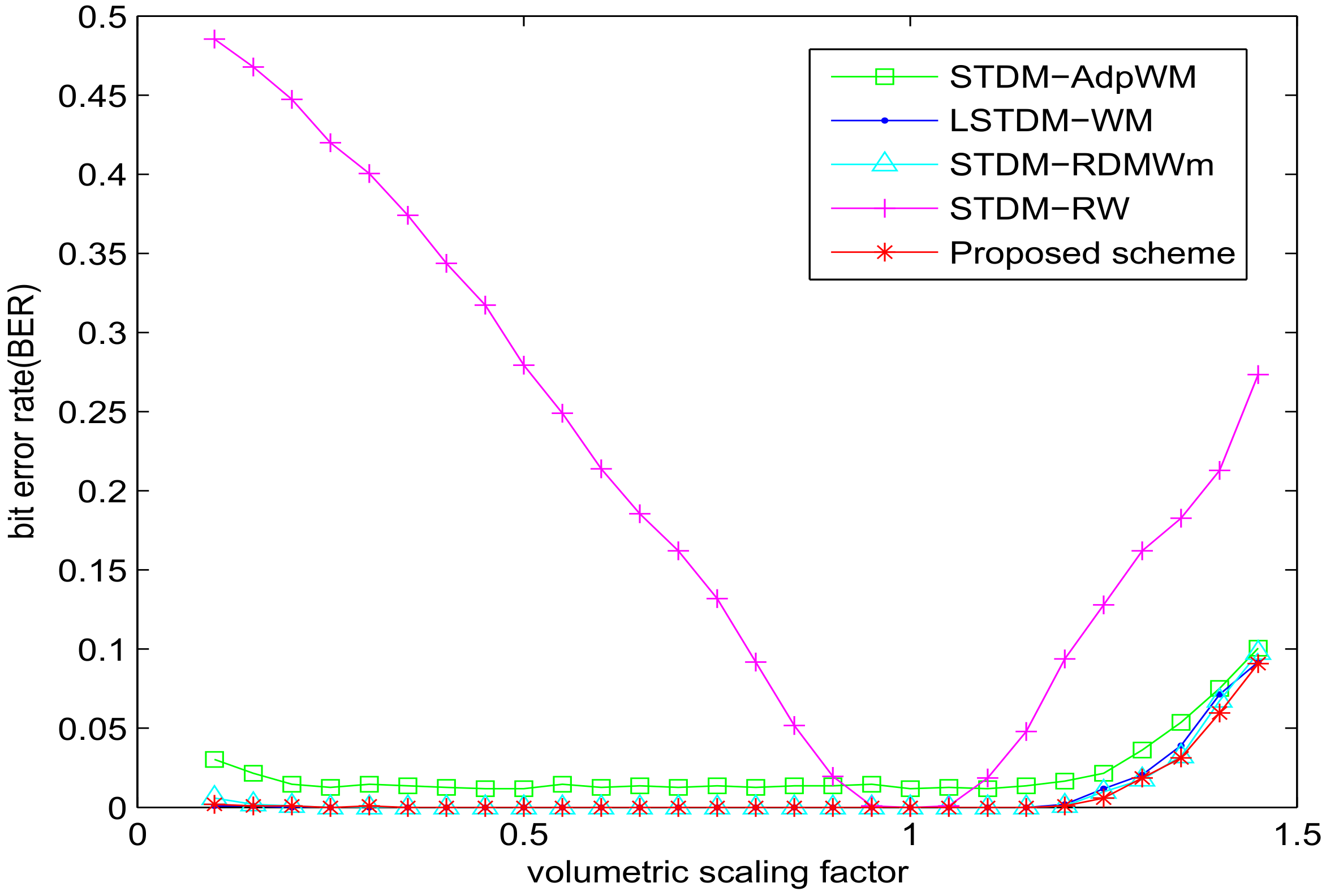
5. Experimental Results and Analysis
5.1. Experiment of Robustness with SSIM = 0.982
5.2. Experiment of Robustness with VSI = 0.982
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kang, H.; Iwamura, K. Information Hiding Method Using Best DCT and Wavelet Coefficients and Its Watermark Competition. Entropy 2015, 17, 1218–1235. [Google Scholar] [CrossRef]
- Abdullatif, M.; Zeki, A.M.; Chebil, J.; Gunawan, T.S. Properties of digital image watermarking. In Proceedings of the 2013 IEEE 9th International Colloquium on Signal Processing and Its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 235–240. [Google Scholar]
- Qi, H.; Zheng, D.; Zhao, J. Human visual system based adaptive digital image watermarking. Signal Process. 2008, 88, 174–188. [Google Scholar] [CrossRef]
- Papakostas, G.; Tsougenis, E.; Koulouriotis, D. Fuzzy knowledge-based adaptive image watermarking by the method of moments. Complex Intell. Syst. 2016, 2, 205–220. [Google Scholar] [CrossRef]
- Chen, B.; Wornell, G.W. Quantization index modulation: A class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theor. 2001, 47, 1423–1443. [Google Scholar] [CrossRef]
- Yu, D.; Ma, L.; Wang, G.; Lu, H. Adaptive spread-transform dither modulation using an improved luminance-masked threshold. In Proceedings of the 15th IEEE International Conference on Image Processing, ICIP 2008, San Diego, CA, USA, 12–15 October 2008; pp. 449–452. [Google Scholar]
- Li, Q.; Doerr, G.; Cox, I.J. Spread Transform Dither Modulation using a Perceptual Model. In Proceedings of the 2006 IEEE Workshop on Multimedia Signal Processing, Victoria, BC, Canada, 3–6 October 2006; pp. 98–102. [Google Scholar]
- Watson, A.B. DCT quantization matrices optimized for individual images. In Human Vision, Visual Processing, and Digital Display IV, Proceedings of the IS and T/SPIE’s Symposium on Electronic Imaging: Science and Technology, San Jose, CA, USA, 31 January–5 February 1993; Allebach, J.P., Rogowitz, B.E., Eds.; SPIE: Bellingham, WA, USA, 1993. [Google Scholar]
- Li, Q.; Cox, I.J. Improved Spread Transform Dither Modulation using a Perceptual Model: Robustness to Amplitude Scaling and JPEG Compression. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; pp. II-185–II-188. [Google Scholar]
- Zhang, X.H.; Lin, W.S.; Xue, P. Improved estimation for just-noticeable visual distortion. Signal Process. 2004, 85, 795–808. [Google Scholar] [CrossRef]
- Wei, Z.; Ngan, K.N. Spatial just noticeable distortion profile for image in DCT domain. In Proceedings of the 2008 IEEE International Conference on Multimedia and Expo, Hannover, Germany, 23–26 June 2008; pp. 925–928. [Google Scholar]
- Ma, L.; Yu, D.; Wei, G.; Tian, J.; Lu, H. Adaptive Spread-Transform Dither Modulation Using a New Perceptual Model for Color Image Watermarking. IEICE Trans. Inf. Syst. 2010, 93, 843–857. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Sun, J.; Yang, X.; Liu, W. Step-projection-based spread transform dither modulation. IET Inf. Secur. 2011, 5, 170–180. [Google Scholar] [CrossRef]
- Tang, W.; Wan, W.; Liu, J.; Sun, J. Improved Spread Transform Dither Modulation Using Luminance-Based JND Model. In Image and Graphics, Proceedings of the 8th International Conference on Image and Graphics, ICIG 2015, Tianjin, China, 13–16 August 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 430–437. [Google Scholar]
- Bae, S.H.; Kim, M. A Novel DCT-Based JND Model for Luminance Adaptation Effect in DCT Frequency. IEEE Signal Process. Lett. 2013, 20, 893–896. [Google Scholar]
- Zhang, L.; Shen, Y.; Li, H. VSI: A visual saliency-induced index for perceptual image quality assessment. IEEE Trans. Image Process. 2014, 23, 4270–4281. [Google Scholar] [CrossRef] [PubMed]
- Gu, K.; Zhai, G.; Yang, X.; Chen, L.; Zhang, W. Nonlinear additive model based saliency map weighting strategy for image quality assessment. In Proceedings of the 2012 IEEE 14th International Workshop on Multimedia Signal Processing (MMSP), Banff, AB, Canada, 17–19 September 2012; pp. 313–318. [Google Scholar]
- Ling, J.; Liu, J.; Sun, J.; Sun, X. Visual model based iterative AQIM watermark algorithm. Acta Electron. Sin. 2010, 38, 151–155. [Google Scholar]
- Amrutha, I.; Shylaja, S.; Natarajan, S.; Murthy, K. A smart automatic thumbnail cropping based on attention driven regions of interest extraction. In Proceedings of the 2nd International Conference on Interaction Sciences: Information Technology, Culture and Human, Seoul, Korea, 24–26 November 2009; pp. 957–962. [Google Scholar]
- Niu, Y.; Todd, R.M.; Anderson, A.K. Affective salience can reverse the effects of stimulus-driven salience on eye movements in complex scenes. Front. Psychol. 2012, 3, 336. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Liu, J.; Sun, J.; Ge, C.; Nie, X. Logarithmic STDM watermarking using visual saliency-based JND model. Electron. Lett. 2015, 51, 758–760. [Google Scholar] [CrossRef]
- Lubin, J. A human vision system model for objective picture quality measurements. In Proceedings of the 1997. International Broadcasting Convention, Amsterdam, Netherlands, 12–16 September 1997; pp. 498–503. [Google Scholar]
- Treisman, A.M.; Gelade, G. A feature-integration theory of attention. Cogn. Psychol. 1980, 12, 97–136. [Google Scholar] [CrossRef]
- Han, J.; Ngan, K.N.; Li, M.; Zhang, H.J. Unsupervised extraction of visual attention objects in color images. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 141–145. [Google Scholar] [CrossRef]
- Rutishauser, U.; Walther, D.; Koch, C.; Perona, P. Is bottom-up attention useful for object recognition? In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. II-37–II-44. [Google Scholar]
- Fang, Y.; Lin, W.; Chen, Z.; Tsai, C.M.; Lin, C.W. A Video Saliency Detection Model in Compressed Domain. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 27–38. [Google Scholar] [CrossRef]
- Rust, B.W.; Rushmeier, H.E. A New Representation of the Contrast Sensitivity Function for Human Vision. In Proceedings of the International Conference on Imaging Science, System, Technology, Las Vegas, NV, USA, 30 June–3 July 1997. [Google Scholar]
- Ahumada, A.J., Jr.; Peterson, H.A. Luminance-model-based DCT quantization for color image compression. Proc. SPIE 1992, 1666, 365–374. [Google Scholar]
- Zhang, L.; Gu, Z.; Li, H. SDSP: A novel saliency detection method by combining simple priors. In Proceedings of the 2013 20th IEEE International Conference on Image Processing (ICIP), Melbourne, Australia, 15–18 September 2013; pp. 171–175. [Google Scholar]
- Achanta, R.; Hemami, S.; Estrada, F.; Susstrunk, S. Frequency-tuned salient region detection. In Proceedings of the CVPR 2009 IEEE Conference on Computer vision and pattern recognition, Miami, FL, USA, 20–25 June 2009; pp. 1597–1604. [Google Scholar]
- Field, D.J. Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 1987, 4, 2379–2394. [Google Scholar] [CrossRef] [PubMed]
- Judd, T.; Ehinger, K.; Durand, F.; Torralba, A. Learning to predict where humans look. In Proceedings of the 2009 IEEE 12th international conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 2106–2113. [Google Scholar]
- USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 20 August 2017).
- Wan, W.; Liu, J.; Sun, J.; Yang, X.; Nie, X.; Wang, F. Logarithmic spread-transform dither modulation watermarking based on perceptual model. In Proceedings of the 2013 20th IEEE International Conference on Image Processing (ICIP), Melbourne, Australia, 15–18 September 2013; pp. 4522–4526. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]


| Attack | STDM-RW | STDM-AdpWM | STDM-RDMWm | LSTDM-WM | Proposed |
|---|---|---|---|---|---|
| Salt-and-peppers noise | |||||
| 0.015 | 0.2881 | 0.2292 | 0.2393 | 0.2185 | 0.2093 |
| Wiener filtering | |||||
| 0.1611 | 0.1264 | 0.1889 | 0.1533 | 0.1189 | |
| Median filtering | |||||
| 0.1631 | 0.1201 | 0.1194 | 0.1631 | 0.1130 | |
| Average | 0.2041 | 0.1585 | 0.1825 | 0.1783 | 0.1471 |
| Attack | STDM-RW | STDM-AdpWM | STDM-RDMWm | LSTDM-WM | Proposed |
|---|---|---|---|---|---|
| Salt-and-peppers noise | |||||
| 0.015 | 0.2129 | 0.1885 | 0.1885 | 0.1221 | 0.1145 |
| Wiener filtering | |||||
| 0.0869 | 0.0938 | 0.0549 | 0.1064 | 0.0479 | |
| Median filtering | |||||
| 0.1143 | 0.1094 | 0.0840 | 0.1038 | 0.0645 | |
| Average | 0.1380 | 0.1306 | 0.1091 | 0.1107 | 0.0756 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, T.; Wan, W.; Han, X.; Xu, M. A Novel STDM Watermarking Using Visual Saliency-Based JND Model. Information 2017, 8, 103. https://doi.org/10.3390/info8030103
Wang C, Zhang T, Wan W, Han X, Xu M. A Novel STDM Watermarking Using Visual Saliency-Based JND Model. Information. 2017; 8(3):103. https://doi.org/10.3390/info8030103
Chicago/Turabian StyleWang, Chunxing, Teng Zhang, Wenbo Wan, Xiaoyue Han, and Meiling Xu. 2017. "A Novel STDM Watermarking Using Visual Saliency-Based JND Model" Information 8, no. 3: 103. https://doi.org/10.3390/info8030103





