Physical Layer Security and Optimal Multi-Time-Slot Power Allocation of SWIPT System Powered by Hybrid Energy
Abstract
:1. Introduction
2. The System Model and Mathematical Modeling
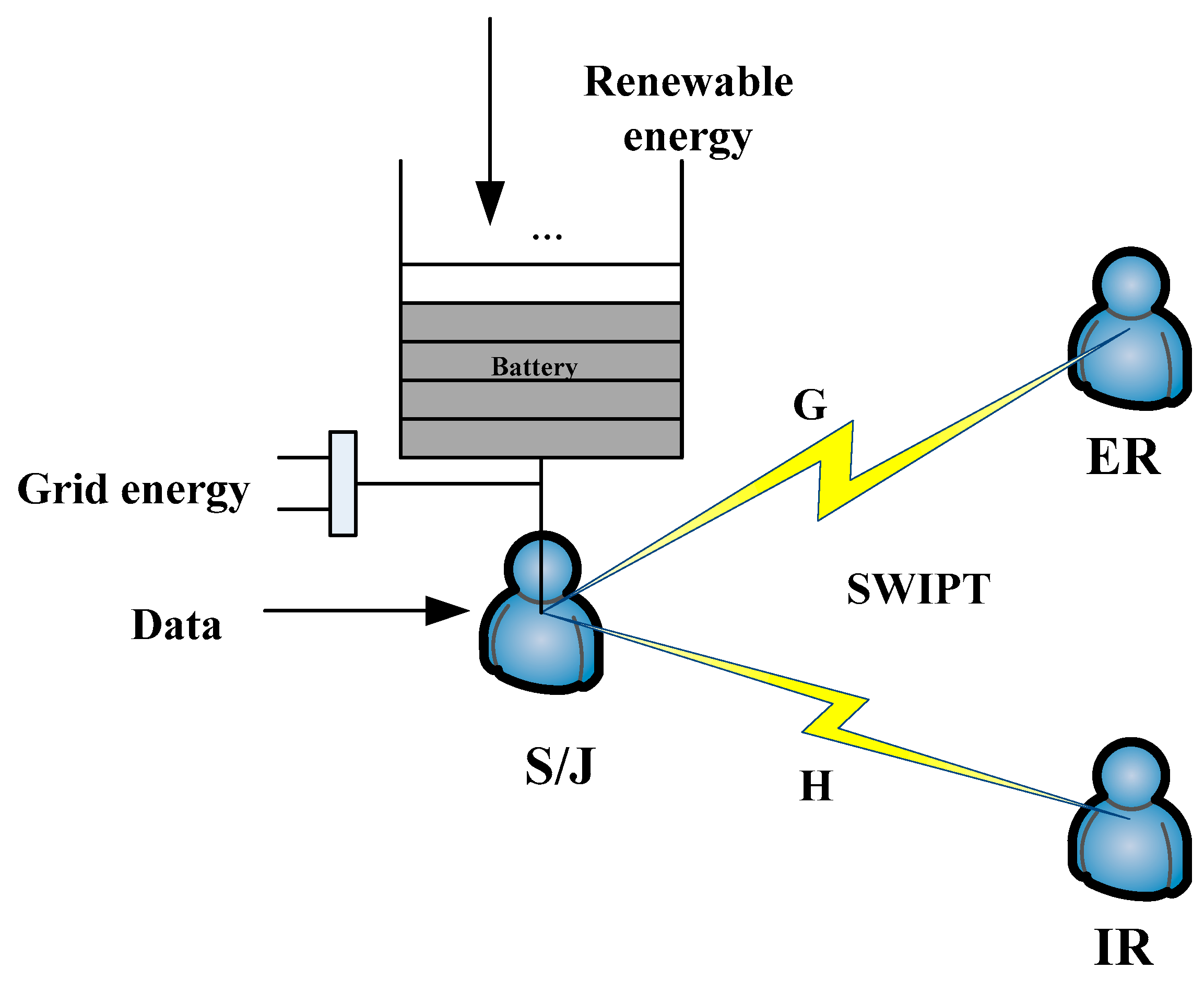
2.1. The System Model
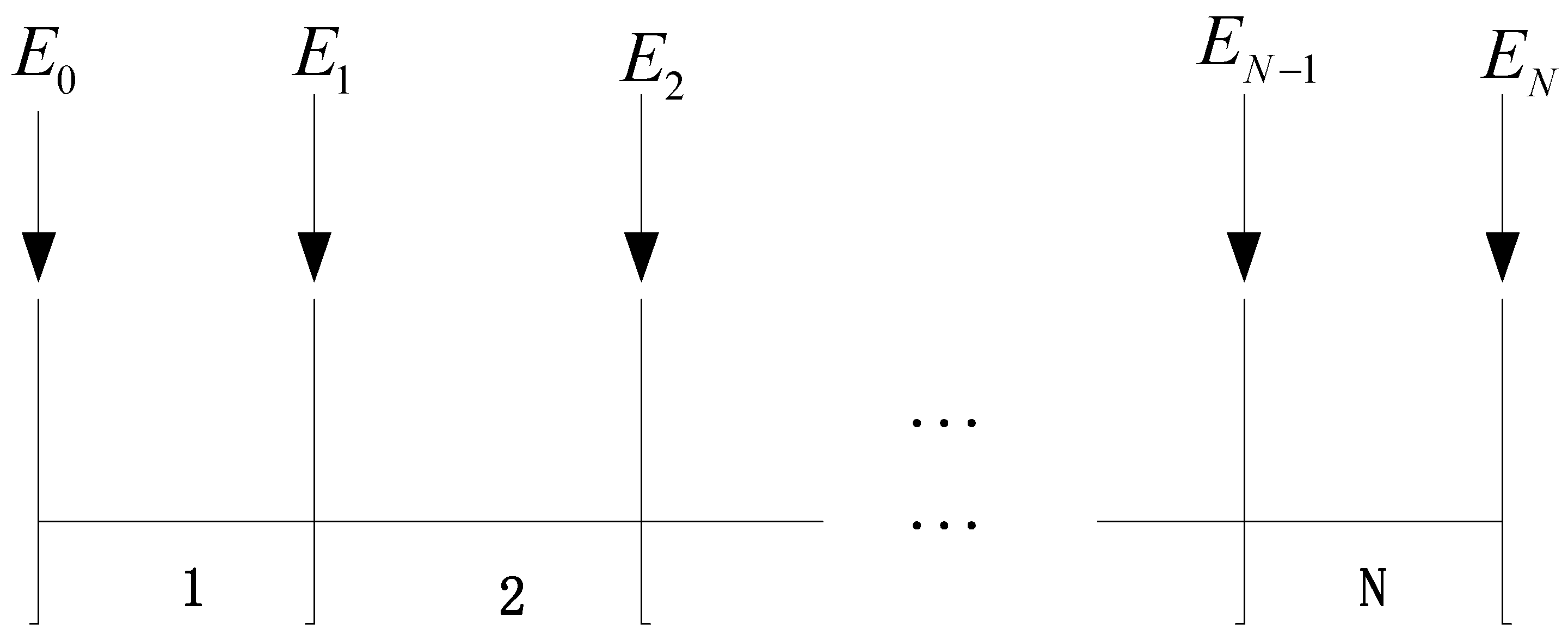
2.2. The Mathematical Modeling
3. The Optimal Power Splitting Ratio and Transmit Power
3.1. The Power Splitting Ratio
3.2. The Optimal Transmit Power
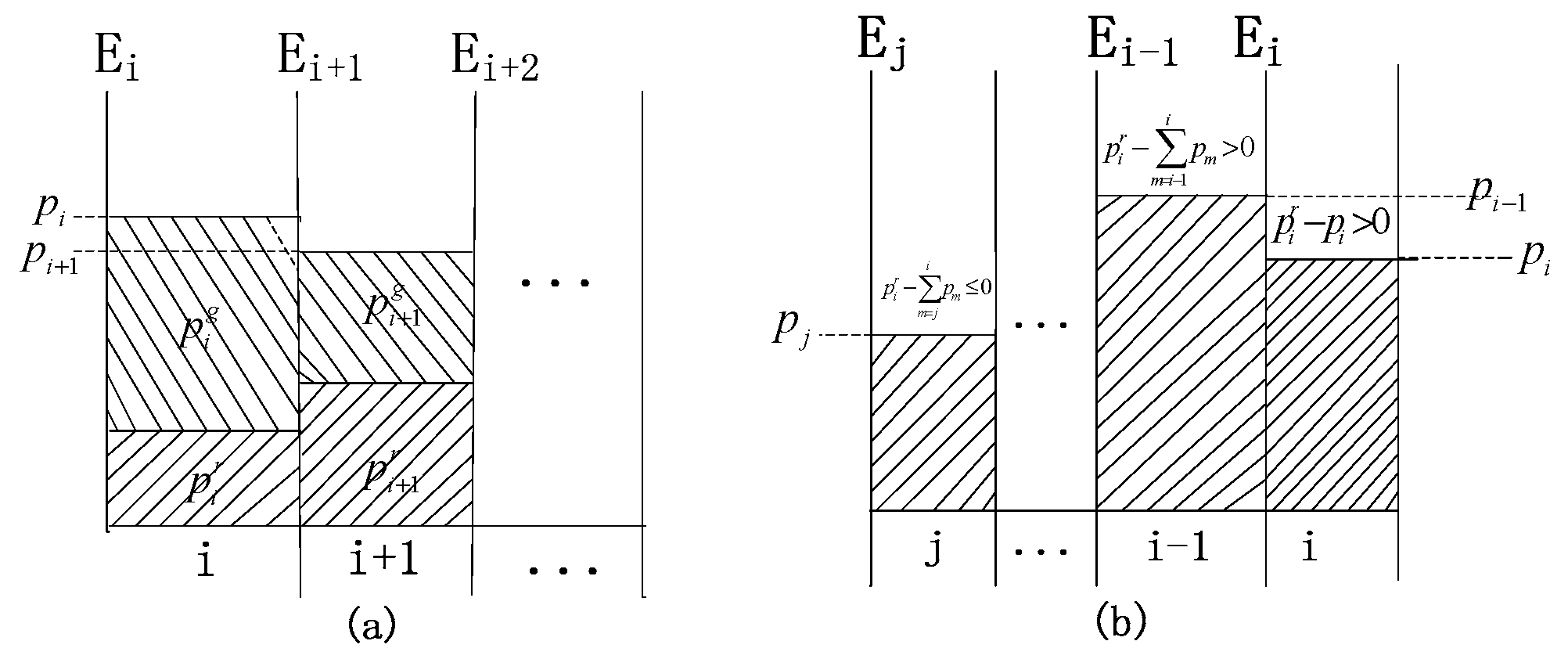
4. A Power Allocation Algorithm
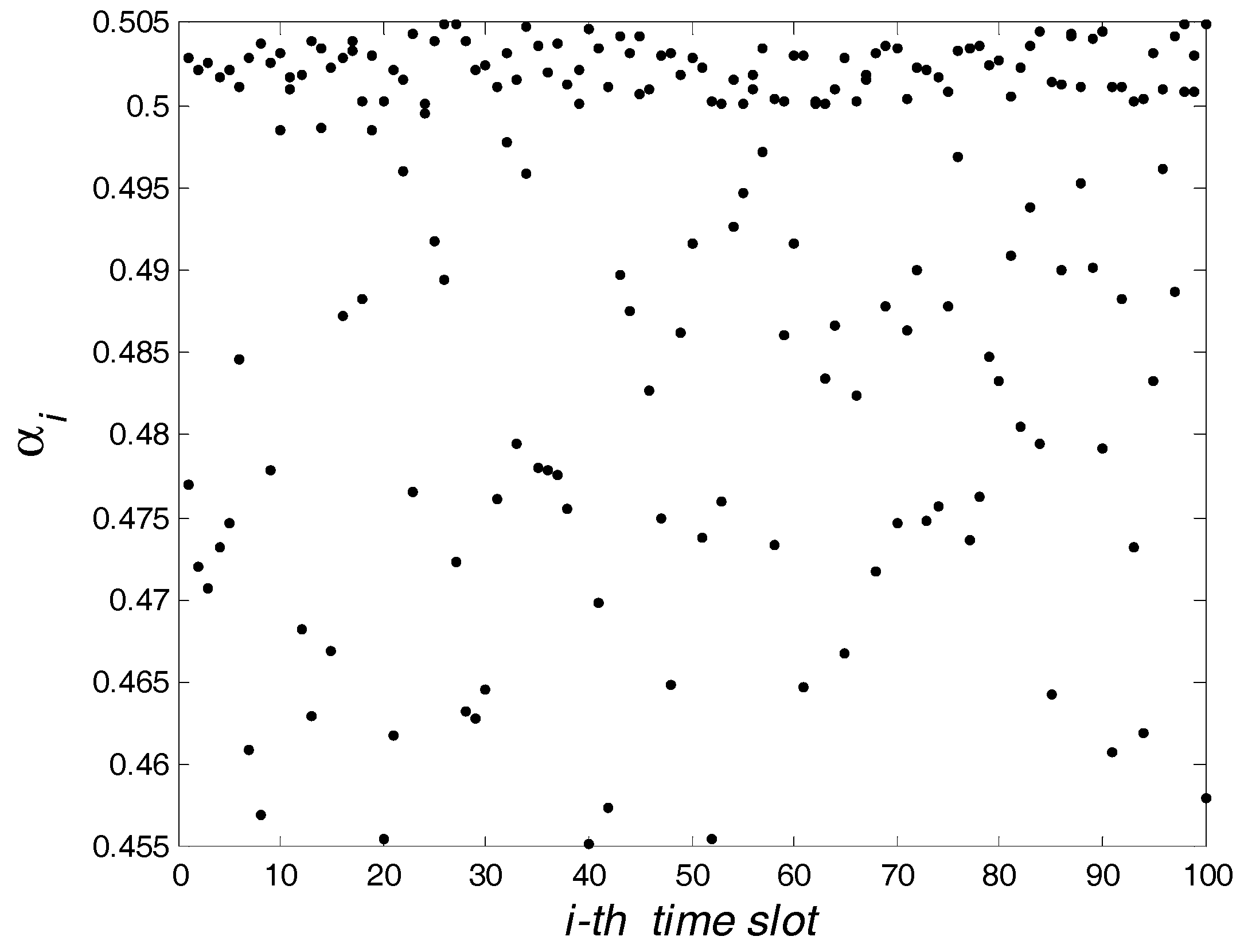
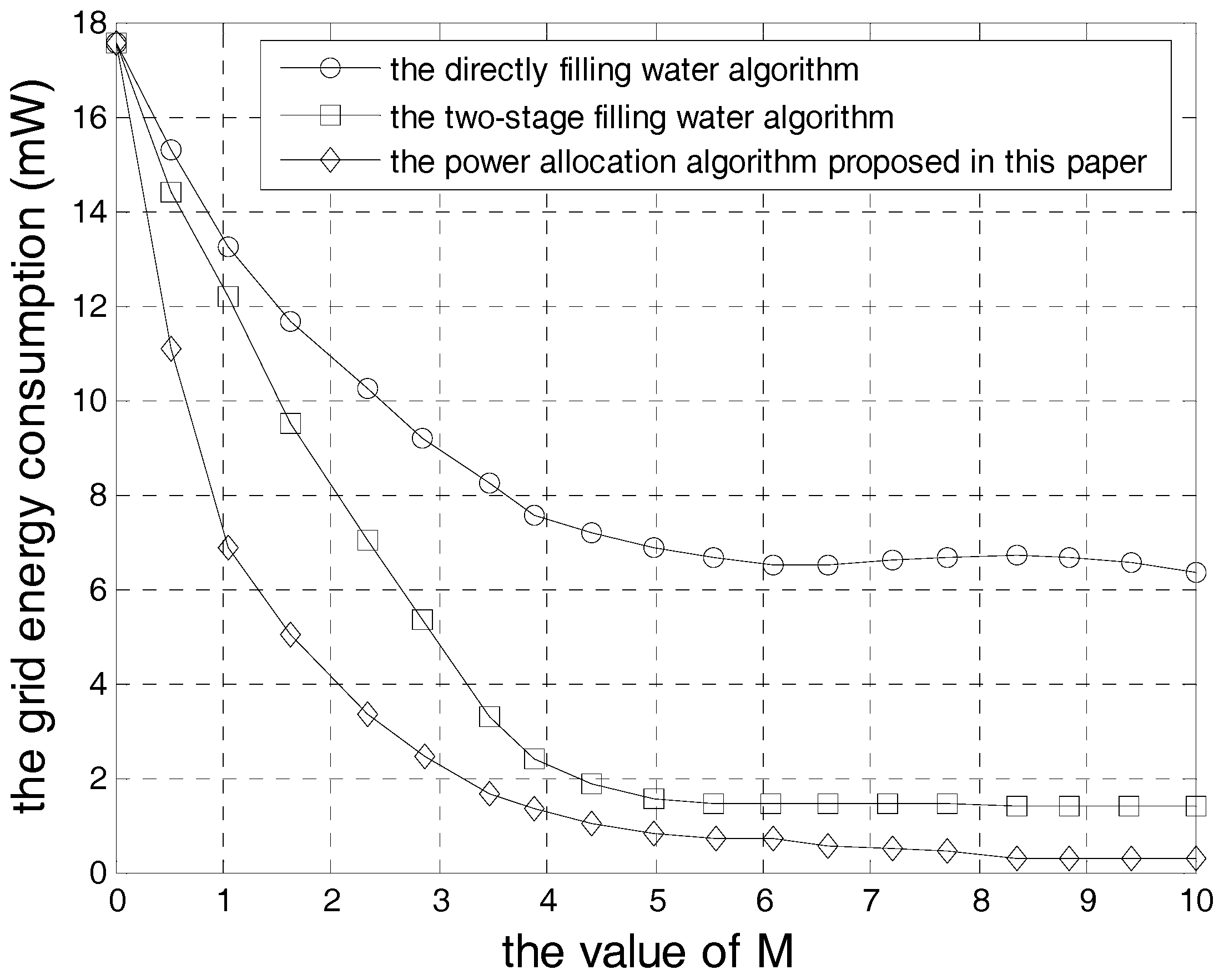
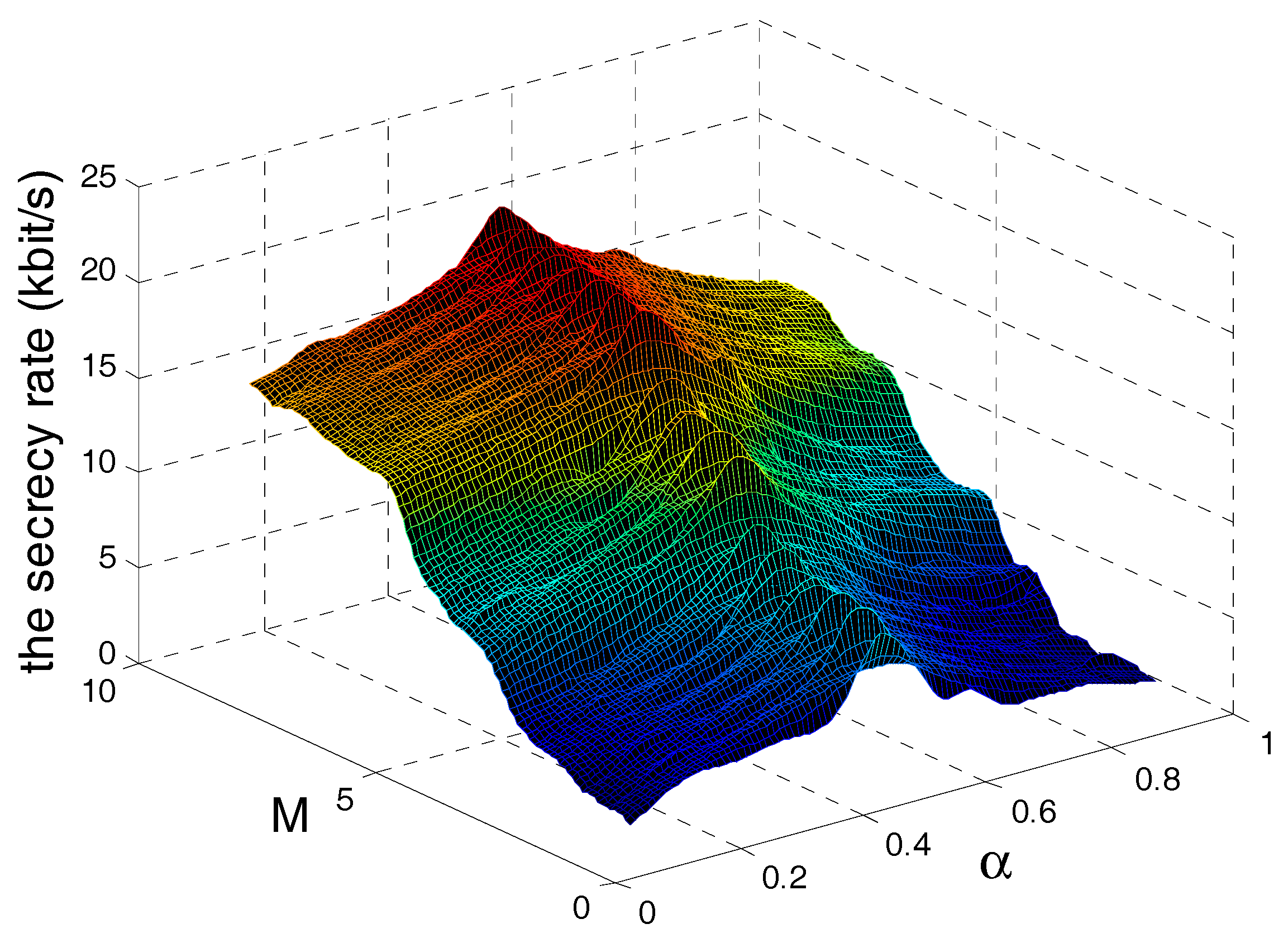
5. Simulation Results
6. Conclusions and Future Works
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bockelmann, C.; Prata, N.; Nilopour, H.; Au, K.; Svensson, T.; Stefanovic, C.; Popovski, P.; Dekorsy, A. Massive machine-type communications in 5G: Physical and MAC-layer solu tions. IEEE Commun. Mag. 2016, 54, 59–65. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, W.C.; Zhang, H.L. Full-duplex transmission in PHY and MAC layers for 5G mobile wireless networks. IEEE Wirel. Commun. 2015, 22, 112–121. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Lee, K.J.; Wang, Z.Y.; Lee, I. Robust beamforming and power splitting design in distributed antenna system with SWIPT under bounded channel uncertainty. In Proceedings of the IEEE 81st Vehicular Technology Conference, Glasgow, UK, 11–14 May 2015. [Google Scholar]
- Zhu, Z.Y.; Chu, Z.; Wang, Z.Y.; Lee, I. Joint optimization of AN-aided beamforming and power splitting designs for MISO secrecy channel with SWIPT. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016. [Google Scholar]
- Zhang, H.; Du, J.; Cheng, J.; Leung, V.C.M. Resource allocation in SWIPT enable heterogeneous cloud small cell networks with incomplete CSI. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Wu, Y.N.; Chen, X.M. Robust beamforming and power splitting for secrecy wireless information and power transfer in cognitive relay networks. IEEE Commun. Lett. 2016, 20, 1152–1155. [Google Scholar] [CrossRef]
- Chen, X.M.; Ng, D.W.K.; Chen, H.H. Secrecy wireless information and power transfer: Challenges and opportunities. IEEE Wirel. Commun. 2016, 23, 54–61. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Li, C.G.; Huang, Y.M.; Yang, L.X. Secure beamforming for SWIPT in multiuser MISO broadcast channels with confidential messages. IEEE Commun. Lett. 2015, 19, 1347–1350. [Google Scholar] [CrossRef]
- Romero-Zurita, N.; Mclernon, D.; Ghogho, M.; Swami, A. PHY layer security based on protected zone and artificial noise. IEEE Signal Process. Lett. 2013, 20, 487–490. [Google Scholar] [CrossRef]
- Zhang, H.; Hong, X.; Cheng, J.; Nallanathan, A.; Leung, V. Secure resource allocation for OFDMA two-way relay wireless sensor networks without and with cooperative jamming. IEEE Trans. Ind. Inf. 2016, 12, 1714–1725. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, H.X.; Wu, D.L.; Yuan, D.F. Improving physical layer security for MISO systems via using artificial noise. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015. [Google Scholar]
- Chu, Z.; Zhu, Z.Y.; Hussein, J. Robust optimization for AN-Aided transmission and power splitting for secure MISO SWIPT system. IEEE Commun. Lett. 2016, 20, 1571–1574. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Schober, R. Secure and green SWIPT in distributed Antenna Networks with limited backhaul capacity. IEEE Trans. Wirel. Commun. 2015, 14, 5082–5097. [Google Scholar] [CrossRef]
- Yuan, B.; Yang, X.; Li, D.H. Analysis and design of a high efficiency current fed multi-resonant converter for high step-up power conversion in renewable energy harvesting. In Proceedings of the 2010 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Hefei, China, 16–18 September 2010; pp. 138–143. [Google Scholar]
- Che, L.; Zhang, X.P.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal interconnection planning of community microgrids with renewable energy sources. IEEE Trans. Smart Grid 2017, 8, 1054–1063. [Google Scholar] [CrossRef]
- Gong, J.; Zhou, S.; Niu, Z.S. Optimal power allocation for energy harvesting and power grid coexisting wireless communication systems. IEEE Trans. Commun. 2013, 61, 3040–3049. [Google Scholar] [CrossRef]
- Ozel, O.; Tutuncuogl, K.; Yang, J.; Ulukus, S.; Yener, A. Transmission with energy harvesting nodes in fading wireless channels: Optimal policies. IEEE J. Sel. Areas Commun. 2011, 29, 1732–1743. [Google Scholar] [CrossRef]
- Yang, J.; Ozel, O.; Ulukus, S. Broadcasting with an energy harvesting rechargeable transmitter. IEEE Trans. Wirel. Commun. 2012, 29, 571–583. [Google Scholar] [CrossRef]
- Yang, J.; Ulukus, S. Optimal packet scheduling in a multiple access channel with rechargeable nodes. In Proceedings of the IEEE ICC, Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Yang, G.J.; Xie, L.P.; Zeng, J.C. A hybrid vector artificial physics optimization with one-dimensional search. In Proceedings of the 2010 International Conference on Computational Aspects of Social Networks (CASoN 2010), Taiyuan, China, 26–28 September 2010; pp. 19–22. [Google Scholar]
- Hong, X.; Liu, L.; Zhang, R. Secrecy wireless information and power transfer in fading wiretap channel. IEEE Trans. Veh. Technol. 2016, 65, 180–190. [Google Scholar]
- Jiang, X.; Zhang, C.; Zhang, Z.; Karagiannidis, G.K. Power beacon assisted wiretap channels with jamming. IEEE Trans. Wirel. Commun. 2016, 15, 8353–8367. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Li, B.; Zhao, W. Physical Layer Security and Optimal Multi-Time-Slot Power Allocation of SWIPT System Powered by Hybrid Energy. Information 2017, 8, 100. https://doi.org/10.3390/info8030100
Guo D, Li B, Zhao W. Physical Layer Security and Optimal Multi-Time-Slot Power Allocation of SWIPT System Powered by Hybrid Energy. Information. 2017; 8(3):100. https://doi.org/10.3390/info8030100
Chicago/Turabian StyleGuo, Dandan, Baogang Li, and Wei Zhao. 2017. "Physical Layer Security and Optimal Multi-Time-Slot Power Allocation of SWIPT System Powered by Hybrid Energy" Information 8, no. 3: 100. https://doi.org/10.3390/info8030100



