2. Results of Analysis of Symmetries in Genetic Alphabets
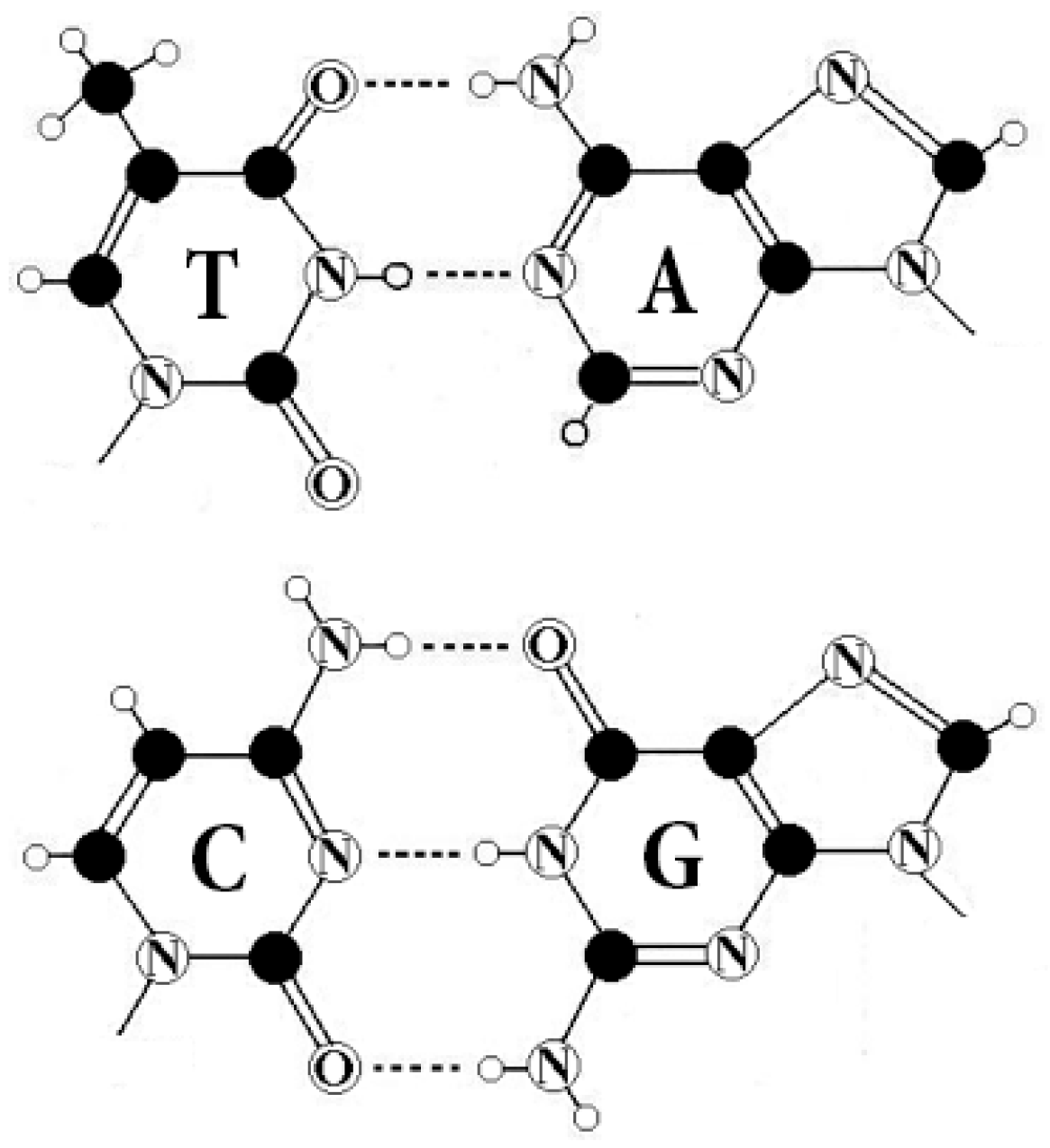
All living organisms are identical from the point of view of the molecular foundations of genetic coding of sequences of amino acids in proteins. This coding is based on molecules of DNA and RNA. In DNA, the genetic information is recorded using different sequences of four nitrogenous bases, which play the role of letters of the alphabet: adenine A, guanine G, cytosine C, and thymine T (uracil U is used in RNA instead of thymine T) (
Figure 1).
Science does not know why the genetic alphabet of DNA has been created by nature from just four letters, and why just these very simple molecules were chosen for the DNA-alphabet (out of millions of possible molecules). But science knows [
2,
3,
5,
6] that these four molecules are interrelated by means of their symmetrical peculiarities into the united molecular ensemble with its three pairs of binary-oppositional traits (
Table 1):
- (1)
Two letters are purines (A and G), and the other two are pyrimidines (C and T). From the standpoint of these binary-oppositional traits one can denote C = T = 0, A = G = 1. From the standpoint of these traits, any of the DNA-sequences are represented by a corresponding binary sequence. For example, GCATGAAGT is represented by 101011110;
- (2)
Two letters are amino-molecules (A and C) and the other two are keto-molecules (G and T). From the standpoint of these traits one can designate A = C = 0, G = T = 1. Correspondingly, the same sequence, GCATGAAGT, is represented by another binary sequence, 100110011;
- (3)
The pairs of complementary letters, A-T and C-G, are linked by 2 and 3 hydrogen bonds, respectively. From the standpoint of these binary traits, one can designate C = G = 0, A = T = 1. Correspondingly, the same sequence, GCATGAAGT, is read as 001101101.
Accordingly, each of the DNA-sequences of nucleotides is the carrier of three parallel messages on three different binary languages. At the same time, these three types of binary representations form a common logical set on the basis of logical operation of modulo-2 addition: modulo-2 addition of any two such binary representations of the DNA-sequence coincides with the third binary representation of the same DNA-sequence. One can be reminded here of the rules of the bitwise modulo-2 addition (denoted by the symbol, ): 0 0 = 0; 0 1 = 1; 1 0 = 1; 1 1 = 0. The mentioned three representations of the sequence GCATGAAGT form a common logical set: for example, 101011110 100110011 = 001101101.
This fact is the initial evidence in favor that the system of genetic coding uses Boolean algebra of logic with its binary tuples and logical operations, such as modulo-2 addition. Correspondingly, one can think that there is a profound analogy between genetic organization of living bodies and computers, which are based on Boolean algebra.
Modulo-2 addition is utilized broadly in the theory of discrete signal processing as a fundamental operation for binary variables and for dyadic groups of binary numbers [
7]. This logic operation serves as the group operation in symmetric dyadic groups of
n-bit binary numbers (
n = 2, 3, 4, …) [
8]. Each of such symmetric groups contains 2
n members. The distance in these groups is known as the Hamming distance. Since the Hamming distance satisfies the conditions of a metric group, any dyadic group is a metric group. The expression (1) shows an example of the dyadic group of 3-bit binary numbers:
The modulo-2 addition of any two binary numbers from (1) always results in a new number from the same series. For example, modulo-2 addition of two binary numbers, 110 and 101, which are equal to 6 and 5, respectively, in decimal notation, gives the result 110
101 = 011, which is equal to 3 in decimal notation. The number 000 serves as the unit element of this group: for example, 010
000 = 010. The reverse element for any number in this group is the number itself: for example, 010
010 = 000. The series (1) is transformed by modulo-2 addition of all its members with the binary number 001 into a new series of the same numbers: 001, 000, 011, 010, 101, 100, 111, 110. Such changes in the initial binary sequence, produced by modulo-2 addition of its members with any of binary numbers from (1), are termed dyadic shifts [
7,
8]. If any system of elements demonstrates its connection with dyadic shifts, it indicates that the structural organization of the system is connected with the logic modulo-2 addition. Works [
2,
3,
9] show additionally that the structural organization of the molecular-genetic system is connected with dyadic shifts and correspondingly with modulo-2 addition. Below dyadic shifts also participate in analysis of molecular-genetic ensembles.
Information from the micro-world of genetic molecules dictates constructions in the macro-world of living bodies under conditions of strong noise and interference. This dictation is realized by means of unknown algorithms of multi-channel noise-immunity coding. For example, in accordance with Mendel’s laws of independent inheritance of traits, colors of human skin, eye, and hairs are genetically defined independently. So, each living organism is an algorithmic machine of multi-channel noise-immune coding. To understand this machine one should use the theory of noise-immune coding, which is based on matrix representations of digital information. This theory was developed by mathematicians for digital communication, where similar problems of noise-immune transfer of information exist, for example, when we need to transmit photos of the Martian surface to Earth via electromagnetic signals traveling through millions of kilometers of interference. Below, we borrow some formalisms of this mathematics to study genetic structures.
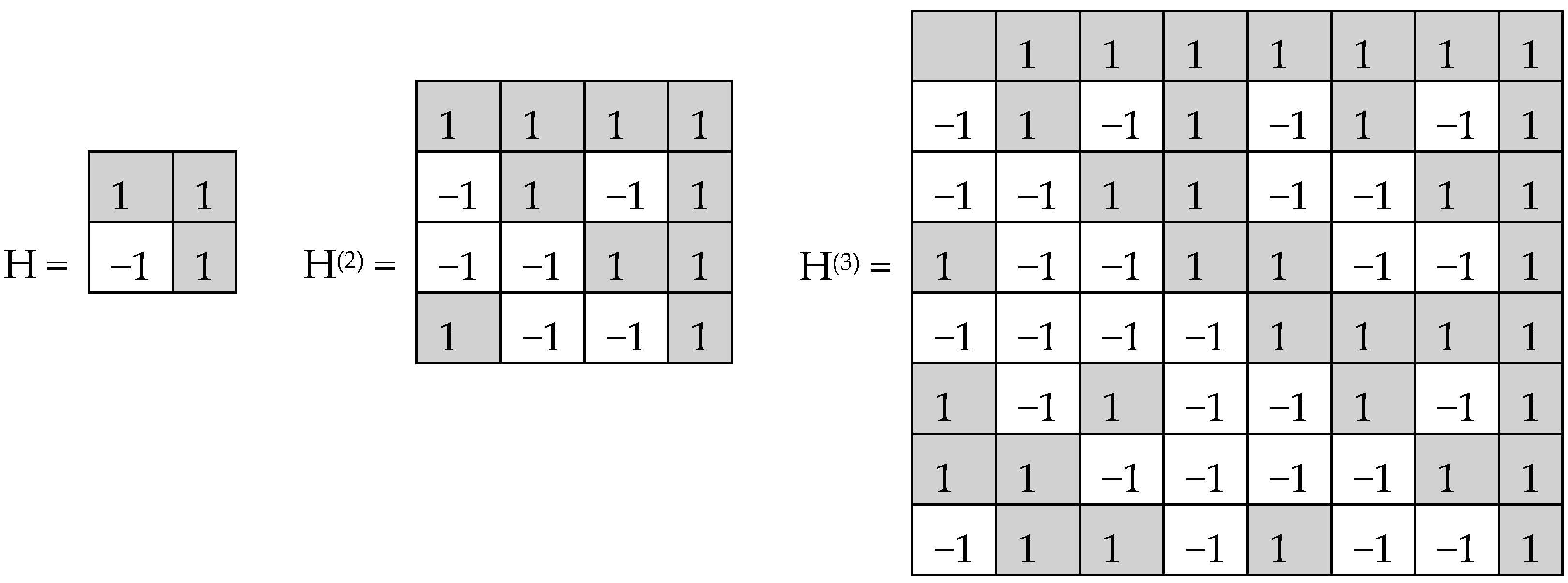
In noise-immune coding and also in quantum mechanics, Hadamard matrices play significant roles. By definition, a Hadamard matrix is a square matrix, H, with entries ±1, which satisfies H*H
T =
n*E, where H
T—transposed matrix, E—identity matrix. Tensor (or Kronecker) exponentiation of Hadamard (2*2)-matrix H generates a tensor family of Hadamard (2
n*2
n)-matrices H
(n) (
Figure 2), rows and columns of which are Walsh functions [
7].
Hadamard (2
n*2
n)-matrices in
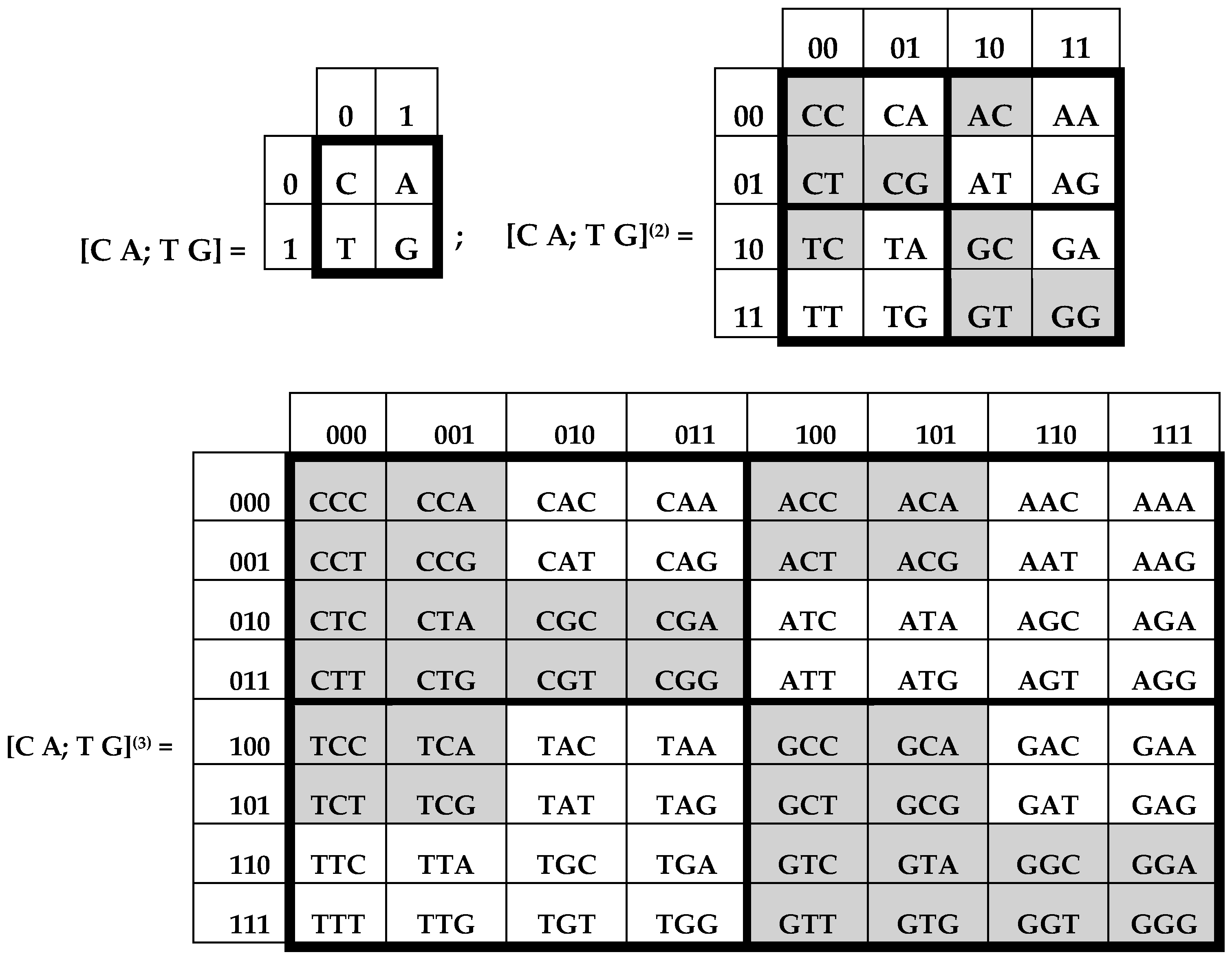
Figure 2 consist of 4, 16, and 64 entries. The DNA-alphabets also consist of 4 nitrogenous bases, 16 doublets and 64 triplets. By analogy, we represent the system of these alphabets in a form of the tensor family of square genetic matrices [C, A; T, G]
(n) in
Figure 3, with additional binary numerations of their rows and columns on the basis of the following principle [
2]. Entries of each column are numerated in accordance with the first sub-alphabet in
Figure 1 (for example, the triplet CAG and all other triplets in its column are the combinations, “pyrimidine-purin-purin”, and so this column is correspondingly numerated 011). By contrast, entries of each row are numerated in accordance with the second sub-alphabet (for example, the same triplet CAG and all other triplets in its row are the combinations, “amino-amino-keto”, and so this row is correspondingly numerated 001).
Black and white cells of genetic matrices [C, A; T, G]
(2) and [C, A; T, G]
(3) in
Figure 3 reflect the known phenomenon of segregation of the set of 64 triplets into two equal sub-sets on the basis of strong and weak roots, i.e., the first two positions in triplets [
10]: (a) black cells contain 32 triplets with strong roots, i.e., with 8 “strong” doublets AC, CC, CG, CT, GC, GG, GT, TC; (b) white cells contain 32 triplets with weak roots, i.e., with 8 “weak” doublets AA, AG, AT, GA, TA, TG, TT. Code meanings of triplets with strong roots do not depend on the letters in their third position; code meanings of triplets with weak roots depend on their third letter (see details in [
11]).
Figure 3 shows the unexpected phenomenological fact of a symmetrical disposition of black and white triplets in the genetic matrix [C, T; A, G]
(3), which was constructed formally without any mention about strong and weak roots, amino acids, and the degeneracy of the genetic code:
- (1)
The left and right halves of the matrix mosaic are mirror-anti-symmetric each to the other in its colors: any pair of cells, disposed by a mirror-symmetrical manner in the halves, possesses the opposite colors;
- (2)
Both quadrants along each diagonal are identical from the standpoint of their mosaic;
- (3)
The mosaics of all rows have meander configurations (each row has black and white fragments of equal lengths) and they are identical to mosaics of some Walsh functions, which coincide with Rademacher functions as the particular cases of Walsh functions;
- (4)
Each pair of adjacent rows of decimal numeration 0–1, 2–3, 4–5, 6–7 has an identical mosaic (the realization of the principle “even-odd”).
It should be noted that a huge quantity, 64! ≈ 10
89, of variants exists for locations of 64 triplets in a separate (8*8)-matrix. For comparison, modern physics estimates time of existence of the Universe in 10
17 s. It is obvious that an accidental disposition of black and white triplets (and corresponding amino acids) in an (8*8)-matrix will almost never give symmetries. However, in our approach, this matrix of 64 triplets (
Figure 3) is not a separate matrix, but is one of members of the tensor family of matrices of genetic alphabets, and, in this case, wonderful symmetries are revealed in the location of black and white triplets. These symmetries testify that the location of black and white triplets in the set of 64 triplets is not accidental. Below, additional facts of symmetries also indicate that this is a regular distribution.
In digital signal processing, bit-reversal permutations play an important role; they are connected, in particularly, with quasi-holographic models, noise-immunity coding, and with algorithms of fast Fourier transform [
12,
13,
14,
15,
16]. The bit-reversal permutation is a permutation of a sequence of
n items, where
n = 2
k,
k—positive integer. It is defined by decimal indexing the elements of the sequence by the numbers from 0 to
n − 1 and then reversing the binary representation of each of these decimal numbers (each of these binary numbers has a length of exactly
k). Each item is then mapped to the new position given by this reversed value. For example, consider the sequence of eight letters,
abcdefgh. Their indexes are the binary numbers, 000, 001, 010, 011, 100, 101, 110, and 111 (in decimal notation, 0, 1, …, 7), which when bit-reversed become 000, 100, 010, 110, 001, 101, 011, and 111 (in decimal notation, 0, 4, 2, 6, 1, 5, 3, 7, where the first half of the series contains even numbers and the second half contains odd numbers). This permutation of indexes transforms the initial sequence,
abcdefgh, into the new sequence,
aecgbfdh. Repeating the same permutation on this new sequence returns to the starting sequence. In particular, bit-reverse permutations are applied to (2
n*2
n)-matrices, which represent visual images in tasks of noise-immunity coding these images. In these cases, bit-reverse permutations are applied to binary numerations of columns and rows of such matrices. Illustrations of results of bit-reverse permutations in such tasks are given in [
15,
16].
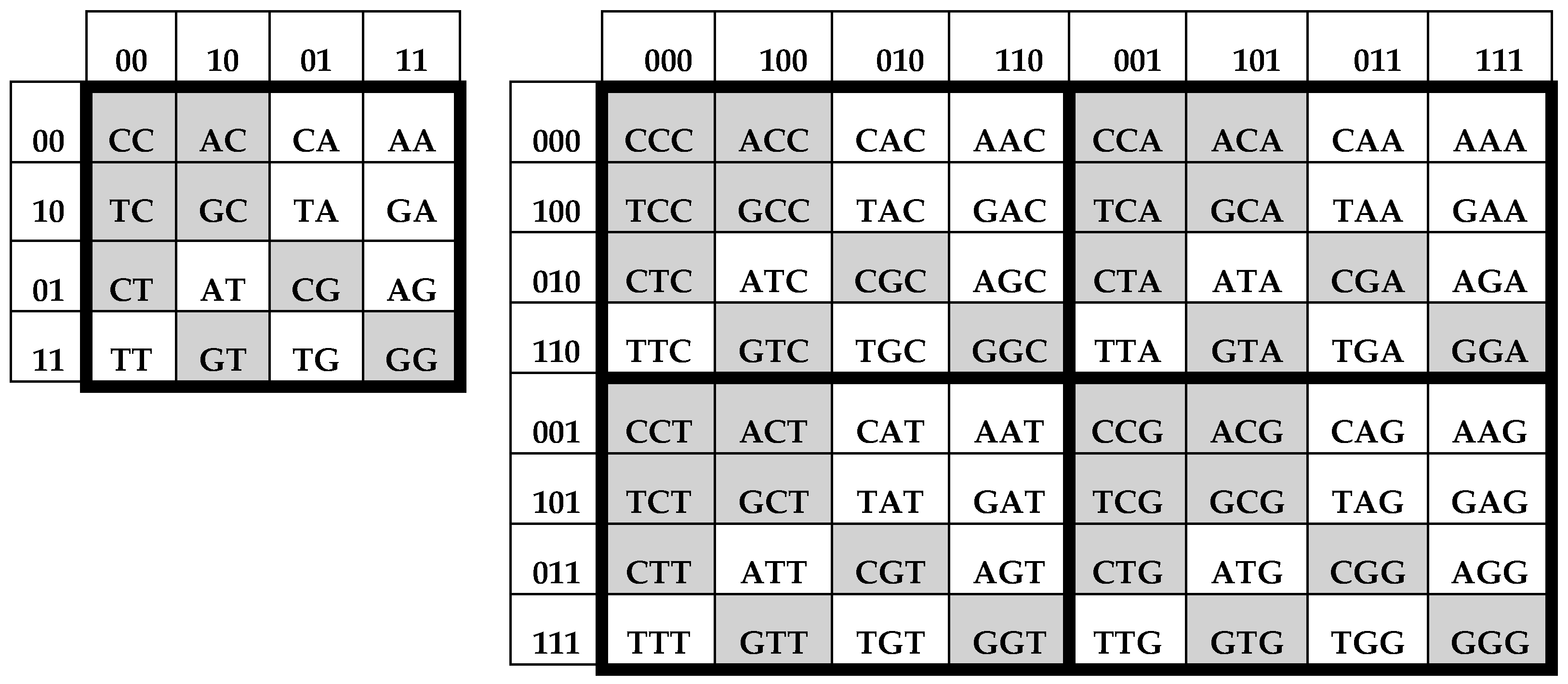
By analogy, bit-reverse permutations can be applied to binary numerations of columns and rows of the genetic matrices, [C, A; T, G]
(2) and [C, A; T, G]
(3), in
Figure 3. This action leads to new matrices of 16 doublets and 64 triplets, whose mosaics are interrelated (
Figure 4).
These matrices, which can be conditionally termed “bit-reversed matrices” (BR-matrices), have the following symmetric features of their mosaics (
Figure 4):
Mosaics of all 4 quadrants of the (8*8)-matrix of 64 triplets are identical;
The mosaic of each of the (4*4)-quadrants of the (8*8)-matrix of 64 triplets is identical to the mosaic of the (4*4)-matrix of 16 doublets. From the point of view of the black-and-white mosaics, the (8*8)-matrix of 64 triplets can be considered as a tetra-reproduction of the (4*4)-matrix of 16 doublets. This phenomenological relation between the molecular alphabets reminds one of the tetra-reproduction of biological cells in meiosis, that is, at the molecular genetic level, there is a structural analog of reproduction at the cellular level;
The mosaics of all rows have, again, meander configurations and they are identical to meander mosaics of some Walsh functions;
The mosaics of the left and right halves of the matrices are mirror-antisymmetric.
In relation to their mosaics, the matrices of 64 triplets (
Figure 3 and
Figure 4) possess a quasi-holographic property. If all entries of the lower half of the (8*8)-matrix in
Figure 4 are deleted (that is, these cells become empty), the bit-reverse permutations of the binary numeration of columns and rows of this matrix will lead to the changed variant of the (8*8)-matrix in
Figure 3, where all rows with odd numeration 1, 3, 5, 7 will be empty. However, in accordance with the abovementioned symmetric properties of the matrix in
Figure 3, the mosaics of these odd rows should be identical to the mosaics of adjacent even rows 0, 2, 4, 6, and so, they can be restored.
The double helix of DNA has the following correspondence to the bit-reverse permutations. As known, nucleotide sequences of two complementary filaments of DNA are read in opposite directions. If each of these complementary sequences is represented from the standpoint of the third binary sub-alphabet (
Figure 1), where A = T = 1, C = G = 0, then the binary representations of the sequences are the bit-reverse analogues to each other. For example, if one DNA-filament contains the sequence, ATGGCATTC, then the complementary filament contains the sequence, ТАССGTAAG, which is read in the opposite direction as GAATGCCAT. From the standpoint of the sub-alphabet A = T = 1, C = G = 0, the sequences ATGGCATTC and GAATGCCAT are represented by binary numbers 110001110 and 011100011, correspondingly, which are the bit-reverse analogues to each other.
We use the method of bit-reverse permutations to analyze the degeneracy of the genetic code in its different dialects and also to analyze nucleotide sequences of DNA in their binary representations, but these materials are beyond the scope of this article and they should be published separately.
From
Figure 3 and
Figure 4 one can see that entries of matrices in
Figure 3 are replaced in their cells by entries with the reverse order of positions of their letters. For example, all triplets, which have the order of positions 1-2-3 in
Figure 3, are replaced by their reversed analogues with the order of positions 3-2-1 (the triplet CGA is replaced by the triplet AGC, etc.). In studies of genetic coding, special attention is paid to cyclic codes connected with cyclic shifts [
17,
18,
19,
20,
21,
22]. Let us analyze transformations of genetic matrices of 64 triplets in
Figure 3 and
Figure 4 in cases of simultaneous cyclic permutations of 3 positions in each of the triplets. For the matrix in
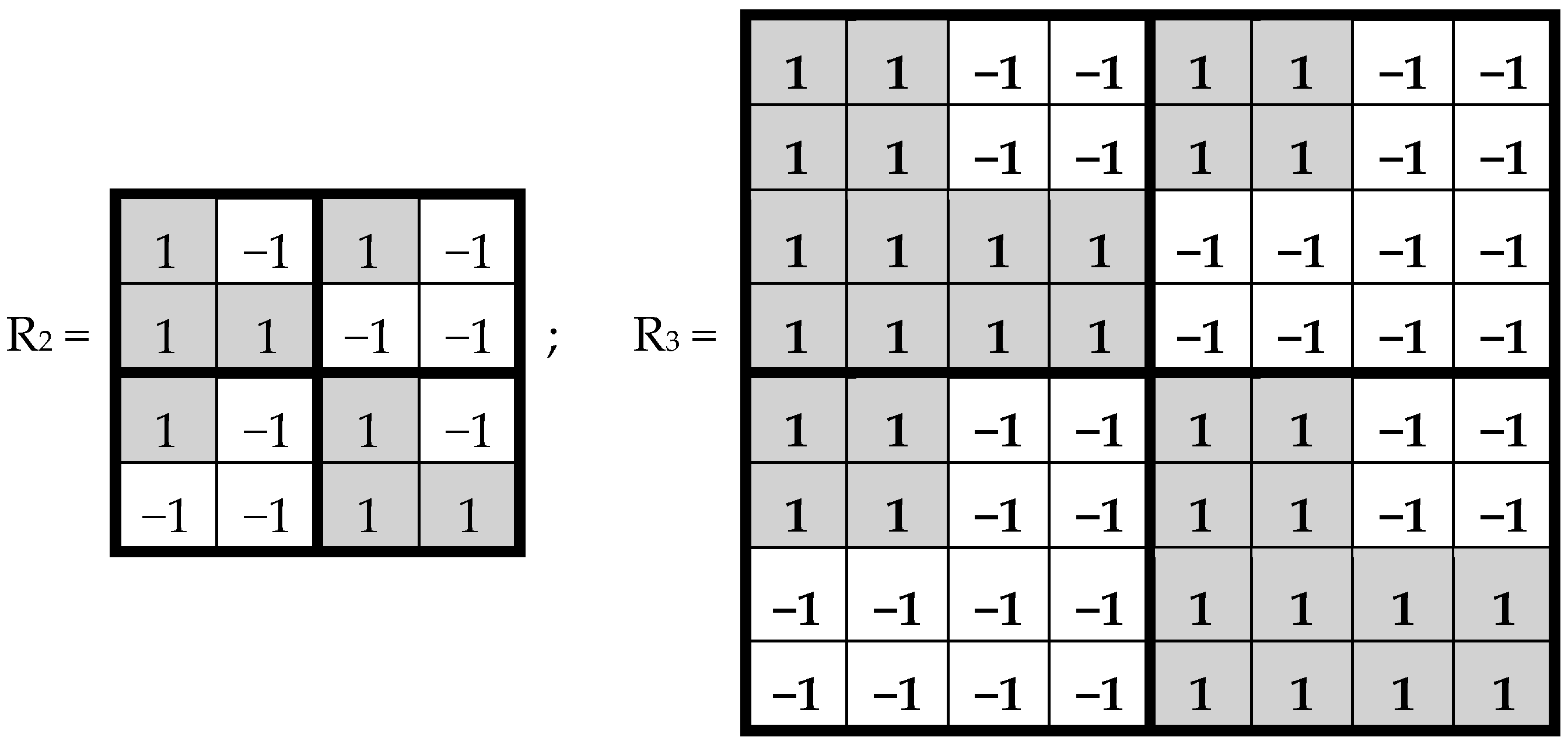
Figure 3, cyclic shifts define three possible orders of positions in triplets: 1-2-3, 2-3-1, 3-1-2. For the bit-reverse matrix in
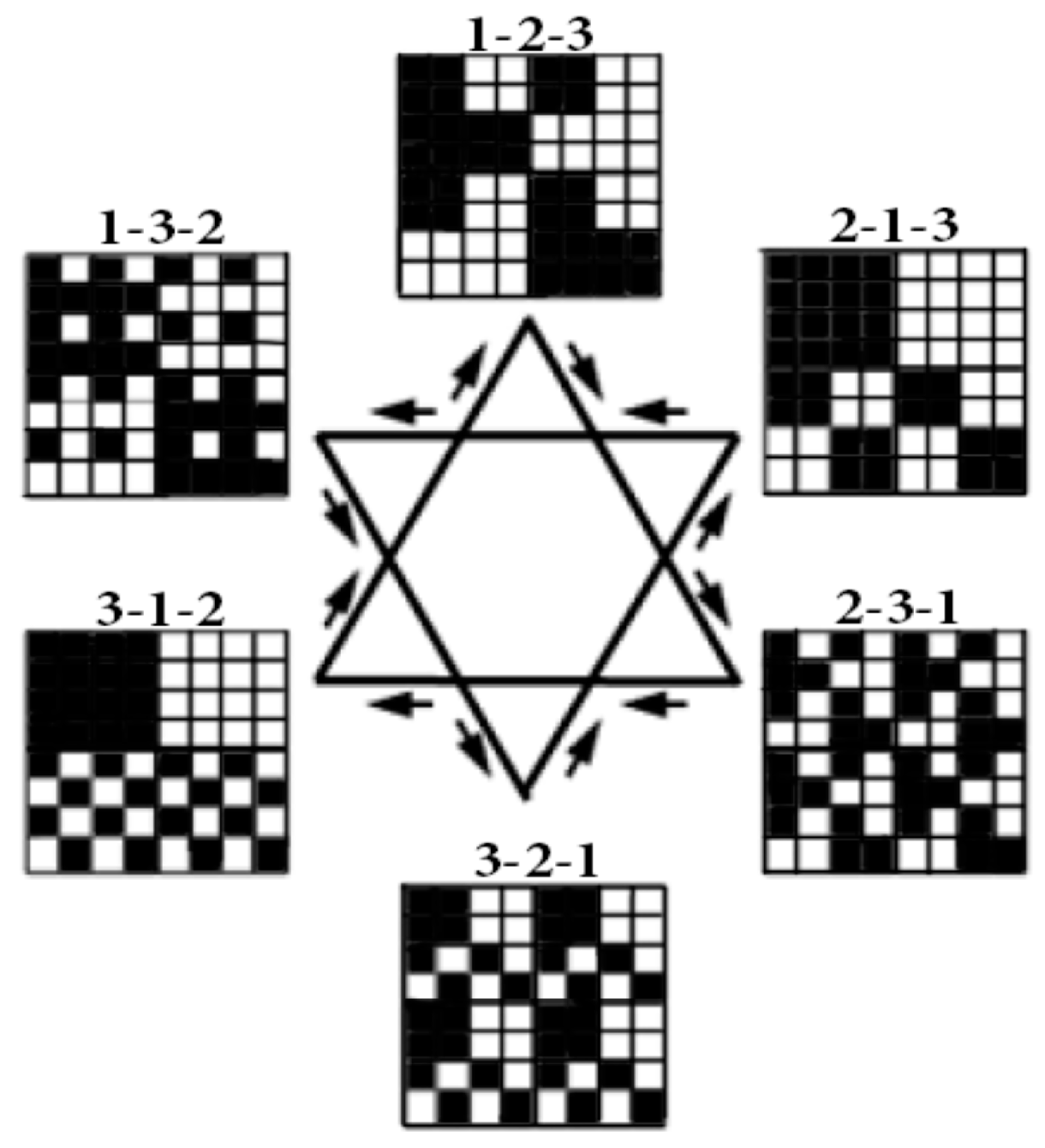
Figure 4, cyclic shifts define three reverse orders of positions in triplets: 3-2-1, 1-3-2, 2-1-3. Each of the corresponding 6 matrices of 64 triplets has an individual black-and-white mosaic of its location of triplets, with strong and weak roots.
Figure 5 shows the mosaics of the set of these 6 genetic matrices in a visual form of the six-vertex star (the Star of David), where vertices of one triangle correspond to the cases of the direct orders 1-2-3, 2-3-1, 3-1-2 and vertices of the second triangle correspond to the cases of the reverse orders 3-2-1, 1-3-2, 2-1-3 of positions in the triplets.
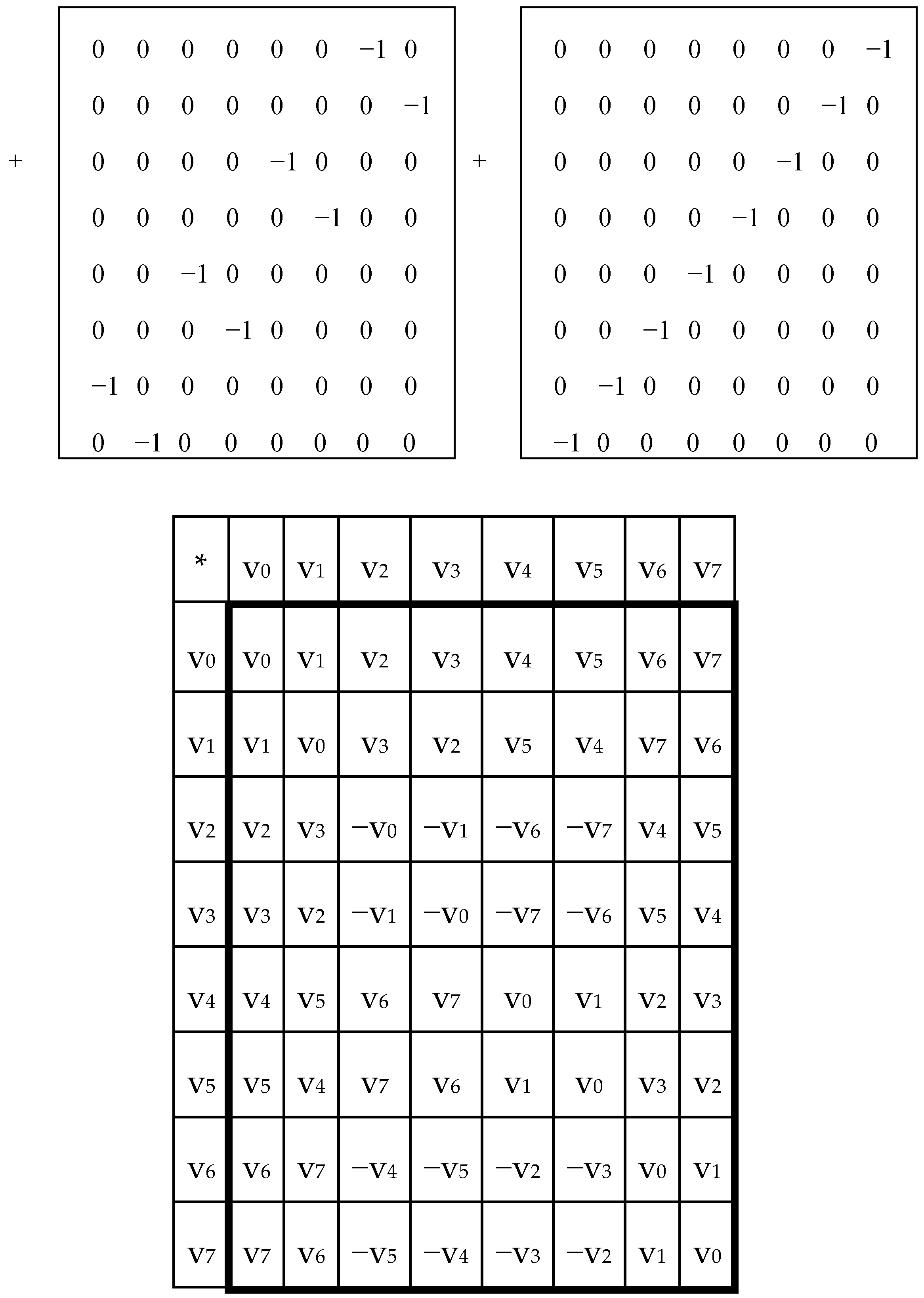
In each of these six matrices, each row has again a meander configuration, which corresponds to one of Walsh functions for eight-dimensional space. Let us show now that each of these six matrices is formally connected with one of kinds of eight-dimensional hypercomplex numbers.
4. About Hadamard Matrices, Genetic Alphabets, and Logical Holography
Inside the DNA-alphabet A, C, G, and T, thymine T has a unique status and differs from the other three letters:
Only thymine T is replaced by another molecule, U (uracil), in transferring from DNA to RNA;
Only thymine T does not have the functionally important amino group NH2.
This binary opposition can be expressed as: A = C = G = +1, T = −1. Correspondingly, in each of the triplets, its letters can be replaced by these numbers to represent numerically the triplet as the product of these numbers (for example, the triplet CTA is represented by number 1*(−1)*1 = −1). In this case, the symbolic matrices, [C, A; T, G]
(2) and [C, A; T, G]
(3), in
Figure 3 become Hadamard matrices, H
(2) and H
(3), in
Figure 2, which represent matrices of 16 doublets and 64 triplets from the tensor family of genetic matrices. The sets of rows in H
(2) and H
(3) contain complete orthogonal systems of Walsh function for 4-dimensional and 8-dimensional spaces correspondingly. The term “complete” means here that any numeric vector of 4-dimensional or 8-dimensional spaces can be represented in a form of a superposition of these Walsh functions.
Hadamard matrices and their systems of Walsh functions are widely used in noise-immunity coding of information and in many other tasks of digital signals processing [
7,
27]. For example, they are employed on the spacecrafts “Mariner” and “Voyager” for the noise-immune transfer of photos of Mars, Jupiter, Saturn, Uranus, and Neptune to Earth. Hadamard matrices are also used in quantum computers (“Hadamard gates”), and in quantum mechanics as unitary operators. Complete systems of Walsh functions serve as a basis of the “sequency theory” [
8,
28], which has led to effective decisions in radio-engineering, acoustics, optics, etc. In particular, the problem of absorption of radio waves and acoustic waves, which is important for biological systems, is bypassed by means of “sequency analysis”. Hadamard matrices are employed in logical holography [
29] and in the spectral analysis of systems of Boolean functions [
30]. Let us say more about the logical holography.
Living organisms possess properties, which seem to be analogical to properties of holography with its non-local record of information. For example, in his experiments, German embryologist Hans Driesch separated from each other two or four blastomeres of sea urchin eggs. The main result of Driesch’s experiments was that fairly normal (although proportionally diminished) larvae with all of their organs properly arranged could be obtained from a single embryonic cell (blastomere) containing no more than 1⁄2 (if the two first blastomeres were separated), or even 1⁄4 (in the case of four blastomeres separation) of the entire egg’s material. Rather soon, these effects (defined by Driesch as “embryonic regulations”) were numerously confirmed and extended to the species belonging to almost all taxonomic groups of metazoans, from sponges to mammalians [
31,
32]. In 1901, Hans Spemann conducted an experiment on the separation of the amphibian embryo into individual cells, from which quite normal tadpoles grew (in 1935 he won the Nobel Prize for the discovery of organizing effects in embryonic development) [
31]. These experimental results testify that complete sets of “causes” required for further development are contained not only within whole eggs/embryos but also in their halves, quarters, etc. Similar properties exist in holograms, where one can restore a whole holographic image of a material object from a part of the hologram. A hologram has such a property since each part of the hologram possesses information about all parts of the object (in contrast to ordinary photos).
One can mention also, the known hypothesis about possible connections of holography with brain functions, including associative memory, physiological processing, visual information, etc. (see, for example, [
33,
34]). Yet the brain and the nervous system have appeared at a relatively late stage of biological evolution. A great number of species of organisms lived perfectly up to this, and are now living without neuronal networks. It is clear that the origins of the similarity between holography and nonlocal informatics of living organisms should be searched at the level of the genetic system.
Physical holography, which possesses the highest properties of noise-immunity, is based on a record of standing waves from two coherent physical waves of the object beam and of the reference beam [
35]. However, physical waves can be modeled digitally. Correspondingly, noise-immunity and other properties of optical and acoustical holography can be modeled digitally, in particular, using Walsh functions and logic operations concerning dyadic groups of binary numbers, because Walsh transforms are Fourier transforms on the dyadic groups. This can be done on the basis of discrete electrical or other signals without any application of physical waves. The pioneer work about “holography by Walsh waves” was [
29]. The work was devoted to Walsh waves (or Walsh functions), which propagate through electronic circuits—composed of logical and analog elements—by analogy with the optical Fourier transform holography. In this digital Walsh-holography, objects, whose digital holograms could be made, are represented in forms of 2
n-dimensional vectors. Each component of these vectors corresponds to one of 2
n input channels of appropriate electric circuits; the same is true for 2
n output channels, which are related with components of resulting vectors. Examples of electrical circuits for th logic holography are shown in the works [
29,
36]. Due to application of Walsh transformation, information about such vector is written in each component of the appropriate hologram, which is also a 2
n-dimensional vector, to provide nonlocal character of storing information.
One should specially note that Walsh functions are closely related with dyadic groups, since Walsh functions are algebraic characters of dyadic groups [
37]. Therefore, the Fourier analysis on dyadic groups is defined in terms of Walsh functions. In the same way, the discrete Walsh functions are algebraic characters of the finite dyadic groups, on which the switching functions are defined. Therefore, the Fourier analysis for switching functions, considered as a subset of complex valued functions, is formulated in terms of the Walsh functions [
30].
This digital Walsh-holography under the title “logical holography” was also considered later in [
36,
38,
39]. All these and other works about logical Walsh-holography considered possibilities of its application in engineering technologies without any supposition of its application in biology, in particular, in genetics. On the basis of our results about connections of the genetic code system with Walsh functions, Hadamard matrices, dyadic groups, bit-reversal permutations, and logical modulo-2 addition, we put forward the hypothesis that principles of logical holography are appropriate for mathematical modeling properties of the genetic system [
9,
40]. This hypothesis leads to a new class of mathematical models of genetic structures and phenomena on the basis of logical holography and appropriate logical operations. Correspondingly, we develop the theory of “genetic logical holography”, where mathematics of the logical holography and logical operations is used for modeling genetic phenomena. The mathematical basis of this modeling approach is lattice functions, logical operations with them, dyadic spaces, dyadic groups of binary numbers, logic modulo-2 addition, dyadic convolution, and dyadic derivatives of J. Gibbs, in close relation with peculiarities of molecular-genetic systems. In our opinion, a realization of the mechanisms of logical holography in biological organisms is provided by Nature on the basis of binary bio-computers on resonances [
10]. The new kind of mathematics in modeling genetic phenomena gives possibilities of new heuristic associations and new understanding of natural phenomena. Initial examples of models from this new field of the genetic logical holography are the following: (1) models of different kinds of repetitions of fragments in nucleotide sequences (complementary palindromes, simple palindromes, etc.) on the basis of the dyadic convolution of vector-signals; (2) the model of the zipper reproduction of DNA molecules [
9] (pp. 78–88).
Mathematical formalisms of logical holography and the theory of logic functions, including the dyadic convolutions and the dyadic derivatives of J. Gibbs, can be applied for comparative studying of nucleotide sequences and also other biological string-like patterns and repetitions in them, which are under influence of genetic templates [
9] (pp. 83–86). For example, the dyadic derivatives can be used in medical diagnosis for comparative analysis of bio-rhythms, including cardiac arrhythmias. In the last case, components of each vector for calculation of its dyadic derivative coincide with values of time intervals in cardiac pulsations. Returning to the Mendel’s laws of independent inheritance of traits (for example, colors of human skin, eye, and hairs are inherited independently), it seems to be interesting to develop models of a multiplex-logical holography, where each of the inherited traits is represented by its own logical hologram. In such an approach, a living body is a set of individual logical holograms of inherited traits.
As known, holographic methods in engineering allow quickly detecting individual elements in a huge image. The theory of genetic logical holography allows assuming that one of the secrets of noise-immunity of genetic informatics is based on the similar possibilities of genetic logical holography. In an appropriate modeling approach, if one of the DNA molecules mutates, the genetic logical holography—by analogy with classic physical holography—allows quickly detecting the mutated DNA in the whole logical hologram of a set of DNA molecules. As a result, the genetic information of this individual DNA molecule could automatically be found to be incorrect for further using in an organism.
5. The Concept of Geno-Logical Coding
The epoch-making discovery of the genetic code of the amino acid sequences in proteins has revealed the molecular genetic commonality in the diversity of species of living organisms. Some authors supposed that other kinds of genetic coding could also exist. For example, a supposition about the histone code is well known [
41]. The histone code is a hypothesis that the transcription of genetic information encoded in DNA is in part regulated by chemical modifications to histone proteins, primarily on their unstructured ends. Together with similar modifications, such as DNA methylation, it is part of the epigenetic code (see for example [
42]). No mathematical approaches have been proposed to model such additional kinds of the genetic code.
It is obvious that the knowledge of the regularities of the genetic encode of structures of amino acid sequences is not enough for understanding and explaining the enormous class of inherited processes and principles of an algorithmic character: congenital coordinated motions of living bodies, innate principles of sensory information processing (including the psychophysical law of Weber-Fechner), congenital instincts and spatial representations, and so forth. We postulate that another kind of biological code exists in parallel with the genetic code of amino acid sequences. We name conditionally this second code “the geno-logical code”, since—on the basis of our researches—we believe that this biological code is connected with logical operations and logical functions, dyadic groups of binary numbers, Walsh functions, logical holography, and the spectral logic of systems of Boolean functions. We believe that molecules, DNA and RNA, are not only the carriers of the genetic code of amino acid sequences but also they are participants of the geno-logic code, which encodes logical functions and which is connected with epigenetic mechanisms. DNA is an important part of this integrated coding system, peculiarities of which are reflected in structures of DNA-alphabets and in features of the degeneracy of the genetic code of amino acids. The integrated coding system contains not only the code of amino acid sequences but also the code of sets of logic functions. We are developing a relevant mathematical doctrine about this biological code. Below, we describe our approaches to this theme.
As known, newborn turtles and crocodiles, when they hatched from eggs, crawl with quite coordinated movements to water without any training from anybody. Celled organisms, which have no nervous systems and muscles, move themselves by means of perfectly coordinated motions of cilia on their surfaces (the genetically inherited “dances of cilia”). In these inherited motions, a huge number of muscle fibers, nerve cells, contractile proteins, enzymes, and so forth are acting in concert, by analogy with the coordinated work of a plurality of parts of computers.
Computers work on the basis of networks of two-positional switches (triggers), each of which can be in one of two states: “yes” or “no”. Also in physiology, a similar law “all-or-none” [
43] for excitable tissues exists: a nerve cell or a muscle fiber give only their answers “yes” or “no” under action of a different stimulus by analogy with Boolean variables. If a stimulus is above a certain threshold, a nerve or muscle fiber will fire with full response. Essentially, there will either be a full response or there will be no response [
44,
45]. A separate muscle, which contains many muscle fibers, can reduce its length to a different degree due to the combined work of the plurality of its muscle fibers. The nervous system also can react differently to stimulus of a different force by means of combined excitations of its many nerve fibers (and also due to the ability to change the frequency of the generation of nerve impulses at their fixed amplitude).
R. Penrose [
46]—in his thoughts about biological quantum computers—appeals to the known fact that tubulin proteins exist in two different configurations, and they can switch between these configurations like triggers to provide bio-computer functions.
Taking these known facts into account, we propose to consider a living organism as a genetically inherited huge network of triggers of different types and different biological levels, including trigger subnets of tubulin proteins, muscle fibers, neurons, etc. From this perspective, biological evolution can be represented as a process of self-organization and self-development of systems of biological trigger networks. Correspondingly, the Darwinian principle of natural selection can be interpreted in a certain degree as natural selection of biological networks of triggers, together with appropriate systems of Boolean functions for coordinated work of these networks. In light of this, it is not so surprising that the genetic system, which provides transmission of corresponding logic networks along the chain of generations, is also built on the principles of dyadic groups and operations of Boolean algebra of logic.
Digital computers work on the basis of binary numbers and Boolean algebra. Hypotheses about analogies between the functioning of living organisms and computers existed long ago (see, for example, [
46,
47,
48,
49,
50,
51]). Our results of studying molecular-genetic systems led to the pieces of evidence that genetic systems work on the base of logical operations of Boolean algebra and dyadic groups of binary numbers; it is important, since the level of the molecular-genetic system is a deeper level than secondary levels of the inherited nervous system, or separate kinds of proteins such as the abovementioned tubulin. According to our concept of the systemic-resonant genetics [
10], binary-oppositional kinds of molecular resonances of oscillatory systems with many degrees of freedom can be the natural basis of binary bio-computers working with genetic systems of dyadic groups and Boolean functions.
As known, for the creation of a computer, the usage of material substances for its hardware is not enough, but logical operations should also be included for the working of the computer. These logical operations can successfully work with different kinds of hardware made from very different materials. The same situation is true for living bodies, where genetical systems should provide genetic information not only about material substances (proteins) but also about the logic of interrelated operations in biological processes. One can be reminded that informatics is a scientific branch, which exists independent of physics or chemistry. For example, a physicist, who knows all the physical laws but does not know the informatics, cannot understand the working of computers. We think that the known genetic code of amino acid sequences defines material aspects of biological bodies and the geno-logic code defines logic rules and functions of their operating work. In the proposed new modeling approach about the geno-logic code, molecular-genetic elements (nitrogenous bases, doublets, triplets, etc.) and their ensembles are represented as Boolean functions or systems of these functions [
9,
40].
Genetics can be additionally developed as a science about genetic systems of logic functions. Results of this development can be used not only for deeper understanding living matter but also for progress in the fields of artificial intellect and artificial life (A-life), where mathematical logic plays a key role. In this case, computer systems and theoretical models should be developed, which are based on the special set of logic functions related with genetic systems. As known, artificial intellect, which possesses an ability of reproducing features of biological intellect, cannot be constructed without usage of mathematical logic [
52], and so the idea of geno-logical coding is very natural.
6. Geno-Logical Coding and Questions of Modern Genetics
Our postulate on geno-logical coding allows, in particular, explanations of some difficult questions of contemporary genetics, including the following four questions.
The first question concerns the degeneracy of the genetic code of amino acids, where 64 triplets encode 20 amino acids and stop-signals of protein synthesis, and where several triplets encode each of the amino acids. By this reason, any fragment of amino acid sequences in proteins has many different variants of its encoding by different triplets. For example, let us consider the short sequence of 3 amino acids: Ser-Pro-Leu. In the Standard genetic code, the amino acid, Ser, is encoded by 6 triplets (TCC, TCT, TCA, TCG, AGC, AGT), the amino acid, Pro—by 4 triplets (CCC, CCT, CCA, CCG), and the amino acid Leu—by 6 triplets (CTC, CTT, CTA, CTG, TTA, TTG). Due to this, the short sequence, Ser-Pro-Leu, can be encoded by means of 144 (=6*4*6) different variants of a sequence of 3 triplets: TCC-CCC-CTC, TCT-CCT-CTG, AGT-CCT-TTG, etc. If more and more long sequences of amino acids are taken into consideration (some proteins have sequences with many thousands of amino acids in them), the number of variants of their encoding increases rapidly to astronomic quantities. Why does living matter need such a tremendously excessive number of encoding variants, which can greatly complicate the work of a reliable coding system? This is a difficult question without a satisfactory explanation in modern science.
The standpoint of the geno-logical code gives the following answer on the question. DNA (RNA) molecules are carriers of at least two different genetic codes: in one of them triplets encode amino acids, and in the second code the same triplets (or n-plets in a general case) encode genetic systems of Boolean functions. In this case, the existence of many different variants of sequences of triplets, which encode the same amino acid sequence, has a sense, because any two different sequences of triplets, which encode the same amino acid sequence, simultaneously encode different systems of Boolean functions. One can suppose that the amino acid sequence, encoded by the first set of triplets, is designed to work in cooperation with one of the genetic systems of Boolean functions; by contrast, the same amino acid sequence, encoded by another set of triplets, is designed to work in cooperation with another genetic system of Boolean functions. This implies that, in living bodies, each of proteins is intended for use in different encoded systems of Boolean functions, if this protein can be encoded by different sequences of triplets. In other words, each protein is potentially connected with many variants of encoded genetic Boolean functions. Correspondingly, the fate of the protein in a living body depends on its connection with one of the encoded genetic systems of Boolean functions, which is possible for it. It correlates with the known phenomenon that the same kinds of proteins can be used in constructions of very different organs, each of which is built by means of its own algorithmic-logical processes. One can also note that the same kind of organs in different biological species can be built from very different proteins even though they provide the same function and frequently they are similar to each other in their morphology (for example, eyes as organs of vision in different species). These facts give additional pieces of evidence about the biological importance of encoded algorithmic processes founded on genetic logical programs of geno-logical coding.
The second question concerns the existence of introns, which do not encode proteins (by contrast to exons in nucleotide sequences). From the standpoint of the geno-logical code, introns participate in the definition of genetic systems of Boolean functions, which are needed for inherited algorithmic processes. They do this in cooperation with exons.
The third question concerns the problem of jumping genes [
53], which also can be related with the existence of the geno-logical code, together with the genetic code of amino acid sequences: jumping of DNA fragments is needed for changing of the encoded systems of Boolean functions without changing the amino acid sequence in the encoded protein.
The fourth question: why the alphabets of DNA and RNA—together with the numeric characteristics of the degeneracy of the genetic code—are related with dyadic groups of binary numbers and with Walsh functions? From the standpoint of the geno-logic code, this relationship plays a key role in inheritance of algebra-logical processes, since dyadic groups are closely related, not only with Boolean algebra of logic but also with Walsh functions, which are algebraic characters of dyadic groups. The dyadic-group structure of the DNA- and RNA-alphabets connects genetics with Boolean algebra of logic for inheritance of algorithmic processes and for combining individual elements into a whole organism with its quasi-holographic properties, work abilities, etc.
For developing the theory of the geno-logical code, one needs to study possible variants of natural relations of molecular-genetic ensembles with systems of Boolean functions and their methods of analysis developed in mathematics, including spectral logic using Walsh functions and the tensor (or Kronecker) product of matrices [
29,
54,
55]. These known mathematical methods pay special attention to the Walsh-Hadamard spectra and dyadic autocorrelation characteristics of systems of Boolean functions. Different classes of Boolean functions exist: linear, self-dual, anti-self-dual, threshold, and others. Knowledge of a class of Boolean functions is important for the synthesis of devices that implement complex logic functions or their systems, since specific synthesis methods are known for each of such classes. To get this knowledge, dyadic autocorrelation characteristics are traditionally used, which coincide with dyadic convolutions [
6]. The paper [
9] (pp. 91–99) is the first work where initial models of molecular-genetic ensembles as systems of Boolean functions and elements of algebra of logic are described in connection with the concept of geno-logical coding. From the point of view of the geno-logical approach, the genetic system is a part of such an intellectual substance, which is a living organism. One can think that the genetic system also is an intellectual substance, which communicates with other intellectual parts of the living body to provide coordinated mutual functions. The point of view about intellectual abilities of parts of a living body has associations with works about the Double Homunculus model [
56], and an emergence of formal logic induced by an internal agent [
57]. Of course, the described representations should be considered as initial material for further research of genetic systems and biological organisms from the standpoint of Boolean algebra of logic and spectral logic, for deeper understanding of living matter and for developing “algebraic-logical biology”. In particular, the development of algebraic-logical biology should include a new theory of morphogenesis and of inherited phenomena of resemblances with the surroundings (biological camouflage, or mimicry in a wide sense); in our opinion, geno-logical coding plays an important role in these phenomena.
E. Schrödinger noted [
58]: “from all we have learnt about the structure of living matter, we must be prepared to find it working in a manner that cannot be reduced to the ordinary laws of physics… because the construction is different from an anything we have yet tested in the physical laboratory”. For comparison, the enzymes in the biological organism work a million times more effectively than catalysts in the laboratory. Biological enzymes can accelerate receiving of results of chemical reactions 10
10–10
14 times [
59] (p. 5). We believe that such ultra-efficiency of enzymes in biological bodies is defined not only by laws of physics, but also by algebra-logical algorithms of geno-logic coding, and therefore—in accordance with Schrödinger—this ultra-efficiency cannot be reduced to the ordinary laws of physics. Concerning enzymes, one should note that reading of genetic information of DNA is closely related with biological catalysis; encoding of the protein by the polynucleotide can be interpreted as catalysis of the protein by the polynucleotide [
1].
The American journal, Time, in 2008, announced “personalized genetics” from the company, 23andMe, as the best innovation of the year [
60]. This innovation was recognized to be much more important than many others, including the Large Hadron Collider from the field of nuclear physics. The company, 23andMe, proposes information about genetic peculiarities of persons at a low price. Now possibilities of personalized genetics are developed intensively in many countries, with huge financial support. Yet this initial kind of “personalized genetics”, which has limited possibilities, uses knowledge about the genetic code of protein sequences of amino acids without knowledge about the geno-logic code. It is natural to think that the cause of the body‘s genetic predisposition to various diseases is not only violations in amino acid sequences of proteins, but that geno-logical disorders in inheritance of various processes also play an important role. We believe that development of knowledge about geno-logic coding will lead to “geno-logical personalized genetics” as a next step in human progress.
George Boole created his mathematics of logic to describe the laws of thought: his book in 1854 was titled,
An Investigation of the Laws of Thoughts [
61]. Our reasoned statement about the existence of geno-logical coding shows that our genetically encoded body is created on the basis of the same laws of logic on which our thoughts are constructed (the unity of the laws of thoughts and body). It gives new material for a discussion about the old problem: what is primary—thoughts or matter?
Materials about the geno-logical coding and about living matter as a territory of systems of Boolean functions gives rise to many new questions, including the question on non-Euclidean bio-symmetries and generalized crystallography [
62,
63,
64,
65]. One of them is the question concerning the role of water in living bodies. As known, jellyfishes consist of 99% water, but despite this they live perfectly. If such living bodies are genetically organized on the base of logical functions, then one can assume that structural water in living bodies is also related with logical functions in it, which can be provided by systems of its molecular resonances. We think that structural water can also be a carrier of logical functions and logical operations. It seems to be a new aspect of the study of water, which is usually analyzed only from a physico-chemical standpoint without the idea of a participation of laws of algebra of logic in water properties.