Passivity-Based Nonlinear Excitation Control of Power Systems with Structure Matrix Reassignment
Abstract
:1. Introduction
2. IDA-PBC Methodology of Nonlinear Systems
- (i)
- Fix the desired structure of the interconnection and damping matrix.
- (ii)
- Derive a partial differential equation (PDE) parameterized by the chosen matrices whose solutions characterize all the energy functions that can be assigned.
- (iii)
- Choose one solution that satisfies the minimum requirement and computer the control.
3. IDA-PBC Excitation Control of Power Systems
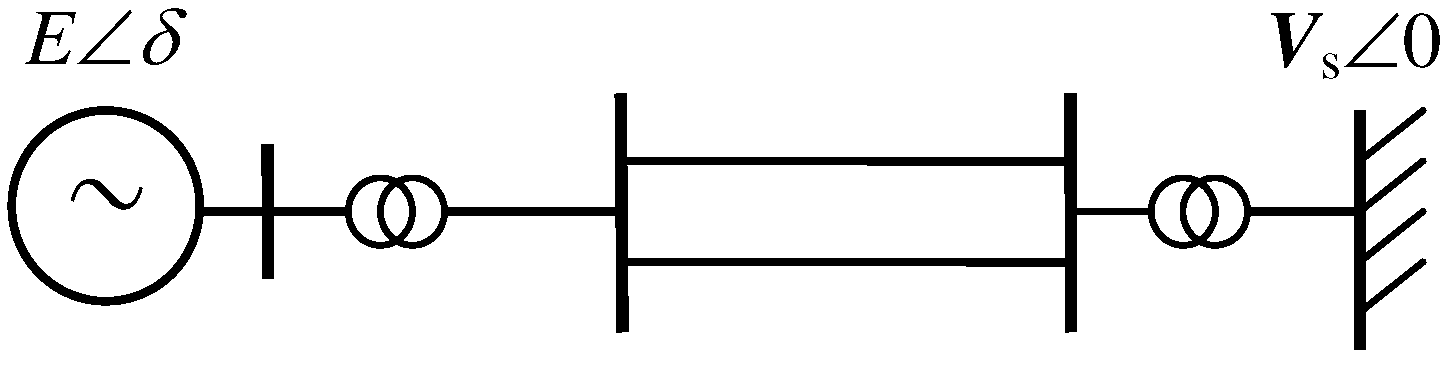
4. Simulation
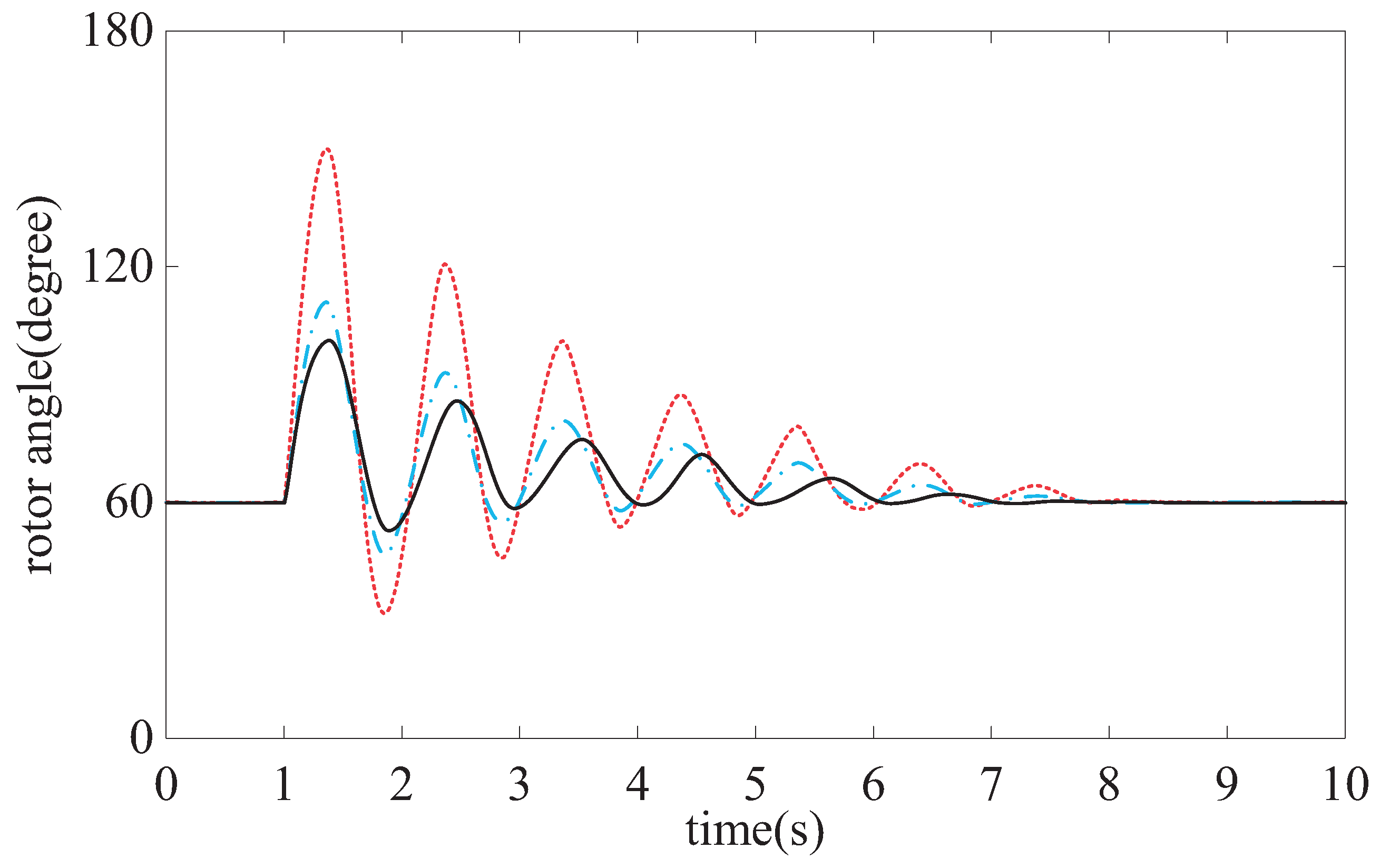
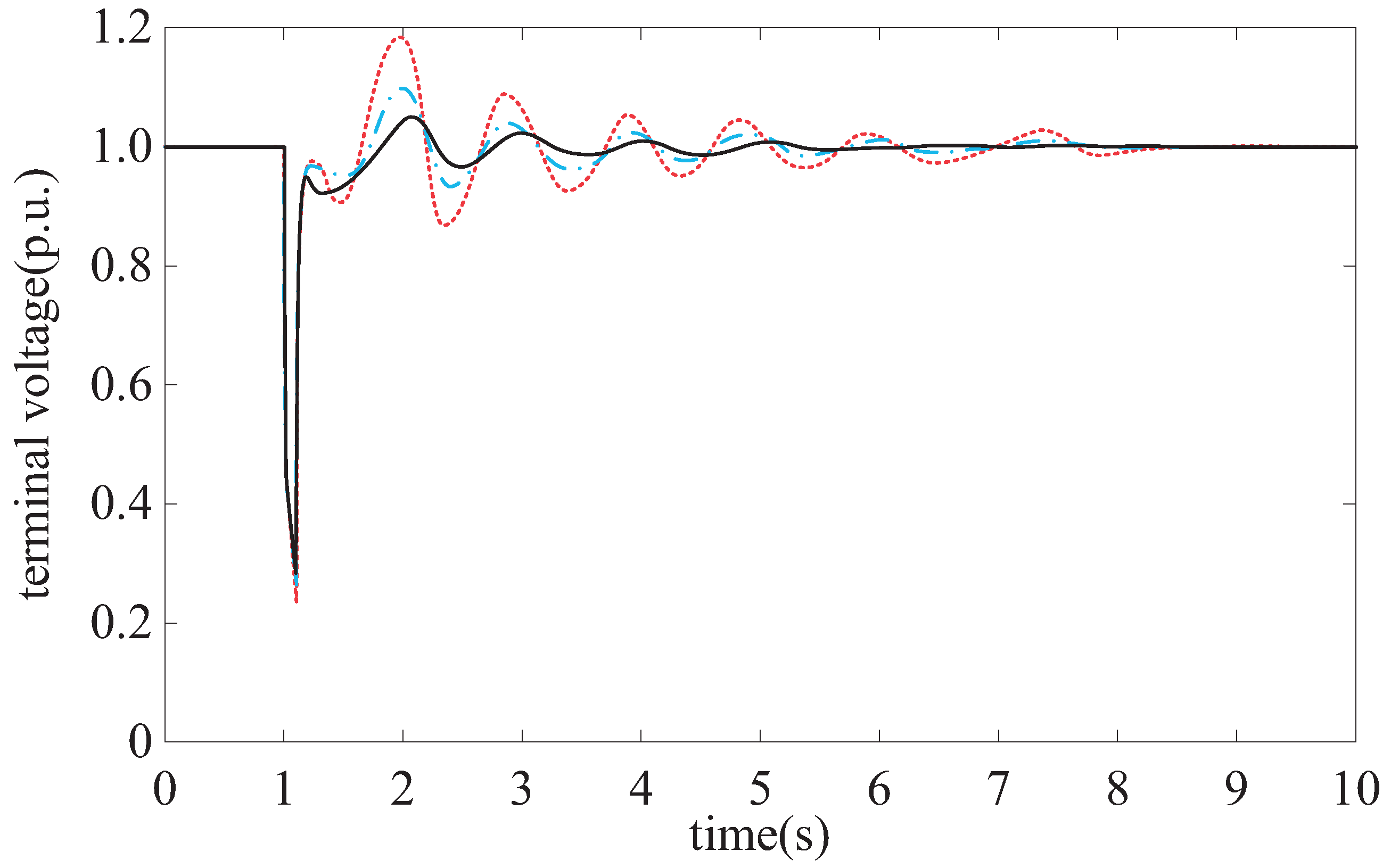
5. Conclusions
Acknowledgements
Conflict of Interest
References
- Van der Schaft, A.J. Port-Hamiltonian Systems: Network Modeling and Control of Nonlinear Physical Systems. In Advanced Dynamics and Control of Structures and Machines; CISM Courses and Lectures, Volume 444; Springer: New York, NY, USA, 2004. [Google Scholar]
- Ortega, R.; van der Schaft, A.J.; Mareels, I.; Maschke, B. Putting energy back in control. IEEE Control Syst. Mag. 2001, 21, 18–33. [Google Scholar] [CrossRef]
- Ortega, R.; van der Schaft, A.J.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Ortega, R.; García-Causeco, E. Interconnection and damping assignment passivity-based control: A survey. Eur. J. Control 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Ortega, R.; Castaños, F.; Astolfi, A. Control by interconnection and standard passivity-based control of Port-Hamiltonian systems. IEEE Trans. Autom. Control 2008, 53, 2527–2542. [Google Scholar] [CrossRef]
- Fujimoto, K.; Sakurama, K.; Surgie, T. Trajectory Tracking Control of Portcontrolled Hamiltonian Systems and its Application to a Magnetic Levitation System. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 3388–3393.
- Rodríguez, H.; Ortega, R. Stabilization of electromechanical systems via interconnection and damping assignment. Int. J. Robust Nonlinear Control 2003, 13, 1095–1111. [Google Scholar] [CrossRef]
- Batlle, C.; Dòria-Cerezo, A.; Fossas, E. Bidirectional power flow control of a power converter using passive Hamiltonian techniques. Int. J. Circuit Theory Appl., 2008, 36, 769–788. [Google Scholar] [CrossRef]
- Cheng, D.; Xi, Z.; Hong, Y.; Qin, H. Energy-based Stabilization in Power Systems. In Proceedings of the 14th IFAC World Congress, Beijing, China, 5–9 July 1999; pp. 297–303.
- Xi, Z.; Cheng, D.; Lu, Q.; Mei, S. Nonlinear decentralized controller design for multimachine power systems using Hamiltonian function method. Automatica 2002, 38, 527–534. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, D.; Hong, Y. Stabilization of synchronous generators with Hamiltonian function approach. Int. J. Syst. Sci. 2001, 32, 971–978. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, T.; Ortega, R.; Lu, Q. Decentralized Controller Design for Multi-machine Power Systems on Hamiltonian Structure. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, USA, 4–7 December 2001; pp. 3045–3050.
- Xi, Z.; Cheng, D.; Lu, Q.; Mei, S. Nonlinear decentralized controller design for multimachine power systems using Hamiltonian function method. Automatica 2002, 38, 527–534. [Google Scholar] [CrossRef]
- Galaz, M.; Ortega, R.; Bazanella, A.S.; Stankovic, A.M. An energy-shapping approach to the design of excitation control of synchronous generators. Automatica 2003, 39, 111–119. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Li, C.; Zhang, L. Interconnection and Damping Assignment Passivity-based Excitation Control of Power Systems. In Proceedings of IEEE Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 954–958.
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, J.; Liu, Y.; Li, C.; Chu, B. Passivity-Based Nonlinear Excitation Control of Power Systems with Structure Matrix Reassignment. Information 2013, 4, 342-350. https://doi.org/10.3390/info4030342
Li J, Liu Y, Li C, Chu B. Passivity-Based Nonlinear Excitation Control of Power Systems with Structure Matrix Reassignment. Information. 2013; 4(3):342-350. https://doi.org/10.3390/info4030342
Chicago/Turabian StyleLi, Jianyong, Yanhong Liu, Chunwen Li, and Bing Chu. 2013. "Passivity-Based Nonlinear Excitation Control of Power Systems with Structure Matrix Reassignment" Information 4, no. 3: 342-350. https://doi.org/10.3390/info4030342




