1. Introduction
In his paper “The Method of Levels of Abstraction” [
1] Luciano Floridi introduces arguments in defence of the need of forms of “levelism” to study the reality. As argued in the mentioned paper, “more recently the concept of simulation has been used in computer science to relate levels of abstraction to satisfy the requirement that systems constructed in levels (in order to tame their complexity) function correctly”. In accordance with this argument, an increasing interest in the development of discussions about the epistemology of computer simulations is testified by a flourishing of literature on the argument [
2]. Advanced computer-based simulation methods and techniques have been developed thanks to the creation of innovative computational models (e.g., cellular automata, agent-based systems) and related powerful distributed technologies (e.g., grid computing) allowing computer-based experiments to be performed. This algorithmic and computational power allowed also for the representation and modelling of complex phenomena not only circumscribed to natural sciences, but also social and economic phenomena, showing novel fields of scientific investigation and epistemological discussions [
3,
4,
5]. Additional discussions, more on the field of the computer science side of this research effort, include [
6,
7,
8].
The computer-based simulation of the dynamical behaviour of crowds and pedestrians is a challenging field of research naturally involving knowledge coming from different disciplines, producing interesting results from physics and applied mathematics, to computer science, often in collaboration with anthropological, psychological, sociological studies and the humanities in general. Sometimes, these results allowed also the design and development of commercial software packages, due to the pressure of decision makers and crowd managers of public spaces. (See [
9] for a significant although not necessarily comprehensive list of simulation platforms.) Despite the presence of commercial packages, the modelling and simulation of crowd and pedestrians requires much more knowledge and epistemological discussions [
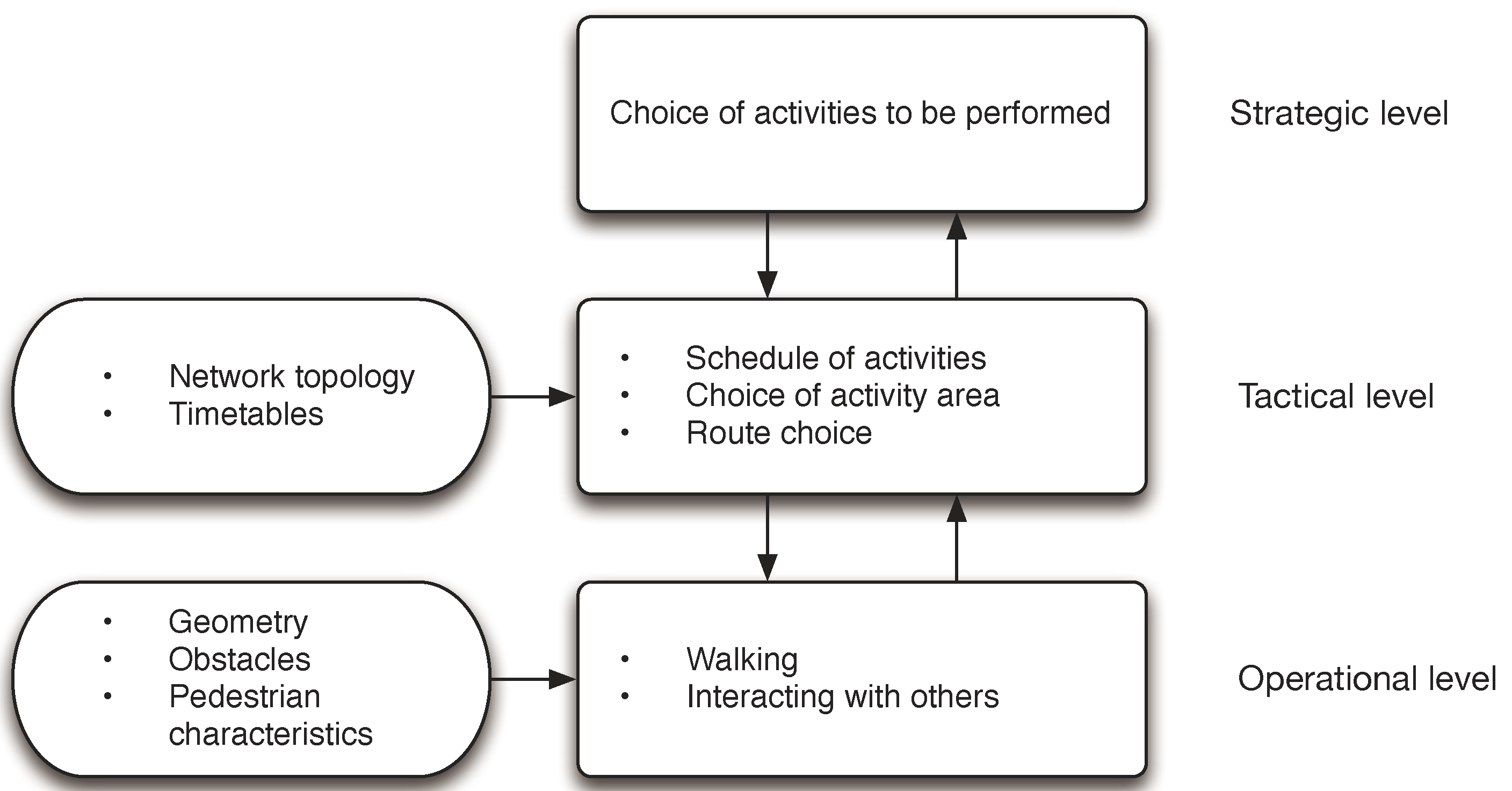
10]. In particular, in the following we will show how the notion of
levels of abstraction can be very useful to clarify what are the actual goals of the simulation effort, what is the object of the analysis and therefore correctly set the research effort in the wide and heterogeneous relevant literature. A level of abstraction formally defines “the scope or granularity of a single mode”; Floridi also introduces the notion of
gradient of abstractions as “a way of varying the level of abstraction in order to make observations at differing levels of abstractions”. Even though it is possible to observe the crowd phenomenon at different levels of granularity, it is not simple (and possibly not really useful) to put different and heterogeneous models into a hierarchical relation such as one inspired by the notion of gradient of abstraction. Nonetheless, it is important to notice that notions of
observables and
system behaviours, instrumental in the definition of the levels and gradients of abstractions, can be very important to describe and discuss the results of simulations and, therefore, to evaluate and compare models. These concepts support the definition of “standard outputs” of models that support their evaluation and also the actual comparison of their effectiveness (in a process of alignment [
11] that still represents an open issue despite being well-known in the field).
In the following, we will briefly describe some relevant influences from different areas of the Humanities to this research effort;
Section 3 will instead provide a compact review of the current state of the art of the area of pedestrian and crowd modelling and simulation.
Section 4 will present and sample model for the simulation of pedestrian movement, while
Section 5 will clarify the relevant system behaviours in this area, even beyond the scientific research context, considering the practitioner’s perspective. Conclusions and future developments will end the paper.
2. Elements of an Interdisciplinary Approach
Pedestrian and crowd modelling research context regards events in which a large number of people may be gathered or bound to move in a limited area; this can lead to serious safety and security issues for the participants and the organisers. The understanding of the dynamics of large groups of people is very important in the design and management of any type of public events. In addition to safety and security concerns, also the comfort of event participants is another aim of the organisers and managers of crowd related events. Large people gatherings in public spaces (like pop-rock concerts or religious rites participation) represent scenarios in which crowd dynamics can be quite complex due to different factors (the large number and heterogeneity of participants, their interactions, their relationship with the performing artists and also exogenous factors like dangerous situations and any kind of different stimuli present in the environment [
10]). The traditional and current trend in social sciences studying crowds is still characterised by a non-dominant behavioural theory on individuals and crowds dynamics, although it is recognised that a behavioural theory is needed to improve the current state of the art in pedestrian and crowd modelling and simulation [
12].
2.1. Proxemics
The term
proxemics was first introduced by Hall with respect to the study of set of measurable distances between people as they interact [
13]. In his studies, Hall carried out analysis of different situations in order to recognise behavioural patterns. These patterns are based on people’s culture as they appear at different levels of awareness. In [
14] Hall proposed a system for the notation of proxemic behaviour in order to collect data and information on people sharing a common space. Hall defined proxemic behaviour and four types of perceived distances:
intimate distance for embracing, touching or whispering;
personal distance for interactions among good friends or family members;
social distance for interactions among acquaintances;
public distance used for public speaking. Perceived distances depend on some additional elements that characterise relationships and interactions between people: posture and sex identifiers, sociofugal-sociopetal (SFP) axis, kinesthetic factor, touching code, visual code, thermal code, olfactory code and voice loudness.
Proxemic behaviour includes different aspects that could be useful and interesting to integrate in crowd and pedestrian dynamics simulation. In particular, the most significant aspect among them is the existence of two kinds of distance: physical distance and perceived distance. While the first depends on physical position associated to each person, the latter depends on proxemic behaviour based on culture and social rules.
It must be noted that some recent research effort was aimed at evaluating the impact of proxemics and cultural differences on the fundamental diagram [
15], a graph showing how the average velocity of pedestrians in a section of the environment (e.g., one of the ends of a corridor) varies according to the density of the observed environment, a typical way of evaluating both real crowding situations and simulation results that will be more thoroughly described in
Section 5. The work has essentially confirmed, better quantified and extended Hall’s findings, and together with recent results in nonverbal behaviour studies [
16] it has renewed the interest in this kind of observation.
2.2. Crowds: Canetti’s Theory
Elias Canetti’s work [
17] proposes a classification and an ontological description of the crowd; it represents the result of 40 years of empirical observations and studies from psychological and anthropological viewpoints. Elias Canetti can be considered as belonging to the tradition of social studies that refer to the crowd as an entity dominated by uniform moods and feelings. We preferred this work among others dealing with crowds due to its clear semantics and explicit reference to concepts of loss of individuality, crowd uniformity, spatial-temporal dynamics and
discharge as a triggering entity generating the crowd, which could be fruitfully represented by computationally modelling approaches like MAS.
The normal pedestrian behaviour, according to Canetti, is based upon what can be called the fear to be touched principle:
“There is nothing man fears more than the touch of the unknown. He wants to see what is reaching towards him, and to be able to recognise or at least classify it.”
“All the distance which men place around themselves are dictated by this fear.”
A discharge is a particular event, a situation, a specific context in which this principle is not valid anymore, since pedestrians are willing to accept being very close (within touch distance). Canetti provided an extensive categorization of the conditions, situations in which this happens and he also described the features of these situations and of the resulting types of crowds. Finally, Canetti also provides the concept of crowd crystal, a particular set of pedestrians that are part of a group willing to preserve its unity, despite crowd dynamics. Canetti’s theory (and precisely the fear to be touched principle) is apparently compatible with Hall’s proxemics, but it also provides additional concepts that are useful to describe phenomena that take place in several relevant crowding phenomena, especially from the Hajj perspective.
Recent developments aimed at formalizing, embedding and employing Canetti’s crowd theory into computer systems (for instance supporting crowd profiling and modelling) can be found in the literature [
18,
19] and they represent a useful contribution to the present work.
4. An Agent-Based Proxemic Model
This section introduces an agent-based model including abstractions and mechanisms based on fundamental considerations about proxemics and basic group behaviour in pedestrians. We first defined a very general and simple model for agents, their environment and interaction, then we realised a proof-of-concept prototype to have an immediate idea of the implications of our modelling choices. The present model does not represent an answer to all of the open issues introduced in the previous sections but rather a first step in this line of research already presenting some interesting results; further extensions of the model and its application to more complex scenarios in the context of the Hajj are object of current project activities. The results of this first steps in the modelling and
in-silico experimentation phase of the project are also discussed in [
44].
The simulated environment is based on a simplified real built environment: a corridor with two exits (North and South); different experiments will be described with corridors of different size (10 m wide and 20 m long as well as 5 m wide and 10 m long). We represented this environment as a simple Euclidean bi-dimensional space, which is discrete (meaning that coordinates are integer numbers) but not “discretised” (as in a CA). Pedestrians, in other words, are characterised by a position that is a pair 〈
x,
y〉 that does not denote a cell but rather admissible coordinates in an Euclidean space. Movement, the fundamental agent’s action is represented as a displacement in this space,
i.e., a vector. The approach is essentially based on the Boids model [
45], in which rules have been modified to represent the phenomenologies described by the basic theories on pedestrian movement. Boundaries can also be defined: in the example Eastern and Western borders cannot be crossed and the movement of pedestrians is limited by the pedestrian position update function, which is an environmental responsibility. Every agent
a ∈ A (where
A is the set of agents representing pedestrians of the modelled scenario) is characterised by a position
posa represented by a pair of coordinates 〈
xa, ya〉. Agent’s action is thus represented by a vector
![Information 04 00075 i007]()
=
〈δxa , δya 〉 where |
![Information 04 00075 i008]()
|=
![Information 04 00075 i009]()
<
M , where
M is a parameter depending on the specific scenario representing the maximum displacement per time unit.
More complex environments could be modelled, for instance by means of a set of relevant objects in the scene, like points of interest but also obstacles. These objects could be perceived by agents according to their position and perceptual capabilities, and they could thus have implications on their movement. Objects can in fact (but they do not necessarily have to) be considered as attractive or repulsive by them. The effect of the perception of objects and other pedestrians, however, is part of agents’ behavioural specifications. For this specific application, however, the perceptive capability of an agent
a are simply defined as the set of other pedestrians that are present at the time of the perception in a circular portion of space or radius
rp centred at the current coordinates of agent
a. In particular, each agent
a ∈ A is provided with a perception distance
pera; the set of perceived agents is defined as
Pa=
p1, . . . , pi where
d(
a,i) =
![Information 04 00075 i010]()
≤
pera.Pedestrians are modelled as agents situated in an environment, each occupying about 40 cm
2, characterised by a state representing individual properties. Their behaviour has a goal driven component, a preferred direction; in this specific example it does not change over time and according to agent’s position in space (agents want to get out of the corridor from one of the exits, whether north or south), but it generally changes according to the position of the agent, generating a path of movement from its starting point to its own destination. The preferred direction is thus generally the result of a stochastic function possibly depending on time and current position of the agent. The goal driven component of the agent behavioural specification, however, is just one the different elements of the agent architectures that must include elements properly capturing elements related to general proxemic tendencies and group influence (at least), and we also added a small random contribution to the overall movement of pedestrians, as suggested by [
46]. The actual layering of the modules contributing to the overall is object of current and future work. In the scenario, agents’ goal driven behavioural component is instead rather simple: agents heading North (respectively South) have a deliberate contribution to their overall movement
![Information 04 00075 i013]()
= 〈0, M〉 (respectively
![Information 04 00075 i014]()
= 〈0, −M〉).
We realised a simulation scenario in a rapid prototyping framework [
47] and we employed it to test the simple behavioural model that will be described in the following. In the realised simulator, the environment is responsible for updating the position of agents, actually triggering their action choice in a sequential way, in order to ensure fairness among agents. In particular, we set the turn duration to 100 ms and the maximum covered distance in one turn is 15 cm (
i.e., the maximum velocity for a pedestrian is 1.5 m/s).
4.1. Basic Proxemic Rules
Every pedestrian is characterised by a culturally defined proxemic distance
p; this value is in general related to the specific culture characterising the individual, so the overall system is designed to be potentially heterogeneous. In a normal situation, the pedestrian moves (according to his/her preferred direction) maintaining the minimum distance from the others above this threshold (rule
P1). More precisely, for a given agent
a, this rule defines that the proxemic contribution to the overall agent movement
![Information 04 00075 i015]()
= 0 if ∀
b ∈ Pa:
d(
a, b) ≥
p.
However, due to the overall system dynamics, the minimum distance between one pedestrian and another can drop below
p. In this case, given a pedestrian
a, we have that ∃
b∈ Pa:
d(
a, b)
< p; the proxemic contribution to the overall movement of
a will try to restore this condition (rule
P2) (please notice that pedestrians might have different thresholds, so
b might not be in a situation so that his/her
P2 rule is activated). In particular, given
p1, . . . , pk∈ Pa:
d(
a, pi)
< p for 1 ≤
i ≤
k, given
c the centroid of
posp1 , . . . , pospk, the proxemic contribution to the overall agent movement
![Information 04 00075 i016]()
, where
ka is a parameter determining the intensity of the proxemic influence on the overall behaviour.
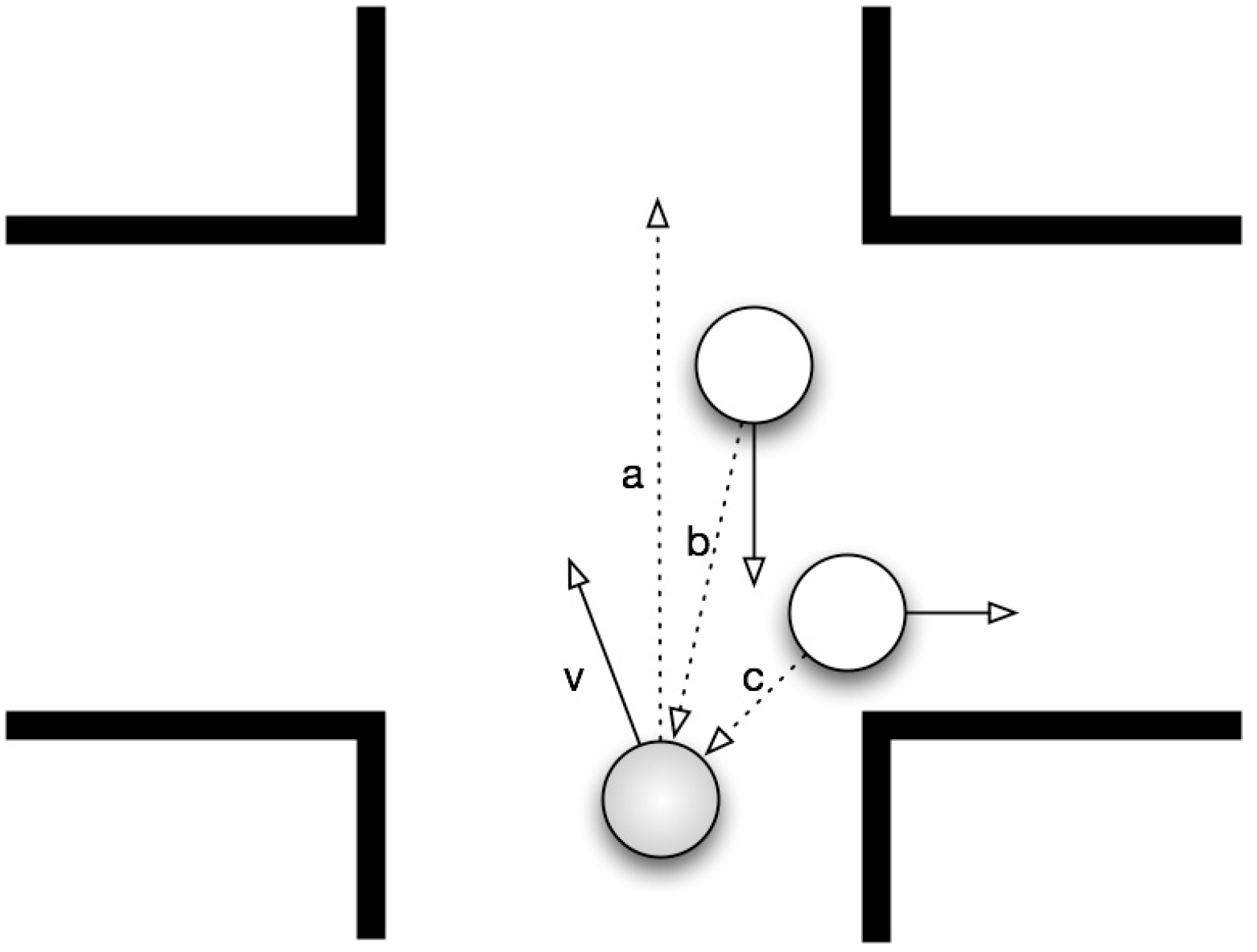
These basic considerations, also schematised in
Figure 4a, lead to the definition of rules that support a basic proxemic behaviour for pedestrian agents; these agents are not characterised by any particular relationship binding them, with the exception of a shared goal,
i.e., they are not a group but rather an unstructured set of pedestrians.
Figure 4.
Basic behavioural rules: a basic proxemic rule drives an agent to move away from other agents that entered/are present in his/her own personal space (delimited by the proxemic distance p) (a), whereas a member of a group will pursue members of his/her group that have moved/are located beyond a certain distance (g) but within his/her perception radius (r) (b).
4.2. Group Dynamic Rules
We extended the behavioural specification of agents by means of an additional contribution representing the tendency of group members to stay close to each other. First of all, every pedestrian may be thus part of a group, that is, a set of pedestrians that mutually recognise their belonging to the same group and that are willing to preserve the group unity. This is clearly a very simplified non-hierarchical notion of group, and in particular it does not account for hierarchical relationships in groups (e.g., leader and followers), but we wanted to start defining basic rules for the simplest form of group.
Every pedestrian is thus also characterised by a culturally defined proxemic distance
g determining the way the pedestrian interprets the minimum distance from any other group member. In particular, in a normal situation a pedestrian moves (according to his/her preferred direction and also considering the basic proxemic rules) keeping the maximum distance from the other members of the group below
g (Rule
G1). More precisely, for a given agent
a, member of a group
G, this rule defines that the group dynamic contribution to the overall agent movement
![Information 04 00075 i018]()
.
However, due to the overall system dynamics, the maximum distance between one pedestrian and other members of his group can exceed
g. In this case, the pedestrian will try to restore this condition by moving towards the group members he/she is able to perceive (rule
G2). In particular, given
p1, . . . , pk∈ (
Pa ∩ (
G − {
a})) :
d(
a, pi) ≥
g for 1 ≤
i ≤
k, given
c the centroid of
posp1, . . . , pospk , the proxemic contribution to the overall agent movement
![Information 04 00075 i020]()
, where
ka is a parameter determining the intensity of the group dynamic influence on the overall behaviour.
This basic idea of group influence on pedestrian dynamics, also schematised in
Figure 4b, lead to the extension of the basic proxemic behaviour for pedestrian agents of the previous example. We tested the newly defined rules in a similar scenario but including groups of pedestrians. In particular, two scenarios were analysed. In the first one, we simply substituted 4 individual pedestrians in the previous scenario with a group of 4 pedestrians. The group was able to preserve its unity in all the tests we conducted, but the average travel time for the group members actually increased. Individuals, in other words, trade some of their potential speed to preserve the unity of the group. In a different scenario, we included 10 pedestrians and a group of 4 pedestrians heading north, 10 pedestrians and a group of 4 pedestrians heading south. In these circumstances, the two groups sometimes face and they are generally able to find a way to form two lanes, actually avoiding each other. However, the overall travel time for group members actually increases in many of the simulations we conducted.
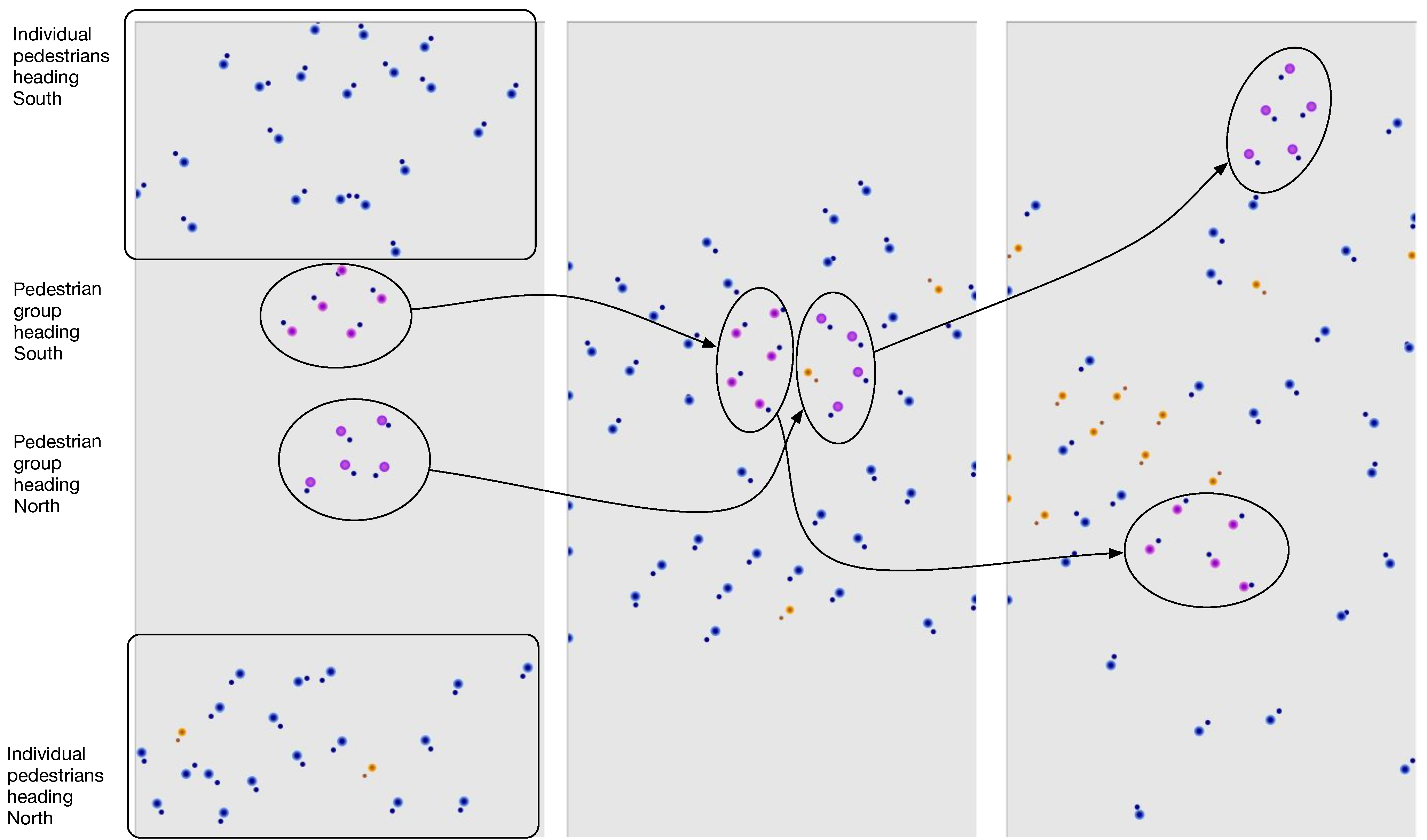
Figure 5 shows two screenshots of the prototype of the simulation system that was briefly introduced here. Individual agents that are not part of a group are depicted in blue, but those for which rule P2 is activated (they are afraid to be touched) are in orange to highlight the invasion of their personal space. Members of groups are depicted in violet and pink. The two screenshots show how two groups directly facing each other must manage to “turn around” each other to preserve their unity but at the same time advance towards their destination.
Figure 5.
Screenshots of the prototype of the simulation system.
5. Observable Behaviours in Crowd Simulation Models
After introducing a sample pedestrian and crowd model, it is now possible to introduce in a more systematic way those relevant measurements and analyses of the simulation results that represent the effecttveness side of the way to evaluate a simulation model (the efficiency dimension of this kind of research effort is out of the scope of this section). In Floridi's framework, these measurements and analyses would be called system behaviours.
Once a model has been defined and a simulation system implementing it has been realised, it is possible to execute such system and to analyse its results. First of all, this can be done to understand if the model and the simulator implementing it produce dynamics that match, to a certain extent, those that can be observed in reality (at least when the simulated scenario does represent a real situation, not, for instance, a designed or planned one). After the model has proven its merits in a sufficiently representative set of scenarios, it can be used for the sake of explanation or prediction. Leaving aside the issues related to the usage of simulation as a method for scientific investigation (for a more comprehensive discussion on these topics please consider [
6] or [
8] in the specific context of agent-based approaches), we are now going to focus on the nature of the "results" of a pedestrians or crowd simulation.
One of the first type of relevant data that can be generated by a pedestrian simulation system is represented by the time that is necessary for a simulated pedestrian to complete a certain specific type of composite path in the environment: questions like "considering this arrangement of the environment and these crowding conditions, how long does it take to move from point A to point B?" represent a significant motivation behind the whole modelling and simulation effort. Considering the specific nature of the involved models, but also the nature of the simulated reality, it is more appropriate to talk about average travel time associated with a given path (and sometimes to a given type of pedestrian, whenever the model can deal with different types of agents in the simulated scenario). Some of the considerations introduced in [
48], in fact, effectively highlight the potential limits of pedestrian models: in the cited paper, a well known and widely adopted model [
49], which is able to generate plausible and realistic dynamics from both qualitative and quantitative perspectives (e.g., formation of lanes, patterns at intersections and bottlenecks), does not faithfully reproduce a pedestrian avoidance pattern among just two individuals. Results of pedestrian and crowd models should therefore be considered and analysed at an aggregate level.
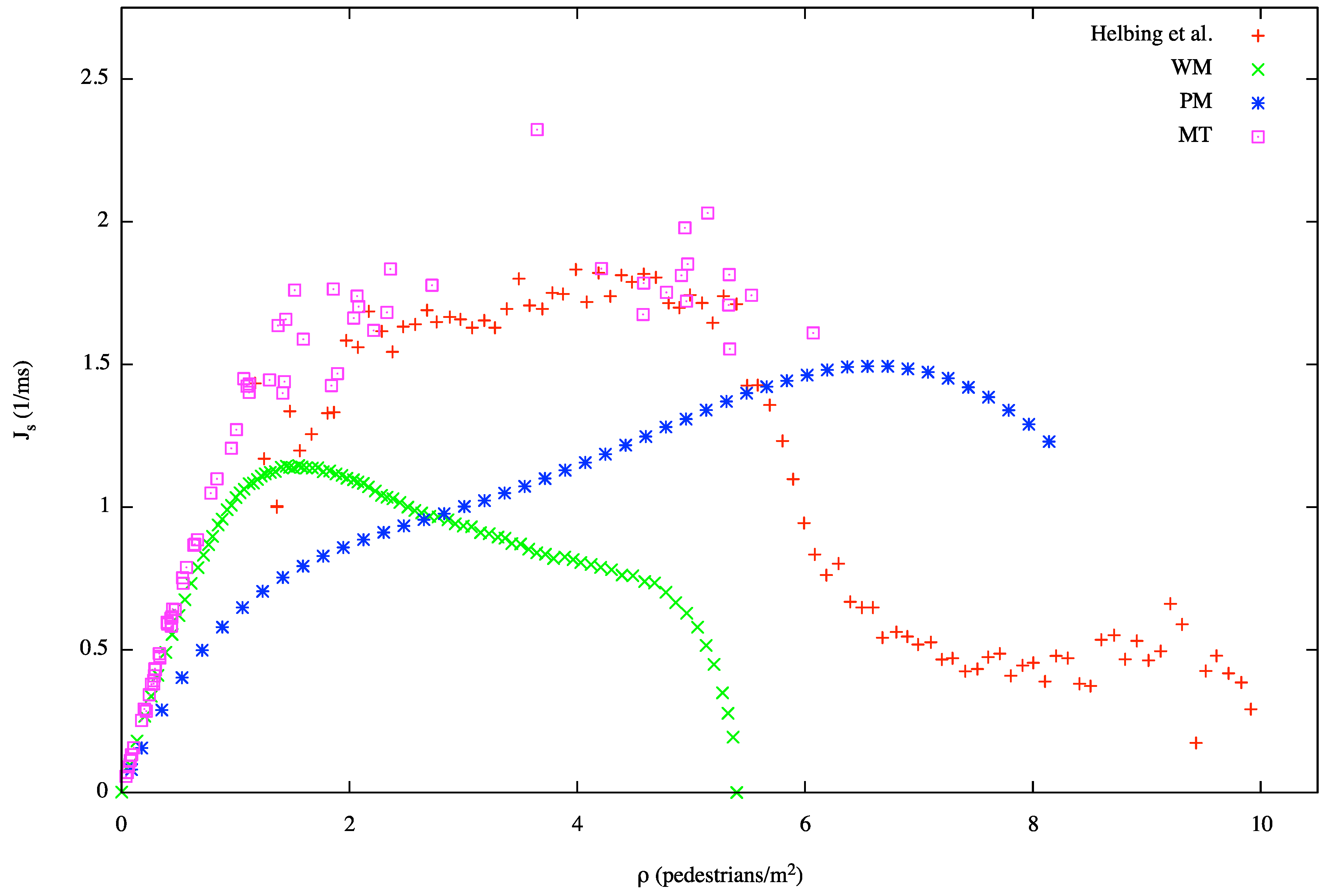
A different kind of analysis of simulation results that represents a further step in the above direction is represented by the so-called
fundamental diagram [
10]: this graph shows how the average velocity of pedestrians in a section of the environment (e.g., one of the ends of a corridor) varies according to the density of the observed environment. Since the flow of pedestrians is directly proportional to their velocity, this diagram is sometimes presented in an equivalent form that shows the variation of flow according to the density. In general, we expect to have a decrease in the velocity when density grows; the flow, instead, initially grows, since it is also directly proportional to the density, until a certain threshold value is reached (also called
critical density), then it decreases. Despite being of great relevance, different experiments gathered different values of empirical data. Consensus on the shape of the function is wide, but the range of the possible values has even big differences from different versions, as one can see from the set of different diagrams in
Figure 6 where both lines are related to design manuals ([
50,
51]) and also data points are related to experimental measurements (respectively carried out in the context of the Hajj in Saudi Arabia by [
52] and in the city of Osaka, in Japan, by [
53]). The maximum possible value for density before congestions arise is also disputed. In the several versions of the fundamental diagram presented, this value ranges between 3.8 m
2 and 10 m
2, which is more than double. In [
54], the authors report densities of 8 m
−2 during the Tawaf, one of the Islamic rituals of pilgrimage, and in general values higher than 6.25 m
−2 (the limit of several CA-based models) are reported to be found. Nonetheless, the capability of a model to generate a plausible fundamental diagram represents a sort of necessary condition for the possibility of actually reproducing in a faithful way pedestrian dynamics in more complex situations than a single corridor or section of a larger scenario.
Finally, one of the most interesting possibilities offered by pedestrian simulation system is the chance to actually visualise the plausible utilisation of space in the actual map of the environment in order to identify potentially problematic situations. This measure is essentially related to the frequency of occupation of a “spot” of the simulated environment by a pedestrian on the overall simulated time; this value is essentially related to the geometry of the environment and the planned flows, and it is strongly related to local average density of pedestrians (relating to the so-called “level of service” for pedestrian facilities [
55]).
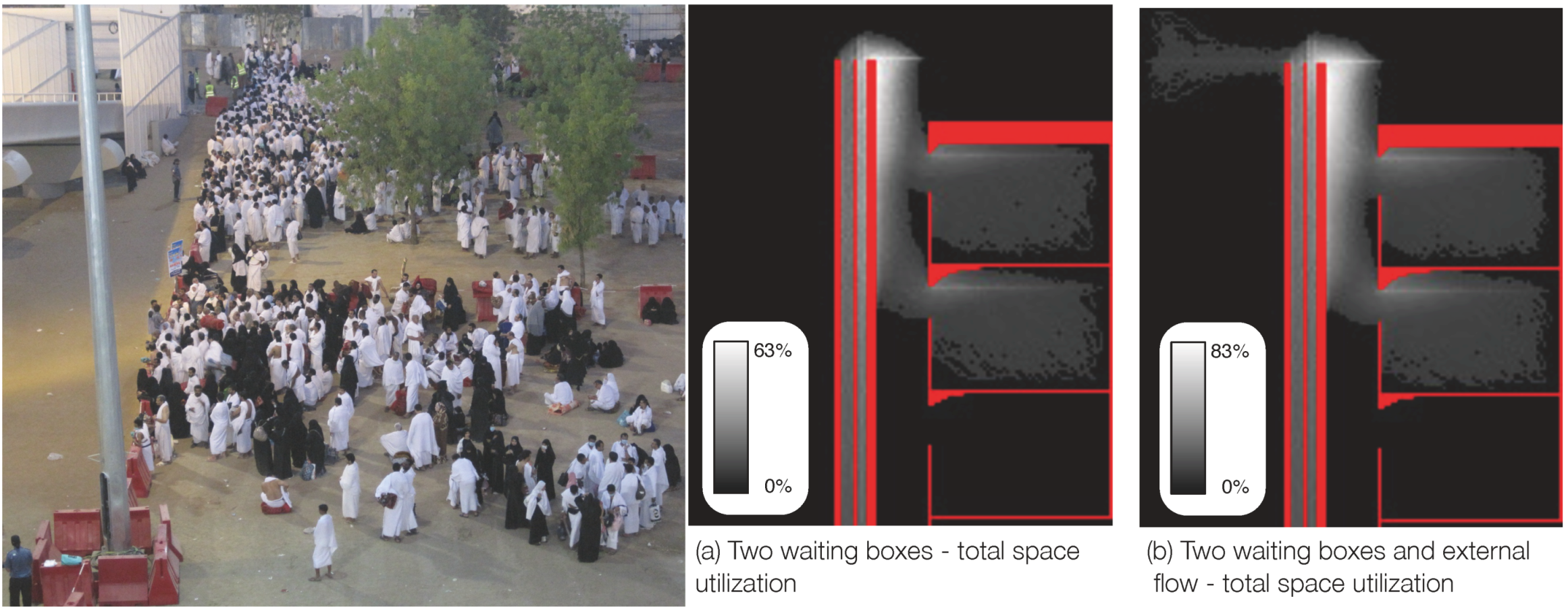
Figure 7 shows an sample situation in the context of the Hajj, more thoroughly described in [
56]: in this scenario, each pilgrim moves from a waiting area towards a ramp to reach a train station. The overall process of arrival of pilgrims to the station must be organised in order to avoid congestion and a simulation system can help in understanding how different crowd management schemes perform from this perspective. The diagrams of
Figure 7 respectively show the level of space utilisation (a) in the simultaneous arrival of pilgrims from two waiting areas and (b) when a group of pilgrims move directly to the ramp in addition to the pilgrims moving from the previous two waiting areas.
Figure 6.
Empirical fundamental diagrams for pedestrian movement in planar facilities as reported by design manuals design manuals [
50,
51] and also data points related to experimental measurements (respectively carried out in the context of the Hajj in Saudi Arabia by Helbing [
52] and in the city of Osaka, in Japan, by [
53]).
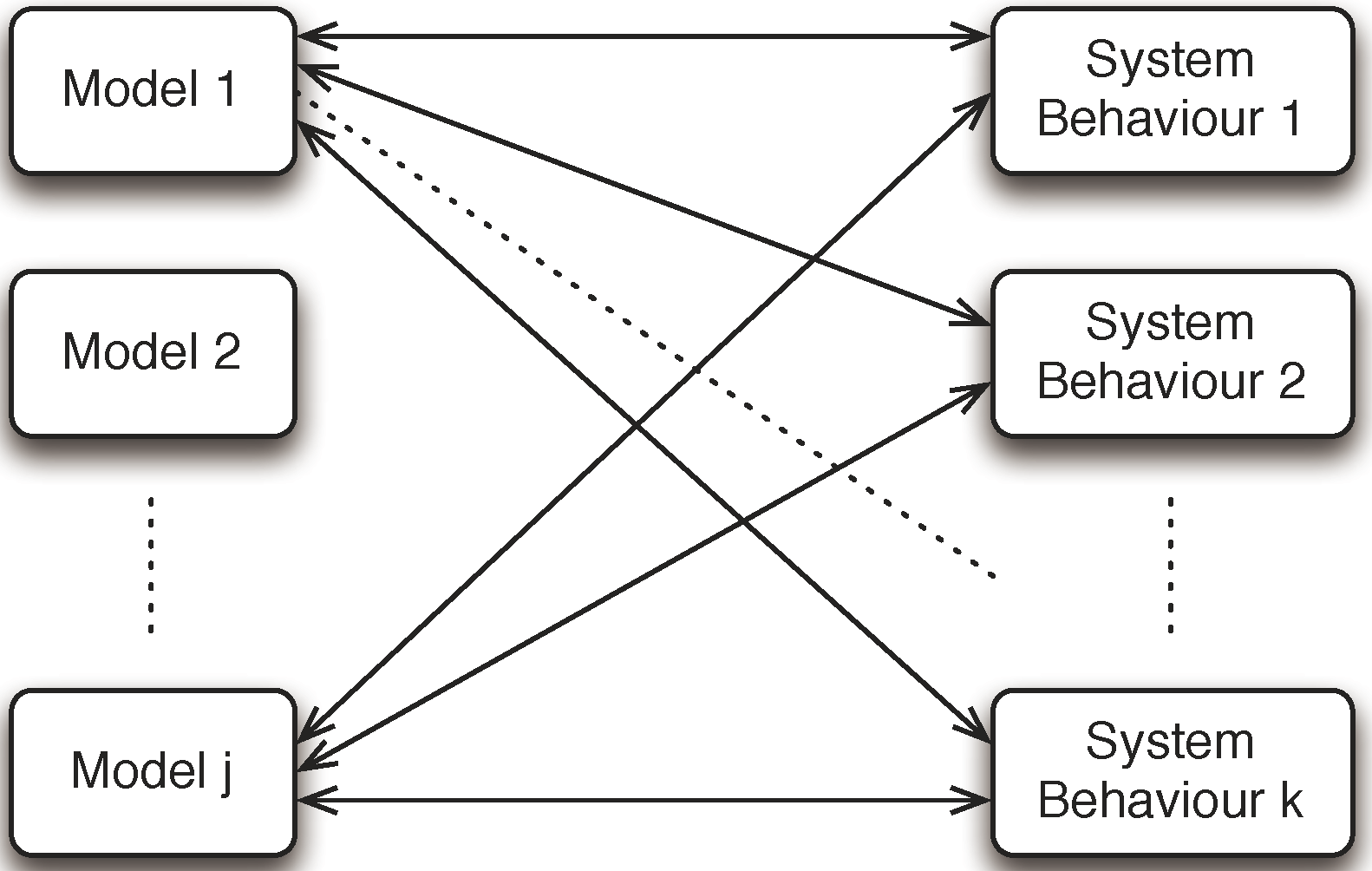
It must be emphasised that the substantial number, variety and level of formalisation of relevant system behaviour are actually an important factor supporting the possibility to evaluate and compare the results of a modelling approach. In fact, given the heterogeneity in the modelling approaches, briefly introduced in
Section 3, it might be difficult to put them in relation in terms of different levels of abstractions, in Floridi’s sense. Nonetheless, it is generally quite simple to achieve the necessary information from the model to analyse its results in terms of the above system behaviours and therefore to actually compare the performance of models on the basis of the outcomes of their application, as shown in
Figure 8: the analysis described in [
57], for instance, shows how different (commercial) simulation platforms, working respectively with a discrete and a continuous spatial representation of the environment, can actually produce comparable results in terms of analysis of the “level of service”.
Figure 7.
A portion of a simulated scenario on the left and two schematic representations ofthe level of space utilisation on the right.
Figure 8.
A mapping scheme between models and relevant system behaviours.
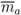 = 〈δxa , δya 〉 where |
= 〈δxa , δya 〉 where | 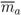 |=
|=  < M , where M is a parameter depending on the specific scenario representing the maximum displacement per time unit.
< M , where M is a parameter depending on the specific scenario representing the maximum displacement per time unit.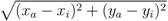 ≤ pera.
≤ pera.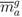 = 〈0, M〉 (respectively
= 〈0, M〉 (respectively  = 〈0, −M〉).
= 〈0, −M〉).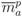 = 0 if ∀b ∈ Pa: d(a, b) ≥p.
= 0 if ∀b ∈ Pa: d(a, b) ≥p.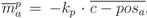 , where ka is a parameter determining the intensity of the proxemic influence on the overall behaviour.
, where ka is a parameter determining the intensity of the proxemic influence on the overall behaviour.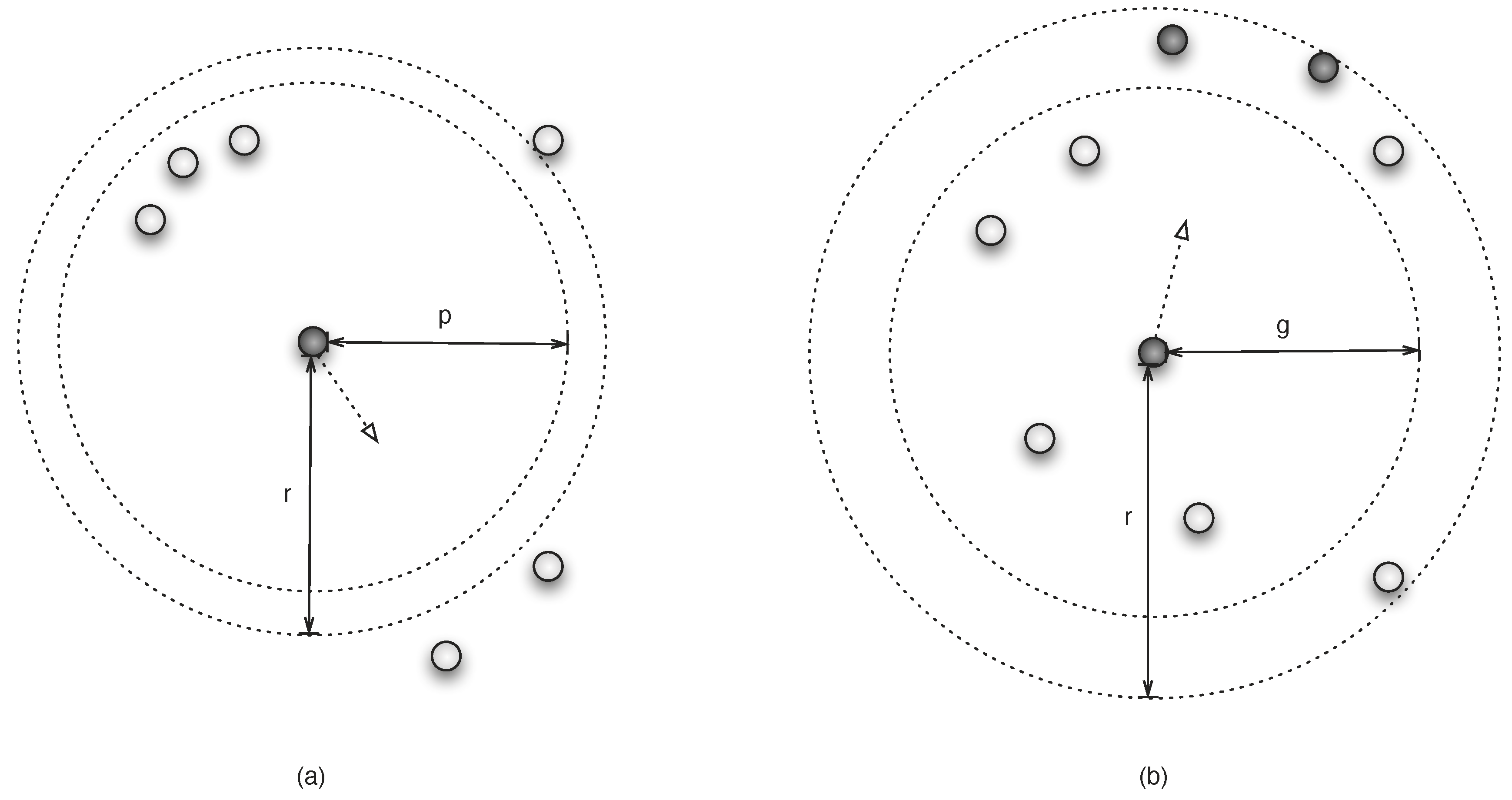
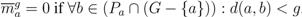 .
.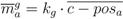 , where ka is a parameter determining the intensity of the group dynamic influence on the overall behaviour.
, where ka is a parameter determining the intensity of the group dynamic influence on the overall behaviour.