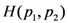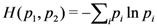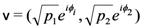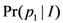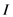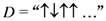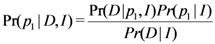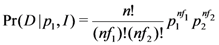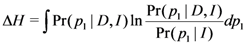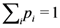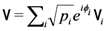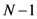Information Physics—Towards a New Conception of Physical Reality
Abstract
:1. Introduction
2. The Role of Information in Quantum Physics
2.1. Classical Physics
- A conception of the physical world, namely the mechanical conception of reality;
- A precise conceptual and mathematical framework, which formalizes this mechanical conception;
- Classical physical theories—in particular Newtonian mechanics and Maxwellian electrodynamics—which are built within this framework.
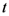 , the physical state of a physical system is described by a mathematical object,
, the physical state of a physical system is described by a mathematical object, 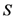 , simply called the state. The state
, simply called the state. The state 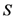 completely describes the physical state insofar as predictions of the outcomes of all possible measurements performed on the system are concerned. The state is a
completely describes the physical state insofar as predictions of the outcomes of all possible measurements performed on the system are concerned. The state is a 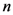 -tuple of real numbers since it is assumed that the properties it encodes (which are in turn revealed by performing measurements on the system) have a continuum of possible values. The state space of the system is the set of all possible states of the system. The temporal evolution of the state of the system during the interval
-tuple of real numbers since it is assumed that the properties it encodes (which are in turn revealed by performing measurements on the system) have a continuum of possible values. The state space of the system is the set of all possible states of the system. The temporal evolution of the state of the system during the interval 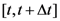 is represented by a continuous bijective map,
is represented by a continuous bijective map, 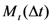 , over state space.
, over state space.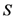 , and the dynamical map
, and the dynamical map 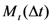 . For example, in Newton’s theory of gravity, matter is composed of mutually-gravitating particles represented by geometrical points in Euclidean space, moving in geometrically-precise trajectories. The state of a system of
. For example, in Newton’s theory of gravity, matter is composed of mutually-gravitating particles represented by geometrical points in Euclidean space, moving in geometrically-precise trajectories. The state of a system of 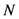 such particles is given by a list of the real-valued positions and velocities of these
such particles is given by a list of the real-valued positions and velocities of these 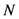 particles, and the dynamical map is obtained from Newton’s laws of motion by taking into account the gravitational forces between these particles via Newton’s law of gravitation. In principle, there exists an informationally-complete measurement whose outcome is simply a read-out of the positions and velocities of the
particles, and the dynamical map is obtained from Newton’s laws of motion by taking into account the gravitational forces between these particles via Newton’s law of gravitation. In principle, there exists an informationally-complete measurement whose outcome is simply a read-out of the positions and velocities of the 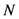 particles that constitute the physical system.
particles that constitute the physical system.2.2. Quantum Physics
2.2.1. Quantum Model of the Measurement Process
- Discreteness. The number of possible outcomes of a measurement may be finite or countably infinite;
- Probabilistic Outcomes. The outcome of a measurement performed on a physical system is only predictable on a probabilistic level;
- Disturbance. A measurement almost invariably changes the state of the system upon which it is performed;
- Complementarity. A measurement only yields information about some of the parameters needed to specify the state of the system, at the expense of the others.
 . A Stern-Gerlach measurement consists of a pair of magnets oriented in some specific direction,
. A Stern-Gerlach measurement consists of a pair of magnets oriented in some specific direction, 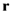 , which deflect the silver atom up or down by an amount that, classically, depends upon the component of
, which deflect the silver atom up or down by an amount that, classically, depends upon the component of  in the direction
in the direction 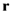 . Accordingly, in the classical framework, a Stern-Gerlach measurement oriented in the
. Accordingly, in the classical framework, a Stern-Gerlach measurement oriented in the  -direction records
-direction records 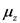 , the component of
, the component of  in the
in the  -direction. Since measurements are ideally non-disturbing in the classical framework, subsequent Stern-Gerlach measurements oriented in the
-direction. Since measurements are ideally non-disturbing in the classical framework, subsequent Stern-Gerlach measurements oriented in the 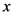 - and
- and 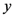 -directions can be made on the spin to record the
-directions can be made on the spin to record the 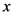 - and
- and 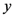 -components of
-components of  . In this way, an experimenter can, in principle, precisely determine
. In this way, an experimenter can, in principle, precisely determine  by performing a sequence of Stern-Gerlach measurements on a single spin.
by performing a sequence of Stern-Gerlach measurements on a single spin.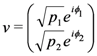
 -direction performed on the spin will yield just one of two possible outcomes, conventionally labelled up (
-direction performed on the spin will yield just one of two possible outcomes, conventionally labelled up ( 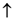 ) and down (
) and down ( 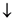 ). This discreteness does not arise due to a discretization of a real-valued quantity, but, rather, is—according to the quantum formalism—an inherent feature of certain measurements on quantum systems.
). This discreteness does not arise due to a discretization of a real-valued quantity, but, rather, is—according to the quantum formalism—an inherent feature of certain measurements on quantum systems.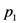 and down with probability
and down with probability 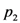 . If the measurement is now repeated immediately afterwards, then, due to the property of repeatability, the measurement will (at least ideally) yield the same outcome with certainty. Suppose, for the sake of argument, that the first measurement yields the outcome up. Then, in order that the second measurement also yields up, the state of the spin in between the two measurements be
. If the measurement is now repeated immediately afterwards, then, due to the property of repeatability, the measurement will (at least ideally) yield the same outcome with certainty. Suppose, for the sake of argument, that the first measurement yields the outcome up. Then, in order that the second measurement also yields up, the state of the spin in between the two measurements be
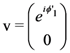
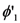 is arbitrary. Hence, the first measurement disturbs the state of the system. In fact, the disturbance is almost total: the post-measurement state carries almost no trace of the degrees of freedom in the pre-measurement state. As a result, after the first measurement is made, no further information about the pre-measurement state can be obtained by performing additional measurements on the system.
is arbitrary. Hence, the first measurement disturbs the state of the system. In fact, the disturbance is almost total: the post-measurement state carries almost no trace of the degrees of freedom in the pre-measurement state. As a result, after the first measurement is made, no further information about the pre-measurement state can be obtained by performing additional measurements on the system. -direction yields information about
-direction yields information about 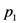 and
and 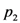 , but no information about
, but no information about 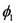 and
and 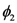 , and we have already established that subsequent measurements on the same system yields no additional information. Thus, in choosing to perform this particular Stern-Gerlach measurement (oriented in the
, and we have already established that subsequent measurements on the same system yields no additional information. Thus, in choosing to perform this particular Stern-Gerlach measurement (oriented in the  -direction), the experimentalist has effectively chosen to learn about
-direction), the experimentalist has effectively chosen to learn about 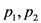 at the expense of
at the expense of  . In other words, she learns about one-half of the degrees of freedom in the state at the expense of learning nothing about the other half [2]. This trade-off—which is one way of expressing the idea of complementarity—is not something which can be alleviated by performing a more sophisticated repeatable measurement, but is a fundamental limitation built into the quantum framework [3]. If the experimentalist wishes to learn about
. In other words, she learns about one-half of the degrees of freedom in the state at the expense of learning nothing about the other half [2]. This trade-off—which is one way of expressing the idea of complementarity—is not something which can be alleviated by performing a more sophisticated repeatable measurement, but is a fundamental limitation built into the quantum framework [3]. If the experimentalist wishes to learn about  , she would need to perform Stern-Gerlach measurements in different directions (for example, in the
, she would need to perform Stern-Gerlach measurements in different directions (for example, in the 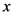 - and
- and 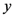 -directions) on other identical copies of the spin.
-directions) on other identical copies of the spin.- (1) Limited information about future measurement outcomes.Given the state of the system and the measurement to be performed, the experimenter lacks information about the outcome that will be obtained. In the above example, prior to performing a Stern-Gerlach measurement in the
-direction on the spin, the experimenter does not know which outcome (up or down) will occur, but only that the probabilities of the two possible outcomes are
and
, respectively.
Quantitatively, prior to performing the measurement, the experimenter has uncertaintyabout which outcome will be obtained. The
-function here is an uncertainty function, such as the Shannon entropy function,
. After performing the measurement and obtaining a definite outcome, the experimenter’s uncertainty has been removed. Hence, the uncertainty,
, can be interpreted as the amount of information the experimenter lacks prior to performing the measurement about which the outcome will be obtained.
- (2) Limited information about the unknown state of a physical system.If an experimenter is presented with a system in an unknown state and wishes to learn what that state is, the quantum framework imposes two kinds of fundamental limits. First, due to the probabilistic and disturbance features of measurements, the outcome of a single measurement performed on the system provides scant information about the state of the system. In practice, in order to build up any useful knowledge of the state, the experimenter must perform a large number of measurements on identically-prepared copies of the system. Furthermore, due to complementarity, a single type of measurement only provides access to one-half of the degrees of freedom of the state of the system, so that the experimenter must perform other types of measurement in order to build up information about all of the degrees of freedom in the state.In the electron spin example, the experimenter wishes to learn about the unknown state,
. The experimenter’s information about the outcome probabilities,
, prior to performing the Stern-Gerlach measurement is encoded in the Bayesian prior probability
, where
symbolizes the experimenter’s prior state of knowledge. After the experimenter has performed
identical Stern-Gerlach measurements on
identically prepared copies of the system, obtaining data which can be summarized in the data string
of length
, the prior can be updated to the posterior,
, using Bayes’ rule:
If the experimenter obtainscases of outcome up and
of outcome down, then
The amount of information the data thus provides the experimenter aboutcan readily be quantified using, for example, the continuum form of the Shannon entropy,
which is finite for finite. Hence, for finite
, the experimenter only has finite, imperfect information about
. Only in the practically unattainable limit as
does the experimenter gain perfect knowledge of
.
Furthermore, the data string,, provides no information about the
. In order to obtain information about the
, the experimenter needs to perform Stern-Gerlach measurements in other directions.
2.2.2. Quantum Description of Composite Systems
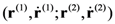 of two particles is a list of the two states,
of two particles is a list of the two states, 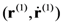 ,
, 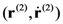 of the particles considered separately.
of the particles considered separately.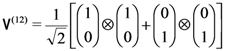
 denotes the tensor product operation, and where the state has been written down with respect to Stern-Gerlach measurements in the
denotes the tensor product operation, and where the state has been written down with respect to Stern-Gerlach measurements in the  -direction. This state is entangled, meaning that it cannot be expressed in the form
-direction. This state is entangled, meaning that it cannot be expressed in the form 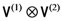 , where
, where 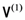 and
and 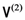 are the spin states of the respective particles.
are the spin states of the respective particles. -direction on the first particle, the above entangled state yields equal probability of obtaining up or down. The quantum formalism further predicts that a Stern-Gerlach measurement in any direction performed on the first particle has equal probability of yielding the two possible outcomes. This prediction holds true even for a different entangled state such as
-direction on the first particle, the above entangled state yields equal probability of obtaining up or down. The quantum formalism further predicts that a Stern-Gerlach measurement in any direction performed on the first particle has equal probability of yielding the two possible outcomes. This prediction holds true even for a different entangled state such as
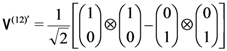
 -direction separately on the two particles then, for both states
-direction separately on the two particles then, for both states 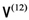 and
and 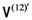 , the agents would each have equal probability of obtaining “up, up” or “down, down”, and zero probability of obtaining “up, down” or “down, up”, and hence would not be able to distinguish between them [4].
, the agents would each have equal probability of obtaining “up, up” or “down, down”, and zero probability of obtaining “up, down” or “down, up”, and hence would not be able to distinguish between them [4].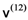 , the post-measurement state is
, the post-measurement state is
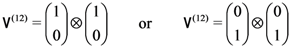
 -direction on the two particles in the spin state
-direction on the two particles in the spin state 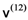 , their respective outcomes would be perfectly correlated—they would either both get up or both get down.
, their respective outcomes would be perfectly correlated—they would either both get up or both get down. -direction on their respective spins, they will find that the spin directions they measure are perfectly correlated with one another. However, a pair of quantum systems admits correlations which are much richer, and Bell showed that, if a pair of quantum systems is allowed to interact and are then separated by an arbitrarily great distance, and the two agents are then allowed to freely perform different measurements upon the two subsystems, then the outcomes of their measurements can be correlated in a way that cannot be accounted for if we assume that reality behaves in accordance with the mechanical conception of classical physics (being local, in particular). An excellent and accessible self-contained exposition of Bell’s theorem requiring only high school algebra and no prior knowledge of quantum theory can be found in [10]. In short, Bell showed that entanglement indeed leaves an experimentally detectable fingerprint—non-local correlations—which cannot be accounted for within the classical framework.
-direction on their respective spins, they will find that the spin directions they measure are perfectly correlated with one another. However, a pair of quantum systems admits correlations which are much richer, and Bell showed that, if a pair of quantum systems is allowed to interact and are then separated by an arbitrarily great distance, and the two agents are then allowed to freely perform different measurements upon the two subsystems, then the outcomes of their measurements can be correlated in a way that cannot be accounted for if we assume that reality behaves in accordance with the mechanical conception of classical physics (being local, in particular). An excellent and accessible self-contained exposition of Bell’s theorem requiring only high school algebra and no prior knowledge of quantum theory can be found in [10]. In short, Bell showed that entanglement indeed leaves an experimentally detectable fingerprint—non-local correlations—which cannot be accounted for within the classical framework.3. The Rise of the Informational View
3.1. Mach and the Primacy of Experience over Concepts
“The goal which it (physical science) has set itself is the simplest and most economical abstract expression of facts.”
“In mentally separating a body from the changeable environment in which it moves, what we really do is to extricate a group of sensations on which our thoughts are fastened and which is of relatively greater stability than the others, from the stream of all our sensations. Suppose we were to attribute to nature the property of producing like effects in like circumstances; just these like circumstances we should not know how to find. Nature exists once only. Our schematic mental imitation alone produces like events.”
3.2. Thermodynamics, Statistical Mechanics, and Maxwell’s Demon
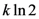 if he determines whether a molecule is in one half or the other half of a box, and acts appropriately on this information) in order to offset the reduction in thermodynamic entropy of the system due to his activity.
if he determines whether a molecule is in one half or the other half of a box, and acts appropriately on this information) in order to offset the reduction in thermodynamic entropy of the system due to his activity.3.3. Shannon’s Theory of Information, and Its Applications
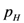 (heads) and
(heads) and 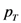 (tails), one’s gain of information is maximal when these probabilities are both
(tails), one’s gain of information is maximal when these probabilities are both  , is zero when one of these probabilities is zero, and varies smoothly between these extremes for intermediate probability distributions.
, is zero when one of these probabilities is zero, and varies smoothly between these extremes for intermediate probability distributions.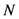 possible outcomes with probabilities
possible outcomes with probabilities 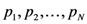 , he showed that the information gain is given by
, he showed that the information gain is given by
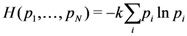
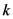 is an arbitrary positive constant. At the suggestion of John von Neumann, Shannon decided to call
is an arbitrary positive constant. At the suggestion of John von Neumann, Shannon decided to call 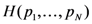 the entropy of the probability distribution, in conscious acknowledgment of the connection to the work of Szilard described in Section 3.2.
the entropy of the probability distribution, in conscious acknowledgment of the connection to the work of Szilard described in Section 3.2.Principle of Maximum Entropy: In assigning a probability distribution, select the distribution which has maximum entropy,
subject to the normalization constraint
and any other constraints on
.
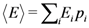 , is known, where
, is known, where 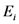 is the energy of the
is the energy of the 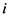 th microstate of the system. Thus, the Shannon entropy of the canonical distribution can be regarded as a precise measure of the amount of information an agent lacks about the microstate of the system if he knows only the average energy of the system.
th microstate of the system. Thus, the Shannon entropy of the canonical distribution can be regarded as a precise measure of the amount of information an agent lacks about the microstate of the system if he knows only the average energy of the system.3.4. Black Hole Physics
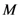 . The solution showed a coordinate singularity along a sphere of radius
. The solution showed a coordinate singularity along a sphere of radius 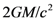 centered on the mass. Subsequent work showed that this coordinate singularity represented a kind of real physical boundary—once in-falling matter passes the boundary, neither it nor the light it emits is able to penetrate the boundary. Hence, according to general relativity, no detailed information about matter within the spherical boundary can be obtained by an observer external to the boundary, a situation which led Wheeler to name this object a black hole. General relativity also implies that a black hole, no matter how it is formed, is completely characterized by just three parameters, namely mass, angular momentum, and electric charge. Thus, whatever the internal constitution of a black hole may be, the only information available to an external observer about its internal constitution are these three real-valued parameters.
centered on the mass. Subsequent work showed that this coordinate singularity represented a kind of real physical boundary—once in-falling matter passes the boundary, neither it nor the light it emits is able to penetrate the boundary. Hence, according to general relativity, no detailed information about matter within the spherical boundary can be obtained by an observer external to the boundary, a situation which led Wheeler to name this object a black hole. General relativity also implies that a black hole, no matter how it is formed, is completely characterized by just three parameters, namely mass, angular momentum, and electric charge. Thus, whatever the internal constitution of a black hole may be, the only information available to an external observer about its internal constitution are these three real-valued parameters. for a non-rotating, chargeless black hole of mass
for a non-rotating, chargeless black hole of mass 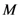 ) and a temperature, and obeys four laws analogous to the four laws of thermodynamics [18]. Viewed from the point of view of statistical physics, the entropy of a black hole quantifies an external observer’s lack of information about the internal structure of the black hole. The interpretation of the Bekenstein-Hawking expression for the entropy of a black hole (which is derived using thermodynamic arguments [18]) from a microscopic point view is supported by calculations from a microscopic point of view within the frameworks of string theory [19] and loop quantum gravity [20] that both yield the Bekenstein-Hawking expression. For example, for a non-rotating, chargeless black hole, the information that an external observer lacks can be written down in a binary string of length given by
) and a temperature, and obeys four laws analogous to the four laws of thermodynamics [18]. Viewed from the point of view of statistical physics, the entropy of a black hole quantifies an external observer’s lack of information about the internal structure of the black hole. The interpretation of the Bekenstein-Hawking expression for the entropy of a black hole (which is derived using thermodynamic arguments [18]) from a microscopic point view is supported by calculations from a microscopic point of view within the frameworks of string theory [19] and loop quantum gravity [20] that both yield the Bekenstein-Hawking expression. For example, for a non-rotating, chargeless black hole, the information that an external observer lacks can be written down in a binary string of length given by 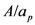 , where
, where 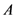 is the area of the event horizon and
is the area of the event horizon and 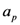 is the area
is the area 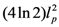 with
with 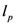 being the Planck length (approximately
being the Planck length (approximately 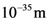 ).
).3.5. Computation as a Physical Process
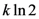 of thermodynamic entropy. Turing’s machine did not take into account any such fundamental physical cost of reading, erasing, and writing a symbol to a tape. In 1961, following Szilard, Laudauer postulated that there indeed exists such an entropic cost, associated with the irreversibility of certain logical operations involved in a computation [22], and Bennett subsequently argued that the entropic cost is specifically associated with the erasure step [23]. A computing device within infinite memory could side-step this entropic cost since it could operate indefinitely without performing an erase operation. However, a device with finite memory would eventually fill up all available working memory and, from that point onward, need to perform erase operations, and would thus eventually be forced to start paying this entropic cost.
of thermodynamic entropy. Turing’s machine did not take into account any such fundamental physical cost of reading, erasing, and writing a symbol to a tape. In 1961, following Szilard, Laudauer postulated that there indeed exists such an entropic cost, associated with the irreversibility of certain logical operations involved in a computation [22], and Bennett subsequently argued that the entropic cost is specifically associated with the erasure step [23]. A computing device within infinite memory could side-step this entropic cost since it could operate indefinitely without performing an erase operation. However, a device with finite memory would eventually fill up all available working memory and, from that point onward, need to perform erase operations, and would thus eventually be forced to start paying this entropic cost.4. Information Physics
“ ‘It from bit’ symbolizes the idea that every item of the physical world has at bottom—at a very deep bottom, in most instances—an immaterial source and explanation; that which we call reality arises in the last analysis from the posing of yes-no questions and the registering of equipment-evoked responses; in short, that all things physical are information-theoretic in origin, and this in a participatory universe.”
“What we call reality consists of a few iron posts of observation between which we fill an elaborate papier-mâché of imagination and theory.”
- Shift from the view of a physical theory as a description of reality in itself to a description of reality as experienced by an agent. Mach’s emphasis on the primacy of the experience of an agent over the concepts of a physical theory, thermodynamics as a theory explicitly constructed to interrelate the macro-variables accessible to limited agents, and quantum theory with its highly non-trivial model of the measurement process have all helped to shift the focus of physical theory from being a description of reality in itself to a description of reality as experienced by an agent.
- Breakdown of the classical notion of an ideal agent who has unfettered access to the state of reality. Szilard’s proposal that there is a physical entropic cost associated with measurement (itself arising from the tension between the second law of thermodynamics and the reversible dynamics of classical mechanics), the quantum model of measurement (with its features of discreteness, probabilistic outcomes, disturbance and complementarity), and the limited access to information of the internal constitution of a black hole by an external observer all point to the breakdown of the classical notion of an ideal agent who has unfettered access to the state of reality without bringing about any reciprocal change as a result, and all suggest that the interface between an agent and the physical world is a highly non-trivial one governed by precise rules which we can come to know.
- Recognition that the informational view might lead to new quantitative understanding of the reality described by existing physics. Szilard’s quantification of the entropy generation associated with information acquisition, Shannon’s quantification of the information gain resulting from learning the outcome of a probabilistic process, Jaynes’ derivation of statistical mechanics on the basis of Shannon’s information measure, the quantification and statistical interpretation of black hole entropy, and the constructive use of the mathematical tools of information theory to discover and explore unexpected phenomena in the quantum world have all lent support to the hope that the informational view might lead to new quantitative understanding of the reality described by existing physics and that it is important that information be taken into account in the development of new physical theories.
4.1. Understanding Quantum Theory
4.1.1. Information-based Reconstruction of Quantum Theory
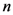 identically-prepared copies of the system are analyzed, and postulates that, if one holds the experimental situation fixed but imagines varying the physical laws which govern the situation, then the actual laws are those which maximize the amount of information that the experimenter gains about the system.
identically-prepared copies of the system are analyzed, and postulates that, if one holds the experimental situation fixed but imagines varying the physical laws which govern the situation, then the actual laws are those which maximize the amount of information that the experimenter gains about the system.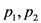 of a two-dimensional quantum system are a function of the angle
of a two-dimensional quantum system are a function of the angle 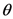 between the preparation and analysis stages of an experiment, then
between the preparation and analysis stages of an experiment, then 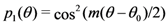 , where
, where  , which is a generalized form of Malus’ law, a well-verified prediction of quantum theory.
, which is a generalized form of Malus’ law, a well-verified prediction of quantum theory. with a block in the negative channel, which prepares incoming electron spins. The analysis is performed by a vertically-oriented Stern-Gerlach apparatus. Suppose that the experimenter does not know the angles
with a block in the negative channel, which prepares incoming electron spins. The analysis is performed by a vertically-oriented Stern-Gerlach apparatus. Suppose that the experimenter does not know the angles 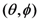 because, for example, the preparation stage is physically removed from the laboratory. The aim of the experimenter is to learn about
because, for example, the preparation stage is physically removed from the laboratory. The aim of the experimenter is to learn about 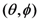 from the data he obtains from performing measurements on
from the data he obtains from performing measurements on 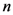 identically-prepared spins.
identically-prepared spins.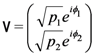
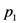 and
and 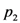 are the probabilities that the analysis will yield the outcomes up and down, respectively. If
are the probabilities that the analysis will yield the outcomes up and down, respectively. If 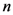 spins identically prepared by this arrangement are analyzed, the experimenter can learn about the values of the parameters
spins identically prepared by this arrangement are analyzed, the experimenter can learn about the values of the parameters 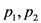 from the frequency data that he obtains. According to quantum theory, the
from the frequency data that he obtains. According to quantum theory, the 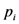 are functions of
are functions of 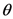 , and quantum theory permits the precise determination of these functions. Using these functions, the experimenter can transform his knowledge about the
, and quantum theory permits the precise determination of these functions. Using these functions, the experimenter can transform his knowledge about the 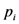 into knowledge about
into knowledge about 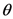 . Viewed in this way, the
. Viewed in this way, the 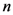 electrons are “transmitting” information about the preparation parameter
electrons are “transmitting” information about the preparation parameter 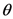 to the experimenter. Wootters’ strategy is to try to fix the function
to the experimenter. Wootters’ strategy is to try to fix the function 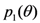 by requiring that the information conveyed to the experimenter is maximized.
by requiring that the information conveyed to the experimenter is maximized.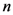 analyses, the experimental data,
analyses, the experimental data, 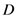 , thus consists of the frequencies
, thus consists of the frequencies  , where
, where 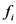 is the frequency with which outcome
is the frequency with which outcome 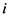
 has been obtained. The posterior probability,
has been obtained. The posterior probability, 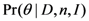 can be calculated from Bayes rule,
can be calculated from Bayes rule,
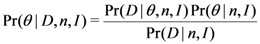
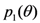 as
as
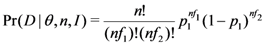
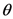 itself depends upon the value of
itself depends upon the value of 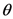 . The expected amount of information gained about
. The expected amount of information gained about 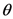 is given by
is given by
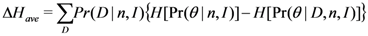
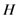 , the average being taken over all possible data,
, the average being taken over all possible data, 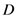 , obtainable in a fixed number,
, obtainable in a fixed number, 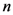 , of detections. The evaluation of
, of detections. The evaluation of 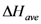 requires the specification of the prior probability
requires the specification of the prior probability 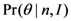 which is equal to
which is equal to 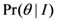 since the choice of
since the choice of 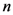 has no bearing on
has no bearing on 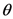 . Wootters assumes that
. Wootters assumes that 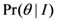 is a constant on the grounds that, for any
is a constant on the grounds that, for any 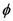 , all
, all 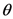 are equally likely. In the limit
are equally likely. In the limit 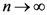 , one finds that the maximization of
, one finds that the maximization of 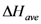 yields a generalized form of Malus’ law,
yields a generalized form of Malus’ law,
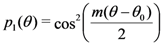
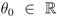 and
and  remain undetermined. Wootters’ information maximization principle thus becomes:
remain undetermined. Wootters’ information maximization principle thus becomes:Wootters’ Information Maximization Principle: The laws of quantum physics are such that the expected gain in the Shannon information about the state of a quantum system after analysis of a large number of identically-prepared systems is maximized. The average is taken over all possible data that can be obtained in a given number of analyses.
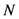 dimensional quantum system, but the derivation invokes additional assumptions which presuppose prior knowledge of rather abstract features of the quantum formalism itself. Nevertheless, the derivation of Malus’ law is striking in its simplicity and economy of means, and clearly demonstrates that it is not unreasonable to hope to be able to reconstruct the quantum formalism from information-theoretic principles.
dimensional quantum system, but the derivation invokes additional assumptions which presuppose prior knowledge of rather abstract features of the quantum formalism itself. Nevertheless, the derivation of Malus’ law is striking in its simplicity and economy of means, and clearly demonstrates that it is not unreasonable to hope to be able to reconstruct the quantum formalism from information-theoretic principles.5. Towards a New Conception of Reality
References and Notes
- More generally, the knowledge that an agent (be the agent ideal or non-ideal) possesses about the state of a system can be represented by a probability distribution over the state space of the system. This distribution itself is often also referred to as “the state” of the system. If the distribution picks out a single state, as would it be in the case of an ideal agent, it is said to be pure.
- This characterization holds true for an N-dimensional quantum system. In that case, the state is represented by
where Viis the
th eigenstate of measurement operator
, and measurement A will yield information about the
(which constitute
independent degrees of freedom since
) at the expense of information about the
(which constitute
independent degrees of freedom since the overall phase of the state is predictively irrelevant).
- If one is willing to sacrifice repeatability, then it is possible to perform measurements—known as informationally-complete measurements—which are capable of accessing all of the degrees of freedom of a quantum state.
- It is, however, possible for the two agents to distinguish between these two entangled states if they allowed to perform a sufficient number of different measurements on many identically-prepared copies of the two spins.
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Blaylock, G. The EPR paradox, Bell’s inequality, and the question of locality. Am. J. Phys. 2010, 78, 111–120. [Google Scholar] [CrossRef]
- Griffiths, R.B. EPR, Bell, and quantum locality. Am. J. Phys. 2011, 79, 954–965. [Google Scholar] [CrossRef]
- Maudlin, T. What Bell proved: A reply to Blaylock. Am. J. Phys. 2010, 78, 121–125. [Google Scholar] [CrossRef]
- Maudlin, T. How Bell reasoned: A reply to Griffiths. Am. J. Phys. 2011, 79, 966–970. [Google Scholar] [CrossRef]
- Maudlin, T. Quantum Non-Locality and Relativity, 3rd ed.; Wiley-Blackwell: Malden, MA, USA, 2011. [Google Scholar]
- Bennett, C.; Wiesner, S. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar]
- Ekert, A. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Z. für Physik 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black hole thermodynamics. Phys. Today 1980, 33, 24–31. [Google Scholar] [CrossRef]
- Strominger, A.; Vafa, C. Microscopic origin of the Bekenstein-Hawking Entropy. Phys. Lett. B 1996, 379, 99–104. [Google Scholar] [CrossRef]
- Rovelli, C. Black hole entropy from loop quantum gravity. Phys. Rev. Lett. 1996, 77, 3288–3291. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, 2, 230–265. [Google Scholar]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C. The thermodynamics of computation—a review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Zurek, W.H.; Wootters, W.K. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Wheeler, J.A. It from Bit. In Proceedings of the 3rd International Symposium on the Foundations of Quantum Mechanics, Tokyo, Japan, 1989.
- Wheeler, J.A. Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Bohr, N. Causality and complementarity. Philos. Sci. 1937, 4, 289–298. [Google Scholar]
- Pais, A. Niels Bohr’s Times; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Heisenberg, W. Physics and Beyond; HarperCollins Publishers Ltd.: Hammersmith, London, UK, 1971; Translated from the German original. [Google Scholar]
- Pauli, W. Writings on Physics and Philosophy; Springer-Verlag: Berlin, Germany, 1994. [Google Scholar]
- Fuchs, C.A. Quantum mechanics as quantum information. Available online: http://arxiv.org/abs/quant-ph/0205039 (accessed on 27 September 2012).
- Grinbaum, A. Reconstructing instead of interpreting quantum theory. Philos. Sci. 2007, 74, 761–774. [Google Scholar] [CrossRef]
- Grinbaum, A. Reconstruction of quantum theory. Br. J. Philos. Sci. 2007, 58, 387–408. [Google Scholar] [CrossRef]
- Wootters, W.K. The Acquisition of Information from Quantum Measurements. Ph.D. thesis, University of Texas at Austin, Austin, TX, USA, 1980. [Google Scholar]
- Fuchs, C.A. Quantum mechanics as quantum information, mostly. J. Mod. Opt. 2003. Available online: http://perimeterinstitute.ca/personal/cfuchs/Oviedo.pdf (accessed on 27 September 2012).
- Brassard, G. Is information the key? Nat. Phys. 2005, 1, 2–4. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Causality and nonlocality as axioms for quantum mechanics. Available online: http://arxiv.org/abs/quant-ph/9709026 (accessed on 27 September 2012).
- Pawlowski, M. Information causality as a physical principle. Nature 2009, 461, 1101–1104. [Google Scholar] [CrossRef]
- Barrett, J. Information processing in generalized probabilistic theories. Phys. Rev. A 2007, 75, 032304:1–032304:21. [Google Scholar]
- Bergia, S.; Cannata, F.; Cornia, A.; Livi, R. On the actual measurability of the density matrix of a decaying system by means of measurements on the decay products. Found. Phys. 1980, 10, 723–730. [Google Scholar] [CrossRef]
- Hardy, L. Quantum theory from five reasonable axioms. Available online: http://arxiv.org/abs/quant-ph/0101012 (accessed on 27 September 2012).
- Hardy, L. Why Quantum Theory? Available online: http://arxiv.org/abs/quant-ph/0111068 (accessed on 27 September 2012).
- Chiribella, G.; Perinotti, P.; D’Ariano, G.M. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311:1–012311:47. [Google Scholar]
- Goyal, P.; Knuth, K.H.; Skilling, J. Origin of complex quantum amplitudes and Feynman’s Rules. Phys. Rev. A 2010, 81, 022109:1–022109:12. [Google Scholar]
- Goyal, P.; Knuth, K.H. Quantum theory and probability theory: Their relationship and origin in symmetry. Symmetry 2011, 3, 171–206. [Google Scholar] [CrossRef]
- Norton, J.D. Time really passes. Humana. Mente 2010, 13, 23–34. [Google Scholar]
- Ghirardi, G.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar]
- Whitehead, A.N. Process and Reality; Free Press: New York, NY, USA, 1929. [Google Scholar]
- Weart, S.R.; Szilard, G.W. The Collected Works of Leo Szilard: Scientific Papers; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Rosenkrantz, R.D. E.T. Jaynes: Papers on Probability, Statistics, and Statistical Physics; Kluwer Boston: Dordrecht, the Netherland, 1983. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Goyal, P. Information Physics—Towards a New Conception of Physical Reality. Information 2012, 3, 567-594. https://doi.org/10.3390/info3040567
Goyal P. Information Physics—Towards a New Conception of Physical Reality. Information. 2012; 3(4):567-594. https://doi.org/10.3390/info3040567
Chicago/Turabian StyleGoyal, Philip. 2012. "Information Physics—Towards a New Conception of Physical Reality" Information 3, no. 4: 567-594. https://doi.org/10.3390/info3040567
APA StyleGoyal, P. (2012). Information Physics—Towards a New Conception of Physical Reality. Information, 3(4), 567-594. https://doi.org/10.3390/info3040567