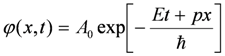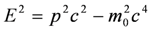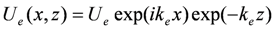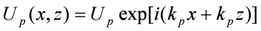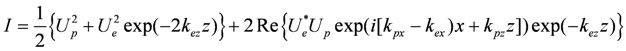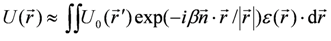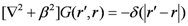1. Introduction
Daniel Pollen and Michael Trachtenberg [
1] proposed the holographic brain theory [
2] to help explain the existence of photographic memories in some people. They suggested that such individuals had more vivid memories because they somehow could access a very large region of their memory holograms. S.R. Hameroff suggested in his paper that a centriole cylinder composed of microtubules functions as a waveguide for the evanescent photons for quantum signal processing [
3]. Georgiev also proposed the idea that consciousness can be the result of quantum computation via applied laser-like pulses in quantum gates within the brain cortex [
4]. Subsequently, Georgiev concluded that this mechanism cannot be used for manipulation of the qubits inside the microtubule cavities, or centrioles, because the photon wavelength is two orders of magnitude longer than the size of these centrioles [
5]; super radiant photons in the microtubule cavities could have wavelength of λ = 100 nm or more suggested by Smith [
6], incompatible with the length of a moderate-sized microtubule cavity, which is about 1 nm. Therefore, super-radiant emissions could not be used to signal qubits in a fashion similar to standing wave lasers in an ion trap computation.
As an alternative mechanism, the author proposes that the cylinder formed by the microtubule cavity may have a negative refractive index, similar to a metamaterial [
7]. Typically, metamaterials are artificial materials, engineered to have a negative refractive index, a property that is not normally found in nature [
8]. They usually gain their properties from structure rather than composition, using microscopic inhomogeneities to create an effective macroscopic behavior.
Negative refractive index materials appear to permit the creation of super lenses that can have a spatial resolution below that of the wavelength [
9]. If the inner medium of the cylinder of microtubules possesses the characteristics of negative refractive index, the generation of evanescent photons is enhanced, and they propagate lossless inside the neurons according to the properties of a metamaterial.
2. Evanescent Superluminal Photons in the Microtubule
Due to the high performance of quantum computation, there is much research into how quantum computing could explain the performance behaviors of human brains, including consciousness itself. As Feynman proposed: The optical computing network is the most realizable quantum mechanical computer, and Hameroff suggested that microtubule cavities in the brain were acting as waveguides for photons and as holographic processors [
10].
The cytoskeleton of biological cells, including neurons of the brain, is made up of microtubules.
Microtubules are composed of subunits of the protein, named tubulin [
11]. Each microtubule is a hollow cylindrical tube of tubulin proteins as shown in
Figure 1, the outer core diameter of which is 25 nm. Each tubulin molecule within each microtubule can function as a switch between two conformations that exist in quantum superposition of both conformational states [
12]. The dimensions of centrioles are close to the wavelengths of light in the infrared and visible spectrum such that they may act as phase coherent, resonant waveguides [
13].
Figure 1.
Structure of microtubules forming a centriole cavity.
According to Jibu
et al. [
14,
15,
16], microtubule quantum states link to those of other neurons by quantum coherent photons tunneling through membranes in biological systems, and the cytoskeletal protein conformational states are entangled by these photons which form coherent domains in their interaction with the local electromagnetic field. They claimed that human consciousness could be understood as arising from those creation-annihilation dynamics of a finite number of evanescent (tunneling) photons in the brain.
E. Recami [
17,
18] claimed in his papers that tunneling photons traveling in an evanescent mode could move with superluminal group speed, which can be shown as follows:
The evanescent photon generated in the quantum domain satisfies the following Klein-Fock-Gordon equation, given by:
Where c is light speed, m0 is an absolute value of the proper mass of the evanescent photon and ħ is Plank’s constant divided by 2π.
This equation has the solution for the photon traveling in an evanescent mode given by:
which corresponds to the elementary particle with an imaginary mass im0 that travels at a superluminal speed satisfying:
where E is the energy of the superluminal particle and p is its momentum. Hence, it can be seen that tunneling photons traveling in an evanescent mode can move at a superluminal speed.
From the assumption that the evanescent photon is a superluminal particle, the author has shown that a microtubule in the biological brain can achieve quantum bit (qubit) computations on large data sets, which would account for the high performance computation as compared with conventional processors [
19].
It therefore seems highly plausible that macroscopic quantum ordered dynamic systems of evanescent photons in the brain could play an essential role in realizing long-range biological order in living systems. Ziolkowski pointed out in his paper that superluminal pulse propagation that permits consequent superluminal exchange without a violation in causality is possible in electromagnetic metamaterials [
20]. If the inner medium of a cylinder of microtubules possesses the characteristics of a metamaterial with negative refractive index, tunneling photons will propagate losslessly inside the neurons in a way that is not restricted by wavelength, and therefore infrared photons could be used for the manipulation of qubits in the brain.
3. Evanescent Wave Holography in the Microtubule Cavity
Similar to Hameroff’s idea, Georgiev presented an idea that consciousness could be the result of quantum computation via short laser-like pulses controlling quantum gates within the brain cortex.
However, he later rejected this theory because the wavelength of super radiant photon emission in the infrared spectrum is two orders of magnitude longer than a microtubule cavity of any size [
4]. Thus if one proposes this mechanism, the infrared photon cannot be used for manipulation of the quantum qubits inside the microtubule cavity.
To avoid this problem, we suppose that the substance in the microtubule cylinder has the characteristics of a metamaterial composed of sub-wavelength structures. As evanescent waves inside the microtubule cavity waveguide can propagate below the cutoff frequency defined by
fc =
c/2
d, where
d is a diameter of the waveguide, then we can model the evanescent wave according to the theory of evanescent wave holography [
21], shown as follows:
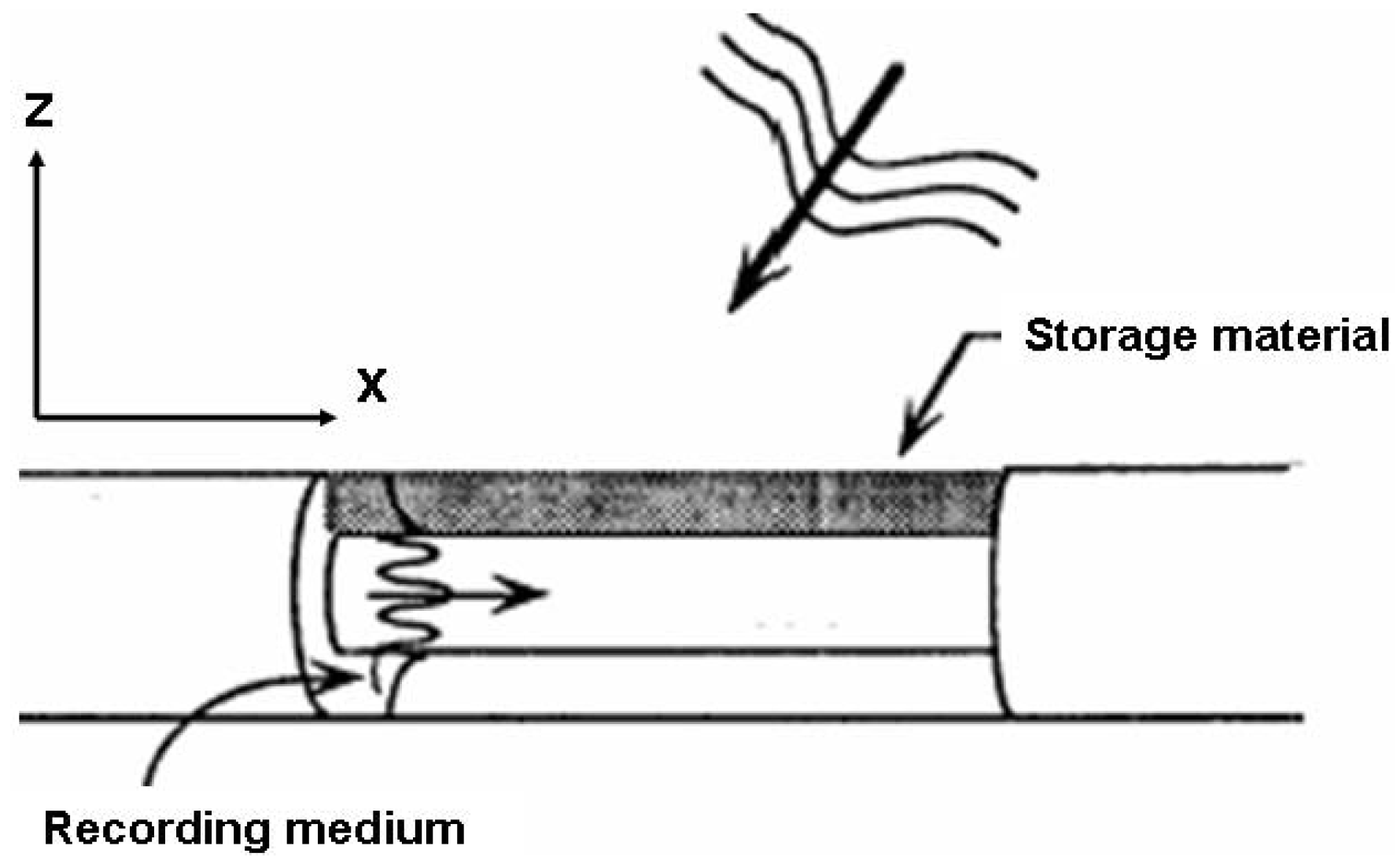
The basic idea of evanescent wave holography is to use an evanescent wave as a reference wave and as a readout wave. Suppose that the field distribution of a wave propagating in a microtubule is periodic inside the core, and evanescent outside this region given by:
and
where
Ue is an evanescent wave and
Up is a propagating wave from outside of the microtubule waveguide as shown in
Figure 2.
Figure 2.
Recording of an evanescent wave hologram in the microtubule waveguide.
As shown in
Figure 2,
Up interferes with
Ue and this interference is recorded.
This interference in the storage material will produce a proportional variation of the index of refraction that is periodic along the length of each microtubule. From Equations (4) and (5), the intensity of the wave can be given by:
We suppose that the cylinder of the microtubule consists of a storage material, whose thickness is much smaller compared with the penetration depth of evanescent waves. The response of the recoding medium to this intensity distribution is that the dielectric constant ε is a function of the local intensity given by ε = f (I·τ), where τ is an exposure time.
Then, the total field consists of an illuminated wave and a diffracted wave and can be described by:
as the wavelet scattered by each volume element of the hologram can be obtained using Green’s function and integrated over the volume of the hologram. According to the integral equation for hologram reconstruction, it can be given by:
where U0 is an illuminating wave, U is a wave including the information of object wave field and β is a parameter satisfying:
This means that the guided readout wave propagates in the same direction as the reference wave during recording. It is diffracted by the hologram structure and the object field can be reconstructed. This is the mechanism of holographic memory of the brain, which was also proposed by Pribram
et al. [
2].
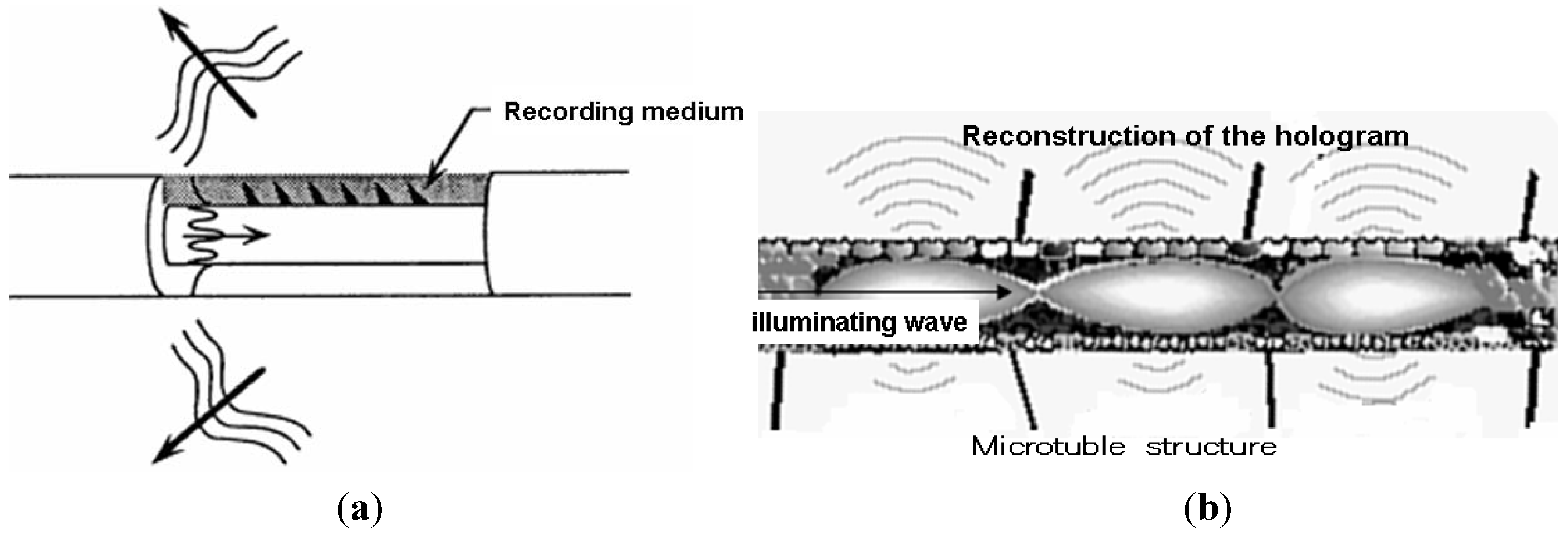
Figure 3(a) shows the schematic diagram of the reconstruction of stored memory by the propagating evanescent wave inside the microtubule structure. As shown in this figure, an illumination with the reference wave
Ur reconstructs the objective wave field
U0 by interaction with the term
UrU0 in the dielectric structure of the physical substrate for memory inside the microtubule structure.
By this mechanism, the evanescent photon propagating inside the microtubule can manipulate the storage and provide for the retrieval of stored data, or memory, as shown in
Figure 3(b). The holographic mechanism would also explain how our brains could store so many memories in so little space. The microtubules store memories by the evanescent wave holography suggests that impairment of consciousness, such as Alzheimer’s disease, may be due in part to the loss of metamaterial characteristics of the substructure inside the microtubule in the brain. Furthermore, a new design for an artificially constructed computer system could be constructed using a similar technique for data storage and retrieval, with memories which rely on interfering waves of photons passing through multiplexed holographic gratings similar to the brain’s neural structure;
i.e., a holographic brain system could now be constructed as hardware using the same mechanism.
Figure 3.
(a) Reconstruction of wave field by the guided readout wave;(b) Microtubule structure and the reconstruction of the hologram image.