1. Introduction
Many forms of organized complexity have arisen in nature’s long journey from uniformity to maximal entropy. On earth, biological systems have created diverse forms of adaptively self-organized complexity despite the ever present forces of noise and disorder. This self-organization occurs in open, holistic, far-from-equilibrium, “non-linear” systems with feedback, which makes them highly diverse and hard to predict. They depend on information about their world and themselves, and this information is used for inference-inferences about distal things from proximal signals, and inferences about the likely consequences of possible activities. Though usually implicit, probabilistic inference is central to such systems because adaptation depends upon information about the conditions to which the systems are adapted. Useful inference is possible because the laws of physics are sufficiently reliable, but the endless variety of individual circumstances and the prevalence of deterministic chaos make many things unpredictable. So, to thrive, biological systems must combine local reliability with holistic flexibility.
These arguments suggest several issues on which we need to make progress. What is self-organized complexity? What are the capabilities and constraints of the various forms of inductive inference, e.g., classical
versus Bayesian [
1], conscious
versus unconscious [
2]? How is local reliability combined with holistic flexibility? What is context, and how can it be used? How can the information theory measures that have been applied to these issues be tested, and what do they contribute to our understanding?
Better formalisation of these issues is clearly needed, so I will first give a brief outline of some conceptions of self-organized complexity, and then of the theory of Coherent Infomax which uses information theory measures to formalize these issues [
3,
4,
5,
6]. This theory was initially developed as a theory of mammalian neocortex, but here the possibility of a broader relevance is considered. A summary of Jaynes’s theory of probability and inference will then be given, followed by discussion relating it to self-organized complexity and then to Coherent Infomax. Finally, objectives of probabilistic inference in self-organized systems will be briefly discussed.
2. Organized Complexity
An obvious tension underlies the notion of organized complexity. Complexity can most simply be thought of as the amount of information in a system. That kind of complexity is increased by increasing the number of elements in a system and by
increasing their independence. In contrast to that, organisation implies
decreasing theirindependence. Shannon’s information entropy quantifies the former as it increases with independence. What is referred to here as organized complexity is often referred to simply as “complexity”, but I prefer to emphasize the tension by using terminology that makes it explicit. Many ways of quantifying the broad notion of organized complexity have been suggested. They typically combine order (organization/coherence) with disorder (entropy/information), and they often do so using measures of mutual information [
7]. These measures are designed to ascribe high complexity to systems of many elements that interact in such a way as to achieve effective integration but without imposing such uniformity that their joint entropy is low.
Self-organisation is emphasized here for two basic reasons. First, it relates to a major dilemma underlying Jaynes’s account of inference, i.e., does it or does it not imply someone, such as a scientist, who draws the inferences? Second, Jaynes’s views will be related to a theory of the inference that is implicit in biological systems, which I assume to be self-organized.
Self-organisation is also common in inanimate physical systems. Bénard convection is a well-known example, and has been used to extract general principles of self-organisation that apply even to highly evolved biological systems such as the mammalian neocortex [
8].
I assume that life is adaptively self-organized complexity. This adaptation, which is achieved by both genetic selection and ontogenetic plasticity, implies the selection and improvement of constructive processes that require a high capacity for information transmission. The window of possibility for life in all conceivable universes seems to be extremely small. Furthermore, if it depends on liquid water, as seems likely, it may also be small in our own actual universe. In addition to being dependent on information, life creates an information explosion [
9] because living things are highly diverse, even down to the molecular level, while also being well coordinated both within and across individual organisms. Macroscopic thermodynamic properties can be accurately estimated by averaging over vast numbers of elements that are assumed to be identical and with independent dynamics. Within living things even a single molecule can have significant effects on its macroscopic properties, and the activities of their elements are not independent, but highly interdependent. Their diversity and ability to surprise us is what makes them so interesting.
3. Coherent Infomax
The centrality of probabilistic inference to life is most obvious in neural systems. Helmholtz correctly emphasized the role of unconscious inference in perception, and many demonstrations of this can be given [
10]. Friston [
11] has now shown formally how such unconscious inference may also be central to both reinforcement learning and motor control, which extends its relevance to much of neural function. Neural systems will therefore be of particular relevance to the following discussions.
The apparent conflict between the requirements of local reliability and holistic flexibility has been prominent in the history of neuroscience, with one or the other being dominant at different times [
12]. The perspective outlined here shows how these two requirements are not necessarily mutually exclusive, as has long been assumed, but can be mutually supportive. Its central hypothesis is that there are two classes of neuronal interaction: driving interactions that specify the information content of the output signals to be transmitted by the local neuronal processor, and coordinating contextual interactions that modulate the gain and timing of response to the driving inputs. This theory shows how contextual inputs can disambiguate local signals and dynamically group them into coherent subsets. It is based upon much detailed psychophysical, neurobiological, and clinical evidence [
13,
14,
15]. The great volume and diversity of that evidence suggests that formal clarification of the role of context-sensitivity in probabilistic inference would be a major advance.
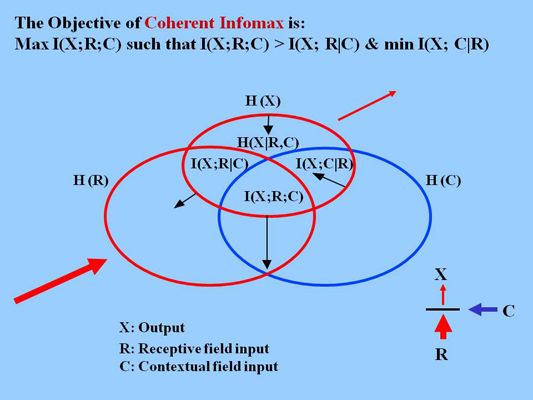
Our contribution to this effort has produced the theory of Coherent Infomax [
3,
4,
5,
6]. For full formal presentations see the original publications; only a brief outline is given here. It is closely related to several other influential theories [
11,
16,
17,
18,
19,
20,
21,
22,
23]. Though unification of all these theories is a task for the future, it seems feasible. The theory of Coherent Infomax is founded on an objective function that specifies the goal toward which both the short-term dynamics and the long-term plasticity of local neuronal processing elements are directed. Minimally, the function of local processors is to select and compress that information in their primary driving input that is relevant to the current task and situation, as indicated by the contextual input. This is formalized in information theoretic terms as an objective function describing the signal processing work to be done. In short, the goal is to maximize the information transmitted about the driving inputs, giving priority to the three-way mutual information between output, driving, and contextual inputs while minimizing the information transmitted specifically about the context. This objective therefore uses context to control the gain of response to the driving inputs. To show how that objective could be met in neural systems, a biologically plausible activation function for idealized local neural processors was formulated to include the required gain-control, and a learning rule for modifying the synaptic strengths of the connections between these local processors was derived analytically from the objective function [
3,
4,
5]. The learning rule derived has much in common with synaptic plasticity that has been independently discovered using neurophysiological techniques [
13].
Endlessly many system architectures can be constructed from such local processing elements. A system architecture suggested by the anatomy of mammalian neocortex is that of at most a few tens of hierarchical layers of processing, with many specialized but interactive local processors at each stage [
13]. Feedforward connections between layers are driving, whereas lateral and feedback connections provide coordinating gain-control. Though it is the dynamics of
local processors that are specified by Coherent Infomax, its objective requires them to coordinate their activities with other local processors, thus producing patterns of activity that tend to maximize overall
holistic coherence. This shows, in principle, how neural systems can use the information that is available to them to perform probabilistic inference in a way that combines local reliability with holistic flexibility.
The Coherent Infomax objective can be seen as a form of statistical latent structure analysis [
3,
4,
5,
6]. Its goal is to discover variables defined upon each of many distinct datasets that have predictive relations with variables defined upon other datasets. In short, its goal is to discover what predicts what. Therefore it concurrently discovers related variables and their relations; the variables do not need to be known in advance. So far, it has been mostly studied in relation to perceptual data-processing tasks, which has the advantage of drawing attention to the fact that inference is not at all restricted to the prediction of future events. It can equally well apply across space, or backwards in time. In visual perception, predictive relationships between concurrent datasets can be used to resolve local ambiguities within them. In auditory perception, inferences from later inputs can similarly be used to resolve ambiguities in earlier inputs. Current astronomical data can be used to predict events in the distant past.
The objective of Coherent Infomax is related to conceptions of organized complexity, such as “effective complexity”, though it was not derived from them. The contextual interactions central to the theory maximize organized complexity because they coordinate activities while not becoming confounded with the information that those activities variously transmit. Furthermore, Coherent Infomax is highly compatible with the small-world network architectures conducive to high complexity on these measures [
7]. It assumes a system composed of many local processors with logically independent inputs, and with dynamics that allows them to communicate while preserving their distinct identities. This communication discovers and amplifies regularities on their inputs that are statistically related across processors. It can be thought of as a kind of internal mutual observation that seeks agreement. The optimal state specified by the Coherent Infomax objective is computationally tractable only in simple situations, however. Therefore, in more complex situations it is a direction of travel, not a terminus. There are endless possibilities for specialized sensors, effectors, and connection architectures. This is consistent with the great diversity that is seen in the findings of neuroscience. The hypothesis being examined here is that the probabilistic inference underlying all that diversity is subject to a single, unified, coherent logic, or computational theory.
4. Jaynes’s Probability Theory
Edwin T. Jaynes (1922-1998) was a physicist who worked on quantum electrodynamics, statistical mechanics, information theory, and probability theory mostly in Washington University, St. Louis, but also in Stanford, Berkeley, Princeton, and MIT in the USA, and at Cambridge in the UK. His arguments for and developments of probability as a measure of uncertainty, rather than as the relative frequency of an outcome in the “long-run”, remain highly influential in physics, mathematics, engineering, and machine-learning. Though a few neurobiologists have used Jaynes’s ideas [
24,
25], they are not yet widely known in either biology or psychology. Of his many publications, those most used in preparing this outline are: “Probability theory as logic” [
26]; “Where do we stand on maximum entropy? [
27]; “Information theory and statistical mechanics” [
28], and the posthumous book, edited by G. Larry Bretthorst, “Probability Theory: The Logic of Science” [
1]. Specific references to particular writings will be given below only where necessary.
His central contribution to probability theory was an in-depth study of its use to quantify uncertainty. This rejected the frequentist definitions that had been dominant in statistics for many decades. Such a change in the definition of “probability” may seem unimportant, but it has major consequences, both conceptually and in real applications. Jaynes defines probability as quantifying the uncertainty of inferences drawn from given conditions. It is therefore often referred to as epistemic. By classical frequentist definitions probability quantifies properties of the observed world, i.e., it is ontological. Frequentist definitions apply only to populations of observations, but epistemic probabilities apply also to individual cases. Furthermore, epistemic probabilities allow inferences to use all relevant information, whereas frequentist conceptions use only relative frequencies. Jaynes’s logic assumes that scientific inferences should be treated as working hypotheses that are continually improved by new observations. His theory shows how to update estimates of the plausibility of hypotheses by appropriately weighting new observations and priors according to the strength of the evidence on which they are based. Unjustified bias in estimating that weighting is minimized by using maximum entropy methods. These do not apply any law of physics, but are simply a way of making predictions without making arbitrary unjustified assumptions. In the simple case of dice throwing, for example, this allocates equal probability to all six possible outcomes, if no other information is available. Other information, of endless forms, can modify these probabilities, including inspection of the dice and the surface on which it is thrown, knowledge of the honesty of the owner, and the relative frequencies of previously observed outcomes. Frequentist conceptions of probability are thus treated as a special limited case of Jaynes’s more general interpretation of probability.
Within Jaynes’s theory nothing is assumed to happen by chance or “at random” in reality; instead, he argued that randomness is a slippery, undefined, and unverifiable notion [
26]. As a physicist, he argued against the widely held Copenhagen interpretation of quantum mechanics, in which quantal uncertainty is assumed to be a property of the world. He insisted, instead, that that could never be proved, so that all we can say is that no deterministic rules governing quantal events have yet been discovered. Discussing Boltzmann’s statistical mechanics, he notes that it is sometimes asked where the randomness necessary for statistical behavior comes from if the universe is at heart an orderly, deterministic place. Jaynes sees this as a non-problem because to him probability theory as logic easily explains what we see, as a consequence of physical laws even if they are deterministic. The theorems of statistical mechanics are then interpreted as inferences predicting macroscopic behavior as best we can when given only knowledge of macroscopic variables that are interpreted as averages over microstates. More generally, he makes no use of the notion of a “random variable”, even though that is usually presented as fundamental to all statistics. He noted that use of this notion requires assumptions that are usually unnecessary and often implausible, such as ergodicity. Fortunately, resolution of this debate concerning ultimate determinism is not crucial here because adaptively self-organized systems depend upon what is in practice predictable, and, even in a deterministic world, that is severely constrained by incomplete information, deterministic chaos, or computational feasibility. Thus, probabilistic inference will usually be needed in practice because uncertainty is so common.
It is often asked “whose” uncertainties are quantified by using epistemic probabilities. When discussing Shannon’s information entropy, Jaynes [
1] explicitly concludes that it is the uncertainty of the designer of the communication system,
i.e., the engineer. Self-organized systems do not have a designer, however, so here we need a different answer. When thinking about this problem we may be misled by phenomenological connotations of “uncertainty”, but they can be avoided by further study of Jaynes’s theory. It extends logic to show what inferences concerning the plausibility of given hypotheses can be validly drawn from given conditions. Deductive logic is the special case where inferred probabilities are 0 or 1. Putting it this way shows that probabilistic inference is relative to the given conditions, as is deduction. As that relativity is unavoidable, this shows that Jaynes’s logic is as “objective” as deductive logic.
Though Jaynes played a leading role in initiating the “Bayesian” revival in statistics and beyond, and refers to his theory throughout as Bayesian, very little was actually contributed by Thomas Bayes himself. The terms “Bayes” and “Bayesian” are little more than custom without content; replacing them with “Jaynes” and “Jaynesian” would be both more accurate and more useful. It was Laplace whose writings pre-figured more of the conception for which Jaynes argued so passionately and extensively. Jaynes goes well beyond both. He formally derived the whole framework from a few elementary logical desiderata, the most fundamental being the requirement of consistency. He showed how probability theory applies to non-equilibrium states. He showed how thermodynamic entropy and information-theory entropy (uncertainty) can be interpreted as the same concept, and not merely as sharing a mathematical expression. He emphasised the importance of distinguishing epistemic from frequentist definitions, which Bayes did not. He showed how classical statistical methods and frequentist probability definitions are essentially special cases of his methods and definitions. He established Maximum Entropy methods as the best way to set priors for things unknown. These methods are now used for data analysis and prediction in a wide range of applications. For all of these contributions he deserves widespread acknowledgement and attention.
5. Relations Between Jaynes’s Probability Theory and Adaptively Self-Organized Complexity
Jaynes presents his probability theory as the logic of science [
1]. Here it is considered as the logic of life. There is a deep ambiguity within Jaynes’s theory. It is primarily concerned with the logic by which scientists should make explicit inferences. The logic proposed is so general and unified, however, that, if correct, it underlies all valid inference, whether made explicitly by scientists or implicitly by anything. If living organisms adapt to their environment by implicitly making inferences about it, then it is possible that probability theory could provide a conceptual framework within which to understand how they do so. I assume that any such contribution would be at the level of computational theory.
i.e., it would clarify the logic underlying all inference, while leaving open issues concerning the particular strategies (representations and algorithms) and physical mechanisms by which requirements of that logic are met or approximated.
Jaynes [
27] related his theory to biology by discussing potential uses of his probability theory to infer organisms’ macroscopic properties from knowledge of their molecular structure. He suggested that this might be possible in some simple cases within a few decades. The issue here is not with what inferences science can draw about biological systems, however, but with principles of inference implicit in biological activity. We must therefore take a “first-person” view of information and inference from the perspective of the system itself [
24,
25]. This requires us to make inferences about inferential systems.
Jaynes himself was very inconsistent on this issue. His logic is often presented as
prescriptive, showing how inferences should be drawn, and as requiring a scientist, or someone else, to specify the issues to be studied, to propose hypotheses, to provide the priors, and select the relevant data. He sometimes explicitly denied that the theory was
descriptive of the way in which people or other organisms do in fact infer. In 1958 he submitted a paper to a physics journal using the title “How does the brain do plausible reasoning?” In response to its rejection he said that the theory presented was not meant seriously as a description of how real brains actually do perform plausible reasoning, but as showing how an idealized “robot” brain should reason. Elsewhere, he argued that familiar problems of everyday life are typically so much more complicated than scientific problems, and depend on so many unknown and uncontrolled factors, that a full Bayesian analysis is out of the question in practice [
1]. In replying to criticisms of the utility of Bayesian methods, he says “The first critic objected to Bayesian methods on the grounds that they do not tell us how to create hypotheses (although neither do any other methods). This is like criticizing a computer because it will not push its own buttons; of course, it is up to us to tell Bayesian theory which problem we want it to solve. Would anybody want it otherwise?” [
26].
In contrast to such denials of probability theory as descriptive of implicit inference in biological systems, Jaynes more often argues for its applicability to inference of any kind. He showed in detail how his probability theory can be applied to irreversible non-equilibrium processes as well as to equilibrium processes [
29], and that suggests potential relevance to self-organized complexity. His belief in the wider underlying generality of his proposed inferential principles is also made clear in his first paper on information theory and statistical mechanics [
28], where he concludes that Shannon entropy, used as a measure of uncertainty, becomes the primitive concept with which we work, more fundamental even than energy. He later concluded that “seeing is inference from incomplete information”, and that probability theory is “telling us something about the way our own minds operate” when we unconsciously form intuitive judgments [
1]. He explicitly argued that any reasoning which conflicts with Bayesian principles would place a creature at a decided survival disadvantage, so evolution by natural selection would automatically produce brains which reason in the Bayesian format. In reply to the claim that human reasoning is often not Bayesian, Jaynes says: “One disadvantage of having a little intelligence is that one can invent myths out of his own imagination, and come to believe them. Wild animals, lacking imagination, almost never do disastrously stupid things out of false perceptions of the world about them. But humans create artificial disasters for themselves when their ideology makes them unable to perceive where their own self-interest lies.” [
26]. This implies that Bayesian inference is common across species, but in humans operates under special limitations that are a consequence of their own creative imagination. He also suggests that conscious human reasoning is sometimes misled by “false indoctrination”.
Science has done for humans what nothing has done for any other species. Therefore, principles of Jaynes’s probability theory that distil the essence of inference in general cannot also distil any special essence unique to science. My working assumption is that science depends upon distinctively human cognitive capabilities that have somehow overcome constraints under which more widely embodied strategies, or algorithms, for inference operate. Probability theory, construed as the logic of science, requires explicit conscious hypothesis creation and testing by people such as scientists and engineers. In life more generally it must be self-organized, but how is that possible? In response to that fundamental mystery the following section reconsiders Coherent Infomax in the light of Jaynes’s logic.
6. Relations Between Jaynes’s Probability Theory and Coherent Infomax
Coherent Infomax was originally proposed as a multi-purpose algorithm implemented in mammalian neocortex [
13]. In short, its task was to discover predictive relationships latent within rich datasets. Encouraged by the much greater generality of Jaynes’s probability theory, and by the broad conception of biological inference in Friston’s “free energy” theory [
10,
30], our working hypothesis is now that the relevance of Coherent Infomax extends well beyond neocortex. This broader potential is clearly implied by its formulation in terms of Shannon entropy. So, can it be combined with Jaynes’s unified theory of probability as extended logic to provide a unified conception of brain function?
6.1. Challenges Faced by Theories of Self-Organized Inference in Neural Systems
Creation of such a unified theory faces difficult challenges, however. First, it must be shown how inference can be self-organized. Second, though the logical desiderata from which Jaynes begins seem simple, they are councils of unattainable perfection at the system level. We cannot guarantee that all our beliefs are consistent, and we can rarely be sure that we use all relevant knowledge. Furthermore, it could be argued that some inconsistencies should be tolerated, or even welcomed. Therefore, it may be better to treat Jaynes’s desiderata at the system level as goals to be approximated, rather than as absolute requirements. Third, there is the difficulty well-known as the “curse-of-dimensionality” [
31]. Most raw sensory data occurs within a space of such high dimensionality that individual events are distributed very sparsely throughout it, with most locations within the space being empty, and few with more than one prior sample. This is true for all realistic lifetimes, whether of individual or species, because the number of locations grows exponentially with dimensionality. Therefore, prior events within the raw sensory space
taken as a whole cannot serve directly as a basis for inference. As there are enduring regularities within the real world, however, most events actually occur on or near manifolds of much lower dimension. Discovery of such manifolds is therefore a crucial problem to be solved. Fourth, inferential tractability decreases exponentially with the number of constraints to be consistently satisfied. How can that difficulty be alleviated? Fifth, another major difficulty arises from the ubiquity of ambiguity. This is best resolved by using predictions arising from the context, but how can that be done while avoiding self-fulfilling prophecies? Finally, any major transitions through which inferential capabilities have evolved need to be identified.
The following discussion outlines ways in which Coherent Infomax responds to these challenges, emphasizing the distinction between driving and contextual interactions. It then examines ways in which this distinction may be related to Jaynes’s probability theory. Limitations in the extent to which Coherent Infomax explains higher cognitive functions will then be mentioned, together with a discussion of the need for a more differentiated account of major transitions in cognitive evolution.
6.2. How Coherent Infomax Responds to These Challenges
The Infomax component of Coherent Infomax formalizes a widely accepted principle for the self-organisation of efficient coding in neural systems. It was originally called the “reduction of redundancy” by Horace Barlow [
32], then formalised and called Infomax by Ralph Linsker [
33]. It maximizes the mutual information between input and output of a local processor under the constraint of substantial data compression, so it greatly eases the curse-of-dimensionality. Infomax is formulated using Shannon entropy, and increases information transmission by maximizing the variance of outputs given the actual inputs received. It can therefore be directly related to Maximum Entropy methods in the case of Gaussian noise [
33].
Useful inference requires more than efficient coding, however. Sensory systems can provide so much information that the more difficult problem is separating the crucial variables from the “noise”. When there is far too much information for any given purpose, more is required than compression of all the available information into a smaller amount of data. Coherent Infomax suggests a way of specifying what information to transmit; its objective is to discover and amplify those variables that are predictively related to the particular context in which they occur. It therefore provides a way of specifying what information is important. Elementary variables discovered to be crucial to survival by adaptive evolution can then be specified directly rather than having to be discovered through further learning. Coherent Infomax can then discover and amplify new variables defined upon richer data-sets that predict the crucial variables. Once evolved because of their contribution to survival, however, mechanisms implementing Coherent Infomax can be used to discover and create statistical structure that may have little or no relevance to survival. Similarly, in a practical application of Coherent Infomax, the engineer could directly specify any relevant variables that are known, and then use Coherent Infomax to find new variables that are predictively related to them. In addition, however, he could also use it for open, exploratory, data mining.
An unavoidable consequence of the curse-of-dimensionality is that large amounts of data must be divided into subsets that are small enough to make learning feasible. If they were processed independently, however, then relations between the subsets would be unobservable. Success in finding the relevant manifolds would then be completely dependent upon the original division into subsets, but that is unlikely to be adequate unless the manifolds were already known. Coherent Infomax responds to this dilemma by dividing data at each level of an interpretive hierarchy into many small subsets, and searching for variables defined on them that are predictively related across subsets. This strategy allows for endlessly many ways in which the data can be divided into subsets, and linked across subsets.
Grouping large datasets into smaller subsets can also make inference more tractable by limiting the number of constraints within which consistency is sought. Within many real situations, with large knowledge bases, the best that can be done is to maximise the local consistencies and minimize the local inconsistencies [
34]. When performed dynamically within perception this is known as Gestalt grouping, and psychophysical studies have discovered many criteria on which it is based in biological perceptual systems. The importance and difficulty of these grouping processes is clearly demonstrated by the existence of a whole sub-discipline within machine perception devoted to the task of “perceptual organization”. The information required for such dynamic grouping overlaps greatly with that required for contextual disambiguation, and much evidence suggests that within neural systems there is overlap between the mechanisms involved; furthermore, those mechanisms can be interpreted as implementing Coherent Infomax [
14].
Contextual disambiguation is central to the Coherent Infomax strategy. Because the data to be interpreted by local processors within each level of the hierarchy arises only from a subset of the data, it will typically be compatible with a range of possible interpretations. Coherent choices across the system as a whole can be facilitated by amplifying those local choices that are most likely within the context of the activity of other processors. These contextual predictions must not by themselves be sufficient to drive local processor activity, however, because, if they were, self-fulfilling prophecy would remove the ability to learn about the real world. This is formalized within Coherent Infomax as the minimization of the conditional mutual information between outputs and contextual inputs given the driving inputs. Information specifically about the context is therefore not transmitted, thus ensuring that it does not corrupt the information transmitted specifically about the driving inputs. In neural systems this is implemented by using the contextual inputs to control the gain of the response to the driving inputs, and several synaptic and local circuit mechanisms for doing this have been discovered [
13,
14,
15,
35].
6.3. Can the Asymmetry Between the Effects of Contextual and Driving Inputs Be Related to Jaynes’s Probability Theory?
The theory of Coherent Infomax is based on a fundamental asymmetry between the effects of contextual and driving inputs. In short, contextual inputs are neither necessary nor sufficient to produce an output; driving inputs are both necessary and sufficient. Can this asymmetry be related to Jaynes’s probability theory? Prima facie, the most obvious possibility is that in Bayesian inference priors provide context-sensitivity. That is what I had long assumed, and it may seem obvious to many that context must operate via the prior. However, Jim Kay recently showed that not to be so [
6]. In Coherent Infomax context contributes to the posterior via the likelihood, not via the prior. In Bayesian inference posteriors are proportional to the product of priors and likelihoods. There is no essential asymmetry between them. Strong priors can outweigh weak likelihoods, and
vice versa. In its standard form, Bayesian inference is simply a way of accumulating data, and the distinction between earlier and later data is essentially arbitrary [
1]. Priors are neither necessarily nor usually context-sensitive. What Jim Kay’s new perspective shows is that, in our approach, driving inputs are used to compute prior probability distributions, and that context contributes to the computation of the likelihood of the data to be interpreted given the “hypothesis” whose probability is to be updated [
6]. This is therefore equivalent to using context as part of the generative model in context-sensitive Bayesian techniques as mentioned below.
Bayesian inference does seem to imply an asymmetry in that the data is a “given” that is assumed to be true. Data is also “fixed” in the sense that probability distributions are computed for likelihoods over varied model parameters for the given data. This asymmetry is less relevant here than at first appears, however, because the hypotheses whose probabilities are estimated by Bayesian inference concern unknown things. The objects of inference are not the observations themselves, but uncertain things about which the data provides evidence, such as the parameters in a model of the underlying processes that generate the data, or future data yet to be observed. Priors can provide evidence about those parameters that is as strong as, or stronger than, the current data. Consider a gambler who uses some system or inside knowledge to bet on a horse that loses. He may nevertheless be justified in making further bets on the same grounds if that strategy pays off over many races. No single outcome has a privileged status in determining that.
An asymmetry equivalent to that emphasized by Coherent Infomax does occur in some uses of maximum entropy and Bayesian methods, however. In machine learning, for example, a probability distribution of possible translations of a new occurrence of a familiar word in a body of text may be estimated from a sample of prior translations. Conditional maximum entropy methods do this using context [
36]. The item to be translated must have previously occurred at least once previously, and preferably many times, so it should be defined on a space of low dimensionality. The particular combination of item and context may be entirely novel, however; so it can occur within a space of much higher dimensionality. Presence of the item to be translated is both necessary and sufficient to produce an output distribution; the context is neither necessary nor sufficient. This is equivalent to the effects of context in Coherent Infomax. Context-sensitivity has also been added to Bayesian techniques in some other applications. In bioinformatic data mining, for example, context-sensitivity was found to make dramatic improvements in both the precision and the sensitivity of predictions [
37]. Context-sensitive Bayesian techniques have also been applied to the task of correcting spelling errors that result in valid words, but where the context indicates that some other word was intended [
38]. The role of context in all these applications is essentially equivalent to that in Coherent Infomax, so their practical success greatly encourages our study of its theoretical significance.
6.4. What Are the Major Transitions in the Evolution of Inferential Capabilities?
When showing how learning can proceed without necessitating storage of all the details of past experience, Jaynes [
1] distinguished between conscious and subconscious inference. He suggests that subconscious processes continually update a density function for each probability to be estimated. This function has a broad distribution when the prior evidence is weak. It has a single high peak when prior evidence for the stored probability is strong. The former, but not the latter, is easily changed by new evidence. He suggests that in humans the subconscious system (which is similar to what psychologists call “procedural memory”) may more reliably reflect the inferential principles that he proposes than does the conscious system. In contrast to that suggestion, advances in the cognitive and neurosciences support the view that Bayesian principles play a leading role in both conscious human reasoning [
39], and unconscious inference [
11,
40]. Though that work still has far to go [
41], and has so far made little use of Jaynes’s advances on Bayes, it shows that, as he thought, his preliminary explorations of these issues, were early steps into a large new territory.
A crucial issue within that territory concerns the possibility of major transitions in the evolution of inferential capabilities. Szmatháry and Maynard Smith [
42] identified seven major transitions in the evolution of life, such as the transition from asexual to sexual reproduction. Only one of those concerned cognition,
i.e., the transition to language. Major transitions in the evolution of inferential capabilities prior to language are also possible, however, and it is crucial to determine whether this is so because empirical studies of inferential capabilities will be misinterpreted if they are assumed to reflect a single strategy, when instead they reflect a mixture of strategies, either across or within species.
Probability theory could contribute to this issue by proposing various possible inferential strategies. For example, these could range from those with requirements that are simple to meet but with severely limited capacities, through intermediate stages of development, to those having more demanding requirements but with enhanced capabilities. Some possible transitions are as follows: from predictions only of things that are directly observable to estimates of things not directly observable; from generative models averaged over various contexts to those that are context specific; from hypotheses determined by input data to those that are somehow more internally generated; from probabilistic inference to syntactic structure, and, finally, from hypothesis testing to pure hypothesizing freed from testing. Within stages marked by such transitions there would still be much to be done by gradual evolutionary processes. For example, context-sensitive computations can make astronomical demands on computational resources, so they are only useful if appropriate constraints are placed on the sources and size of contextual input, as already shown for its use in natural language processing [
38]. Thus, even given the ability to use contextual information, the search for useful sources of contextual input could still be a lengthy process, even on an evolutionary timescale, and produce much diversity.
Transition from non-conscious to conscious strategies was not included in the list of possible transitions just given for the simple reason that all of those mentioned were explicitly related to probabilistic inference. It is not clear how that can be done for consciousness. Though it is not necessary for inference, the possibility that various aspects of consciousness are associated with one or more of the possible transitions listed may be an important issue for further research.
These speculations go far beyond the current theory of Coherent Infomax. Limitations of the theory are discussed elsewhere [
43], but one of particular relevance here is that the theory does not even account for intentional representation [
13]. It neither assumes nor explains the existence of an interpreter who knows of, and distinguishes, both signs and what they signal. Our hope is that the theory will contribute to our understanding of such higher cognitive functions by showing what can be done without them, thus revealing both the foundations on which they build, and the constraints they overcome.
The tension between creation and discovery implicit in Jaynes’s view of the human imagination is memorably expressed in the quote from Montaigne with which he begins his 1990 paper [
26]: “Man is surely mad. He cannot make a worm; yet he makes Gods by the dozen.” Man’s ability to make a worm is now closer to reality than Montaigne thought, and, creativity underlies life in general; not only does it form and reform itself, but it also transforms the world in which it lives. Our susceptibility to delusion may therefore be a price we pay for the capabilities that enable us to create organized worlds of ever-increasing complexity [
15,
44], though that hypothesis needs careful formulation [
45].
7. Does Self-Organized Inference in Living Things Have an Objective?
Several theories of brain function derive system properties from a formally specified objective function whose value tends to change in one direction over time as the system evolves, in both the short-term and the long-term. Coherent Infomax is one of them. Though Jaynes proposed an underlying logic for plausible inference, he did not specify inferential objectives, which were assumed to be supplied by the scientist, engineer, or whoever else is making the inferences. Coherent Infomax adds to Jaynes’s logic by proposing a formal objective function, and by showing, in principle, how that objective can drive the dynamics of adaptively self-organized complex systems. This objective is Jaynesian in spirit, however, because it produces patterns of activity in which the mutual information shared by elements is high, even though it also increases their joint information. This is “Jaynesian” because it increases the amount of information from which useful inferences can be drawn.
The theory of Coherent Infomax was developed independently of any particular definition of probability, but Fiorillo [
46] argues strongly that the use of a unified Jaynesian definition would enable neuroscience advance beyond the state currently reached by using Bayesian theories without acknowledging any distinction between frequentist and epistemic probabilities. From that perspective, he argues that the computational goal of neural systems is to infer or predict states of the world for the purpose of deciding which motor outputs to select. Quantitatively he describes this as minimizing uncertainty about biologically relevant aspects of the world, or, equivalently, as maximizing information about those aspects [
46]. This goal is similar to that of Coherent Infomax, and in both Fiorillo’s theory [
24,
46] and ours inference is seen as central to brain function, and Jaynes’s ideas are seen as providing an insight into its underlying logic that is far more profound than the mere Bayesian inversion of conditional probabilities.
If it is not only entropy, but also self-organized complexity that increases over much of cosmic history, then Richard Dawkins’ selfishness is not the only option for a scientifically based conception of long-term objectives. We can think of life at the ecological and species levels, not as “evolved to reproduce”, but as “reproducing to evolve”; i.e., in the direction of the formally specified objective. One answer to the question “Why does it do that?” is then simply “Because it can”. From that perspective we can think of our own individual efforts as directed, not merely towards survival, but as directed towards whatever organized complexities we choose to create.