Methodology for Assessment and Optimization of Industrial Eco-Systems
Abstract
:1. Introduction
- (i) Increased systemic energy efficiency leading to reduced systemic energy use.
- (ii) Increase in the amount and types of process outputs that have market value.
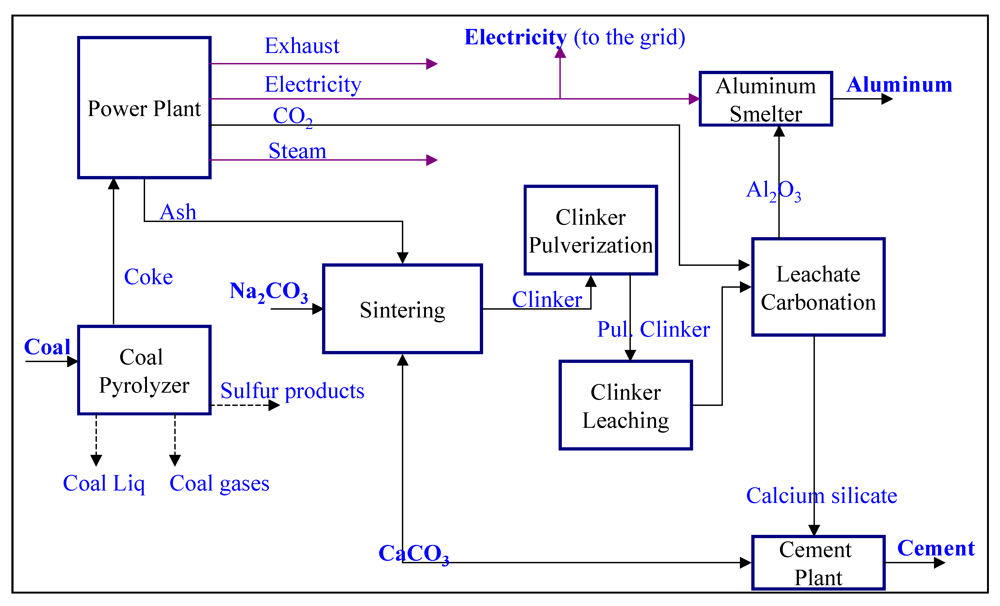
2. Process System Engineering (PSE) in Chemical Process Industries
2.1. Developing Optimization Techniques
| Approach | References |
|---|---|
| Deterministic approaches | Biegler, L.T. & Grossmann, I.E. (2004). Retrospective on optimization. Computers & chemical engineering, 28(8), 1169–1192 |
Mixed integer non-linear (MINLP)
| Grossmann, I.E. & Kravanja, Z. (1995). Mixed-integer nonlinear programming techniques for process systems engineering.Computers & Chemical Engineering, V19, S1, 189–204 |
| Gupta, O.K. & Ravindran, A. (1985). Branch and Bound Experiments in Convex Nonlinear Integer Programming. Management Science, 31 (12), 1533–1546 | |
| Kagan, N. & Adams, R.N. (1993). A Benders’ decomposition approach to the multi-objective distribution planning problem. International Journal of Electrical Power and Energy Systems, 15 (5), 259–271. | |
| Dynamic programming | Dadeboa, S.A. & Mcauley, K.B. (1995) Dynamic optimization of constrained chemical engineering problems using dynamic programming, Computers & Chemical Engineering, 19(5), 513–525 |
| Meta-heuristic approaches | Jones, D. F., Mirrazavi, S. K., & Tamiz, M. (2002) Multi-objective meta-heuristics: An overview of the current state-of-the-art. European Journal of Operational Research, 137(1), 1–9. |
| Expert systems | Yamin, H.Y. (2004). Review on methods of generation scheduling in electric power systems. Electric Power Sys. Res., 69, (2-3), 227–248 |
| Neural networks | Nascimento, C., Giudici, R., Guardani, R. (2000), Neural network based approach for optimization of industrial chemical processes. Computers & Chemical Engineering, 24 (9-10), 2303–2314 |
| Genetic algorithms | Shopova, E.G. & Vaklieva-Bancheva, N.G. (2006). BASIC—A genetic algorithm for engineering problems solution. Computers and Chemical Engineering, 30, 1293–1309 |
| Multi-objective Optimization Solution Methods | References |
|---|---|
| Normal Boundary Intersection method | Vahidinasab, V. & Jadid, S. (2010). Normal boundary intersection method for suppliers’ strategic bidding in electricity markets: An environmental/economic approach. Energy Conversion and Management, 51, 1111–1119. |
| Enhanced normalized normal constraint | Sanchis, J., Martínez, M., Blasco, X., &Salcedo, J.V. (2008). A new perspective on multiobjective optimization by enhanced normalized normal constraint method. |
| Structural and Multidisciplinary Optimization, 36, 537–546 | |
| Successive Pareto Optimization method | Ancau, M. & Caizar, C. (2010), The computation of Pareto-optimal set in multicriterial optimization of rapid prototyping processes. Computers & Industrial Engineering, 58, 696–708 |
| Multi-objective Optimization Evolutionary Algorithms | Tan, K.C., Lee, T.H. & Khor, E.F. (2002) Evolutionary Algorithms for Multi-Objective Optimization: Performance Assessments and Comparisons. Artificial Intelligence Review, 17, 253–290. |
| Genetic algorithms | Summanwar, V.S., Jayaraman, V.K., Kulkarni, B.D., Kusumakar, H.S., Gupta, K., & Rajesh, J. (2002). Solution of constrained optimization problems by multi-objective genetic algorithm. Computers and Chemical Engineering, 26 (10), 1481–1492 |
| Non-dominated Sorting Genetic Algorithms | Inamdar, S.V., Gupta, S.K., & Saraf, D.N. (2004). Multi-objective Optimization of an Industrial Crude Distillation Unit Using the Elitist Non-Dominated Sorting Genetic Algorithm.Chem. Ind. Res. Des., 82(A5), 611–623 |
| Strength Pareto Evolutionary Approach | Sarker,R., Liang, K., & Newton, C. (2002). New multiobjective evolutionary algorithm |
| European Journal of Operational Research,1, 12–23 | |
| Chaotic Particle swarm optimization | Cai, J, Mab, X., Li,Q, Li, L., & Peng, H. (2009). A multi-objective chaotic particle swarm optimization for environmental/economic dispatch. Energy Conversion and Management, 50, 1318–1325 |
| Simulated annealing algorithms | Suman, B. (2004). Study of simulated annealing based algorithms for multiobjective optimization of a constrained problem. Computers and Chemical Engineering, 28, 1849–1871 |
| Analytic hierarchy process (AHP) and Goal Programming (GP) | Arunraj, N.S. & Maiti, J. (2010), Risk-based maintenance policy selection using AHP and goal programming. Safety Science, 48, 238–247 |
2.2. PSE Approach Towards Addressing Rising Environmental Concerns
2.3. Managing Complex Systems
- Combining ecological balance of an industrial system with their other goals of productivity and economic profitability.
- Developing new operating model for industries
- (i) The industrial complex in Kalundburg, Denmark, is a famous example of IE [19]. This project was triggered in 1961 with the objective to save or minimize ground water for a new oil refinery. Now, it contains a power station, an oil refinery, a biotechnology company, a plasterboard producer, a soil remediation firm and a waste management company; exchanging various resources, including steam, water, gas, gypsum, fly ash, sludge, liquid fertilizer, etc. through a co-operative network and protocol developed local municipality [20]. In this industrial complex, different industries together formed a highly integrated industrial system that was optimized for the use of its byproducts in order to minimize the amount of net waste material or heat disposed of, resulting in substantial savings [21]. For example, the combination of heat and power production resulted in ~30% improvement of fuel utilization compared to a separate production of heat and power: using wastewater recycling the power plant has reduced water consumption by ~60%. The reduction in the use of ground water has been estimated at close to 2 million cubic meters per year.
- (ii) A second example may be taken from Asian developing countries during recent years, where industrial ecology is emerging as a potential approach to reduce the environmental burden of rapid economic expansion [22]. Fang et al. [23] have studied industrial sustainability in China, where they described the Lubei industrial case. This ecosystem has 52 member enterprises and 5300 employees, with total assets of 5 billion yuan. Since 2001, the Lubei Group has been the largest producer of phosphate fertilizer in China as well as the largest manufacturer of ammonium phosphate, sulfuric acid and cement in the world. There are three major industrial value chains. The first comprises the industries which are producing ammonium phosphate–sulfuric acid–cement. The major focus of the second chain is integrated sea water utilization, mainly consisting of chemical process units producing salt, gypsum, potassium sulfate, magnesium chloride, bromine etc. The third is a salt–alkali–electricity manufacturing chain. The Lubei integrated industrial system reveals synergy in the re-use of by-products, both within and among the three production chains. Sulfuric acid and seawater are the basic material flows, steam and electricity are the energy flows, and gypsum and furnace slag are the main “waste” flows. Fang et al. [23] also reviewed the sustainable development created by promoting a circular economy (CE) with optimal utilization of resources and energy; and maximization of integrated community profit.
- (iii) Heeres et al. [24] compared IE systems in The Netherlands and in the US and found that Dutch EIP projects are more successful in their initial development than the US cases. Although most of the projects were in the early stages, the initial success of the Dutch projects was attributed to two factors, the first being the active participation of companies in the project. This may be addressed by an association of the local entrepreneurs, which could be an effective platform to educate and inform companies of the potential benefits that can be achieved through the establishment of an IE. The second factor is the willingness to share the costs of EIP planning by companies. Participating companies should also be financially committed rather than depending on the government to fund such initiatives. This would help to ensure the commitment of the participating companies in the later phases of the program.
- (iv) The Synergy Industrial Park at Carole Park is an important initiative by the Queensland government and private sector partners in demonstrating the application of industrial ecology in Australia. The important lesson learned from the Synergy Park project is the need to engage business and the community in a program of education to support eco-industrial development [25].
- (v) In the US, the Mississippi River Corridor Industrial Complex comprises around 150 chemical plants. Research activities are in progress to minimize waste disposal and maximize material and energy reuse in such complexes [26].
3. Sustainability Assessment of an IE
3.1. Environmental Performance Indicators
- (i) Higher degree of uncertainty or lack of data in the impact assessment of various categories, such as global warming, ozone depletion, eco-toxicity, human toxicity etc. We believe that the majority of these are due to the lack of a quantitative assessment of ecological processes and the impact of their emissions.
- (ii) Difficulty in the traceability or quantification of some of the streams or species. This is mainly due to the fact that the ecological system boundaries are not well established or understood, and also that these streams or species are not included in the economic analysis, as the industrial system does not pay a price to these, hence, the go unaccounted.
- (iii) Not all types of impacts are equally well covered in a typical LCA. For example, assessment of land use, including impacts on biodiversity and resource aspects, including freshwater resources, are problematic and need significant improvement.
3.2. Input-Output Analysis (IOA)
3.3. Challenges with “LCA-Centered Optimization” and Traditional Optimization Tools for IEs
3.4. Sustainability Assessment of An IE Using Embodied Energy
- (i) Index of Economic Performance (IEcP): This index is the ratio the sum of the emergy of the main product and byproduct and the yield generated from waste, divided by the emergy of the total investment to obtain the required quantity and quality of the product while satisfying environmental regulations. A process can be made profitable by maximizing the production while minimizing the total investment.
- (ii) Index of Environmental Performance: The index of environmental performance (IEvP) is the ratio of the sum of the emergy of non-renewable resources consumed and the waste disposed of into the environment, with or without treatment, during the production process to the total emergy of the renewable resources used in the process and the internal recycle streams for renewable and non-renewable resources generated from treated as well as untreated waste. A low value of IEvP is always desirable, because it indicates less pressure on the environment. The value of IEvP can be improved by replacing non-renewable resources with appropriate renewable resources. Implementing the internal recycling of waste as renewable or non-renewable resources can also largely reduce the value of the IEvP.
- (iii) Index of Sustainable Performance: The index of sustainable performance (ISP) is the ratio of IEcP and IEvP. It is a measure of the overall sustainability of a process, because it combines the economic as well as the environmental performance of a process.
4. Simplified Approach for Optimization of an IE
5. Robust Optimization of Chemical Processes
6. Towards Robust Optimization of An IE
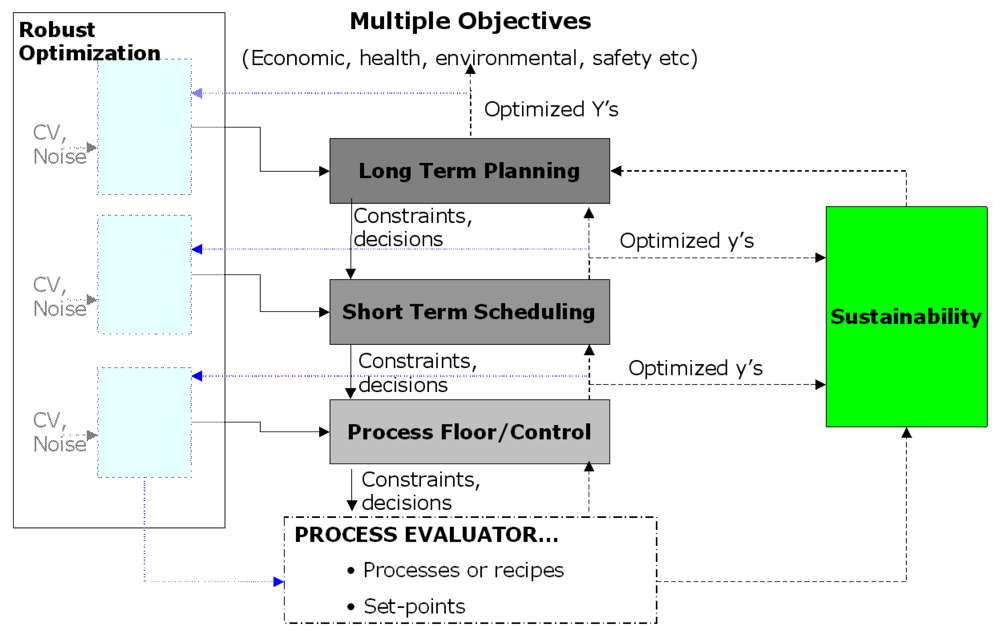
References
- Hau, J.L.; Bakshi, B.R. Expanding exergy analysis to account for ecosystem products and services. Environ. Sci. Technol. 2004, 38, 3768–3777. [Google Scholar] [CrossRef]
- Bakshi, B.R.; Fiksel, J. The quest for sustainability: Challenges for process systems engineering. AIChE J. 2003, 49, 1350–1358. [Google Scholar] [CrossRef]
- Allenby, B.R.; Richards, D.J. The Greening of Industrial Ecosystems; National Academy Press: Washington, DC, USA, 1994. [Google Scholar]
- Gertler, N. Industrial Ecosystems: Developing Sustainable Industrial Structures.
- Sinkin, C.; Wright, C.J.; Burnett, R.D. Eco-efficiency and firm value. J. Account. Public Policy 2008, 27, 167–176. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Kravanja, Z. Mixed-integer nonlinear programming techniques for process systems engineering. Comput. Chem. Eng. 1995, 19, 189–204. [Google Scholar]
- Biegler, L.T.; Grossmann, I.E. Retrospective on optimization. Comput. Chem. Eng. 2004, 28, 1169–1192. [Google Scholar] [CrossRef]
- Irwin, A.; Hooper, P.D. Clean technology, successful innovation and the greening of industry: A case-study analysis. Bus. Strateg. Environ. 1992, 1, 1–11. [Google Scholar] [CrossRef]
- Alidi, A.S. A multiobjective optimization model for the waste management of the petrochemical industry. Appl. Math. Modell. 1996, 20, 925–933. [Google Scholar] [CrossRef]
- Halim, I.; Srinivasan, R. Integrated decision support system for waste minimization analysis in chemical processes. Environ. Sci. Technol. 2002, 36, 1640–1648. [Google Scholar] [CrossRef]
- Halim, I.; Srinivasan, R. Systematic waste minimization in chemical processes. 1. Methodology. Ind. Eng. Chem. Res. 2002, 41, 196–207. [Google Scholar] [CrossRef]
- Halim, I.; Srinivasan, R. Systematic waste minimization in chemical processes. 2. Intelligent decision support system. Ind. Eng. Chem. Res. 2002, 41, 208–210. [Google Scholar] [CrossRef]
- Halim, I.; Srinivasan, R. Systematic waste minimization in chemical processes. 3. Batch operations. Ind. Eng. Chem. Res. 2006, 45, 4693–4705. [Google Scholar] [CrossRef]
- Halim, I.; Srinivasan, R. Designing sustainable alternatives for batch operations using an intelligent simulation-optimization framework. Chem. Eng. Res. Des. 2008, 86, 809–822. [Google Scholar] [CrossRef]
- Karuppiah, R.; Grossmann, I.E. Global optimization for the synthesis of integrated water systems in chemical processes. Comput. Chem. Eng. 2006, 30, 650–673. [Google Scholar] [CrossRef]
- Clift, R. Sustainable development and its implications for chemical engineering. Chem. Eng. Sci. 2006, 61, 4179–4187. [Google Scholar] [CrossRef]
- Batterham, R.J. Sustainability—The next chapter. Chem. Eng. Sci. 2006, 61, 4188–4193. [Google Scholar] [CrossRef]
- Lambert, A.J.D.; Boons, F.A. Eco-industrial parks: Stimulating sustainable development in mixed industrial parks. Technovation 2002, 22, 471–484. [Google Scholar] [CrossRef]
- Ehrenfeld, J.; Gertler, N. Industrial ecology in practice: The evolution of interdependence at Kalundborg. J. Ind. Ecol. 1997, 1, 67–79. [Google Scholar] [CrossRef]
- Yang, Y. Feasibility Study for a Design of an Industrial Park with Low Energy Consumption. Lulea University of Technology: Lulea, Sweden, 2006. Available online: http://epubl.luth.se/1653-0187/2006/29/LTU-PB-EX-0629-SE.pdf (accessed on 18 June 2012). Master’s Thesis. 2006:29 PB..
- Jacobsen, N.B. Industrial symbiosis in Kalundborg, Denmark: A quantitative assessment of economic and environmental aspects. J. Ind. Ecol. 2006, 10, 239–255. [Google Scholar] [CrossRef]
- Chiu, A.S.F.; Yong, G. On the industrial ecology potential in Asian developing countries. J. Clean. Prod. 2004, 12, 1037–1045. [Google Scholar] [CrossRef]
- Fang, Y.; Cote, R.P.; Qin, R. Industrial sustainability in China: Practice and prospects for eco-industrial development. J. Environ. Manag. 2007, 83, 315–328. [Google Scholar] [CrossRef]
- Heeres, R.R.; Vermeulen, W.J.V.; de Walle, F.B. Eco-industrial park initiatives in the USA and the Netherlands: First lessons. J. Clean. Prod. 2004, 12, 985–995. [Google Scholar] [CrossRef]
- Roberts, B.H. The application of industrial ecology principles and planning guidelines for the development of eco-industrial parks: An Australian case study. J. Clean. Prod. 2004, 12, 997–1010. [Google Scholar] [CrossRef]
- Singh, A.; Lou, H.H.; Yaws, C.R.; Hopper, J.R.; Pike, R.W. Environmental impact assessment of different design schemes of an industrial ecosystem. Resour. Conserv. Recycl. 2007, 51, 294–313. [Google Scholar] [CrossRef]
- Hezri, A.A.; Dovers, R. Sustainability indicators, policy and governance: Issues for ecological economics. Ecol. Econ. 2006, 60, 86–99. [Google Scholar] [CrossRef]
- Spangenberg, J.H. Institutional sustainability indicators: An analysis of the institutions in Agenda 21 and a draft set of indicators for monitoring their effectivity. Sustain. Dev. 2002, 10, 103–115. [Google Scholar] [CrossRef]
- Niemeijer, D.; de Groot, R.S. A conceptual framework for selecting environmental indicator sets. Ecol. Indic. 2008, 8, 14–25. [Google Scholar] [CrossRef]
- Huijbregtsa, M.A.J.; Hellweg, S.; Frischknecht, R.; Hungerbühlerd, K.; Hendriks, A.J. Ecological footprint accounting in the life cycle assessment of products. Ecol. Econ. 2008, 64, 798–807. [Google Scholar] [CrossRef]
- Goedkoop, M.; Hofstetter, P.; Müller-Wenk, R.; Spriemsma, R. The Eco-Indicator 98 explained. Int. J. Life Cycle Assess. 1998, 3, 352–360. [Google Scholar] [CrossRef]
- Finnveden, G.; Hauschild, M.Z.; Ekvall, T.; Guinée, J.; Heijungs, R.; Hellweg, S.; Koehler, A.; Pennington, D.; Suh, S. Recent developments in life cycle assessment. J. Environ. Manag. 2009, 91, 1–21. [Google Scholar] [CrossRef]
- Hau, J.L.; Bakshi, B.R. Expanding exergy analysis to account for ecosystem products and services. Environ. Sci. Technol. 2004, 38, 3768–3777. [Google Scholar] [CrossRef]
- Bailey, R.; Allen, J.K.; Bras, B. Applying ecological input-output flow analysis to material flows in industrial systems-Part I: Tracing flows and Part II Flow metrics. J. Ind. Ecol. 2004, 8, 45–91. [Google Scholar]
- Piluso, C.; Huang, Y.; Lou, H.H. Ecological input-output analysis-based sustainability analysis of industrial systems. Ind. Eng. Chem. Res. 2008, 47, 1955–1966. [Google Scholar] [CrossRef]
- Hugo, A.; Pistikopoulos, E.N. Environmentally conscious long-range planning and design of supply chain networks. J. Clean. Prod. 2005, 13, 1428–1448. [Google Scholar]
- Guillén-Gosálbez, G.; Grossmann, I.E. Optimal design and planning of sustainable chemical supply chains under uncertainty. AIChE J. 2009, 55, 99–121. [Google Scholar] [CrossRef]
- Gebreslassie, B.H.; Guillén-Gosálbez, G.; Jiménez, L.; Boer, D. Design of environmentally conscious absorption cooling systems via multi-objective optimization and life cycle assessment. Appl. Energy 2009, 86, 1712–1722. [Google Scholar] [CrossRef]
- Gnansounou, E.; Dauriat, A. Techno-economic analysis of lignocellulosic ethanol: A review. Bioresour. Technol. 2010, 101, 4980–4991. [Google Scholar] [CrossRef]
- Odum, H.T. Environmental Accounting; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Odum, H.T. Self organization, transformity, and information. Science 1988, 242, 1132–1139. [Google Scholar]
- Wang, L.; Ni, W.; Li, Z. Emergy evaluation of combined heat and power plant eco-industrial park (CHP plant EIP). Resour. Conserv. Recycl. 2006, 48, 56–70. [Google Scholar] [CrossRef]
- Ulgiati, S.; Brown, M.T. Monitoring patterns of sustainability in natural and man-made ecosystems. Ecol. Modell. 1998, 108, 23–36. [Google Scholar] [CrossRef]
- Brown, M.T.; Herendeen, R.A. Embodied energy analysis and EMERGY analysis: A comparative View. Ecol. Econ. 1996, 19, 219–235. [Google Scholar] [CrossRef]
- Lou, H.H.; Kulkarni, M.A.; Singh, A.; Hopper, J.R. Sustainability assessment of industrial systems. Ind. Eng. Chem. Res. 2004, 43, 4233–4242. [Google Scholar] [CrossRef]
- Cao, K.; Xiao Feng, X. Distribution of emergy indices and its application. Energy Fuels 2007, 21, 1717–1723. [Google Scholar] [CrossRef]
- Zondervan, E.; Betlem, B.H.L.; Blankert, B.; Roffel, B. Modeling and optimization of a sequence of chemical cleaning cycles in dead-end ultrafiltration. J. Membr. Sci. 2008, 308, 207–217. [Google Scholar] [CrossRef]
- Logist, F.; van Erdeghem, P.M.M.; van Impe, J.F. Efficient deterministic multiple objective optimal control of (bio) chemical processes. Chem. Eng. Sci. 2009, 64, 2527–2538. [Google Scholar] [CrossRef]
- Singh, A.; Lou, H.H. Hierarchical pareto optimization for the sustainable development of industrial ecosystems. Ind. Eng. Chem. Res. 2006, 45, 3265–3279. [Google Scholar] [CrossRef]
- Diwekar, U.M. Greener by design. Environ. Sci. Technol. 2003, 37, 5432–5444. [Google Scholar] [CrossRef]
- Diwekar, U.M. A novel sampling approach to combinatorial optimization under uncertainty. Comput. Optim. Appl. 2003, 24, 335–371. [Google Scholar] [CrossRef]
- Diwekar, U. Green process design, industrial ecology, and sustainability: A systems analysis perspective. Resour. Conserv. Recycl. 2005, 44, 215–235. [Google Scholar] [CrossRef]
- Palmer, K.; Realff, M. Metamodeling approach to optimization of steady-state flowsheet simulators: Model generation. Chem. Eng. Res. Des. 2002, 80, 760–772. [Google Scholar] [CrossRef]
- Caballero, J.A.; Grossmann, I.E. Rigorous flow sheet optimization using process simulators and surrogate models. In Proceedings of the 18th European Symposium on Computer Aided Process Engineering–ESCAPE 18, Lyon, France, June 2008.
- Henao, C.A.; Maravelias, C.T. Surrogate-based superstructure optimization frame work. AIChE J. 2011, 57, 1216–1232. [Google Scholar] [CrossRef]
- Sammons, N.E., Jr.; Yuana, W.; Edena, M.R.; Aksoyb, B.; Cullinanb, H.T. Optimal biorefinery product allocation by combining process and economic modeling. Chem. Eng. Res. Des. 2008, 86, 800–808. [Google Scholar] [CrossRef]
- Zondervan, E.; de Haan, A.B. Modeling Techniques for Integration of Process Systems. In Proceedings of the European Conference on Modelling and Simulation, Madrid, Spain, June 2009; pp. 334–337.
- Zondervan, E.; Roffel, B.; de Haan, A.B. Flexible optimization of industrial process systems. In Proceedings of the fifth international conference on Foundations of Computer-Aided Process Operations (FOCAPO), Boston, USA, July 2008; pp. 397–401.
- Munawar, S.A.; Gudi, R.D. A multilevel control-theoretic framework for integration of planning, scheduling, and rescheduling. Ind. Eng. Chem. Res. 2005, 44, 4001–4021. [Google Scholar] [CrossRef]
- Gupta, O.K.; Ravindran, A. Branch and bound experiments in convex nonlinear integer programming. Manage Sci. 1985, 31(12), 1533–1546. [Google Scholar] [CrossRef]
- Kagan, N.; Adams, R.N. A Benders’ decomposition approach to the multi-objective distribution planning problem. Int. J. Elec. Power 1993, 15(5), 259–271. [Google Scholar] [CrossRef]
- Dadeboa, S.A.; Mcauley, K.B. Dynamic optimization of constrained chemical engineering problems using dynamic programming. Comput. Chem. Eng. 1995, 19(5), 513–525. [Google Scholar]
- Jones, D.F.; Mirrazavi, S.K.; Tamiz, M. Multi-objective meta-heuristics: An overview of the current state-of-the-art. Eur. J. Oper. Res. 2002, 137(1), 1–9. [Google Scholar] [CrossRef]
- Yamin, H.Y. Review on methods of generation scheduling in electric power systems. Electric Power Sys. Res. 2004, 69, 227–248. [Google Scholar] [CrossRef]
- Nascimento, C.; Giudici, R.; Guardani, R. Neural network based approach for optimization of industrial chemical processes. Comput. Chem. Eng. 2000, 24, 2303–2314. [Google Scholar] [CrossRef]
- Shopova, E.G.; Vaklieva-Bancheva, N.G. BASIC—A genetic algorithm for engineering problems solution. Comput. Chem. Eng. 2006, 30, 1293–1309. [Google Scholar] [CrossRef]
- Vahidinasab, V.; Jadid, S. Normal boundary intersection method for suppliers’ strategic bidding in electricity markets: An environmental/economic approach. Energ. Convers. Manage. 2010, 51, 1111–1119. [Google Scholar] [CrossRef]
- Sanchis, J.; Martínez, M.; Blasco, X.; Salcedo, J.V. A new perspective on multiobjective optimization by enhanced normalized normal constraint method. Struct. Multidiscip. O. 2008, 36, 537–546. [Google Scholar] [CrossRef]
- Ancau, M.; Caizar, C. The computation of Pareto-optimal set in multicriterial optimization of rapid prototyping processes. Comput. Ind. Eng. 2010, 58, 696–708. [Google Scholar] [CrossRef]
- Tan, K.C.; Lee, T.H.; Khor, E.F. Evolutionary algorithms for multi-objective optimization: Performance assessments and comparisons. Artif. Intell. Rev. 2002, 17, 253–290. [Google Scholar]
- Summanwar, V.S.; Jayaraman, V.K.; Kulkarni, B.D.; Kusumakar, H.S.; Gupta, K.; Rajesh, J. Solution of constrained optimization problems by multi-objective genetic algorithm. Comput. Chem. Eng. 2002, 26(10), 1481–1492. [Google Scholar] [CrossRef]
- Inamdar, S.V.; Gupta, S.K.; Saraf, D.N. Multi-objective optimization of an industrial crude distillation unit using the elitist non-dominated sorting genetic algorithm. Chem. Ind. Res. Des. 2004, 82(A5), 611–623. [Google Scholar]
- Sarker, R.; Liang, K.; Newton, C. New multiobjective evolutionary algorithm. Eur. J. Oper. Res. 2002, 1, 12–23. [Google Scholar]
- Cai, J.; Mab, X.; Li, Q.; Li, L.; Peng, H. A multi-objective chaotic particle swarm optimization for environmental/economic dispatch. Energ. Convers. Manage. 2009, 50, 1318–1325. [Google Scholar] [CrossRef]
- Suman, B. Study of simulated annealing based algorithms for multiobjective optimization of a constrained problem. Comput. Chem. Eng. 2004, 28, 1849–1871. [Google Scholar] [CrossRef]
- Arunraj, N.S.; Maiti, J. Risk-based maintenance policy selection using AHP and goal programming. Safety Sci. 2010, 48, 238–247. [Google Scholar] [CrossRef]
- Vahidinasab, V.; Jadid, S. Normal boundary intersection method for suppliers’ strategic bidding in electricity markets: An environmental/economic approach. Energ. Convers. Manage. 2010, 51, 1111–1119. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gondkar, S.; Sreeramagiri, S.; Zondervan, E. Methodology for Assessment and Optimization of Industrial Eco-Systems. Challenges 2012, 3, 49-69. https://doi.org/10.3390/challe3010049
Gondkar S, Sreeramagiri S, Zondervan E. Methodology for Assessment and Optimization of Industrial Eco-Systems. Challenges. 2012; 3(1):49-69. https://doi.org/10.3390/challe3010049
Chicago/Turabian StyleGondkar, Shyamal, Sivakumar Sreeramagiri, and Edwin Zondervan. 2012. "Methodology for Assessment and Optimization of Industrial Eco-Systems" Challenges 3, no. 1: 49-69. https://doi.org/10.3390/challe3010049




