Research on the Tensile Mechanical Properties of a Braided Corrugated Hose and Its Axial Stiffness Model
Abstract
:1. Introduction
2. Mathematic Model of Braided Corrugated Hose
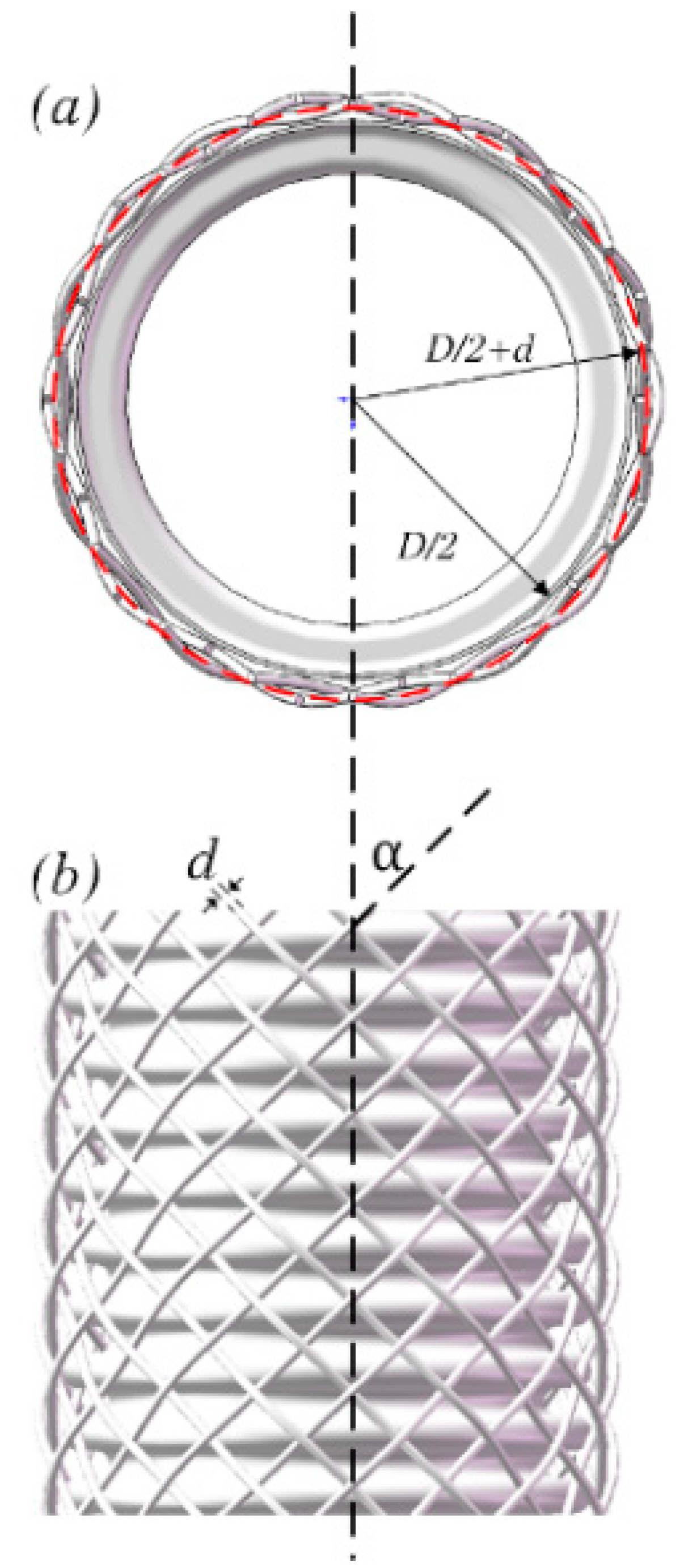
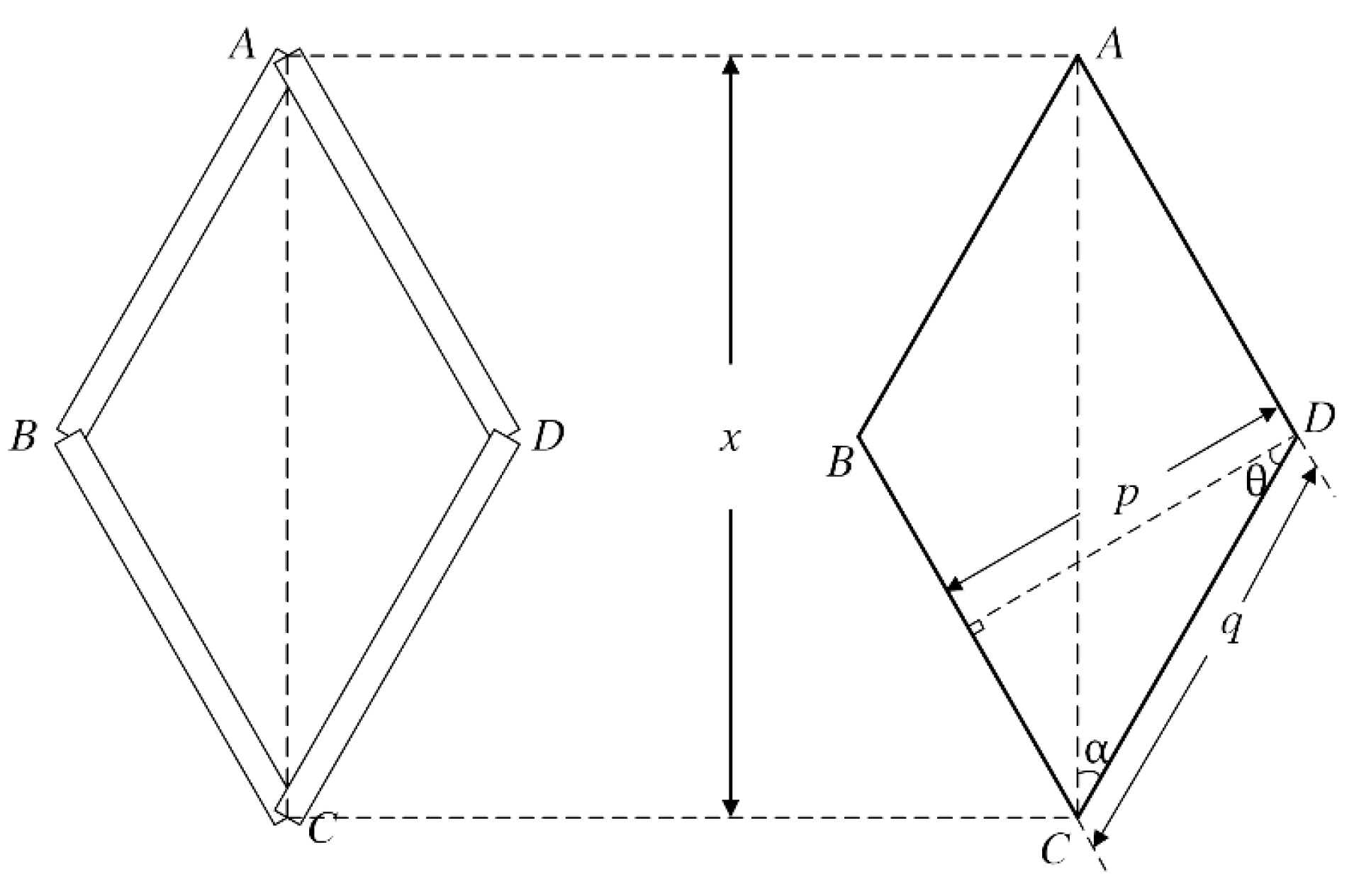
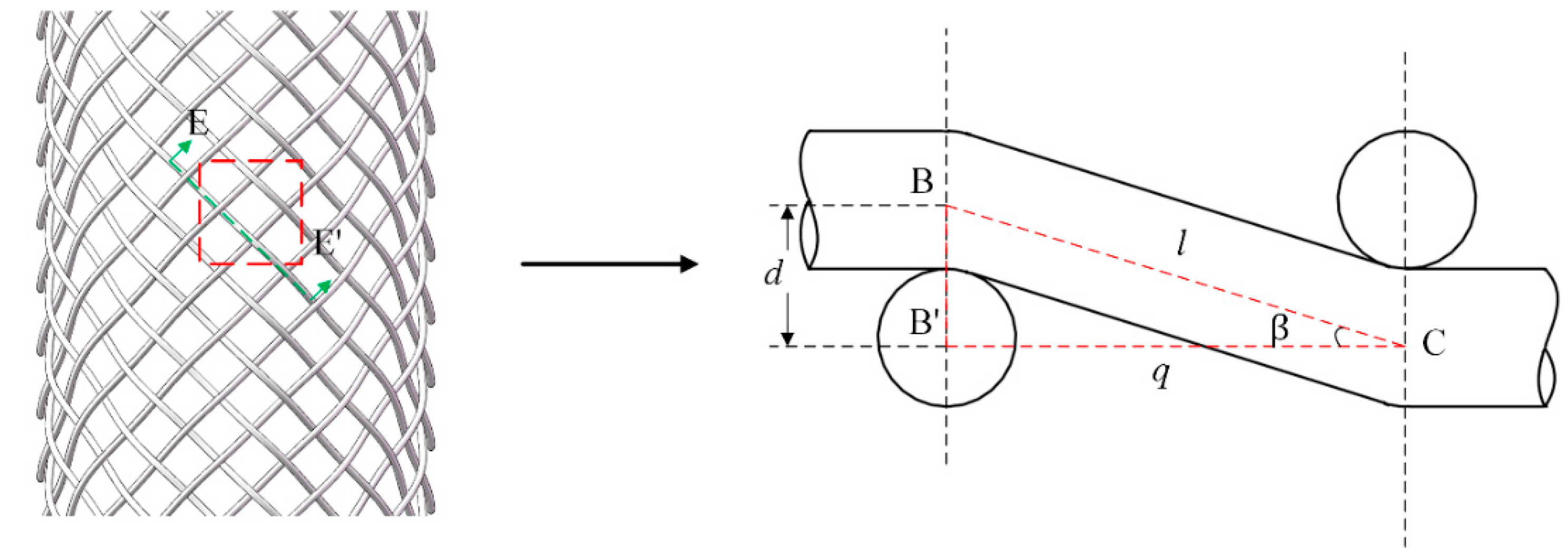
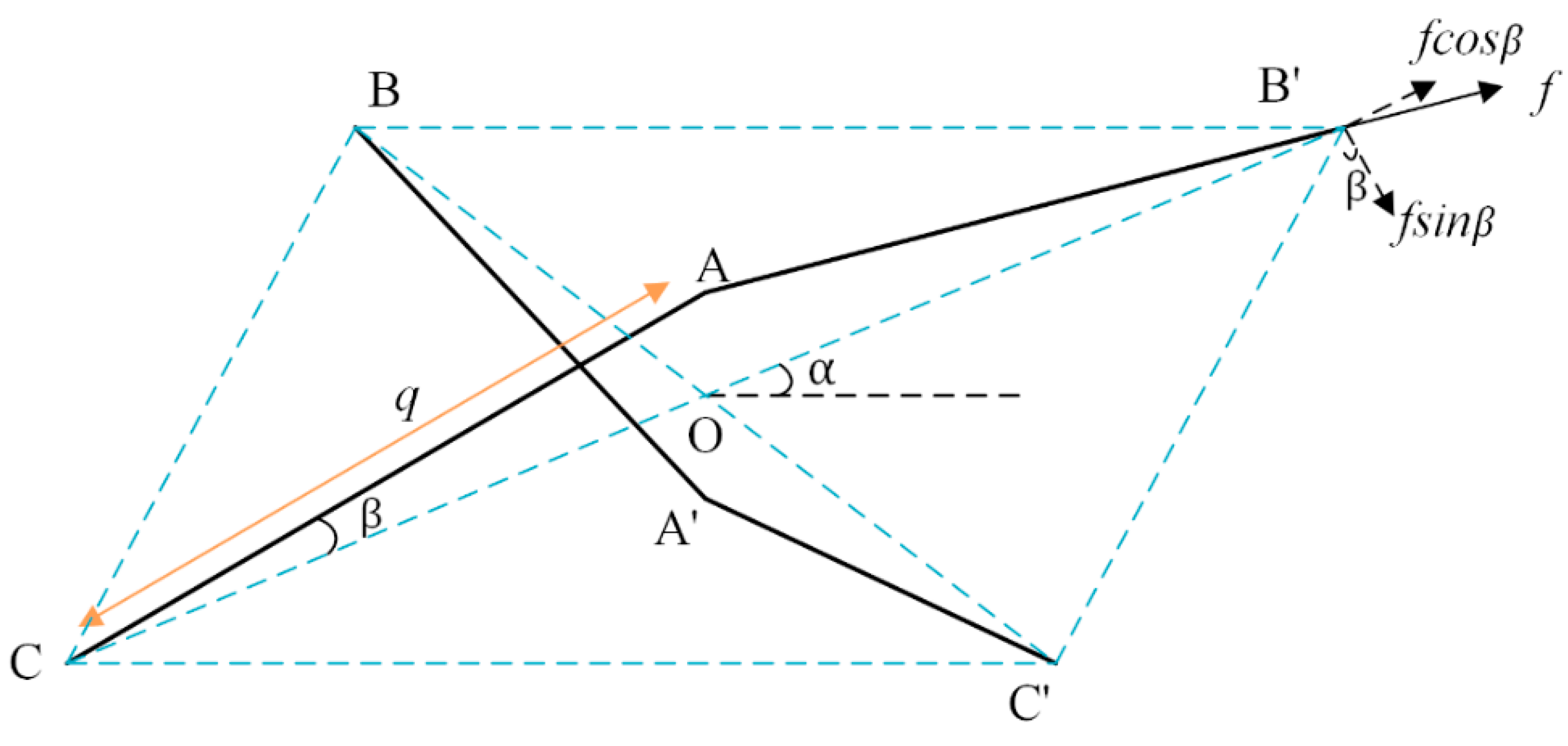
2.1. The Structure of the Metallic Braided Tube
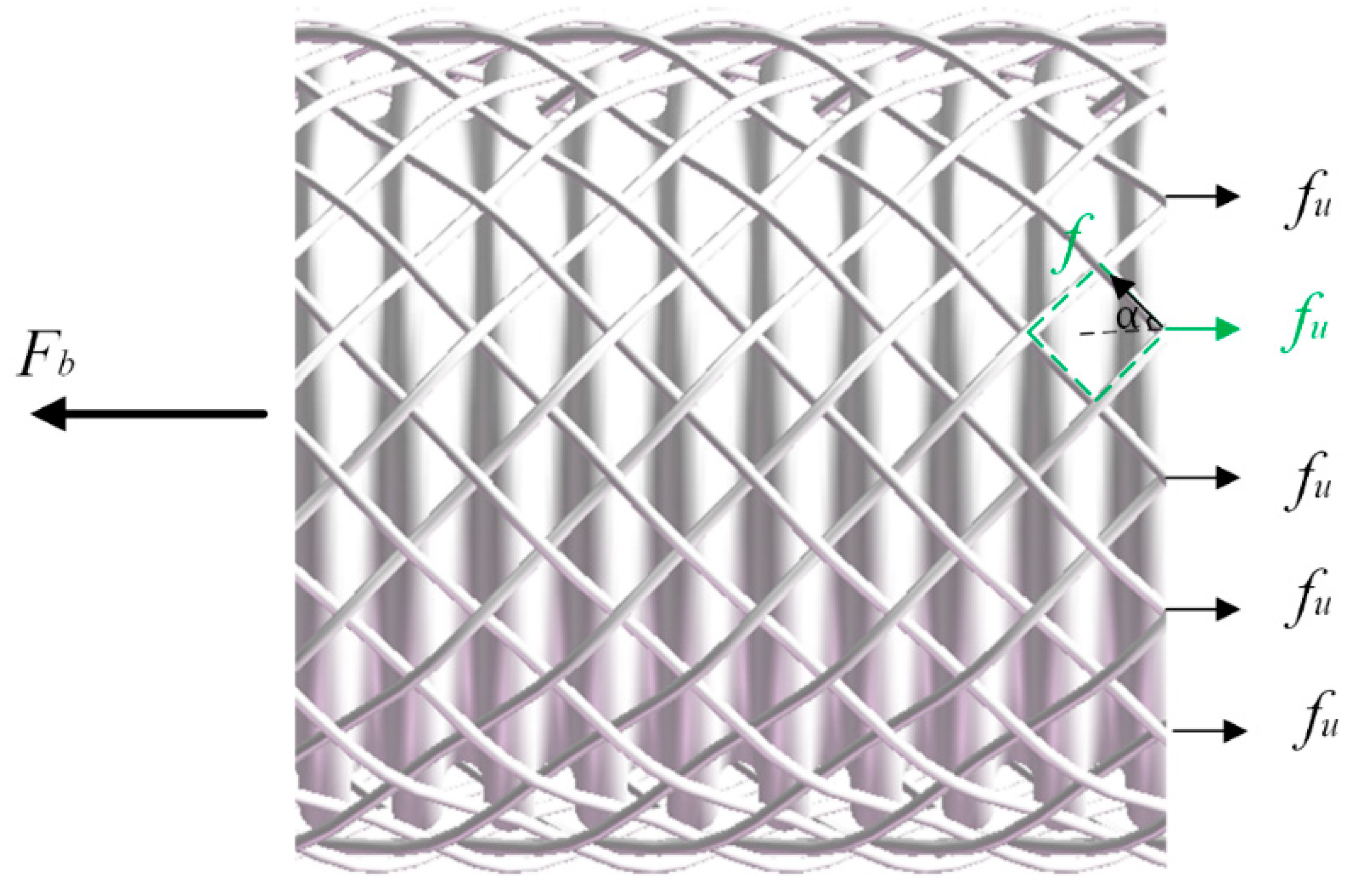
2.2. The Mechanical Properties of Wires under Tensile Load
- (1)
- Assuming that the wire has a circular cross-section, the diameter and cross-section of the wire are unaffected by the applied load;
- (2)
- The wire elongation is based on Hooke’s law, , where σ is the stress in the wire, E is the modulus of elasticity of the wire, and ε is the strain in the wire;
- (3)
- The bending of the filament is based on the theory , where M is the moment, κ is the yarn curvature, and .
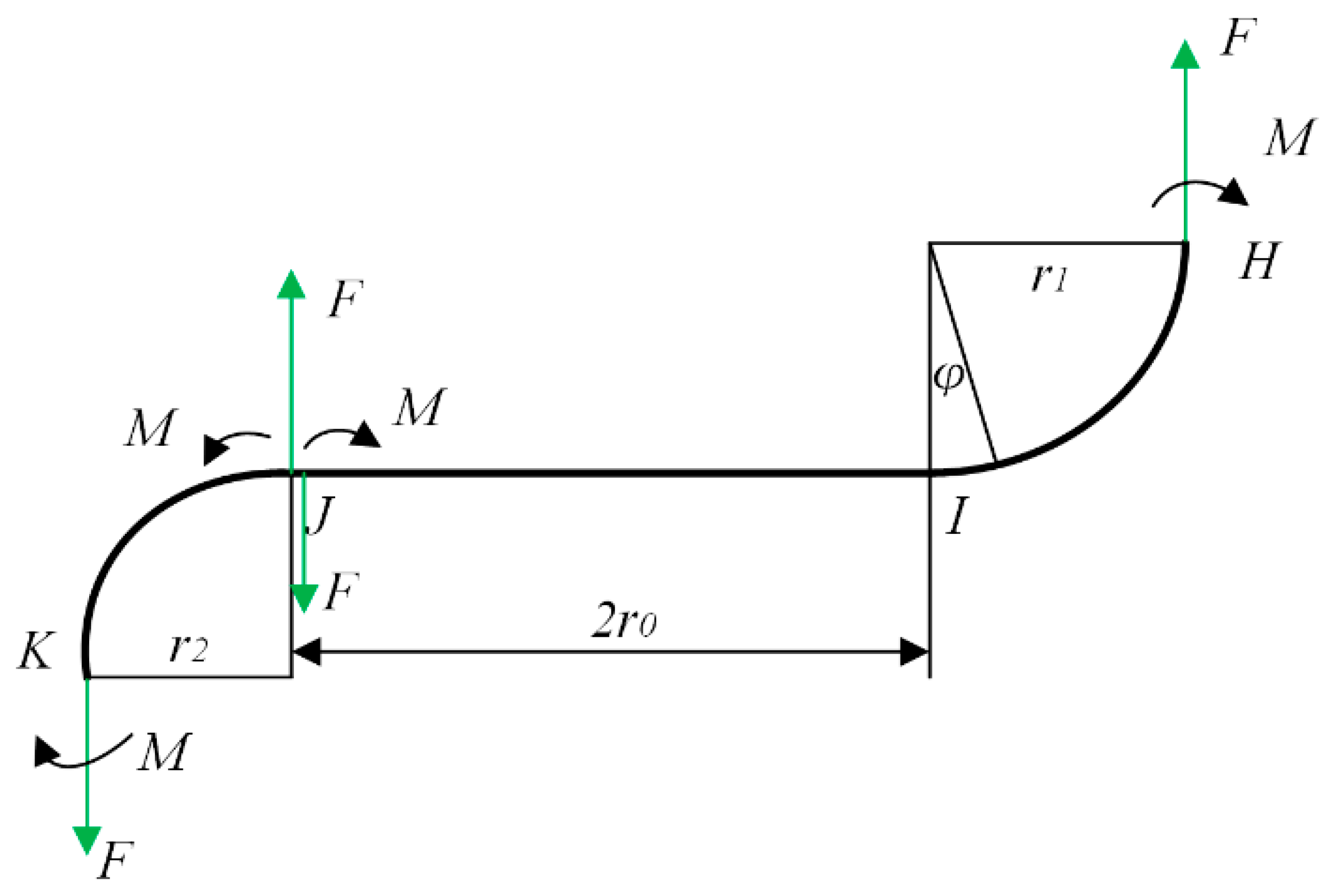
2.3. The Stiffness of the Bellows
2.4. The Axial Stiffness of the Braided Corrugated Hose
3. Numerical Experiment with the Braided Corrugated Hose
3.1. The Material and Structure of the Braided Corrugated Hose
3.2. Simulation Setup
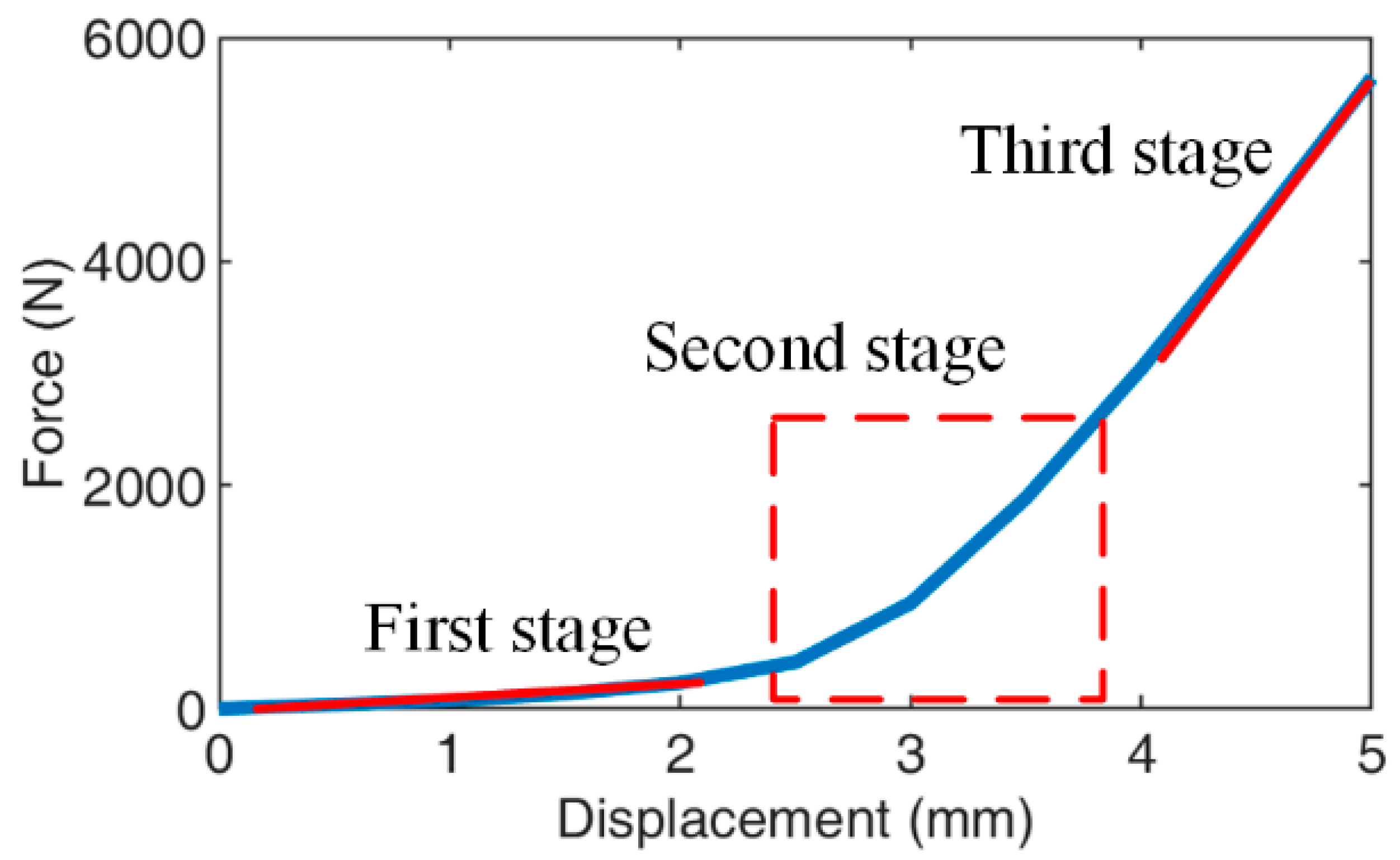
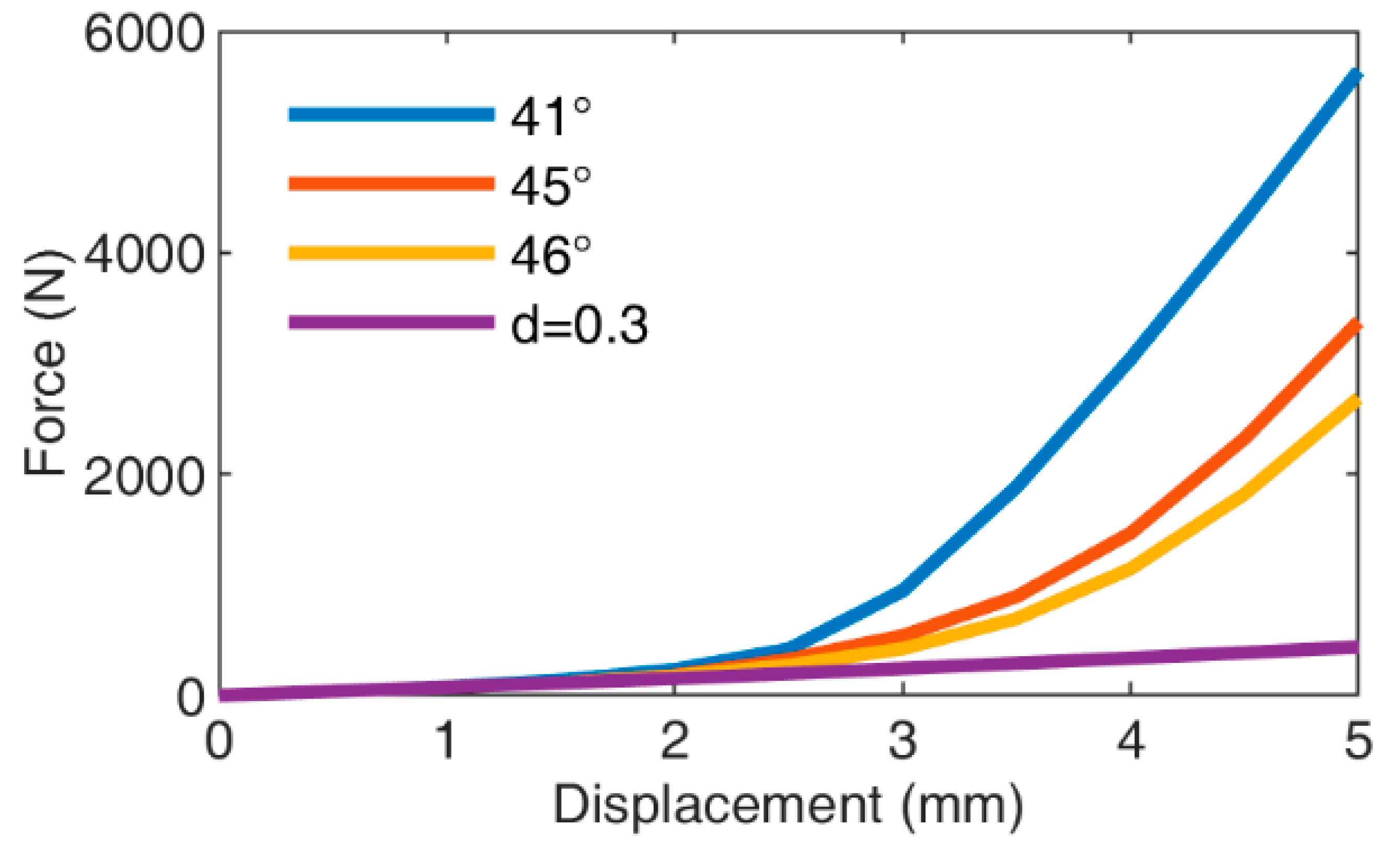
3.3. Numerical Results and Analysis
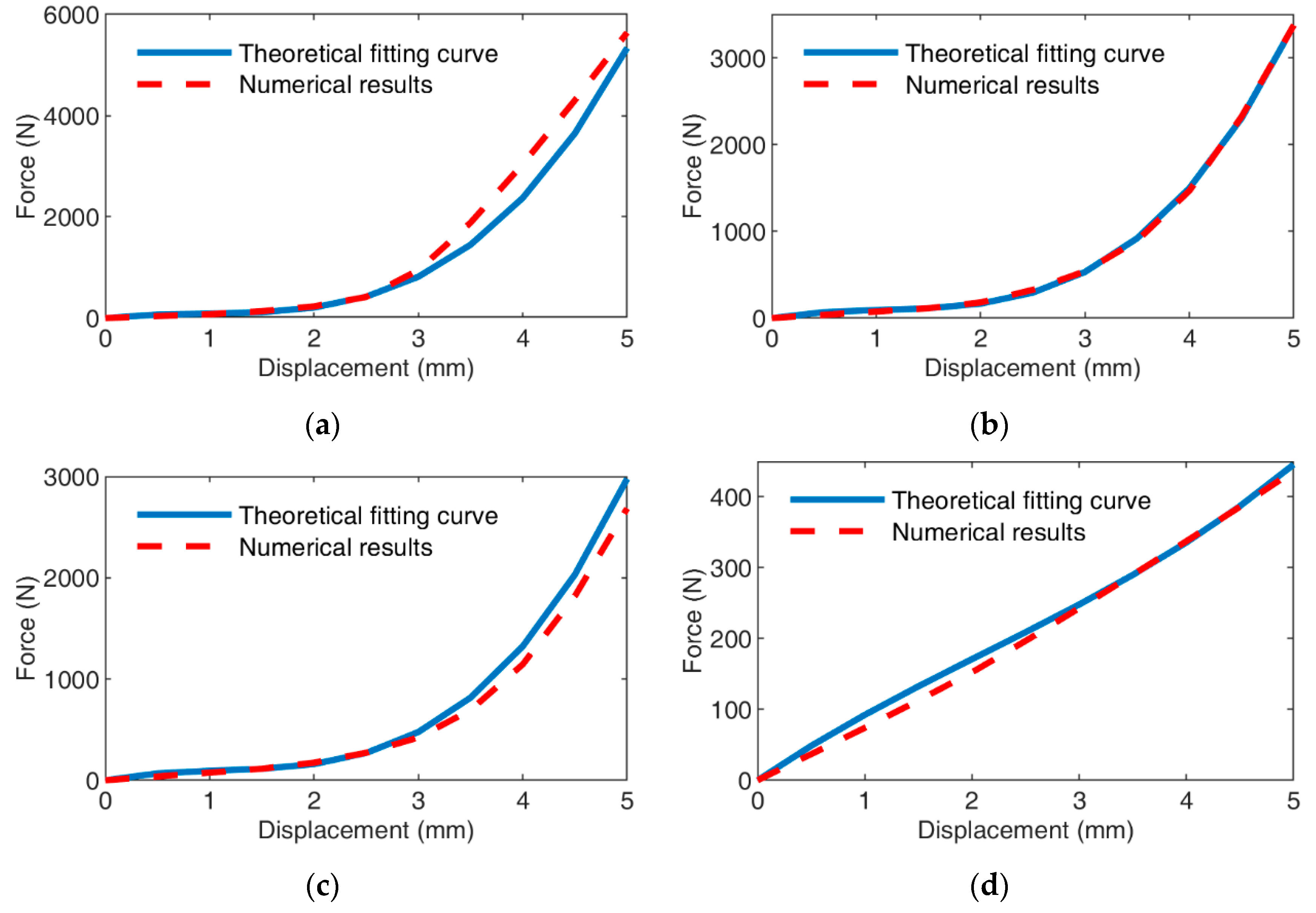
4. Model Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, D.; Zhang, J. Numerical Simulation and Experimental Study on Axial Stiffness and Stress Deformation of the Braided Corrugated Hose. Appl. Sci. 2021, 11, 4709. [Google Scholar] [CrossRef]
- Pierce, S.O.; Evans, J.L. Failure analysis of a metal bellows flexible hose subjected to multiple pressure cycles. Eng. Fail. Anal. 2012, 22, 11–20. [Google Scholar] [CrossRef]
- Anderson, W.F. Analysis of Stresses in Bellows. Part I. Design Criteria and Test Results. Technical Report Archive & Image Library; UNT Digital Library: Denton, TX, USA, 1964. [Google Scholar]
- Chien, W. Calculations for semi-Circular Arc Type Corrugated Tube-Application of the Theory of Slender Ring Shells. J. Tsinghua Univ. 1979, 1, 84–99. [Google Scholar]
- Chien, H. Calculation of Stresses and Deformations of Bellows by Initial parameter Method of Numerical Integation. Appl. Math. Mech. 1982, 3, 101–112. [Google Scholar] [CrossRef]
- Laupa, A.; Weil, N.A. Analysis of u-shaped expansion joints. J. Appl. Mech. Trans. ASME 1960, 29, 115–123. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Gu, B. The finite element analysis to the U-shape bellows by the ANSYS program. Press. Vessel. Technol. 2000, 17, 34–36. [Google Scholar]
- Yang, Y.; Wang, X. Nonlinear finite element analysis of the multiply bellows. Press. Vessel. Technol. 2003, 20, 13–16. [Google Scholar]
- Zhu, J.; Ma, W.; Liu, Y. Finite element analysis of high-damped multilayer U-shaped bellows’ axial equivalent stiffness. Press. Vessel. Technol. 2011, 28, 28–32. [Google Scholar]
- Zhou, L.; Li, L.; Zhao, C.Y. Performance analysis of the multi U-shaped bellows based on CAE. Mater. Sci. Forum 2014, 800–801, 390–393. [Google Scholar] [CrossRef]
- Brunnschweiler, D. Braids and braiding. J. Text. Inst. Proc. 1953, 44, P666–P686. [Google Scholar] [CrossRef]
- Hristov, K.; Armstrong-Carroll, E.; Dunn, M.; Pastore, C.; Gowayed, Y. Mechanical Behavior of Circular Hybrid Braids Under Tensile Loads. Text. Res. J. 2004, 74, 20–26. [Google Scholar] [CrossRef]
- Phoenix, S.L. Mechanical Response of a Tubular Braided Cable with an Elastic Core. Text. Res. J. 1978, 48, 81–91. [Google Scholar] [CrossRef]
- Grosberg, P. The Mechanical Properties of Woven Fabrics Part II: The Bending of Woven Fabrics. Text. Res. J. 1966, 36, 205–211. [Google Scholar] [CrossRef]
- Hearle, J.W.S.; Potluri, P.; Thammandra, V.S. Modelling Fabric Mechanics. J. Text. Inst. 2001, 92, 53–69. [Google Scholar] [CrossRef]
- Dabiryan, H.; Johari, M.S. Analysis of the tensile behavior of tubular braids using energy method, part I: Theoretical analysis. J. Text. Inst. 2016, 107, 553–561. [Google Scholar] [CrossRef]
- Brunnschweiler, D. 5—The structure and tensile properties of braids. J. Text. Inst. Trans. 1954, 45, T55–T77. [Google Scholar] [CrossRef]
- Hachemi, H.; Kebir, H.; Roelandt, J.M.; Wintrebert, E. A study of the braided corrugated hoses: Behavior and life estimation. Mater. Des. 2011, 32, 1957–1966. [Google Scholar] [CrossRef]
- Fu, H.; Hua, Z.; Zou, L.; Wang, Y.; Ye, J. Combined stiffness characteristic of metal rubber material under vibration loads. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6076–6088. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Y.; Liu, W. The comparison of common static stiffness theory model of metal rubber. Gongneng Cailiao/J. Funct. Mater. 2017, 48, 11141–11146. [Google Scholar] [CrossRef]
- Zou, G.P.; Liu, Z.; Chang, Z.L.; Li, Y.L. Constitutive relation of metal-net rubber. Hangkong Dongli Xuebao/J. Aerosp. Power 2016, 31, 2318–2324. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Q.; Teng, H.D. Stiffness estimation of corrugated-pipe elements for vibration isolator design. Zhendong Gongcheng Xuebao/J. Vib. Eng. 2011, 24, 280–286. [Google Scholar]




| Young’s Modulus /MPa | Poisson’s Ration | |||
|---|---|---|---|---|
| 0.3 |
| Number | Number of Strands | Wires per Strand | Braiding Angle | Diameter of Wire /mm | Length of Unit Cell /mm |
|---|---|---|---|---|---|
| A | 36 | 1 | 41° | 0.6 | 4.4109 |
| B | 36 | 1 | 45° | 0.6 | 4.0855 |
| C | 36 | 1 | 46° | 0.6 | 4.0077 |
| D | 36 | 1 | 45° | 0.3 | 4.0855 |
| Outer Diameter /mm | Inner Diameter /mm | Pitch of Wave /mm | Wave Height /mm | Radius of Wave Trough/mm | Radius of Wave Crest /mm | Thickness /mm | Length/mm |
|---|---|---|---|---|---|---|---|
| 31.5 | 25.4 | 3.7 | 2.8 | 0.8 | 0.8 | 0.25 | 200 |
| Coefficients | |||
|---|---|---|---|
| Value | 0.4578 | 0.001728 | 0.000001763 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Zhang, J. Research on the Tensile Mechanical Properties of a Braided Corrugated Hose and Its Axial Stiffness Model. J. Mar. Sci. Eng. 2021, 9, 1029. https://doi.org/10.3390/jmse9091029
Huang D, Zhang J. Research on the Tensile Mechanical Properties of a Braided Corrugated Hose and Its Axial Stiffness Model. Journal of Marine Science and Engineering. 2021; 9(9):1029. https://doi.org/10.3390/jmse9091029
Chicago/Turabian StyleHuang, Dacheng, and Jianrun Zhang. 2021. "Research on the Tensile Mechanical Properties of a Braided Corrugated Hose and Its Axial Stiffness Model" Journal of Marine Science and Engineering 9, no. 9: 1029. https://doi.org/10.3390/jmse9091029





