A State-Dependent Constitutive Model for Gas Hydrate-Bearing Sediments Considering Cementing Effect

Abstract

This paper presents a state-dependent constitutive model for gas hydrate-bearing sediments (GHBS), considering the cementing effect for simulating the stress–strain behavior of GHBS. In this work, to consider the influence of hydrate on matrix samples in theory, some representative GHBS laboratory tests were analyzed, and it was found that GHBS has obvious state-related characteristics. At the same time, it was found that GHBS has high bonding strength. In order to describe these characteristics of GHBS, the cementation strength related to hydrate saturation is introduced in the framework of a sand state correlation model. In addition, in order to accurately reflect the influence of cementation on the hardening law of GHBS, the degradation rate of cementation strength is introduced, and the mixed hardening theory is adopted to establish the constitutive model. The model presented in this paper reproduces the experimental results of Masui et al. and Miyazaki et al., and the prediction performance of the model is satisfactory, which proves the rationality of this work.

1. Introduction

With the continuous development and progress of exploration technology and equipment, the exploitation of oil and gas resources has gradually shifted from land and shallow sea to deep sea [1]. There are abundant resources in the ocean, especially natural gas hydrate, which can reach twice the total amount of traditional fossil fuels [2]. Gas hydrates are considered as one of the most promising strategic resources for commercial development in the future [3].

Gas hydrates are caged crystalline compounds formed by water and natural gas under certain temperature and pressure conditions. They are widely distributed in seabed strata and have the advantages of being clean, with large reserves and high heat value [3]. Some countries have carried out on-site exploitation of hydrate, and Mallik in Canada was the first place to carry out gas hydrate test mining [4]. Gas hydrate test mining was carried out three times, in 1998, 2002, and 2007–2008, respectively, and the production response characteristics of gas hydrate-bearing sediments (GHBS) were directly identified for the first time. However, due to the limitations of the production test cycle, this study is not enough to fully evaluate the resource potential of gas hydrate. In 2012, American researchers conducted the world’s first hydrate production test project combining the carbon dioxide replacement method and depressurization method on the northern slope of Alaska, and it confirmed the feasibility of developing hydrate by using the replacement method on the technical level [5]. Since 2000, Japan has carried out the world’s first sea area hydrate test production in Nankai Trough, and the second test production was carried out in this area from May to June, 2017 [6]. However, the long-term production feasibility of the existing technology cannot be confirmed by the current gas production time. In May 2017 and February 2020, China successfully carried out gas hydrate test production [3]. Generally speaking, the exploitation of gas hydrates still faces great challenges. At present, the common mining technologies mainly include the depressurization mining method [7], thermal stimulation method [8], CO₂ replacement mining method [9] and a combination of several mining methods [7]. In addition to these mining technologies, there are mainly horizontal wells and vertical wells in a wellbore layout, among which horizontal wells are considered as the most feasible commercial mining method.

Geological survey data show that the cementation of gas hydrate significantly improves the strength of marine sediments [10]. However, the formation and decomposition of gas hydrate are affected by temperature, pressure, gas type and seawater salinity [11]. When these conditions change, the occurrence state of gas hydrate will also change. Under unfavorable conditions, hydrate will decompose to produce a large amount of natural gas. With the decomposition of gas hydrate, the void ratio of GHBS increases and becomes loose sand, while the cementation of soil particles weakens and the strength of soil decreases [12]. On the other hand, a large amount of free gas is released by dissociation, which leads to a rapid increase in pore pressure in GHBS, a decrease in effective stress of soil, static liquefaction of the submarine slope and submarine landslide [13]. Therefore, studying and analyzing the strength and deformation of GHBS, and expressing their mechanism and general rules in an appropriate constitutive model for application to theoretical analysis and for handling practical engineering problems, have gained importance in the task of guaranteeing the safe exploitation of hydrates.

On the basis of mastering the mechanical properties of GHBS, it is an important issue to carry out numerical simulation of the submarine slope [14]. Combined with the mechanical properties of GHBS, which are similar to sand or special soil, based on different model frameworks, several types of constitutional models have been proposed. Yu et al. [15] and Yan et al. [16] put forward a modified nonlinear elastic model of GHBS under the framework of the Duncan–Chang model, considering the influence of hydrate saturations (S_h), but the model cannot describe the softening behavior of GHBS. Sultan et al. [17] put forward an elastoplastic model based on the modified Cambridge model, which can consider strain softening and dilatancy. However, due to the adoption of the associated flow rule, the calculation of volume deformation is not ideal. Yan et al. [18] referred to the mathematical model of cemented soil, regarded GHBS as composite cemented material, introduced additional internal variables to describe the effect of hydrates on the yield strength and established a constitutive model of GHBS. The model suggests that the cementation has different decline rates before and after the peak value, which has not been effectively confirmed by experiments. Klar et al. [19] established an ideal elastoplastic model based on the Mohr–Coulomb strength criterion. Although its parameters are few, strain softening and dilatancy cannot be considered. So far, there have been few constitutive models for the state dependent properties of GHBS, and almost all the established models adopt isotropic hardening theory, which can not fully reflect the mechanical properties of GHBS.

To sum up, the hydrate exploitation activities that have been carried out now are facing many challenges. In order to exploit natural gas hydrate safely, scholars have conducted a profound study on the mechanical behavior of energy soil from both qualitative and quantitative perspectives. In this study, combined with the state-related characteristics of GHBS, under the framework of the state-related model of sand, the cementation strength of GHBS is introduced, the evolution law of cementation strength is established, and the state-related constitutive model of GHBS is established by adopting the mixed hardening theory.

2. State-Related Characteristics of GHBS

Many scholars have conducted indoor experiments on GHBS. Winters et al. [20] and Hyodo et al. [21] synthesized samples and studied the effects of initial void ratio and hydrate saturation on the stress–strain behavior of GHBS. Masui et al. [22] prepared two types of GHBS using percolated methane gas in a specimen of Toyoura sand mixed with powder ice and excessive water and later carried out a series of triaxial tests with different effective confining pressures. Yun et al. [23], Miyazaki et al. [24], Ghiassian et al. [25], Liu et al. [26], Madhusudhan et al. [27] and Dong et al. [28] conducted experimental studies on GHBS.

On the basis of existing research results, Soga et al. [29] have described the mechanical properties of GHBS in detail, but because the mechanical properties of GHBS are the basis of this study, in order to facilitate understanding, this paper briefly introduces the main mechanical properties of hydrate sediments:

(1)

GHBS may show strain hardening or softening during shearing, and its characteristics depend on S_h, compactness and stress level.

(2)

For the deformation characteristics of GHBS, shear shrinkage and dilatancy may occur, which are mainly related to internal states, such as hydrate occurrence mode and S_h.

(3)

The cementation of GHBS has an important influence on its characteristics of strength and deformation. With the decline of cementation, it often shows a more obvious phenomenon of softening and dilatancy.

To sum up, the strength characteristics of GHBS not only depend on the void ratio and stress level, making it similar to sand, but are also related to S_h and cementation, thus producing essential differences in the mechanical properties of the ordinary soil and sand. Therefore, GHBS is also a kind of state-dependent material. By constructing appropriate expressions of the state parameter, the state-dependent characteristics of GHBS can be described.

3. State-Dependent Elastoplastic Constitutive Model of GHBS

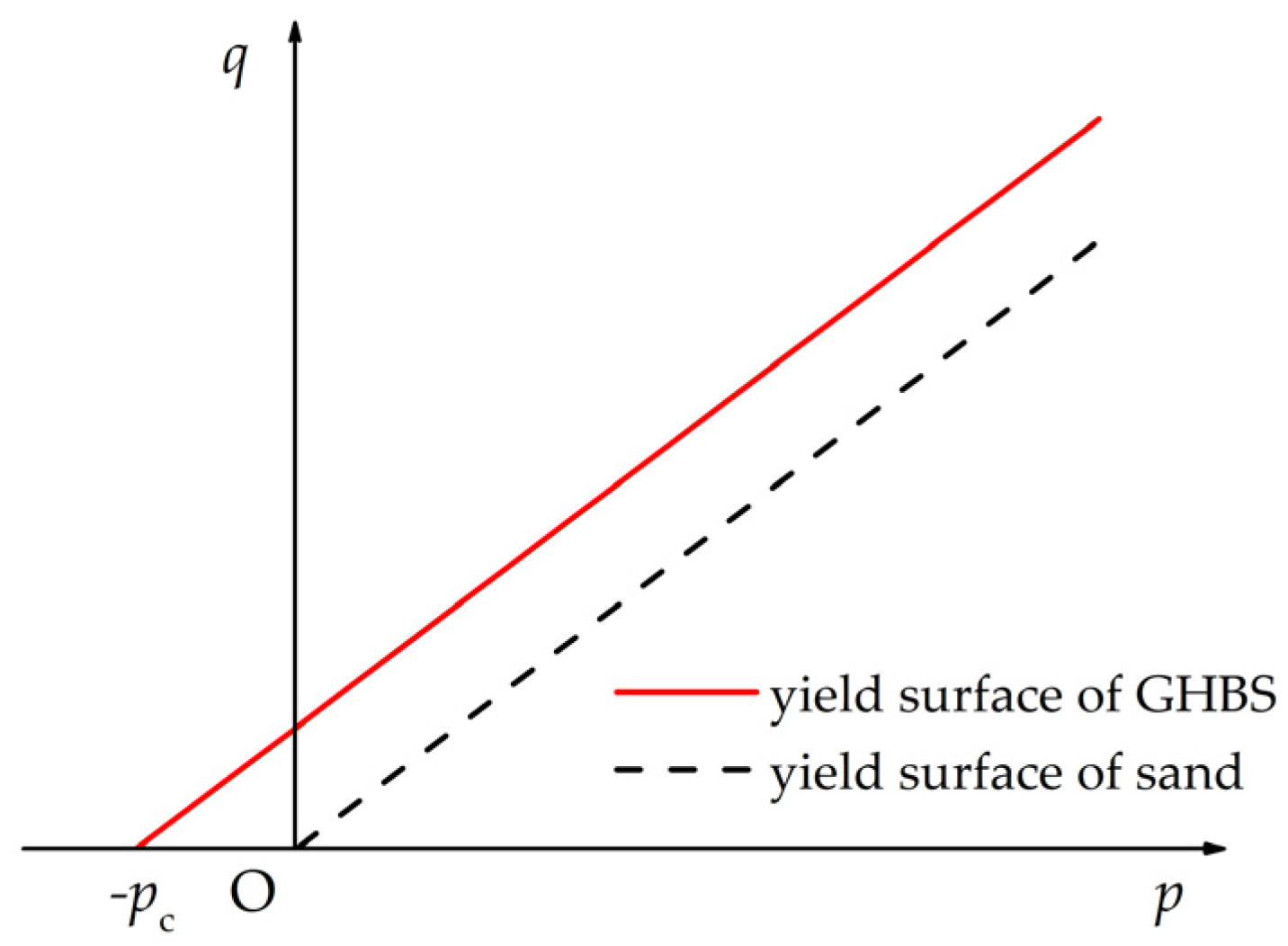
3.1. Yield Function

Since GHBS exhibits characteristics similar to sand, the yield function of the sand model is modified. A large number of studies on sand have shown that the deformation caused by consolidation is very small, while the deformation of sand is mainly caused by stress ratio [30,31,32]. Poorooshasb et al. [33] assumed that the yield trajectory of sand is a series of straight lines with a constant stress ratio. In Figure 1, the schematic diagram of the yield surface shows the shape of the yield surface, which is represented by Equation (1).

f = q* − M*p*

(1)

where q*, and p* are the mean normal stress and generalized shear stress of sand, respectively, and M* is the stress ratio of critical state.

Considering that the cementation of GHBS has an important influence on the yield strength, the straight line represented by Equation (1) is translated to the left to establish the yield function of GHBS, as shown by Equation (2), whereas the shape of the yield surface is shown in Figure 1. If the attenuation of cementation is considered, the subsequent yield surface of GHBS will simultaneously move to the right with the loading process.

f = q − M(p + p_c )

(2)

where q and p are the mean normal stress and generalized shear stress of the GHBS, respectively, p_c is the cementation of GHBS, and M is the critical state stress ratio, which is equal to M*.

When the stress ratio reaches M, GHBS enters the state of destruction. The stress ratio η is given by Equation (3).

η = q/(p + p_c)

(3)

3.2. Cementation

Referring to Sanchez’s and Uchida’s method for determining the cementation of GHBS [14,34], it is assumed that the initial value of cementation p_c0 satisfies the exponential relationship with S_h (see Equation (4)).

$$p_{\mathrm{c}0} = {\alpha S}_h^{\beta }$$

(4)

where α and β are the model parameters, while all other terms have the same meaning as defined previously.

Compared with ordinary sand, shear behavior not only causes rotation, slip and redistribution of particles in the material, but it also causes hydrate breakage and debonding between the hydrate and sand particles [35]. With the development of strain, cementation will decline. This difference directly affects the macroscopic mechanical behavior of GHBS. In research on the evolutionary pattern of cementation of GHBS, several authors [14,18,34] assume that it is a function of plastic shear strain (${\epsilon }_s^p$) and have obtained ideal prediction effect. In this paper, the same assumption is made, and it is found that ${\epsilon }_s^p$ cannot be recovered. The evolutionary pattern of cementation of GHBS is expressed using Equation (5).

$$\mathrm{d}{p}_{\mathrm{c}} = -a_{\mathrm{c}}{p}_{\mathrm{c}0} \mathrm{d}{\epsilon }_s^p$$

(5)

where a_c indicates the attenuation rate of the cementation of GHBS.

3.3. State Parameters and Dilatancy

The dilatancy of GHBS depends on the internal state and stress level, which can be reflected by the yield function. Therefore, it is necessary to construct a state parameter expression that reflects the internal state and then to clarify the dilatancy of GHBS by describing the current state.

If e is the current void ratio of the material, and e_c is the critical void ratio, then the state parameter φ can be expressed as the difference [36] and the ratio [37] between e and e_c. Yao et al. [32] use the void ratio e_η corresponding to the mean normal stress p under the condition of equal stress ratio to replace e_c and construct the state parameter φ considering the stress ratio. In this paper, the state parameter φ is expressed using Equation (6).

φ = e/e_c

(6)

According to the basic theory of soil mechanics, the relationship between the current void ratio e of GHBS, the initial void ratio e₀ and the volume strain ε_v is given by Equation (7).

e = e₀ − (1 + e₀)ε_v

(7)

In order to obtain the expression of the state parameter φ of the GHBS, it is necessary to establish the expression of the initial void ratio e₀ and the critical void ratio e_c. The hydrate has the effects of filling and cementation on GHBS. Furthermore, for the GHBS mainly filled with the filling effect, e₀ may decrease with the increase of S_h; however, for the GHBS-containing structure, the larger the S_h, the smaller is the e₀. The influence of the content and occurrence mode of hydrate on e₀ is not completely clear at present. Additionally, the samples of GHBS prepared indoors are affected by methane gas scouring, which may lead to uneven samples. Therefore, it is difficult to establish the mathematical relationship between e₀ and S_h. In order to reduce the model parameters, this paper assumes that e₀ and S_h of GHBS satisfy a simple inverse proportional relationship, as given by Equation (8).

$$e_0=e_0^{*}-\frac{k{S}_{\mathrm{h}}}{1+S_{\mathrm{h}}}$$

(8)

where $e_0^{*}$ is the initial void ratio of the host sand, and k is the model parameter that reflects the influence of hydrate occurrence mode and formation conditions on the initial void ratio of GHBS.

Yoneda et al. [38] verified that the deformation process affects the occurrence conditions of hydrate and leads to hydrate decomposition, whereas the consolidation line of GHBS gradually approaches the consolidation line of the host sand, due to which the GHBS should have the same critical state line (CSL) as the host sand. The CSL of sand can be expressed using Equation (9).

e_c = e_c0 − λ(p/p_a)^ξ

(9)

where e_c0 is the void ratio of CSL when p = 1kPa, λ is the slope of CSL in e-lnp space, ξ is the material parameter with the generally accepted value of 0.7 for sand, and p_a is the atmospheric pressure (101kPa) introduced for dimensional unification.

Using the expression of dilatancy equation proposed by Wan and Guo [37], the state parameter φ, as given by Equation (6), is introduced into the dilatancy equation, which is given by Equation (10).

d = Mφ ^m − η

(10)

where m is the model parameter, which can be obtained from the results of the triaxial test. It can be seen that when m = 0, Equation (10) is reduced to the dilatancy equation of the Cambridge model.

3.4. Hardening Modulus

The plastic strain of GHBS can be divided into two parts. One part is related to the expansion of the yield surface. For this part, η is used to reflect the isotropic hardening of GHBS with the evolution of plastic strain. The other part results from the movement of the yield surface. Cementation reflects the motion hardening of GHBS with the evolution of plastic shear strain. Both of them constitute the mixed hardening of GHBS.

The hardening caused by the stress ratio is the same as the hardening modulus expression of sand, while the isotropic hardening modulus A₁ is given by Equation (11).

A₁ = hG(M/η − φ)

(11)

where h is the model parameter and G is the shear modulus of GHBS.

For sand, the shear modulus has the following empirical correlation (Equation (12)).

$$G^{*}=G_0^{*}\frac{{(2.97-e^{*})}^2}{1+e^{*}}\sqrt{p{p}_{\mathrm{a}}}$$

(12)

where G* is the shear modulus of sand and $G_0^{*}$ is the model parameter.

Yoneda et al. [38] have given the empirical correlation of the shear modulus of GHBS under 1MPa effective confining pressure, which is given by Equation (13).

G = 91.482 [( 1 + e₀ )(1 − S_h)]^−1.363

(13)

Based on Equations (12) and (13), the shear modulus of GHBS is rewritten and given by Equation (14).

$$G={\left(1-S_{\mathrm{h}}\right)}^{-\chi }{G}_0^{*}\frac{{(2.97-e)}^2}{1+e}\sqrt{p{p}_{\mathrm{a}}}$$

(14)

where χ is the material parameter of GHBS and reflects the degree of influence of the hydrate on the hardening modulus.

The cementation of GHBS also causes material hardening during shearing, which has the characteristics of kinematic hardening. In this paper, the kinematic hardening modulus is represented by Equation (15).

A₂ = − a_cηp_c0

(15)

Therefore, the hardening modulus of GHBS can be expressed using Equation (16).

A = A₁ + A₂ = hG(M/η − φ) − a_cηp_c0

(16)

It can be seen that, when S_h = 0, and p_c0 = 0, Equation (16) returns to the hardening modulus expression of sand.

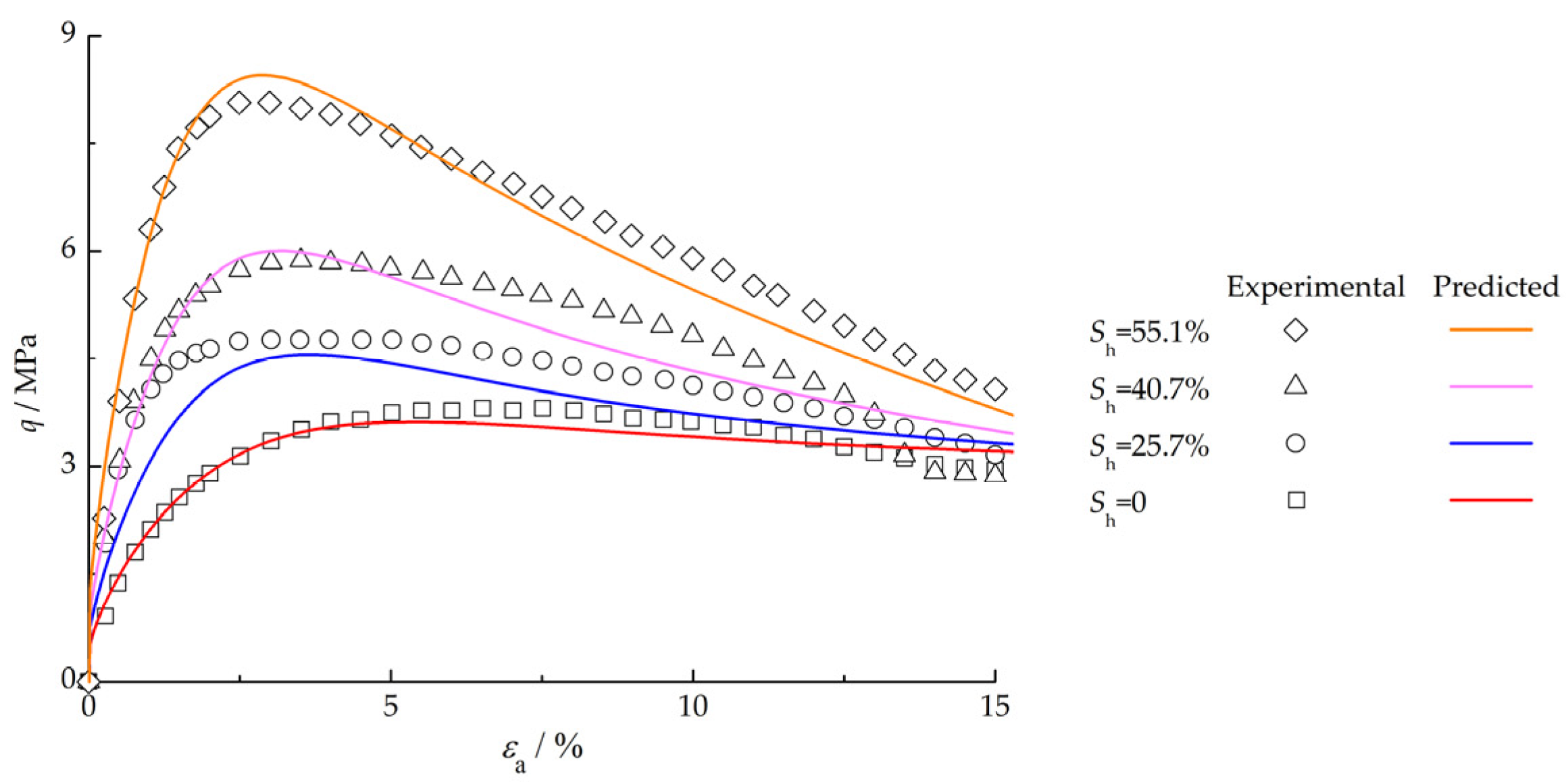
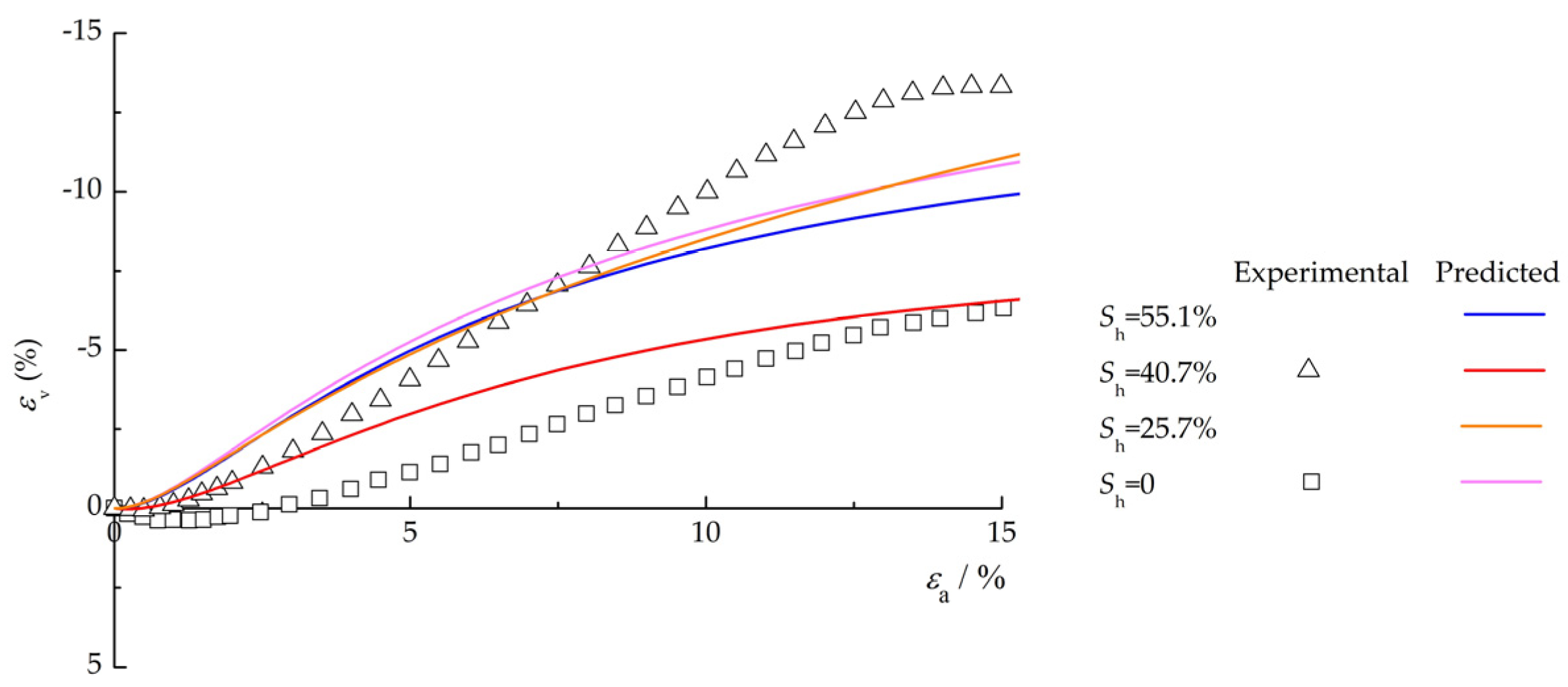
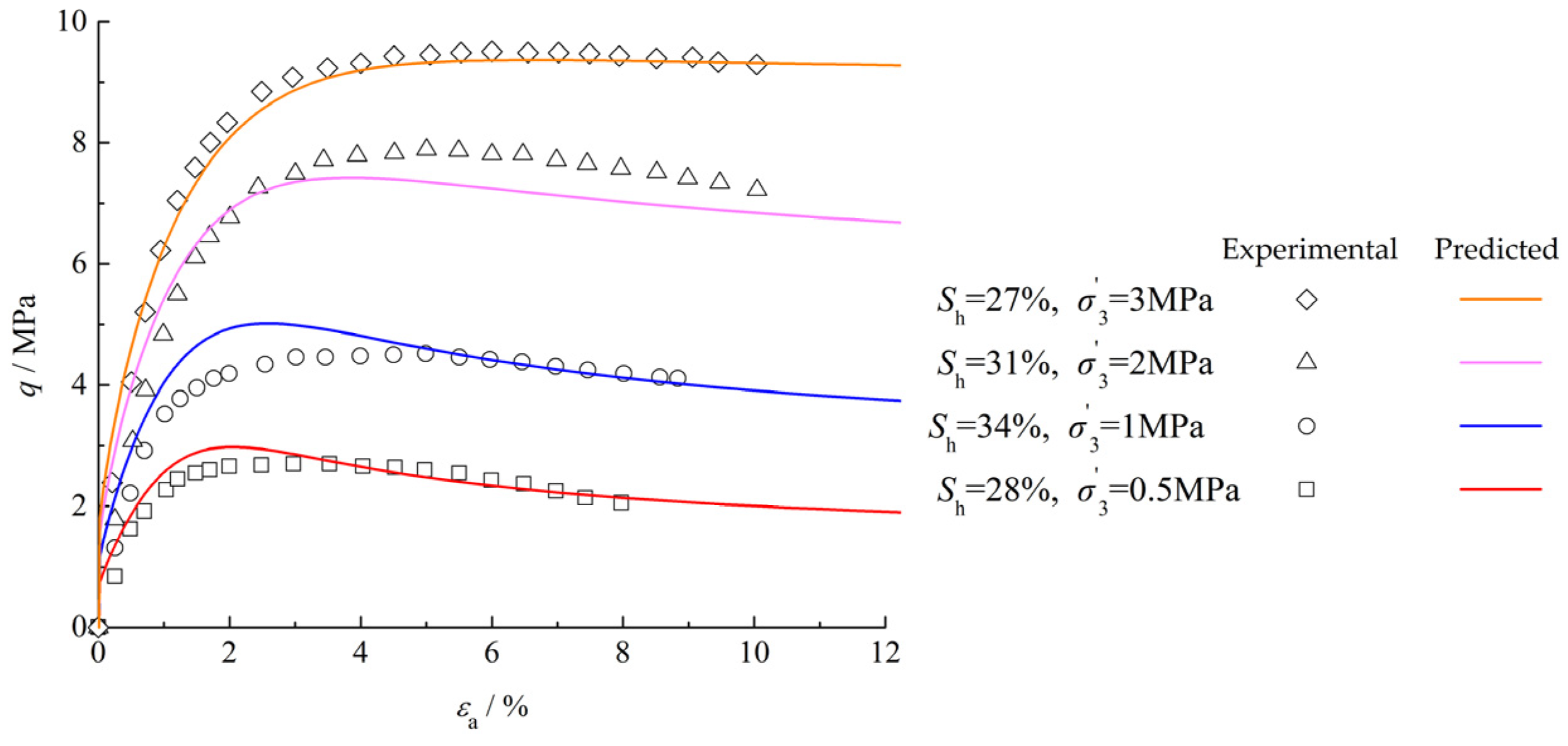
4. Model Verification

4.1. Model Parameters

The model established in this paper contains thirteen parameters and can be divided into two categories, as represented by the parameters given in

Table 1. Sand material parameters.

Parameter	Value	Parameter	Value
ξ	0.7	M	1.5
λ	0.0191	h	0.0533
ec0	0.9344	m	3.16
μ	0.3	$G_0^{*}$	1944

and

Table 2. Hydrate-related parameters.

Parameter	Value
k	0.29
α(MPa)	7.75
β	2.90
ac	4.97
χ	0.94

. Among them, sand material parameters ξ, λ, e_c0 and μ can be obtained through the isotropic compression test of the host sand, while M, h, m and $G_0^{*}$ are calibrated according to the results of the triaxial test. The hydrate-related parameters k, α, β and a_c are obtained by fitting the triaxial test results of different S_h values, whereas χ is calculated using Equation (14).

4.2. Model Prediction

Masui et al. [22] took Toyoura sand as the matrix material with an initial void ratio of 0.65, prepared GHBS samples with different S_h and conducted triaxial drained tests under the effective confining pressure of 1MPa. The test data of Masui are predicted using the model proposed in the current paper, and the parameters used are presented in Table 1 and Table 2.

Figure 2 shows the comparison between experimental and model results for different S_h values in terms of deviatoric stress. It can be seen that the predicted results of the model are consistent with the test data, and the model can satisfactorily reflect the strength and strain softening characteristics of GHBS. With the increase in S_h, the stiffness and strength of GHBS gradually increase, and the phenomenon of strain-softening becomes more obvious. The prediction curve of the volume strain of GHBS is shown in Figure 3. Compared to the experimental data, it can be seen that the model can satisfactorily describe the effect of hydrates on dilatancy. When the strain is small, GHBS mainly shows shear shrinkage. With the increase in axial strain, the volume strain gradually increases. Furthermore, higher the value of S_h, more obvious is the dilatancy.

In order to test the applicability of the model under different effective confining pressures, it is compared with the test data of Miyazaki [24]. Miyazaki et al. also used Toyoura sand and methane to prepare samples with approximately equal S_h values. The initial void ratio of host sand samples is 0.6, while the effective confining pressures are varied consecutively through values of 0.5MPa, 1MPa, 2MPa and 3MPa. During the tests, the axial strain ε_a and radial strain ε_r of GHBS are monitored.

As the test conditions of Miyazaki et al. [24] and Masui et al. [22] are not the same, the model parameters are changed.

Table 3. Calculation parameters for model prediction.

Parameter	Value	Parameter	Value
$G_0^{*}$	2496	β	3.49
k	0.08	ac	1.95
α(MPa)	7.71	χ	1.08

presents the parameters used to predict the test data of Miyazaki et al. The results predicted by the model are compared with the experimental data. It can be seen from Figure 4 that, for the same S_h, the increase in effective confining pressure makes the GHBS change from strain-softening to strain-hardening, because the constraint effect of effective confining pressure improves the rigidity and strength of GHBS. Meanwhile, the rate of decline of cementation of GHBS decreases. Figure 5 shows the comparison between the relationship curve of predicted radial strain and the experimental data. The predicted curve is in good agreement with the experimental data, indicating that the model proposed in the current paper has a very good applicability.

5. Conclusions

In this study, an elastoplastic model is proposed based on the framework of the sand state-dependent constitutive model, in which GHBS is considered as a bonded material. The main conclusions are as follows:

(1)

By summarizing the test rules of GHBS, it is found that GHBS has certain cohesive strength and obvious state-related characteristics. In this paper, GHBS is regarded as a special cementing material, and the sand state correlation model is selected as the basic framework.

(2)

By constructing appropriate state parameter expressions, introducing the cementation and its evolutionary pattern and adopting the mixed hardening rule, the state-dependent constitutive model of GHBS is established.

(3)

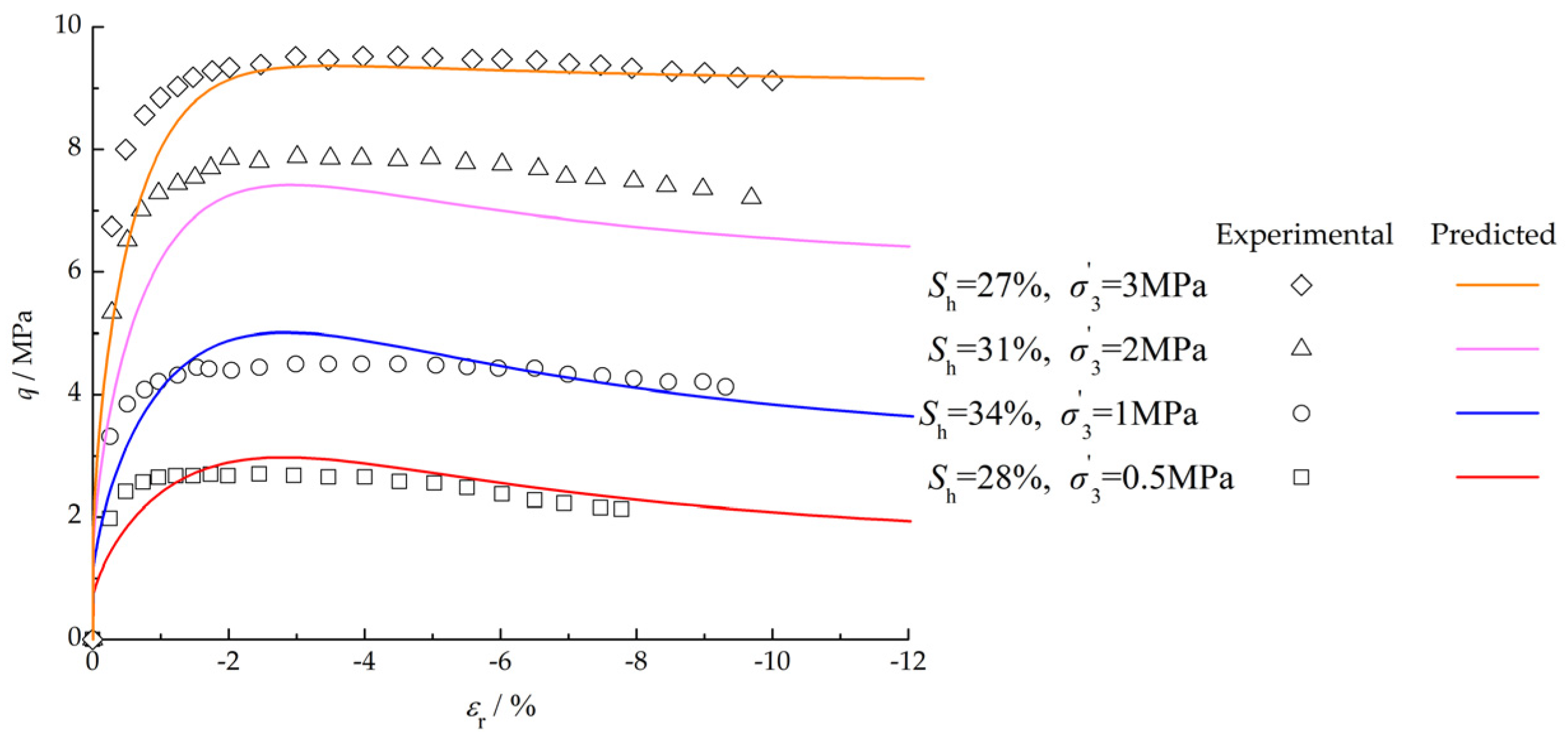
The comparison between the predicted results using the proposed model and the experimental data shows that the established constitutive model is in good agreement with the experimental data. The model can satisfactorily describe the strain-hardening and strain-softening characteristics of GHBS and can effectively reflect the correlation characteristics of strength and stiffness with hydrate saturation, effective confining pressure and other factors.