Numerical Study on Wave Radiation by a Barge with Large Amplitudes and Frequencies
Abstract
:1. Introduction
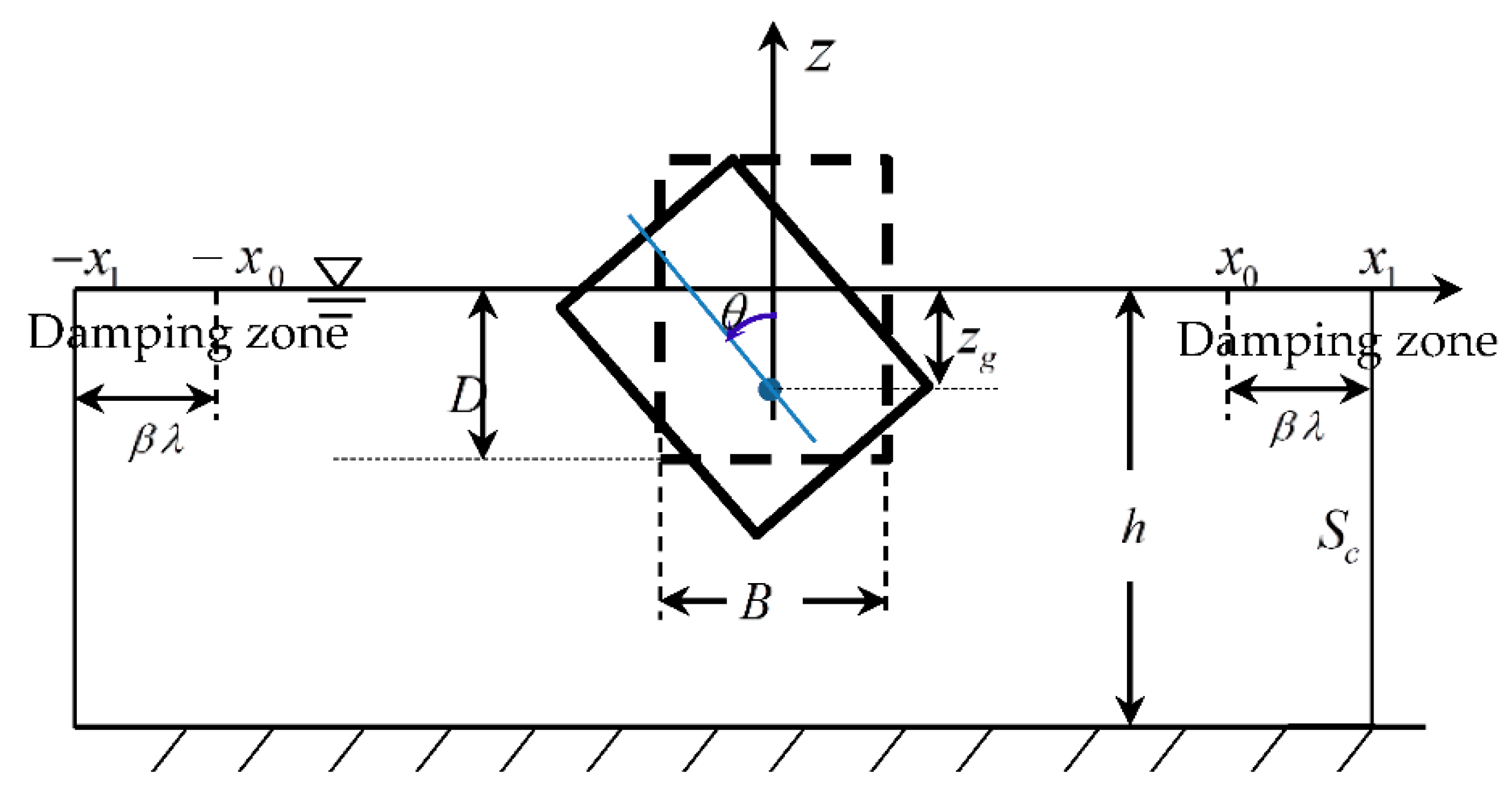
2. Mathematical Model and Its Numerical Implementation
2.1. Governing Equations and Boundary Conditions
2.2. Hydrodynamic Forces and Moments
2.3. Numerical Procedures
2.4. Special Treatments
2.4.1. Plunging Wave Cutting
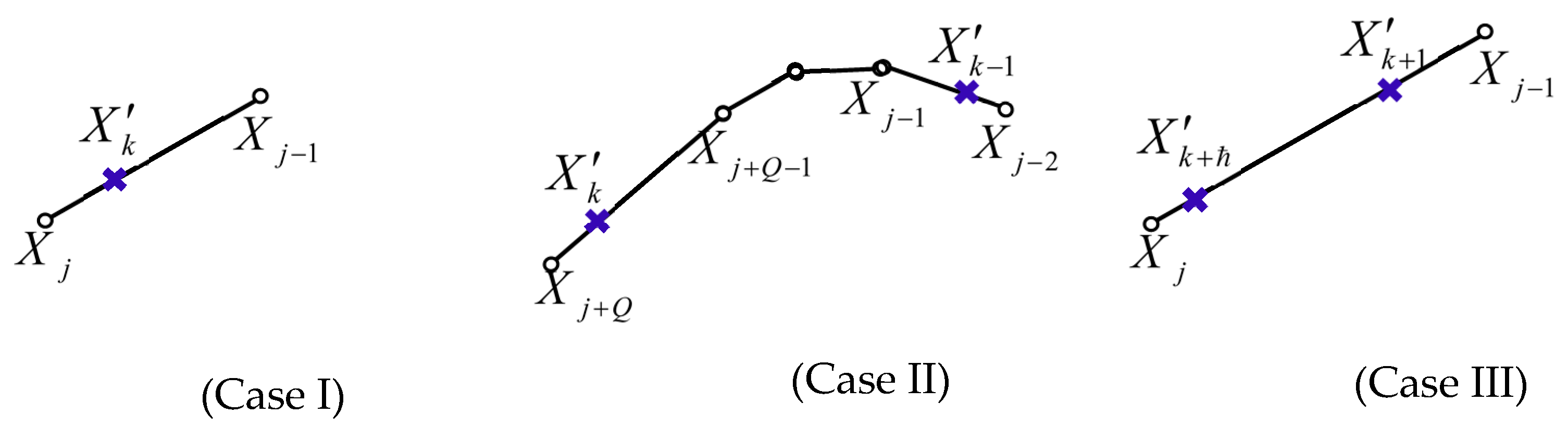
2.4.2. Remeshing
3. Numerical Results and Discussion
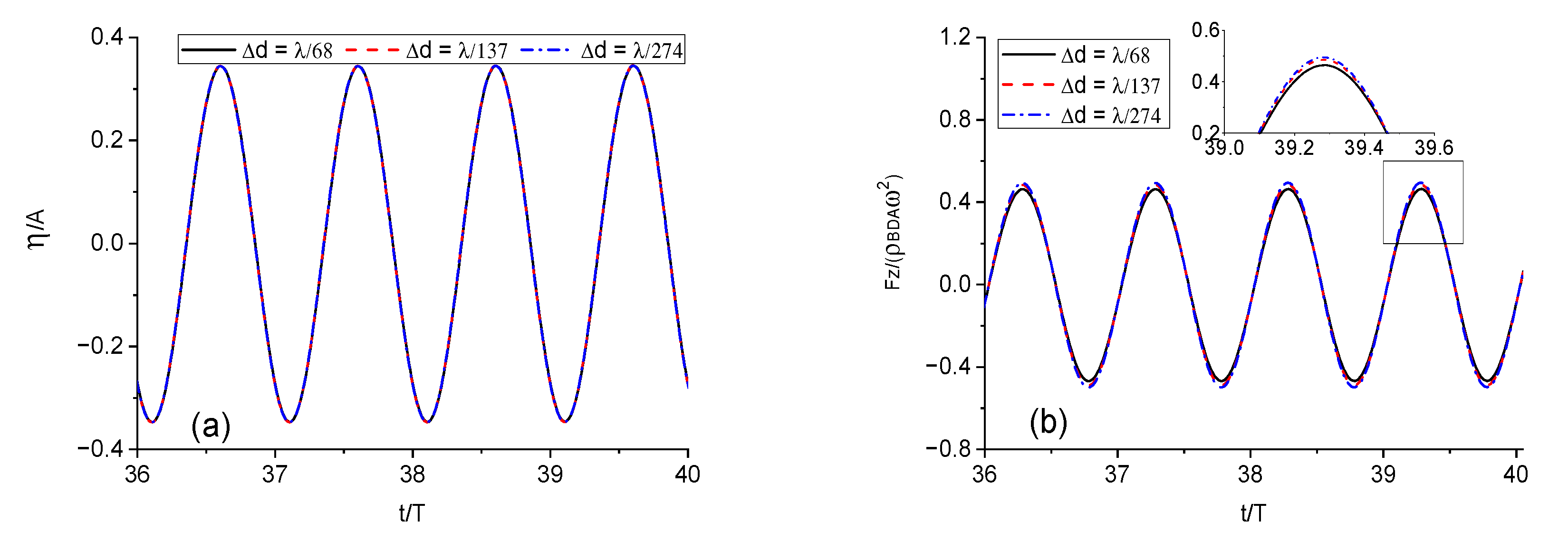
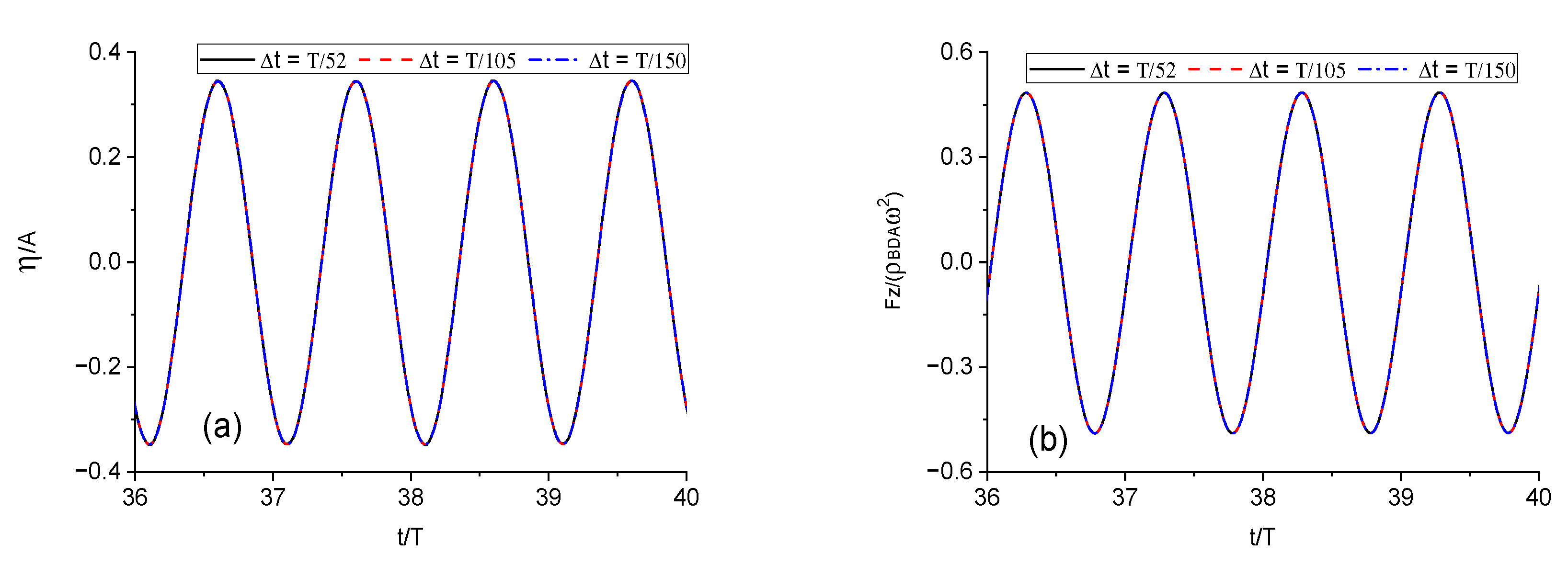
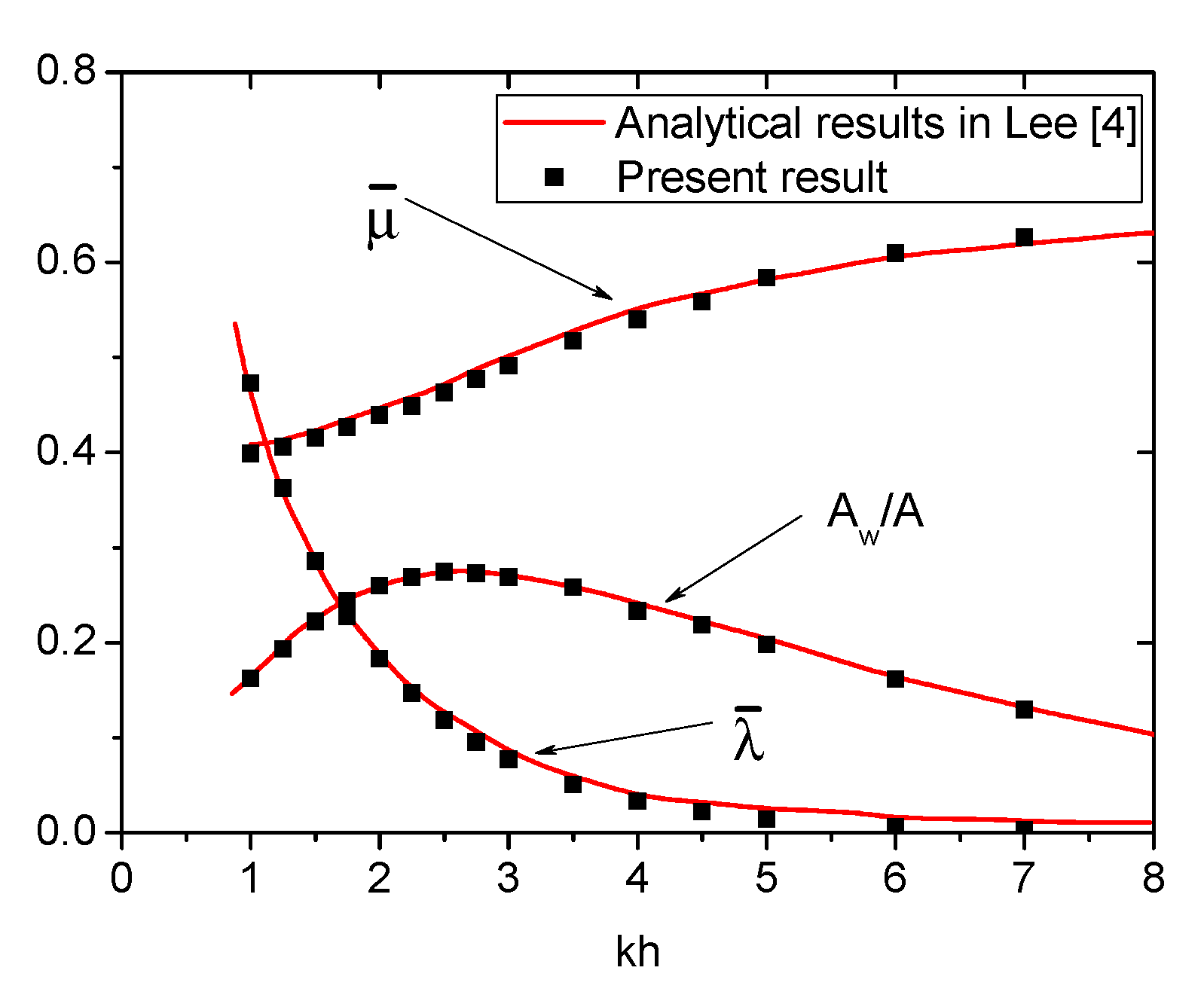
3.1. Convergence Study and Validation
3.2. Wave Radiation by a Single Motion Mode
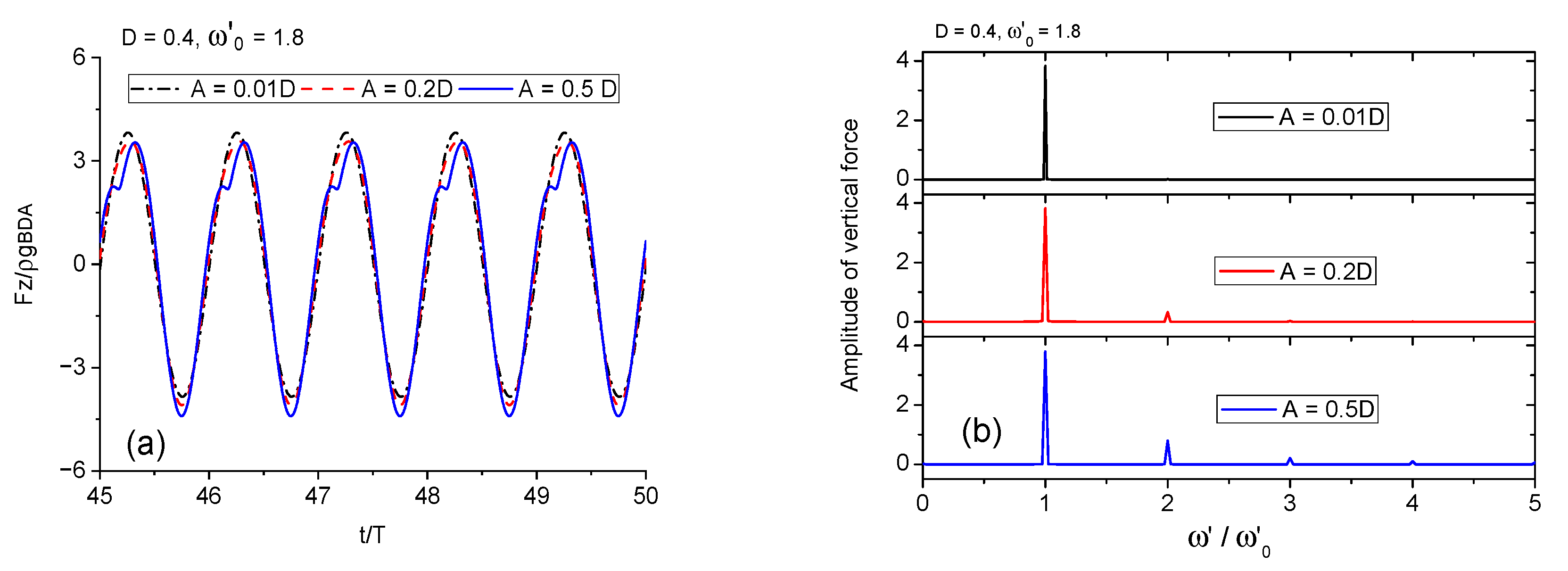
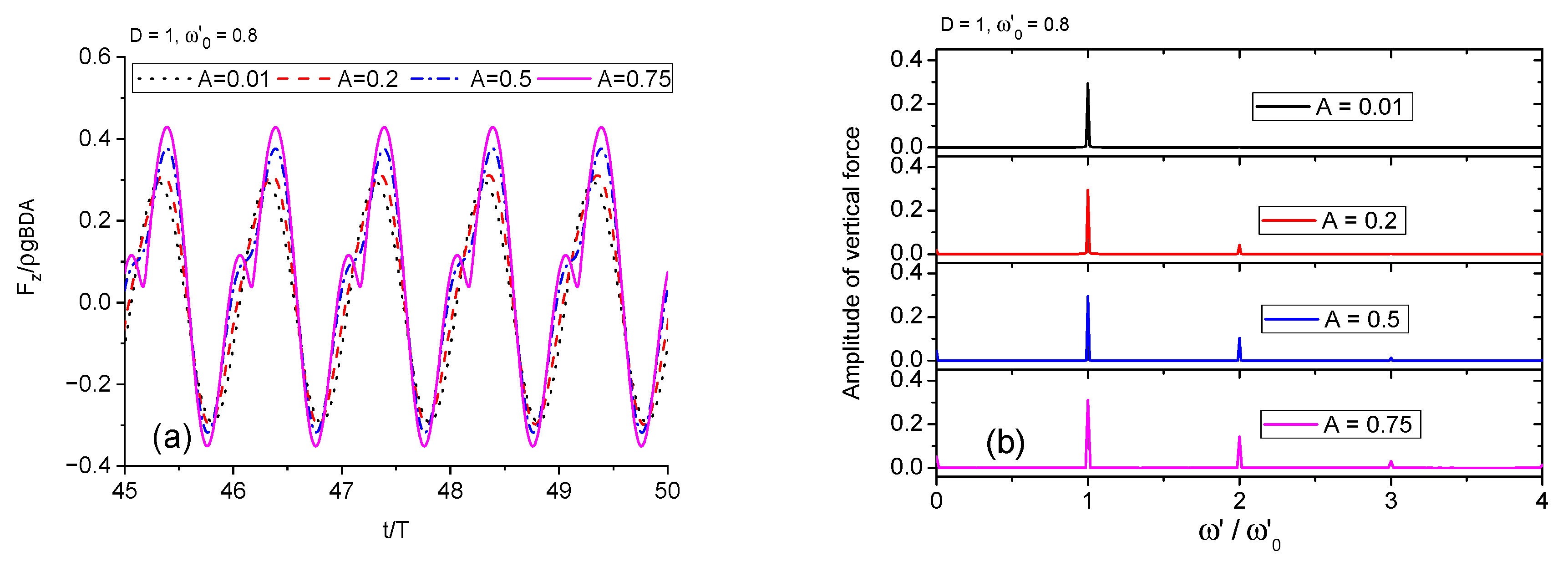
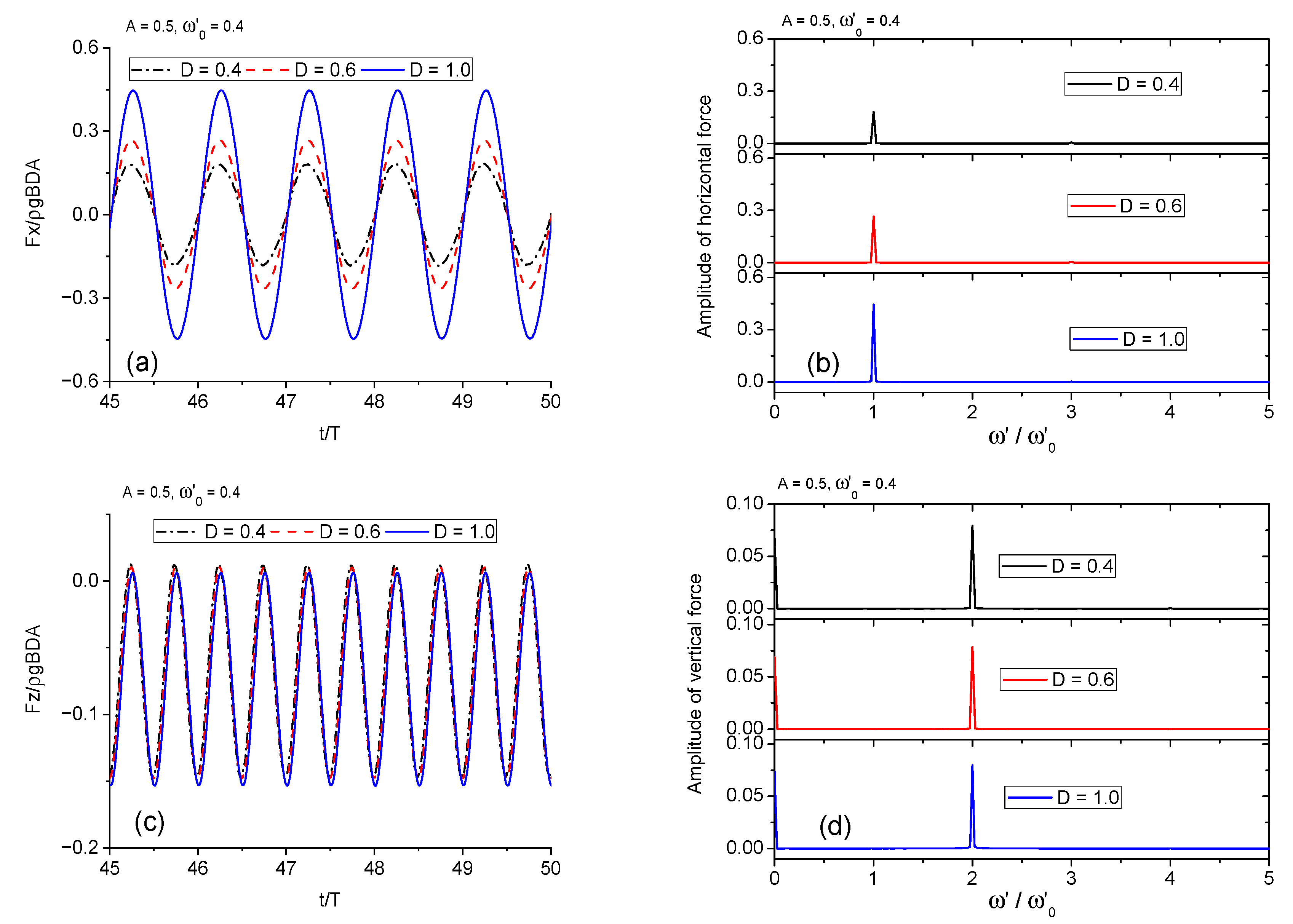
3.2.1. Forced Heave Motion
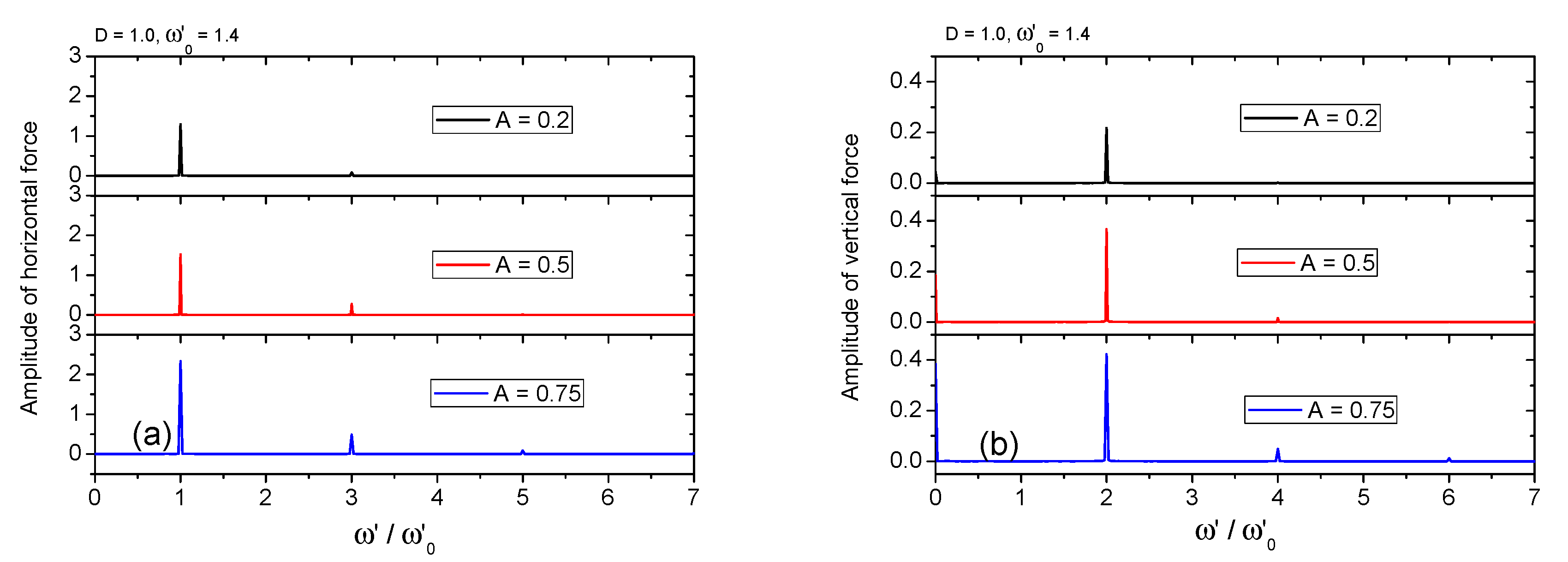
3.2.2. Forced Sway Motion
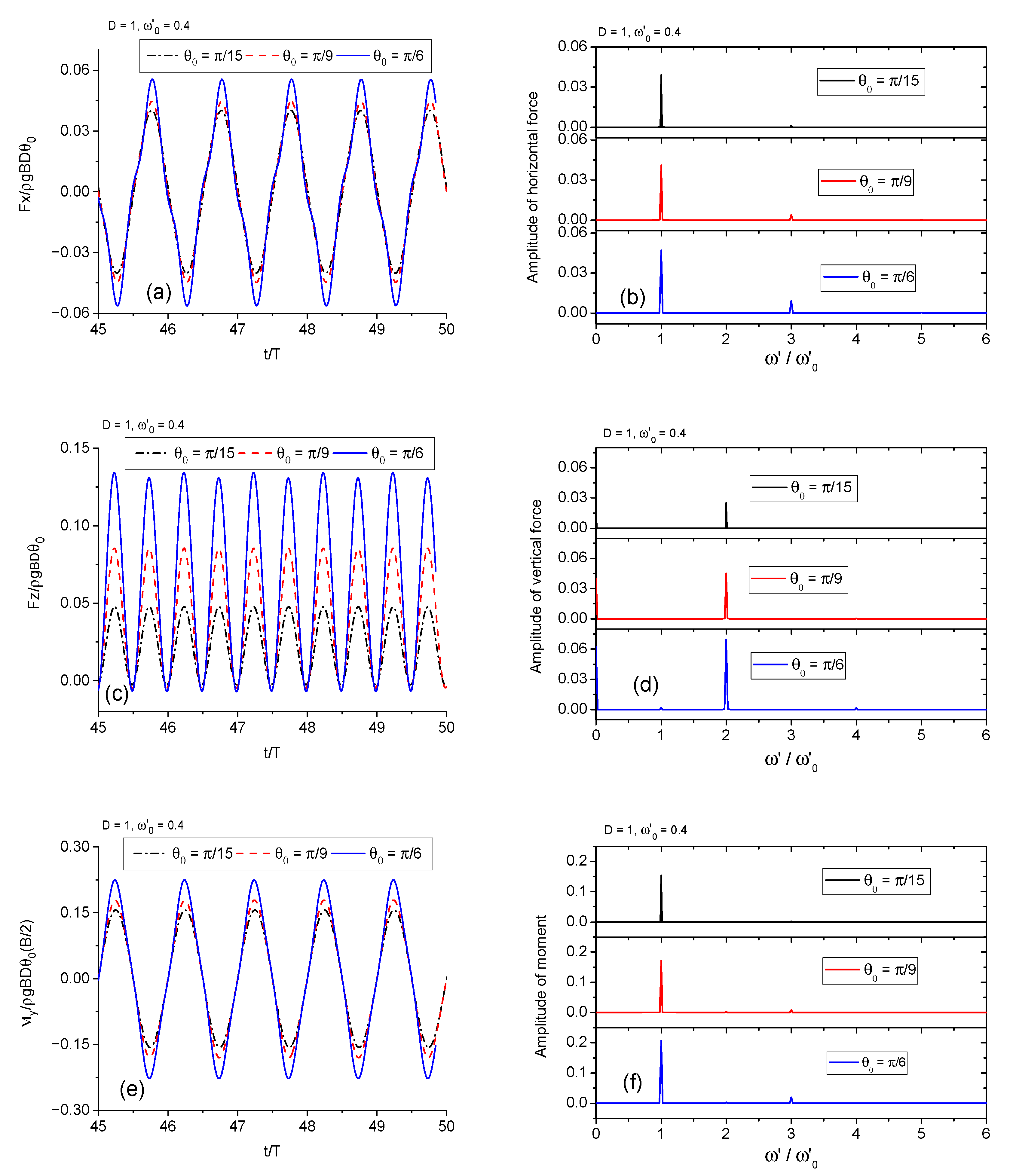
3.2.3. Forced Roll Motion
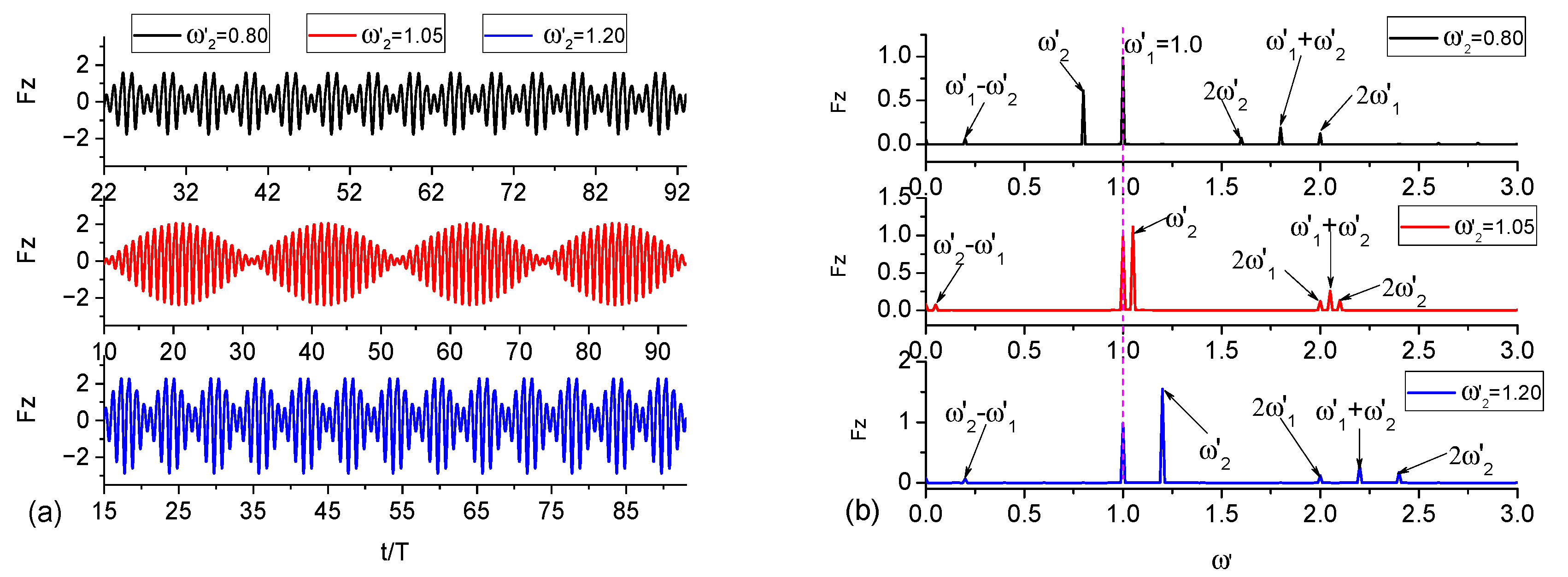
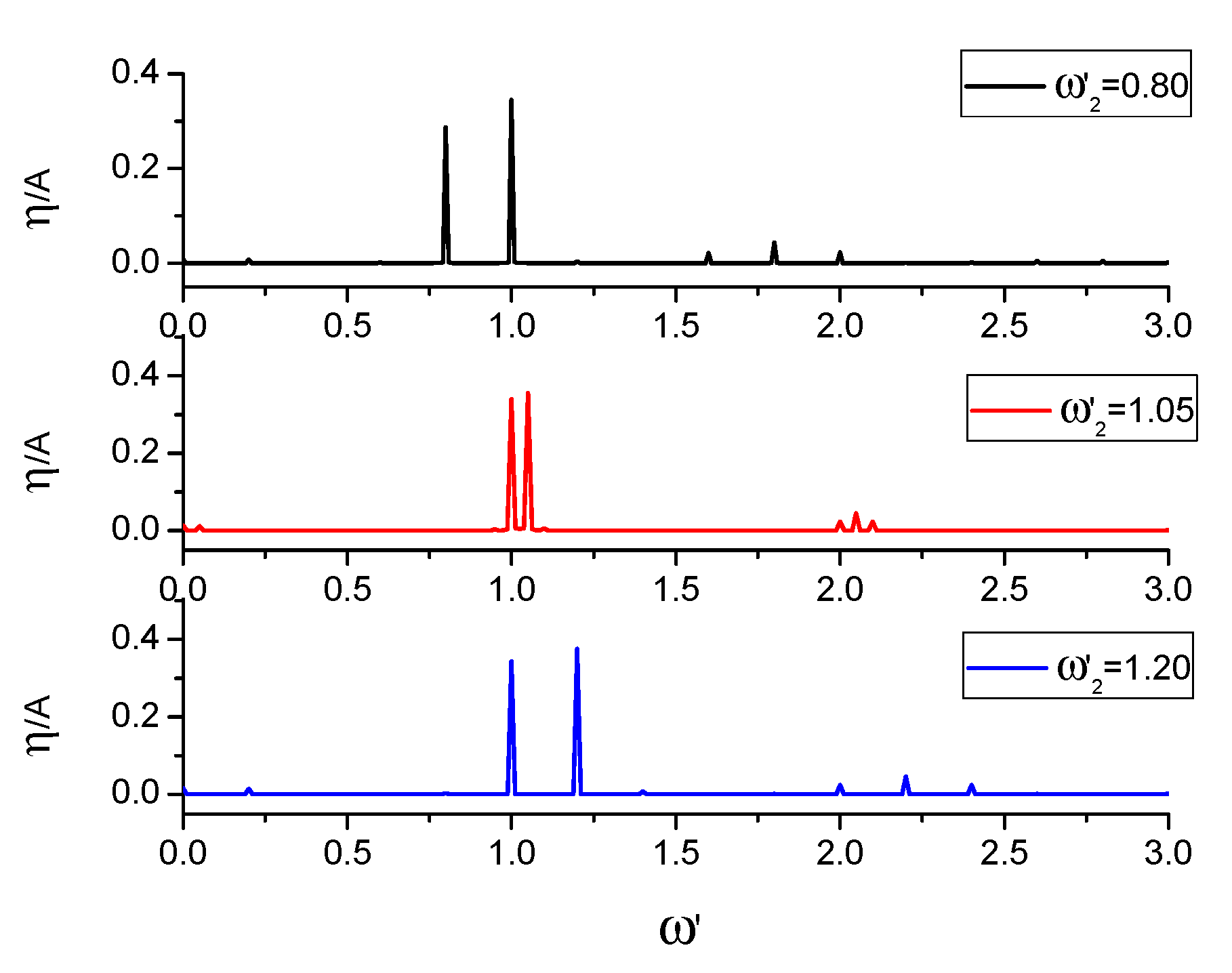
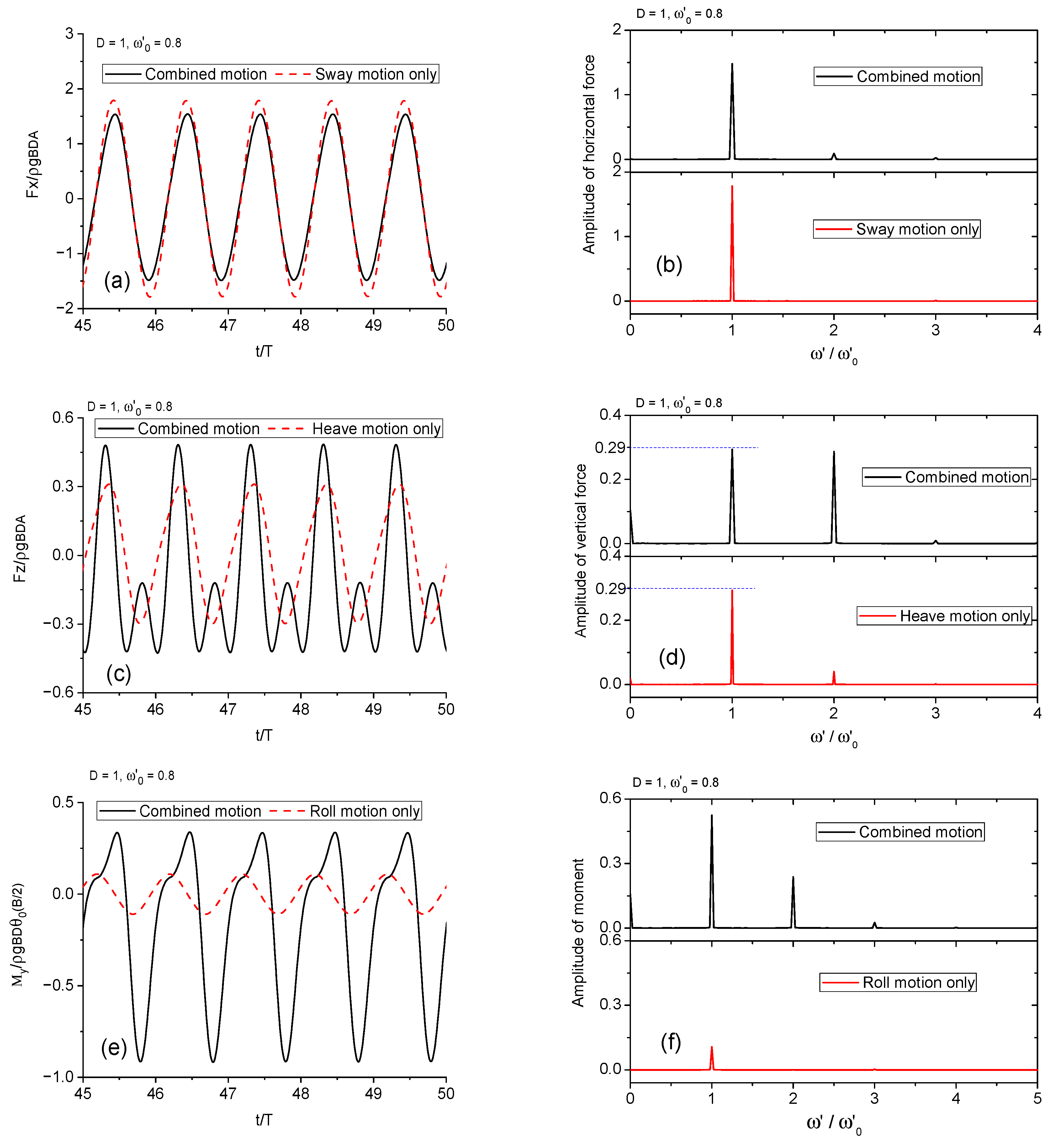
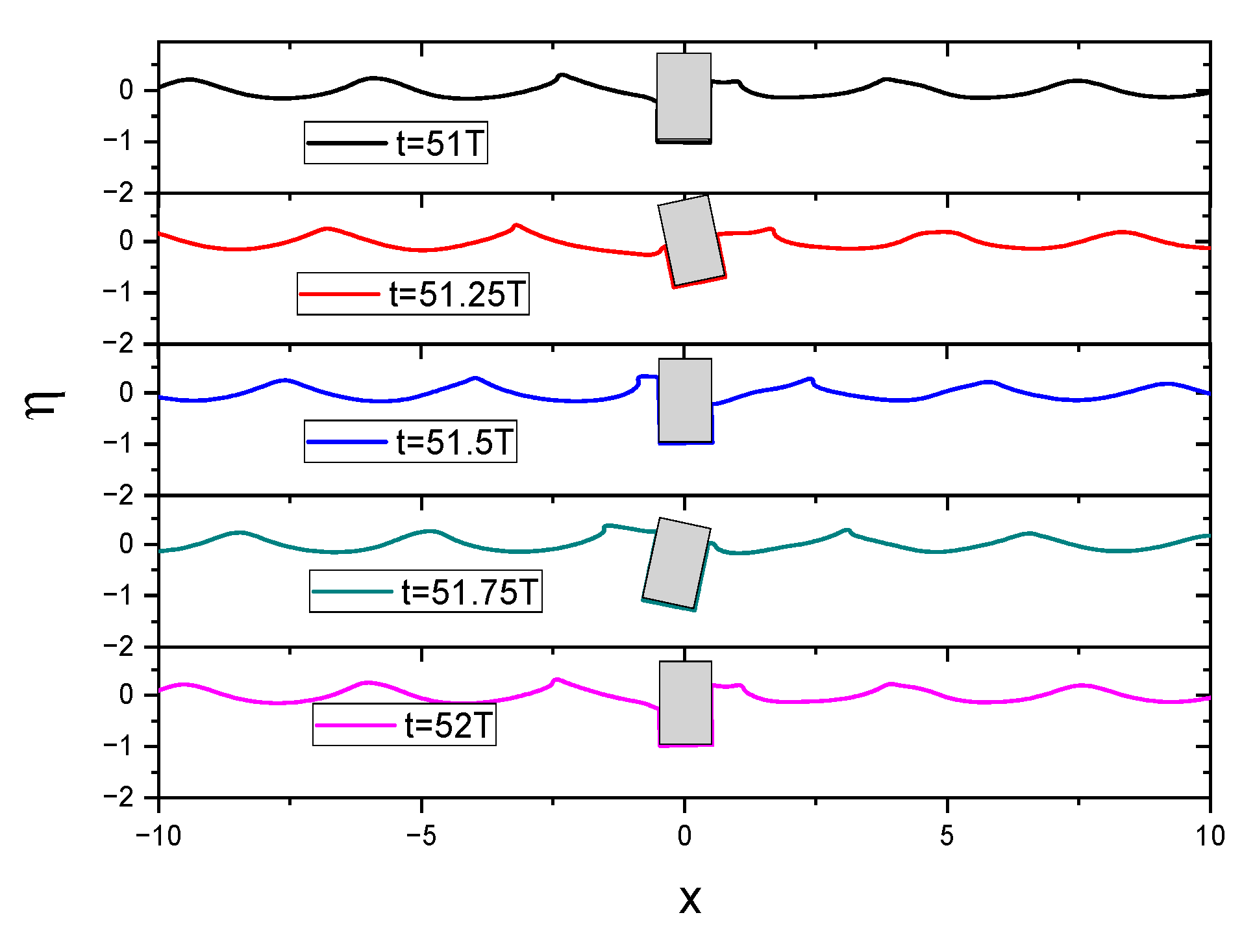
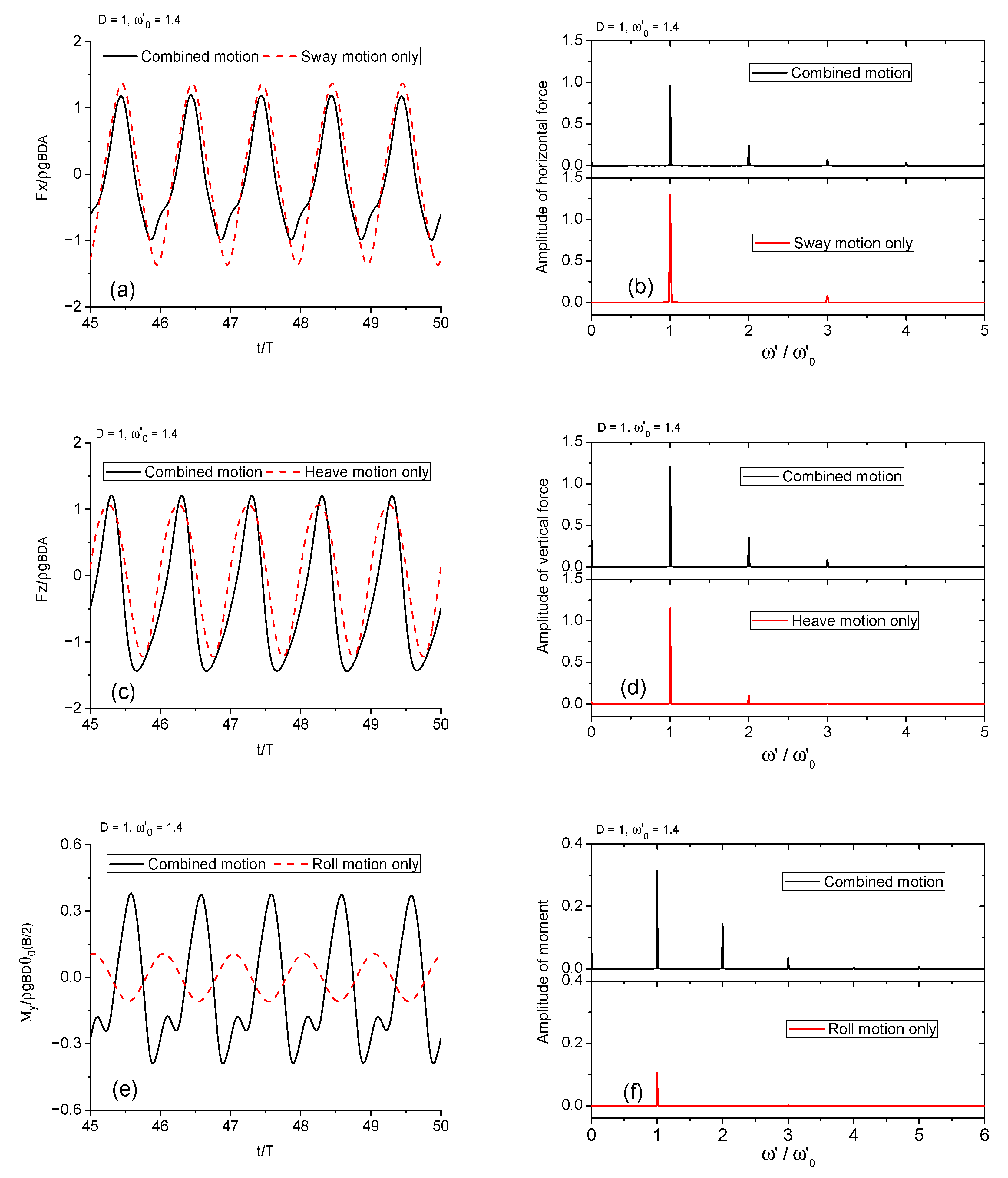
3.3. Wave Radiation by Combined Motion
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ursell, F. On the heaving motion of a circular cylinder on the surface of a fluid. Q. J. Mech. Appl. Math. 1949, 2, 218–231. [Google Scholar] [CrossRef] [Green Version]
- Kim, W.D. On the harmonic oscillations of a rigid body on a free surface. J. Fluid Mech. 1965, 21, 427–451. [Google Scholar] [CrossRef]
- Black, J.L.; Mei, C.C.; Bray, M.C.G. Radiation and scattering of water waves by rigid bodies. J. Fluid Mech. 1971, 46, 151–164. [Google Scholar] [CrossRef]
- Lee, J.F. On the heave radiation of a rectangular structure. Ocean Eng. 1995, 22, 19–34. [Google Scholar] [CrossRef]
- Li, Z.F.; Wu, G.X.; Ji, C.Y. Wave radiation and diffraction by a circular cylinder submerged below an ice sheet with a crack. J. Fluid Mech. 2018, 845, 682–712. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, L.; Zhao, X.; Huang, Z. Hydrodynamic performance of a T-shaped floating breakwater. Appl. Ocean Res. 2019, 82, 325–336. [Google Scholar] [CrossRef]
- Lee, C.M. The second-order theory of heaving cylinders in a free surface. J. Ship Res. 1968, 12, 313–327. [Google Scholar]
- Papanikolaou, A.; Nowacki, H. Second-Order Theory of Oscillating Cylinders in a Regular Steep Wave. In Proceedings of the 13th Symposium on Naval Hydrodynamics, Tokyo, Japan, 6–10 October 1980. [Google Scholar]
- Isaacson, M.; Ng, J.Y.T. Time-Domain Second-Order Wave Radiation in Two Dimensions. J. Ship Res. 1993, 37, 25–33. [Google Scholar]
- Wu, G.X. Second-order wave radiation by a submerged horizontal circular cylinder. Appl. Ocean Res. 1993, 15, 293–303. [Google Scholar] [CrossRef]
- Wu, G.X.; Eatock Taylor, R. Time stepping solutions of the two-dimensional nonlinear wave radiation problem. Ocean Eng. 1995, 22, 785–798. [Google Scholar] [CrossRef]
- Maiti, S.; Sen, D. Nonlinear heave radiation forces on two-dimensional single and twin hulls. Ocean Eng. 2001, 28, 1031–1052. [Google Scholar] [CrossRef]
- Hu, P.; Wu, G.X.; Ma, Q.W. Numerical simulation of nonlinear wave radiation by a moving vertical cylinder. Ocean Eng. 2002, 29, 1733–1750. [Google Scholar] [CrossRef]
- Bai, W.; Eatock Taylor, R. Higher-order boundary element simulation of fully nonlinear wave radiation by oscillating vertical cylinders. Appl. Ocean Res. 2006, 28, 247–265. [Google Scholar] [CrossRef]
- Wang, C.Z.; Wu, G.X.; Drake, K.R. Interactions between nonlinear water waves and non-wall-sided 3D structures. Ocean Eng. 2007, 34, 1182–1196. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Ning, D.; Teng, B.; Bai, W. Numerical investigation of wave radiation by a vertical cylinder using a fully nonlinear HOBEM. Ocean Eng. 2013, 70, 1–13. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Ning, D.; Teng, B.; Zhao, M. Fully nonlinear modeling of radiated waves generated by floating flared structures. Acta Mech. Sin. 2014, 30, 667–680. [Google Scholar] [CrossRef]
- Sun, S.Y.; Sun, S.L.; Ren, H.L.; Wu, G.X. Splash jet and slamming generated by a rotating flap. Phys. Fluids 2015, 27, 092107. [Google Scholar] [CrossRef]
- Li, Y.; Xu, B.; Zhang, D.; Shen, X.; Zhang, W. Numerical analysis of combined wave radiation and diffraction on a floating barge. Water 2020, 12, 205. [Google Scholar] [CrossRef] [Green Version]
- Tanizawa, K. Long time fully nonlinear simulation of floating body motions with artificial damping zone. J. Soc. Nav. Arch. Jpn. 1996, 180, 311–319. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.X.; Eatock Taylor, R. The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies. Ocean Eng. 2003, 30, 387–400. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.D.; Duan, W.Y.; Wu, G.X. Numerical simulation of water entry of a cone in free-fall motion. Q. J. Mech. Appl. Math. 2011, 64, 265–285. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, C. Analysis of wave resonance in gap between two heaving barges. Ocean Eng. 2016, 117, 210–220. [Google Scholar] [CrossRef]
- Sun, H.; Faltinsen, O.M. The influence of gravity on the performance of planing vessels in calm water. J. Eng. Math. 2007, 58, 91–107. [Google Scholar] [CrossRef]
- Xu, G.D.; Duan, W.Y.; Wu, G.X. Simulation of water entry of a wedge through free fall in three degrees of freedom. Proc. R. Soc. Lond. 2010, 466, 2219–2239. [Google Scholar] [CrossRef]
- Wang, C.Z.; Wu, G.X. An unstructured-mesh-based finite element simulation of wave interactions with non-wall-sided bodies. J. Fluids Struct. 2006, 22, 441–461. [Google Scholar] [CrossRef]
- Isaacson, M.; Cheung, K.-F. Second order wave diffraction around two-dimensional bodies by time-domain method. Appl. Ocean Res. 1991, 13, 175–186. [Google Scholar] [CrossRef]
- Wu, G.X. A note on non-linear hydrodynamic force on a floating body. Appl. Ocean Res. 2000, 22, 315–316. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Long, Y. Numerical Study on Wave Radiation by a Barge with Large Amplitudes and Frequencies. J. Mar. Sci. Eng. 2020, 8, 1034. https://doi.org/10.3390/jmse8121034
Li Y, Long Y. Numerical Study on Wave Radiation by a Barge with Large Amplitudes and Frequencies. Journal of Marine Science and Engineering. 2020; 8(12):1034. https://doi.org/10.3390/jmse8121034
Chicago/Turabian StyleLi, Yajie, and Yun Long. 2020. "Numerical Study on Wave Radiation by a Barge with Large Amplitudes and Frequencies" Journal of Marine Science and Engineering 8, no. 12: 1034. https://doi.org/10.3390/jmse8121034




