Influence of Membrane Equivalent Weight and Reinforcement on Ionic Species Crossover in All-Vanadium Redox Flow Batteries
Abstract
:1. Introduction
2. Experimental Section
2.1. Membrane Selection and Pretreatment
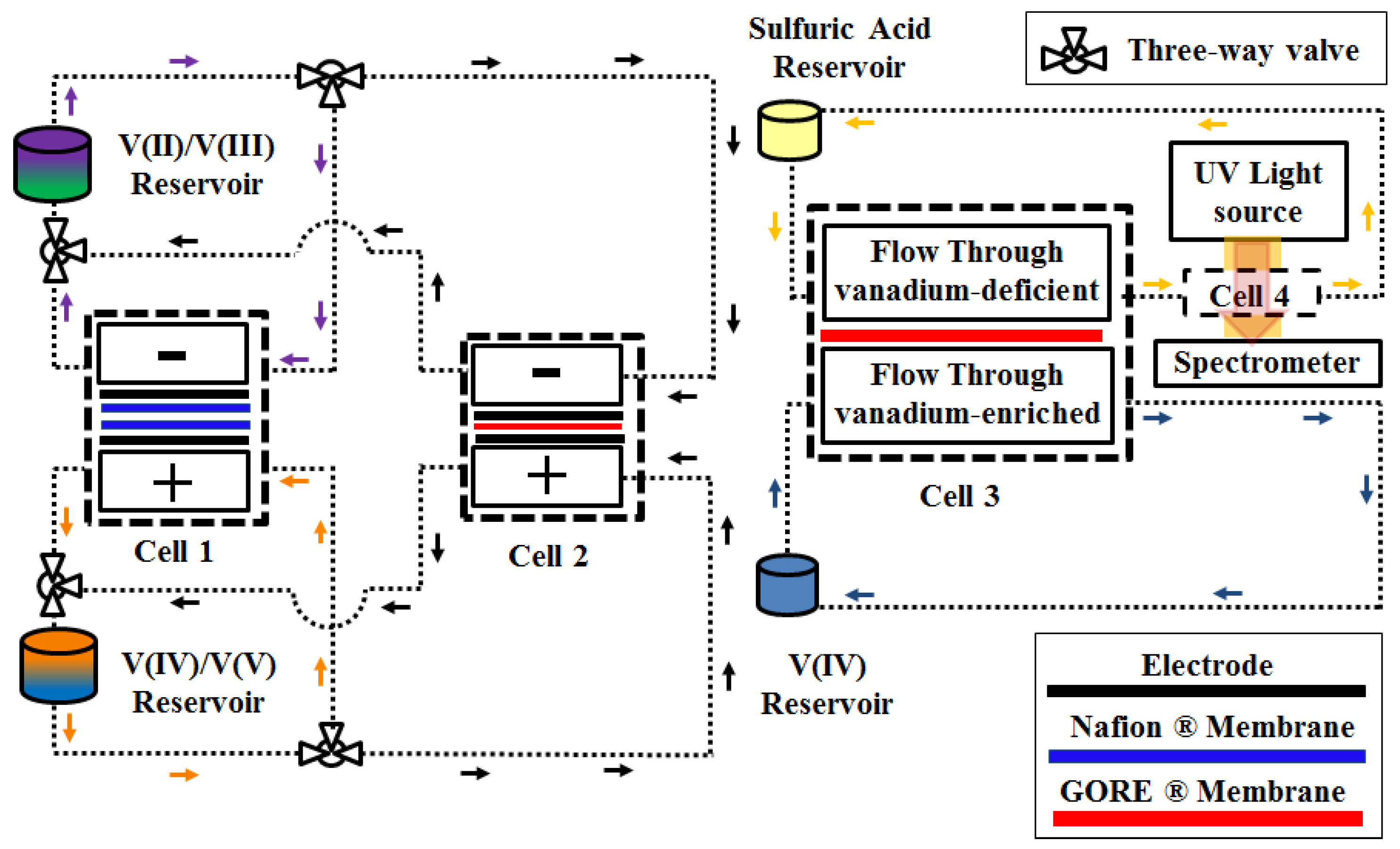
2.2. Method of Approach
2.3. Testing Protocol
2.4. UV-Vis Spectroscopy
3. Vanadium Ion Permeability Assessment
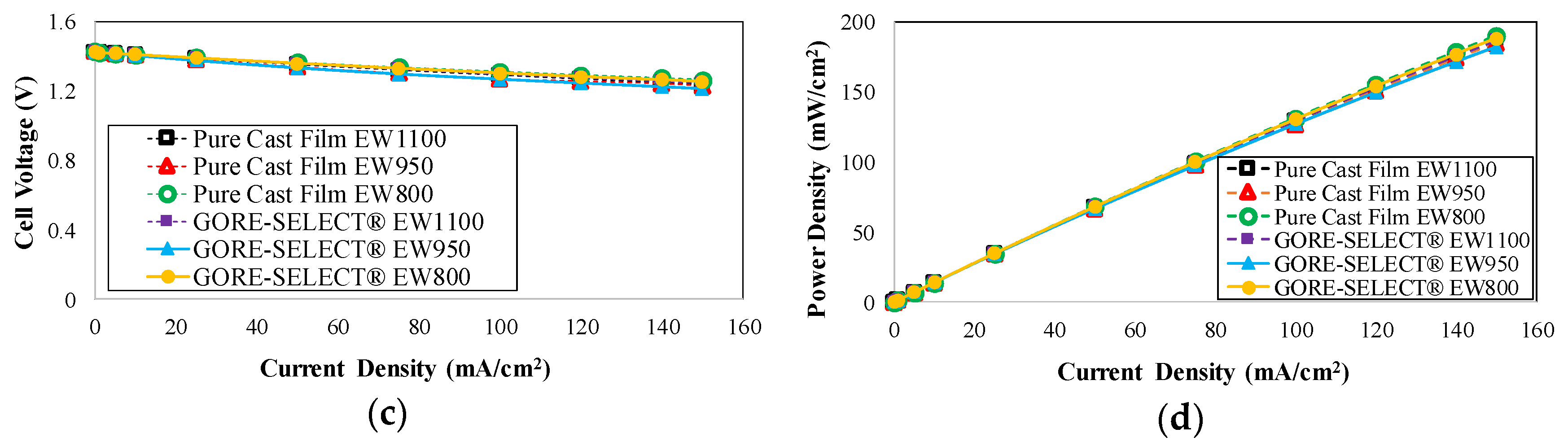
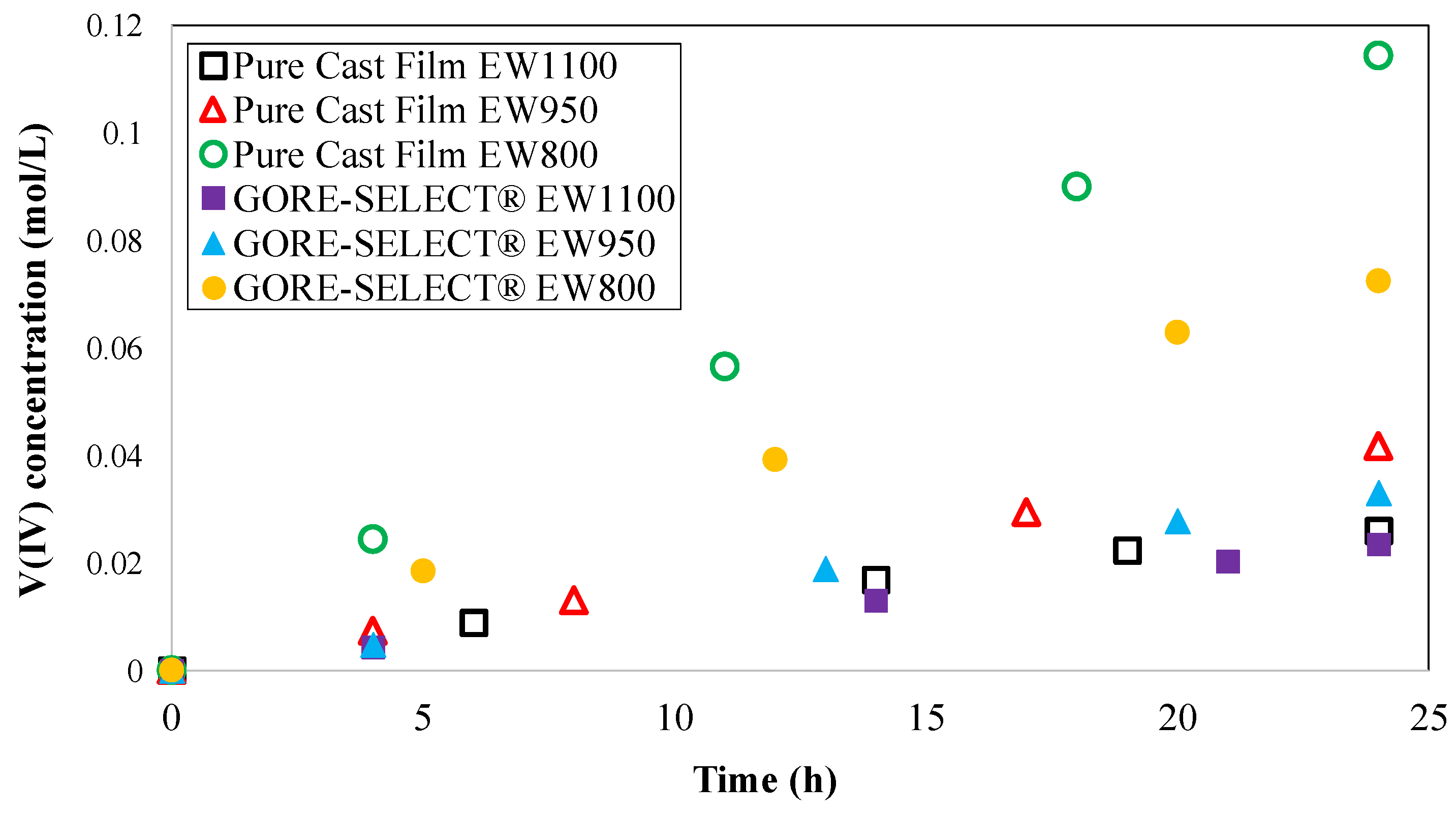
4. Results
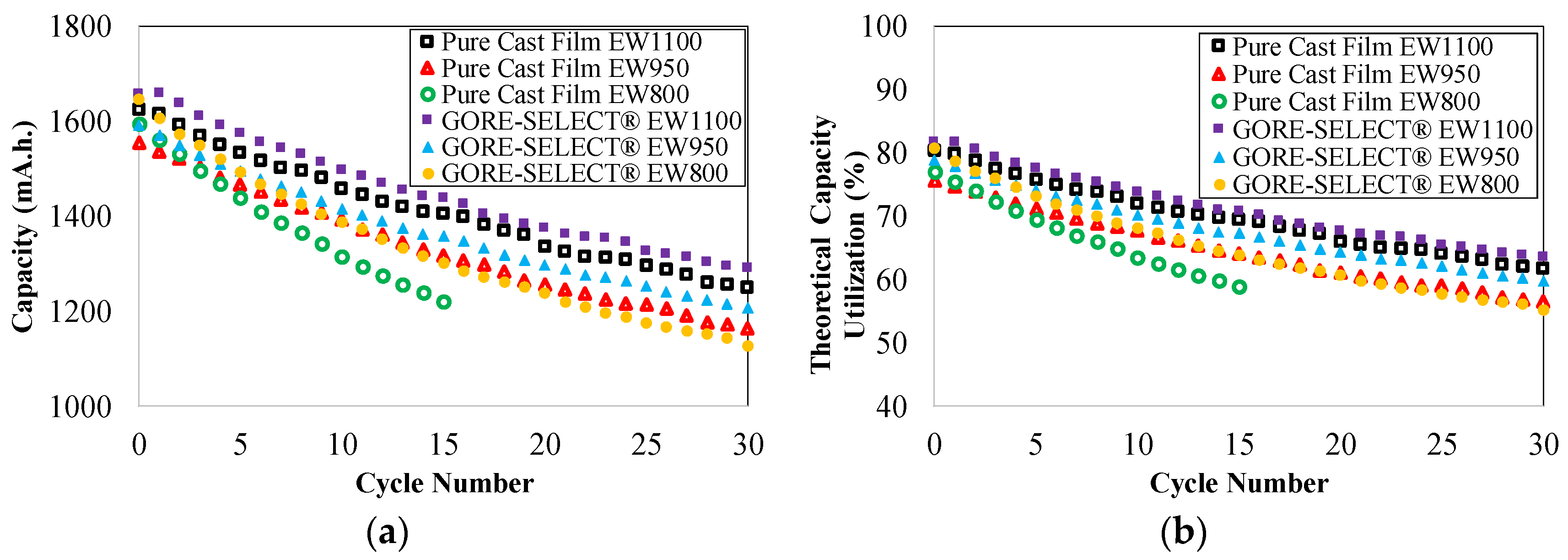
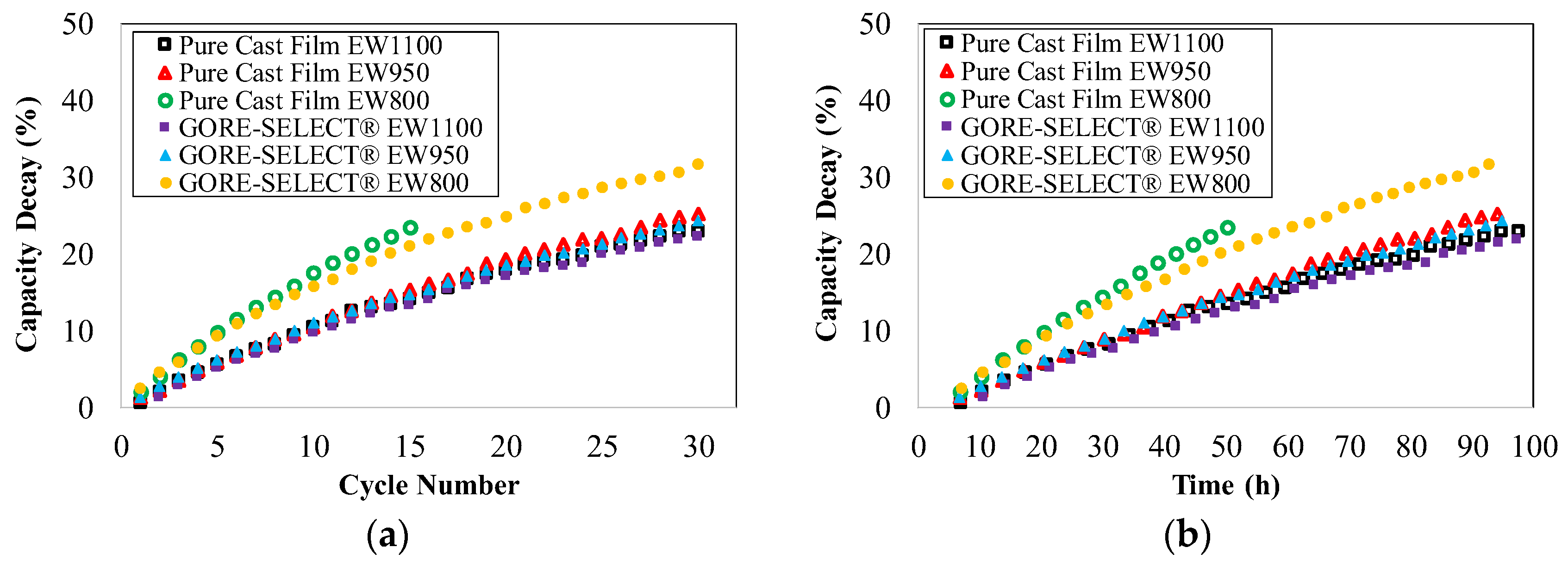
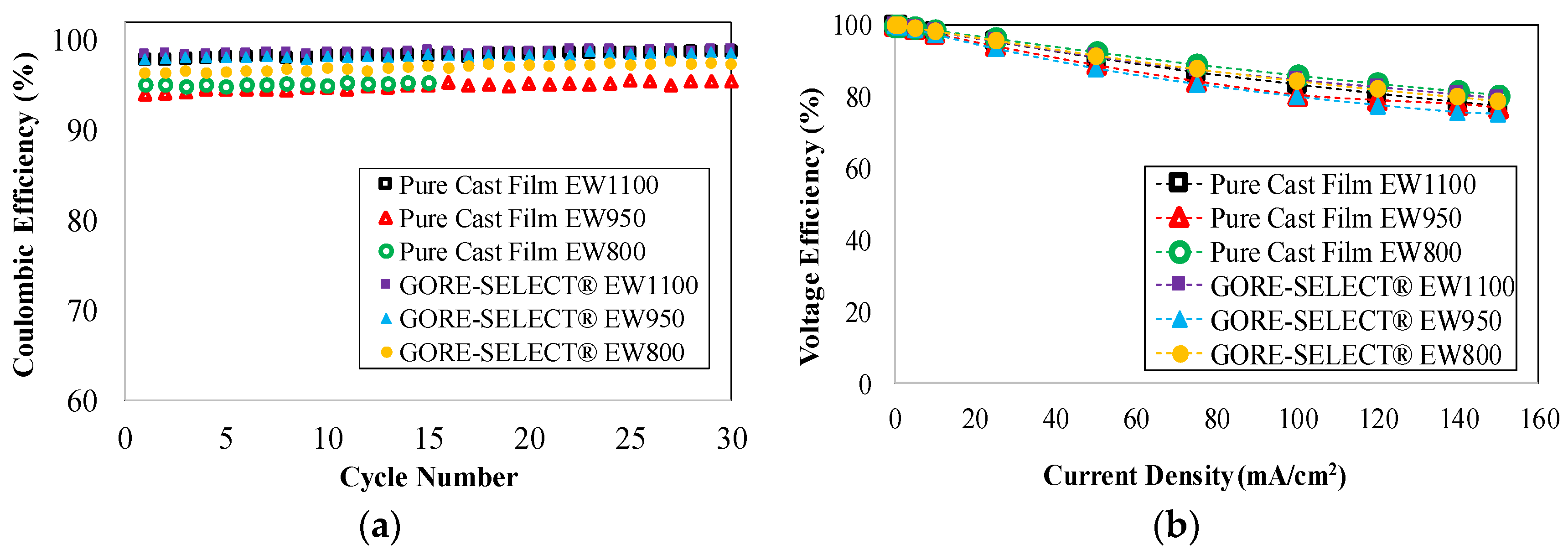
4.1. Capacity Decay during Long-Term Cycling
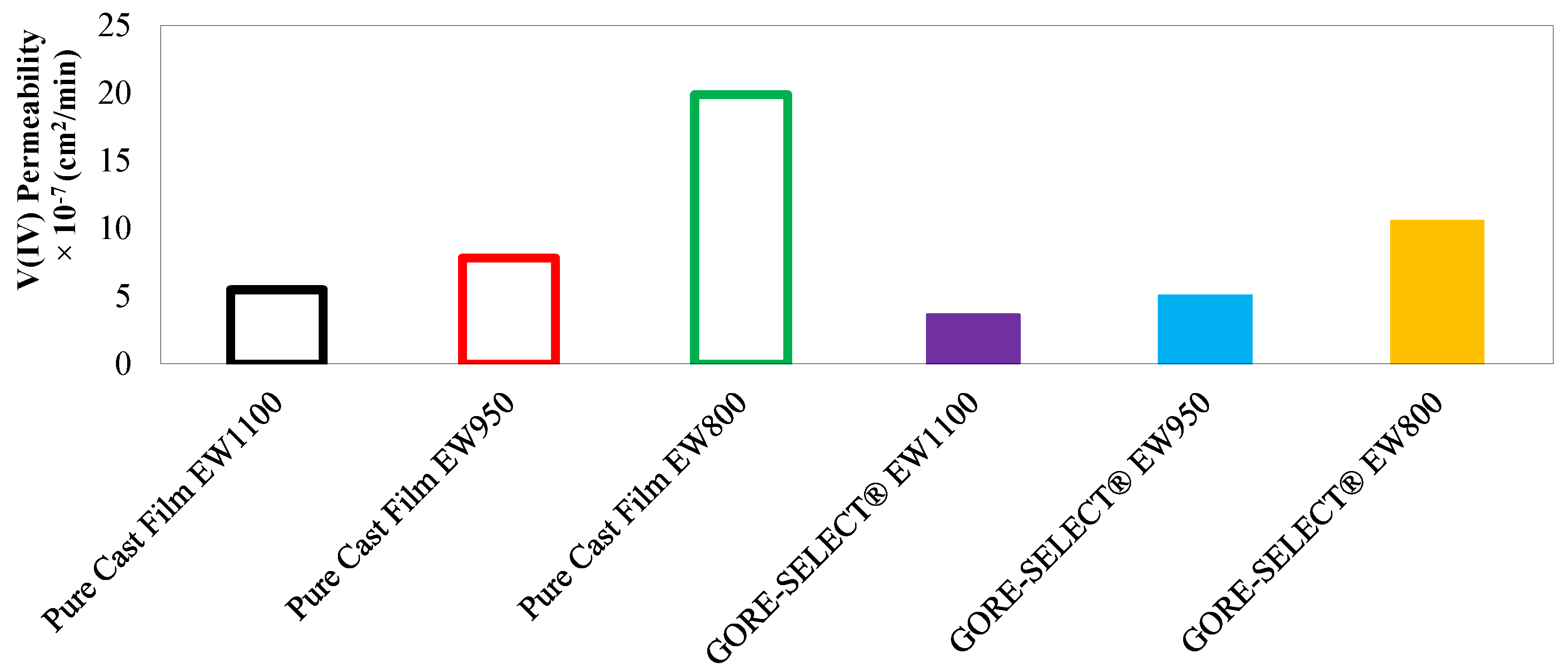
4.2. Crossover of Vanadium Ions
5. Summary and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Volume of the vanadium-deficient electrolyte (m3) | |
| Concentration of V(IV) ion in vanadium-deficient electrolyte (mol/m3) | |
| Concentration of V(IV) ion in vanadium-enriched electrolyte (mol/m3) | |
| Permeability of V(IV) ion through membrane m (m2/s) | |
| Thickness of ion-exchange membrane (m) | |
| Area of the ion-exchange membrane (m2) | |
| Diffusive transport parameter of V(IV) ion through membrane m (m/s) |
References
- Weber, A.Z.; Mench, M.M.; Meyers, J.P.; Ross, P.N.; Gostick, J.T.; Liu, Q. Redox flow batteries: A review. J. Appl. Electrochem. 2011, 41, 1137–1164. [Google Scholar] [CrossRef]
- Aaron, D.S.; Liu, Q.; Tang, Z.; Grim, G.; Papandrew, A.; Turhan, A.; Zawodzinski, T.A.; Mench, M.M. Dramatic performance gains in vanadium redox flow batteries through modified cell architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
- Sum, E.; Skyllas-Kazacos, M. A study of the V(II)/V(III) redox couple for redox flow cell applications. J. Power Sources 1985, 15, 179–190. [Google Scholar] [CrossRef]
- Sum, E.; Rychcik, M.; Skyllas-Kazacos, M. Investigation of the V(V)/V(IV) system for use in the positive half-cell of a redox battery. J. Power Sources 1985, 16, 85–95. [Google Scholar] [CrossRef]
- Pezeshki, A.M.; Clement, J.T.; Veith, G.M.; Zawodzinski, T.A.; Mench, M.M. High performance electrodes in vanadium redox flow batteries through oxygen-enriched thermal activation. J. Power Sources 2015, 294, 333–338. [Google Scholar] [CrossRef]
- Dennison, C.; Agar, E.; Akuzum, B.; Kumbur, E. Enhancing mass transport in redox flow batteries by tailoring flow field and electrode design. J. Electrochem. Soc. 2016, 163, A5163–A5169. [Google Scholar] [CrossRef]
- Li, L.; Kim, S.; Wang, W.; Vijayakumar, M.; Nie, Z.; Chen, B.; Zhang, J.; Xia, G.; Hu, J.; Graff, G. A stable vanadium redox-flow battery with high energy density for large-scale energy storage. Adv. Energy Mater. 2011, 1, 394–400. [Google Scholar] [CrossRef]
- Leung, P.; Li, X.; de León, C.P.; Berlouis, L.; Low, C.J.; Walsh, F.C. Progress in redox flow batteries, remaining challenges and their applications in energy storage. RSC Adv. 2012, 2, 10125–10156. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Chakrabarti, M.; Hajimolana, S.; Mjalli, F.; Saleem, M. Progress in flow battery research and development. J. Electrochem. Soc. 2011, 158, R55–R79. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, Y.; Zhu, X.; Wei, L.; Zhao, T.S. A high-performance dual-scale porous electrode for vanadium redox flow batteries. J. Power Sources 2016, 325, 329–336. [Google Scholar] [CrossRef]
- Derr, I.; Fetyan, A.; Schutjajew, K.; Roth, C. Electrochemical analysis of the performance loss in all vanadium redox flow batteries using different cut-off voltages. Electrochim. Acta 2016, 224, 9–16. [Google Scholar] [CrossRef]
- Pezeshki, A.M.; Sacci, R.L.; Veith, G.M.; Zawodzinski, T.A.; Mench, M.M. The cell-in-series method: A technique for accelerated electrode degradation in redox flow batteries. J. Electrochem. Soc. 2016, 163, A5202–A5210. [Google Scholar] [CrossRef]
- Knehr, K.; Agar, E.; Dennison, C.; Kalidindi, A.; Kumbur, E. A transient vanadium flow battery model incorporating vanadium crossover and water transport through the membrane. J. Electrochem. Soc. 2012, 159, A1446–A1459. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Dynamic modelling of the effects of ion diffusion and side reactions on the capacity loss for vanadium redox flow battery. J. Power Sources 2011, 196, 10737–10747. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Aaron, D.S.; Mench, M.M. Coupled membrane transport parameters for ionic species in all-vanadium redox flow batteries. Electrochim. Acta 2016, 218, 174–190. [Google Scholar] [CrossRef]
- Wiedemann, E.; Heintz, A.; Lichtenthaler, R. Transport properties of vanadium ions in cation exchange membranes: Determination of diffusion coefficients using a dialysis cell. J. Membr. Sci. 1998, 141, 215–221. [Google Scholar] [CrossRef]
- Sun, C.; Chen, J.; Zhang, H.; Han, X.; Luo, Q. Investigations on transfer of water and vanadium ions across nafion membrane in an operating vanadium redox flow battery. J. Power Sources 2010, 195, 890–897. [Google Scholar] [CrossRef]
- Xi, J.; Wu, Z.; Qiu, X.; Chen, L. Nafion/SiO2 hybrid membrane for vanadium redox flow battery. J. Power Sources 2007, 166, 531–536. [Google Scholar] [CrossRef]
- Xie, W.; Darling, R.M.; Perry, M.L. Processing and pretreatment effects on vanadium transport in nafion membranes. J. Electrochem. Soc. 2016, 163, A5084–A5089. [Google Scholar] [CrossRef]
- Yang, X.-G.; Ye, Q.; Cheng, P.; Zhao, T.S. Effects of the electric field on ion crossover in vanadium redox flow batteries. Appl. Energy 2015, 145, 306–319. [Google Scholar] [CrossRef]
- Darling, R.M.; Weber, A.Z.; Tucker, M.C.; Perry, M.L. The influence of electric field on crossover in redox-flow batteries. J. Electrochem. Soc. 2016, 163, A5014–A5022. [Google Scholar] [CrossRef]
- Lawton, J.S.; Jones, A.; Zawodzinski, T. Concentration dependence of VO2+ crossover of nafion for vanadium redox flow batteries. J. Electrochem. Soc. 2013, 160, A697–A702. [Google Scholar] [CrossRef]
- Elgammal, R.A.; Tang, Z.; Sun, C.-N.; Lawton, J.; Zawodzinski, T.A. Species uptake and mass transport in membranes for vanadium redox flow batteries. Electrochim. Acta 2017, 237, 1–11. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Zawodzinski, T.A.; Mench, M.M. Concentrated solution model of transport in all vanadium redox flow battery membrane separator. ECS Trans. 2014, 61, 23–32. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Edmundson, M.D.; Busby, F.C.; Mench, M.M. Water management in polymer electrolyte fuel cells through asymmetric thermal and mass transport engineering of the micro-porous layers. J. Electrochem. Soc. 2016, 163, F933–F944. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Mench, M.M. Assessing the limits of water management using asymmetric micro-porous layer configurations. ECS Trans. 2013, 58, 1375–1382. [Google Scholar] [CrossRef]
- Ashraf Gandomi, Y.; Aaron, D.S.; Zawodzinski, T.A.; Mench, M.M. In situ potential distribution measurement and validated model for all-vanadium redox flow battery. J. Electrochem. Soc. 2016, 163, A5188–A5201. [Google Scholar] [CrossRef]
- Won, S.; Oh, K.; Ju, H. Numerical analysis of vanadium crossover effects in all-vanadium redox flow batteries. Electrochim. Acta 2015, 177, 310–320. [Google Scholar] [CrossRef]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A critical review of modeling transport phenomena in polymer-electrolyte fuel cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Darling, R.; Gallagher, K.; Xie, W.; Su, L.; Brushett, F. Transport property requirements for flow battery separators. J. Electrochem. Soc. 2016, 163, A5029–A5040. [Google Scholar] [CrossRef]
- Luo, J.; Conrad, O.; Vankelecom, I.F.J. Imidazolium methanesulfonate as a high temperature proton conductor. J. Mater. Chem. A 2013, 1, 2238–2247. [Google Scholar] [CrossRef]
- Luo, J.; Conrad, O.; Vankelecom, I.F.J. Physicochemical properties of phosphonium-based and ammonium-based protic ionic liquids. J. Mater. Chem. 2012, 22, 20574–20579. [Google Scholar] [CrossRef]
- Viswanathan, V.; Crawford, A.; Stephenson, D.; Kim, S.; Wang, W.; Li, B.; Coffey, G.; Thomsen, E.; Graff, G.; Balducci, P.; et al. Cost and performance model for redox flow batteries. J. Power Sources 2014, 247, 1040–1051. [Google Scholar] [CrossRef]
- Darling, R.M.; Gallagher, K.G.; Kowalski, J.A.; Ha, S.; Brushett, F.R. Pathways to low-cost electrochemical energy storage: A comparison of aqueous and nonaqueous flow batteries. Energy Environ. Sci. 2014, 7, 3459–3477. [Google Scholar] [CrossRef]
- Luo, Q.; Li, L.; Nie, Z.; Wang, W.; Wei, X.; Li, B.; Chen, B.; Yang, Z. In-situ investigation of vanadium ion transport in redox flow battery. J. Power Sources 2012, 218, 15–20. [Google Scholar] [CrossRef]
- De Leon, C.P.; Frías-Ferrer, A.; González-García, J.; Szánto, D.; Walsh, F.C. Redox flow cells for energy conversion. J. Power Sources 2006, 160, 716–732. [Google Scholar] [CrossRef]
- Sepehr, F. Multiscale modeling of electrolytes for energy storage and conversion. Univ. Tenn. 2016, 92. Available online: http://trace.tennessee.edu/utk_graddiss/4165 (accessed on 11 February 2017).
- Humplik, T.; Lee, J.; O’hern, S.; Fellman, B.; Baig, M.; Hassan, S.; Atieh, M.; Rahman, F.; Laoui, T.; Karnik, R. Nanostructured materials for water desalination. Nanotechnology 2011, 22, 292001. [Google Scholar] [CrossRef] [PubMed]
- Humplik, T.; Raj, R.; Maroo, S.C.; Laoui, T.; Wang, E.N. Effect of hydrophilic defects on water transport in MFI zeolites. Langmuir 2014, 30, 6446–6453. [Google Scholar] [CrossRef] [PubMed]
- Fasano, M.; Humplik, T.; Bevilacqua, A.; Tsapatsis, M.; Chiavazzo, E.; Wang, E.N.; Asinari, P. Interplay between hydrophilicity and surface barriers on water transport in zeolite membranes. Nat. Commun. 2016, 7, 12762. [Google Scholar] [CrossRef] [PubMed]
- Yousefzadi Nobakht, A.; Shin, S. Anisotropic control of thermal transport in graphene/Si heterostructures. J. Appl. Phys. 2016, 120. [Google Scholar] [CrossRef]
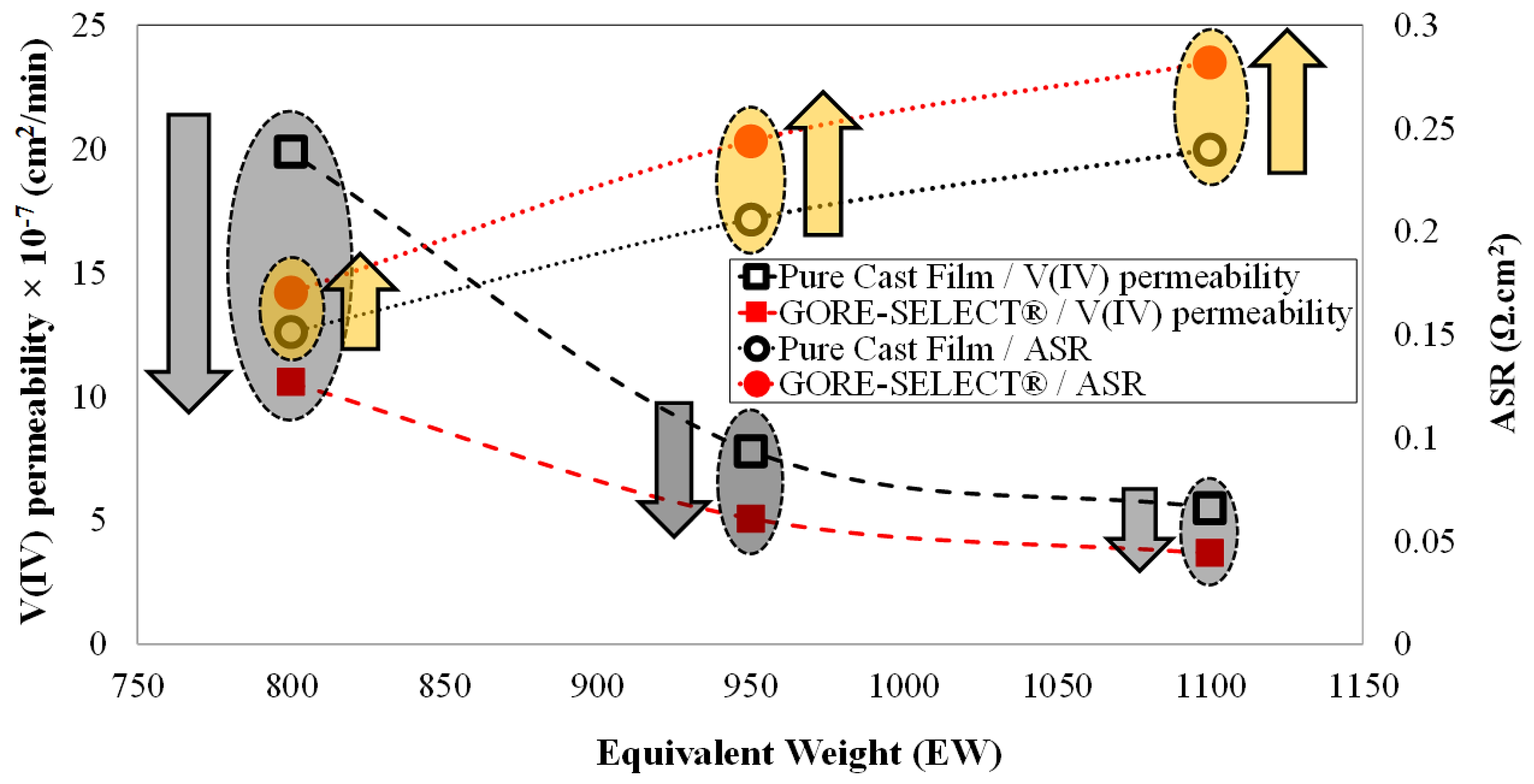
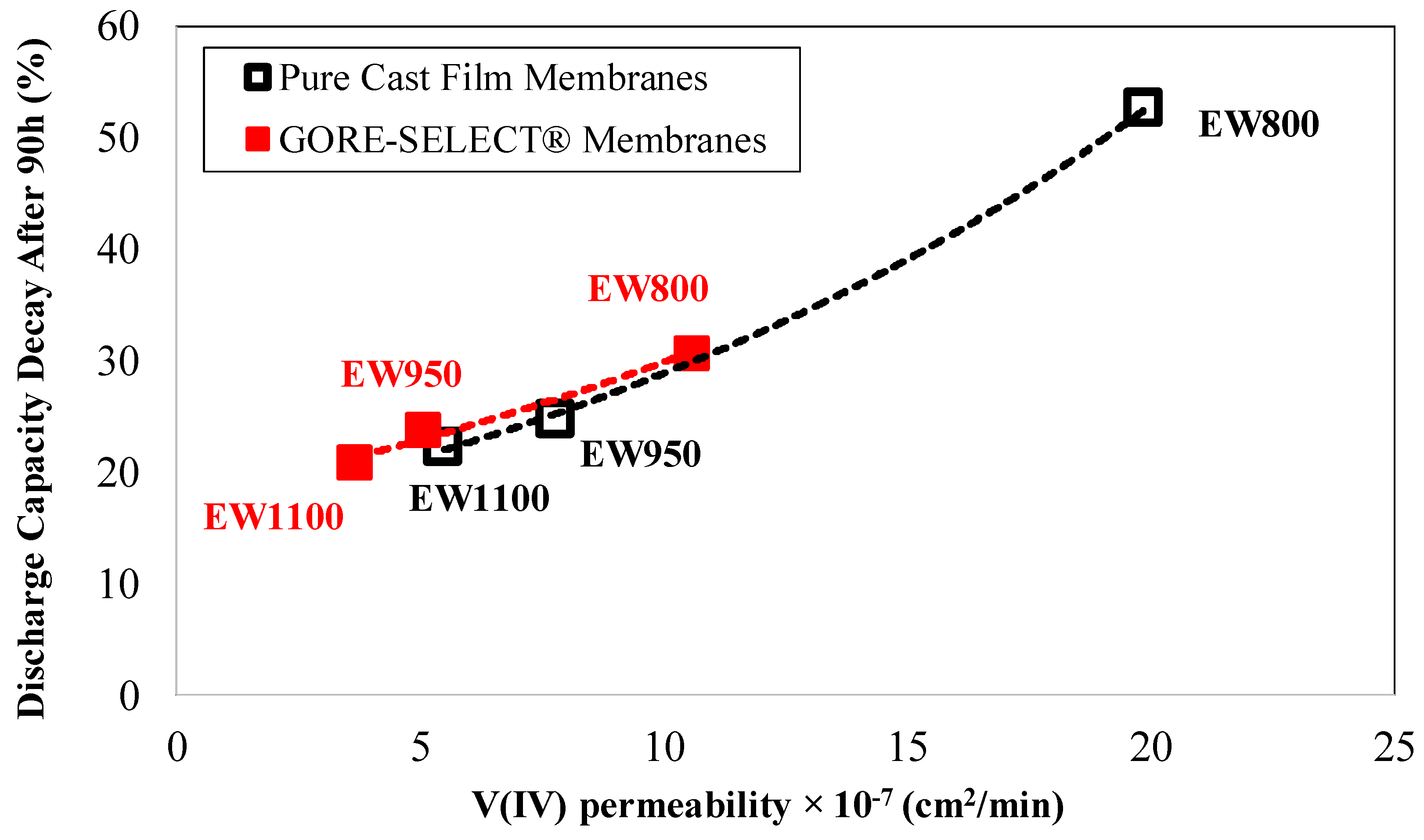
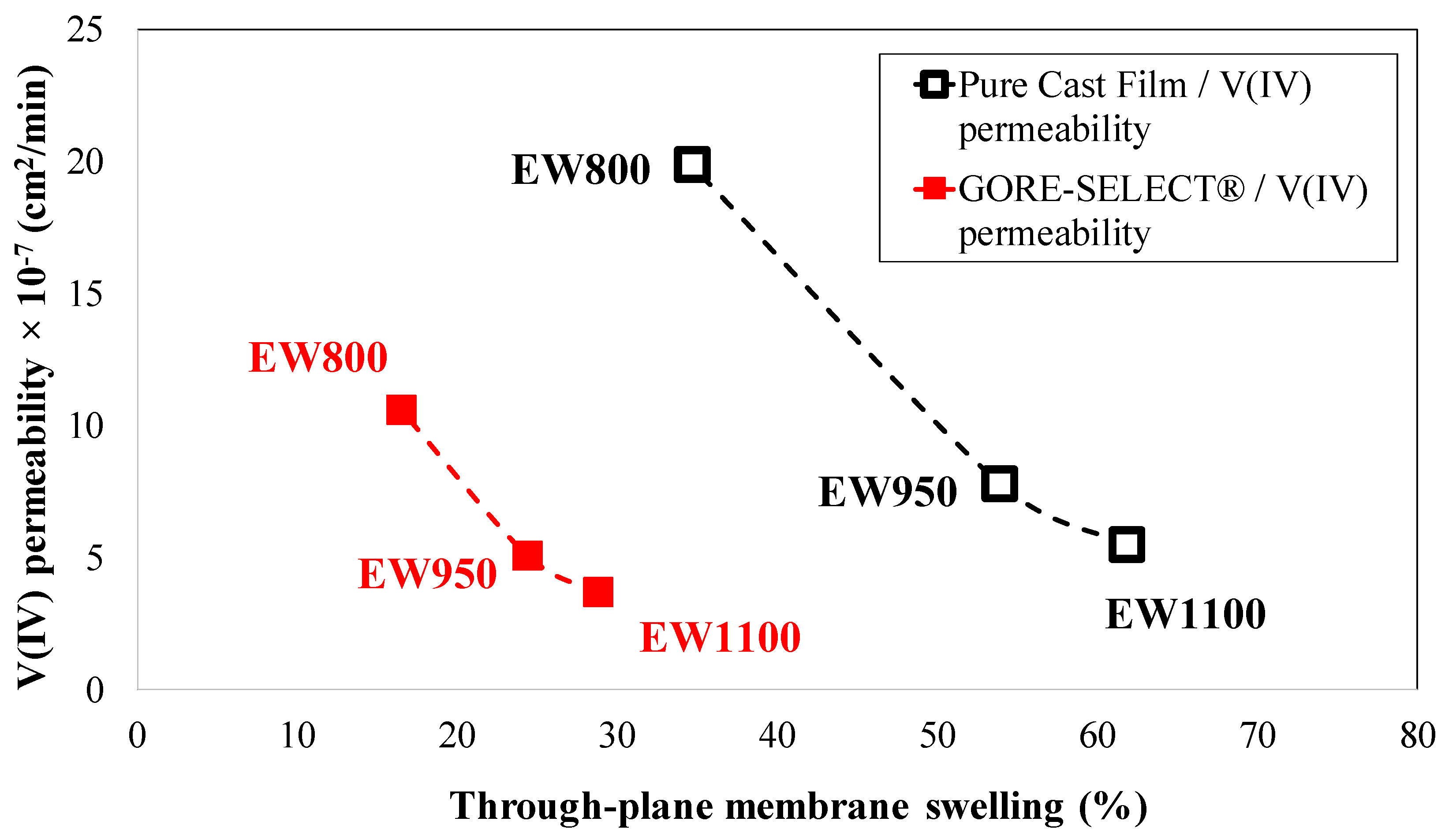
| Membrane Type | Initial ASR (Ω·cm2) | Relative Increase in ASR (%) | Initial Ohmic Overpotential at 100 mA·cm−2 (mV) | Increase in Ohmic Overpotential at 100 mA·cm−2 during 30 Cycles (mV) |
|---|---|---|---|---|
| Pure Cast Film EW1100 | 0.240 | 14.17 | 24.0 | 3.41 |
| Pure Cast Film EW950 | 0.206 | 14.08 | 20.6 | 2.94 |
| Pure Cast Film EW800 | 0.151 | 17.88 | 15.1 | 2.74 |
| GORE-SELECT® EW1100 | 0.282 | 16.67 | 28.2 | 4.66 |
| GORE-SELECT® EW950 | 0.244 | 12.70 | 24.4 | 3.11 |
| GORE-SELECT® EW800 | 0.171 | 16.96 | 17.1 | 2.93 |
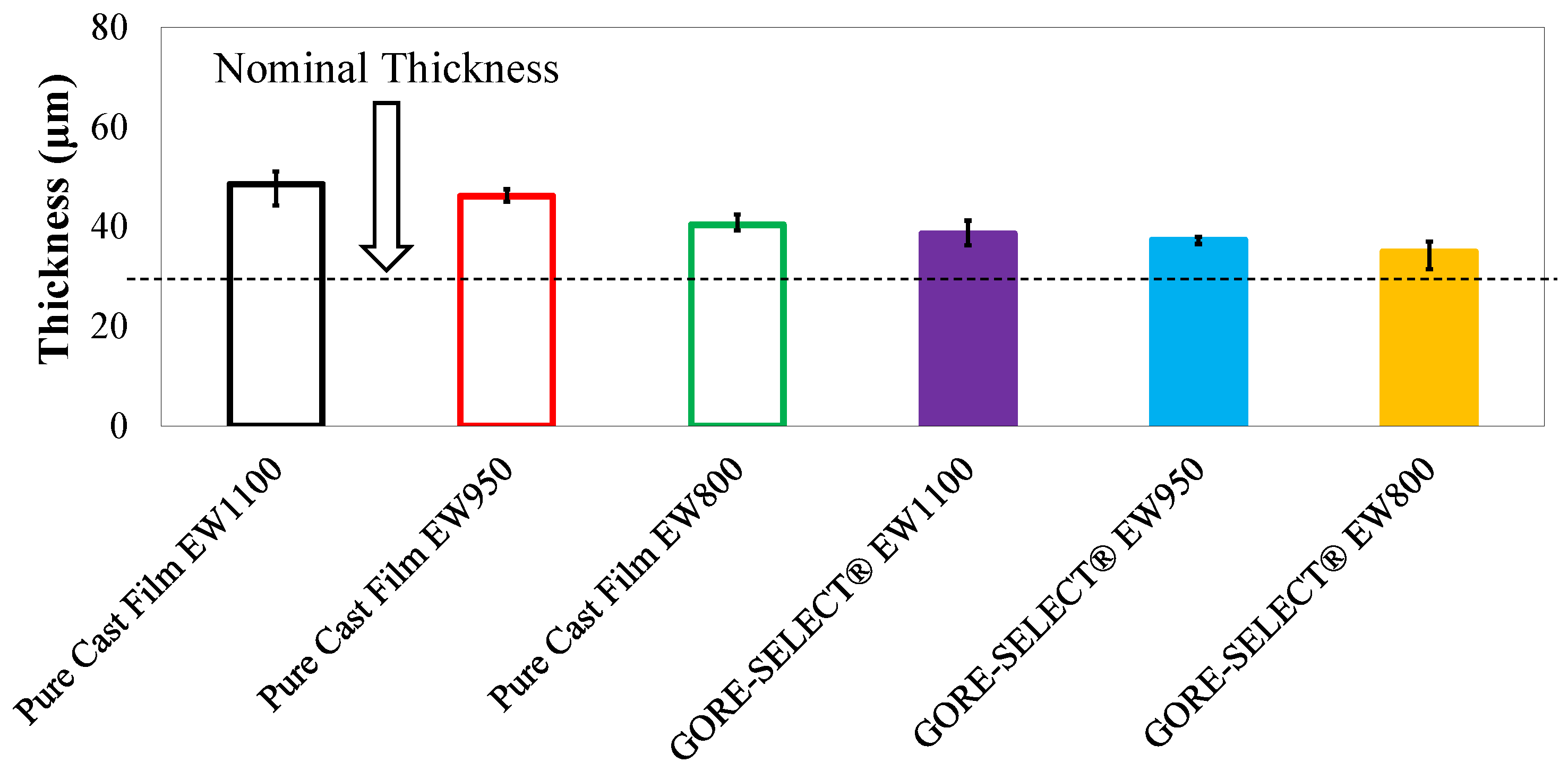
| Membrane Type | Manufacturing Details | Nominal Thickness (μm) | Average Thickness after Soak (μm) | Through-Plane Swelling (%) |
|---|---|---|---|---|
| Pure Cast Film EW1100 | Cast film | 30 | 49 | 62 |
| Pure Cast Film EW950 | Cast film | 30 | 46 | 54 |
| Pure Cast Film EW800 | Cast film | 30 | 40 | 35 |
| GORE-SELECT® EW1100 | Reinforced | 30 | 39 | 29 |
| GORE-SELECT® EW950 | Reinforced | 30 | 37 | 24 |
| GORE-SELECT® EW800 | Reinforced | 30 | 35 | 16 |
| Membrane Type | ||
|---|---|---|
| Pure Cast Film EW1100 | 5.49 | 1131 |
| Pure Cast Film EW950 | 7.80 | 1689 |
| Pure Cast Film EW800 | 19.87 | 4919 |
| GORE-SELECT® EW1100 | 3.66 | 948 |
| GORE-SELECT® EW950 | 5.08 | 1361 |
| GORE-SELECT® EW800 | 10.59 | 3029 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf Gandomi, Y.; Aaron, D.S.; Mench, M.M. Influence of Membrane Equivalent Weight and Reinforcement on Ionic Species Crossover in All-Vanadium Redox Flow Batteries. Membranes 2017, 7, 29. https://doi.org/10.3390/membranes7020029
Ashraf Gandomi Y, Aaron DS, Mench MM. Influence of Membrane Equivalent Weight and Reinforcement on Ionic Species Crossover in All-Vanadium Redox Flow Batteries. Membranes. 2017; 7(2):29. https://doi.org/10.3390/membranes7020029
Chicago/Turabian StyleAshraf Gandomi, Yasser, Doug S. Aaron, and Matthew M. Mench. 2017. "Influence of Membrane Equivalent Weight and Reinforcement on Ionic Species Crossover in All-Vanadium Redox Flow Batteries" Membranes 7, no. 2: 29. https://doi.org/10.3390/membranes7020029
APA StyleAshraf Gandomi, Y., Aaron, D. S., & Mench, M. M. (2017). Influence of Membrane Equivalent Weight and Reinforcement on Ionic Species Crossover in All-Vanadium Redox Flow Batteries. Membranes, 7(2), 29. https://doi.org/10.3390/membranes7020029






