Experimental Investigation into the Transmembrane Electrical Potential of the Forward Osmosis Membrane Process in Electrolyte Solutions
Abstract
:1. Introduction
2. Results and Discussion
2.1. Influence of Membrane Orientation

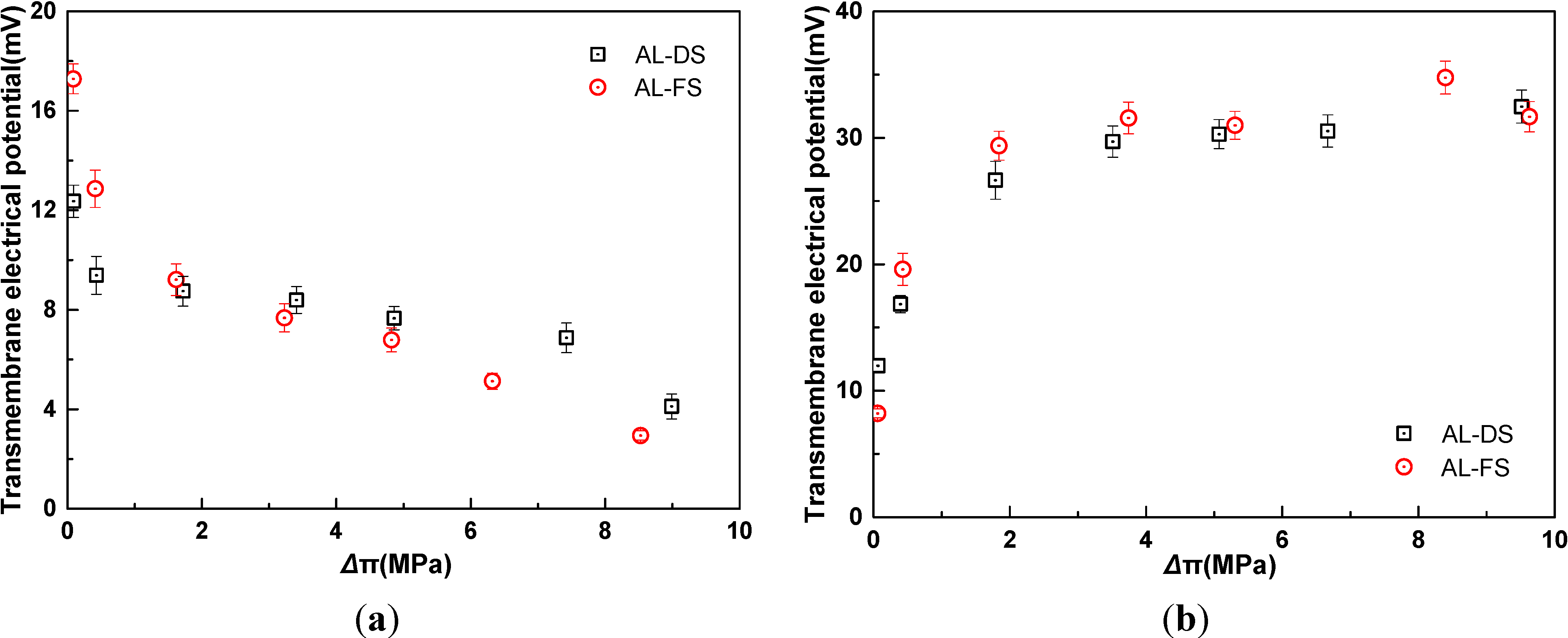
2.2. Influence of Solution Concentration Ratio

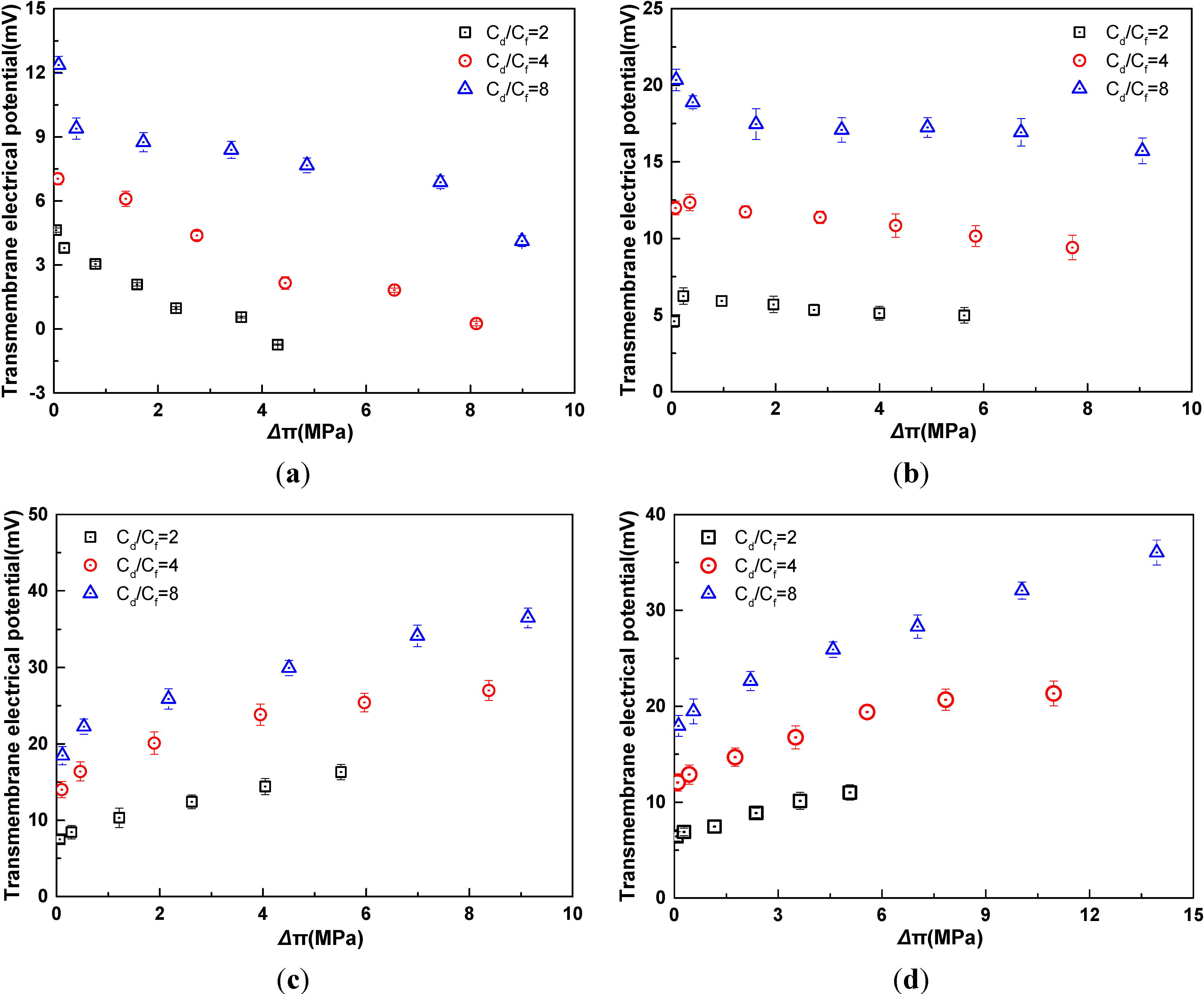
2.3. Influence of Electrolyte Species

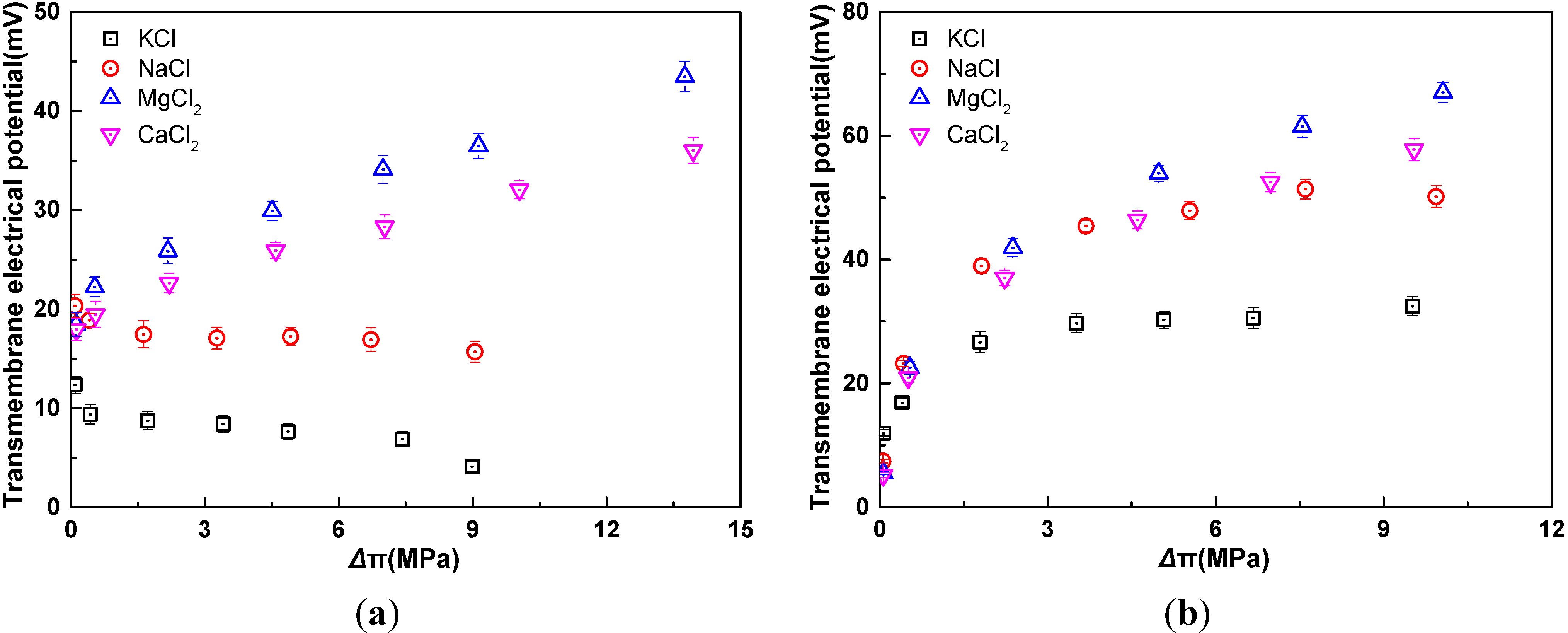
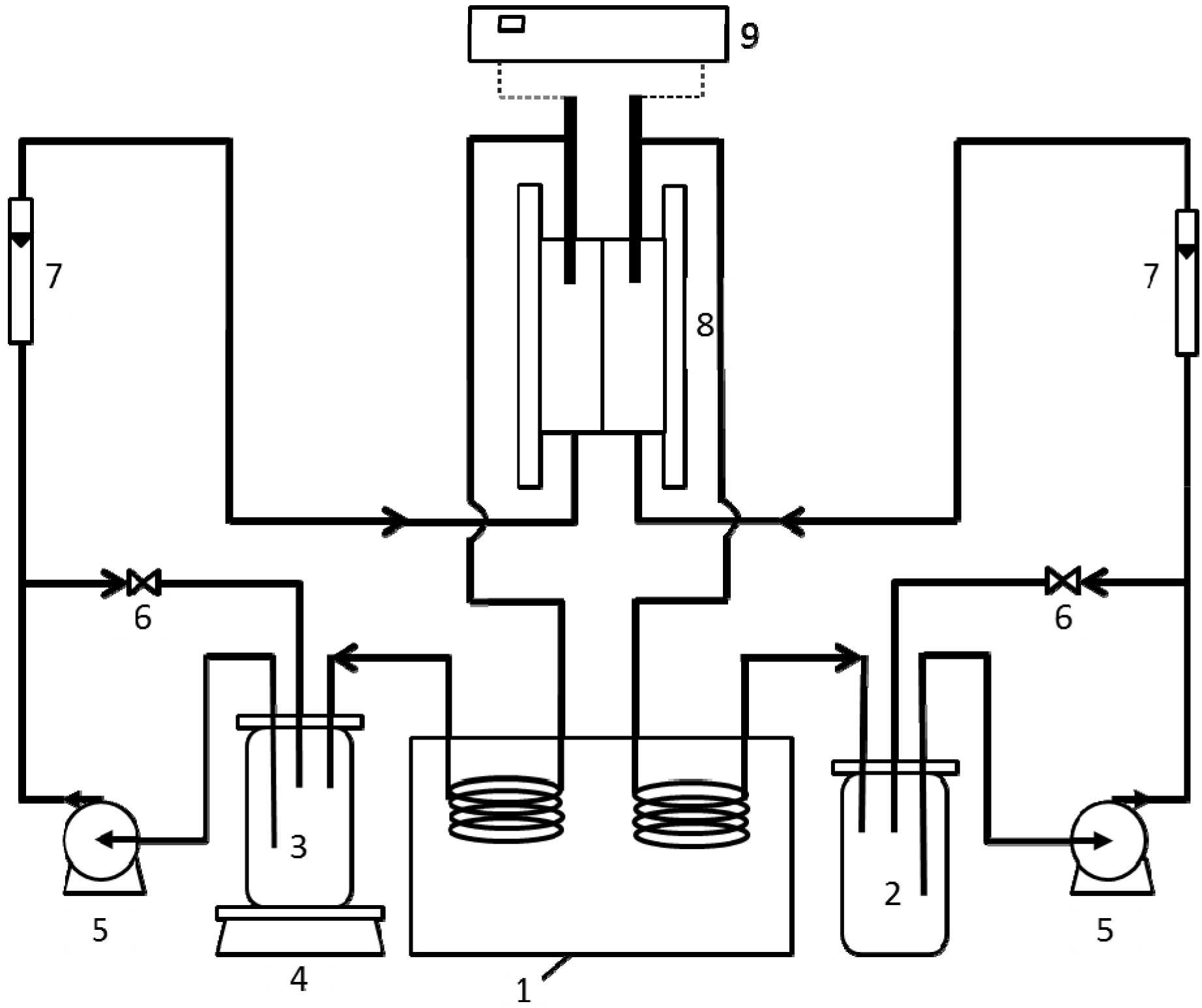
3. Experimental Section
3.1. Membrane and Chemicals
3.2. Water Flux and TMEP Measurements
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Zhao, S.F.; Zou, L.; Tang, C.Y.Y.; Mulcahy, D. Recent developments in forward osmosis: Opportunities and challenges. J. Membr. Sci. 2012, 396, 1–21. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Desalination by ammonia-carbon dioxide forward osmosis: Influence of draw and feed solution concentrations on process performance. J. Membr. Sci. 2006, 278, 114–123. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; McGinnis, R.L.; Elimelech, M. A novel ammonia-carbon dioxide forward (direct) osmosis desalination process. Desalination 2005, 174, 1–11. [Google Scholar] [CrossRef]
- Sim, V.S.T.; She, Q.H.; Chong, T.H.; Tang, C.Y.Y.; Fane, A.G.; Krantz, W.B. Strategic co-location in a hybrid process involving desalination and pressure retarded osmosis (PRO). Membranes 2013, 3, 98–125. [Google Scholar] [CrossRef] [Green Version]
- Holloway, R.W.; Childress, A.E.; Dennett, K.E.; Cath, T.Y. Forward osmosis for concentration of anaerobic digester centrate. Water Res. 2007, 41, 4005–4014. [Google Scholar] [CrossRef]
- Achilli, A.; Cath, T.Y.; Marchand, E.A.; Childress, A.E. The forward osmosis membrane bioreactor: A low fouling alternative to MBR processes. Desalination 2009, 239, 10–21. [Google Scholar] [CrossRef]
- Xiao, D.; Tang, C.Y.; Zhang, J.; Lay, W.C.L.; Wang, R.; Fane, A.G. Modeling salt accumulation in osmotic membrane bioreactors: Implications for FO membrane selection and system operation. J. Membr. Sci. 2011, 366, 314–324. [Google Scholar] [CrossRef]
- Hancock, N.T.; Black, N.D.; Cath, T.Y. A comparative life cycle assessment of hybrid osmotic dilution desalination and established seawater desalination and wastewater reclamation processes. Water Res. 2012, 46, 1145–1154. [Google Scholar] [CrossRef]
- Xie, M.; Nghiem, L.D.; Price, W.E.; Elimelech, M. Comparison of the removal of hydrophobic trace organic contaminants by forward osmosis and reverse osmosis. Water Res. 2012, 46, 2683–2692. [Google Scholar] [CrossRef]
- Petrotos, K.B.; Quantick, P.; Petropakis, H. A study of the direct osmotic concentration of tomato juice in tubular membrane-module configuration. I. The effect of certain basic process parameters on the process performance. J. Membr. Sci. 1998, 150, 99–110. [Google Scholar] [CrossRef]
- Petrotos, K.B.; Lazarides, H.N. Osmotic concentration of liquid foods. J. Food Eng. 2001, 49, 201–206. [Google Scholar] [CrossRef]
- Jiao, B.; Cassano, A.; Drioli, E. Recent advances on membrane processes for the concentration of fruit juices: A review. J. Food Eng. 2004, 63, 303–324. [Google Scholar] [CrossRef]
- Lee, K.L.; Baker, R.W.; Lonsdale, H.K. Membrane for power-generation by pressure-retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Loeb, S. Energy production at the Dead Sea by pressure-retarded osmosis: Challenge or chimera? Desalination 1998, 120, 247–262. [Google Scholar] [CrossRef]
- Loeb, S. One hundred and thirty benign and renewable megawatts from Great Salt Lake? The possibilities of hydroelectric power by pressure-retarded osmosis with spiral module membranes. Desalination 2001, 141, 85–91. [Google Scholar] [CrossRef]
- Loeb, S. Large-scale power production by pressure-retarded osmosis, using river water and sea water passing through spiral modules. Desalination 2002, 143, 115–122. [Google Scholar] [CrossRef]
- Gray, G.T.; McCutcheon, J.R.; Elimelech, M. International concentration polarization in forward osmosis: Role of membrane orientation. Desalination 2006, 197, 1–8. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Influence of membrane support layer hydrophobicity on water flux in osmotically driven membrane processes. J. Membr. Sci. 2008, 318, 458–466. [Google Scholar] [CrossRef]
- Qin, J.H.; Chen, S.; Oo, M.H.; Kekre, K.A.; Cornelissen, E.R.; Ruiken, C.J. Experimental studies and modeling on concentration polarization in forward osmosis. Water Sci. Technol. 2010, 61, 2897–2904. [Google Scholar] [CrossRef]
- Tan, C.H.; Ng, H.Y. Modified models to predict flux behavior in forward osmosis in consideration of external and internal concentration polarizations. J. Membr. Sci. 2008, 324, 209–219. [Google Scholar] [CrossRef]
- Hancock, N.T.; Cath, T.Y. Solute coupled diffusion in osmotically driven membrane processes. Environ. Sci. Technol. 2009, 43, 6769–6775. [Google Scholar] [CrossRef]
- Kim, C.; Lee, S.; Shon, H.K.; Elimelech, M.; Hong, S. Boron transport in forward osmosis: Measurements, mechanisms, and comparison with reverse osmosis. J. Membr. Sci. 2012, 419–420, 42–48. [Google Scholar] [CrossRef]
- Yaroshchuk, A.E.; Boiko, Y.P.; Makovetskiy, A.L. Filtration potential across membranes containing selective layers. Langmuir 2002, 18, 5154–5162. [Google Scholar] [CrossRef]
- Szymczyk, A.; Sbai, M.; Fievet, P. Analysis of the pressure-induced potential arising through composite membranes with surface layers. Langmuir 2005, 21, 1818–1826. [Google Scholar] [CrossRef]
- Tu, C.H.; Wang, H.L.; Wang, X.L. Study on transmembrane electrical potential of nanofiltration membranes in KCl and MgCl2 solutions. Langmuir 2010, 26, 17656–17664. [Google Scholar]
- Fang, Y.Y.; Bian, L.X.; Wang, X.L. Understanding membrane parameters of a forward osmosis membrane based on nonequilibrium thermodynamics. J. Membr. Sci. 2013, 437, 72–81. [Google Scholar] [CrossRef]
- Li, Y.H.; Gregory, S. Diffusion of ions in sea water and in deep-sea sediments. Geochim. Cosmochim. Acta 1974, 38, 703–714. [Google Scholar] [CrossRef]
- Shang, W.J.; Wang, X.L.; Yu, Y.X. Theoretical calculation on the membrane potential of charged porous membranes in 1-1, 1-2, 2-1 and 2-2 electrolyte solutions. J. Membr. Sci. 2006, 285, 362–375. [Google Scholar] [CrossRef]
- Hamer, W.J.; Wu, Y.C. Osmotic coefficients and mean activity coefficients of uni-univalent electrolytes in water at 25 °C. J. Phys. Chem. Data 1972, 1, 1047–1100. [Google Scholar] [CrossRef]
- Goldberg, R.N.; Nuttall, R.L. Evaluated activity and osmotic coefficients for aqueous solutions: The alkaline earth metal halides. J. Phys. Chem. Data 1978, 7, 263–310. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Influence of concentrative and dilutive internal concentration polarization on flux behavior in forward osmosis. J. Membr. Sci. 2006, 284, 237–247. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bian, L.; Fang, Y.; Wang, X. Experimental Investigation into the Transmembrane Electrical Potential of the Forward Osmosis Membrane Process in Electrolyte Solutions. Membranes 2014, 4, 275-286. https://doi.org/10.3390/membranes4020275
Bian L, Fang Y, Wang X. Experimental Investigation into the Transmembrane Electrical Potential of the Forward Osmosis Membrane Process in Electrolyte Solutions. Membranes. 2014; 4(2):275-286. https://doi.org/10.3390/membranes4020275
Chicago/Turabian StyleBian, Lixia, Yanyan Fang, and Xiaolin Wang. 2014. "Experimental Investigation into the Transmembrane Electrical Potential of the Forward Osmosis Membrane Process in Electrolyte Solutions" Membranes 4, no. 2: 275-286. https://doi.org/10.3390/membranes4020275




