Membrane Potential Generated by Ion Adsorption
Abstract
:1. Introduction
2. Experimental Section
2.1. Potential across the Anion Exchange Membrane
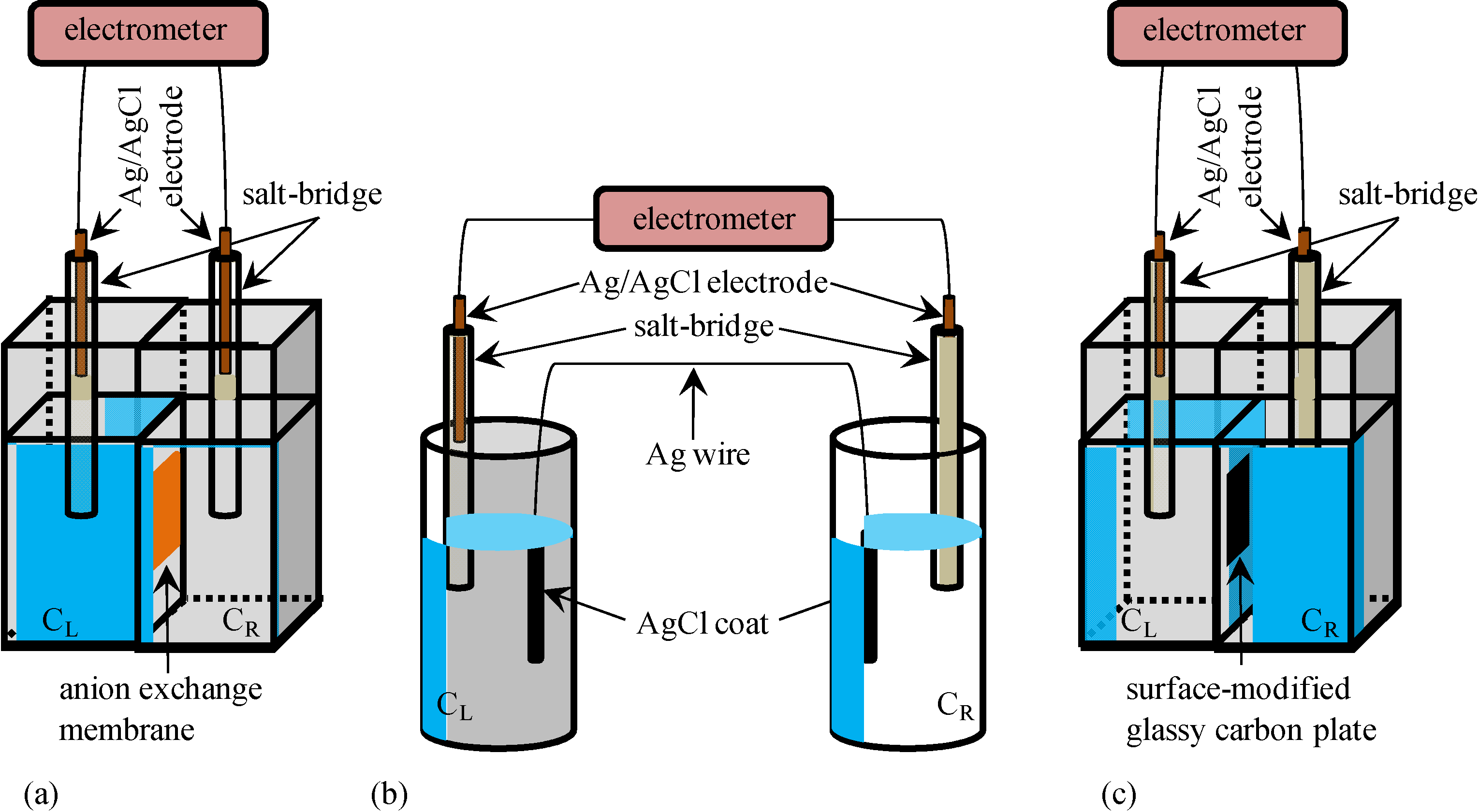
2.2. Potential across the Ag Wire Coated with AgCl

2.3. Potential across the Glassy Carbon Plate Covered with –COOH Groups
3. Results and Theoretical Analysis
3.1. Potential Generation across the Anion Exchange Membrane
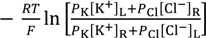
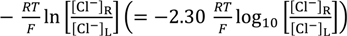
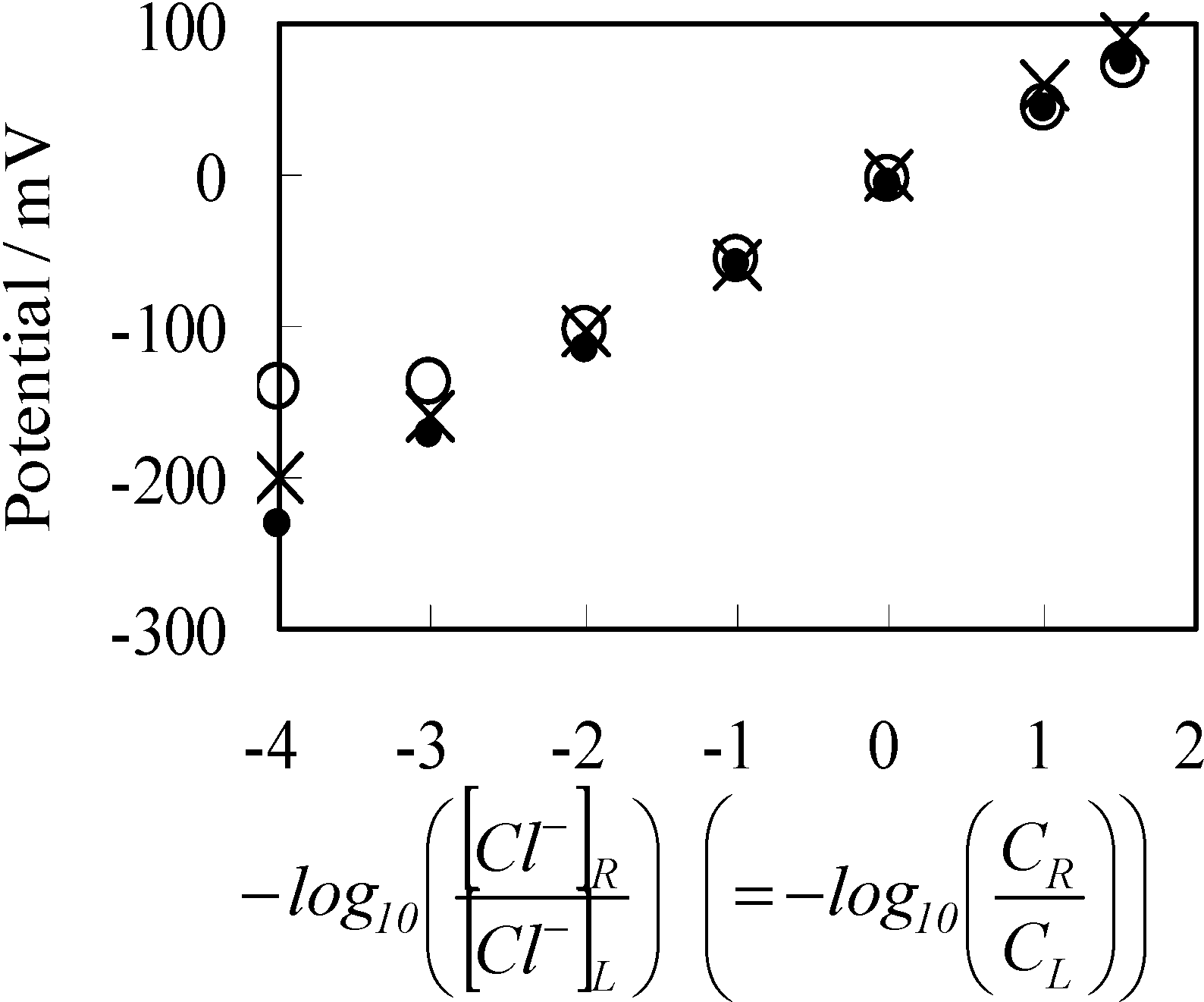
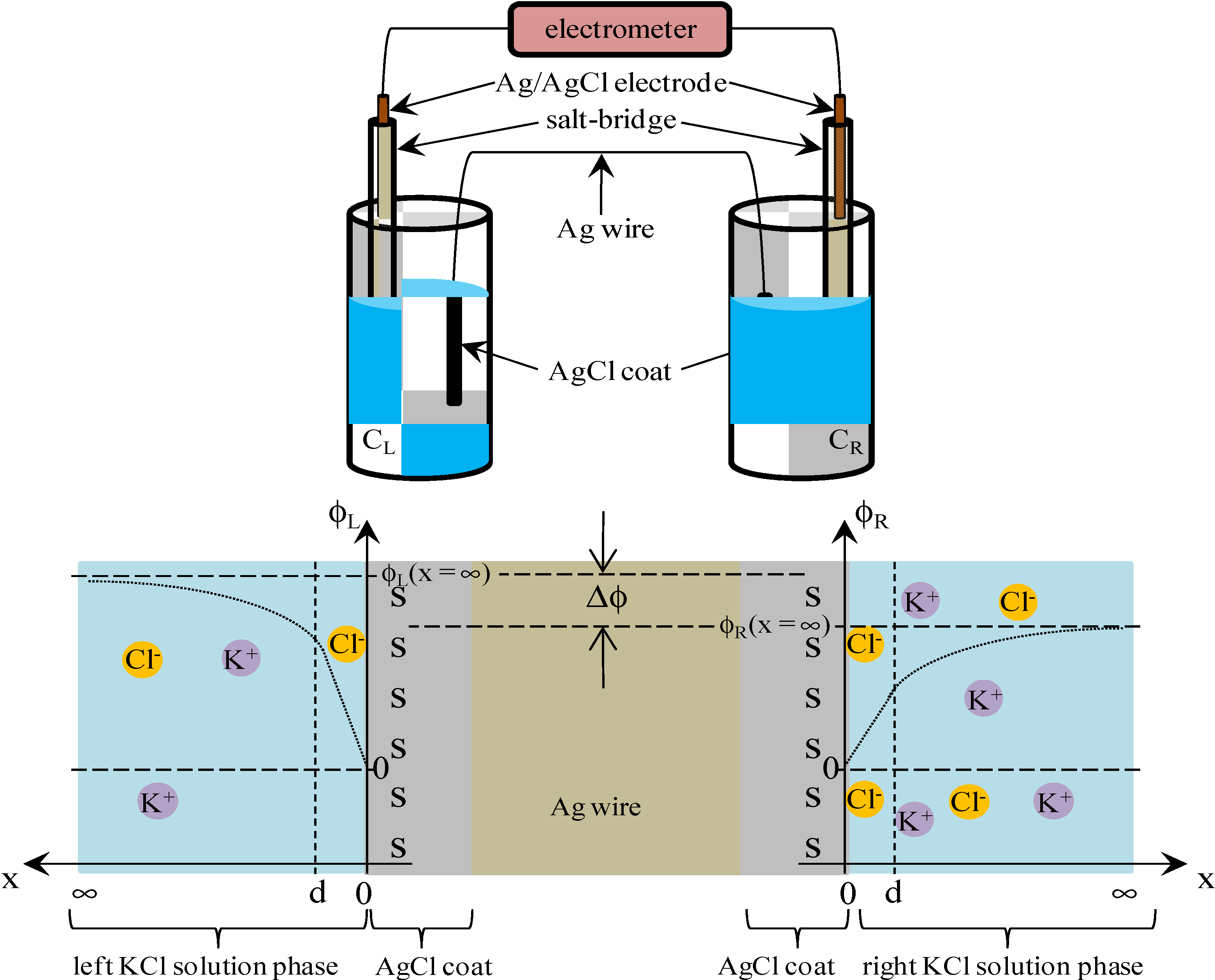
3.2. Potential Generation across the Ag Wire
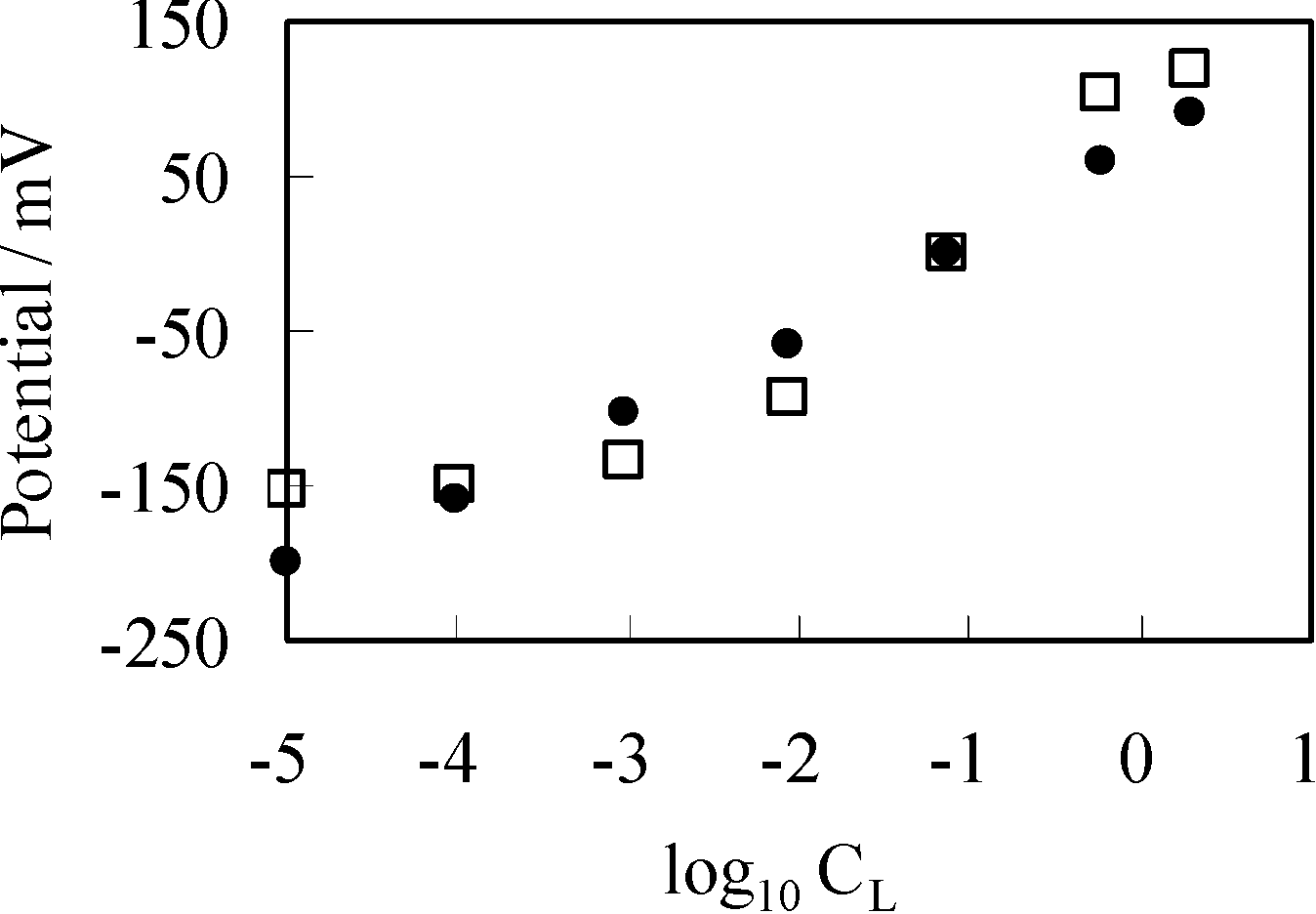
3.2.1. Experimental
3.2.2. Theoretical Analysis
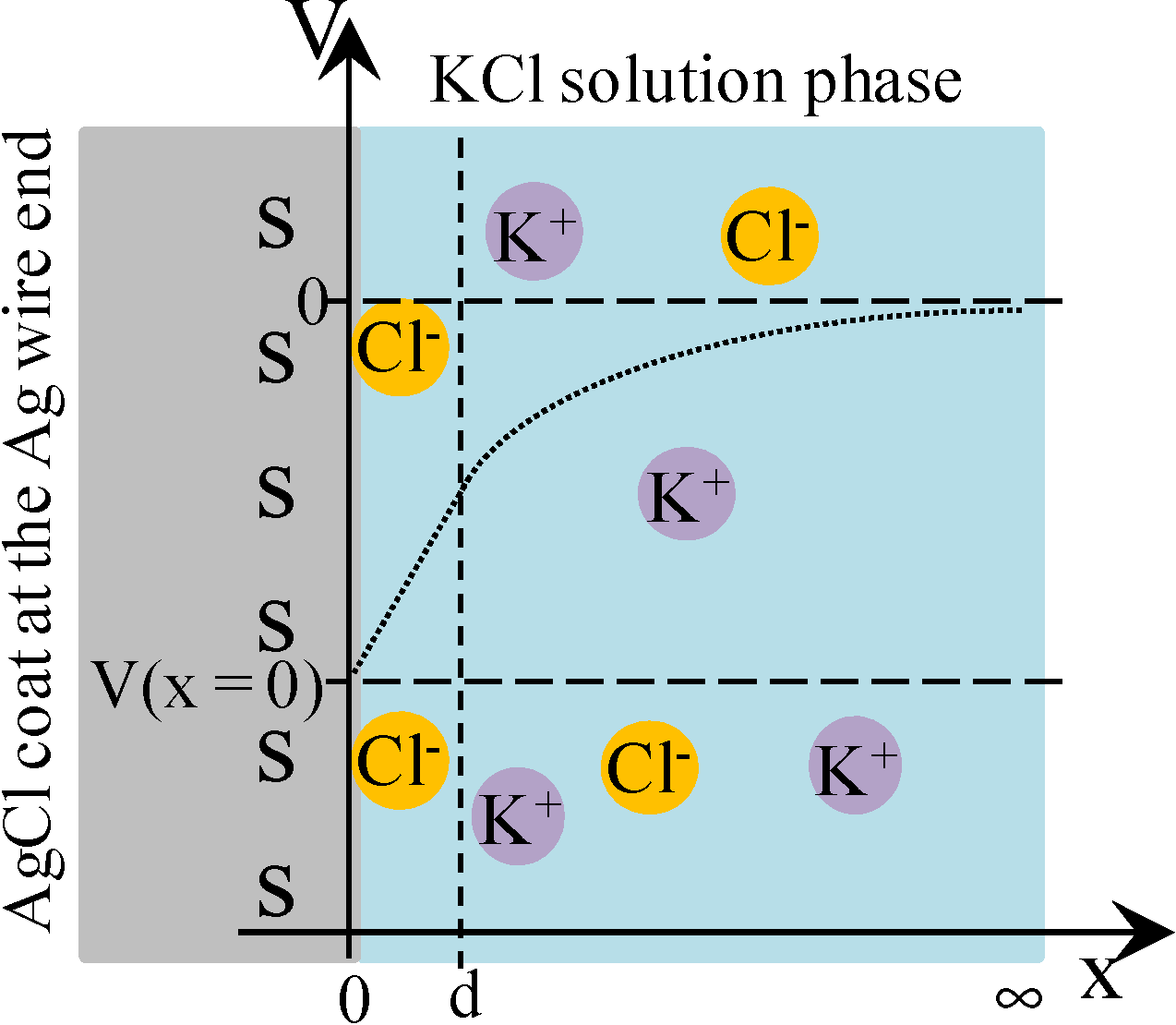
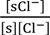
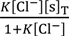
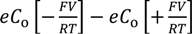
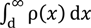 = 0
= 0
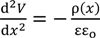
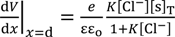
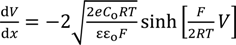
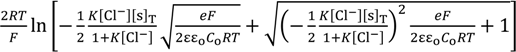
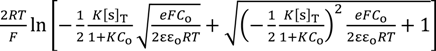
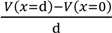 = Esur
= Esur
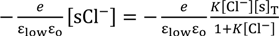
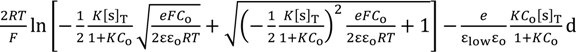

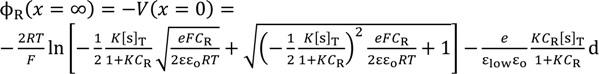
3.3. Potential Generation across the Glassy Carbon Plate
3.3.1. Experimental
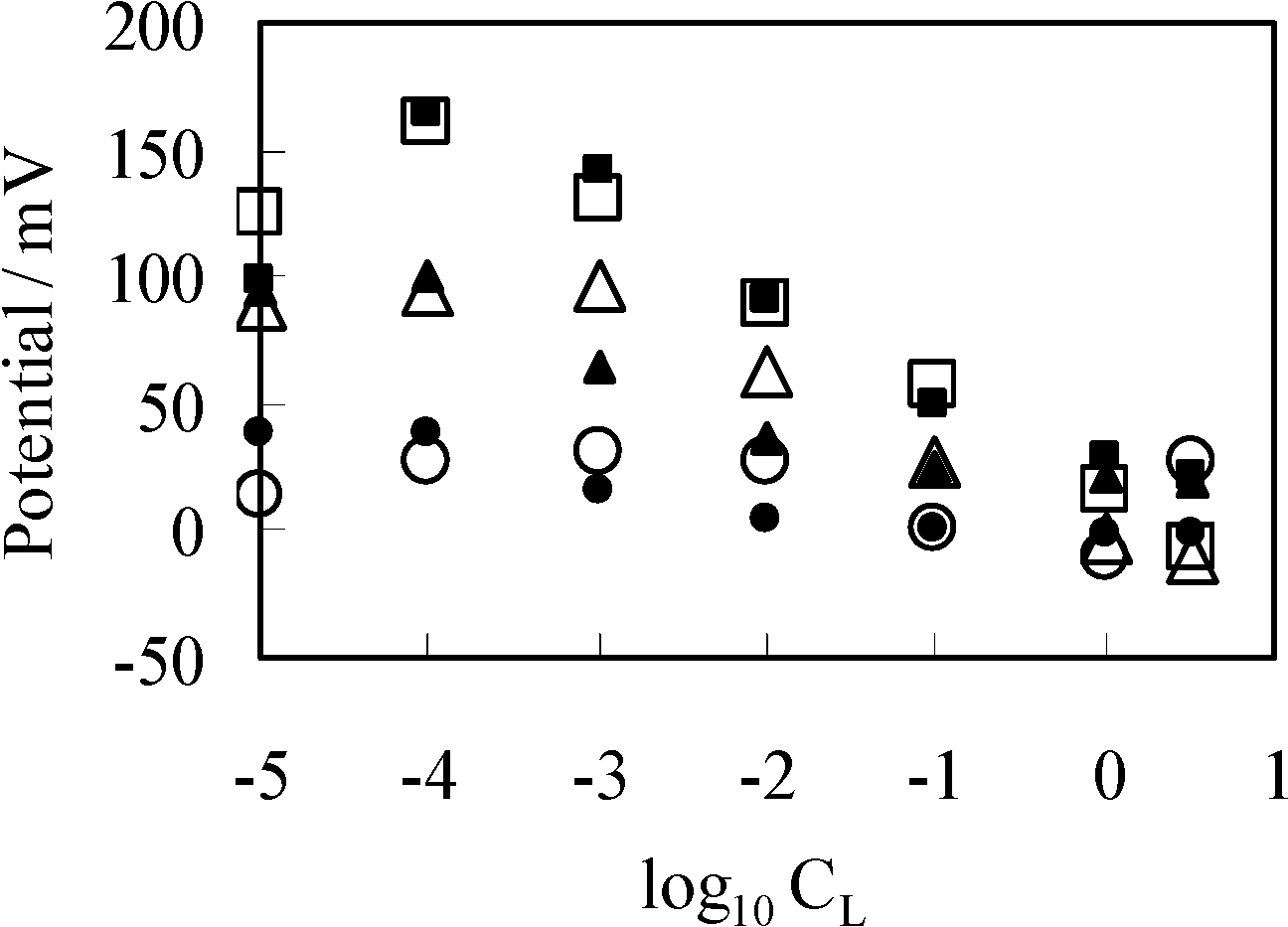
3.3.2. Theoretical Analysis
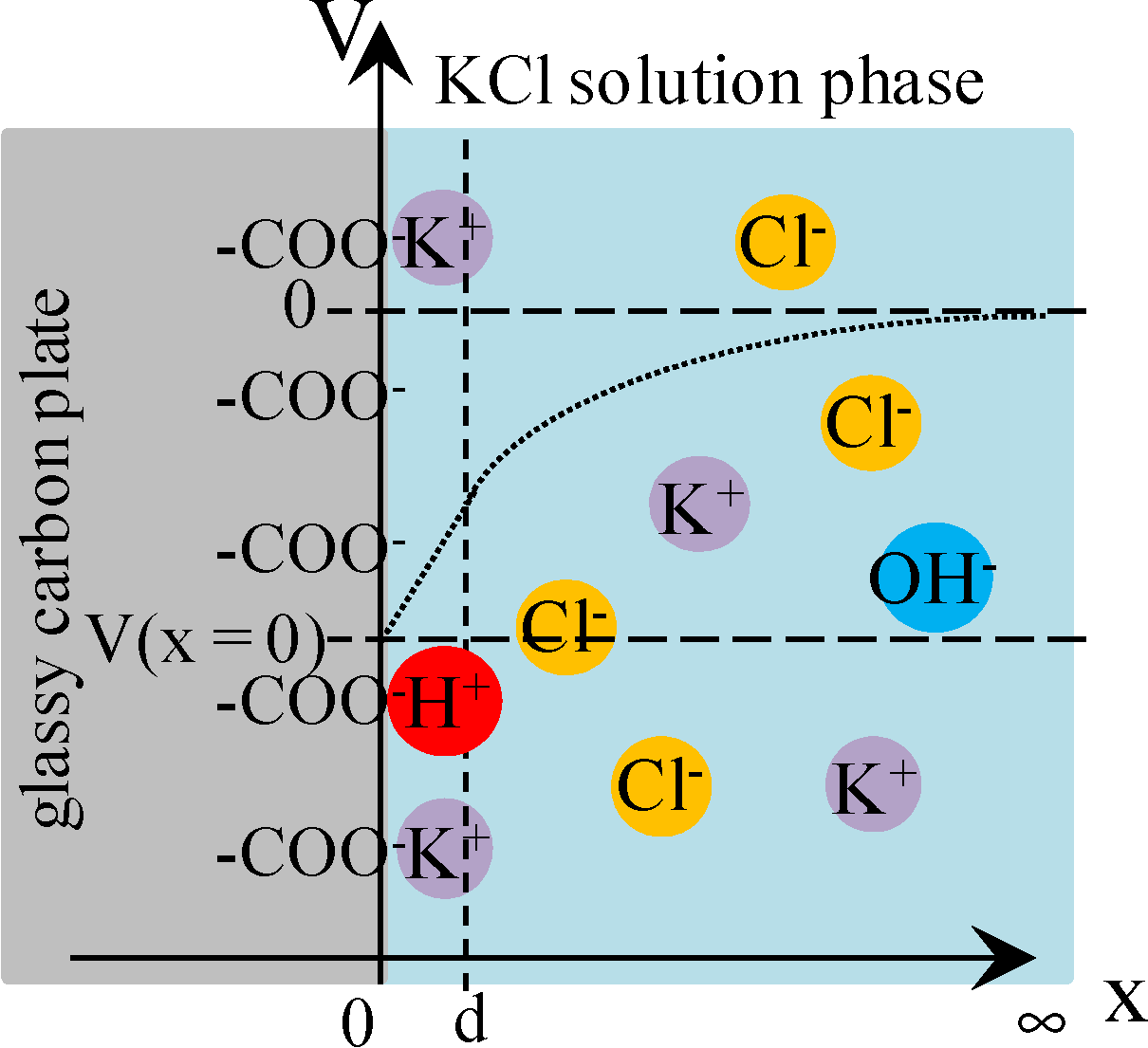
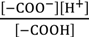
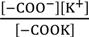
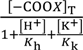
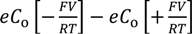
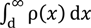 = 0
= 0
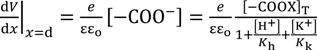

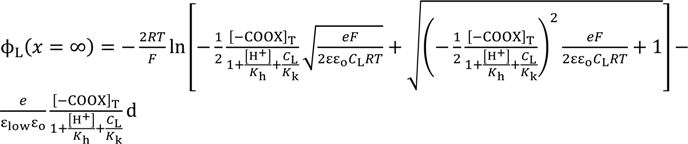
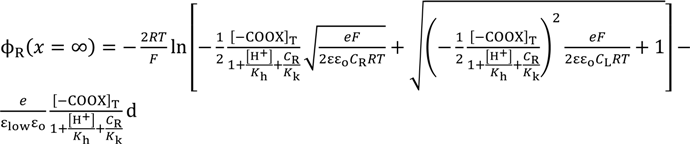
3.4. Potential Generation across the Impermeable Ion Exchange Membrane

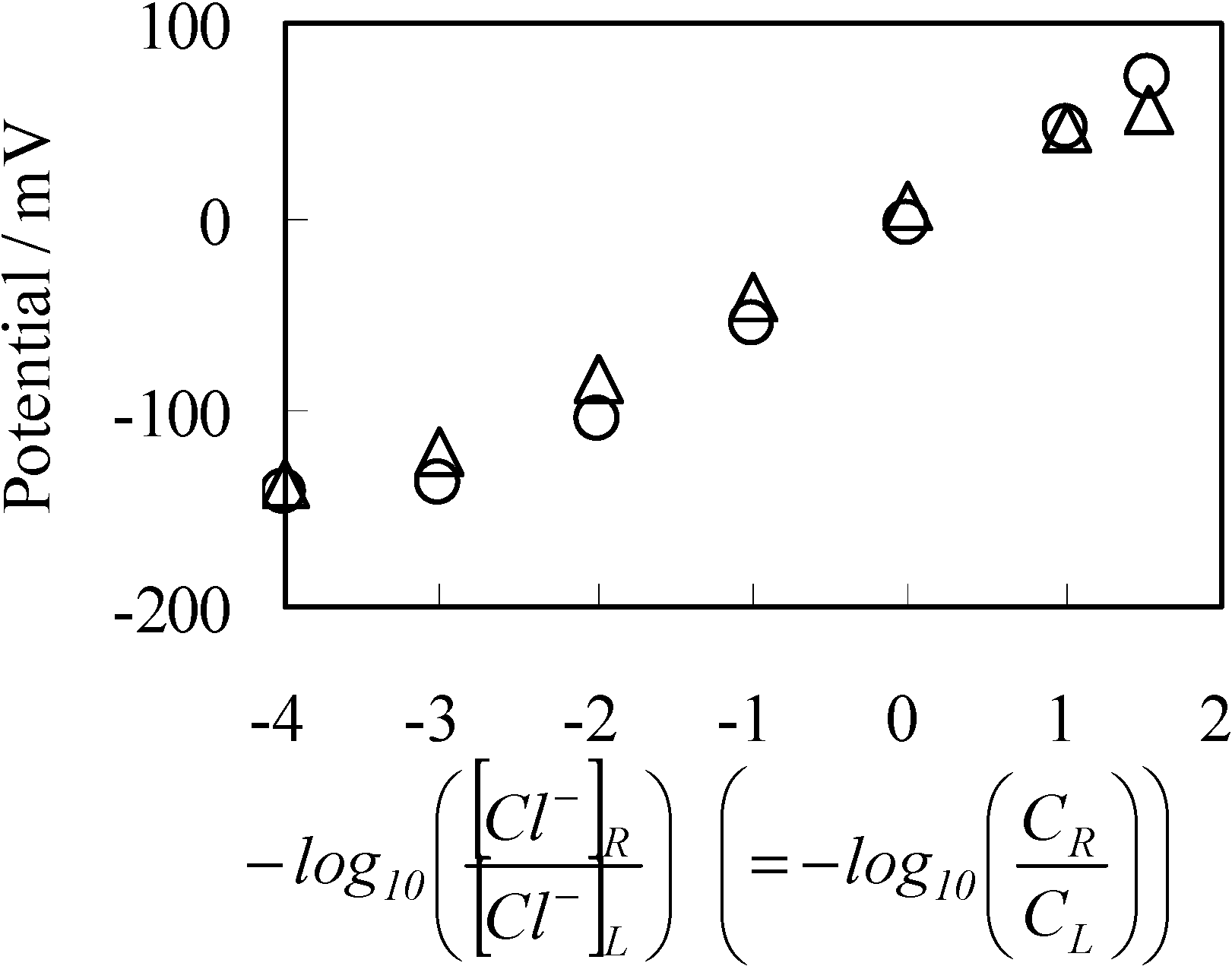
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ling, G. Revolution in the Physiology of the Living Cell; Krieger Pub Co.: Malabar, FL, USA, 1991. [Google Scholar]
- Ling, G. Life at the Cell and Below-Cell Level: The Hidden History of a Fundamental Revolution in Biology; Pacific Press: New York, NY, USA, 2001. [Google Scholar]
- Miyakawa, H.; Inoue, M. Nyuuron no Seibutsubuturi (Biophysics of Neuron); Maruzen: Tokyo, Japan, 2003. (In Japanase) [Google Scholar]
- Ermentrout, G.B.; Terman, D.H. Mathematical Foundations of Neuroscience; Springer: Berlin, Germany, 2010. [Google Scholar]
- Colacicco, G. Electrical potential at an oil/water interface. Nature 1965, 207, 936–938. [Google Scholar] [CrossRef]
- Colacicco, G. Reversal of potential across a liquid non-aqueous membrane with regard to membrane excitability. Nature 1965, 207, 1045–1047. [Google Scholar]
- Adrian, R.H. The effect of internal and external potassium concentration on the membrane potential of frog muscle. J. Physiol. 1956, 133, 631–658. [Google Scholar]
- Hodgkin, A.L.; Horowicz, P.J. The influence of potassium and chloride ions on the membrane potential of single muscle fibre. J. Physiol. 1959, 148, 127–160. [Google Scholar]
- Cheng, K.L. Capacitor theory for nonfaradaic potnetiometry. Microchem. J. 1990, 42, 5–24. [Google Scholar] [CrossRef]
- Huang, C.-M.; Jean, Y.C.; Cheng, K.L. Isotopic evidence disproving Ion exchange reaction between H+ and Na+ in pH glass electrode. J. Electrochem. Soc. 1995, 142, L175–L176. [Google Scholar] [CrossRef]
- Cheng, K.L. Explanation of misleading Nernst slope by Boltzmann equation. Microchem. J. 1998, 59, 457–461. [Google Scholar] [CrossRef]
- Temsamani, K.R.; Cheng, K.L. Studies of chloride adsorption on the Ag/AgCl electrode. Sens. Actuators B 2001, 76, 551–555. [Google Scholar] [CrossRef]
- Cheng, K.L. Recent development of non-faradaic potentiometry. Microchem. J. 2002, 72, 269–276. [Google Scholar] [CrossRef]
- Sin, M.L.Y.; Chow, G.C.T.; Wong, G.M.K.; Li, W.J. Ultralow-power alcohol vapor sensors using chemically functionalized multiwalled carbon nanotubes. IEEE Trans. Nanotechnol. 2007, 6, 571–577. [Google Scholar] [CrossRef]
- Ouyang, M.; Sin, M.L.Y.; Tsoi, B.K.H.; Chow, G.C.T.; Wong, G.M.K.; Li, W.J. Constant-Power Operation of Functionalized Carbon Nanotube Sensors for Alcohol Vapor Detection. In Proceedings of the 3rd IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Sanya, China, 6–9 January 2008; pp. 747–752.
- Lide, D.R. CRC Handbook of Chemistry and Physics; Internet Version 2005; Lide, D.R., Ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Bockris, J.O’M.; Khan, S.U.M. Surface Electrochemistry: A Molecular Level Approach; Springer: New York, NY, USA, 1993. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces with Applications to Colloidal and Biological Systems; Academic Press: San Diego, CA, USA, 1985. [Google Scholar]
- Plouraboue, F.; Chang, H.-C. Symmetry Breaking and Electrostatic Attraction Between Two Identical Surfaces. Phys. Rev. E 2009, 79, 041404:1–041404:9. [Google Scholar]
- Basuray, S.; Chang, H.-C. Designing a Sensitive and Quantifiable Nanocolloid Assay with Dielectrophoretic Cross-Over Frequency. Biomicrofluidics 2010, 4, 013205:1–013205:11. [Google Scholar]
- Parsegian, V.A.; Gingell, D. On the electrostatic interaction across a salt solution between two bodies bearing unequal charges. Biophys. J. 1972, 12, 1192–1204. [Google Scholar] [CrossRef]
- Kitahara, A.; Watanabe, A. Surfactant Science Series Volume 15, Electrical Phenomena at Interface Fundamentals, Measurements, and Applications; Kitahara, A., Watanabe, A., Eds.; Dekker: New York, NY, USA, 1984. [Google Scholar]
- Ohshima, H.; Makino, K.; Kondo, T. Electrostatic interaction of two parallel plates with surface charge layers. J. Colloid Interface Sci. 1987, 116, 196–199. [Google Scholar] [CrossRef]
- Brett, C.M.A.; Brett, A.M.O. Electrochemistry Principles, Methods and Applications; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Anandarajah, A.; Chen, J. Double-Layer Repulsive Force between Two Inclined Platy Particles According to the Gouy-Chapman Theory. J. Colloid Interface Sci. 1994, 168, 111–117. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Adsorption of large ions from an electrolyte solution: A modified Poisson–Boltzmann equation. Electrochim. Acta 2000, 46, 221–229. [Google Scholar] [CrossRef]
- Chapot, D.; Bocquet, L.; Trizac, E. Electrostatic potential around charged finite rodlike macromolecules: Nonlinear Poisson–Boltzmann theory. J. Colloid Interface Sci. 2005, 285, 609–618. [Google Scholar] [CrossRef]
- Zhang, J.; Drechsler, A.; Grundke, K.; Kwok, D.Y. The similarity of electric double-layer interaction from the general Poisson–Boltzmann theory. J. Colloid Interface Sci. 2006, 300, 391–395. [Google Scholar] [CrossRef]
- Polat, M.; Polat, H. Analytical solution of Poisson–Boltzmann equation for interacting plates of arbitrary potentials and same sign. J. Colloid Interface Sci. 2010, 341, 178–185. [Google Scholar] [CrossRef]
- Alijó, P.H.R.; Tavaresa, F.W.; Biscaia, E.C., Jr. Double layer interaction between charged parallel plates using a modified Poisson–Boltzmann equation to include size effects and ion specificity. Colloids Surf. A 2012, 412, 29–35. [Google Scholar] [CrossRef]
- Trefalt, G.; Szilagyi, I.; Borkovec, M. Poisson–Boltzmann description of interaction forces and aggregation rates involving charged colloidal particles in asymmetric electrolytes. J. Colloid Interface Sci. 2013, 406, 111–120. [Google Scholar] [CrossRef]
- Tamagawa, H. Ishudenkawo motsu Koubunshigeru kanno sougosayou (in Japanese) (Interaction between Cationic and Anionic Polymer Gels). Master’s Thesis, Tokyo Institute of Technology, Tokyo, Japan, March 1994. [Google Scholar]
- Velikonja, A.; Perutkova, S.; Gongadze, E.; Kramar, P.; Polak, A.; Macek-Lebar, A.; Iglic, A. Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations. Int. J. Mol. Sci. 2013, 14, 2846–2861. [Google Scholar] [CrossRef]
- Gongadze, E.; van Rienen, U.; Igli, A. Generalized Stern models of the electric double layer considering the spatial variation of permittivity and finite size of ion in saturation regime. Cell. Mol. Biol. Lett. 2011, 16, 576–594. [Google Scholar] [CrossRef]
- Khalil, M.I.; Al-Resayes, S.I. The role of dielectric constant in sodium chloride solution chemistry: Magnitude of super saturation. Int. J. Phys. Sci. 2012, 7, 578–583. [Google Scholar]
- Aguilella-Arzo, M.; Andrio, A.; Aguilella, V.M.; Alcaraz, A. Dielectric saturation of water in a membrane protein channel. Phys. Chem. Chem. Phys. 2009, 11, 358–365. [Google Scholar] [CrossRef]
- Mentré, P. Water in the Cell a Heterogeneous and Dynamic Interface of Macromolecules; Masson: Paris, France, 1995. [Google Scholar]
- Chatterjee, S.; Basumallick, I. Transfer Thermodynamics of Protein in Denaturing and Stabilizing Media. J. Chin. Chem. Soc. 2008, 55, 17–22. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tamagawa, H.; Morita, S. Membrane Potential Generated by Ion Adsorption. Membranes 2014, 4, 257-274. https://doi.org/10.3390/membranes4020257
Tamagawa H, Morita S. Membrane Potential Generated by Ion Adsorption. Membranes. 2014; 4(2):257-274. https://doi.org/10.3390/membranes4020257
Chicago/Turabian StyleTamagawa, Hirohisa, and Sachi Morita. 2014. "Membrane Potential Generated by Ion Adsorption" Membranes 4, no. 2: 257-274. https://doi.org/10.3390/membranes4020257




