Validation and Analysis of Forward Osmosis CFD Model in Complex 3D Geometries
Abstract
:Nomenclature
| Symbol | Description | Unit |
| A | water permeability | m (s Pa)−1 |
| B | solute permeability | m s−1 |
| C | solute concentration | kg m−3 |
| DAB | diffusion coefficient | m2 s−1 |
| g | gravitational acceleration | m s−2 |
| Js | solute flux | kg (m2 s)−1 |
| Jw | water flux | m s−1 |
| K | diffusion resistivity | s m−1 |
| kd | mass transfer coefficient | s m−1 |
| mA | solute mass fraction | kg kg−1 |
| n | surface normal vector | m |
| n | surface normal direction | m |
| µ | viscosity of fluid | Pa s |
| p | pressure | Pa |
| π | osmotic pressure | Pa |
| R | seperation coefficient | - |
| Re | Reynolds number | - |
| ρ | fluid denisty | kg m−3 |
| S | structural parameter | m |
| U | fluid velocity vector | ms-1 |
 | mean cross-flow velocity | ms−1 |
| Index | Description | |
| d | draw-side of membrane | |
| f | feed-side of membrane | |
| i | between active layer and support | |
| m | at the membrane surface |
1. Introduction
2. Experimental
2.1. FO Experiments
2.2. Governing Equations and Boundary Conditions
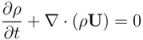
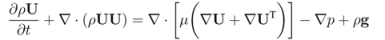
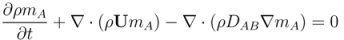
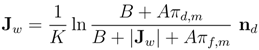
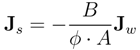
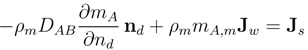
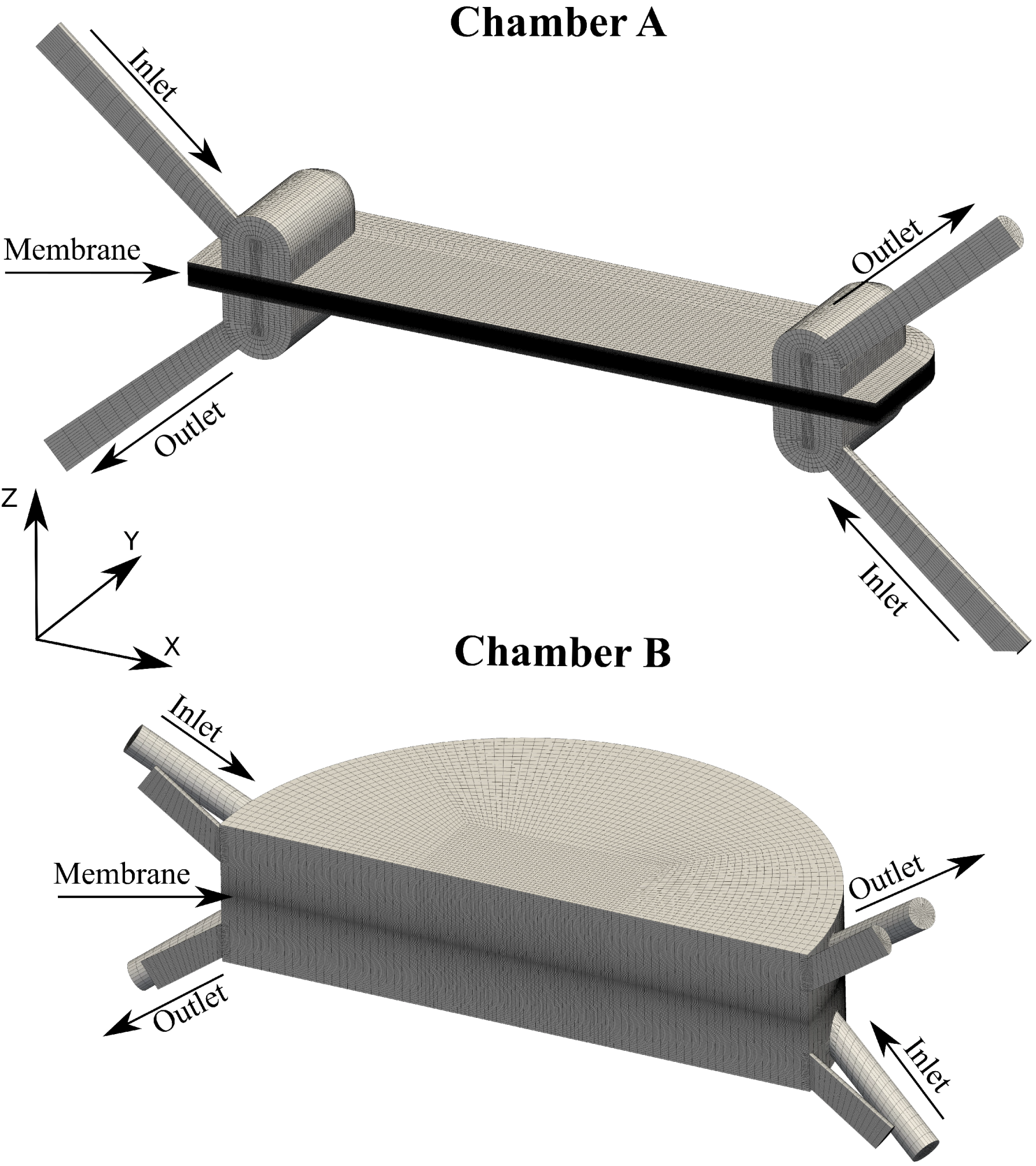
2.3. Case Geometry
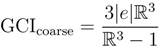
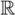 is the ratio of cells between the fine and coarse grid, and |e| is the relative error in an integral function between the two grids; e.g., the water or solute flux. In order to ensure that the results obtained in our CFD model were accurate, we required that GCIcoarse < 1% when comparing coarse grids of 500,000 cells with finer grids consisting of approximately 1,500,000 cells. The total solute on the draw solution side of the membrane was used as the integral function in the GCI-analysis, since this was the parameter that was found to vary the most with grid density. Interpolated data from the steady-state solutions obtained from coarse grids were used as initial guesses in simulations with finer grids.
is the ratio of cells between the fine and coarse grid, and |e| is the relative error in an integral function between the two grids; e.g., the water or solute flux. In order to ensure that the results obtained in our CFD model were accurate, we required that GCIcoarse < 1% when comparing coarse grids of 500,000 cells with finer grids consisting of approximately 1,500,000 cells. The total solute on the draw solution side of the membrane was used as the integral function in the GCI-analysis, since this was the parameter that was found to vary the most with grid density. Interpolated data from the steady-state solutions obtained from coarse grids were used as initial guesses in simulations with finer grids. 2.4. Fluid Parameters
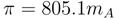
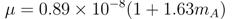
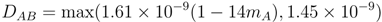
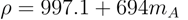
2.5. Membrane Properties
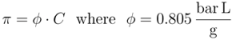
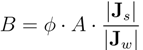
2.6. Numerical Procedure
3. Results and Discussions
3.1. Membrane Characteristics
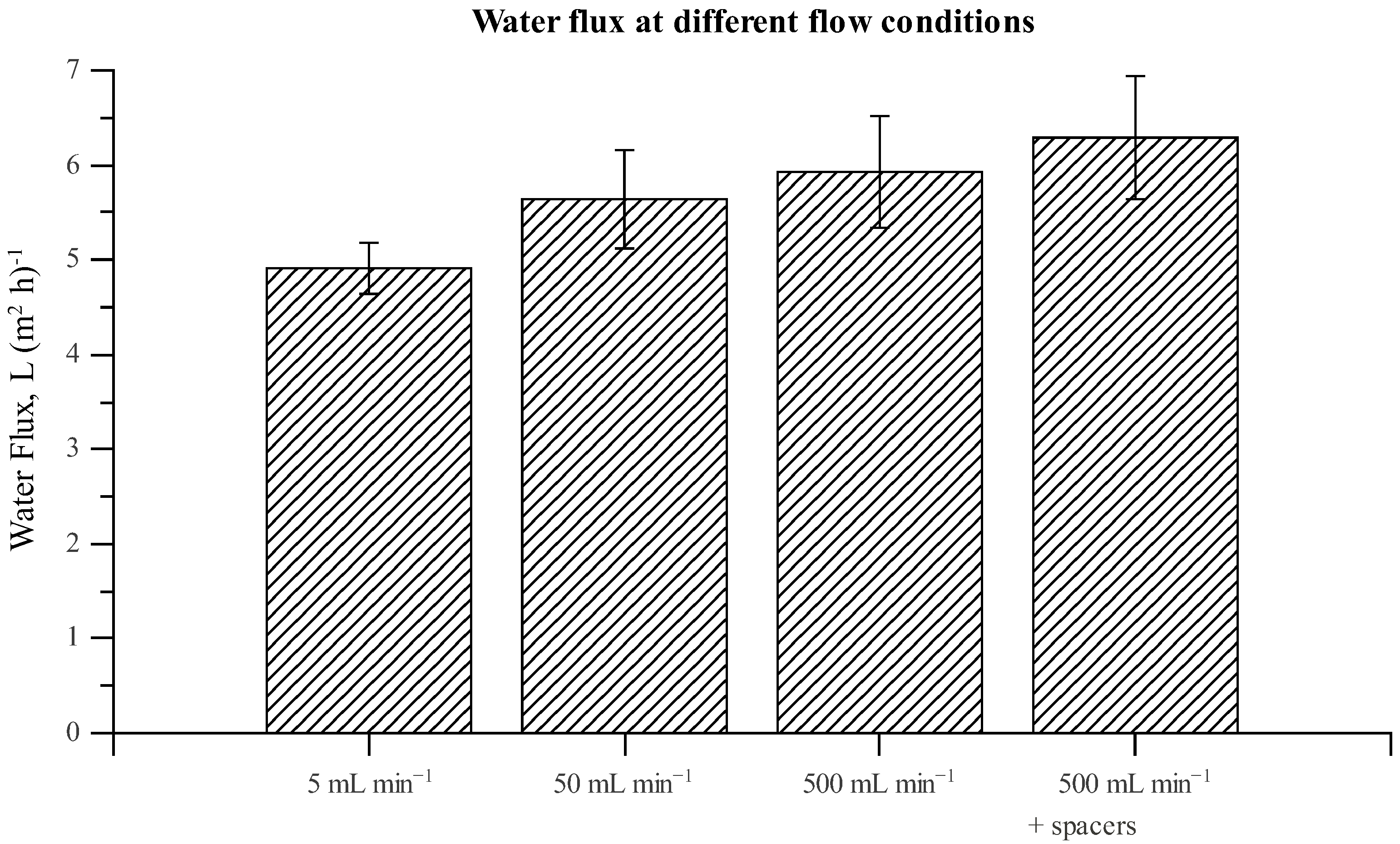
| Parameter | Value | Unit | i | n |
|---|---|---|---|---|
| A | 0.44 ± 0.05 | L (m2 h bar)−1 | 5 | 3 |
| B | 0.087 ± 0.018 | L (m2 h)−1 | 5 | 2 |
| K | 0.72 ± 0.23 | s µm−1 | 5 | 5 |
3.2. Membrane Chamber Meshing
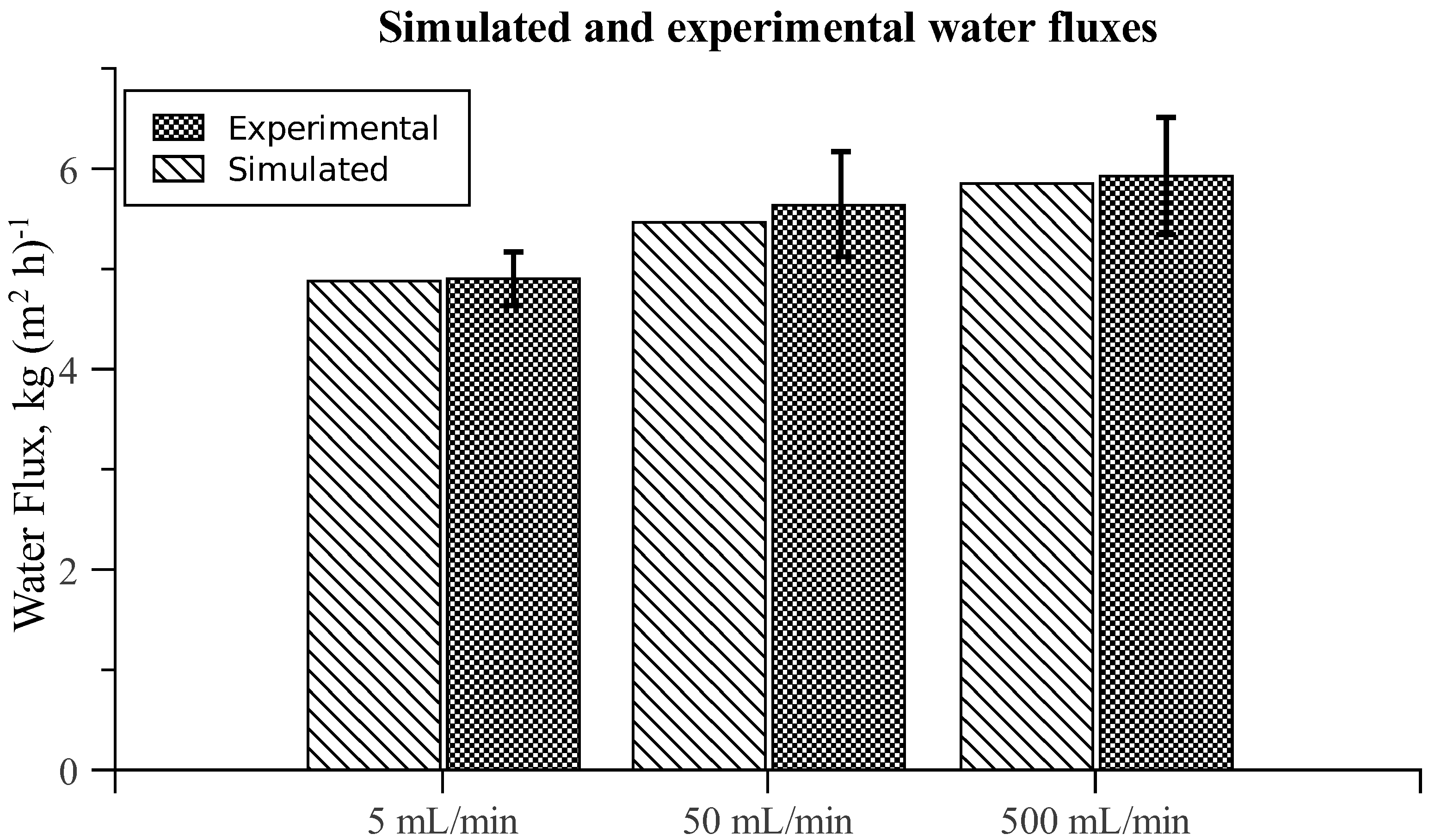
3.3. Chamber Comparison and Optimization
| Simulated | Experimental | |||
|---|---|---|---|---|
| Chamber | J w | Js | J w | Js |
| A | 5.46 | 1.35 | 5.64 ± 0.52 | 1.44 ± 0.28 |
| B | 5.54 | 1.37 | 5.72 ± 0.40 | 1.60 ± 0.39 |



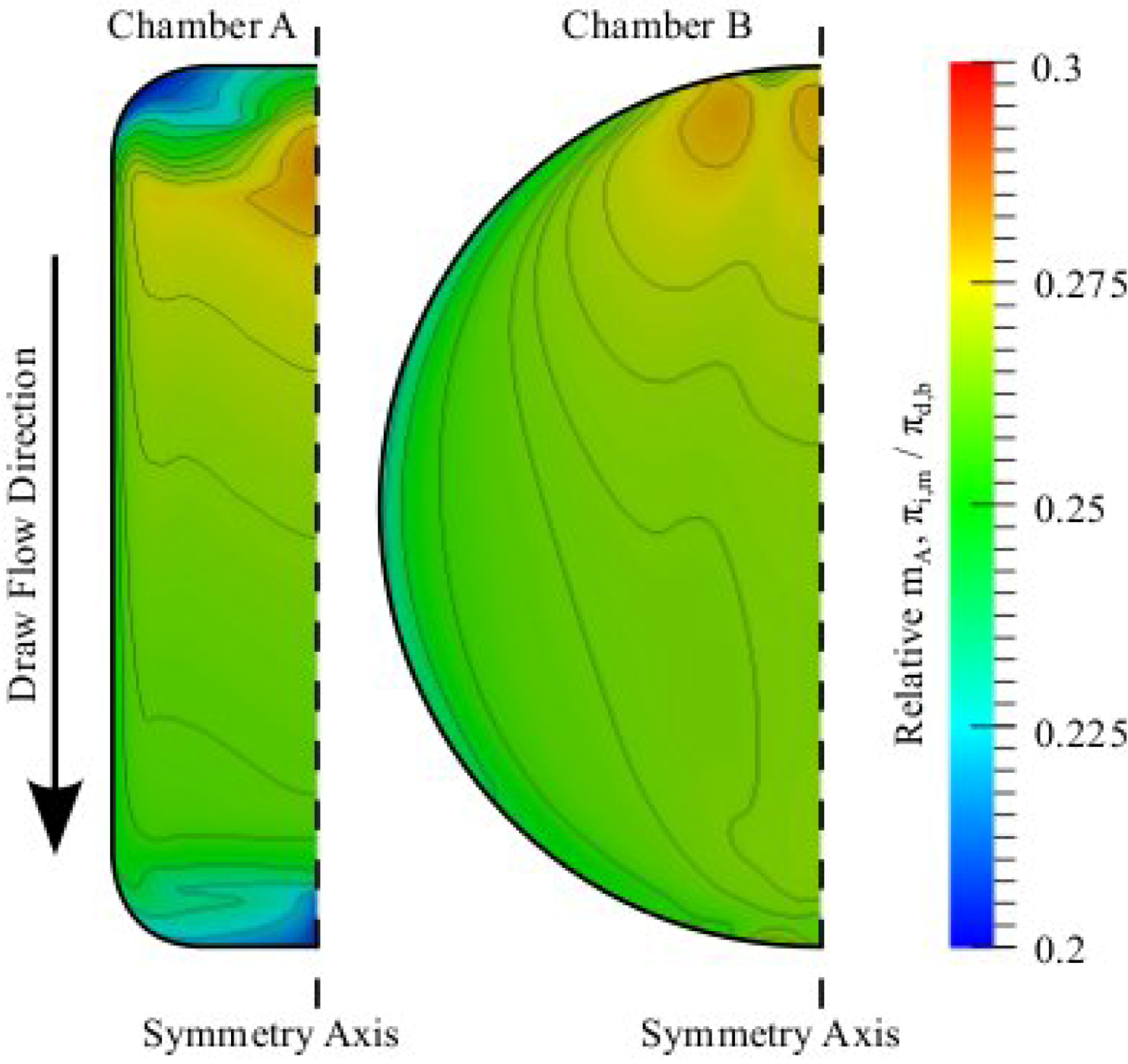
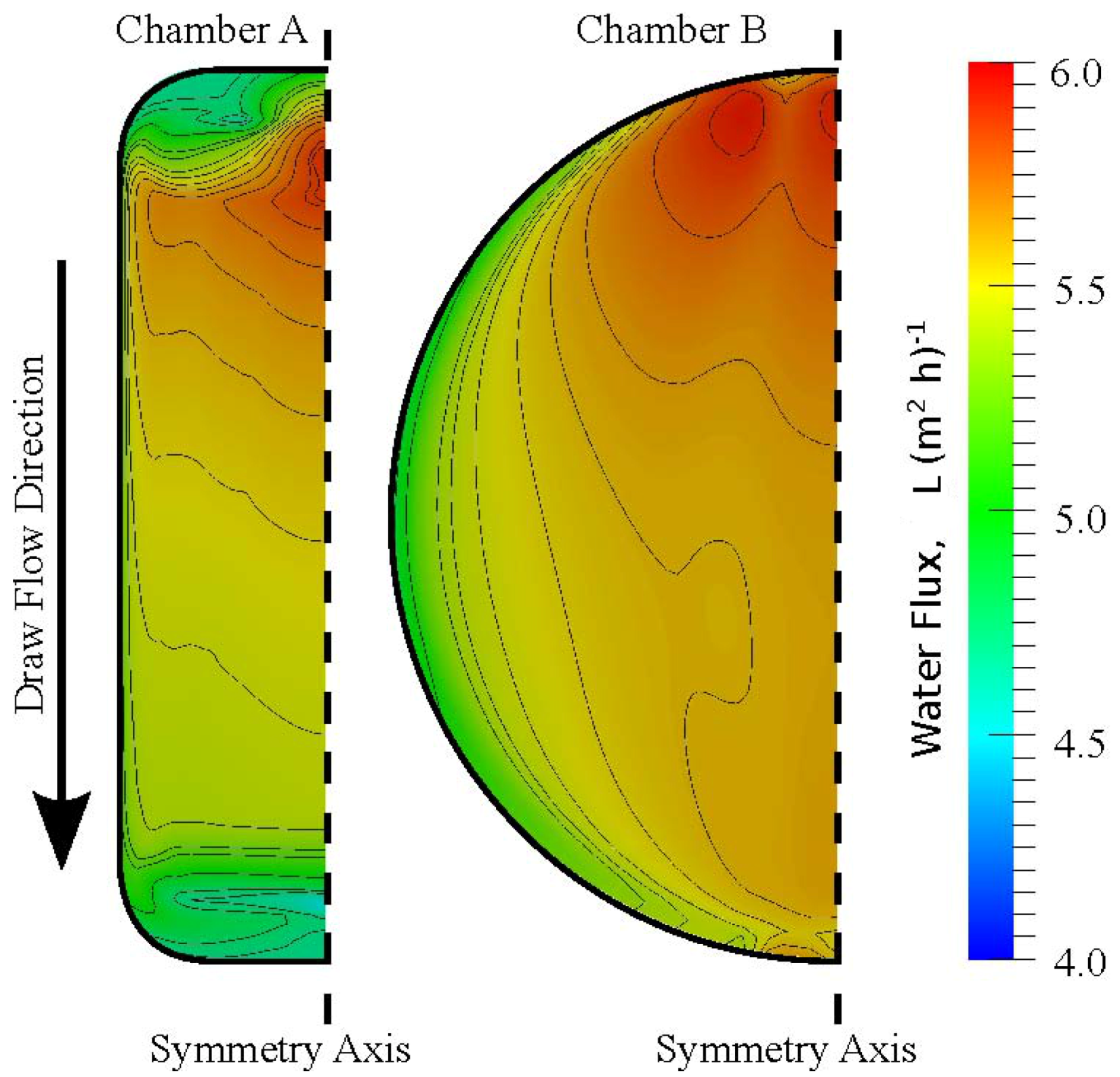
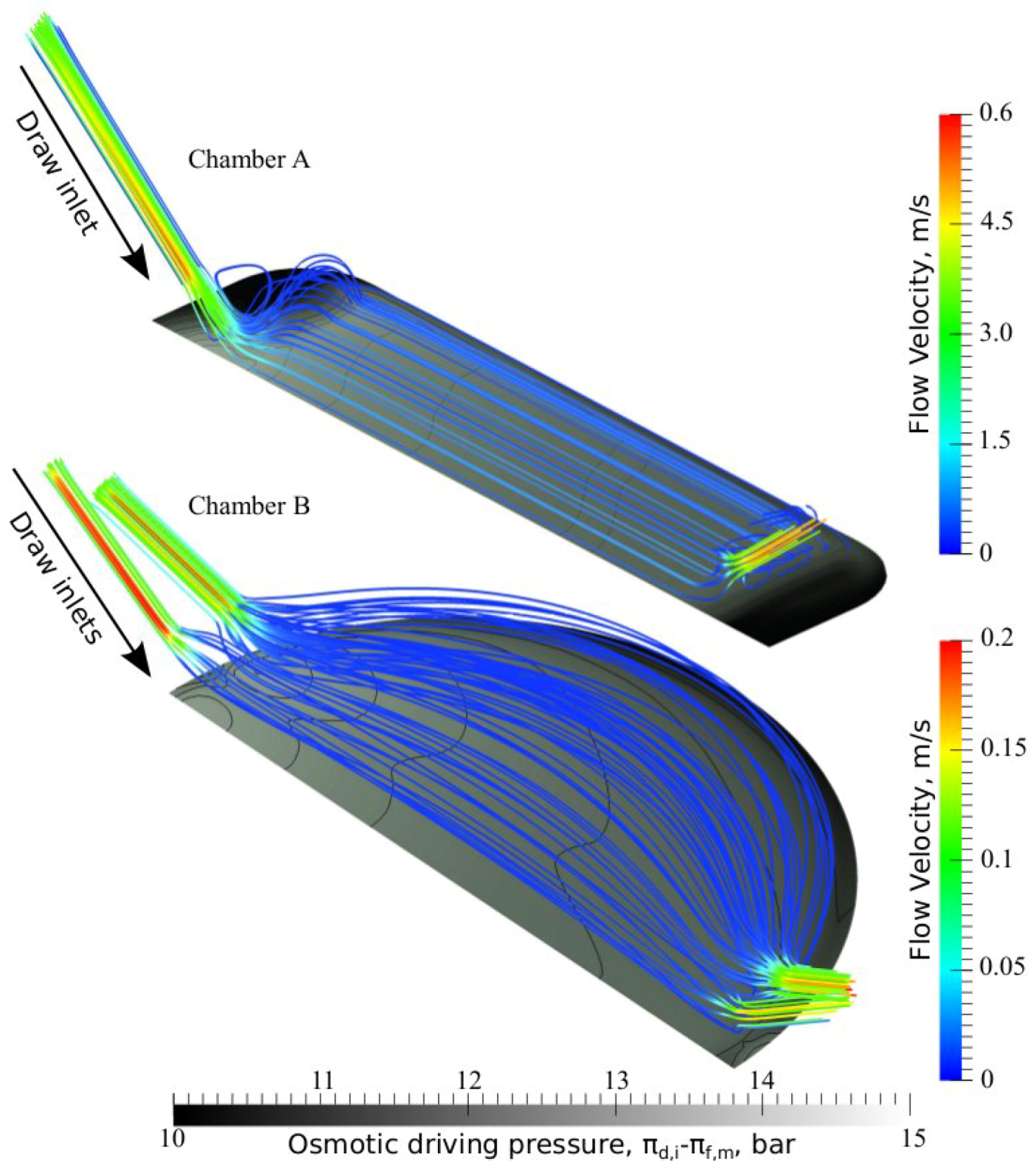
4. Conclusions
Acknowledgments
References
- McGinnis, R.L.; Elimelech, M. Energy requirements of ammonia-carbon dioxide forward osmosis desalination. Desalination 2007, 207, 370–382. [Google Scholar] [CrossRef]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Achilli, A.; Cath, T.Y.; Marchand, E.A.; Childress, A.E. The forward osmosis membrane bioreactor: A low fouling alternative to MBR processes. Desalination 2009, 239, 10–21. [Google Scholar] [CrossRef]
- Holloway, R.W.; Childress, A.E.; Dennett, K.E.; Cath, T.Y. Forward osmosis for concentration of anaerobic digester centrate. Water Res. 2007, 41, 4005–4014. [Google Scholar] [CrossRef]
- Tang, C.Y.; She, Q.; Lay, W.C.L.; Wang, R.; Fane, A.G. Coupled effects of internal concentration polarization and fouling on flux behavior of forward osmosis membranes during humic acid filtration. J. Membr. Sci. 2010, 354, 123–133. [Google Scholar] [CrossRef]
- Mi, B.; Elimelech, M. Organic fouling of forward osmosis membranes: Fouling reversibility and cleaning without chemical reagents. J. Membr. Sci. 2010, 348, 337–345. [Google Scholar] [CrossRef]
- Lee, S.; Boo, C.; Elimelech, M.; Hong, S. Comparison of fouling behavior in forward osmosis (FO) and reverse osmosis (RO). J. Membr. Sci. 2010, 365, 34–39. [Google Scholar] [CrossRef]
- Hélix-Nielsen, C. Osmotic water purification: Insights from nanoscale biomimetics. Environ. Nano Technol. 2010, 1, 58–66. [Google Scholar]
- McCutcheon, J.R.; Elimelech, M. Modeling water flux in forward osmosis: Implications for improved membrane design. Am. Inst. Chem. Eng. 2007, 53, 1736–1744. [Google Scholar] [CrossRef]
- Yip, N.Y.; Tiraferri, A.; Phillip, W.A.; Schiffman, J.D.; Elimelech, M. High performance thin-film composite forward osmosis membrane. Environ. Sci. Technol. 2010, 44, 3812–3818. [Google Scholar] [CrossRef]
- Wang, R.; Shi, L.; Tang, C.Y.; Chou, S.; Qiu, C.; Fane, A.G. Characterization of novel forward osmosis hollow fiber membranes. J. Membr. Sci. 2010, 355, 158–167. [Google Scholar] [CrossRef]
- Zydney, A.L. Stagnant film model for concentration polarization in membrane systems. J. Membr. Sci. 1997, 130, 275–281. [Google Scholar] [CrossRef]
- Kim, S.; Hoek, E.M.V. Modeling concentration polarization in reverse osmosis processes. Desalination 2005, 186, 111–128. [Google Scholar] [CrossRef]
- Lee, K.L.; Baker, R.W.; Lonsdale, H.K. Membranes for power generation by pressure-retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Loeb, S.; Titelman, L.; Korngold, E.; Freiman, J. Effect of porous support fabric on osmosis through a Loeb-Sourirajan type asymmetric membrane. J. Membr. Sci. 1997, 129, 243–249. [Google Scholar] [CrossRef]
- Brian, P.L.T. Concentration polarization in reverse osmosis desalination with variable flux and incomplete salt rejection. Ind. Eng. Chem. Fundam. 1965, 4, 439. [Google Scholar] [CrossRef]
- Yeh, H.M.; Cheng, T.W. Analysis of the slip effect on the permeate flux in membrane ultrafiltration. J. Membr. Sci. 1999, 154, 41–51. [Google Scholar]
- Chellam, S.; Wiesner, M.R.; Dawson, C. Slip at a uniformly porous boundary: Effect on fluid flow and mass transfer. J. Eng. Math. 1992, 26, 481–492. [Google Scholar]
- Youm, K.H.; Fane, A.G.; Wiley, D.E. Effects of natural convection instability on membrane performance in dead-end and cross-flow ultrafiltration. J. Membr. Sci. 1996, 116, 229–241. [Google Scholar] [CrossRef]
- Wiley, D.E.; Fletcher, D.F. Computational fluid dynamics modelling of flow and permeation for pressure-driven membrane processes. Desalination 2002, 145, 183–186. [Google Scholar] [CrossRef]
- Wiley, D.E.; Fletcher, D.F. Techniques for computational fluid dynamics modelling of flow in membrane channels. J. Membr. Sci. 2003, 211, 127–137. [Google Scholar] [CrossRef]
- Wardeh, S.; Morvan, H.P. CFD simulations of flow and concentration polarization in spacer-filled channels for application to water desalination. Chem. Eng. Res. Des. 2008, 86, 1107–1116. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.A.; Wiley, D.E. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Gruber, M.F.; Johnson, C.J.; Yde, L.; Hèlix-Nielsen, C. Computational Fluid Dynamics simulations of flow and concentration polarization in forward osmosis membrane systems. J. Membr. Sci. 2011, 379, 488–495. [Google Scholar] [CrossRef]
- Fletcher, D.F.; Wiley, D.E. A computational fluids dynamics study of buoyancy effects in reverse osmosis. J. Membr. Sci. 2004, 245, 175–181. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid. Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Geraldes, V.; Semiao, V.; de Pinho, M.N. Flow and mass transfer modelling of nanofiltration. J. Membr. Sci. 2001, 191, 109–128. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications, 2nd ed; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed; Dover Publications: Mineola, NY, USA, 2002. [Google Scholar]
- Issa, R.I. Solution of the implicitly discretized fluid-flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes, the Art of Scientific Computing, 3rd ed; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wei, J.; Qiu, C.; Tang, C.Y.; Wang, R.; Fane, A.G. Synthesis and characterization of flat-sheet thin film composite forward osmosis membranes. J. Membr. Sci. 2011, 372, 292–302. [Google Scholar] [CrossRef]
- Iwatsu, R.; Hyun, J.M.; Kuwahara, K. Analyses of three-dimensional flow calculations in a driven cavity. Fluid Dynam. Res. 1990, 6, 91–102. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.A.; Wiley, D.E. Numerical study of mass transfer in three-dimensional spacer-filled narrow channels with steady flow. J. Membr. Sci. 2007, 306, 228–243. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Kim, A.S.; Elimelech, M. Influence of crossflow membrane filter geometry and shear rate on colloidal fouling in reverse osmosis and nanofiltration separations. Environ. Eng. Sci. 2002, 19, 357–372. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Influence of concentrative and dilutive internal concentration polarization on flux behavior in forward osmosis. J. Membr. Sci. 2006, 284, 237–247. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gruber, M.F.; Johnson, C.J.; Tang, C.; Jensen, M.H.; Yde, L.; Hélix-Nielsen, C. Validation and Analysis of Forward Osmosis CFD Model in Complex 3D Geometries. Membranes 2012, 2, 764-782. https://doi.org/10.3390/membranes2040764
Gruber MF, Johnson CJ, Tang C, Jensen MH, Yde L, Hélix-Nielsen C. Validation and Analysis of Forward Osmosis CFD Model in Complex 3D Geometries. Membranes. 2012; 2(4):764-782. https://doi.org/10.3390/membranes2040764
Chicago/Turabian StyleGruber, Mathias F., Carl J. Johnson, Chuyang Tang, Mogens H. Jensen, Lars Yde, and Claus Hélix-Nielsen. 2012. "Validation and Analysis of Forward Osmosis CFD Model in Complex 3D Geometries" Membranes 2, no. 4: 764-782. https://doi.org/10.3390/membranes2040764




