Ion Separations Based on Spontaneously Arising Streaming Potentials in Rotating Isoporous Membranes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
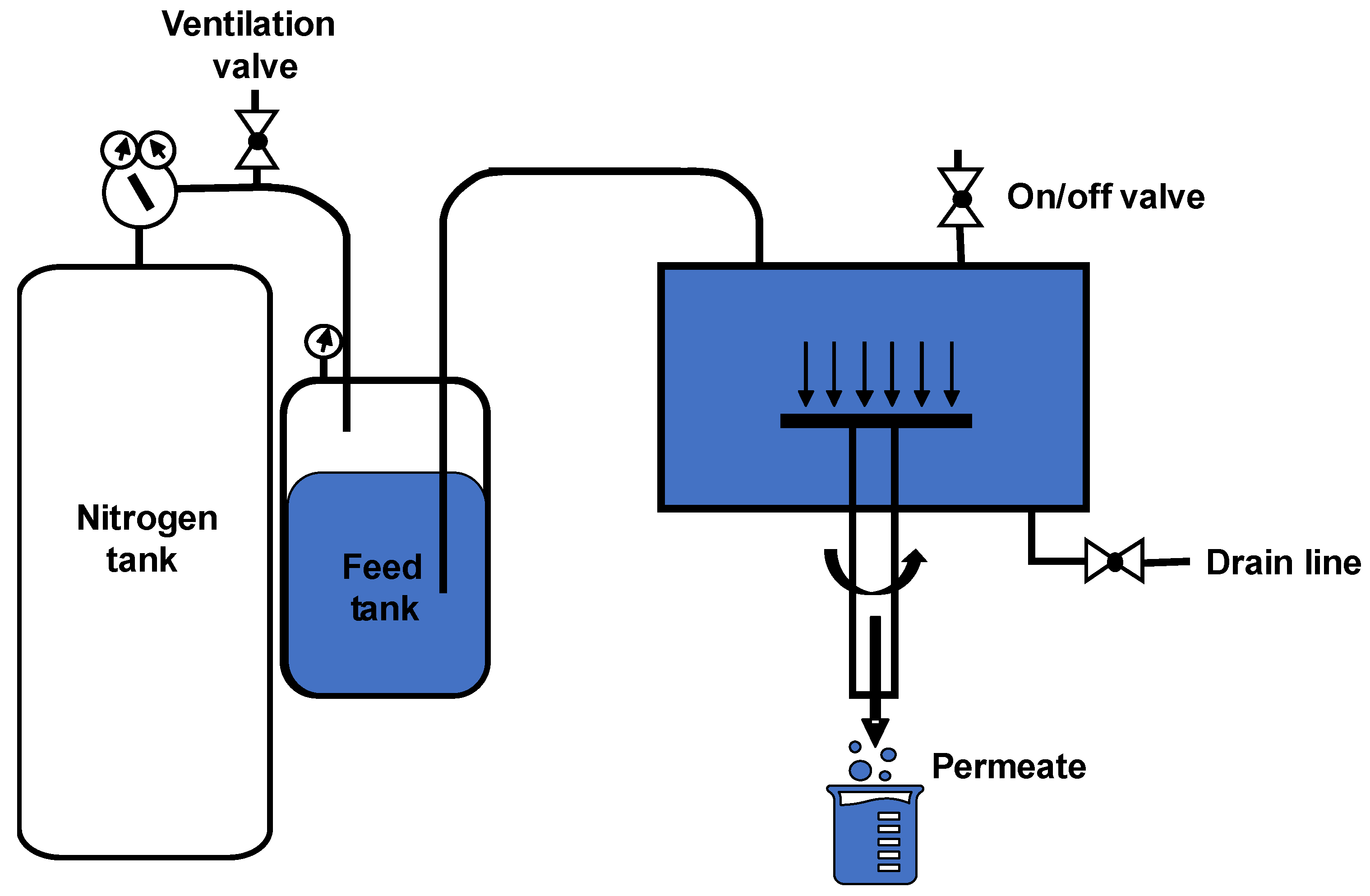
2.2. Rotating-Membrane Filtration Cell
2.3. Filtration Setup
2.4. Permeability Measurements
2.5. Single-Salt and Mixed-Salt Filtration
2.6. Numerical Simulations
3. Results and Discussion
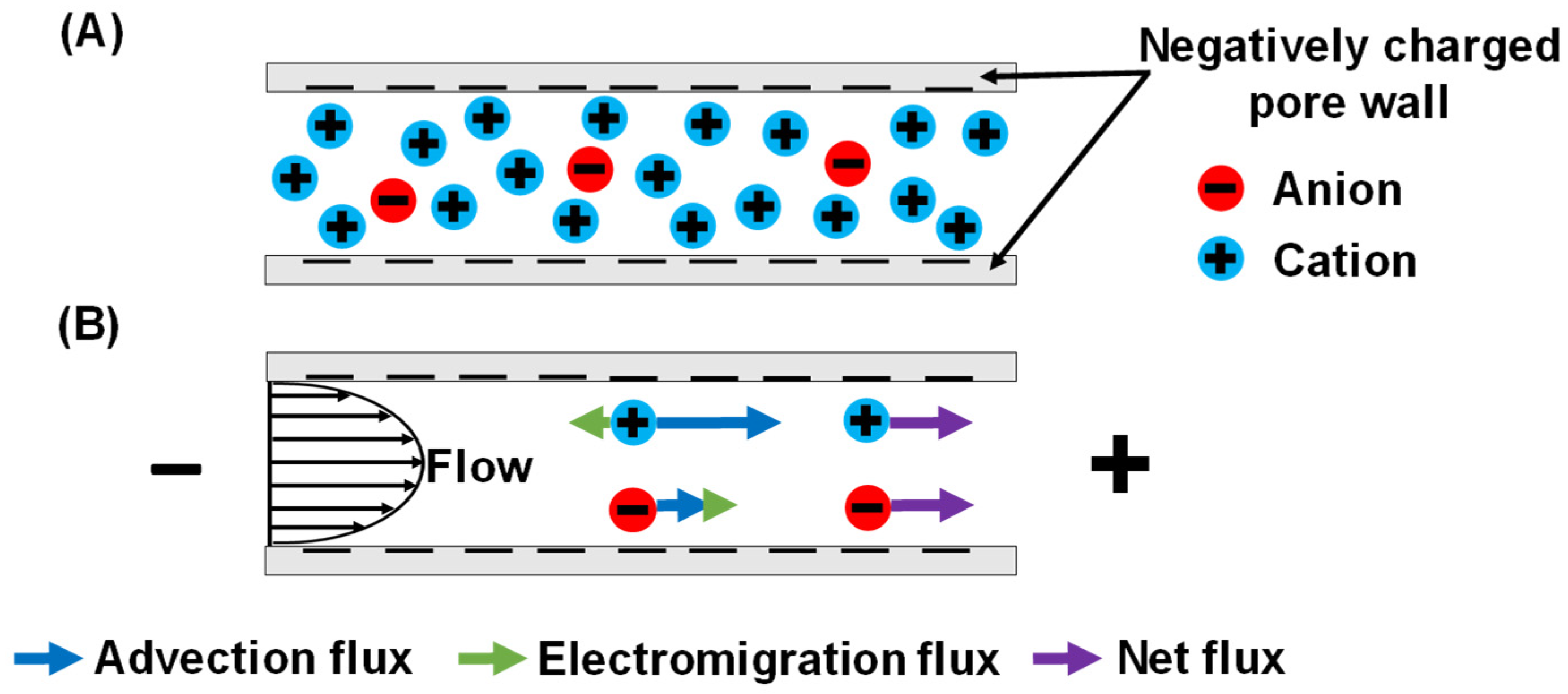
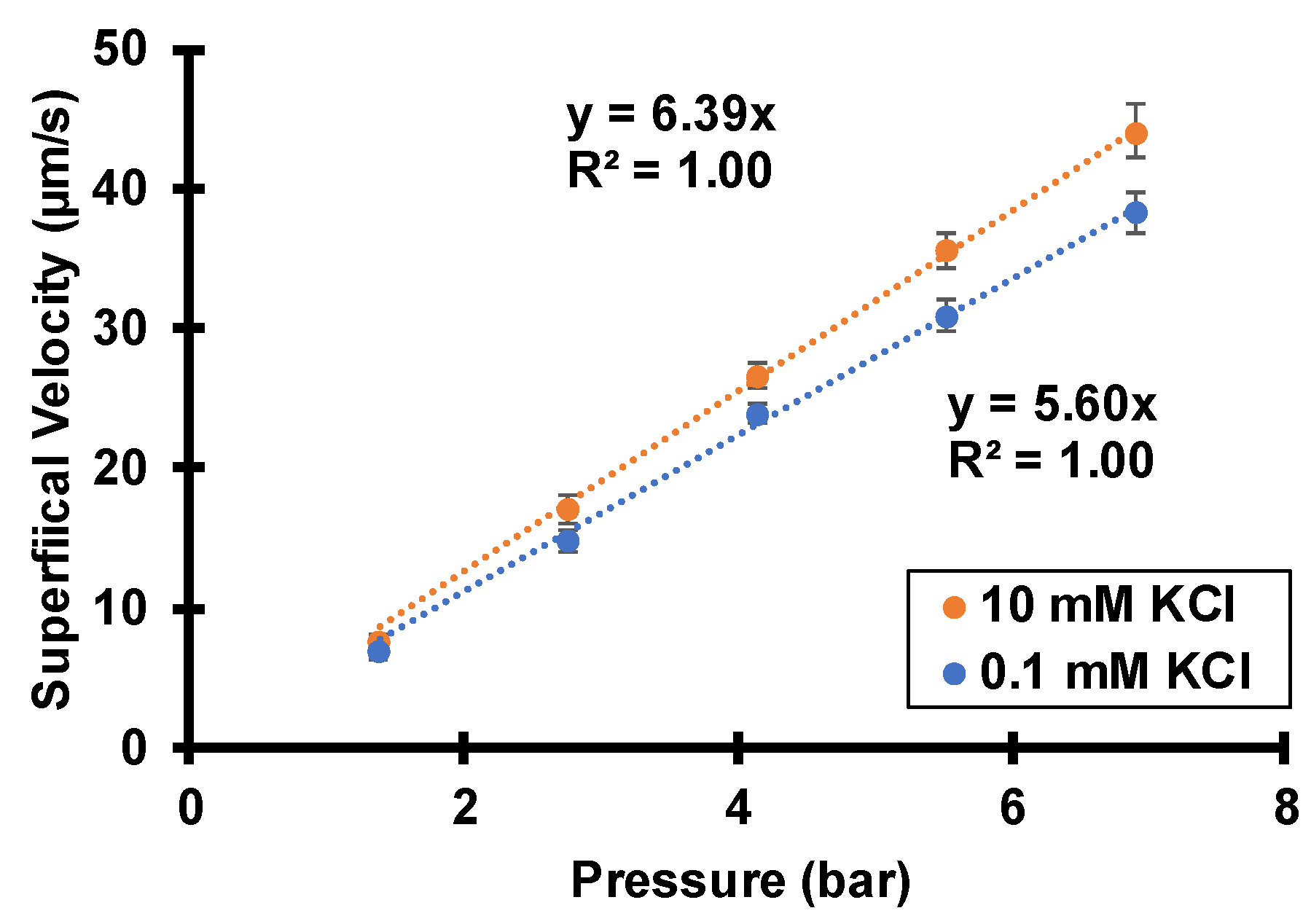
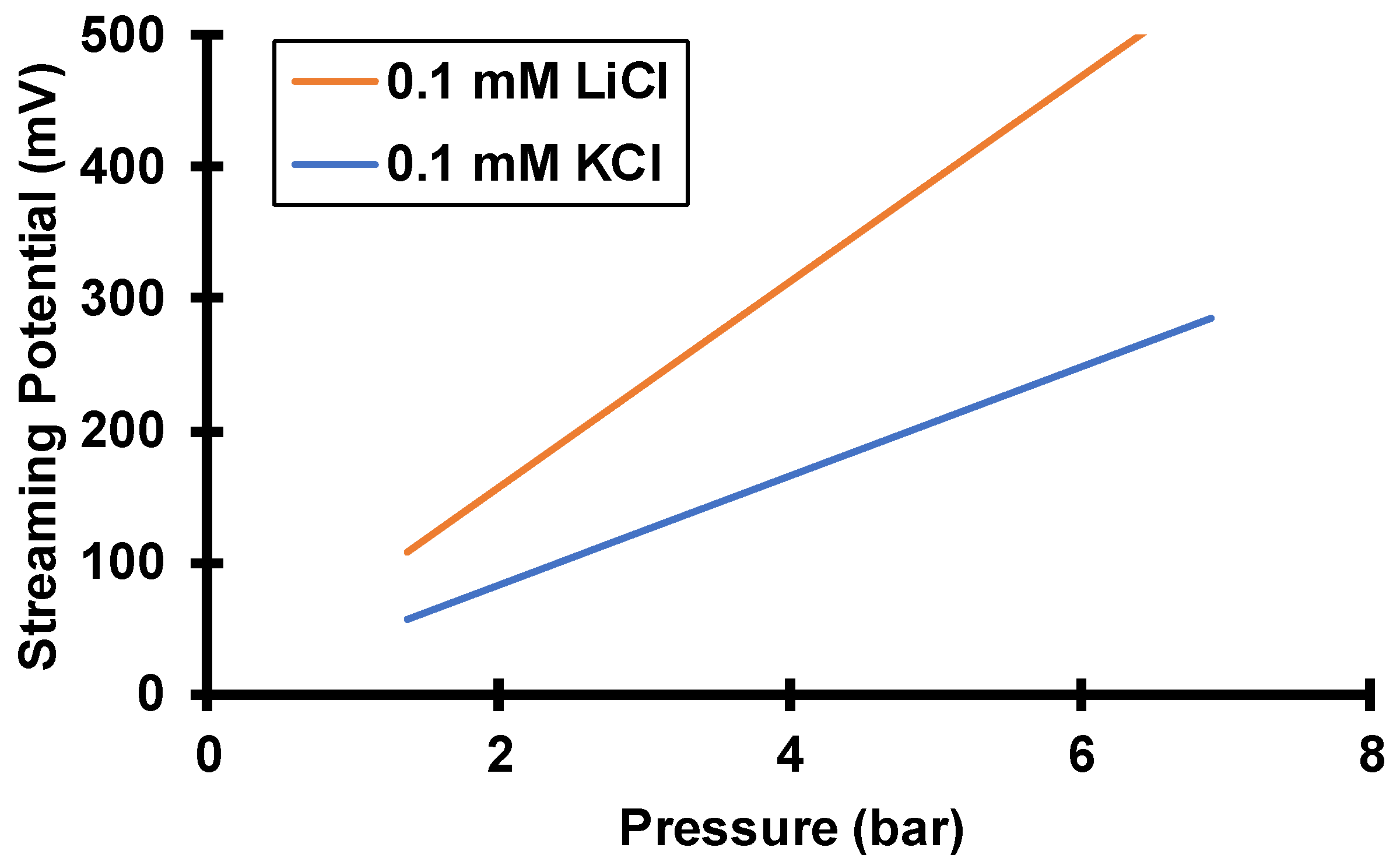
3.1. Peameability Measurements and Electroosmosis
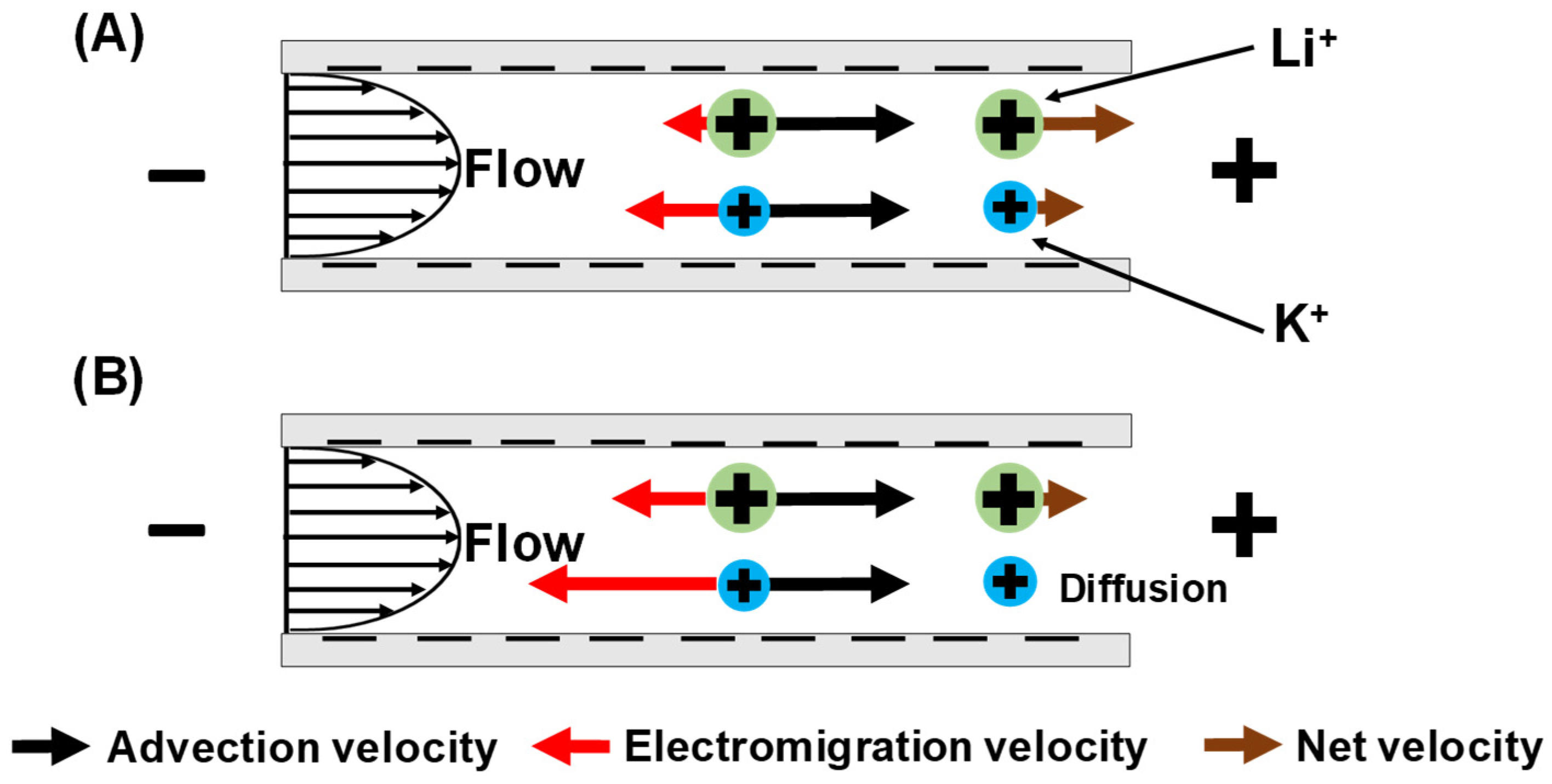
3.2. Single-Salt Studies
3.3. Mixed-Salt Studies
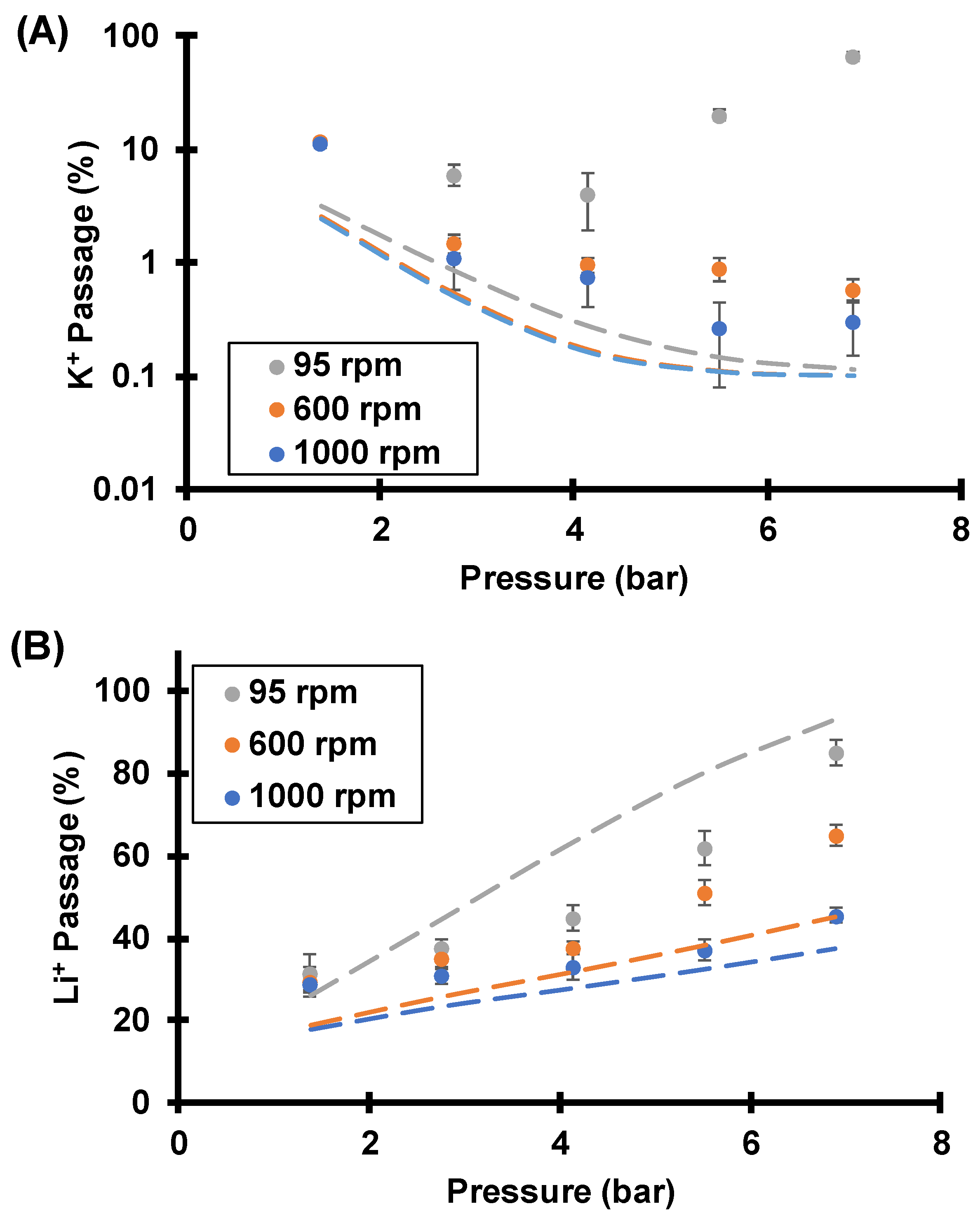
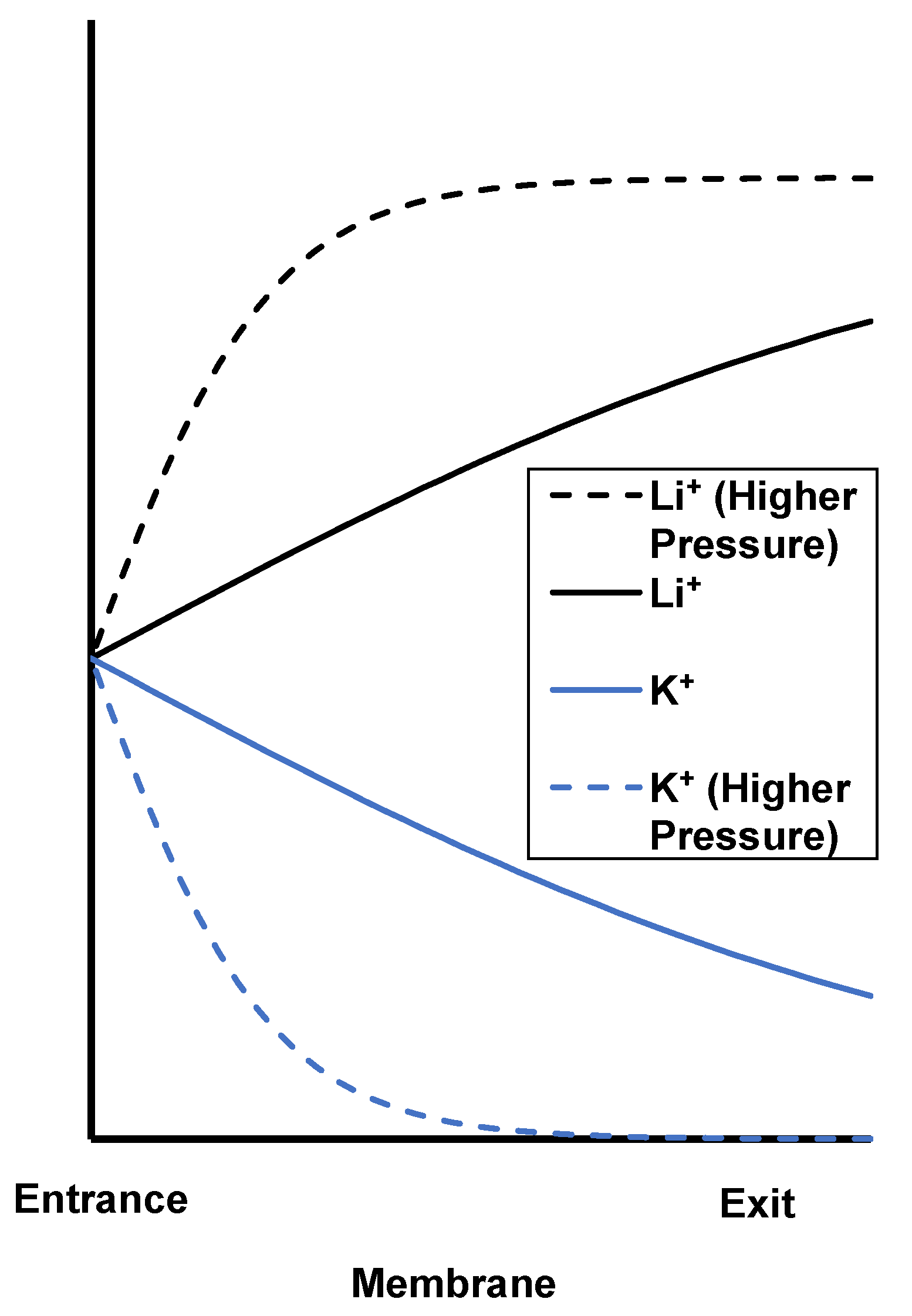
3.3.1. Effect of Rotation Rate (Concentration Polarization)
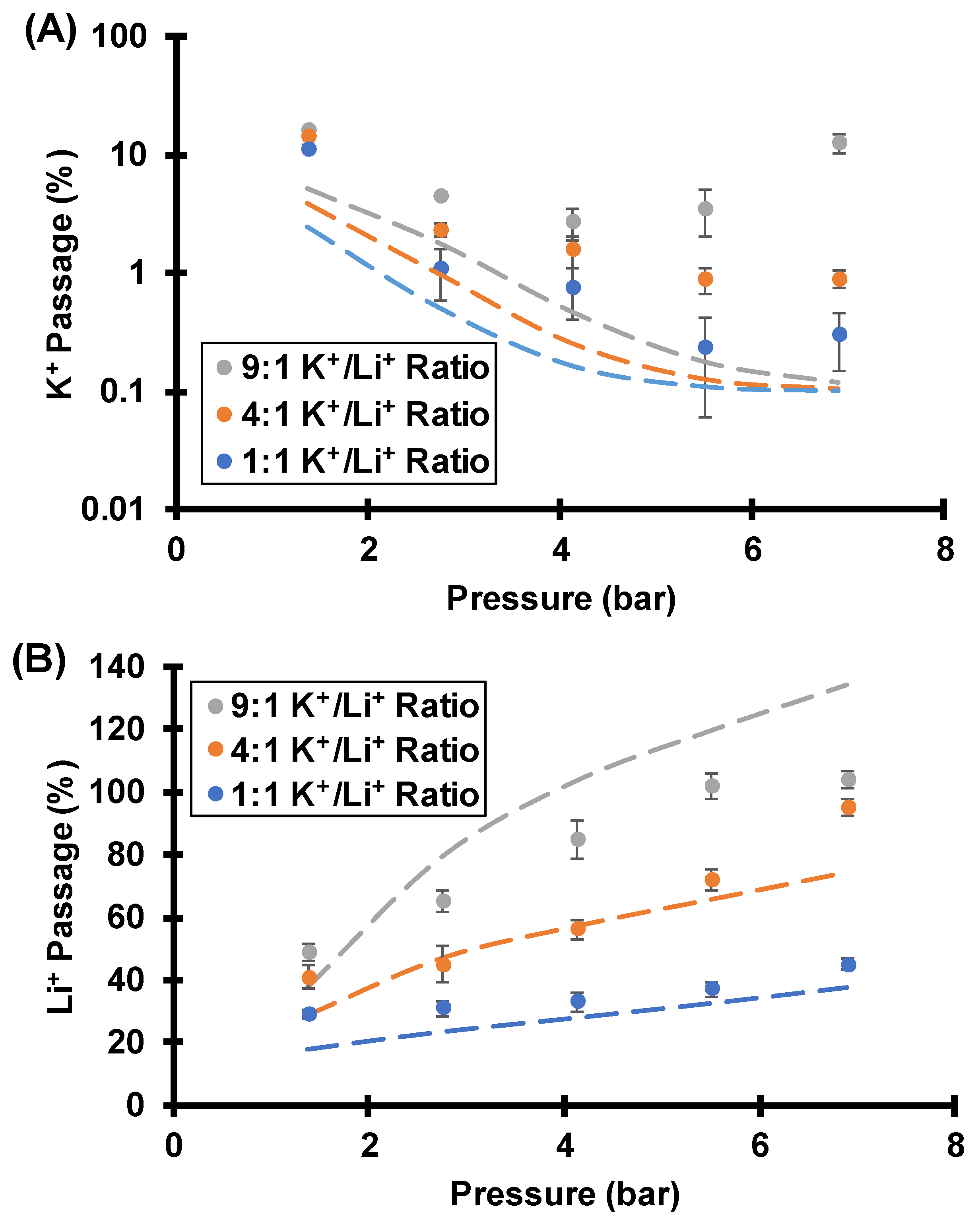
3.3.2. Effect of Feed K+/Li+ Molar Ratios on Separations
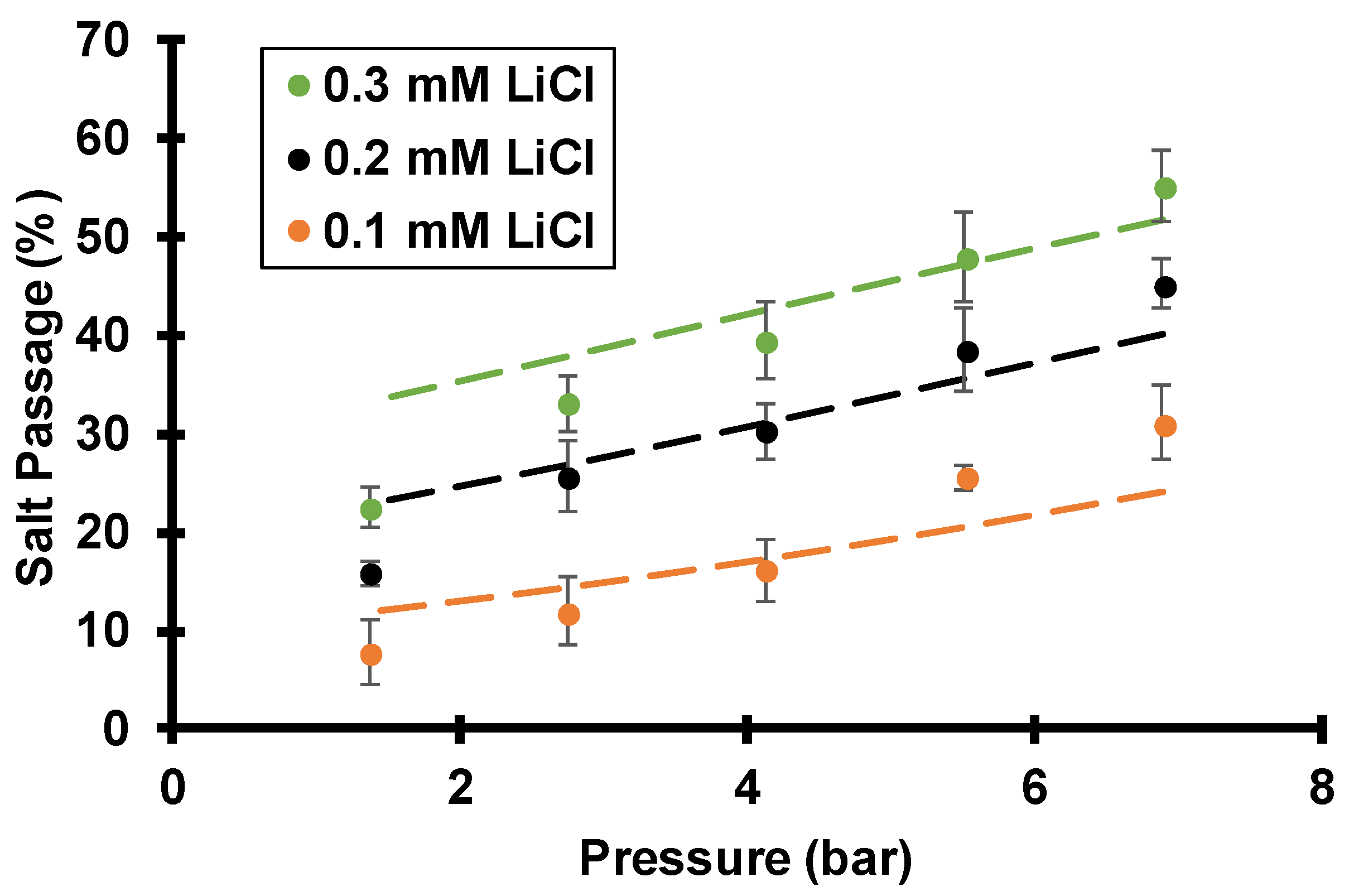
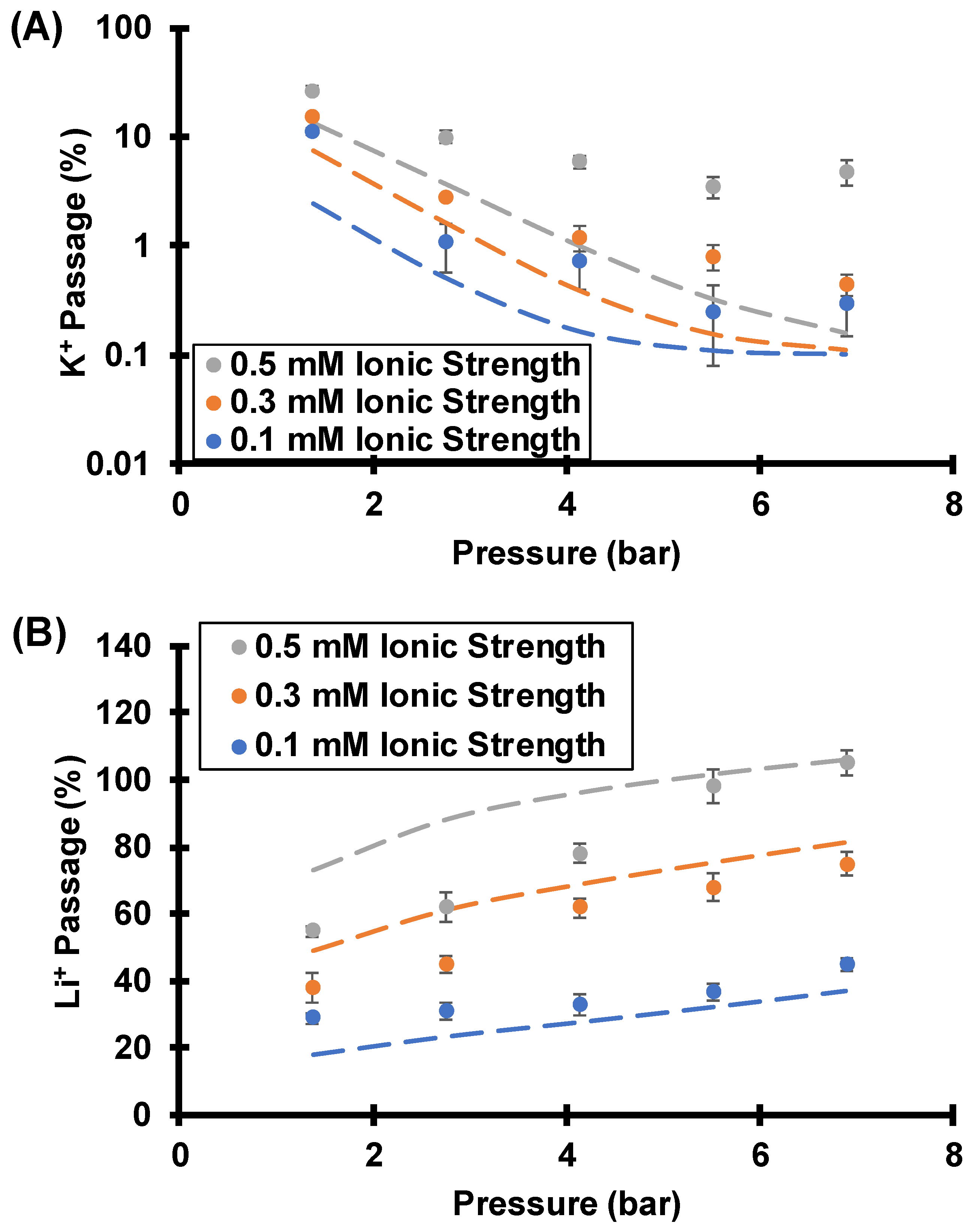
3.3.3. Effect of Feed Ionic Strength
3.3.4. Comparison to Other Studies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef] [PubMed]
- Stamp, A.; Lang, D.J.; Wäger, P.A. Environmental impacts of a transition toward e-mobility: The present and future role of lithium carbonate production. J. Clean. Prod. 2012, 23, 104–112. [Google Scholar] [CrossRef]
- Peiró, L.T.; Méndez, G.V.; Ayres, R.U. Lithium: Sources, production, uses, and recovery outlook. JOM 2013, 65, 986–996. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Bruening, M.L. Ion separations with membranes. J. Polym. Sci. 2020, 58, 2831–2856. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Lee, M.S. A review on the separation of lithium ion from leach liquors of primary and secondary resources by solvent extraction with commercial extractants. Processes 2018, 6, 55. [Google Scholar] [CrossRef] [Green Version]
- Xie, F.; Zhang, T.A.; Dreisinger, D.; Doyle, F. A critical review on solvent extraction of rare earths from aqueous solutions. Miner. Eng. 2014, 56, 10–28. [Google Scholar] [CrossRef]
- Ding, D.; Yaroshchuk, A.; Bruening, M.L. Electrodialysis through Nafion membranes coated with polyelectrolyte multilayers yields >99% pure monovalent ions at high recoveries. J. Membr. Sci. 2022, 647, 120294. [Google Scholar] [CrossRef]
- Abdu, S.; Martí-Calatayud, M.-C.; Wong, J.E.; García-Gabaldón, M.; Wessling, M. Layer-by-layer modification of cation exchange membranes controls ion selectivity and water splitting. ACS Appl. Mater. Interfaces 2014, 6, 1843–1854. [Google Scholar] [CrossRef]
- Amara, M.; Kerdjoudj, H. Modified membranes applied to metallic ion separation and mineral acid concentration by electrodialysis. Sep. Purif. Technol. 2002, 29, 79–87. [Google Scholar] [CrossRef]
- Lambert, J.; Avila-Rodriguez, M.; Durand, G.; Rakib, M. Separation of sodium ions from trivalent chromium by electrodialysis using monovalent cation selective membranes. J. Membr. Sci. 2006, 280, 219–225. [Google Scholar] [CrossRef]
- Pérez-González, A.; Ibáñez, R.; Gómez, P.; Urtiaga, A.M.; Ortiz, I.; Irabien, J.A. Nanofiltration separation of polyvalent and monovalent anions in desalination brines. J. Membr. Sci. 2015, 473, 16–27. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, W. Positively charged hollow-fiber composite nanofiltration membrane prepared by quaternization crosslinking. J. Appl. Polym. Sci. 2013, 129, 2806–2812. [Google Scholar] [CrossRef]
- Li, Q.; Liu, H.; He, B.; Shi, W.; Ji, Y.; Cui, Z.; Yan, F.; Mohammad, Y.; Li, J. Ultrahigh-efficient separation of Mg2+/Li+ using an in-situ reconstructed positively charged nanofiltration membrane under an electric field. J. Membr. Sci. 2022, 641, 119880. [Google Scholar] [CrossRef]
- Epsztein, R.; Shaulsky, E.; Dizge, N.; Warsinger, D.M.; Elimelech, M. Role of ionic charge density in Donnan exclusion of monovalent anions by nanofiltration. Environ. Sci. Technol. 2018, 52, 4108–4116. [Google Scholar] [CrossRef] [PubMed]
- Apel, P.; Bondarenko, M.; Yamauchi, Y.; Yaroshchuk, A. Osmotic pressure and diffusion of ions in charged nanopores. Langmuir 2021, 37, 14089–14095. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Vasu, K.S.; Williams, C.D.; Gopinadhan, K.; Su, Y.; Cherian, C.T.; Dix, J.; Prestat, E.; Haigh, S.J.; Grigorieva, I.V.; et al. Tunable sieving of ions using graphene oxide membranes. Nat. Nanotechnol. 2017, 12, 546–550. [Google Scholar] [CrossRef]
- Chen, L.; Shi, G.; Shen, J.; Peng, B.; Zhang, B.; Wang, Y.; Bian, F.; Wang, J.; Li, D.; Qian, Z.; et al. Ion sieving in graphene oxide membranes via cationic control of interlayer spacing. Nature 2017, 550, 380–383. [Google Scholar] [CrossRef]
- Joshi, R.K.; Carbone, P.; Wang, F.C.; Kravets, V.G.; Su, Y.; Grigorieva, I.V.; Wu, H.A.; Geim, A.K.; Nair, R.R. Precise and ultrafast molecular sieving through graphene oxide membranes. Science 2014, 343, 752–754. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Ying, Y.; Mao, Y.; Peng, X.; Chen, B. Polystyrene sulfonate threaded through a metal–organic framework membrane for fast and selective lithium-ion separation. Angew. Chem. Int. Ed. 2016, 55, 15120–15124. [Google Scholar] [CrossRef]
- Wen, Y.; Dai, R.; Li, X.; Zhang, X.; Cao, X.; Wu, Z.; Lin, S.; Tang, C.Y.; Wang, Z. Metal-organic framework enables ultraselective polyamide membrane for desalination and water reuse. Sci. Adv. 2022, 8, 10. [Google Scholar] [CrossRef]
- Li, J.; Yi, H.; Wang, M.; Yan, F.; Zhu, Q.; Wang, S.; Li, J.; He, B.; Cui, Z. Preparation of crown-ether-functionalized polysulfone membrane by in situ surface grafting for selective adsorption and separation of Li+. ChemistrySelect 2020, 5, 3321–3329. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhang, Y.; Zheng, X.; Sun, W.; Li, B.; Wang, D.; Li, Z. High specific surface crown ether modified chitosan nanofiber membrane by low-temperature phase separation for efficient selective adsorption of lithium. Sep. Purif. Technol. 2021, 262, 118312. [Google Scholar] [CrossRef]
- Acar, E.; Buchsbaum, S.; Combs, C.; Fornasiero, F.; Siwy, Z. Biomimetic potassium-selective nanopores. Sci. Adv. 2019, 5, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, C.; Yaroshchuk, A.; Bruening, M.L. Flow through negatively charged, nanoporous membranes separates Li+ and K+ due to induced electromigration. Chem. Commun. 2020, 56, 10954–10957. [Google Scholar] [CrossRef] [PubMed]
- Déjardin, P.; Vasina, E.N.; Berezkin, V.V.; Sobolev, V.D.; Volkov, V.I. Streaming potential in cylindrical pores of poly(ethylene terephthalate) track-etched membranes: variation of apparent ζ potential with pore radius. Langmuir 2005, 21, 4680–4685. [Google Scholar] [CrossRef] [PubMed]
- Lettmann, C.; Möckel, D.; Staude, E. Permeation and tangential flow streaming potential measurements for electrokinetic characterization of track-etched microfiltration membranes. J. Membr. Sci. 1999, 159, 243–251. [Google Scholar] [CrossRef]
- Vanysek, P. Ionic conductivity and diffusion at infinite dilution. In CRC Handbook of Chemistry and Physics; Lide, D.R., Ed.; CRC Press: Boca Raton, FL, USA, 2000; Volume 83, pp. 76–78. [Google Scholar]
- Helfferich, F. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Dresner, L. Stability of the extended Nernst-Planck equations in the description of hyperfiltration through ion-exchange membranes. J. Phys. Chem. 1972, 76, 2256–2267. [Google Scholar] [CrossRef]
- Dresner, L. Some remarks on the integration of the extended Nernst-Planck equations in the hyperfiltration of multicomponent solutions. Desalination 1972, 10, 27–46. [Google Scholar] [CrossRef]
- de Labastida, M.F.; Licón, E.E.; Bondarenko, M.; Yaroshchuk, A. Rotating disk-like membrane cell for pressure-driven measurements with equally-accessible membrane surface: Numerical simulation and experimental validation. J. Membr. Sci. 2018, 550, 492–501. [Google Scholar] [CrossRef]
- de Labastida, M.F.; Yaroshchuk, A. Nanofiltration of multi-ion solutions: Quantitative control of concentration polarization and interpretation by solution-diffusion-electro-migration model. Membranes. 2021, 11, 272. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Ferain, E.; Legras, R. Pore shape control in nanoporous particle track etched membrane. Nucl. Instrum. Methods Phys. Res. B: Beam Interact. Mater. At. 1997, 131, 97–102. [Google Scholar] [CrossRef]
- Kozinski, A.; Lightfoot, E. Protein ultrafiltration: A general example of boundary layer filtration. AIChE J. 1972, 18, 1030–1040. [Google Scholar] [CrossRef]
- Elimelech, M.; Chen, W.H.; Waypa, J.J. Measuring the zeta (electrokinetic) potential of reverse-osmosis membranes by a streaming potential analyzer. Desalination 1994, 95, 269–286. [Google Scholar] [CrossRef]
- Huisman, I.H.; Prádanos, P.; Calvo, J.I.; Hernández, A. Electroviscous effects, streaming potential, and zeta potential in polycarbonate track-etched membranes. J. Membr. Sci. 2000, 178, 79–92. [Google Scholar] [CrossRef]
- Kim, K.J.; Fane, A.G.; Nyström, M.; Pihlajamaki, A. Chemical and electrical characterization of virgin and protein-fouled polycarbonate track-etched membranes by FTIR and streaming-potential measurements. J. Membr. Sci. 1997, 134, 199–208. [Google Scholar] [CrossRef]
- Kestin, J.; Khalifa, H.E.; Correia, R.J. Tables of the dynamic and kinematic viscosity of aqueous NaCl solutions in the temperature range 20–150 °C and the pressure range 0.1–35 MPa. J. Phys. Chem. Ref. Data 1981, 10, 71–88. [Google Scholar] [CrossRef]
- Bowen, W.R.; Jenner, F. Electroviscous effects in charged capillaries. J. Colloid Interface Sci. 1995, 173, 388–395. [Google Scholar] [CrossRef]
- Ren, L.; Li, D.; Qu, W. Electro-viscous effects on liquid flow in microchannels. J. Colloid Interface Sci. 2001, 233, 12–22. [Google Scholar] [CrossRef]
- Kong, J.; Bo, Z.; Yang, H.; Yang, J.; Shuai, X.; Yan, J.; Cen, K. Temperature dependence of ion diffusion coefficients in NaCl electrolyte confined within graphene nanochannels. Phys. Chem. Chem. Phys. 2017, 19, 7678–7688. [Google Scholar] [CrossRef]
- Tang, C.; Bondarenko, M.P.; Yaroshchuk, A.; Bruening, M.L. Highly selective ion separations based on counter-flow electromigration in nanoporous membranes. J. Membr. Sci. 2021, 638, 119684. [Google Scholar] [CrossRef]
- Qian, Z.; Miedema, H.; Sahin, S.; de Smet, L.C.P.M.; Sudhölter, E.J.R. Separation of alkali metal cations by a supported liquid membrane (SLM) operating under electro dialysis (ED) conditions. Desalination 2020, 495, 114631. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; He, B.; Sun, Z.; Yan, F.; Cui, Z.; Li, J. High-Efficiency Separation of Mg2+/Sr2+ through a NF Membrane under Electric Field. Membranes 2021, 12, 57. [Google Scholar] [CrossRef] [PubMed]
- Ounissi, T.; Dammak, L.; Fauvarque, C.L.J.-F.; Hmida, E.S.B.H. Novel lithium selective composite membranes: Synthesis, characterization and validation tests in dialysis. J. Mater. Sci. 2020, 55, 16111–16128. [Google Scholar] [CrossRef]
- Butylskii, D.Y.; Pismenskaya, N.D.; Apel, P.Y.; Sabbatovskiy, K.G.; Nikonenko, V.V. Highly selective separation of singly charged cations by countercurrent electromigration with a track-etched membrane. J. Membr. Sci. 2021, 635, 119449. [Google Scholar] [CrossRef]
- Kelson, N.; Desseaux, A. Note on porous rotating disk flow. ANZIAM J. 2000, 42, C837–C855. [Google Scholar] [CrossRef]



| Properties | Value |
|---|---|
| Pore diameter | 30 nm |
| Pore length | 6 µm |
| Membrane surface charge density | −2.2 mC/m2 |
| Transmembrane pressure | 20–100 psi (1.4–6.9 bar) |
| Flow velocity within the boundary layer | Obtained from permeability measurements |
| Fluid dynamic viscosity | 0.00089 Pa/s at 25 °C |
| Flow velocity within the pores | Calculated from Hagen–Poiseuille model |
| K+ diffusion coefficient 1 | 1.96 × 10−9 m2/s |
| Li+ diffusion coefficient 1 | 1.03 × 10−9 m2/s |
| Cl− diffusion coefficient 1 | 2.03 × 10−9 m2/s |
| Boundary layer thickness (from Levich equation for K+) | 19.4 µm @ 1000 rpm 25.1 µm @ 600 rpm 63.1 µm @ 95 rpm |
| Mechanism | Selectivity |
|---|---|
| Differences in dehydration energy and mobility between ion species | K+/Na+ ~850 in electrodialysis [44] Sr2+/Mg2+ ~900 in electric field-assisted nanofiltration [45] K+/Li+ and Na+/Li+ selectivities ~ 100 [16] |
| Molecular recognition | Li+/Na+ ~280 and Li+/K+ ~360 in dialysis [46] K+/Na+ ~20 in conductivity measurements [23] |
| Opposing flow and electric field | Li+/K+ ~150 in dead-end filtration (this work) K+/Li+ ~30 in hybrid electro-baromembrane process [47] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.; Yaroshchuk, A.; Bruening, M.L. Ion Separations Based on Spontaneously Arising Streaming Potentials in Rotating Isoporous Membranes. Membranes 2022, 12, 631. https://doi.org/10.3390/membranes12060631
Tang C, Yaroshchuk A, Bruening ML. Ion Separations Based on Spontaneously Arising Streaming Potentials in Rotating Isoporous Membranes. Membranes. 2022; 12(6):631. https://doi.org/10.3390/membranes12060631
Chicago/Turabian StyleTang, Chao, Andriy Yaroshchuk, and Merlin L. Bruening. 2022. "Ion Separations Based on Spontaneously Arising Streaming Potentials in Rotating Isoporous Membranes" Membranes 12, no. 6: 631. https://doi.org/10.3390/membranes12060631
APA StyleTang, C., Yaroshchuk, A., & Bruening, M. L. (2022). Ion Separations Based on Spontaneously Arising Streaming Potentials in Rotating Isoporous Membranes. Membranes, 12(6), 631. https://doi.org/10.3390/membranes12060631






