Modulatory Effects of Acidic pH and Membrane Potential on the Adsorption of pH-Sensitive Peptides to Anionic Lipid Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals and Reagents
2.2. Peptide Synthesis
2.3. Preparation of Large Unilamellar Vesicles
DLS and Zeta Potential
2.4. Peptide Adsorption onto the Membrane: Binding Experiments
2.5. Constant pH Molecular Dynamics Simulations
3. Results
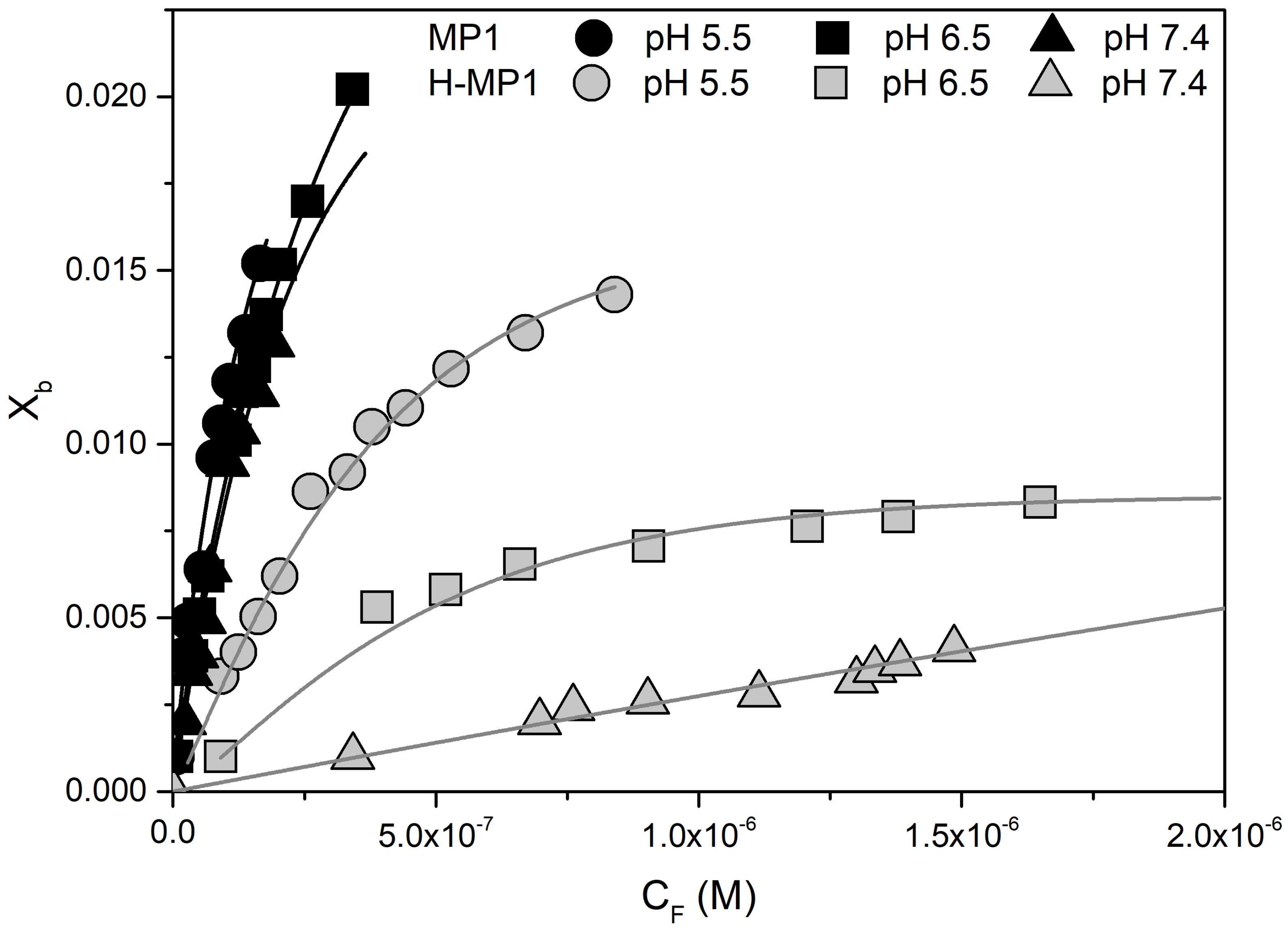
3.1. Peptide Affinity to the Anionic Membrane Investigated by Fluorescence Spectroscopy
Analyses of Adsorption Isotherms Using Gouy–Chapman Theory
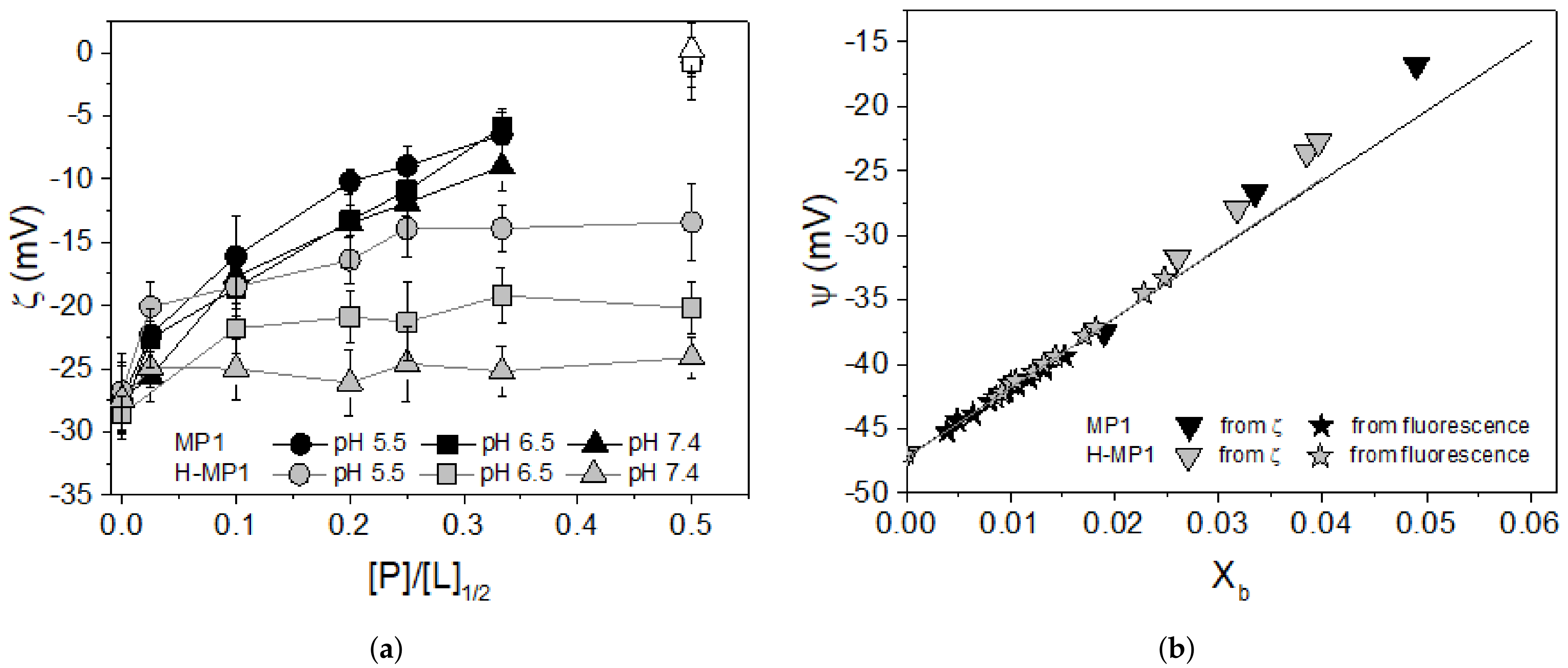
3.2. Zeta Potential Measurements
3.3. Peptide Net Charge Calculated Via CpHMD Simulations
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zasloff, M. Antimicrobial peptides of multicellular organisms. Nature 2002, 415, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Yeaman, M.R. Mechanisms of antimicrobial peptide action and resistance. Pharmacol. Rev. 2003, 55, 27–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blondelle, S.E.; Lohner, K.; Aguilar, M. Lipid-induced conformation and lipid-binding properties of cytolytic and antimicrobial peptides: Determination and biological specificity. Biochim. Biophys. Acta 1999, 1462, 89–108. [Google Scholar] [CrossRef] [Green Version]
- Boman, H.G. Antibacterial peptides: Basic facts and emerging concepts. J. Intern. Med. 2003, 254, 197–215. [Google Scholar] [CrossRef]
- Epand, R.M.; Vogel, H.J. Diversity of antimicrobial peptides and their mechanisms of action. Biochim. Biophys. Acta 1999, 1462, 11–28. [Google Scholar] [CrossRef] [Green Version]
- Hancock, R.E.; Falla, T.; Brown, T. Cationic bactericidal peptides. Adv. Microb. Physiol. 1995, 37, 135–175. [Google Scholar]
- Wade, D.; Boman, A.; Wahlin, B.; Drain, C.M.; Andreu, D.; Boman, H.G.; Merrifield, R.B. All-D amino acid-containing channel-forming antibiotic peptides. Proc. Natl. Acad. Sci. USA 1990, 87, 4761–4765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christof, J.; Harvey, R.D.; Bruce, K.D.; Dolling, R.; Bagheri, M.; Dathe, M. Cyclic antimicrobial R-, W-rich peptides: The role of peptide structure and E. coli outer and inner membranes in activity and the mode of action. Eur. Biophys. J. 2011, 40, 515–528. [Google Scholar]
- Scheinpflug, K.; Krylova, O.; Nikolenko, H.; Thurm, C.; Dathe, M. Evidence for a novel mechanism of antimicrobial action of a cyclic R-, W-rich hexapeptide. PLoS ONE 2015, 10, 4e0125056. [Google Scholar] [CrossRef]
- Chen, Y.; Mant, C.T.; Farmer, S.W.; Hancock, R.E.W.; Vasil, M.L.; Hodges, R.S. Rational design of α-helical antimicrobial peptides with enhanced activities and specificity/therapeutic index. J. Biol. Chem. 2005, 280, 12316–12329. [Google Scholar] [CrossRef] [Green Version]
- Dathe, M.; Nikolenko, H.; Meyer, J.; Beyermann, M.; Bienert, M. Optimization of the antimicrobial activity of magainin peptides by modification of charge. FEBS Lett. 2001, 501, 146–150. [Google Scholar] [CrossRef] [Green Version]
- Souza, B.M.; Dos Santos Cabrera, M.P.; Gomes, P.C.; Dias, N.B.; Stabeli, R.G.; Leite, N.B.; Ruggiero Neto, J.; Palma, M.S. Structure-activity relationship of mastoparan analogs: Effects of the number and positioning of Lys residues on secondary structure, interaction with membrane-mimetic systems and biological activity. Peptides 2015, 72, 164–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Souza, B.M.; Mendes, M.A.; Santos, L.D.; Marques, M.R.; Cesar, L.M.M.; Almeida, R.N.A.; Pagnocca, F.C.; Konno, K.; Palma, M.S. Structural and functional characterization of two novel peptide toxins isolated from the venom of the social wasp Polybia paulista. Peptides 2005, 26, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zhang, B.; Zhang, W.; Yan, J.; Li, J.; Wang, R. Antitumor effects, cell selectivity and structure–activity relationship of a novel antimicrobial peptide Polybia-MPI. Peptides 2008, 29, 963–968. [Google Scholar] [CrossRef] [PubMed]
- Shai, Y. Mechanism of the binding, insertion and destabilization of phospholipid bilayer membranes by alpha-helical antimicrobial and cell non-selective membrane-lytic peptides. Biochim. Biophys. Acta 1999, 1462, 55–70. [Google Scholar] [CrossRef] [Green Version]
- Leite, N.B.; Da Costa, L.C.; Alvares, D.S.; Dos Santos Cabrera, M.P.; Souza, B.M.; Palma, M.S.; Ruggiero Neto, J. The effect of acidic residues and amphipathicity on the lytic activities of mastoparan peptides studied by fluorescence and CD spectroscopy. Amino Acids 2011, 40, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Kato, Y.; Ozawa, S.; Miyamoto, C.; Maehata, Y.; Suzuki, A.; Maeda, T.; Baba, Y. Acidic extracellular microenvironment and cancer. Cancer Cell Int. 2013, 13, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Korenchan, D.E.; Flavell, R.R. Cancer Progression and Therapeutic Resistance. Cancers 2019, 11, 1026. [Google Scholar] [CrossRef] [Green Version]
- Persi, E.; Duran-Frigola, M.; Damaghi, M.; Roush, W.R.; Aloy, P.; Cleveland, J.L.; Gillies, R.J.; Ruppin, E. Systems analysis of intracellular pH vulnerabilities for cancer therapy. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Utsugi, T.; Schroit, A.J.; Connor, J.; Bucana, C.; Fidler, I.J. Elevated expression of phosphatidylserine in the outer membrane leaflet of human tumor cells and recognition by activated human blood monocytes. Cancer Res. 1991, 11, 3062–3066. [Google Scholar]
- Fadok, V.A.; Voelker, D.R.; Campbell, P.A.; Cohen, J.J.; Bratton, D.L.; Henson, P.M. Exposure of phosphatidylserine on the surface of apoptotic lymphocytes triggers specific recognition and removal by macrophages. J. Immunol. 1992, 148, 2207–2216. [Google Scholar] [PubMed]
- Gouy, G. Sur la constitution de la charge électrique a la surface d’un électrolyte. Ann. Phys. 1910, 4, 457–468. [Google Scholar] [CrossRef] [Green Version]
- Chapman, D.L. A contribution to the theory of electrocapillarity. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1913, 25, 475–481. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, S. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 113–136. [Google Scholar] [CrossRef] [PubMed]
- Aveyard, R.; Haydon, D.A. An Introduction to the Principles of Surface Chemistry; Cambridge University Press: London, UK, 1973. [Google Scholar]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications, 3rd ed.; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Agadi, N.; Vasudevan, S.; Kumar, A. Structural insight into the mechanism of action of antimicrobial peptide BMAP-28(1-18) and its analogue mutBMAP18. J. Struct. Biol. 2019, 204, 435–448. [Google Scholar] [CrossRef] [PubMed]
- Souza, L.M.P.; Nascimento, J.B.; Romeu, A.L.; Estrada-López, E.D.; Pimentel, A.S. Penetration of antimicrobial peptides in a lung surfactant model. Colloids Surf. B Biointerfaces 2018, 167, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Ermakova, E.; Kurbanov, R.; Zuev, Y. Coarse-grained molecular dynamics of membrane semitoroidal pore formation in model lipid-peptide systems. J. Mol. Graph. Model. 2019, 87, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bertrand, B.; Munusamy, S.; Espinosa-Romero, J.F.; Corzo, G.; Arenas Sosa, I.; Galván-Hernández, A.; Ortega-Blake, I.; Hernández-Adame, P.L.; Ruiz-García, J.; Velasco-Bolom, J.L.; et al. Biophysical characterization of the insertion of two potent antimicrobial peptides-Pin2 and its variant Pin2[GVG] in biological model membranes. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183105. [Google Scholar] [CrossRef]
- Sani, M.A.; Le Brun, A.P.; Separovic, F. The antimicrobial peptide maculatin self assembles in parallel to form a pore in phospholipid bilayers. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183204. [Google Scholar] [CrossRef] [PubMed]
- Bogdanova, L.R.; Valiullina, Y.A.; Faizullin, D.A.; Kurbanov, R.K.; Ermakova, E.A. Spectroscopic, zeta potential and molecular dynamics studies of the interaction of antimicrobial peptides with model bacterial membrane. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 242, 118785. [Google Scholar] [CrossRef] [PubMed]
- Baptista, A.M.; Teixeira, V.H.; Soares, C.M. Constant-pH molecular dynamics using stochastic titration. J. Chem. Phys. 2002, 117, 4184–4200. [Google Scholar] [CrossRef]
- Lousa, D.; Pinto, A.R.T.; Campos, S.R.R.; Baptista, A.M.; Veiga, A.S.; Castanho, M.A.R.B.; Soares, C.M. Efect of pH on the influenza fusion peptide properties unveiled by constant-pH molecular dynamics simulations combined with experiment. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef]
- Mongan, J.; Case, D.A.; McCammon, J.A. Constant pH molecular dynamics in generalized Born implicit solvent. J. Comput. Chem. 2004, 25, 2038–2048. [Google Scholar] [CrossRef] [PubMed]
- Khandogin, J.; Brooks, C.L. Toward the accurate first-principles prediction of ionization equilibria in proteins. Biochemistry 2006, 45, 9363–9373. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Radak, B.K.; Chipot, C.; Suh, D.; Jo, S.; Jiang, W.; Phillips, J.C.; Schulten, K.; Roux, B. Constant-pH molecular dynamics simulations for large biomolecular systems. J. Chem. Theory Comput. 2017, 13, 5933–5944. [Google Scholar] [CrossRef]
- Martins, I.B.S.; Viegas, T.G.; Alvares, D.S.; Souza, B.M.; Palma, M.S.; Ruggiero Neto, J.; Araujo, A.S. The effect of acidic pH on the adsorption and lytic activity of the peptides Polybia-MP1 and its histidine-containing analog in anionic lipid membrane: A biophysical study by molecular dynamics and spectroscopy. Amino Acids 2020. accepted. [Google Scholar]
- Ladokhin, A.S.; Jayasinghe, S.; White, S.H. How to measure and analyze tryptophan fluorescence in membranes properly, and why bother? Anal. Biochem. 2000, 285, 235–245. [Google Scholar] [CrossRef]
- Marsh, D. Handbook of Lipid Bilayers, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Santos, N.C.; Prieto, M.; Castanho, M.A.R.B. Quantifying molecular partition into model systems of biomembranes: An emphasis on optical spectroscopic methods. Biochim. Biophys. Acta Biomembr. 2003, 1612, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 16, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, J.; MacKerell, A.D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 25, 2135–2145. [Google Scholar] [CrossRef] [Green Version]
- Mark, P.; Nilsson, L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Jo, S.; Lim, J.B.; Klauda, J.B.; Im, W. CHARMM-GUI membrane builder for mixed bilayers and its application to yeast membranes. Biophys. J. 2009, 97, 50–58. [Google Scholar] [CrossRef] [Green Version]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Davidchack, R.L.; Handel, R.; Tretyakov, M.V. Langevin thermostat for rigid body dynamics. J. Chem. Phys. 2009, 130, 234101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Elber, R.; Ruymgaart, A.P.; Hess, B. SHAKE parallelization. Eur. Phys. J. Spec. Top. 2011, 200, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 1, 33–38. [Google Scholar] [CrossRef]
- Murray, D.; Arbuzova, A.; Honig, B.; McLaughlin, S. The role of electrostatic and non-polar interaction in the association of peripheral proteins with membranes. Curr. Top. Membr. 2002, 52, 277–307. [Google Scholar]
- Tamba, Y.; Yamazaki, M. Magainin 2-induced pore formation in the lipid membranes depends on its concentration in the membrane. J. Phys. Chem. B 2009, 113, 4846–4852. [Google Scholar] [CrossRef] [PubMed]
- Grimsley, G.R.; Scholtz, J.M.; Pace, C.N. A summary of the measured pK values of the ionizable groups in folded proteins. Protein Sci. 2009, 18, 247–251. [Google Scholar] [PubMed] [Green Version]
- Thurlkill, R.L.; Grimsley, G.R.; Scholtz, J.M.; Pace, C.N. pK values of the ionizable groups of proteins. Protein Sci. 2006, 15, 1214–1218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaines, G.L. Insoluble Monolayers at Liquid-Gas Interfaces; Interscience Publishers: New York, NY, USA, 1966. [Google Scholar]
- Dolovv, K. Bioelectrochemistry of cell surfaces. Prog. Surf. Sci. 1964, 15, 245–366. [Google Scholar]
- Haugen, A.; May, S. The influence of zwitterionic lipids on the electrostatic adsorption of macroions onto mixed lipid membranes. J. Chem. Phys. 2007, 127, 215104. [Google Scholar] [CrossRef]


| MP1 | H-MP1 | |||||
|---|---|---|---|---|---|---|
| pH | GC pH | GC pH | CpHMD | GC pH | GC pH | CpHMD |
| 5.5 | ||||||
| 6.5 | ||||||
| 7.4 | ||||||
| In Aqueous Solution | |||
|---|---|---|---|
| pH | |||
| Residues | 5.5 | 6.5 | 7.4 |
| Asp2 | |||
| Lys4 | |||
| Lys5 | |||
| Asp8 | |||
| Lys11 | |||
| Adsorbed on the Lipid Bilayer | |||
| pH | |||
| Residues | 5.5 | 6.5 | 7.4 |
| Asp2 | |||
| Lys4 | |||
| Lys5 | |||
| Asp8 | |||
| Lys11 | |||
| In Aqueous Solution | |||
|---|---|---|---|
| pH | |||
| Residues | 5.5 | 6.5 | 7.4 |
| Asp2 | |||
| His4 | |||
| His5 | |||
| Asp8 | |||
| His11 | |||
| Adsorbed on the Lipid Bilayer | |||
| pH | |||
| Residues | 5.5 | 6.5 | 7.4 |
| Asp2 | |||
| His4 | |||
| His5 | |||
| Asp8 | |||
| His11 | |||
| MP1 | H-MP1 | |||
|---|---|---|---|---|
| Residues | ||||
| Asp2 | ||||
| His4 | - | - | ||
| His5 | - | - | ||
| Asp8 | ||||
| His11 | - | - | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvares, D.d.S.; Martins, I.B.S.; Viegas, T.G.; Palma, M.S.; de Araujo, A.S.; de Carvalho, S.J.; Ruggiero Neto, J. Modulatory Effects of Acidic pH and Membrane Potential on the Adsorption of pH-Sensitive Peptides to Anionic Lipid Membrane. Membranes 2021, 11, 307. https://doi.org/10.3390/membranes11050307
Alvares DdS, Martins IBS, Viegas TG, Palma MS, de Araujo AS, de Carvalho SJ, Ruggiero Neto J. Modulatory Effects of Acidic pH and Membrane Potential on the Adsorption of pH-Sensitive Peptides to Anionic Lipid Membrane. Membranes. 2021; 11(5):307. https://doi.org/10.3390/membranes11050307
Chicago/Turabian StyleAlvares, Dayane dos Santos, Ingrid Bernardes Santana Martins, Taisa Giordano Viegas, Mario Sergio Palma, Alexandre Suman de Araujo, Sidney Jurado de Carvalho, and João Ruggiero Neto. 2021. "Modulatory Effects of Acidic pH and Membrane Potential on the Adsorption of pH-Sensitive Peptides to Anionic Lipid Membrane" Membranes 11, no. 5: 307. https://doi.org/10.3390/membranes11050307







