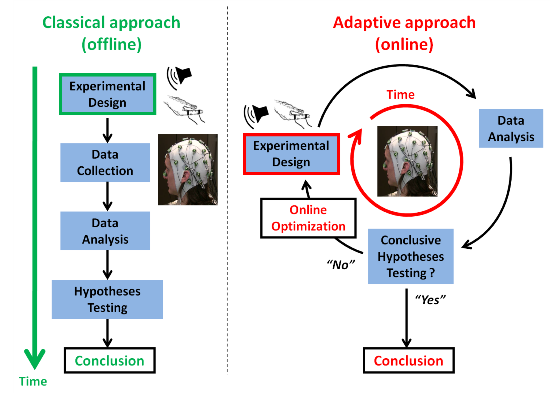
Toward a New Application of Real-Time Electrophysiology: Online Optimization of Cognitive Neurosciences Hypothesis Testing
Abstract
:1. Introduction
1.1. On Common Challenges in BCI (Brain-Computer Interfaces) and Cognitive Neurosciences
1.2. Adaptive Design Optimization
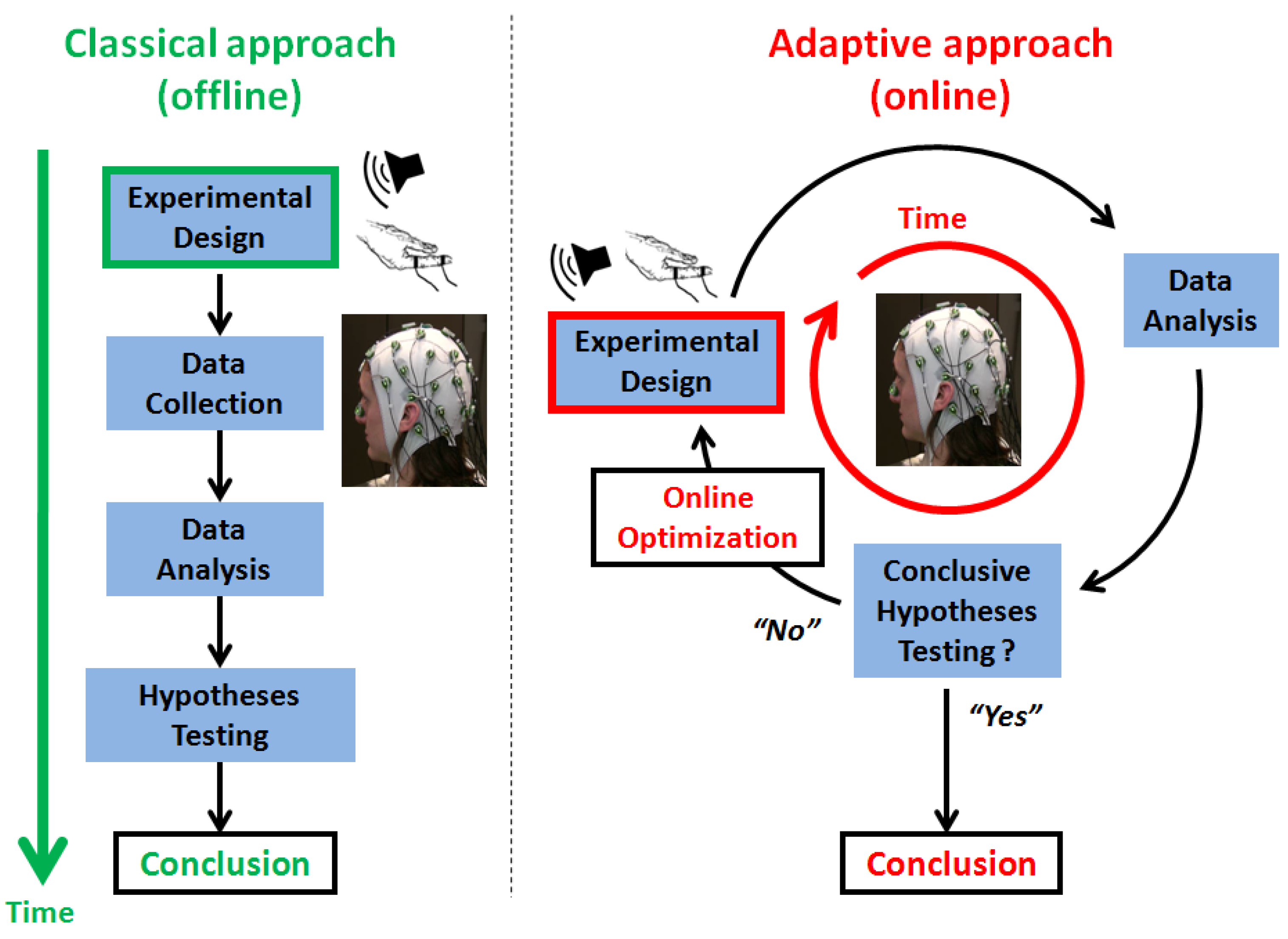
2. Theory and Methods
2.1. Dynamic Causal Models (DCMs)
2.2. Online Optimization of Model Comparison
- (i)
- Running the variational Bayes (VB) inference for each model, M, given past observations and experimental design variables;
- (ii)
- Updating the prior over models with the obtained posteriors;
- (iii)
- Computing the design efficiency or Laplace-Chernoff bound for each possible value of the experimental design variable, u;
- (iv)
- Selecting the optimal design for the next trial or stage.
2.3. Validation
2.3.1. First Study: Synthetic Behavioral Data
2.3.2. Second Study: Synthetic Electrophysiological Data
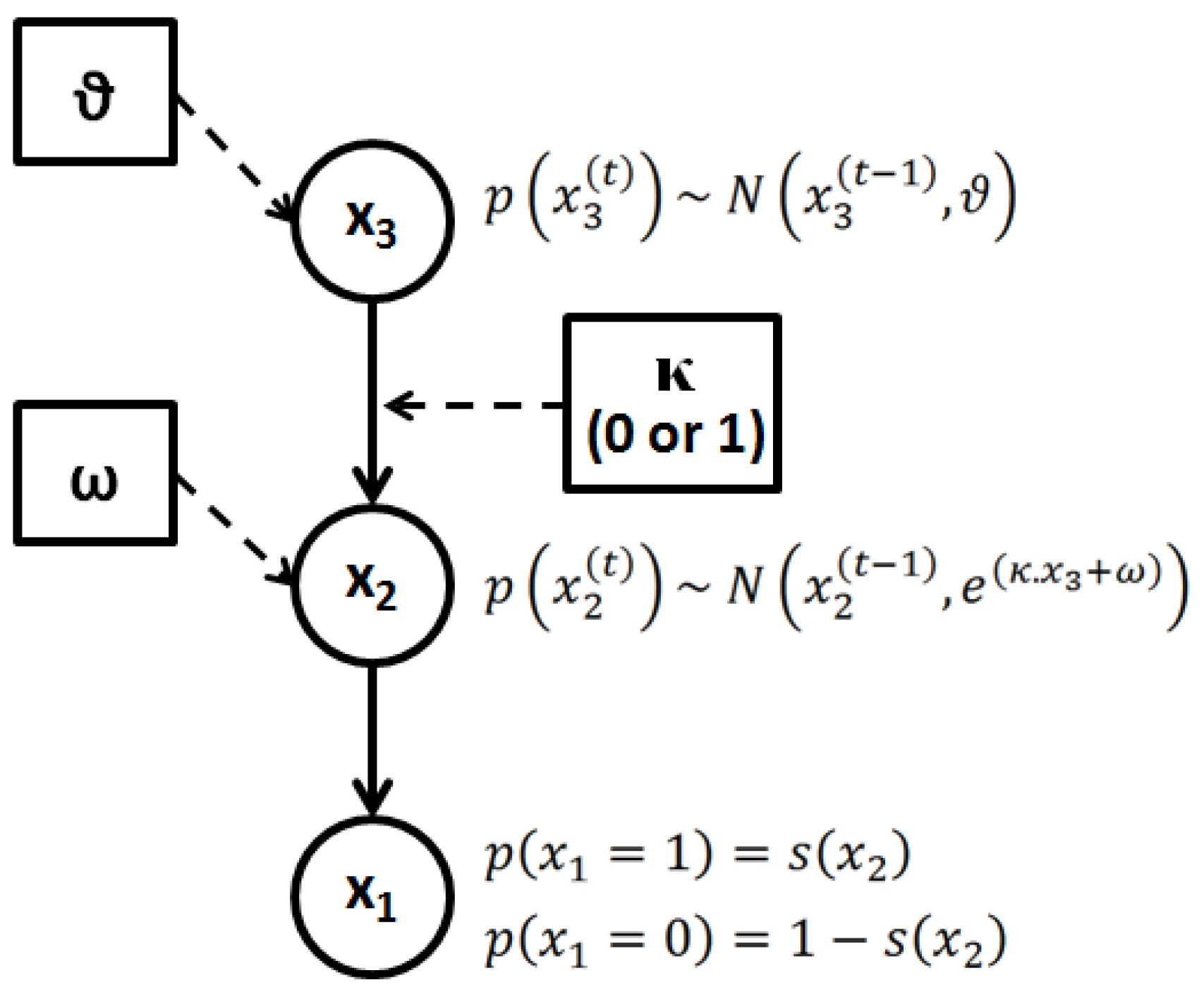
2.3.2.1. Perceptual Learning Model
 , with x1 = 1 for deviant and x1 = 0 for standard stimuli) is governed by a state, x2, at the next level of the hierarchy. The brain perceptual model assumes that the probability distribution of x1 is conditional on x2, as follows:
, with x1 = 1 for deviant and x1 = 0 for standard stimuli) is governed by a state, x2, at the next level of the hierarchy. The brain perceptual model assumes that the probability distribution of x1 is conditional on x2, as follows:
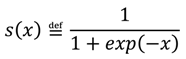
 , is normally distributed with mean
, is normally distributed with mean  and variance
and variance  :
:
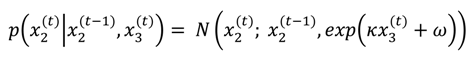
 , on a given trial is normally distributed around
, on a given trial is normally distributed around  , with a variance determined by the constant parameter, ϑ. The latter effectively controls the variability of the log-volatility over time.
, with a variance determined by the constant parameter, ϑ. The latter effectively controls the variability of the log-volatility over time.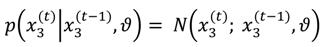
2.3.2.2. Electrophysiological Response Model
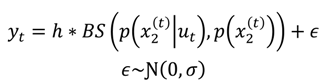
| Models | ω Values | κ Values (If κ = 0, No Third Level) | ϑ Values | Ability to Track Events Probabilities | Ability to Track Environmental Volatility |
|---|---|---|---|---|---|
| M1 | −Inf | 0 | - | No | No |
| M2 | −5 | 0 | - | Low learning | No |
| M3 | −4 | 0 | - | High learning | No |
| M4 | −5 | 1 | 0.2 | Low learning | Yes |
| M5 | −4 | 1 | 0.2 | High learning | Yes |
2.4. Software Note
3. Results
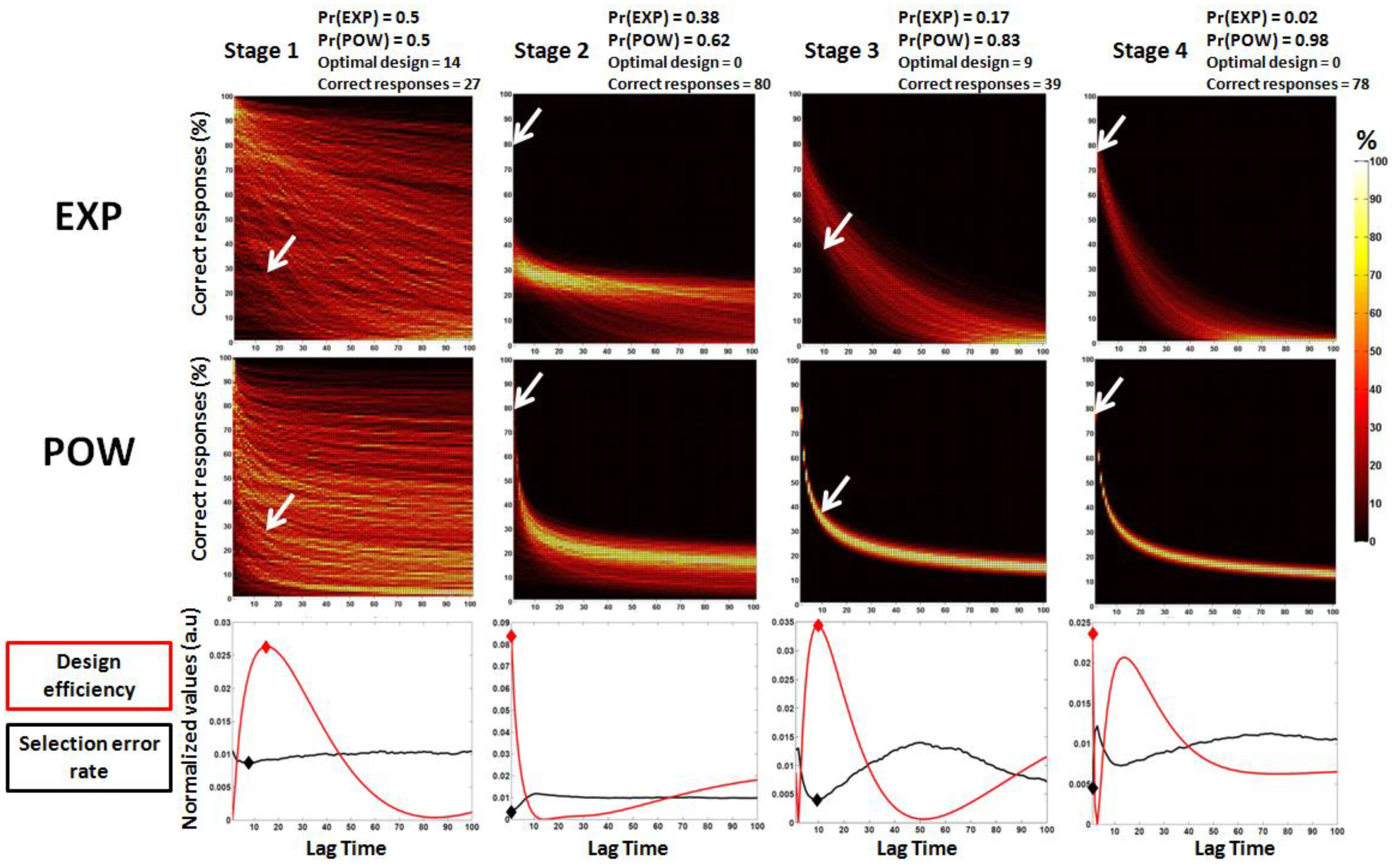
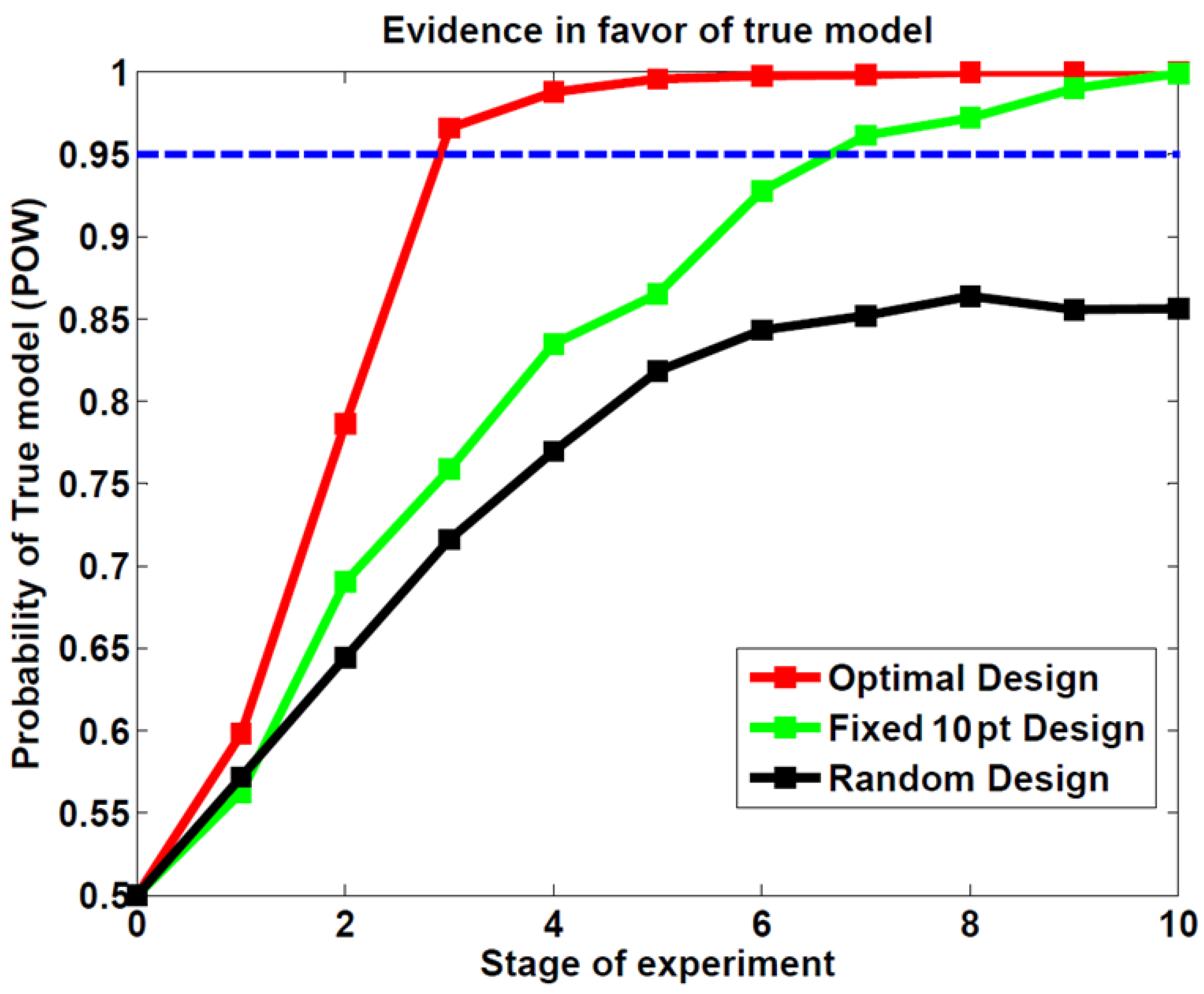
3.1. First Study: Behavioral Synthetic Data

3.2. Second Study: Electrophysiological Synthetic Data

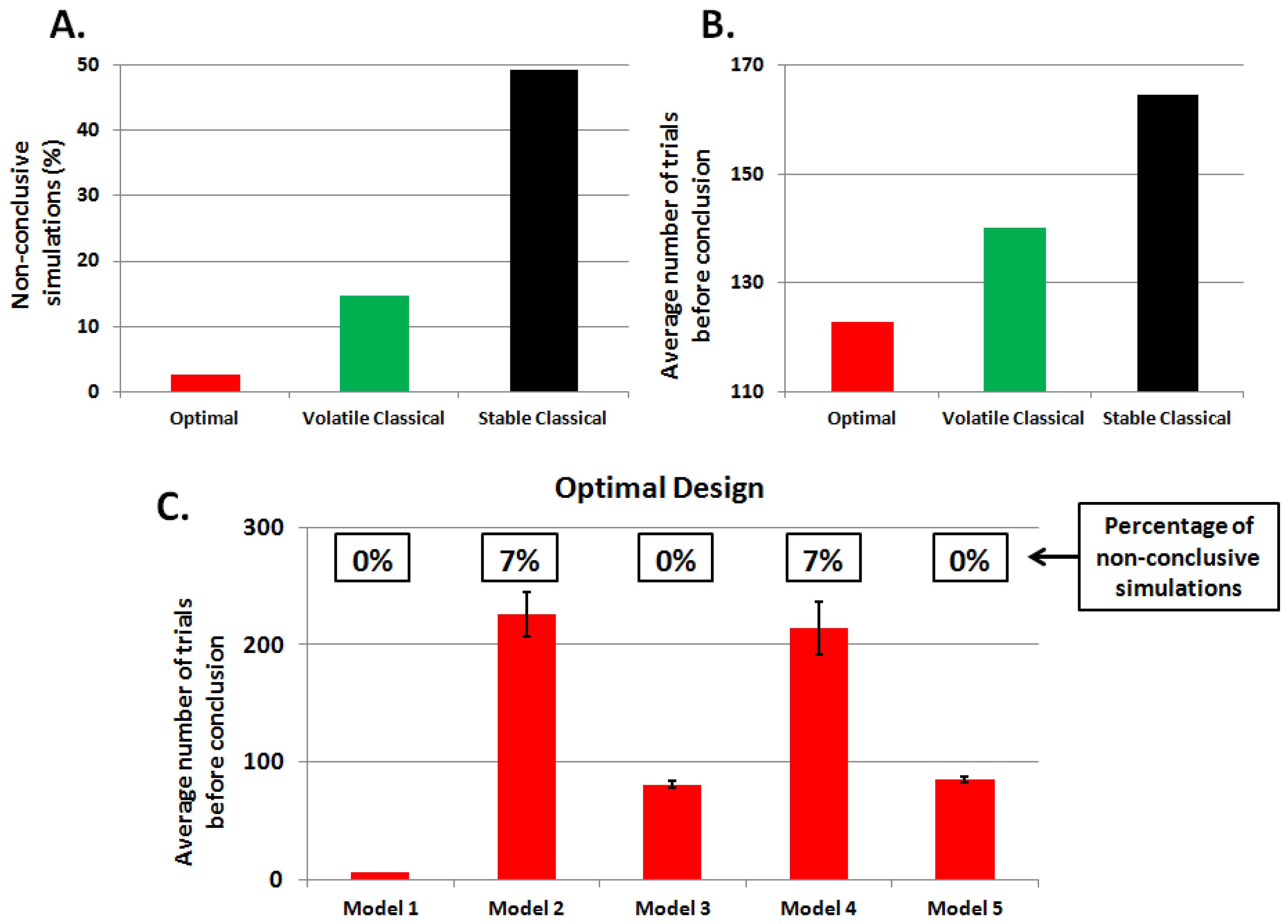
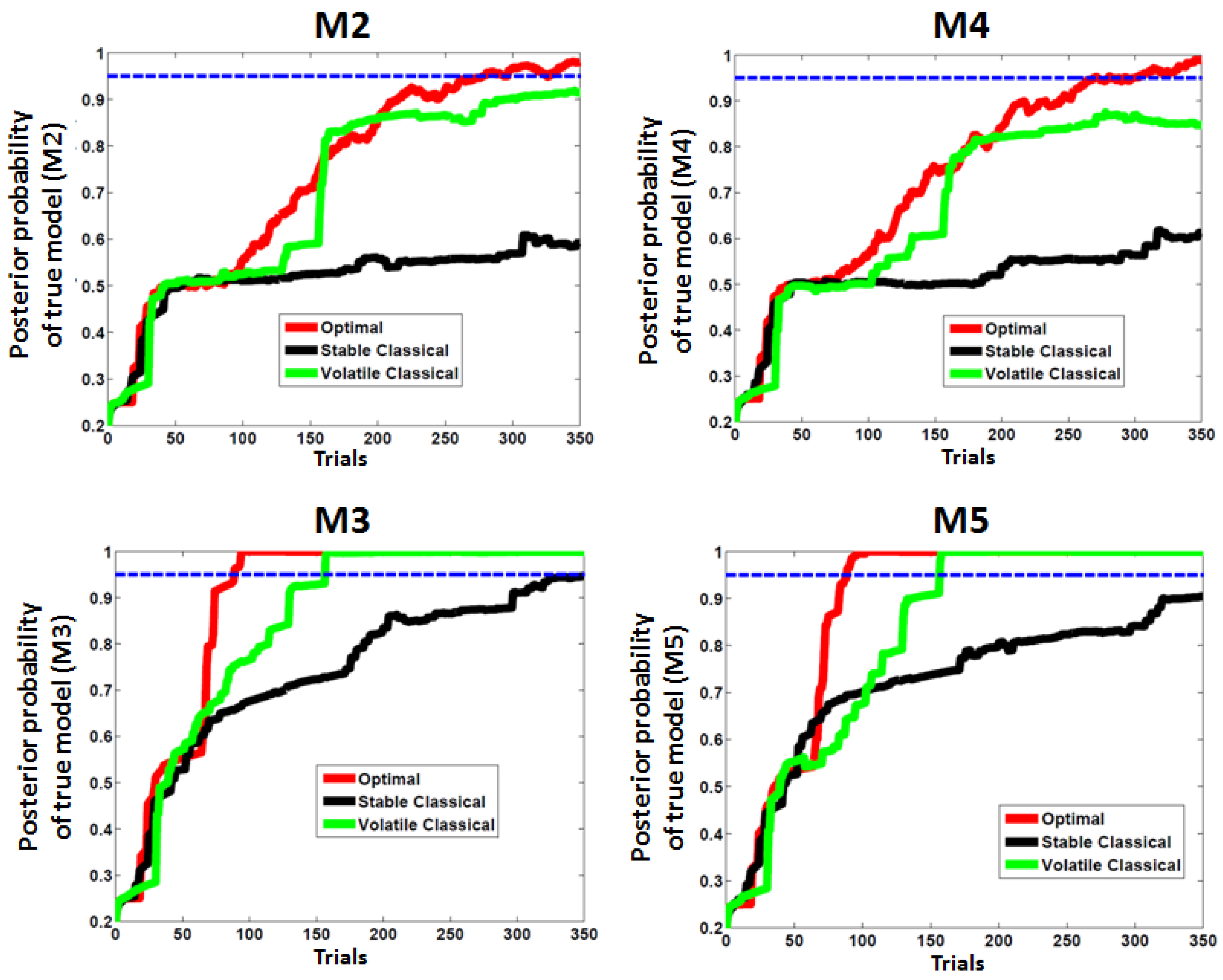
4. Discussion
4.1. Current Limitations
4.2. Perspectives
5. Conclusion
Acknowledgments
Conflicts of Interest
Appendix A
A1. Bayesian Inference
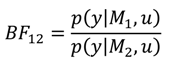
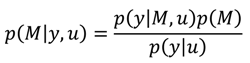
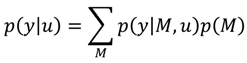
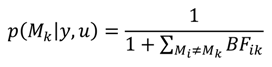
A2. Design Efficiency: A Decision Theoretic Criterion
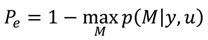
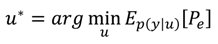
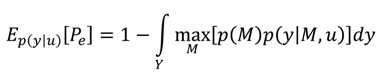
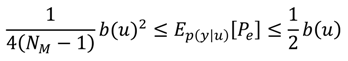
A3. Comparison of the Chernoff Bound with the Other Criterion

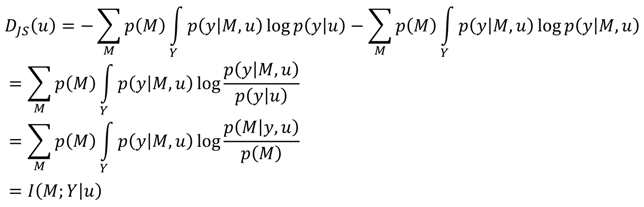
References
- Del R Millán, J.; Carmena, J.M. Invasive or noninvasive: Understanding brain-machine interface technology. IEEE Eng. Med. Biol. Mag. 2010, 29, 16–22. [Google Scholar] [CrossRef]
- Birbaumer, N.; Cohen, L.G. Brain-computer interfaces: Communication and restoration of movement in paralysis. J. Physiol. 2007, 579, 621–636. [Google Scholar] [CrossRef]
- Maby, E.; Perrin, M.; Morlet, D.; Ruby, P.; Bertrand, O.; Ciancia, S.; Gallifet, N.; Luaute, J.; Mattout, J. Evaluation in a Locked-in Patient of the OpenViBE P300-speller. In Proceedings of the 5th International Brain-Computer Interface, Graz, Austria, 22–24 September 2011; pp. 272–275.
- Perrin, M.; Maby, E.; Daligault, S.; Bertrand, O.; Mattout, J. Objective and subjective evaluation of online error correction during P300-based spelling. Adv. Hum. Comput. Interact. 2012, 2012, 578295:1–578295:13. [Google Scholar]
- Johnston, S.J.; Boehm, S.G.; Healy, D.; Goebel, R.; Linden, D.E. Neurofeedback: A promising tool for the self-regulation of emotion networks. NeuroImage 2010, 49, 1066–1072. [Google Scholar] [CrossRef]
- Kübler, A.; Kotchoubey, B. Brain–computer interfaces in the continuum of consciousness. Curr. Opin. Neurol. 2007, 20, 643–649. [Google Scholar] [CrossRef]
- Cruse, D.; Chennu, S.; Chatelle, C.; Bekinschtein, T.A.; Fernández-Espejo, D.; Pickard, J.D.; Laureys, S.; Owen, A.M. Bedside detection of awareness in the vegetative state: A cohort study. Lancet 2011, 378, 2088–2094. [Google Scholar] [CrossRef]
- Mattout, J. Brain-computer interfaces: A neuroscience paradigm of social interaction? A matter of perspective. Front. Hum. Neurosci. 2012. [Google Scholar] [CrossRef]
- Brodersen, K.H.; Haiss, F.; Ong, C.S.; Jung, F.; Tittgemeyer, M.; Buhmann, J.M.; Weber, B.; Stephan, K.E. Model-based feature construction for multivariate decoding. NeuroImage 2011, 56, 601–615. [Google Scholar] [CrossRef] [Green Version]
- Mattout, J.; Gibert, G.; Attina, V.; Maby, E.; Bertrand, O. Probabilistic Classification Models for Brain Computer Interfaces. In Proceedings of the Human Brain Mapping Conference, Melbourne, Australia, 15–19 June 2008.
- Cecotti, H.; Rivet, B.; Congedo, M.; Jutten, C.; Bertrand, O.; Maby, E.; Mattout, J. A robust sensor-selection method for P300 brain–computer interfaces. J. Neural Eng. 2011, 8, 016001. [Google Scholar] [CrossRef]
- Farquhar, J.; Hill, N.J. Interactions between pre-processing and classification methods for event-related-potential classification. Neuroinformatics 2013, 11, 175–192. [Google Scholar] [CrossRef]
- Ekandem, J.I.; Davis, T.A.; Alvarez, I.; James, M.T.; Gilbert, J.E. Evaluating the ergonomics of BCI devices for research and experimentation. Ergonomics 2012, 55, 592–598. [Google Scholar] [CrossRef]
- Schalk, G.; McFarland, D.J.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J.R. BCI2000: A general-purpose brain-computer interface (BCI) system. IEEE Trans. Biomed. Eng. 2004, 51, 1034–1043. [Google Scholar] [CrossRef]
- Renard, Y.; Lotte, F.; Gibert, G.; Congedo, M.; Maby, E.; Delannoy, V.; Bertrand, O.; Lécuyer, A. OpenViBE: An open-source software platform to design, test, and use brain-computer interfaces in real and virtual environments. Presence Teleoperators Virtual Environ. 2010, 19, 35–53. [Google Scholar]
- Jensen, O.; Bahramisharif, A.; Okazaki, Y.O.; van Gerven, M.A.J. Using brain-computer interfaces and brain-state dependent stimulation as tools in cognitive neuroscience. Front. Psychol. 2011, 2011. [Google Scholar] [CrossRef] [Green Version]
- Koush, Y.; Rosa, M.J.; Robineau, F.; Heinen, K.; W. Rieger, S.; Weiskopf, N.; Vuilleumier, P.; van de Ville, D.; Scharnowski, F. Connectivity-based neurofeedback: Dynamic causal modeling for real-time fMRI. NeuroImage 2013, 81, 422–430. [Google Scholar] [CrossRef]
- Garcı́a-Pérez, M.A. Forced-choice staircases with fixed step sizes: Asymptotic and small-sample properties. Vision Res. 1998, 38, 1861–1881. [Google Scholar] [CrossRef]
- Henson, R. Efficient Experimental Design for fMRI. In Statistical Parametric Mapping: The Analysis of Functional Brain Images; Academic Press: London, UK, 2007; pp. 193–210. [Google Scholar]
- Myung, J.I.; Cavagnaro, D.R.; Pitt, M.A. A tutorial on adaptive design optimization. J. Math. Psychol. 2013, 57, 53–67. [Google Scholar] [CrossRef]
- Wald, A. Sequential tests of statistical hypotheses. Ann. Math. Stat. 1945, 16, 117–186. [Google Scholar] [CrossRef]
- Glas, C.A.; van der Linden, W.J. Computerized adaptive testing with item cloning. Appl. Psychol. Meas. 2003, 27, 247–261. [Google Scholar] [CrossRef]
- Kujala, J.V.; Lukka, T.J. Bayesian adaptive estimation: The next dimension. J. Math. Psychol. 2006, 50, 369–389. [Google Scholar] [CrossRef]
- Cavagnaro, D.R.; Pitt, M.A.; Myung, J.I. Model discrimination through adaptive experimentation. Psychon. Bull. Rev. 2010, 18, 204–210. [Google Scholar] [CrossRef]
- Lewi, J.; Butera, R.; Paninski, L. Sequential optimal design of neurophysiology experiments. Neural Comput. 2009, 21, 619–687. [Google Scholar] [CrossRef]
- Friston, K.J.; Dolan, R.J. Computational and dynamic models in neuroimaging. NeuroImage 2010, 52, 752–765. [Google Scholar] [CrossRef]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. NeuroImage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
- Daunizeau, J.; den Ouden, H.E.M.; Pessiglione, M.; Kiebel, S.J.; Stephan, K.E.; Friston, K.J. Observing the observer (I): Meta-bayesian models of learning and decision-making. PLoS One 2010, 5, e15554. [Google Scholar]
- Daunizeau, J.; David, O.; Stephan, K.E. Dynamic causal modelling: A critical review of the biophysical and statistical foundations. NeuroImage 2011, 58, 312–322. [Google Scholar] [CrossRef] [Green Version]
- Körding, K.P.; Wolpert, D.M. Bayesian integration in sensorimotor learning. Nature 2004, 427, 244–247. [Google Scholar] [CrossRef]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference; Gatsby Computational Neuroscience Unit, University College London: London, UK, 2003. [Google Scholar]
- Daunizeau, J.; Preuschoff, K.; Friston, K.; Stephan, K. Optimizing experimental design for comparing models of brain function. PLoS Comput. Biol. 2011, 7, e1002280. [Google Scholar] [CrossRef] [Green Version]
- David, O.; Kiebel, S.J.; Harrison, L.M.; Mattout, J.; Kilner, J.M.; Friston, K.J. Dynamic causal modeling of evoked responses in EEG and MEG. NeuroImage 2006, 30, 1255–1272. [Google Scholar] [CrossRef]
- Chen, C.C.; Kiebel, S.J.; Friston, K.J. Dynamic causal modelling of induced responses. NeuroImage 2008, 41, 1293–1312. [Google Scholar] [CrossRef]
- Moran, R.J.; Stephan, K.E.; Seidenbecher, T.; Pape, H.-C.; Dolan, R.J.; Friston, K.J. Dynamic causal models of steady-state responses. NeuroImage 2009, 44, 796–811. [Google Scholar] [CrossRef]
- Lieder, F.; Daunizeau, J.; Garrido, M.I.; Friston, K.J.; Stephan, K.E. Modelling trial-by-trial changes in the mismatch negativity. PLoS Comput. Biol. 2013, 9, e1002911. [Google Scholar] [CrossRef]
- Friston, K.; Mattout, J.; Trujillo-Barreto, N.; Ashburner, J.; Penny, W. Variational free energy and the Laplace approximation. NeuroImage 2007, 34, 220–234. [Google Scholar] [CrossRef]
- Cavagnaro, D.R.; Myung, J.I.; Pitt, M.A.; Tang, Y. Better Data with Fewer Participants and Trials: Improving Experiment Efficiency with Adaptive Design Optimization. In Proceedings of the 31st Annual Conference of the Cognitive Science Society, Amsterdam, The Netherlands, 29 July–1 August 2009; pp. 93–98.
- Rubin, D.C.; Hinton, S.; Wenzel, A. The precise time course of retention. J. Exp. Psychol. Learn. Mem. Cogn. 1999, 25, 1161–1176. [Google Scholar] [CrossRef]
- Behrens, T.E.J.; Woolrich, M.W.; Walton, M.E.; Rushworth, M.F.S. Learning the value of information in an uncertain world. Nat. Neurosci. 2007, 10, 1214–1221. [Google Scholar] [CrossRef]
- Den Ouden, H.E.M.; Daunizeau, J.; Roiser, J.; Friston, K.J.; Stephan, K.E. Striatal prediction error modulates cortical coupling. J. Neurosci. 2010, 30, 3210–3219. [Google Scholar] [CrossRef] [Green Version]
- Harrison, L.M.; Bestmann, S.; Rosa, M.J.; Penny, W.; Green, G.G.R. Time scales of representation in the human brain: Weighing past information to predict future events. Front. Hum. Neurosci. 2011. [Google Scholar] [CrossRef]
- Mathys, C.; Daunizeau, J.; Friston, K.J.; Stephan, K.E. A bayesian foundation for individual learning under uncertainty. Front. Hum. Neurosci. 2011, 2011. [Google Scholar] [CrossRef] [Green Version]
- Ostwald, D.; Spitzer, B.; Guggenmos, M.; Schmidt, T.T.; Kiebel, S.J.; Blankenburg, F. Evidence for neural encoding of Bayesian surprise in human somatosensation. NeuroImage 2012, 62, 177–188. [Google Scholar] [CrossRef]
- Friston, K.J. Models of brain function in neuroimaging. Annu. Rev. Psychol. 2005, 56, 57–87. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Näätänen, R.; Tervaniemi, M.; Sussman, E.; Paavilainen, P.; Winkler, I. “Primitive intelligence” in the auditory cortex. Trends Neurosci. 2001, 24, 283–288. [Google Scholar] [CrossRef]
- Fischer, C.; Luaute, J.; Morlet, D. Event-related potentials (MMN and novelty P3) in permanent vegetative or minimally conscious states. Clin. Neurophysiol. 2010, 121, 1032–1042. [Google Scholar] [CrossRef]
- Vossel, S.; Mathys, C.; Daunizeau, J.; Bauer, M.; Driver, J.; Friston, K.J.; Stephan, K.E. Spatial attention, precision, and bayesian inference: A study of saccadic response speed. Cereb. Cortex 2013. [Google Scholar] [CrossRef]
- Baldi, P.; Itti, L. Of bits and wows: A bayesian theory of surprise with applications to attention. Neural Netw. 2010, 23, 649–666. [Google Scholar] [CrossRef]
- Penny, W.D. Kullback-Leibler Divergences of Normal, Gamma, Dirichlet and Wishart Densities, Wellcome Department Cognitive Neurology 2001. Available online: http://130.203.133.150/showciting;jsessionid=A0DC3581428F458BF2B759805C684BB3?cid=459356&sort=date (accessed on 15 January 2014).
- Daunizeau, J.; Adam, V.; Rigoux, L. VBA: A probabilistic treatment of nonlinear models for neurobiological and behavioural data. PLoS Comput. Biol. 2013, in press. [Google Scholar]
- Variational bayesian toolbox. Available online: http://code.google.com/p/mbb-vb-toolbox/wiki/InstallingTheToolbox (accessed on 15 January 2014).
- Morlet, D.; Fischer, C. MMN and novelty P3 in coma and other altered states of consciousness: A review. Brain Topogr. 2013, 26. [Google Scholar] [CrossRef] [Green Version]
- Boly, M.; Garrido, M.I.; Gosseries, O.; Bruno, M.-A.; Boveroux, P.; Schnakers, C.; Massimini, M.; Litvak, V.; Laureys, S.; Friston, K. Preserved feedforward but impaired top-down processes in the vegetative state. Science 2011, 332, 858–862. [Google Scholar]
- Bekinschtein, T.A.; Dehaene, S.; Rohaut, B.; Tadel, F.; Cohen, L.; Naccache, L. Neural signature of the conscious processing of auditory regularities. Proc. Natl. Acad. Sci. USA 2009, 106, 1672–1677. [Google Scholar]
- TIDRA. Available online: http://www.tidra.org (accessed on 15 January 2014).
- Penny, W.D. Comparing dynamic causal models using AIC, BIC and free energy. NeuroImage 2012, 59, 319–330. [Google Scholar]
- Pitt, M.A.; Myung, I.J. When a good fit can be bad. Trends Cogn. Sci. 2002, 6, 421–425. [Google Scholar]
- Flandin, G.; Penny, W.D. Bayesian fMRI data analysis with sparse spatial basis function priors. NeuroImage 2007, 34, 1108–1125. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar]
- Topsoe, F. Some inequalities for information divergence and related measures of discrimination. IEEE Trans. Inf. Theory 2000, 46, 1602–1609. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sanchez, G.; Daunizeau, J.; Maby, E.; Bertrand, O.; Bompas, A.; Mattout, J. Toward a New Application of Real-Time Electrophysiology: Online Optimization of Cognitive Neurosciences Hypothesis Testing. Brain Sci. 2014, 4, 49-72. https://doi.org/10.3390/brainsci4010049
Sanchez G, Daunizeau J, Maby E, Bertrand O, Bompas A, Mattout J. Toward a New Application of Real-Time Electrophysiology: Online Optimization of Cognitive Neurosciences Hypothesis Testing. Brain Sciences. 2014; 4(1):49-72. https://doi.org/10.3390/brainsci4010049
Chicago/Turabian StyleSanchez, Gaëtan, Jean Daunizeau, Emmanuel Maby, Olivier Bertrand, Aline Bompas, and Jérémie Mattout. 2014. "Toward a New Application of Real-Time Electrophysiology: Online Optimization of Cognitive Neurosciences Hypothesis Testing" Brain Sciences 4, no. 1: 49-72. https://doi.org/10.3390/brainsci4010049