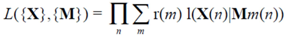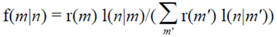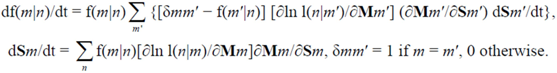1.1. Computational Complexity since the 1950s
Developing mathematical descriptions of the very first recognition step in this seemingly simple association-recognition-understanding process has not been easy, a number of difficulties have been encountered during the past 50 years. These difficulties were summarized under the notion of combinatorial complexity (CC) [
6]. CC refers to multiple combinations of bottom-up and top-down signals, or more generally to combinations of various elements in a complex system; for example, recognition of a scene often requires concurrent recognition of its multiple elements that could be encountered in various combinations. CC is computationally prohibitive because the number of combinations is very large: for example, consider 100 elements (not too large a number); the number of combinations of 100 elements is 100
100, exceeding the number of all elementary particle events in the life of the Universe; no computer would ever be able to compute that many combinations. Although, the story might sound “old”, we concentrate here on those aspects of mathematical modeling of the brain-mind, which remain current and affect thinking in computational modeling and in cognitive science of many scientists today.
The problem of CC was first identified in pattern recognition and classification research in the 1960s and was named “the curse of dimensionality” [
7]. It seemed that adaptive self-learning algorithms and neural networks could learn solutions to any problem “on their own”, if provided with a sufficient number of training examples. The following decades of developing adaptive statistical pattern recognition and neural network algorithms led to a conclusion that the required number of training examples often was combinatorially large. This remains true about recent generation of algorithms and neural networks, which are much more powerful than those in the 1950s and 60s. Training had to include not only every object in its multiple variations, angles,
etc., but also combinations of objects. Thus, self-learning approaches encountered CC of learning requirements.
Rule systems were proposed in the 1970s to solve the problem of learning complexity [
8,
9]. Minsky suggested that learning was a premature step in artificial intelligence; Newton “learned” Newtonian laws, most of scientists read them in the books. Therefore, Minsky has suggested, knowledge ought to be input in computers “ready made” for all situations and artificial intelligence would apply these known rules. Rules would capture the required knowledge and eliminate a need for learning. Chomsky’s original ideas concerning mechanisms of language grammar related to deep structure [
10] were also based on logical rules. Rule systems work well when all aspects of the problem can be predetermined. However, in the presence of variability, the number of rules grew; rules became contingent on other rules and combinations of rules had to be considered. The rule systems encountered CC of rules.
In the 1980s, model systems were proposed to combine advantages of learning and rules-models by using adaptive models [
11,
12,
13,
14,
15,
16,
17,
18]. Existing knowledge was to be encapsulated in models and unknown aspects of concrete situations were to be described by adaptive parameters. Along similar lines went the principles and parameters idea of Chomsky [
19]. Fitting models to data (top-down to bottom-up signals) required selecting data subsets corresponding to various models. The number of subsets, however, is combinatorially large. A general popular algorithm for fitting models to the data, multiple hypotheses testing [
20] is known to face CC of computations. Model-based approaches encountered computational CC (N and NP complete algorithms). None of the past computational approaches modeled specifically human, “aesthetic emotions” (discussed later) related to knowledge, cognitive dissonances, beautiful, and “higher” cognitive abilities.
1.2. Logic, CC, and Amodal Symbols
Amodal symbols and perceptual symbols described by perceptual symbol system (PSS) [
21] differ not only in their representations in the brain, but also in their properties that are mathematically modeled in the referenced papers. This mathematically fundamental difference and its relations to CC of matching bottom-up and top-down signals are the subjects of this section. (A specific reason for connecting our cognitive-mathematical analysis to PSS is that it is a well recognized cognitive theory, giving a detailed non-mathematical description of many cognitive processes; later we discuss that PSS is incomplete and mathematically untenable for abstract concepts, language-cognition interaction, and for aesthetic emotions; necessary modifications are described in the following references [
22,
23,
24].)
The fundamental reasons for CC are related to the use of formal logic by algorithms and neural networks [
6,
25,
26]. Logic serves as a foundation for many approaches to cognition and linguistics; it underlies most of computational algorithms. But its influence extends far beyond, affecting cognitive scientists, psychologists, and linguists, who do not use complex mathematical algorithms for modeling the mind. All of us operate under the influence of formal logic, which roots are more than 2000 years old, making a more or less conscious assumption that the mechanisms of logic serve as the basis of human cognition. As discussed in details later, our minds are unconscious about its illogical foundations. We are mostly conscious about a small part of the mind mechanisms, which is approximately logical. Our intuitions, therefore, are unconsciously affected by the bias toward logic. Even when the laboratory data drive thinking away from logical mechanisms, humans have difficulties overcoming the logical bias [
1,
4,
25,
27,
28,
29,
30,
31,
32,
33,
34].
The relationships between logic, cognition, and language have been a source of longstanding controversy. The widely accepted story is that Aristotle founded logic as a fundamental mind mechanism, and only during the recent decades science overcame this influence. We would like to emphasize the opposite side of this story. Aristotle assumed a close relationship between logic and language. He emphasized that logical statements should not be formulated too strictly and language inherently contains the necessary degree of precision. According to Aristotle, logic serves to communicate already made decisions [
32]. The mechanism of the mind relating language, cognition, and the world Aristotle described as forms. Today we call similar mechanisms mental representations, or concepts, or simulators in the mind. Aristotelian forms are similar to Plato’s ideas with a marked distinction, forms are dynamic: their initial states, before learning, are different from their final states of concepts [
35]. Aristotle emphasized that initial states of forms, forms-as-potentialities, are not logical (
i.e., vague), but their final forms, forms-as-actualities, attained in the result of learning, are logical. This fundamental idea was lost during millennia of philosophical arguments. As discussed below, this Aristotelian process of dynamic forms corresponds to the mathematical model, DL, for processes of perception and cognition, and to Barsalou idea of PSS simulators.
The founders of formal logic emphasized a contradiction between logic and language. In the 19th century George Boole and the great logicians following him, including Gottlob Frege, Georg Cantor, David Hilbert, and Bertrand Russell (see [
36] and references therein) eliminated the uncertainty of language from mathematics, and founded formal mathematical logic, the foundation of the current classical logic. Hilbert developed an approach named formalism, which rejected intuition as a matter of scientific investigation and formally defined scientific objects in terms of axioms or rules. In 1900 he formulated famous Entscheidungsproblem: to define a set of logical rules sufficient to prove all past and future mathematical theorems. This was a part of “Hilbert’s program”, which entailed formalization of the entire human thinking and language. Formal logic ignored the dynamic nature of Aristotelian forms and rejected the uncertainty of language. Hilbert was sure that his logical theory described mechanisms of the mind. “The fundamental idea of my proof theory is none other than to describe the activity of our understanding, to make a protocol of the rules according to which our thinking actually proceeds.” [
37]. However, Hilbert’s vision of formalism explaining mysteries of the human mind came to an end in the 1930s, when Gödel [
38] proved internal inconsistency of formal logic. This development called Gödel theory is considered among most fundamental mathematical results of the previous century. Logic, that was believed to be a sure way to derive truths, turned out to be basically flawed. This is a reason why theories of cognition and language based on formal logic are inherently flawed.
There is a close relation between logic and CC. It turned out that combinatorial complexity of algorithms is a finite-system manifestation of the Gödel’s theory [
30]. If Gödelian theory is applied to finite systems (all practically used or discussed systems, such as computers and brain-mind, are finite), CC is the result, instead of the fundamental inconsistency. Algorithms matching bottom-up and top-down signals based on formal logic have to evaluate every variation in signals and their combinations as separate logical statements. A large, practically infinite number of combinations of these variations cause CC.
This general statement manifests in various types of algorithms in different ways. Rule systems are logical in a straightforward way, and the number of rules grows combinatorially. Pattern recognition algorithms and neural networks are related to logic in learning procedures: every training sample is treated as a logical statement (“this is a chair”) resulting in CC of learning. Multivalued logic and fuzzy logic were proposed to overcome limitations related to logic [
39]. Yet the mathematics of multivalued logic is no different in principle from formal logic [
31]. Fuzzy logic uses logic to set a degree of fuzziness. Correspondingly, it encounters a difficulty related to the degree of fuzziness: if too much fuzziness is specified, the solution does not achieve a needed accuracy, and if too little, it becomes similar to formal logic. If logic is used to find the appropriate fuzziness for every model at every processing step, then the result is CC. The mind has to make concrete decisions, for example one either enters a room or does not; this requires a computational procedure to move from a fuzzy state to a concrete one. But fuzzy logic does not have a formal procedure for this purpose; fuzzy systems treat this decision on an ad-hoc logical basis. A more general summary of this analysis relates CC to logic in the process of learning. Learning is treated in all past algorithms and in many psychological theories as involving learning from examples. An example such as “this is a chair” is a logical statement. Hence the ubiquitous role of logic and CC.
Is logic still possible after Gödel’s proof of its incompleteness? The contemporary state of this field was reviewed in [
26]. It appears that logic after Gödel is much more complicated and much less logical than was assumed by founders of artificial intelligence. CC cannot be solved within logic. Penrose thought that Gödel’s results entail incomputability of the mind processes and testify for a need for new physics “correct quantum gravitation”, which would resolve difficulties in logic and physics [
40]. An opposite position in [
25,
30,
31] is that incomputability of logic does not entail incomputability of the mind. These references add mathematical arguments to Aristotelian view that logic is not the basic mechanism of the mind.
To summarize, various manifestations of CC are all related to formal logic and Gödel theory. Rule systems rely on formal logic in a most direct way. Even mathematical approaches specifically designed to counter limitations of logic, such as fuzzy logic and the second wave of neural networks (developed after the 1980s) rely on logic at some algorithmic steps. Self-learning algorithms and neural networks rely on logic in their training or learning procedures: Every training example is treated as a separate logical statement. Fuzzy logic systems rely on logic for setting degrees of fuzziness. CC of mathematical approaches to the mind is related to the fundamental inconsistency of logic. All past algorithms and theories capable of learning involved logic in their learning procedures. Therefore logical inspirations, leading early cognitive scientists to amodal brain mechanisms, could not realize their hopes for mathematical models of the brain-mind.
Why did the outstanding mathematicians of the 19th and early 20th century believe in logic to be the foundation of the mind? Even more surprising is the belief in logic after Gödel. Gödelian theory was long recognized among most fundamental mathematical results of the 20th century. How is it possible that outstanding minds, including founders of artificial intelligence, and many cognitive scientists and philosophers of mind insisted that logic and amodal symbols implementing logic in the mind are adequate and sufficient? The answer, in our opinion, might be in the “conscious bias”. As we discuss, non-logical operations making up more than 99.9% of the mind functioning are not accessible to consciousness [
4,
25,
27,
29,
30]. However, our consciousness functions in a way that makes us unaware of this. In subjective consciousness we usually experience perception and cognition as logical. Our intuitions are “consciously biased”. This is why amodal logical symbols, which describe a tiny fraction of the mind mechanisms, have seemed to many the foundation of the mind [
4,
25,
28,
29,
30,
31,
32,
33,
34,
41].
Another aspect of logic is that it lacks dynamics; logic operates with static statements such as “this is a chair”. Classical logic is good at modeling structured statements and relations, yet it misses the dynamics of the mind and faces CC, when attempts to match bottom-up and top-down signals. The essentially dynamic nature of the brain-mind is not represented in mathematical foundations of logic. Dynamic logic discussed in the next section is a logic-process. It overcomes CC by automatically choosing the appropriate degree of fuzziness-vagueness for every mind’s concept at every moment. DL combines advantages of logical structure and connectionist dynamics. This dynamics mathematically represents the learning process of Aristotelian forms (which are opposite to classical logic as mentioned) and serves as a foundation for PSS concepts and simulators.
1.3. Dynamic Logic-Process
DL models perception as an interaction between bottom-up and top-down signals [
25,
30,
31,
32,
33,
34]. This section concentrates on the basic relationship between the brain processes and the mathematics of DL. To concentrate on this relationship, we much simplify the discussion of the brain structures. We discuss visual recognition of objects as if the retina and the visual cortex each consist of a single processing level of neurons where recognition occurs (which is not true, detailed relationship of the DL process to brain is considered in given references). Perception consists of the association-matching of bottom-up and top-down signals. Sources of top-down signals are mental representations, memories of objects created by previous simulators [
21]; these representations model the patterns in bottom-up signals. In this way they are concepts (of objects), symbols of a higher order than bottom-up signals; we call them concepts or mental models. In perception processes the models are modified by learning and new models are formed; since an object is never encountered exactly the same as previously, perception and cognition are always learning processes. The DL processes along with concept-representations are mathematical models of the PSS simulators. The bottom-up signals, in this simplified discussion, are a field of neuronal synapse activations in visual cortex. Sources of top-down signals are mental representation-concepts or, equivalently, model-simulators (for short, models; please notice this dual use of the word model, we use “models” for mental representation-simulators, which match-model patterns in bottom-up signals; and we use “models” for mathematical modeling of these mental processes). Each mental model-simulator projects a set of priming, top-down signals, representing the bottom-up signals expected from a particular object. The salient property of DL is that initial states of mental representations are vague and unconscious (or not fully conscious). In the processes of perception and cognition representations are matched to bottom-up signals and become more crisp and conscious. This is discussed in detail later along with references to experimental publications proving that this is a valid model for brain-mind processes of perception and cognition. Mathematical models of mental models-simulators characterize these mental models by parameters. Parameters describe object position, angles, lightings,
etc. (In case of learning situations considered later, parameters characterize objects and relations making up a situation.) To summarize this highly simplified description of a visual system, the learning-perception process “matches” top-down and bottom-up activations by selecting “best” mental models-simulators and their parameters and fitting them to the corresponding sets of bottom-up signals. This DL process mathematically models multiple simulators running in parallel, each producing a set of priming signals for various expected objects.
Mathematical criteria of the “best” fit between bottom-up and top-down signals were given in [
16,
25,
30,
31]. They are similar to probabilistic or informatics measures. In the first case they represent probabilities that the given (observed) data or bottom-up signals correspond to representations-models (top-down signals) of particular objects. In the second case they represent information contained in representations-models about the observed data (in other words, information in top-down signals about bottom-up signals). These similarities are maximized over the model parameters. Results can be interpreted correspondingly as a maximum likelihood that models-representations fit sensory signals, or as maximum information in models-representations about the bottom-up signals. Both similarity measures account for all expected models and for all combinations of signals and models. Correspondingly, a similarity contains a large number of items, a total of
MN, where
M is a number of models and
N is a number of signals; this huge number is the cause for the combinatorial complexity discussed previously.
Maximization of a similarity measure is a mathematical model of an unconditional drive to improve the correspondence between bottom-up and top-down signals (representations-models). In biology and psychology it was discussed as curiosity, a need to reduce cognitive dissonance, or a need for knowledge since the 1950s [
42,
43,
44]. This process involves knowledge-related emotions evaluating satisfaction of this drive for knowledge [
25,
30,
31,
32,
45,
46]. In computational intelligence it is even more ubiquitous, every mathematical learning procedure, algorithm, or neural network maximizes some similarity measure.
The DL learning process can be understood as both an artificial intelligence system or a cognitive model. Let us repeat, DL consists in estimating parameters of concept-models (mental representations) and associating subsets of bottom-up signals with top-down signals originating from these models-concepts by maximizing a similarity. Although a similarity contains combinatorially many items, DL maximizes it without combinatorial complexity [
25,
27,
30,
31,
32,
34,
47] as follows. First, vague-fuzzy association variables are defined, which give a measure of correspondence between each signal and each model. They are defined similarly to the a posteriori Bayes probabilities, they range between 0 and 1, and as a result of learning they converge to the probabilities, under certain conditions. Often the association variables are close to bell-shapes.
The DL process is defined by a set of differential equations given in the above references; together with models discussed later it gives a mathematical description of perception and cognition processes, including the PSS simulators. To keep the review self-consistent we summarize these equations in Appendix. Those interested in mathematical details can read the Appendix. However, basic principles of DL can be adequately understood from a conceptual description and examples in this and following sections. As a mathematical model of perception-cognitive processes, DL is a process described by differential equations given in the Appendix; in particular, fuzzy association variables
f associate bottom-up signals and top-down models-representations. Among unique DL properties is an autonomous dependence of association variables on models-representations: in the processes of perception and cognition, as models improve and become similar to patterns in the bottom-up signals, the association variables become more selective, more similar to delta-functions. Whereas initial association variables are vague and associate near all bottom-up signals with virtually any top-down model-representations, in the processes of perception and cognition association variables are becoming specific, “crisp”, and associate only appropriate signals. This is a process “from vague to crisp”, and also “from unconscious to conscious mental states” (The exact mathematical definition of crisp corresponds to values of
f = 0 or 1; values of
f in between 0 and 1 correspond to various degrees of vagueness.) The fact that “vague to crisp” is equivalent to “unconsciousness to conscious” has been experimentally demonstrated in [
4].
DL processes mathematically model PSS simulators and not static amodal signals. Another unique aspect of DL is that it explains how logic appears in the human mind; how illogical dynamic PSS simulators give rise of classical logic, and what is the role of amodal symbols. This is discussed throughout the paper, and also in specific details in
section 6.
An essential aspect of DL, mentioned above, is that associations between models and data (top-down and bottom-up signals) are uncertain and dynamic; their uncertainty matches uncertainty of parameters of the models and both change in time during perception and cognition processes. As the model parameters improve, the associations become crisp. In this way the DL model of simulator-processes avoids combinatorial complexity because there is no need to consider separately various combinations of bottom-up and top-down signals. Instead, all combinations are accounted for in the DL simulator-processes. Let us repeat that, initially, the models do not match the data. The association variables are not the narrow logical variables 0, or 1, or nearly logical, instead they are wide functions (across top-down and bottom-up signals). In other words, they are vague, initially they take near homogeneous values across the data (across bottom-up and top-down signals); they associate all the representation-models (through simulator processes) with all the input signals [
25,
30,
33]. Here we conceptually describe the DL process as applicable to visual perception, taking approximately 160 ms, according to the reference below. Gradually, the DL simulator-processes improve matching, models better fit data, the errors become smaller, the bell-shapes concentrate around relevant patterns in the data (objects), and the association variables tend to 1 for correctly matched signal patterns and models, and 0 for others. These 0 or 1 associations are logical decisions. In this way, classical logic appears from vague states and illogical processes. Thus certain representations get associated with certain subsets of signals (objects are recognized and concepts formed logically or approximately logically). This process “from vague-to-crisp” that matches bottom-up and top-down signals has been independently conceived and demonstrated in brain imaging research to take place in human visual system [
4,
48]. Thus DL PSS simulators describe how logic appears from illogical processes, and actually model perception mechanisms of the brain-mind as processes from unconscious to conscious brain states. By connecting conscious and unconscious states DL resolves a long-standing difficulty of free will and explains that past difficulties related to the idea of free will are difficulties of logic, the mind and DL overcomes these difficulties [
49,
50].
Mathematical convergence of the DL process was proven in [
25]. It follows that the simulator-process of perception or cognition assembles objects or concepts among bottom-up signals, which are most similar in terms of the similarity measure. Despite a combinatorially large number of items in the similarity, a computational complexity of DL is relatively low, it is linear in the number of signals, and therefore could indeed model physical systems, like a computer or brain.
1.4. Example of DL, Object Perception in Noise
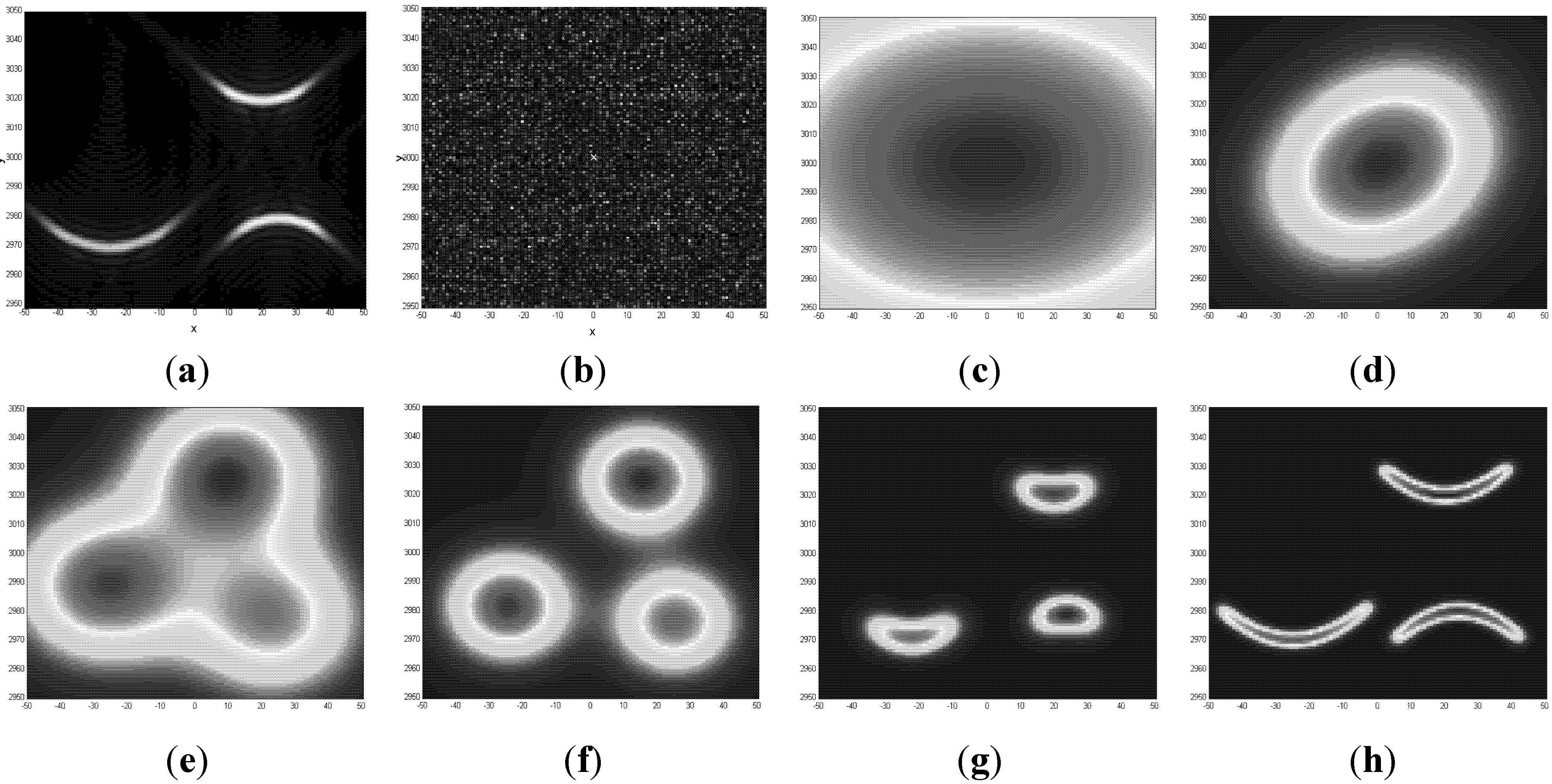
The purpose of this section is to illustrate the DL perception processes, multiple simulators running in parallel as described above. We use a simple example, still unsolvable by other methods, (mathematical details are omitted, they could be found in [
51]). In this example, DL searches for patterns in noise. Finding patterns below noise can be an exceedingly complex problem. If an exact pattern shape is not known and depends on unknown parameters, these parameters should be found by fitting the pattern model to the data. However, when the locations and orientations of patterns are not known, it is not clear which subset of the data points should be selected for fitting. A standard approach for solving this kind of problem, which has already been mentioned, is multiple hypotheses testing [
20]; this algorithm exhaustively searches all logical combinations of subsets and models and is not practically useful because of CC. Nevertheless, DL successfully find the patterns under noise. In the current example, we are looking for “smile” and “frown” patterns in noise shown in
Figure 1a without noise, and in
Figure 1b with noise, as actually measured. Object signals are about 2–3 times below noise and cannot be seen by human visual system (it is usually considered that human visual system is better than any algorithm for perception of objects, therefore we emphasize that DL exceeds performance of human perception in this case because DL models work well with random noise, while human perception was not optimized by evolution for this kind of signals).
To apply DL to this problem, we used DL equations given in the Appendix. Specifics of this example are contained in models. Several types of models are used: parabolic models describing “smiles” and “frown” patterns (unknown size, position, curvature, signal strength, and number of models), circular-blob models describing approximate patterns (unknown size, position, signal strength, and number of models), and noise model (unknown strength). Exact mathematical description of these models is given in several references cited above.
The image size in this example is 100 × 100 points (
N = 10,000 bottom-up signals, corresponding to the number of receptors in an eye retina), and the true number of models is 4 (3 + noise), which is not known. Therefore, at least
M = 5 models should be fit to the data, to decide that 4 fits best. This yields complexity of logical combinatorial search,
MN = 10
5000; this combinatorially large number is much larger than the size of the Universe and the problem was considered unsolvable.
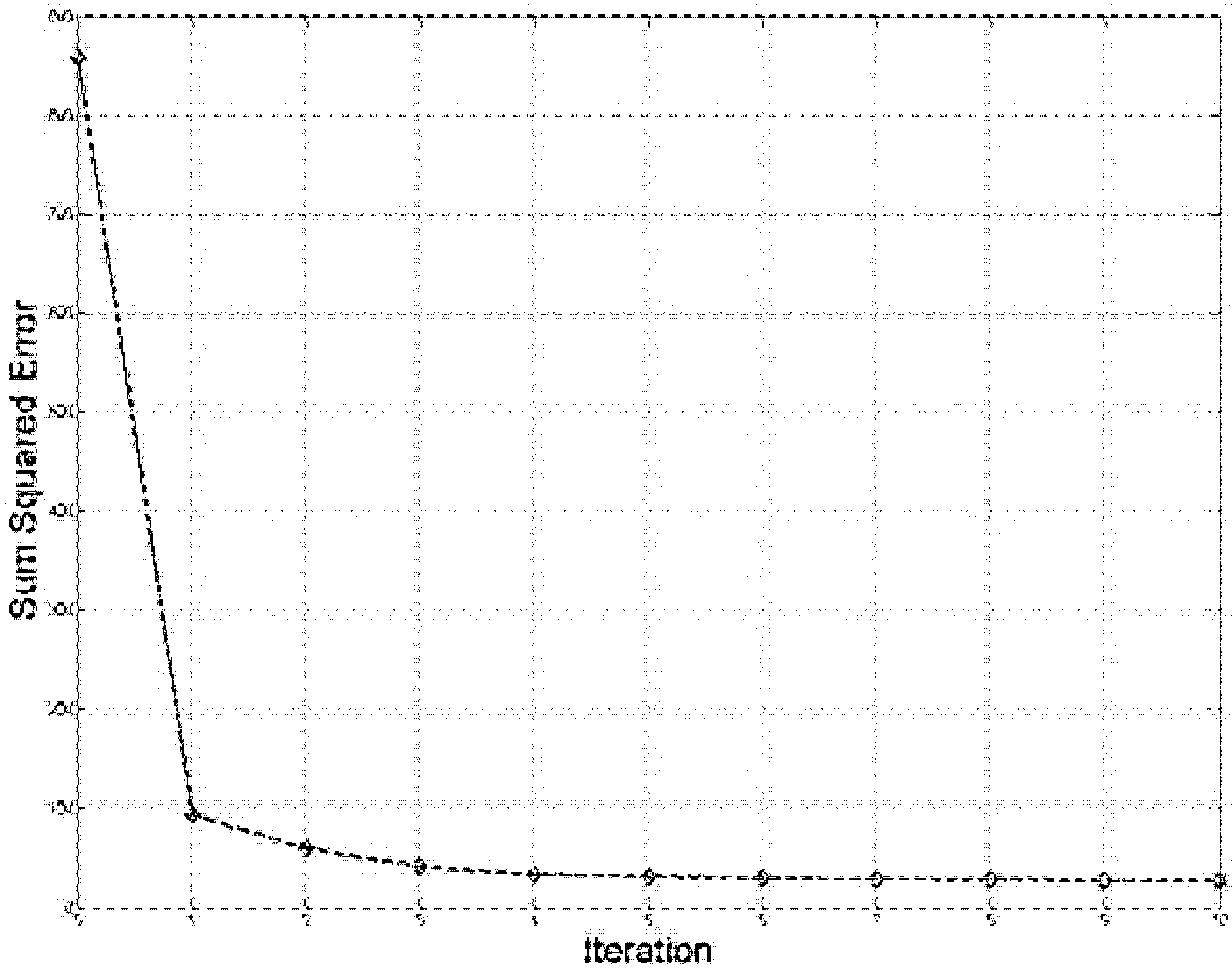
Figure 1 illustrates DL operations: (a) true “smile” and “frown” patterns without noise; (b) actual image available for recognition; (c) through (h) illustrates the DL process, they show improved models at various steps of solving DL equation A3, total of 22 steps (noise model is not shown; figures (c) through (h) show association variables, f, for blob and parabolic models). By comparing (h) to (a) one can see that the final states of the models match patterns in the signal. Of course, DL does not guarantee finding any pattern in noise of any strength. For example, if the amount and strength of noise would increase 10-fold, most likely the patterns would not be found (this would provide an example of “falsifiability” of DL; however more accurate mathematical description of potential failures of DL algorithms is considered later). DL reduced the required number of computations from combinatorial 10
5000 to about 10
9. By solving the CC problem DL was able to find patterns under the strong noise. In terms of signal-to-noise ratio this example gives 10,000% improvement over the previous state-of-the-art. (We repeat that in this example DL actually works better than human visual system; the reason is that human brain is not optimized for recognizing these types of patterns in noise.)
The main point of this example is that DL perception process, or PSS “simulator” is a process “from vague-to-crisp”, similar to visual system processes demonstrated in [
4] (in that publication authors use the term “low spatial frequency” for what we call “vague” in
Figure 1).
Figure 1.
Finding “smile” and “frown” patterns in noise, an example of dynamic logic operation: (a) true “smile” and “frown” patterns are shown without noise; (b) actual image available for recognition (signals are below noise, signal-to-noise ratio is between ½ and ¼, 100 times lower than usually considered necessary); (c) an initial fuzzy blob-model, the vagueness corresponds to uncertainty of knowledge; (d) through (h) show improved models at various steps of dynamic logic (DL) (equation A3 are solved in 22 steps). Between stages (d) and (e) the algorithm tried to fit the data with more than one model and decided that it needs three blob-models to “understand” the content of the data. There are several types of models: One uniform model describing noise (it is not shown) and a variable number of blob-models and parabolic models, which number, location, and curvature are estimated from the data. Until about stage (g) the algorithm “thought” in terms of simple blob models, at (g) and beyond, the algorithm decided that it needs more complex parabolic models to describe the data. Iterations stopped at (h), when similarity (equation A1) stopped increasing.
Figure 1.
Finding “smile” and “frown” patterns in noise, an example of dynamic logic operation: (a) true “smile” and “frown” patterns are shown without noise; (b) actual image available for recognition (signals are below noise, signal-to-noise ratio is between ½ and ¼, 100 times lower than usually considered necessary); (c) an initial fuzzy blob-model, the vagueness corresponds to uncertainty of knowledge; (d) through (h) show improved models at various steps of dynamic logic (DL) (equation A3 are solved in 22 steps). Between stages (d) and (e) the algorithm tried to fit the data with more than one model and decided that it needs three blob-models to “understand” the content of the data. There are several types of models: One uniform model describing noise (it is not shown) and a variable number of blob-models and parabolic models, which number, location, and curvature are estimated from the data. Until about stage (g) the algorithm “thought” in terms of simple blob models, at (g) and beyond, the algorithm decided that it needs more complex parabolic models to describe the data. Iterations stopped at (h), when similarity (equation A1) stopped increasing.
![Brainsci 02 00790 g001]()
We would also like to take this moment to continue the arguments from
section 1.1,
section 1.2, and to emphasize that DL is a fundamental and revolutionary improvement in mathematics [
33,
34]; it was recognized as such in mathematical and engineering communities; it is the theory that has suggested vague initial states; it has been developed for over 20 years; yet it might not be well known in cognitive science community. Those interested in a large number of mathematical and engineering applications of DL could consult given references and references therein. Here we would like to address two specific related concerns, first, if the DL algorithms are falsifiable, second, a possibility that
Figure 1 example could be “lucky” or “erroneous”. We appreciate that some readers could be skeptical about 10,000% improvement over the state of the art. In mathematics there is a standard procedure for establishing average performance of detection (perception) and similar algorithms. It is called “operating curves” and it takes not one example, but tens of thousands examples, randomly varying in parameters, initial conditions,
etc. The results are expressed in terms of probabilities of correct and incorrect algorithm performance (this is an exact mathematical formulation of the idea of “falsifiability” of an algorithm). These careful procedures demonstrated that
Figure 1 represents an average performance of the DL algorithm [
25,
52,
53].
1.5. The Knowledge Instinct (KI)
The word “instinct” fell out of favor in psychology and cognitive science, because of historical uncertainties of what it means. It was mixed up with “instinctual behavior” and other not well defined mechanisms and abilities. However, using a word “drive” is not adequate either, because fundamental inborn drives and culturally evolved drives are mixed up. In this section we follow instinctual-emotional theory of Grossberg and Levine [
45] that gives succinct definition of instincts, enables mathematical modeling of these mechanisms underlying this review, corresponds to psychological, cognitive, and physiological data, and thus restores the scientific credibility of the word “instinct”. According to [
45] instinct is an inborn mechanism that measures vital organism data and determines when these data are within or outside of safe regions. These results are communicated to decision-making brain regions (conscious or unconscious) by emotions (emotional neural signals), resulting in allocating resources to satisfying instinctual needs. Emotional neural signals also result in various physiological and psychological effects, however we would like to emphasize that for mathematical modeling and scientific understanding of the nature of instincts and emotions Grossberg-Levine theory is fundamental, whereas Damasio’s emotions as “bodily markers” are secondary. For some purposes it might be necessary to analyze physiological mechanisms of instincts, as well as physiological and psychological manifestations of emotions. However, within this review the Grossberg-Levine theory is a fundamental level of analysis.
A simplified example of the instinctual-emotional theory is an instinctual need for food. Special sensory-like physiological mechanisms measure sugar level in blood. When it drops below certain level an organism feels an emotion of hunger. Emotional neural signals indicate to decision-making parts of the brain that more resources have to be allocated to finding food. We have dozens of similar instinctual-emotional mechanisms: sensory-like measurements mechanisms and corresponding emotional signals.
Matching bottom-up and top-down signals, as mentioned, is the essence of perception and cognition processes, and constitutes an essential need for understanding the surrounding world. Models stored in memory as representations of past experiences never exactly match current objects and situations. Therefore thinking and even simple perception always require modifying existing models; otherwise the brain-mind would not be able to perceive the surroundings and the organism would not be able to survive. To survive, humans and higher animals have an inborn drive to fit top-down and bottom-up signals. Because the very survival of a higher animal or human depends on this drive, it is even more fundamental than drives for food or procreation; understanding the world around is a condition for satisfying all other instinctual needs. Therefore this drive for knowledge is called the knowledge instinct, KI [
13,
16,
25,
27,
30].
This mechanism is similar to other instincts [
13,
25,
30,
45] in that our mind has a sensor-like mechanism that measures a similarity between top-down and bottom-up signals, between concept-models and sensory percepts. Brain areas participating in the knowledge instinct were discussed in [
54]. As discussed in that publication, biologists considered similar mechanisms since the 1950s; without a mathematical formulation, however, its fundamental role in cognition was difficult to discern. All learning algorithms have some models of this instinct, maximizing correspondence between sensory input and an algorithmic internal structure (knowledge in a wide sense). According to the Grossberg-Levine instinct-emotion theory, satisfaction or dissatisfaction of every instinct is communicated to other brain areas by emotional neural signals. Emotional signals related to KI are felt as harmony or disharmony between our knowledge-models and the world. At lower levels of everyday object recognition these emotions are usually below the threshold of consciousness; at higher levels of abstract and general concepts this feeling of harmony or disharmony could be strong, as discussed in [
13,
28], it is a foundation of human higher mental abilities. Since Kant [
55], emotions related to knowledge are called aesthetic emotions. Here we emphasize that they are related to every process of perception and cognition. They are “higher” emotions in the sense that they are related to knowledge, rather than to bodily needs; we would emphasize that this distinction is not fundamental in terms of mechanisms, all instinctual and emotional mechanisms involve brain. Yet for understanding human psychology it is a fundamental distinction. Their relations to higher cognitive abilities, to emotions of the beautiful and sublime are discussed later.
Mathematical modeling of perception and thinking emphasized fundamental nature of KI: all mathematical algorithms for learning have some variation of this process, matching bottom-up and top-down signals. Without matching previous models to the current reality we will not perceive objects, or abstract ideas, or make plans. This process involves learning-related emotions evaluating satisfaction of KI [
25,
27,
30,
46,
56].
1.6. Emotions of Beautiful and Sublime
DL model of KI inherently involves emotional signals related to satisfaction or dissatisfaction of KI. These emotions are modeled by changes in the similarity between bottom-up and top-down signals, in other world by KI satisfaction. We perceive these emotions as feelings of harmony or disharmony between our knowledge and the world or within the knowledge; these emotions related to knowledge are called aesthetic emotions [
55]. KI and aesthetic emotions drive the brain-mind to improve mental models-concepts for better correspondence to surrounding objects and events. This section relates aesthetic emotions to the beautiful and sublime according to [
25,
28,
30,
34,
57,
58,
59,
60,
61,
62,
63,
64].
Cognitive science and psychology for decades have been at a complete loss when trying to identify cognitive functions of the highest human abilities, the most important and cherished ability to create and perceive the beautiful. Its role in the working of the mind was not understood. Aesthetic emotions discussed above are often below the level of consciousness at lower levels of the mind hierarchy. Simple harmony is an elementary aesthetic emotion related to improvement of mental models of objects. Higher aesthetic emotions are related to the development and improvement of more complex “higher” models at higher levels of the mind hierarchy. At higher levels, when understanding important concepts, aesthetic emotions reach consciousness.
Models at higher levels of the mind hierarchy are more general than lower-level models; they unify knowledge accumulated at lower levels. This is the purpose for which neural mechanisms of concepts emerged in genetic and cultural evolution, and this purpose in inseparable from the content of these models. The highest forms of aesthetic emotions are related to the most general and most important models near the top of the mind hierarchy. The purpose of these models is to unify our entire life experience. This conclusion is identical to the main idea of Kantian aesthetics. According to Kantian analysis among the highest models are models of the meaning of our existence, of our purposiveness or intentionality. KI drives us to develop these models. The reason is in the two sides of knowledge: on one hand knowledge consists in detailed models of objects and events generating bottom-up signals at every hierarchical level, on the other, knowledge is a more general and unified understanding of lower-level models at higher levels, generating top-down signals. These two sides of knowledge are related to viewing the knowledge hierarchy from bottom up or from top down. In the top-down direction, models strive to differentiate into more and more detailed models accounting for every detail of the reality. In the bottom-up direction, models strive to make a larger sense of the detailed knowledge at lower levels. In the process of cultural evolution, higher, general models have been evolving with this purpose, to make more sense, to create more general meanings. In the following sections we consider mathematical models of this process of cultural evolution, in which top mental models evolve. The most general models, at the top of the hierarchy, unify all our knowledge and experience. The mind perceives them as the models of meaning and purpose of existence. In this way KI theory corresponds to Kantian analysis.
Everyday life gives us little evidence to develop models of meaning and purposiveness of our existence. People are dying every day and often from random causes. Nevertheless, belief in one’s purpose is essential for concentrating will and for survival. Is it possible to understand psychological contents and mathematical structures of models of meanings and purpose of human life? It is a challenging problem yet DL gives a foundation for approaching it.
Consider a simple experiment: remember an object in front of your eyes. Then close eyes and recollect the object. The imagined object is vague, not as crisp as this same object a moment ago, when perceived with opened eyes. Imaginations of objects are top-down projections of object representations on the visual cortex. We conclude that mental representations-models of everyday objects are vague (as modeled by DL). We can conclude that models of abstract situations, higher in the hierarchy, which cannot be perceived with “opened eyes”, are much vaguer. Even much vaguer have to be models of the purpose of life at the top of the hierarchy. As mentioned, everyday life gives us no evidence that such a meaning and purpose exist at all. And many people do not believe that life has a meaning. When we ask our colleagues-scientists if life has a meaning, most protest against such a nebulous, indefinable, and seemingly unscientific idea. However, nobody would agree that his or her personal life is as meaningless as a piece of rock at a road wayside.
Is there a scientific way to resolve this contradiction? This is exactly what we intend to do in this section with the help of DL mathematical models and recent results of neuro-psychological experiments. Let us go back again to the closed eye experiment. Vague imaginations with closed eyes cannot be easily recollected when eyes are opened. Vague states of mental models are not easily accessible to consciousness. To imagine vague objects we should close eyes. Can we “close mental eyes” that enable cognition of abstract models? Later we consider mathematical models of this process. Here we formulate the conclusions. “Mental eyes” enabling cognition of abstract models involve language models of abstract ideas. These language models are results of millennia of cultural evolution. High-level abstract models are formulated crisply and consciously in language. To significant extent they are cultural constructs, and they are different in different cultures. Every individual creates cognitive models from his or her experience guided by cultural models stored in language. Whereas language models are crisp and conscious, cognitive models are vague and less conscious. Few individuals in rare moments of their lives can understand some aspects of reality beyond what has been understood in culture over millennia and formulated in language. In these moments “language eyes” are closed and an individual can see “imagined” cognitive images of reality not blinded by culturally received models. Rarely these cognitions better represent reality than millennial cultural models. And even rarer these cognitions are formulated in language so powerfully that they are accepted by other people and become part of language and culture. This is the process of cultural evolution. We will discuss it in more details later.
Understanding the meaning and purpose of one’s life has been important for survival millions of years ago and is important for achieving higher goals in contemporary life. Therefore all cultures and all languages forever have been formulating contents of these models. And the entire humankind has been evolving toward better understanding of the meaning and purpose of life. Those individuals and cultures that do not succeed are handicapped in survival and expansion. But let us set aside cultural evolution for later sections and return to how an individual perceives and feels his or her models of the highest meaning.
As discussed, cognitive models at the very top of the mind hierarchy are vague and unconscious. Even so many people are versatile in talking about these models, and many books have been written about them, cognitive models that correspond to the reality of life are vague and unconscious. Some people, at some points in their life, may believe that their life purpose is finite and concrete, for example to make a lot of money, or build a loving family and bring up good children. These crisp models of purpose are cultural models, formulated in language. Usually they are aimed at satisfying powerful instincts, but not KI and they do not reflect the highest human aspirations. Reasons for this perceived contradiction are related to interaction between cognition and language that we have mentioned and will be discussing in more details later. Anyone who has achieved a finite goal of making money or raising good children knows that this is not the end of his or her aspirations. The psychological reason is that everyone has an ineffable feeling of partaking in the infinite, while at the same time knowing that one’s material existence is finite. This contradiction cannot be resolved. For this reason cognitive models of our purpose and meaning cannot be made crisp and conscious, they will forever remain vague, fuzzy, and mostly unconscious.
As discussed, better understanding of what the model is about leads to satisfaction of KI, and to corresponding aesthetic emotions. Higher in the hierarchy the models are vague, less conscious and emotional contents of mental states are less separated from their conceptual contents. At the top of the mind hierarchy, the conceptual and emotional contents of cognitive models of the meaning of life are not separated. In those rare moments when one improves these models, improves understanding of the meaning of one’s life, or even feels assured that the life has meaning, he or she feels emotions of the beautiful, the aesthetic emotion related to satisfaction of KI at the highest levels.
These issues are not new; philosophers and theologians expounded them from time immemorial. The DL-KI theory gives us a scientific approach to the eternal quest for the meaning. We perceive an object or a situation as beautiful, when it stimulates improvement of the highest models of meaning. Beautiful is what “reminds” us of our purposefulness. This is true about perception of beauty in a flower or in an art object. Just an example, R. Buckminster Fuller, an architect, best known for inventing the geodesic dome wrote: “When I’m working on a problem, I never think about beauty. I think only how to solve the problem. But when I have finished, if the solution is not beautiful, I know it is wrong.” Similar things were told about scientific theories by Einstein and Poincare, emphasizing that the first proof of a scientific theory is its beauty. The KI theory explanation of the nature of the beautiful helps understanding an exact meaning of these statements and resolves a number of mysteries and contradictions in contemporary aesthetics.
Emotions of spiritually sublime are similar to and different from emotions of the beautiful. Emotions of the beautiful are related to
understanding contents of the highest concepts of meaning. Emotions of spiritually sublime are related to
behavior that could make the meaning and beautiful a part of one’s life [
59]. This is the foundation of all religions. It is unfortunate that this foundation has been almost forgotten and often hidden behind fog of pragmatic usefulness of church life, differences among churches, historical enmity between religion and science, neglect and often contempt by scientists toward religion. This explanation is a bridge required by culture to connect science and religion.
Finishing scientific discussion of the beautiful and sublime, we would like to emphasize again that these are emotions related to knowledge at the top of the mind hierarchy, the knowledge of the life meaning. It is governed by KI, not by sex and instinct for procreation. Sexual instinct is among the strongest of our bodily instincts, and it makes use of all our abilities, including knowledge, beauty, and strivings for sublime. And yet the ability for feeling and creating the beautiful and sublime are related not to sexual instinct but to the instinct for knowledge.
A fundamental conclusion from this section is that the brain-mind is not logical, whereas intuition of most lay people and scientists that brain-mind is mostly logical is wrong. This conclusion is difficult to accept and to make sense of for non-mathematicians as well as for many mathematicians. Future developments in psychology and cognitive science require no less than a revolution in scientific intuition and thinking. And the current review might help in this process.