Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur Gears
Abstract
:1. Introduction
2. Influence of Backlash on Time-Varying Mesh Stiffness
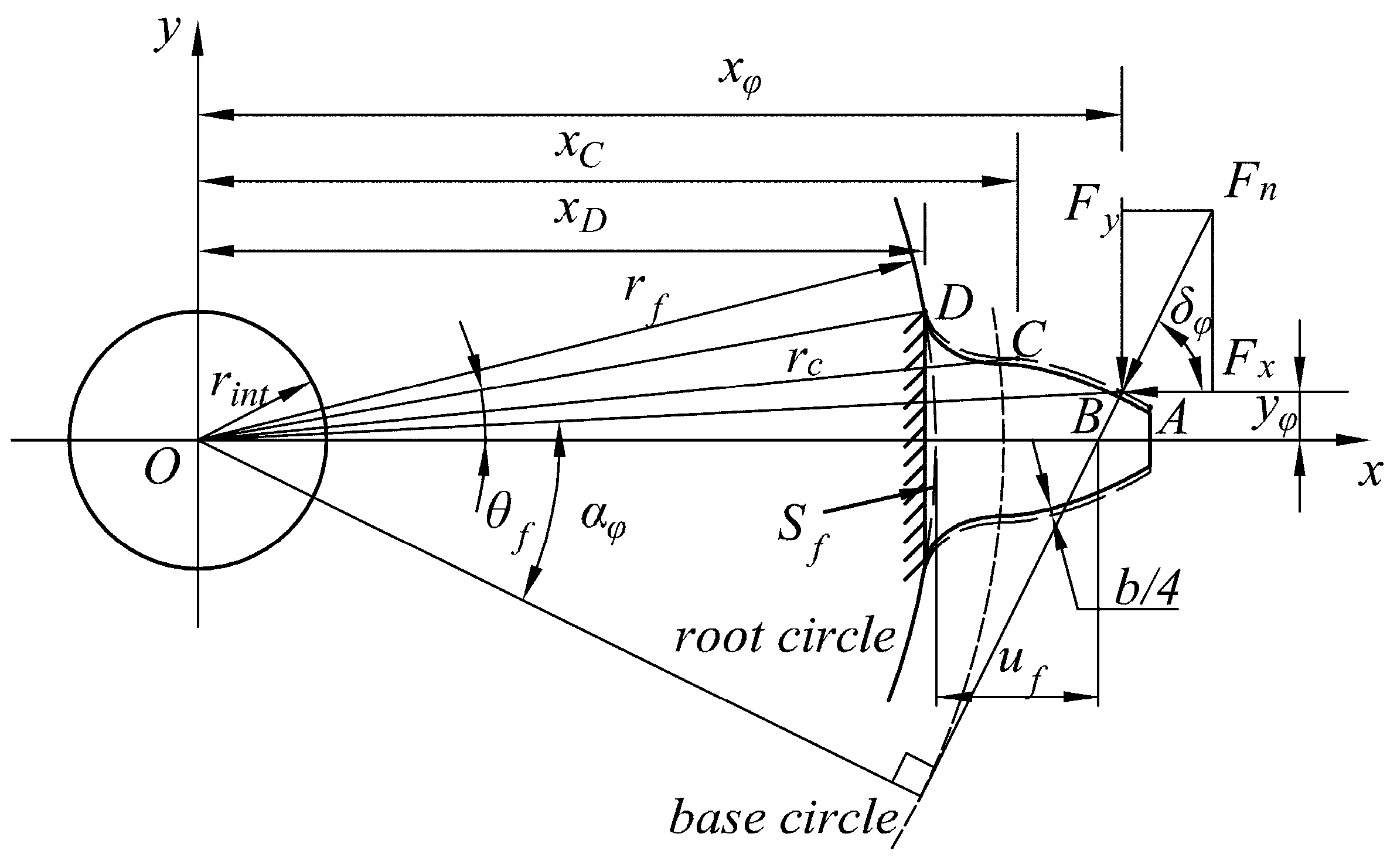
2.1. Mesh Stiffness Model with Backlash
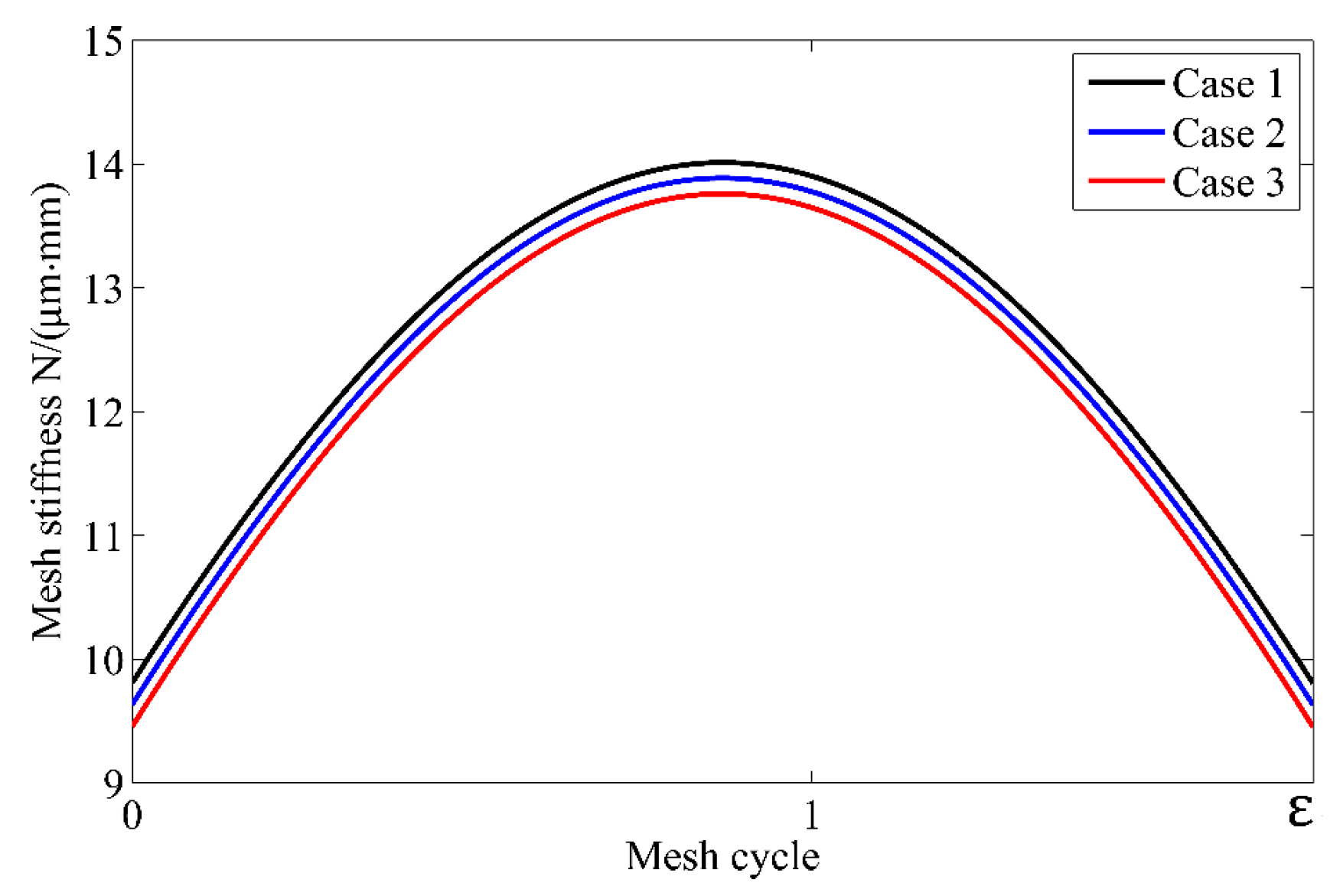
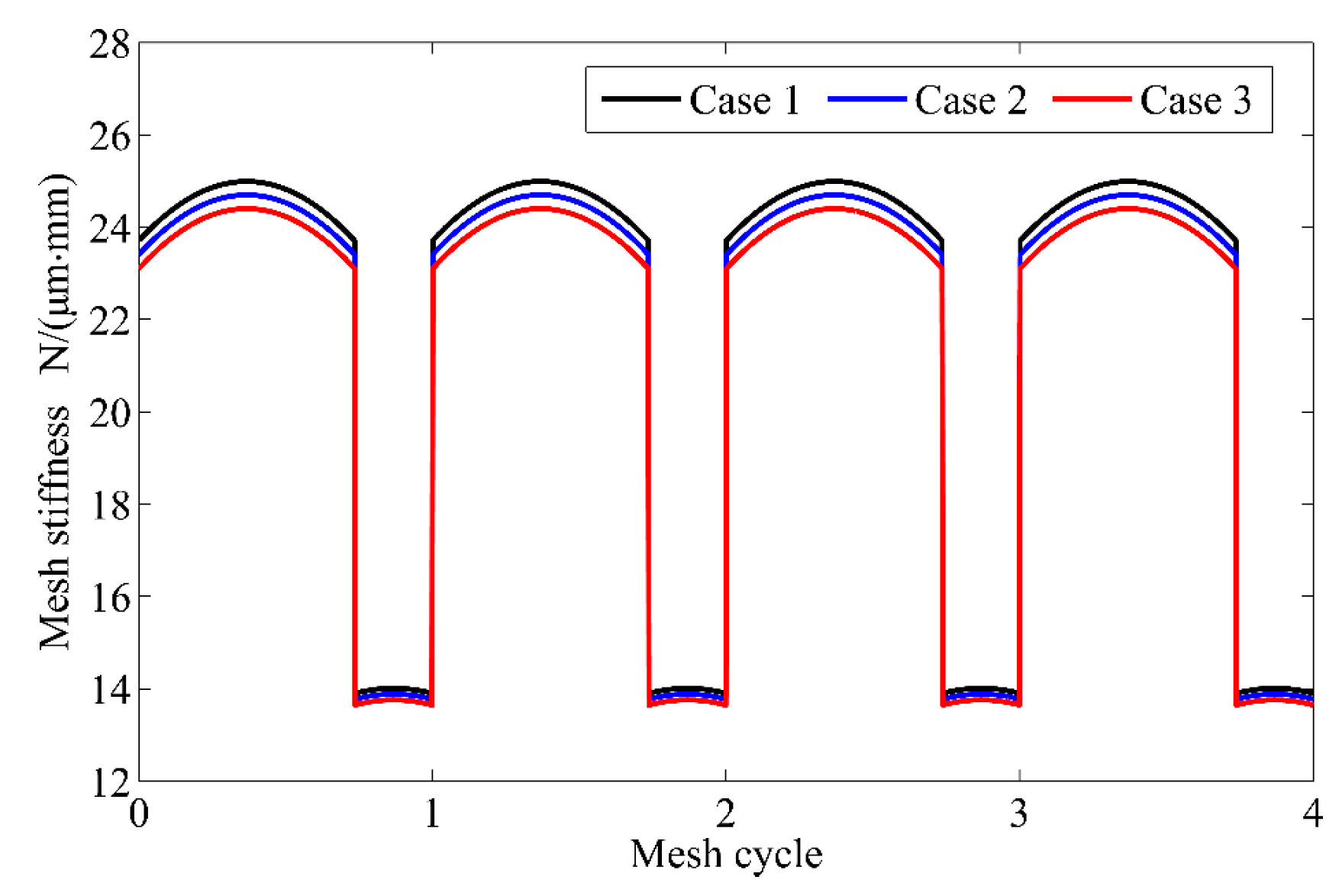
2.2. Influence of Backlash on Stiffness
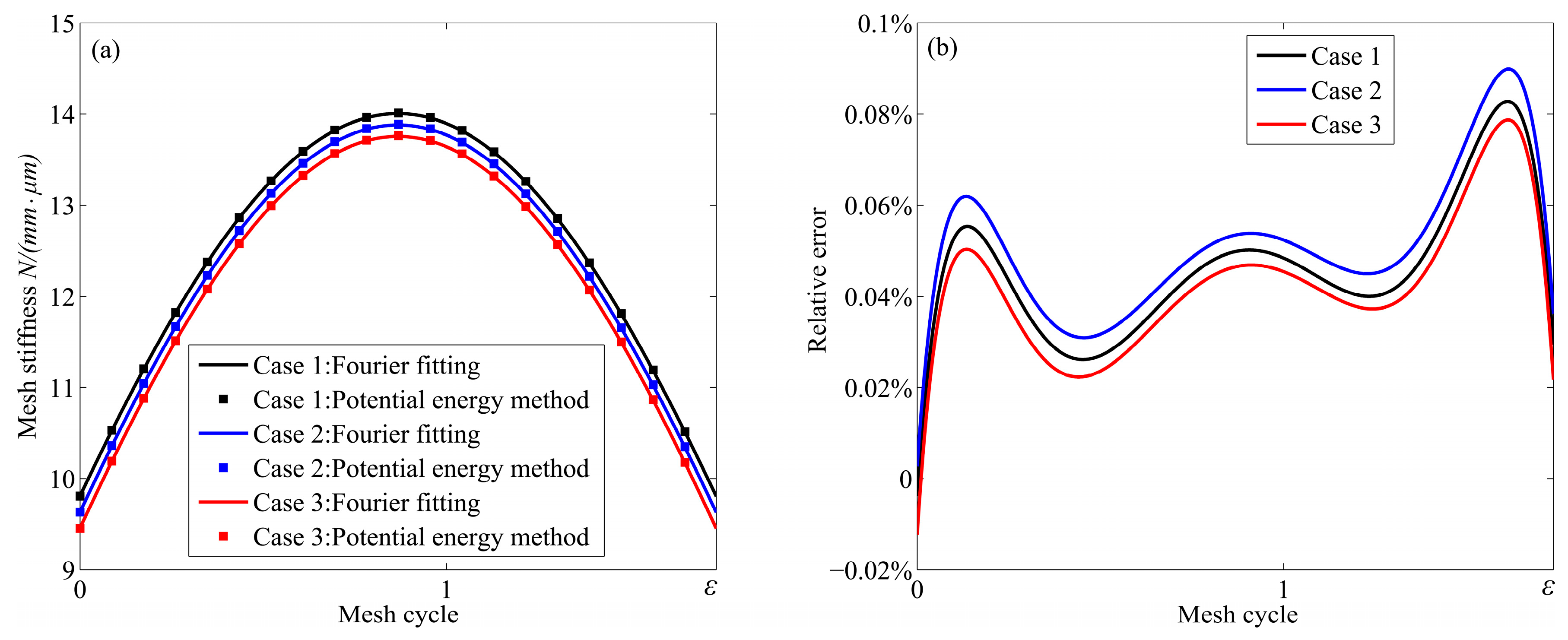
2.3. Mesh Stiffness Fitting Method
3. Influence of Backlash on Dynamics
3.1. Single-Degree-of-Fredom(SDOF) Model and Dynamic Differential Equation
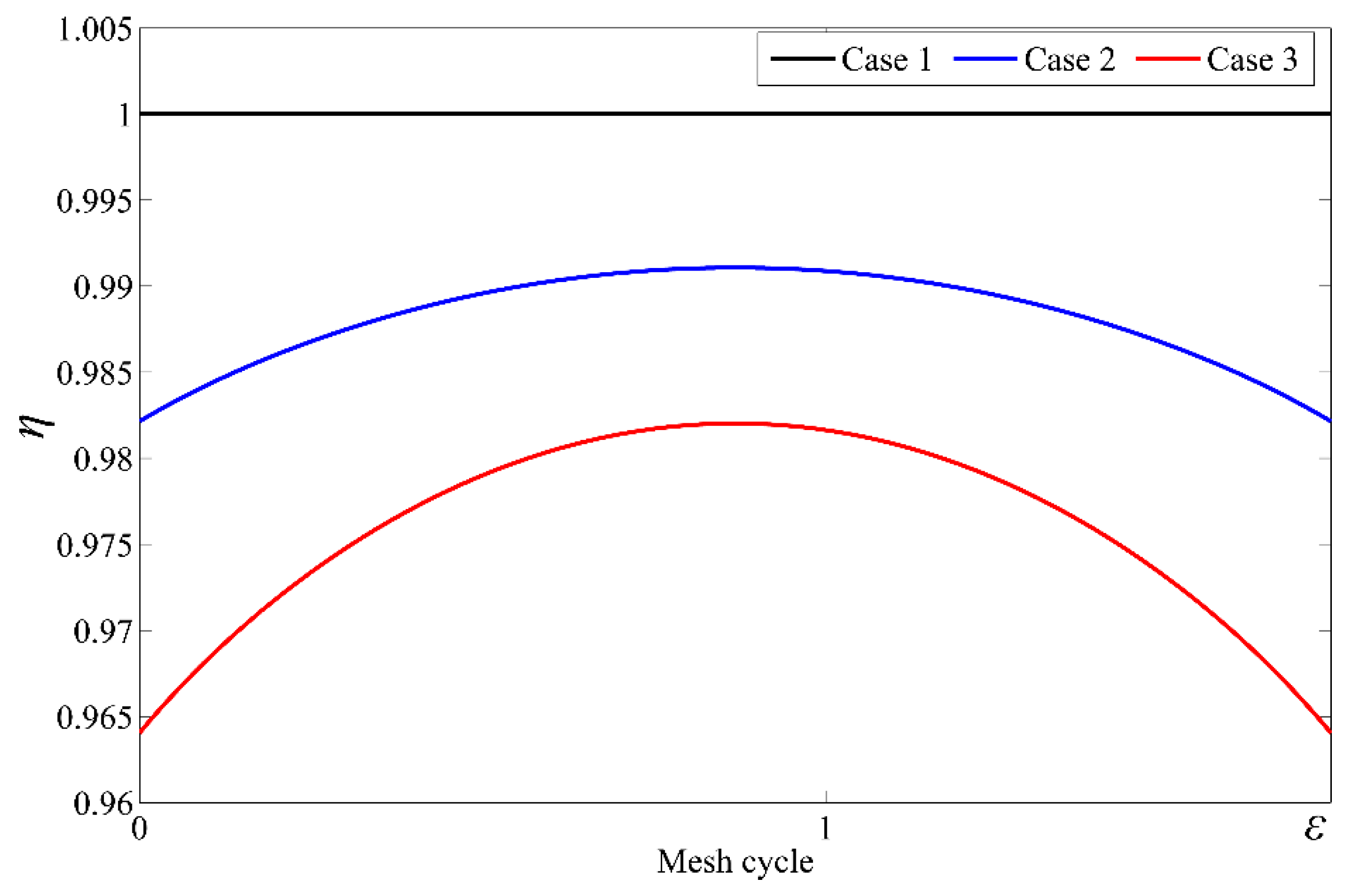
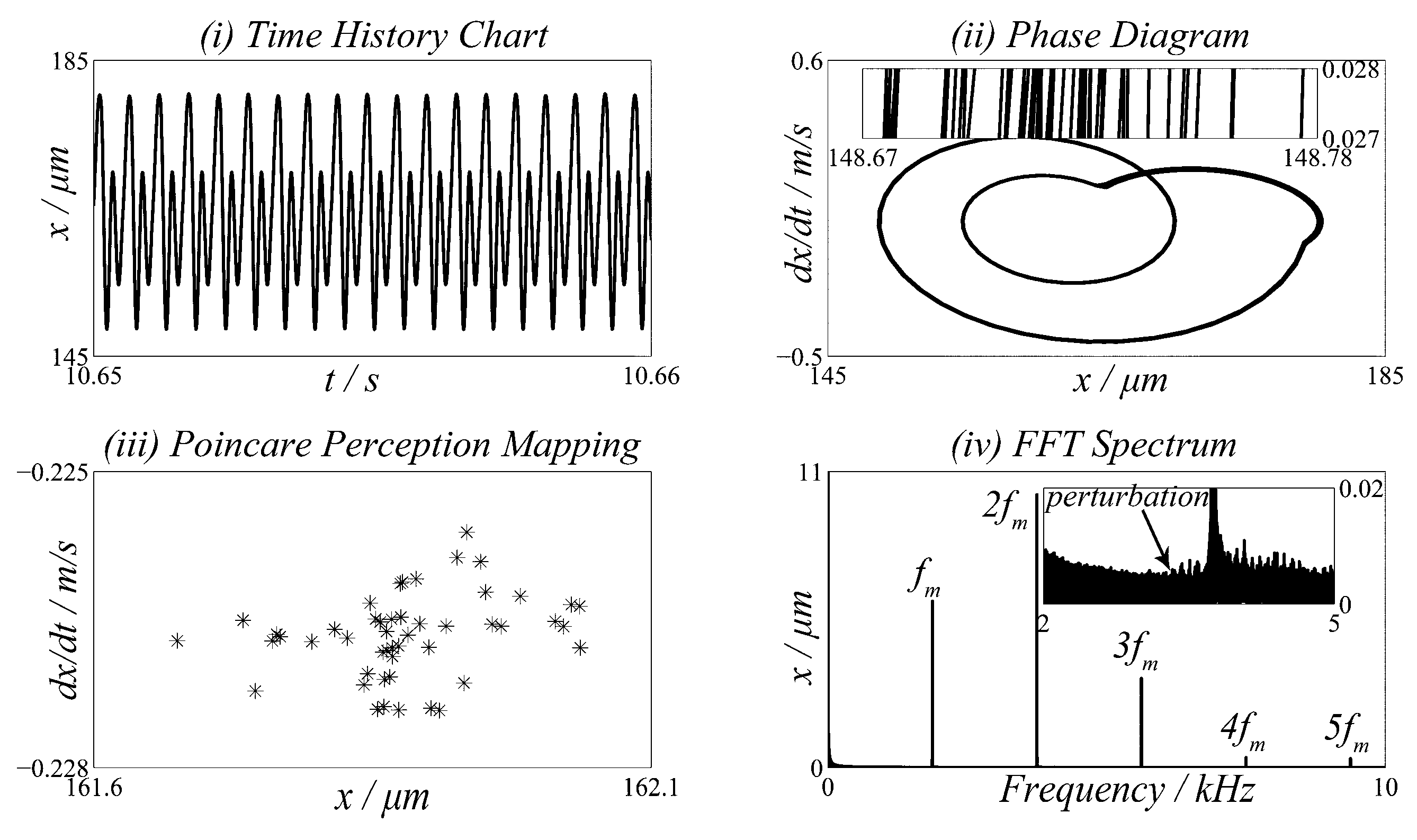
3.2. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Draft International Standard ISO 6336-1. Calculation of Load Capacity of Spur and Helical Gears; Part I: Basic principles and influence factors; International Organization for Standardization: Geneva, Switzerland, 1990; pp. 87–95. [Google Scholar]
- Walha, L.; Fakhfakh, T.; Haddar, M. Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation, bearing flexibility and backlash. Mech. Mach. Theory 2009, 44, 1058–1069. [Google Scholar] [CrossRef]
- Vaishya, M.; Singh, R. Analysis of periodically varying gear mesh systems with Coulomb friction using Floquet theory. J. Sound Vib. 2001, 243, 525–545. [Google Scholar] [CrossRef]
- Yang, J.; Peng, T.; Lim, T.C. An enhanced multi-term harmonic balance solution for nonlinear period-one dynamic motions in right-angle gear pairs. Nonlinear Dyn. 2014, 76, 1237–1252. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, Y.; Mechefske, C.K. Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng. Failure Anal. 2014, 39, 92–107. [Google Scholar] [CrossRef]
- Li, Y.; Ding, K.; He, G.; Lin, H. Vibration mechanisms of spur gear pair in healthy and fault states. Mech. Syst. Signal Process. 2016, 81, 183–201. [Google Scholar] [CrossRef]
- Kuang, J.H.; Yang, Y.T. An estimate of mesh stiffness and load sharing ratio of a spur gear pair. In Proceedings of the ASME Proceedings of International Power Transmission and Gearing Conference, Scottsdale, Arizona, 13–16 September 1992; pp. 1–9. [Google Scholar]
- Parey, A.; El Badaoui, M.; Guillet, F.; Tandon, N. Dynamic modelling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect. J. Sound Vib. 2006, 294, 547–561. [Google Scholar] [CrossRef]
- Hu, Z.; Tang, J.; Zhong, J.; Chen, S.; Yan, H. Effects of tooth profile modification on dynamic responses of a high speed gear-rotor-bearing system. Mech. Syst. Signal Process. 2016, 76–77, 294–318. [Google Scholar] [CrossRef]
- Tang, J.; Cai, W.; Wang, Z. Meshing stiffness formula of modification gear. J. Central South Univ. 2017, 48, 337–342. [Google Scholar]
- Siyu, C.; Jinyuan, T.; Zehua, H. Comparisons of gear dynamic responses with rectangular mesh stiffness and its approximate form. J. Mech. Sci. Technol. 2015, 29, 3563–3569. [Google Scholar]
- Yang, D.C.H.; Lin, J.Y. Hertzian Damping, Tooth Friction and Bending Elasticity in Gear Impact Dynamics. J. Mech. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Philippe, S.; Philippe, V.; Olivier, D. Contribution of gear body to tooth deflections—A new bidimensional analytical formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar]
- Xinhao, T. Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2004. [Google Scholar]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; He, Z. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Eng. Failure Anal. 2014, 42, 157–177. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Yu, W.; Shao, Y.; Mechefske, C.K. The effects of spur gear tooth spatial crack propagation on gear mesh stiffness. Eng. Failure Anal. 2015, 54, 103–119. [Google Scholar] [CrossRef]
- Li, Z.; Ma, H.; Feng, M.; Zhu, Y.; Wen, B. Meshing characteristics of spur gear pair under different crack types. Eng. Failure Anal. 2017, 80, 123–140. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, J.; Zhai, W.; Wang, Y.; Liu, J. Improved analytical methods for calculation of gear tooth fillet-foundation stiffness with tooth root crack. Eng. Failure Anal. 2017, 82, 72–81. [Google Scholar] [CrossRef]
- Ma, H.; Feng, M.; Li, Z.; Feng, R.; Wen, B. Time-varying mesh characteristics of a spur gear pair considering the tip-fillet and friction. Meccanica 2017, 52, 1695–1709. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Wang, D.; Yang, X.; Liu, H.; Lin, J. A probability distribution model of tooth pits for evaluating time-varying mesh stiffness of pitting gears. Mech. Syst. Signal Process. 2018, 106, 355–366. [Google Scholar] [CrossRef]
- Ma, H.; Yang, J.; Song, R.; Zhang, S.; Wen, B. Effects of Tip Relief on Vibration Responses of a Geared Rotor System. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1132–1154. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Analytical determination of back-side contact gear mesh stiffness. Mech. Mach. Theory 2014, 78, 263–271. [Google Scholar] [CrossRef]
- Yogesh, P.; Anand, P. Simulation of crack propagation in spur gear tooth for different gear parameter and its influence on mesh stiffness. Eng. Failure Anal. 2013, 30, 124–137. [Google Scholar]
- Chen, Q.; Ma, Y.; Huang, S.; Zhai, H. Research on gears’ dynamic performance influenced by gear backlash based on fractal theory. Appl. Surface Sci. 2014, 313, 325–332. [Google Scholar] [CrossRef]
- Zhixiong, L.; Zeng, P. Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: A case study on coal cutters. Nonlinear Dyn. 2015, 84, 1–16. [Google Scholar]
- Saghafi, A.; Farshidianfar, A. An analytical study of controlling chaotic dynamics in a spur gear system. Mech. Mach. Theory 2016, 96, 179–191. [Google Scholar] [CrossRef]
- Xianzeng, L.; Yuhu, Y.; Jun, Z. Investigation on coupling effects between surface wear and dynamics in a spur gear system. Tribol. Int. 2016, 101, 383–394. [Google Scholar]
- Yun, Y.J.; Byeongil, K. Effect and feasibility analysis of the smoothening functions for clearance-type nonlinearity in a practical driveline system. Nonlinear Dyn. 2016, 85, 1651–1664. [Google Scholar] [CrossRef]
- Xiangfeng, G.; Lingyun, Z.; Dailin, C. Bifurcation and chaos analysis of spur gear pair in two-parameter plane. Nonlinear Dyn. 2015, 79, 2225–2235. [Google Scholar]
- Wang, J.; Howard, I. The torsional stiffness of involute spur gears. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2004, 218, 131–142. [Google Scholar] [CrossRef]
- Suit, Z. A rotary model for spur gear dynamics. J. Mech. Trans. Autom. Des. 1985, 107, 529–535. [Google Scholar]
- Farshidianfar, A.; Saghafi, A. Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems. Nonlinear Dyn. 2014, 75, 783–806. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Li, Q. Quasi-static analysis of the nonlinear behavior of a railway vehicle gear system considering time-varying and stochastic excitation. Nonlinear Dyn. 2018, 93, 463–485. [Google Scholar] [CrossRef]




| –5.574 10−5 | –1.9986 10−3 | –2.3015 10−4 | 4.7702 10−3 | 0.0271 | 6.8045 | |
| 60.111 10−5 | 28.100 10−3 | –83.431 10−4 | –9.9256 10−3 | 0.1624 | 0.9086 | |
| –50.952 10−5 | 185.50 10−3 | 0.0538 10−4 | 53.3 10−3 | 0.2895 | 0.9236 | |
| –6.2042 10−5 | 9.0889 10−3 | –4.0964 10−4 | 7.8297 10−3 | –0.1472 | 0.6904 |
| Properties | Symbol | Value (Unit) |
|---|---|---|
| Young’s modulus | E | |
| Poisson’s ratio | 0.3 | |
| Pressure angle | ||
| Width of teeth | ||
| Number of teeth | 45/45 | |
| Module | 3 | |
| Radius of the inner hub | 25 | |
| Addendum coefficient | 1 | |
| Clearance coefficient | 0.25 | |
| Contact ratio | 1.7358 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Huang, K.; Xu, F.; Yi, Y.; Sang, M.; Zhai, H. Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur Gears. Appl. Sci. 2019, 9, 1029. https://doi.org/10.3390/app9051029
Xiong Y, Huang K, Xu F, Yi Y, Sang M, Zhai H. Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur Gears. Applied Sciences. 2019; 9(5):1029. https://doi.org/10.3390/app9051029
Chicago/Turabian StyleXiong, Yangshou, Kang Huang, Fengwei Xu, Yong Yi, Meng Sang, and Hua Zhai. 2019. "Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur Gears" Applied Sciences 9, no. 5: 1029. https://doi.org/10.3390/app9051029




