Stepped Spillways and Energy Dissipation: A Non-Uniform Step Length Approach
Abstract
:1. Introduction
- To investigate the effect of uniform step length on the energy dissipation for different slopes.
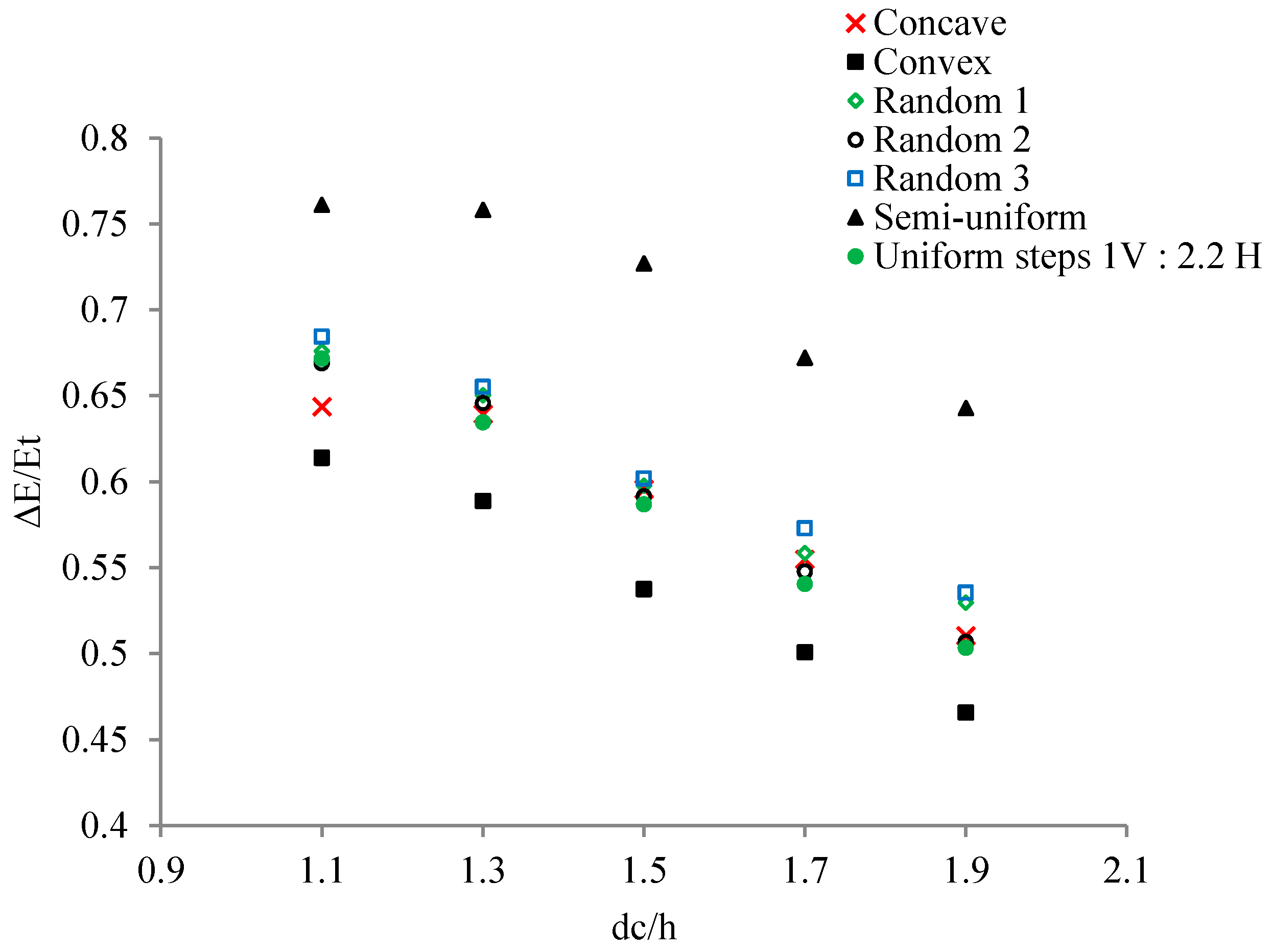
- To investigate the effect of non-uniform step length on the energy dissipation for four different cases:
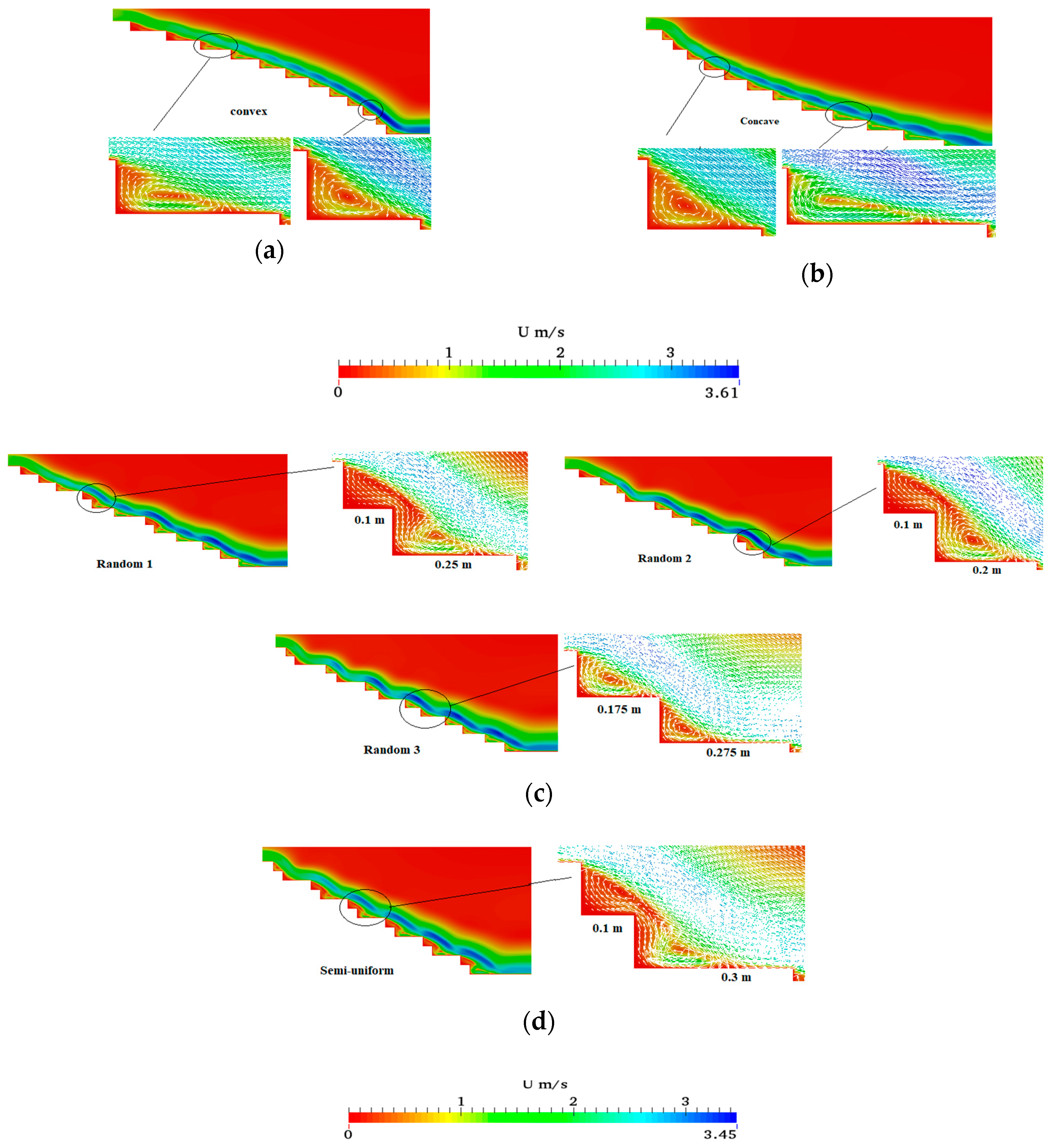
- Longer steps in the beginning, with the step length decreasing progressively toward the end (convex configuration).
- Shorter steps in the beginning, with the step length increasing progressively toward the end (concave configuration).
- Random step length distribution
- Semi-uniform step length distribution
- Investigation of the optimum step length configuration with respect to energy dissipation.
2. Materials and Methods
2.1. Numerical Schemes
2.2. Boundary Conditions
- The water inflow boundary was set as a velocity-inlet condition and obtained based on the range of flow rates 1.1 ≤ dc/h ≤ 1.9. The term (dc/h) represents the ratio of the critical depth (dc) to step height (h), in which critical depth is representative of the discharge.
- The outlet boundary condition was defined as an outlet pressure to allow the water flow out freely.
- The walls were assumed to have a no-slip condition.
- As shown in Figure 1, the atmospheric pressure was considered at the free surface boundary.
3. Results and Discussion
3.1. Mesh-Independence Test and Model Validation
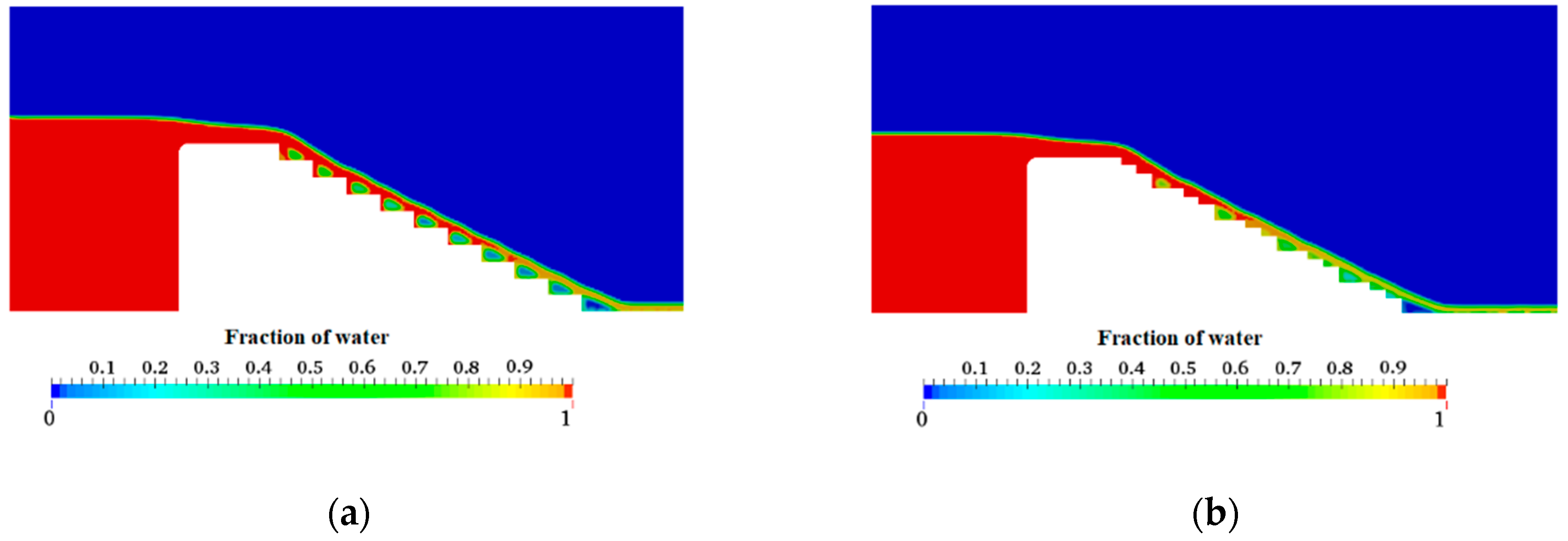
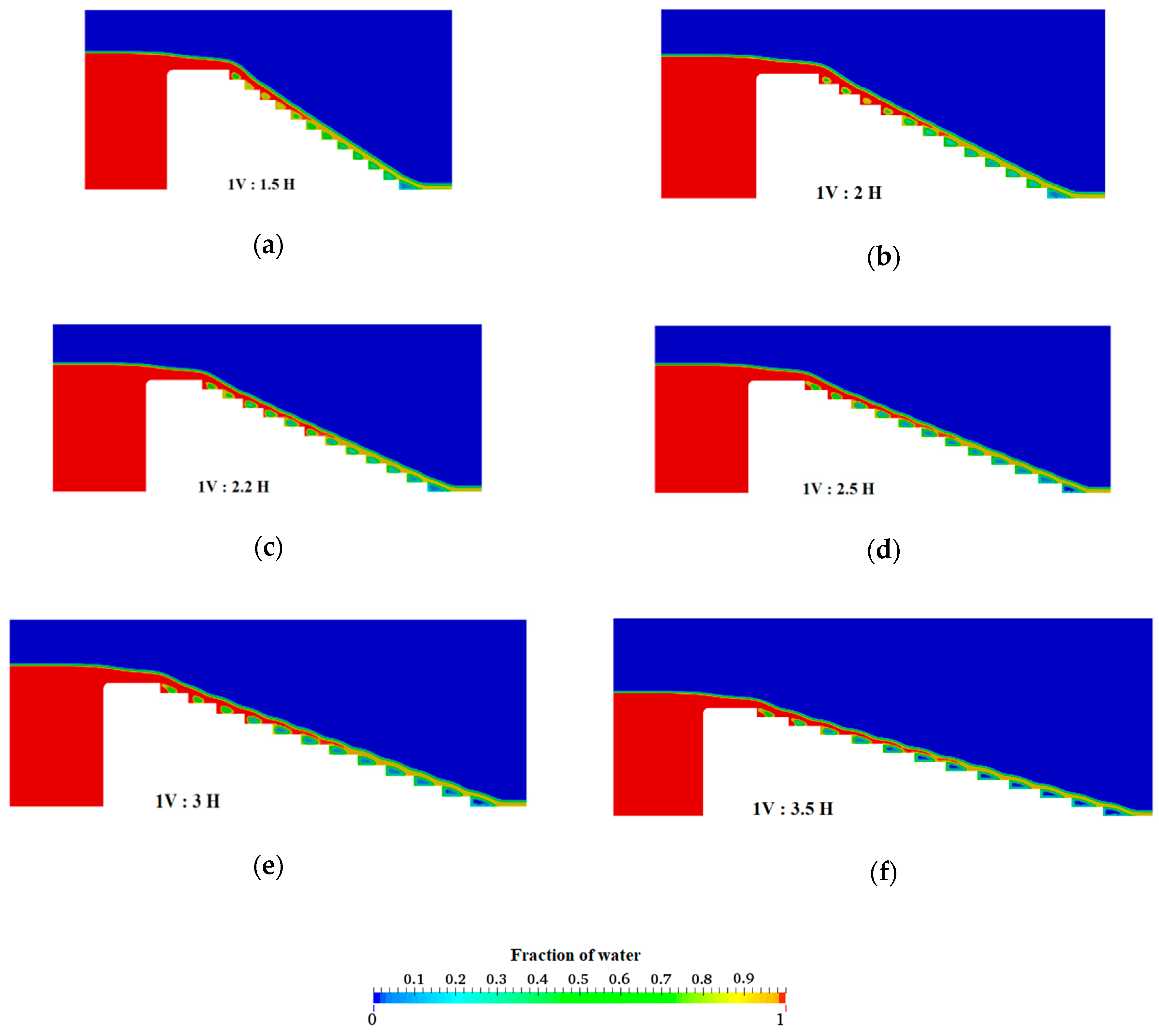
3.1.1. Free Surface Profiles
3.1.2. Velocity Distribution
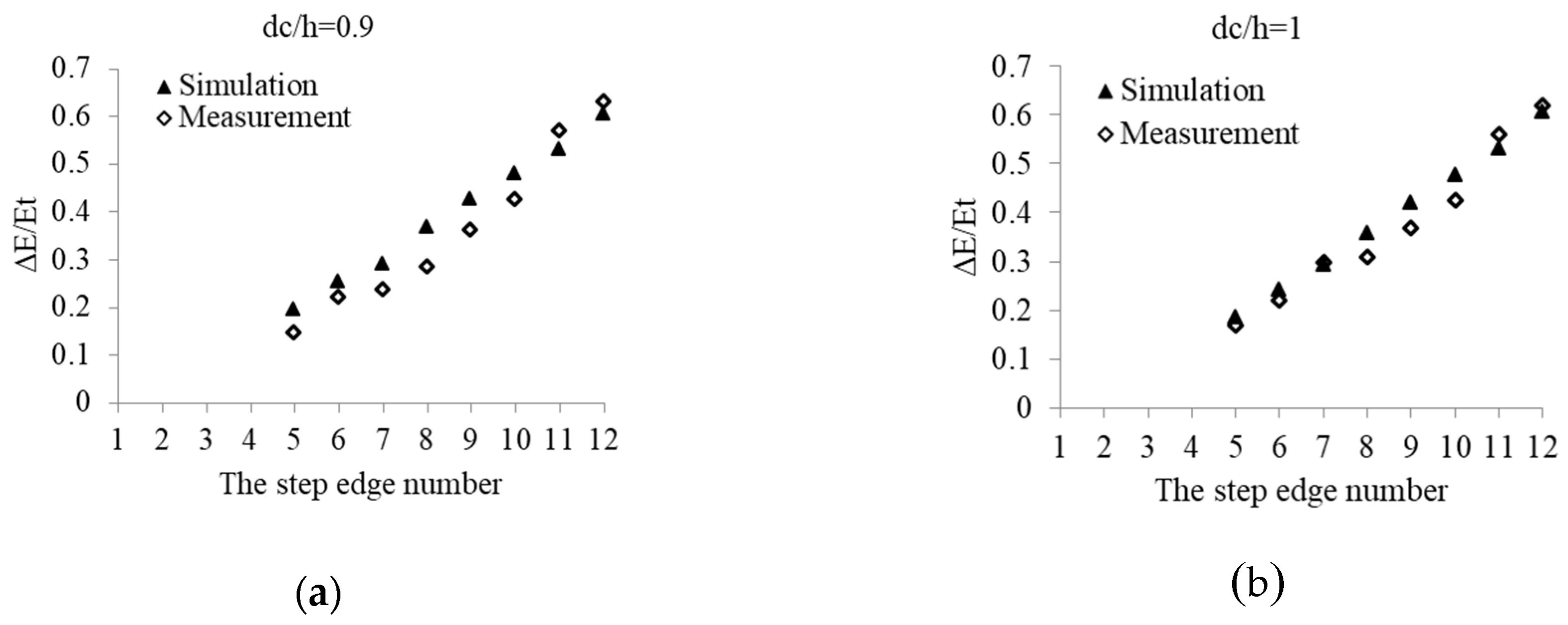
3.1.3. Energy Dissipation
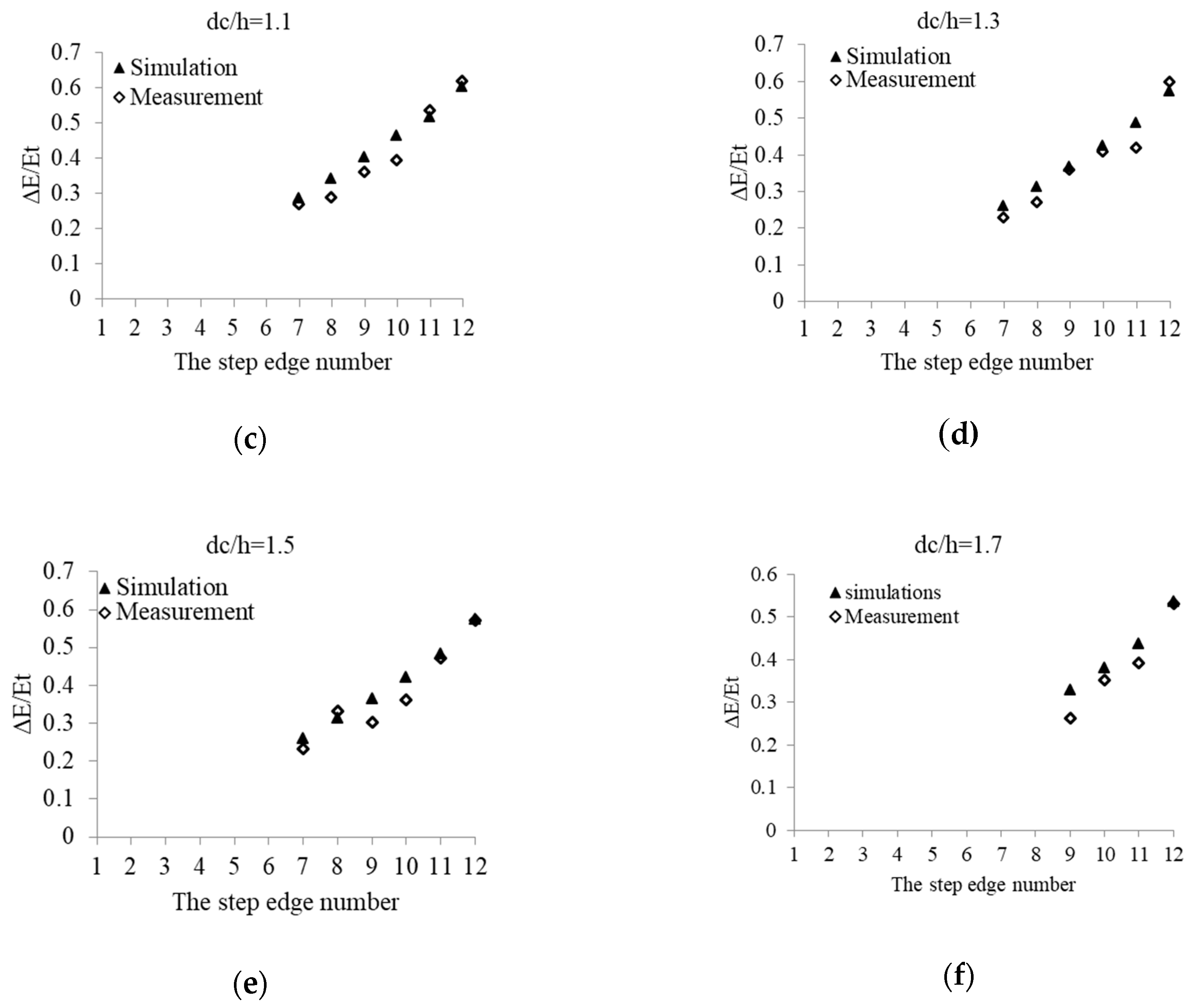
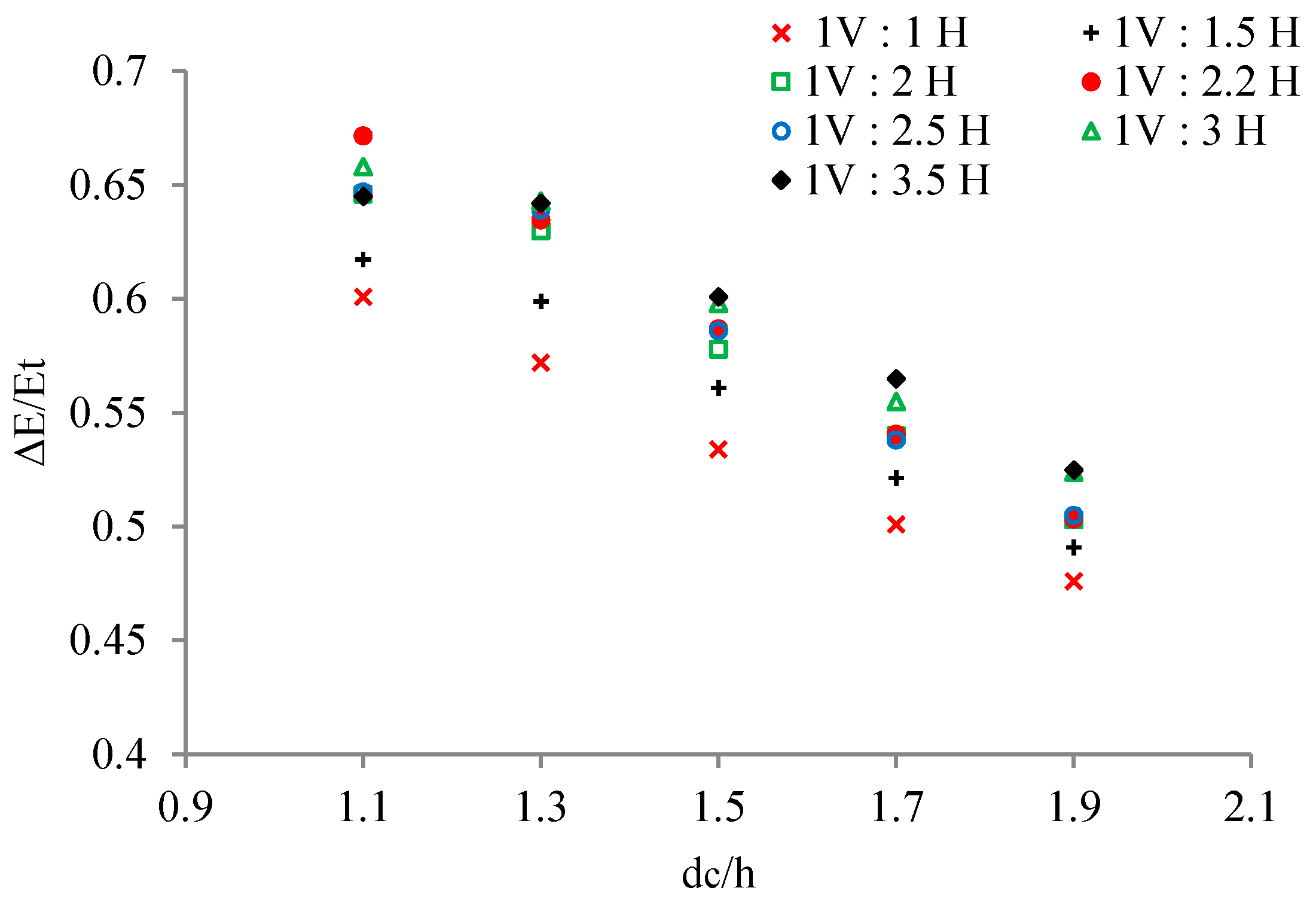
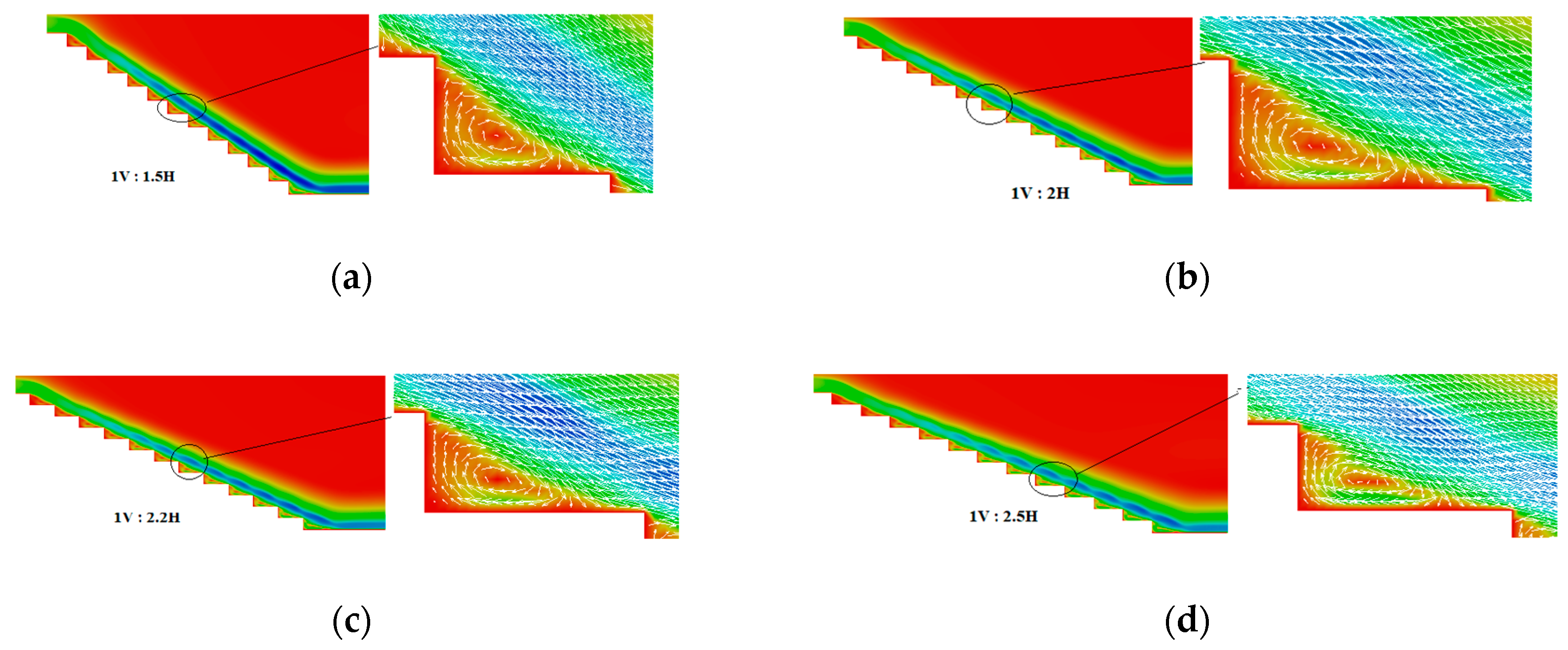
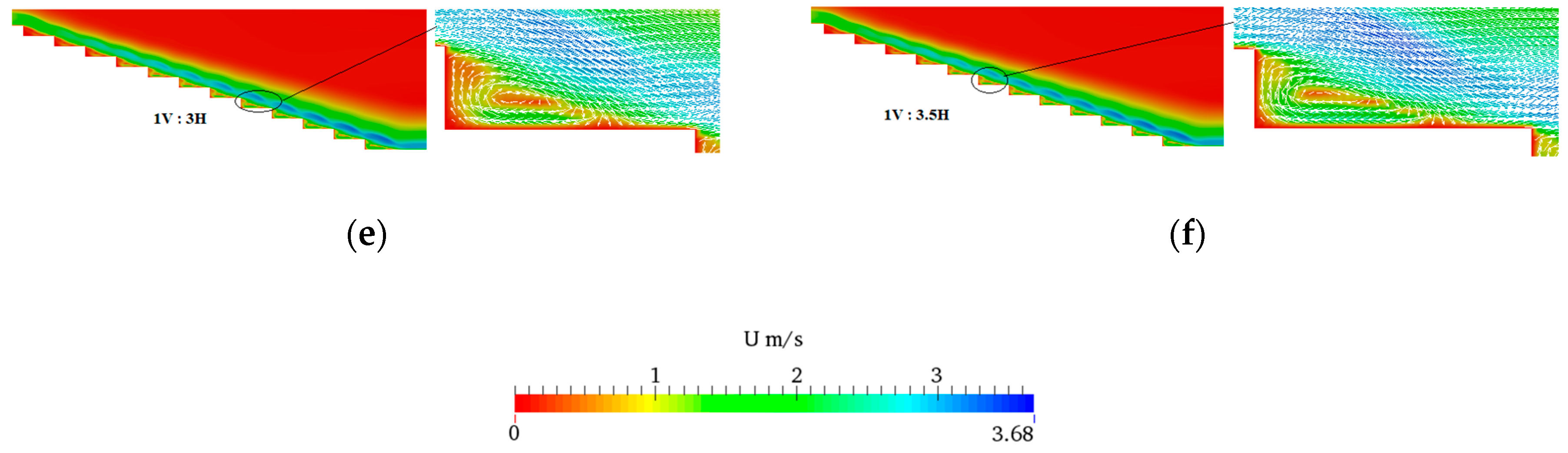
3.2. Uniform Stepped Spillways with Different Slopes
3.3. Non-Uniform Stepped Spillways
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chanson, H. Historical Development of Stepped Cascades for Dissipation of Hydraulic Energy. Trans. Newcom. Soc. 2001, 72, 295–318. [Google Scholar] [CrossRef]
- Felder, S. Air-Water Flow Properties on Stepped Spillways for Embankment Dams: Aeration, Energy Dissipation and Turbulence on Uniform, Non-Uniform and Pooled Stepped Chutes. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 2013. [Google Scholar]
- Gonzalez, C.A.; Chanson, H. Hydraulic Design of Stepped Spillways and Downstream Energy Dissipators for Embankment Dams. Dam Eng. 2007, 17, 223–244. [Google Scholar]
- Padulano, R.; Fecarotta, O.; Del Giudice, G.; Carravetta, A. Hydraulic Design of a USBR Type II Stilling Basin. J. Irrig. Drain. Eng. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Del Giudice, G.; Padulano, R.; Brasca, A.; Pontillo, M. Experimental results on the physical model of an USBR type II stilling basin. In Riverflow 2016; Taylor & Francis Group: London, UK, 2016. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of skimming flows over stepped channels and spillways. J. Hydraul. Res. 1994, 32, 445–460. [Google Scholar] [CrossRef]
- Rajaratnam, N. Skimming flow in stepped spillways. J. Hydraul. Eng. ASCE 1990, 116, 587–591. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-Phase Flow Characteristics of Stepped Spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Chanson, H. Stepped spillway flows and air entrainment. Can. J. Civ. Eng. 1993, 20, 422–435. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Energy dissipation and air entrainment on stepped spillways with non-uniform cavity sizes. In Proceedings of the 34th IAHR Wrld Congress, Brisbane, Australia, 26 June–1 July 2011; pp. 2412–2419. [Google Scholar] [CrossRef]
- Chanson, H. Prediction of the transition nappe/skimming flow on a stepped channel. J. Hydraul. Res. 1996, 34, 421–429. [Google Scholar] [CrossRef]
- Chanson, H.; Toombes, L. Hydraulics of stepped chutes: The transition flow L’hydraulique des chutes en marches d’escalier: L’écoulement de transition. J. Hydraul. Res. 2004, 42, 43–54. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Wongwises, S. Flow Patterns and Energy Dissipation over Various Stepped Chutes. J. Irrig. Drain. Eng. 2006, 132, 70–76. [Google Scholar] [CrossRef]
- Amador, A.; Sánchez-Juny, M.; Dolz, J. Characterization of the nonaerated flow region in a stepped spillway by PIV. J. Fluids Eng. 2006, 128, 1266–1273. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Broad-crested weir operation upstream of a steep stepped spillway. In Proceedings of the 36th IAHR World Congress, Hague, The Netherlands, 28 June–3 July 2015; pp. 2901–2911. [Google Scholar]
- Chamani, M.R.; Rajaratnam, N. Jet flow on stepped spillways. J. Hydraul. Eng. 1994, 120, 254–259. [Google Scholar] [CrossRef]
- Chanson, H. Advective Diffusion of Air Bubbles in Turbulent Water Flows. In Fluid Mechanics of Environmental Interfaces; Taylor & Francis: Leiden, The Netherlands, 2013; pp. 181–219. [Google Scholar]
- Chanson, H.; Felder, S. Energy dissipation on embankment dam stepped spillways, overflow stepped weirs and masonry stepped Spillways. In Proceedings of the 17th Congress of IAHR Asia and Pacific Division, Auckland, New Zealand, 21–24 February 2010; Melville, B., De Costa, G., Swann, T., Eds.; Auckland University: Auckland, New Zealand, 2010. [Google Scholar]
- Felder, S.; Chanson, H. Simple design criterion for residual energy on embankment dam stepped spillways. J. Hydraul. Eng. 2016, 142, 04015062. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C.; Hanson, G.J. Simplistic design methods for moderate-sloped stepped chutes. J. Hydraul. Eng. 2014, 140, 4014062. [Google Scholar] [CrossRef]
- Christodoulou, G.C. Energy dissipation on stepped spillways. J. Hydraul. Eng. 1993, 119, 644–650. [Google Scholar] [CrossRef]
- Stephenson, D. Stepped energy dissipators. In Proceedings of the International Conference on Hydraulics for High Dams, Beijing, China, 15–18 November 1988; IAHR: Beijing, China, 1988. [Google Scholar]
- Felder, S.; Chanson, H. Energy Dissipation down a stepped spillway with nonuniform step heights. J. Hydraul. Eng. 2011, 137, 1543–1548. [Google Scholar] [CrossRef]
- Li, D.; Yang, Q.; Ma, X.; Dai, G. Case study on application of the step with non-uniform heights at the bottom using a numerical and experimental model. Water 2018, 10, 1762. [Google Scholar] [CrossRef]
- Bayon, A.; Toro, J.P.; Bombardelli, F.A.; Matos, J.; López-Jiménez, P.A. Influence of VOF technique, turbulence model and discretization scheme on the numerical simulation of the non-aerated, skimming flow in stepped spillways. J. Hydro-Environ. Res. 2017, 19, 137–149. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Meireles, I.; Matos, J. Laboratory measurements and multi-block numerical simulations of the mean flow and turbulence in the non-aerated skimming flow region of steep stepped spillways. Environ. Fluid Mech. 2011, 11, 263–288. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Volume of fluid model for turbulence numerical simulation of stepped spillway overflow. J. Hydraul. Eng. 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Cheng, X.; Gulliver, J.S.; Zhu, D. Application of displacement height and surface roughness length to determination boundary layer development length over stepped spillway. Water 2014, 12, 3888–3912. [Google Scholar] [CrossRef]
- Kositgittiwong, D.; Chinnarasri, C.; Julien, P.Y. Numerical simulation of flow velocity profiles along a stepped spillway. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2013, 227, 327–335. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J. Numerical investigation on the hydraulic properties of the skimming flow over pooled stepped spillway. Water 2018, 10, 1478. [Google Scholar] [CrossRef]
- Lopes, P.; Leandro, J.; Carvalho, R.F.; Bung, D.B. Alternating skimming flow over a stepped spillway. Environ. Fluid Mech. 2017, 17, 303–322. [Google Scholar] [CrossRef]
- Shahheydari, H.; Nodoshan, E.J.; Barati, R.; Moghadam, M.A. Discharge coefficient and energy dissipation over stepped spillway under skimming flow regime. KSCE J. Civ. Eng. 2015, 19, 1174–1182. [Google Scholar] [CrossRef]
- Tabbara, M.; Chatila, J.; Awwad, R. Computational simulation of flow over stepped spillways. Comput. Struct. 2005, 83, 2215–2224. [Google Scholar] [CrossRef]
- Toro, J.P.; Bombardelli, F.A.; Paik, J.; Meireles, I.; Amador, A. Characterization of turbulence statistics on the non-aerated skimming flow over stepped spillways: A numerical study. Environ. Fluid Mech. 2016, 16, 1195–1221. [Google Scholar] [CrossRef]
- Wan, W.; Raza, A.; Chen, X. Effect of Height and Geometry of Stepped Spillway on Inception Point Location. Appl. Sci. 2019, 9, 2091. [Google Scholar] [CrossRef]
- Eghbalzadeh, A.; Javan, M. Comparison of Mixture and VOF models for numerical simulation of Air-Entrainment in skimming flow over stepped spillways. Procedia Eng. 2012, 28, 657–660. [Google Scholar] [CrossRef] [Green Version]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2002. [Google Scholar] [CrossRef] [Green Version]
- Pendar, M.; Roohi, E. Cavitation characteristics around a sphere: An LES Investigation. Int. J. Multiph. Flow 2018, 98, 1–23. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Hydraulics of the Developing Flow Region of Stepped Cascades: An Experimental Investigation; Hydraulic Model Report No. CH97/15; School of Civil Engineering, The University of Queensland: Brisbane, Australia, 2015; Available online: https://espace.library.uq.edu.au/view/UQ:355818 (accessed on 1 January 2015).
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Bai, Z.; Zhang, J. Comparison of different turbulence models for numerical simulation of pressure Distribution in V-Shaped Stepped Spillway. Math. Probl. Eng. 2017, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Qian, Z.; Hu, X.; Huai, W.; Amador, A. Numerical simulation and analysis of water flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2009, 52, 1958–1965. [Google Scholar] [CrossRef]
- Kositgittiwong, D. Validation of Numerical Model of the Flow Behaviour through Smooth and Stepped Spillways Using Large-Scale Physical Model. Ph.D. Thesis, King Mongkut’s University of Technology, Thonburi, Thailand, 2012. [Google Scholar] [CrossRef]










| Step Height h(m) | Step Length L(m) | Height of Dam Hd (m) | Number of Steps (N) | Slope V:H 1 |
|---|---|---|---|---|
| 0.1 | 0.10 | 1.2 | 12 | 1:1 |
| 0.1 | 0.15 | 1.2 | 12 | 1:1.5 |
| 0.1 | 0.20 | 1.2 | 12 | 1:2 |
| 0.1 | 0.22 | 1.2 | 12 | 1:2.2 |
| 0.1 | 0.25 | 1.2 | 12 | 1:2.5 |
| 0.1 | 0.30 | 1.2 | 12 | 1:3 |
| 0.1 | 0.35 | 1.2 | 12 | 1:3.5 |
| Concave | Convex | Random 1 | Random 2 | Random 3 | Semi-Uniform | ||
|---|---|---|---|---|---|---|---|
| N = 12 h = 0.1 m Hd = 1.2 m | i | L (m) | L (m) | L (m) | L (m) | L (m) | L (m) |
| 1 | 0.1 | 0.35 | 0.2 | 0.25 | 0.1 | 0.1 | |
| 2 | 0.125 | 0.325 | 0.2 | 0.2 | 0.35 | 0.3 | |
| 3 | 0.15 | 0.3 | 0.3 | 0.1 | 0.125 | 0.1 | |
| 4 | 0.175 | 0.275 | 0.1 | 0.35 | 0.325 | 0.3 | |
| 5 | 0.2 | 0.25 | 0.25 | 0.2 | 0.15 | 0.1 | |
| 6 | 0.225 | 0.225 | 0.35 | 0.225 | 0.3 | 0.3 | |
| 7 | 0.25 | 0.2 | 0.1 | 0.2 | 0.175 | 0.1 | |
| 8 | 0.275 | 0.175 | 0.25 | 0.35 | 0.275 | 0.3 | |
| 9 | 0.3 | 0.15 | 0.3 | 0.1 | 0.2 | 0.1 | |
| 10 | 0.325 | 0.125 | 0.2 | 0.2 | 0.25 | 0.3 | |
| 11 | 0.35 | 0.1 | 0.2 | 0.25 | 0.225 | 0.1 | |
| Average Slope (θ) | - | - | 24.20 | 24.40 | 24.00 | 27.7 | |
| Standard deviation (SD) | 0.083 | 0.083 | 0.079 | 0.081 | 0.083 | 0.112 |
| Reference | θ | Hdam | N | h (m) | L (m) | Q m3/sec | dc/h | ΔE/Et | Error % | |
|---|---|---|---|---|---|---|---|---|---|---|
| Experiment Results | Numerical Results | |||||||||
| Zhang and Chanson [16] | 45 | 1.2 | 12 | 0.1 | 0.1 | 0.057 | 0.7 | 0.61 | 0.622 | 1.967 |
| 0.083 | 0.9 | 0.63 | 0.602 | 4.444 | ||||||
| 0.098 | 1 | 0.63 | 0.605 | 3.968 | ||||||
| 0.112 | 1.1 | 0.62 | 0.601 | 3.065 | ||||||
| 0.145 | 1.3 | 0.60 | 0.572 | 4.667 | ||||||
| 0.179 | 1.5 | 0.57 | 0.534 | 6.316 | ||||||
| 0.216 | 1.7 | 0.53 | 0.501 | 5.472 | ||||||
| Felder [2] | 26.56 | 1 | 10 | 0.1 | 0.2 | 0.056 | 0.69 | 0.76 | 0.71 | 6.579 |
| 0.116 | 1.11 | 0.64 | 0.636 | 0.625 | ||||||
| 0.143 | 1.28 | 0.63 | 0.616 | 2.222 | ||||||
| 0.161 | 1.38 | 0.66 | 0.592 | 10.303 | ||||||
| 0.180 | 1.49 | 0.58 | 0.577 | 0.517 | ||||||
| 0.202 | 1.61 | 0.57 | 0.550 | 3.509 | ||||||
| Felder [2] | 0.095 | 0.97 | 0.65 | 0.629 | 3.23 | |||||
| 26.56 | 1 | 15 | h | L | 0.116 | 1.11 | 0.62 | 0.616 | 0.645 | |
| 10 steps (h = 0.05 m) | 0.1 | 0.143 | 1.28 | 0.56 | 0.599 | 6.964 | ||||
| 5 steps (h = 0.1 m) | 0.2 | 0.161 | 1.38 | 0.56 | 0.582 | 3.928 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashoor, A.; Riazi, A. Stepped Spillways and Energy Dissipation: A Non-Uniform Step Length Approach. Appl. Sci. 2019, 9, 5071. https://doi.org/10.3390/app9235071
Ashoor A, Riazi A. Stepped Spillways and Energy Dissipation: A Non-Uniform Step Length Approach. Applied Sciences. 2019; 9(23):5071. https://doi.org/10.3390/app9235071
Chicago/Turabian StyleAshoor, Abdelwanees, and Amin Riazi. 2019. "Stepped Spillways and Energy Dissipation: A Non-Uniform Step Length Approach" Applied Sciences 9, no. 23: 5071. https://doi.org/10.3390/app9235071





