1. Introduction
The methodology of a standard dilatometer test (DMT) is widely known and a detailed procedure for conducting the test was presented by Marchetti [
1] and Marchetti et al. [
2]. Until now, numerous studies have been performed to evaluate and improve some of the original correlations proposed by Marchetti [
1], but most of them have been limited to mineral soils. Comprehensive investigations have been made to assess and expand the application of DMT in geotechnical engineering [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. In most cases, the relationships used to evaluate geotechnical parameters from the dilatometer test such as the corrected first reading
po or corrected second reading
p1, or index parameters such as the material index
ID, horizontal stress index
KD, and dilatometer modulus
ED, are commonly applied.
Undrained shear strength is the basic parameter in the geotechnical design of different structures. Determination of this parameter using dilatometer tests is usually based on empirical formulas. However, it should be noted that most of these formulas have been established in different countries; therefore, regional geotechnical conditions could have substantially affected the empirical relationships and the values of empirical coefficients.
In geotechnical engineering, Artificial Neural Networks (ANNs) have been used to analyse many issues, as reviewed by: Adeli [
18], Rafiq et al. [
19], Shahin et al. [
20,
21], Dihoru et al. [
22], and Sulewska [
23]. The use of ANNs for the prediction of the lateral earth pressure ratio K
o based on a dilatometer test and undrained shear strength of soft clays was presented by Das and Basudhar [
24] and Byeong et al. [
25], respectively. However, Artificial Neural Networks have not yet been applied to evaluate the undrained shear strength of organic soils from dilatometer tests.
This paper presents the results of field and laboratory tests of organic soils such as peat (amorphous and pseudo-fibrous), calcareous soil called “gyttja” (calcareous and calcareous-organic), mud, and organic mud. The undrained shear strength of organic soils can be evaluated based on measurements obtained from the dilatometer test using single- and multi-factor empirical correlations presented in the literature. However, the empirical methods may sometimes show relatively high values of maximum relative error. Therefore, a method for evaluating the undrained shear strength of organic soils using artificial neural networks based on data obtained from a dilatometer test and organic soil properties is presented in this study. The presented neural network, with an architecture of 5-4-1, predicts the normalized undrained shear strength based on five independent variables: the normalized net value of a corrected first pressure reading (po − uo)/σ′v, the normalized net value of a corrected second pressure reading (p1 − uo)/σ′v, the organic content Iom, the void ratio e, and the stress history indictor (oc or nc). The neural model presented in this study provided a more reliable prediction of the undrained shear strength in comparison to the empirical methods, with a maximum relative error of ±10%.
2. Methods and Materials
2.1. Dilatometer Test Procedure
The flat dilatometer was developed in Italy by Silvano Marchetti [
1,
26] as an in situ penetration test. The basic DMT equipment consists of a flat blade-shaped tip, 95 mm wide and 14 mm thick, with a sharp edge, and a 60 mm diameter steel membrane centred on and flushed with one side of the blade. The test procedure involves pushing the blade vertically into the ground with readings at selected test depths. The readings are generally made at every 0.2 m of depth. The first
A-reading pressure occurs at membrane “lift-off” and the second
B-reading pressure after 1.1 mm movement, with both movements being prompted by an audio signal [
16,
27,
28]. After appropriate corrections, the values of
A and
B yield the values of the corrected first reading
po (0.00 mm expansion) and the corrected second reading
p1. Based on the corrected readings
po and
p1, as well as in situ hydrostatic pore pressure
uo and in situ effective vertical stress
σ′vo, the following index parameters were proposed by Marchetti [
1]:
2.2. Evaluation of Undrained Shear Strength From DMT
2.2.1. Marchetti Relationship
Marchetti [
1] developed a correlation between the normalized undrained shear strength
τfu/
σ’vo and the horizontal stress index
KD based on the relationship between the normalized undrained shear strength and the overconsolidation ratio (
OCR) proposed by Ladd et al. [
29] and the correlation of
OCR and
KD. Marchetti [
1] proposed the following basic correlation between the normalized undrained shear strength and the horizontal stress index
KD for cohesive soils (for
ID < 1.2):
Analysis of the DMT and the triaxial test results carried out by Lechowicz [
30,
31] indicates that, particularly for peat and gyttja, the relationship between the normalized undrained shear strength and the horizontal stress index
KD differs from that proposed by Marchetti [
1] and can be modified as follows:
where
S=(τfu/σ’vo)nc is the normalized undrained shear strength for normally consolidated soil. The value of the
S parameter for amorphous peat is equal to 0.5, but for calcareous gyttja and calcareous-organic gyttja, it is at 0.40 and 0.45, respectively [
32].
2.2.2. Roque et al. Relationship
Roque et al. [
33] proposed an alternative approach for estimating the undrained shear strength based on the correlation using the corrected second reading
p1 and the bearing capacity factor
Nc:
where
σho is the in situ horizontal stress, and
NC is the dilatometer factor for clays that varies from about 4 to 7. The value of the bearing capacity factor
NC equals 6 and 7 for gyttja and peat, respectively, and 5 for mud and organic mud [
32].
2.2.3. Smith and Houlsby Relationship
Different approaches have been proposed by Smith and Houlsby [
34], in which the undrained shear strength was a function of the corrected first reading
po and the bearing capacity factor
ND:
where
ND is the dilatometer factor, which varies from about 4 to 7 for clays, and from about 3 to 4 for peat, gyttja, mud, and organic mud.
2.2.4. Rabarijoely Relationship
A multi-factor relationship was proposed by Rabarijoely [
35] to evaluate the undrained shear strength
τfu of organic soils:
where
α0,
α1,
α2,
α3 are the empirical coefficients. In this relationship, three factors are taken into account: the net value of the corrected first pressure reading (
po −
uo), the net value of the corrected second pressure reading (
p1 −
uo), and the effective vertical stress
σ′v. The empirical coefficients in Equation (8) for organic soils can be evaluated as a function of the void ratio
e and empirical coefficients
Ci and
Di shown in
Table 1, according to the following formula:
where subscript
i = 0, 1, 2, 3.
2.3. Characteristics of the Tested Organic Soils
2.3.1. Antoniny Site
The Antoniny test site is located in north-western Poland in the Noteć River valley, where the Department of Geotechnical Engineering of the Warsaw University of Life Sciences in cooperation with the Swedish Geotechnical Institute performed extensive field and laboratory investigations in the 1980s [
36,
37]. Two test embankments (with and without vertical drains) were constructed in three stages between 1983 and 1987. The fill without vertical drains was then brought to failure by successively increasing the height of the fill. The field investigations included dilatometer tests and field vane tests (FVT).
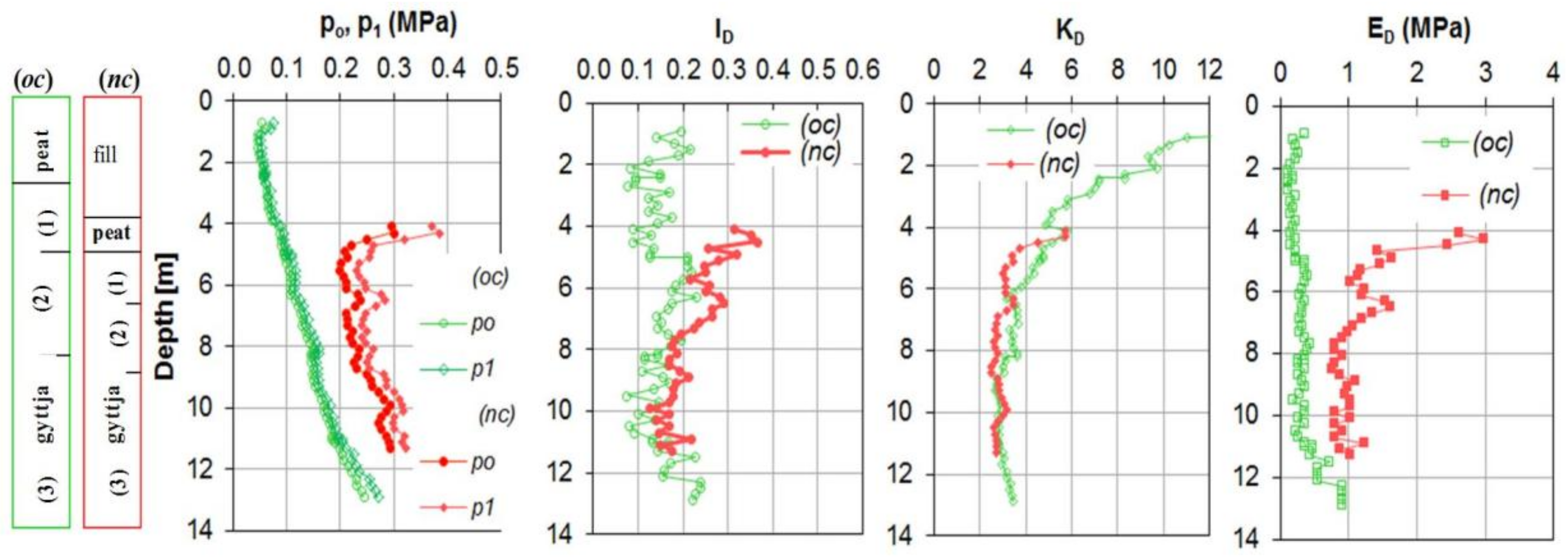
At this site, the virgin organic subsoil, 7.8 m thick, consists of a 3.1 m thick peat layer and a 4.7 m gyttja layer. Based on the index properties, the peat layer was sub-divided into two layers: the first one being pseudo-fibrous peat, occurring from the surface to the depth of 1.0 m, and the second one being amorphous peat, occurring below 1.0 m to the depth of 3.1 m. The gyttja layer was sub-divided into three layers, with the first being calcareous-organic gyttja occurring from the depth of 3.1 m to 4.5 m and the second and third layer being calcareous gyttja occurring from the depth of 4.5 m to 6.8 m and below the depth of 6.8 m, respectively. The organic subsoil is underlined by a sand layer. Organic soils are overconsolidated with an overconsolidation ratio,
OCR, decreasing from 5 to 2 with depth. The results of the index properties of organic soils are summarised in
Table 2. Soil profiles of organic subsoil at the Antoniny site for overconsolidated subsoil (
oc) and normally consolidated subsoil (
nc) are shown in
Figure 1.
2.3.2. Koszyce site
The Koszyce test site is located in north-western Poland in the Ruda River valley, where a laboratory and field testing program was performed below and outside of the main dam embankment of the Koszyce reservoir [
38]. Due to the presence of deep soft organic subsoil, the dam embankment was constructed as a reinforcement mattress. At the Koszyce site, the central part of the dam embankment is founded on organic subsoil with a variable thickness. The soft subsoil consists of organic sediments with a thickness ranging from 4 to 27 m. The uppermost 2.5 m consists of peat. Below the peat layer, there is a layer of calcareous soil called gyttja with a thickness ranging from 2 to 25 m, divided into four sub-layers. The organic subsoil is underlined by a fine sand layer. The field investigations included dilatometer tests and field vane tests (FVT). The index properties of the initial state of organic soils are summarised in
Table 3. Soil profiles of organic subsoil at the Koszyce site for overconsolidated subsoil (
oc) and normally consolidated subsoil (
nc) are shown in
Figure 2.
2.3.3. Nielisz Site
The Nielisz test site is located in south-eastern Poland in the Wieprz River valley where an extensive testing program was performed between 1994 and 1996 [
32,
35,
39], which included laboratory tests and in situ tests such as dilatometer tests and field vane tests (FVT). Due to the appearance of soft soils, the main dam embankment of the Nielisz reservoir was constructed in stages, utilising the increase in shear strength due to consolidation. The main dam embankment was constructed in two stages with preloading fills.
At the Nielisz site, the soft subsoil consists of mineral and organic sediments. The original thickness of soft soils at the site varied from 1.0 to 5.0 m. The upper 0.5–1.0 m mainly consists of sandy silt or silt. Further below, there is a layer of mud or organic mud with a thickness of 1.0–4.0 m, divided into two parts by a layer of silt. A fine sand layer occurs below soft subsoil. The results of the index properties of organic soils are summarised in
Table 4. Soil profiles of organic subsoil at the Nielisz site for overconsolidated subsoil (
oc) and normally consolidated subsoil (
nc) are shown in
Figure 3.
3. Results
3.1. Results of Dilatometer Tests
The DMT data profiles including the corrected readings
po and
p1, as well as the index parameters
ID,
KD, and
ED from dilatometer tests obtained for the overconsolidated subsoil and for normally consolidated organic subsoil at the Antoniny, Koszyce, and Nielisz sites, respectively, are presented in
Figure 1,
Figure 2 and
Figure 3.
3.2. Results of Field Vane Tests
The shear strength of the organic soils at the Antoniny, Koszyce, and Nielisz sites was measured by the field vane test (FVT). In order to evaluate the undrained shear strength
τfu of organic soils from FVT, the measured shear strength
τfv has to be corrected by using the correction factor
μ according to Bjerrum [
40]:
The correction factors for the organic soils from the Antoniny site were evaluated according to the method elaborated by the Swedish Geotechnical Institute (SGI) [
41] based on the liquid limit
wL, and also by the average correction factors determined from the following laboratory tests: triaxial compression, triaxial extension, and direct simple shear (
Table 5).
For organic soils from the Koszyce site, the correction factors for peat, gyttja (calcareous-organic), and gyttja (calcareous), evaluated according to the SGI method based on the liquid limit wL, were μ(wL) = 0.5, μ(wL) = 0.65, and μ(wL) = 0.75, respectively. For organic mud and mud from the Nielisz site, the correction factors evaluated according to the SGI method based on the liquid limit wL were: μ(wL) = 0.6 and μ(wL) = 0.65, respectively.
Shown in
Table 6 are the values of the undrained shear strength
τfv of organic soils obtained from FVT using the corrected value of measured shear strength
τfv.
4. Evaluation of the Undrained Shear Strength Based on Empirical Relationships
Evaluation of the undrained shear strength
τfu of overconsolidated and normally consolidated organic soils from dilatometer tests was carried out on the basis of single- and multi-factor empirical relationships proposed by Marchetti [
1], Lechowicz [
30,
31], Roque et al. [
33], and Smith and Houlsby [
34], as well as the three-factor relationship of Rabarijoely [
35] using Equations (4)–(8), and empirical coefficients determined on the basis of the void ratio
e from Equation (9). In order to compare the undrained shear strength evaluated based on empirical relationships with undrained shear strength obtained from field vane tests, the measurements from dilatometer tests were taken from the same depth where FVT was carried out.
For each relationship, the maximum relative error max
RE (
Table 6) for particular organic soil was selected from values of the relative errors
RE calculated according to the formula:
where
P is the number of cases,
p ∈ {1, …,
P},
d(p) is the measured value, and
y(p) is the calculated value.
Analysis of the calculation results indicates quite high maximum relative error values obtained for the undrained shear strength evaluated on the basis of the single-factor empirical relationship of Marchetti ranging between 47.5–58.7% for peat, 27.6–50.0% for gyttja, and 48.4–50.8% for mud. The max RE values calculated for undrained shear strength evaluated from the Roque et al. relationship with the bearing capacity factor Nc determined for organic soils are smaller, and range between 19.0–50.9% for peat, 7.2–40.6% for gyttja, and 7.7–21.5% for mud. The max RE values calculated for undrained shear strength evaluated from the Smith and Houlsby relationship with the bearing capacity factor ND determined for organic soils are slightly smaller, and range between 8.0–47.0% for peat, 4.8–31.3% for gyttja, and 12.0–17.0% for mud. The comparison carried out for the version of the Marchetti relationship modified by Lechowicz for organic soils indicates that the max RE values obtained for the undrained shear strength of organic soils for the Antoniny, Koszyce, and Nielisz sites vary between 3.3 and 35.1%.
The comparison carried out for the three-factor relationship of Rabarijoely, from which the empirical coefficients were determined on the basis of the void ratio, indicates much smaller max RE values of the undrained shear strength for peat at 0.9–13.4% and for gyttja at 7.2–12.1%. This shows that the evaluation of the undrained shear strength from dilatometer tests for the tested peat and gyttja from the three-factor relationship of Rabarijoely results in a better accuracy; however, it requires the use of empirical coefficients individually determined on the basis of the void ratio. In the case of mud and organic mud, the evaluation of the undrained shear strength from the dilatometer test using the Rabarijoely relationship (Equation (8)) requires additional determination of the empirical coefficients α0, α1, α2, α3.
5. Artificial Neural Networks Analysis
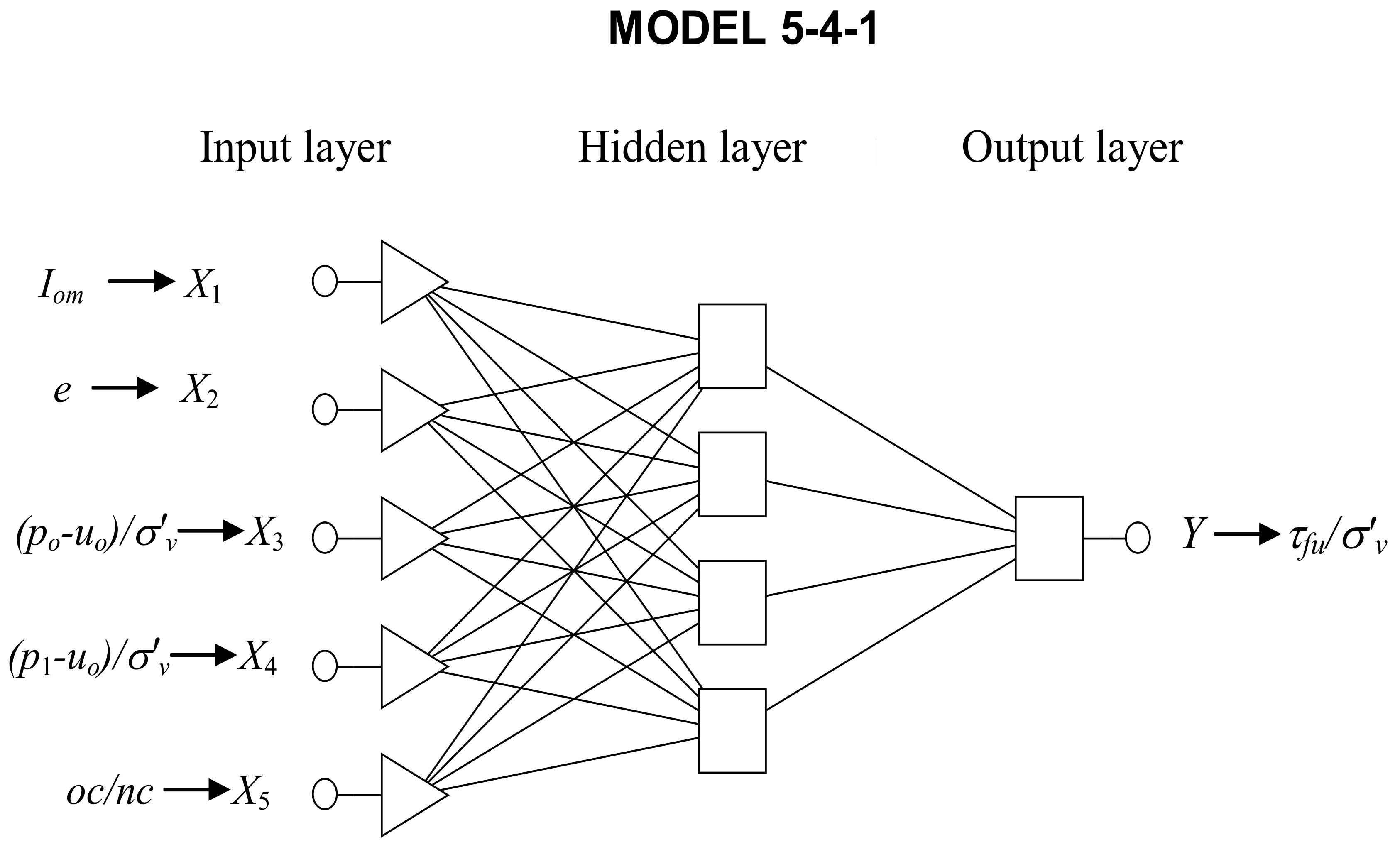
5.1. Determination of the Architecture of the Neural Network
The class of neural network used in this study includes multilayer perceptrons (MLPs) with one hidden layer. The architecture of the
N-H-M type network is defined by the number of nodes
N in the input layer
X1–
XN, the number of nodes
H in one hidden layer, and the number of nodes
M =
Y in the output layer. Neural networks were constructed according to the criterion of minimization of the error function, which was the sum of squares of differences (
SOS) expressed by the formula:
where
P is the number of cases of the set
P,
p ∈ {1, …,
P},
d(p) represents the measured values, and
y(p) represents the corresponding values predicted from neural networks.
5.2. Database Used in the Development of the ANN Method
The dataset used in the ANN analysis consisted of
n = 88 cases of results of index properties tests (organic content and void ratio) and results of dilatometer tests and stress history indicators (
oc or
nc) as independent variables and as dependent variables of normalized undrained shear strength from field vane tests shown in
Table 7. The dataset was described by five independent variables:
X1 = organic content
Iom ∈ {8–85%};
X2 = void ratio
e ∈ {1.9–7.4};
X3 = normalized net value of corrected first pressure reading (
po −
uo)/
σ′v ∈ {1.41–20.0};
X4 = normalized net value of corrected second pressure reading (
p1 −
uo)/
σ′v ∈ {1.87–27.35};
X5 = code of overconsolidated state (
oc) or normally consolidated state (
nc), respectively ∈ {0; 1}, and one dependent variable
Y =
τfu/
σ′v ∈ {0.26–5.00}. Variable
X3 is the same as the horizontal stress index
KD. Variable
X5 was treated as a quantitative variable since it was a zero-one variable [
42].
Sensitivity analysis of the Neural Network was performed based on the network error quotient, with one of the input variables for the basic error of the network calculated for the neural network having all input variables. A larger ratio of errors in the absence of a given input variable means that a larger error is created in the neural network devoid of this input variable. This indicates how the variable is important in the model. In the proposed neural network, the relevant importance of input variables is: X5 = oc or nc (with Ratio = 9.73), X3 = (po − uo)/σ′v, (with Ratio = 9.62), X4 = (p1 − uo)/σ′v, (with Ratio = 5.04), X2 = e (with Ratio = 3.29), and X1 = Iom (with Ratio = 2.28).
5.3. Training and Testing
The quality of prediction of the neural regression model was evaluated on the basis of error analysis, calculated independently for the following subsets: learning
L, testing
T, and validation
V. Neural networks were optimized for the number of neurons in the hidden layer, the activation function in the neurons of the hidden layer and the output layer, and the learning method. The Broyden-Fletcher-Goldfarb-Shanno algorithm (BFGS) was chosen for network learning. An early-stopping method of training was used [
43]. Learning was stopped after 108 learning cycles (epochs). The subsets of learning
L, testing
T for periodic checking of the generalizability acquired by the network, and validation
V for the final evaluation of the trained neural network, were randomly assigned to 75%, 15%, and 15% of the data set, respectively. Neural networks with the best predictive quality were determined on the basis of the highest values of determination coefficients
R2, the lowest mean values of relative errors
RE according to Equation (11) [
43], and the lowest values of mean squared errors
MSE according to the formula:
Based on the analysis of many neural networks, a neural network of 5-4-1 was selected (
Figure 4). Activation functions have been identified: hidden neurons-logistic function (binary sigmoid) and output neuron-exponential function (with a negative exponent). The prediction errors in the subsets
L,
T, and
V are presented in
Table 8.
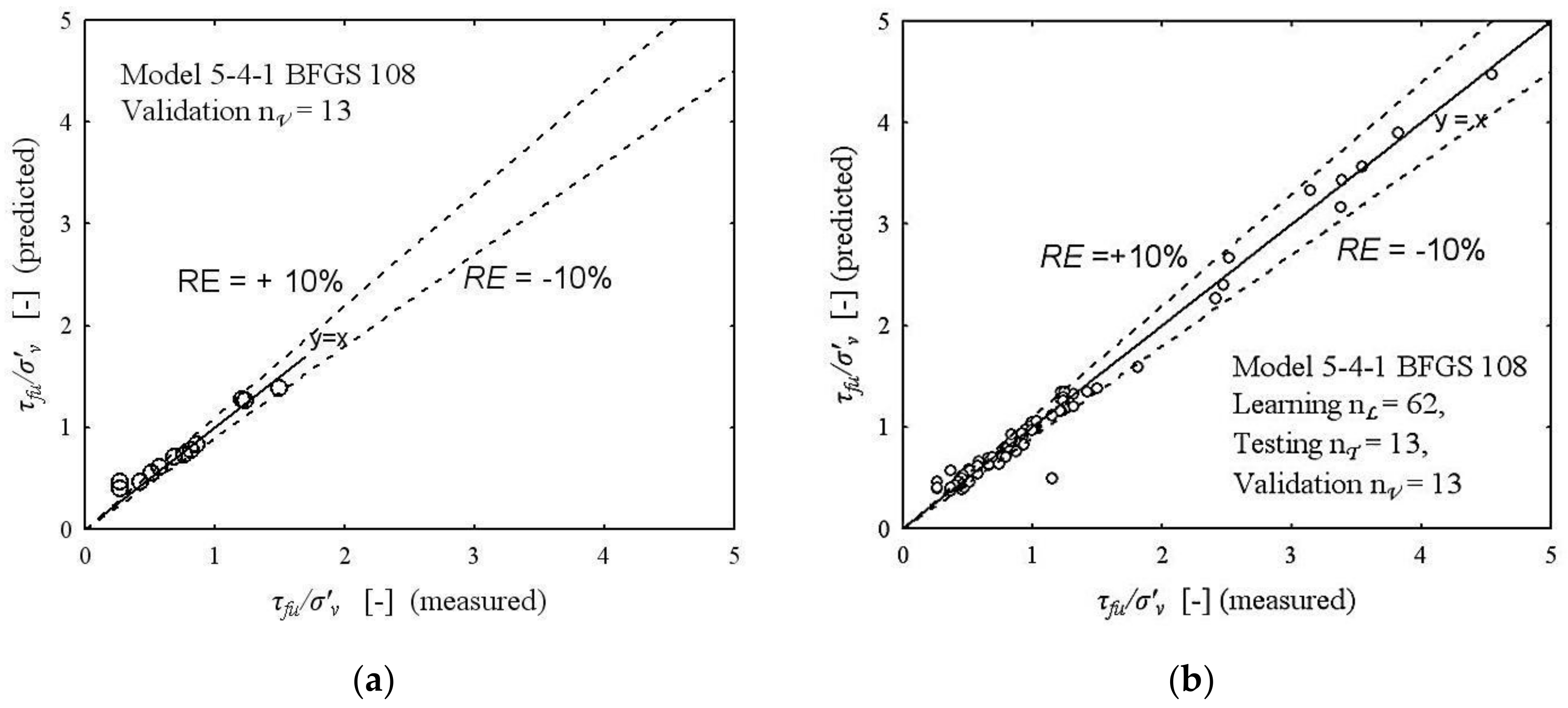
5.4. Evaluation of the Undrained Shear Strength Using a Neural Network
The trained neural network 5-4-1 was tested by applying it for the prediction of the normalized undrained shear strength
τfu/
σ′v of organic soils based on data from subset validation
V and on all data. The accuracy of the prediction using the developed network is illustrated by a graph of the dependence of the measured
τfu/
σ′v values and
τfu/
σ′v values predicted by the neural network (
Figure 5). The maximum relative prediction error of the network 5-4-1 of normalized undrained shear strength
τfu/
σ′v based on the data subset
V and all data is approximately max
RE = ±10%.
6. Conclusions
The analysis carried out for the tested organic soils indicates quite high values of the maximum relative error max RE for the evaluated undrained shear strength τfu from the dilatometer test on the basis of single-factor empirical relationships: Marchetti, Roque et al., Smith and Houlsby, and the Marchetti relationship modified by Lechowicz. It shows that the evaluation of the undrained shear strength τfu from a dilatometer test for the tested peat and gyttja from the three-factor relationship of Rabarijoely presents a better accuracy; however, it requires the use of empirical coefficients individually determined on the basis of the void ratio.
The normalized undrained shear strength τfu/σ′v of organic soils from the dilatometer test can be predicted using the neural model 5-4-1 based on measurements from the dilatometer test as the normalized net value of a corrected first pressure reading (po − uo)/σ′v and the normalized net value of a corrected second pressure reading (p1−uo)/σ′v, and organic soil properties as the organic content Iom, void ratio e and the stress history indicator (oc or nc). A neural model 5-4-1 with values within the data range provides a prediction of relative variable values, with a maximum relative error of approximately ±10%. Further research is needed for organic soils with a higher variability of the organic content Iom, void ratio e, and stress history to extend the proposed neural network by these variables.
Author Contributions
Z.L. and S.R. prepared the research program, performed in situ tests, analysed the test results, and prepared the manuscript. M.F. analysed the test results and prepared the manuscript. M.J.S. performed Artificial Neural Network analysis and prepared the manuscript.
Acknowledgments
This work was carried out in cooperation with the partners from the Warsaw University of Life Sciences, Poland, and the Tokai University, Japan, and between 2017–2018 at the Warsaw University of Life Sciences—SGGW and the Bialystok University of Technology, it was supported by the Polish Ministry of Science and Higher Education.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marchetti, S. In Situ Tests by Flat Dilatometer. J. Geotech. Geoenviron. Eng. 1980, 106, 299–321. [Google Scholar]
- Marchetti, S.; Monaco, P.; Totani, G.; Calabrese, M. The flat dilatometer test (DMT) in soil investigations—A report by the ISSMGE Committee TC16. In Proceedings of the International Conference on Insitu Measurement of Soil Properties and Case Histories, Bali, Indonesia, 21–24 May 2001; p. 41. [Google Scholar]
- Lunne, T.; Lacasse, S.; Rad, N.S. SPT, CPT, pressuremeter testing and recent developments on in situ testing of soils, Part I: All tests except SPT. Publikasjon-Norges Geotekniske Institutt 1989, 4, 2339–2403. [Google Scholar]
- Powell, J.J.M.; Uglow, I.M. Marchetti dilatometer testing in UK soils. In Proceedings of the 1st International Symposium on Penetration Testing (ISOPT-1), Orlando, FL, USA, 20–24 March 1988; Volume 1, pp. 555–562. [Google Scholar]
- Lutenegger, A.J. Current status of the Marchetti dilatometer test. In Proceedings of the 1st International Symposium on Penetration Testing (ISOPT-1), Orlando, FL, USA, 20–24 March 1988; Volume 1, pp. 137–155. [Google Scholar]
- Lutenegger, A.J. Cavity expansion model to estimate undrained shear strength in soft clay from dilatometer. In Proceedings of the Second International Flat Dilatometer Conference, Washington, DC, USA, 2–5 April 2006; pp. 319–326. [Google Scholar]
- Yu, H.S.; Carter, J.P.; Booker, J.R. Analysis of the dilatometer test in undrained clay. In Proceedings of the Predictive Soil Mechanics: Proceedings of the Wroth Memorial Symposium, Oxford, UK, 27–29 July 1993; pp. 783–795. [Google Scholar]
- The flat dilatometer test (DMT) in soil investigations—A Report by the ISSMGE Committee TC16. In Proceedings of the 2nd International Conference on the Flat Dilatometer, Washington, DC, USA, 2–5 April 2006; pp. 7–48.
- Ozer, A.T.; Bartlett, S.F.; Lawton, E.C. DMT testing for consolidation properties of the Lake Bonneville Clay. In Proceedings of the 2nd International Flat Dilatometer Conference, Washington, DC, USA, 2–5 April 2006; pp. 154–161. [Google Scholar]
- Schnaid, F. In Situ Testing in Geomechanic: The Main Tests; Taylor & Francis Group: London, UK, 2009; p. 327. [Google Scholar]
- Hayashi, H.; Yamazoe, N.; Mitachi, T.; Tanaka, H.; Nishimoto, S. Coefficient of earth pressure at rest for normally and overconsolidated peat ground in Hokkaido area. Soils Found. 2012, 52, 299–311. [Google Scholar] [CrossRef]
- Robertson, P.K. Soil behavior type using the DMT. In Proceedings of the 3rd International Flat Dilatometer Conference, Roma, Italy, 14–16 June 2015; pp. 243–250. [Google Scholar]
- Młynarek, Z.; Wierzbicki, J.; Lunne, T. On the influence of overconsolidation effect on the compressibility assessment of subsoil by means of CPTU and DMT. Ann. Warsaw Univ. Life Sci. SGGW Land Reclam. 2016, 48, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Chang, M.F.; Teh, C.I. Analysis of dilatometer test in clay. In Proceedings of the 3rd International Conference on the Flat Dilatometer (DMT’15), Roma, Italy, 14–16 June 2015; pp. 385–392. [Google Scholar]
- Silvestri, V.; Tabib, C. Application of the MCC model for the estimation of undrained geotechnical parameters of clays from dilatometer tests. In Proceedings of the 3rd International Conference on the Flat Dilatometer (DMT’15), Roma, Italy, 14–16 June 2015; pp. 431–438. [Google Scholar]
- Marchetti, S. Some 2015 Updates to the TC16 DMT Report 2001. In Proceedings of the 3rd International Conference on the Flat Dilatometer (DMT’15), Roma, Italy, 14–16 June 2015; pp. 43–65. [Google Scholar]
- Marchetti, S.; Flat dilatometer (DMT). Applications and recent developments. In Proceedings of the Indian Geotechnical Conference, Pune, India, 16–19 December 2015. [Google Scholar]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput. Aided Civ. Inf. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Rafiq, M.Y.; Bugmann, G.; Easterbrook, D.J. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial Neural Network applications in geotechnical engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. State of the art of Artificial Neural Networks in geotechnical engineering. Electron. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Dihoru, L.; Muir Wood, D.; Sadek, T.; Lings, M. A neural network for error prediction in true triaxial apparatus with flexible boundaries. Comput. Geotech. 2005, 32, 59–71. [Google Scholar] [CrossRef]
- Sulewska, M.J. Applying artificial neural networks for analysis of geotechnical problems. Comput. Assist. Mech. Eng. Sci. 2011, 18, 231–241. [Google Scholar]
- Das, S.K.; Basudhar, P.K. Undrained lateral load capacity of piles in clay using artificial neural network. Comput. Geotech. 2006, 33, 454–459. [Google Scholar] [CrossRef]
- Byeon, W.Y.; Lee, S.R.; Kim, Y.S. Application of flat DMT and ANN to Korean soft clay deposits for reliable estimation of undrained shear strength. Int. J. Offshore Polar Eng. 2006, 16, 73–80. [Google Scholar]
- Marchetti, S. A new in situ test for the measurement of horizontal soil deformability. In Proceedings of the Conference on In Situ Measurement of Soil Properties, ASCE, Raleigh, NC, USA, 1–4 June 1975; Volume 2, pp. 255–259. [Google Scholar]
- Marchetti, S.; Crapps, D.K. Flat Dilatometer Manual; Internal Report of GPE; GPE: Princeton, NJ, USA, 1981. [Google Scholar]
- Briaud, J.L.; Miran, J. The Flat Dilatometer Test; Publ. FHWA-SA-91-044; Civil Engineering Department, Texas A&M, for Federal Highway Administration: College Station, TX, USA, 1991. [Google Scholar]
- Ladd, C.C.; Foott, R.; Ishihara, K.; Schlosser, F.; Poulos, H.G. Stress-deformation and strength characteristics. In Proceedings of the IX International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 8–9 July 1977; Volume 2, pp. 421–494. [Google Scholar]
- Lechowicz, Z. Profiling of stress history in organic soils by dilatometer test. Ann. Warsaw Agric. Univ. SGGW Land Reclam. 1997, 28, 97–105. [Google Scholar]
- Lechowicz, Z. Undrained shear strength of organic soils from dilatometer test. Ann. Warsaw Agric. Univ. SGGW Land Reclam. 1997, 28, 85–96. [Google Scholar]
- Lechowicz, Z.; Rabarijoely, S. Use of dilatometer test in evaluation of organic subsoil strengthening. In Proceedings of the Conference on Recent Advances in Soft Soil Engineering, Kuching, Malaysia, 5–7 March 1997; pp. 185–196. [Google Scholar]
- Roque, R.; Janbu, N.; Senneset, K. Basic interpretation procedures of flat dilatometer tests. In Proceedings of the 1st International Symposium on Penetration Testing, Orlando, FL, USA, 20–24 March 1988; Volume 1, pp. 577–587. [Google Scholar]
- Smith, M.G.; Houlsby, G.T. Interpretation of the Marchetti Dilatometer in Clay. In Proceedings of the 11th European Conference on Soil Mechanics and Foundation Engineering, Kopenhaga, Denmark, 28 May–1 June 1995; Volume 1. [Google Scholar]
- Rabarijoely, S. The Use of Dilatometer Test for Evaluation of Organic Soil Parameters. Ph.D. Thesis, Warsaw Agricultural University—SGGW, Land Reclamation, Warszawa, Poland, 2000. (In Polish). [Google Scholar]
- Wolski, W.; Szymański, A.; Mirecki, J.; Lechowicz, Z.; Larsson, R.; Hartlen, J.; Garbulewski, K.; Bergdahl, U. Two Stage-Constructed Embankments on Organic Soils; Report 32; Swedish Geotechnical Institute: Linköping, Sweden, 1988. [Google Scholar]
- Wolski, W.; Szymański, A.; Lechowicz, Z; Larsson, R.; Hartlen, J.; Bergdahl, U. Full-Scale Failure Test on Stage-Constructed Test Fill On Organic Soil; Report 36; Swedish Geotechnical Institute: Linköping, Sweden, 1989. [Google Scholar]
- Lechowicz, Z.; Rabarijoely, S. Evaluation of organic subsoil conditions after large deformations. In Proceedings of the 2nd International Conference on Problematic Soils, Petaling Jaya, Malaysia, 3–5 December 2005; Eastern Mediterranean University Press: Famagusta, Cyprus, 2005; Volume 3, pp. 1075–1082. [Google Scholar]
- Lechowicz, Z.; Bąkowski, J.; Rabarijoely, S. Analysis and performance of an embankment on organic subsoil. In Proceedings of the XI Danube European Conference on Soil Mechanics and Foundation Engineering, Poreč, Croatia; Balkema, 1998; pp. 223–226. [Google Scholar]
- Bjerrum, L. Embankments on soft ground. In Proceedings of the Specialty Conference on Performance of Earth and Earth Supported Structures, ASCE Purdue University, Lafayette, IN, USA, 11–14 June 1972; Volume 1, pp. 1–54. [Google Scholar]
- Larsson, R.; Bergdahl, U.; Eriksson, L. Evaluation of Shear Strength in Cohesive Soils with Special Reference to Swedish Practice and Experience; SGI. Inf.: Linköping, Sweden, 1984; Volume 3, pp. 1–32. [Google Scholar]
- Masters, T. Practical Neural Network Recipes in C++; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
Figure 1.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Antoniny site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 1.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Antoniny site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 2.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Koszyce site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 2.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Koszyce site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 3.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Nielisz site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 3.
Profiles of the corrected readings po and p1 and index parameters ID, KD, and ED from dilatometer tests obtained for organic subsoil at the Nielisz site; (oc): overconsolidated subsoil, (nc): normally consolidated subsoil.
Figure 4.
Architecture of the two-layer artificial neural network 5-4-1.
Figure 4.
Architecture of the two-layer artificial neural network 5-4-1.
Figure 5.
Relative error RE: (a) in the data subset V, (b) in the whole data set.
Figure 5.
Relative error RE: (a) in the data subset V, (b) in the whole data set.
Table 1.
Values of empirical coefficients Ci and Di for Equation (9).
Table 1.
Values of empirical coefficients Ci and Di for Equation (9).
| Coefficients | |
|---|
| i = 0 | i = 1 | i = 2 | i = 3 |
|---|
| Ci | 0.149 | −0.0233 | 0.0065 | 0.0114 |
| Di | 1.003 | 0.3406 | 0.1104 | 0.1847 |
Table 2.
Index properties of organic soils at the Antoniny site.
Table 2.
Index properties of organic soils at the Antoniny site.
| Properties | Peat | Gyttja |
|---|
| (1) | (2) | Calcareous-Organic (1) | Calcareous (2) | Calcareous (3) |
|---|
| Thickness (m) | 0–1.0 | 1.0–3.1 | 3.1–4.5 | 4.5–6.8 | 6.8–7.8 |
| Water content wn (%) | 420–450 | 310–340 | 130–140 | 105–110 | 110–115 |
| Bulk density ρ (t/m3) | 1.05–1.1 | 1.05–1.1 | 1.25–1.30 | 1.35–1.40 | 1.40–1.45 |
| Specific density ρs (t/m3) | 1.4 | 1.45 | 2.2 | 2.3 | 2.4 |
| Liquid limit wL (%) | 450 | 305–310 | 100–110 | 80–90 | 90–100 |
| Organic content Iom (%) | 80–85 | 65–75 | 15–20 | 8–10 | 5–7 |
| CaCO3 content (%) | 5–10 | 10–15 | 65–75 | 80–85 | 85–90 |
Table 3.
Index properties of organic soils at the Koszyce site.
Table 3.
Index properties of organic soils at the Koszyce site.
| Properties | Peat | Gyttja |
|---|
| (1) | Calcareous-Organic (1) | Calcareous (2) | Calcareous (3) | Calcareous (4) |
|---|
| Thickness (m) | 2.5 | 2.5–6.0 | 2.0–5.0 | 3.0–5.0 | 5.0–15.0 |
| Water content wn (%) | 400–500 | 150–160 | 105–115 | 120 | 105–110 |
| Bulk density ρ (t/m3) | 1.03–1.05 | 1.20–1.25 | 1.35–1.40 | 1.40 | 1.45 |
| Specific density ρs (t/m3) | 1.45 | 2.10 | 2.25 | 2.20 | 2.30 |
| Liquid limit wL (%) | 450 | 100–110 | 80–95 | 95–100 | 80–90 |
| Organic content Iom (%) | 80–85 | 15–20 | 8–10 | 10–12 | 6–8 |
| CaCO3 content (%) | 5–10 | 65–70 | 75–80 | 70–75 | 75–80 |
Table 4.
Index properties of organic soils at the Nielisz site.
Table 4.
Index properties of organic soils at the Nielisz site.
| Properties | Organic Mud | Mud |
|---|
| Water content wn (%) | 120–200 | 65–120 |
| Bulk density ρ (t/m3) | 1.2–1.3 | 1.3–1.5 |
| Specific density ρs (t/m3) | 2.1–2.3 | 2.3–2.5 |
| Liquid limit wL (%) | 130–220 | 70–130 |
| Organic content Iom (%) | 21–35 | 8–20 |
Table 5.
Correction factors for field vane tests obtained at the Antoniny site.
Table 5.
Correction factors for field vane tests obtained at the Antoniny site.
| Type of Soil | µ(wL) | µ(lab) |
|---|
| peat (1.0–3.1 m) | 0.50 | 0.51 |
| gyttja 1 (3.1–4.5 m) | 0.70 | 0.56 |
| gyttja 2 and 3 (4.5–7.8 m) | 0.80 | 0.61 |
Table 6.
Summary of calculated maximum relative error max RE of the evaluated undrained shear strength τfu for organic soils from Antoniny, Koszyce, and Nielisz sites.
Table 6.
Summary of calculated maximum relative error max RE of the evaluated undrained shear strength τfu for organic soils from Antoniny, Koszyce, and Nielisz sites.
| Sites | Soil Type | Maximum Relative Error Max RE of Evaluated
Undrained Shear Strength τfu (kPa) for: |
|---|
| Single-Factor Relationships by | Multi-Factor Relationship by |
|---|
Marchetti [1]
Equation (4) | Modified Marchetti
Lechowicz [30,31]
Equation (5) | Roque et al. [33]
Equation (6) | Smith and Houlsby [34]
Equation (7) | Rabarijoely [35]
Equations (8)
and (9) |
|---|
max RE
(%) | max RE
(%) | max RE
(%) | max RE
(%) | max RE
(%) |
|---|
| Antoniny | oc | peat | 56.9 | 19.2 | 19.0 | 47.0 | 13.4 |
| gyttja 1 | 48.4 | 20.3 | 40.6 | 31.3 | 12.1 |
| gyttja 2 | 42.3 | 12.1 | 31.3 | 13.0 | 10.3 |
| nc | peat | 49.9 | 35.1 | 50.9 | 8.0 | 9.5 |
| gyttja 1 | 29.9 | 23.4 | 14.0 | 19.4 | 10.6 |
| gyttja 2 | 27.6 | 22.1 | 31.5 | 25.1 | 12.0 |
| Koszyce | oc | peat | 58.7 | 24.0 | 28.4 | 25.3 | 0.9 |
| gyttja 1 | 50.0 | 14.0 | 19.4 | 8.0 | 7.7 |
| gyttja 2 | 47.7 | 18.6 | 20.3 | 7.4 | 7.2 |
| nc | peat | 47.5 | 25.3 | 23.9 | 22.2 | 2.9 |
| gyttja 1 | 40.6 | 13.8 | 7.2 | 8.6 | 7.8 |
| gyttja 2 | 38.8 | 3.3 | 14.5 | 4.8 | 9.5 |
| Nielisz | oc | organic mud | 50.7 | 10.4 | 13.5 | 17.0 | - |
| mud | 48.8 | 43.1 | 21.5 | 14.0 | - |
| nc | organic mud | 48.4 | 6.2 | 17.5 | 16.0 | - |
| mud | 50.8 | 10.5 | 7.7 | 12.0 | - |
Table 7.
Summary of input and output values for the ANN analysis.
Table 7.
Summary of input and output values for the ANN analysis.
| Site | Soil Type | Iom(%) X1 | e(-) X2 | σ′v
(kPa) | u0
(kPa) | p0
(kPa) | (p0 − u0)/σ′v (-) X3 | p1
(kPa) | (p1 − u0)/σ′v(-) X4 | Stress History oc or nc X5 | τfu (from FVT) (kPa) | τfu/σ′v (from FVT) (-) Y |
|---|
| Antoniny | peat | 75 | 4.8 | 2.9 | 8.9 | 32.6 | 8.29 | 42.0 | 11.61 | oc | 7.2 | 2.52 |
| 70 | 3.6 | 3.2 | 23.6 | 51.5 | 8.86 | 62.0 | 12.19 | oc | 7.8 | 2.48 |
| 65 | 3.1 | 3.4 | 30.4 | 61.5 | 9.14 | 72.0 | 12.23 | oc | 8.2 | 2.41 |
| 75 | 3.6 | 99.5 | 37.0 | 308.0 | 2.72 | 436.1 | 4.01 | nc | 46.0 | 0.46 |
| 75 | 3.6 | 100.3 | 41.0 | 295.0 | 2.53 | 386.4 | 3.44 | nc | 42.3 | 0.42 |
| 75 | 3.6 | 104.9 | 38.0 | 333.0 | 2.81 | 555.6 | 4.93 | nc | 39.2 | 0.37 |
| 75 | 3.6 | 105.3 | 42.0 | 270.0 | 2.17 | 345.6 | 2.88 | nc | 40.6 | 0.39 |
| 70 | 3.2 | 105.7 | 46.0 | 270.0 | 2.12 | 345.6 | 2.83 | nc | 39.1 | 0.37 |
| Antoniny | gyttja
calcareous-organic | 20 | 3.3 | 3.8 | 35.2 | 69.1 | 8.91 | 88.0 | 13.89 | oc | 7.3 | 1.32 |
| 15 | 3.1 | 4.5 | 42.3 | 73.4 | 6.87 | 87.0 | 9.89 | oc | 7.0 | 1.22 |
| 15 | 3.1 | 5.1 | 46.9 | 73.5 | 5.21 | 84.0 | 7.27 | oc | 7.4 | 1.21 |
| 20 | 2.7 | 106.4 | 48.0 | 290.0 | 2.27 | 376.1 | 3.08 | nc | 7.6 | 1.15 |
| 20 | 2.7 | 107.1 | 50.0 | 281.0 | 2.16 | 346.1 | 2.76 | nc | 29.2 | 0.27 |
| 20 | 2.6 | 113.6 | 68.0 | 330.0 | 2.31 | 405.6 | 2.97 | nc | 29.3 | 0.27 |
| 20 | 2.6 | 115.0 | 72.0 | 309.0 | 2.06 | 365.7 | 2.55 | nc | 29.3 | 0.26 |
| Antoniny | Gyttja calcareous | 10 | 2.7 | 5.5 | 54.8 | 84.5 | 5.40 | 95.0 | 7.31 | oc | 7.3 | 1.32 |
| 10 | 2.6 | 5.7 | 60.1 | 89.5 | 5.14 | 101.0 | 7.17 | oc | 7.0 | 1.22 |
| 10 | 2.6 | 6.1 | 68.0 | 99.4 | 5.15 | 112.0 | 7.21 | oc | 7.4 | 1.21 |
| 8 | 2.6 | 6.6 | 73.0 | 105.5 | 4.91 | 117.0 | 6.66 | oc | 7.6 | 1.15 |
| 10 | 2.2 | 108.5 | 54.0 | 242.0 | 1.73 | 291.4 | 2.19 | nc | 29.2 | 0.27 |
| 10 | 2.2 | 110.0 | 58.0 | 257.0 | 1.81 | 295.9 | 2.16 | nc | 29.3 | 0.27 |
| 10 | 2.2 | 111.4 | 62.0 | 256.0 | 1.74 | 295.9 | 2.10 | nc | 29.3 | 0.26 |
| 8 | 2.2 | 112.9 | 66.0 | 267.0 | 1.78 | 311.1 | 2.17 | nc | 30.4 | 0.27 |
| Koszyce | peat | 85 | 7.4 | 3.3 | 6.0 | 60.0 | 16.36 | 71.0 | 19.70 | oc | 15.0 | 4.54 |
| 85 | 7.4 | 3.5 | 12.0 | 46.0 | 9.86 | 53.0 | 11.88 | oc | 12.2 | 3.54 |
| 85 | 7.1 | 42.7 | 58.0 | 250.0 | 4.50 | 320.0 | 6.14 | nc | 39.6 | 0.93 |
| 85 | 7.1 | 43.1 | 62.0 | 209.0 | 3.41 | 256.0 | 4.50 | nc | 35.1 | 0.82 |
| 85 | 7.4 | 3.4 | 12.0 | 80.0 | 20.00 | 105.0 | 27.35 | oc | 17.0 | 5.00 |
| 85 | 7.4 | 4.2 | 20.0 | 75.0 | 13.10 | 95.0 | 17.86 | oc | 16.1 | 3.82 |
| 85 | 7.0 | 57.3 | 61.0 | 234.0 | 3.02 | 285.0 | 3.91 | nc | 39.5 | 0.69 |
| 85 | 7.0 | 58.9 | 70.0 | 250.0 | 3.06 | 280.0 | 3.57 | nc | 38.7 | 0.66 |
| 80 | 4.5 | 106.6 | 55.0 | 253.0 | 1.86 | 310.0 | 2.39 | nc | 49.1 | 0.46 |
| 80 | 4.5 | 105.6 | 45.0 | 242.0 | 1.87 | 330.0 | 2.70 | nc | 50.3 | 0.48 |
| 80 | 6.2 | 28.2 | 47.0 | 113.0 | 2.34 | 135.0 | 3.12 | oc | 24.3 | 0.86 |
| 80 | 6.6 | 5.5 | 23.0 | 84.0 | 11.09 | 105.0 | 14.91 | oc | 17.3 | 3.14 |
| 80 | 6.6 | 4.0 | 7.0 | 44.0 | 9.25 | 62.0 | 13.75 | oc | 13.5 | 3.38 |
| 80 | 6.6 | 4.5 | 12.0 | 65.0 | 11.78 | 78.0 | 14.67 | oc | 15.3 | 3.39 |
| Koszyce | gyttja
calcareous-organic | 20 | 3.2 | 4.6 | 22.0 | 55.0 | 7.17 | 58.2 | 7.86 | oc | 8.3 | 1.81 |
| 20 | 3.2 | 6.6 | 32.0 | 66.0 | 5.15 | 70.2 | 5.79 | oc | 9.4 | 1.42 |
| 20 | 3.2 | 9.1 | 42.0 | 89.0 | 5.16 | 93.2 | 5.63 | oc | 11.3 | 1.25 |
| 20 | 2.9 | 43.7 | 68.0 | 197.0 | 2.95 | 230.0 | 3.71 | nc | 25.5 | 0.58 |
| 20 | 2.9 | 44.6 | 74.0 | 211.0 | 3.07 | 246.0 | 3.86 | nc | 26.1 | 0.59 |
| 20 | 2.9 | 46.6 | 82.0 | 211.0 | 2.77 | 246.0 | 3.52 | nc | 26.0 | 0.56 |
| 20 | 3.2 | 7.0 | 32.0 | 70.0 | 5.43 | 85.0 | 7.57 | oc | 10.5 | 1.50 |
| 20 | 3.2 | 9.0 | 42.0 | 86.0 | 4.89 | 92.0 | 5.56 | oc | 11.2 | 1.24 |
| 20 | 3.2 | 12.0 | 52.0 | 97.0 | 3.75 | 110.0 | 4.83 | oc | 12.4 | 1.03 |
| 20 | 2.8 | 60.2 | 75.0 | 235.0 | 2.66 | 260.0 | 3.07 | nc | 29.5 | 0.49 |
| 20 | 2.8 | 61.0 | 80.0 | 225.0 | 2.38 | 255.0 | 2.87 | nc | 29.5 | 0.48 |
| 20 | 2.7 | 77.9 | 70.0 | 180.0 | 1.41 | 216.0 | 1.87 | nc | 28.5 | 0.37 |
| Koszyce | gyttja
calcareous | 10 | 2.7 | 12.1 | 53.0 | 104.0 | 4.30 | 115.6 | 5.25 | oc | 12.4 | 1.02 |
| 10 | 2.7 | 15.1 | 62.0 | 116.0 | 3.58 | 125.5 | 4.20 | oc | 13.0 | 0.86 |
| 10 | 2.7 | 18.1 | 72.0 | 135.0 | 3.48 | 145.5 | 4.06 | oc | 14.5 | 0.80 |
| 10 | 2.5 | 49.7 | 92.0 | 223.0 | 2.64 | 246.0 | 3.10 | nc | 25.2 | 0.51 |
| 10 | 2.5 | 53.2 | 102.0 | 249.0 | 2.76 | 281.0 | 3.36 | nc | 27.1 | 0.51 |
| 10 | 2.7 | 15.0 | 62.0 | 110.0 | 3.20 | 125.0 | 4.20 | oc | 13.0 | 0.87 |
| 10 | 2.7 | 18.0 | 72.0 | 130.0 | 3.22 | 145.0 | 4.06 | oc | 14.2 | 0.79 |
| 10 | 2.4 | 66.0 | 95.0 | 254.0 | 2.41 | 290.0 | 2.95 | nc | 29.6 | 0.45 |
| 10 | 2.4 | 67.5 | 100.0 | 250.0 | 2.22 | 275.0 | 2.59 | nc | 28.9 | 0.43 |
| 10 | 2.7 | 25.3 | 127.0 | 204.0 | 3.04 | 222.0 | 3.75 | oc | 17.5 | 0.69 |
| 10 | 2.5 | 70.5 | 110.0 | 270.0 | 2.27 | 290.0 | 2.55 | nc | 30.3 | 0.43 |
| Nielisz | mud
organic | 20 | 3.2 | 32.0 | 3.0 | 74.8 | 2.24 | 80.0 | 2.41 | oc | 17.9 | 0.56 |
| 20 | 3.2 | 35.0 | 9.0 | 84.3 | 2.15 | 100.0 | 2.60 | oc | 20.4 | 0.58 |
| 20 | 3.2 | 13.0 | 3.0 | 65.0 | 4.77 | 72.0 | 5.31 | oc | 16.1 | 1.24 |
| 20 | 3.2 | 16.0 | 10.0 | 74.7 | 4.04 | 81.0 | 4.44 | oc | 16.5 | 1.03 |
| 20 | 2.6 | 74.1 | 18.0 | 175.0 | 2.12 | 196.0 | 2.40 | nc | 34.0 | 0.46 |
| 20 | 2.8 | 51.0 | 19.0 | 186.0 | 3.27 | 250.0 | 4.53 | nc | 39.0 | 0.76 |
| 20 | 3.2 | 18.4 | 7.0 | 79.3 | 3.94 | 94.0 | 4.74 | oc | 18.3 | 1.00 |
| 20 | 3.2 | 24.1 | 13.0 | 89.3 | 3.17 | 104.0 | 3.78 | oc | 19.5 | 0.81 |
| 20 | 2.8 | 48.0 | 19.0 | 165.0 | 3.04 | 248.0 | 4.77 | nc | 38.2 | 0.80 |
| 20 | 2.8 | 49.0 | 21.0 | 155.0 | 2.73 | 233.0 | 4.33 | nc | 36.5 | 0.74 |
| 20 | 2.8 | 52.0 | 25.0 | 244.0 | 4.21 | 348.0 | 6.21 | nc | 49.0 | 0.94 |
| 20 | 2.8 | 54.0 | 27.0 | 235.0 | 3.85 | 313.0 | 5.30 | nc | 45.5 | 0.84 |
| 20 | 3.2 | 76.5 | 13.0 | 188.0 | 2.29 | 223.0 | 2.75 | oc | 39.4 | 0.51 |
| 20 | 2.3 | 116.0 | 38.0 | 282.0 | 2.10 | 426.0 | 3.34 | nc | 60.0 | 0.52 |
| Nielisz | mud | 10 | 2.4 | 19.0 | 16.0 | 105.0 | 4.68 | 121.0 | 5.53 | oc | 19.6 | 1.03 |
| 10 | 2.4 | 21.0 | 20.0 | 109.2 | 4.25 | 126.0 | 5.05 | oc | 20.8 | 0.99 |
| 10 | 2.4 | 23.0 | 24.0 | 119.1 | 4.13 | 138.0 | 4.96 | oc | 21.2 | 0.92 |
| 10 | 2.4 | 25.0 | 28.0 | 114.0 | 3.44 | 166.0 | 5.52 | oc | 23.4 | 0.93 |
| 10 | 2.0 | 79.0 | 25.0 | 184.0 | 2.01 | 226.0 | 2.54 | nc | 34.0 | 0.43 |
| 10 | 2.0 | 81.8 | 29.0 | 193.0 | 2.00 | 256.0 | 2.78 | nc | 36.0 | 0.44 |
| 10 | 2.0 | 71.0 | 51.0 | 255.0 | 2.87 | 348.0 | 4.18 | nc | 40.9 | 0.58 |
| 10 | 1.9 | 111.3 | 32.0 | 313.0 | 2.52 | 449.0 | 3.75 | nc | 52.0 | 0.47 |
| 10 | 1.9 | 111.5 | 38.0 | 281.0 | 2.18 | 459.0 | 3.78 | nc | 51.0 | 0.46 |
| 10 | 1.9 | 116.0 | 38.0 | 282.0 | 2.10 | 426.0 | 3.34 | nc | 50.0 | 0.43 |
| 10 | 1.9 | 119.0 | 42.0 | 262.0 | 1.85 | 416.0 | 3.14 | nc | 48.5 | 0.41 |
| 10 | 1.9 | 120.5 | 44.0 | 254.0 | 1.74 | 356.0 | 2.59 | nc | 44.5 | 0.37 |
| 10 | 2.4 | 38.8 | 35.0 | 186.0 | 3.89 | 269.0 | 6.03 | oc | 32.5 | 0.84 |
| 10 | 2.4 | 31.6 | 7.0 | 99.6 | 2.93 | 109.0 | 3.23 | oc | 21.0 | 0.67 |
Table 8.
Measures of network errors 5-4-1 BFGS 108 in the subsets L, T, and V.
Table 8.
Measures of network errors 5-4-1 BFGS 108 in the subsets L, T, and V.
| Measures of Errors | Subset L | Subset T | Subset V |
|---|
| R2 | 0.990 | 0.982 | 0.968 |
| MSE | 0.0058 | 0.0068 | 0.0352 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).