1. Introduction
Modern cities are facing environmental and energy shortage issues, and the large-scale development and utilization of renewable energy sources (RES) in smart cities is a primary strategy for addressing those issues [
1]. However, much wind and solar energy is curtailed due to a lack of reasonable planning and compatibility with conventional energy [
2,
3,
4]. Notably, in 2017, the average curtailment ratios of wind and solar power in Gansu Province, China reached 25% and 20%, respectively [
5]. Moreover, RES will enlarge the peak to valley difference of power demands. These facts have posed great challenges to the smart grid and caused crises in secure operation [
6]. Therefore, strategies to ensure the large-scale utilization of RES in a safe, efficient, and economical way has become a crucial issue in the construction of today’s smart grid and city.
Energy storage has been recognized as an effective means of RES integration and peak-shaving [
7]. Currently, compressed air energy storage (CAES) and pumped storage systems (PHS) are the major large-scale energy storage technologies [
8,
9]. Compared with PHS, CAES has broad application prospects because the geographic conditions or water resources hardly constrain it. Nevertheless, commercial CAES plants, including Huntorf (E.N Kraftwerke, Huntorf, Germany, 1978) and McIntosh (Alabama, America, 1991), strongly depend on natural gas to enhance electricity storage efficiency [
10,
11], which is a restriction in areas without abundant natural gas resources.
Integrated with thermal energy storage (TES), adiabatic CAES (A-CAES) is the main trend of CAES that is independent of fossil fuels. Several A-CAES projects have been announced, are under construction, or are in operation [
12]. Germany has planned to build a large-scale A-CAES power plant with a target cycle power of 70% [
13]. China’s first 500 kW A-CAES demonstration system successfully realized energy storage and power generation in 2014 [
14,
15]. In addition, a national A-CAES demonstration power station led by Tsinghua University, with rated power of 60 MW and rated capacity of 300 MWh, is under construction in China [
16].
However, constrained by the efficiency and structure of compressors and the effectiveness of multi-stage heat exchangers, the heat medium of TES that depend on compression heat cannot reach a high temperature [
17]. Consequently, it is difficult to enlarge electricity production in the discharge process, which may not balance the load demand and confine system efficiency. It is an effective measure to replace the TES of A-CAES with solar thermal collection and storage (STC) of concentrating solar power to overcome deficient heat capacity. Hybrid A-CAES (HA-CAES) notably enhances the storage heat temperature and capacity and can also improve the comprehensive utilization level of clean energy [
18,
19]. Therefore, researchers have recently begun to focus on essential technologies of HA-CAES such as process design, efficiency analysis, and key parameter optimization to improve the system efficiency.
A gas turbine combined solar energy and CAES focusing on process design and efficiency analysis has been proposed, and characteristics of its off-design were studied in [
20]. To cope with the issue of wind and solar curtailment, a novel scheme of wind-energy complementary A-CAES was presented and its thermodynamic characteristics were analyzed in [
21]. A HA-CAES design scheme to optimize cycle efficiency and efficiency for microturbines, solar dish collectors, and A-CAES was described in [
22,
23]. Modeling and analysis of combined cooling heating and power (CCHP) integrated solar thermal energy for its cogeneration characteristics were established in [
24]. Because of the multi-carrier poly-generation capability, an HA-CAES-based multi-carrier clean energy hub is proposed and modeled in [
25] to realize the comprehensive consumption of the renewable energy. A HA-CAES is utilized as an energy hub in a solar-based smart micro-energy grid in [
26].
However, few studies have worked on enhancing the comprehensive efficiency with stable solar thermal resources and utilizing compression heat to supply heat to residents. Unstable thermal resources cause low system electrical storage, round-trip and exergy efficiencies.
In this paper, a novel solar–thermal-assisted A-CAES (ST-CAES) is proposed to attain high efficiency. During the charging process, low-price electricity such as curtailed wind, solar, and off-peak electricity, is used to compress ambient air to high-pressure air and store it in a steel pipeline tank (SPT), recovering compression heat that could be used for heating. Solar–thermal energy is collected and stored by STC, which can supply stable thermal energy. During the discharging process, the stored high-pressure air is released and preheated with the exhaust air of a turbine, and further heated with the stored stable solar–thermal energy to generate electricity. The use of solar thermal energy improves the intake air temperature of the turbine generator, thereby enhancing the efficiency of ST-CAES. In consequence, ST-CAES can provide benefits to the smart grid and integrated RES.
The major contributions of this paper are: (1) A novel hybrid A-CAES based on the utilization of solar energy, which can be used for RES integration and peak-shaving and, furthermore, could significantly improve the round-trip efficiency, is proposed and analyzed; (2) Compared to the current HA-CAES, ST-CAES eliminates the combustion chamber that has already been proposed in [
22]. Consequently, it is a zero-carbon-emission system. Moreover, ST-CAES can provide stable high-grade thermal energy in the discharging process, which is compared with HA-CAES in [
23], and can greatly simplify the regenerative system.
The rest of this paper is organized as follows.
Section 2 elaborates the overall design scheme and mathematic model of ST-CAES.
Section 3 presents an energy and exergy analyses of ST-CAES. This is associated with the influence of primary parameters on system performance in
Section 4, followed by the conclusions in
Section 5.
2. System Description
The implementation of an ST-CAES with four-stage compression and three-stage expansion is illustrated in
Figure 1. The system comprises three main subsystems, including a compression subsystem (COM), a solar thermal collection and storage (STC), and a turbine subsystem (TUR). The COM contains a four-stage compressor train (AC1-AC4), four-stage heat exchangers (HEX1-HEX4), a cold-water tank (CWT), and a hot water tank (HWT). It is worth noting that the number of compression stages is determined by the maximum pressure of the steel pipeline tank (SPT) and the type of compressor in use. The designed maximum pressure of (SPT) is 10 MPa and the conventional single-stage pressure ratio of the reciprocating piston compressor is approximately 3. Therefore, the four-stage compressor can meet the requirement of maximum air pressure in SPT.
The STC consists of a parabolic trough collector (PTC), a low-temperature oil tank (LOT), and a high-temperature oil tank (HOT). The TUR includes a throttle valve (TV), an air turbine chain (AT1-AT3), a heat regenerator (HR), and three heat exchangers (HEX5-HEX7) as well. Moreover, three types of fluids are introduced into the system, namely air (AR), water (WA), and Therminol oil VP-1 (O). To clearly describe the system, all the components and streams are listed and numbered as in
Figure 1.
Although the COM and TUR subsystems are similar to the A-CAES reported in numerous studies [
12,
13,
14,
15], ST-CAES features several distinct characteristics. Firstly, the compression heat is absorbed and stored in HWT and utilized to provide thermal energy to residents. Secondly, low-temperature thermal oil from LOT is heated by the PTC to attain high temperatures and then stored in an HOT that can supply stable heat resources. Thirdly, the compressed air is preheated by exhaust air before entering the air turbine, and further heated by the high-temperature oil from the HOT through heat exchangers (HEX5-HEX7) to improve the system efficiency.
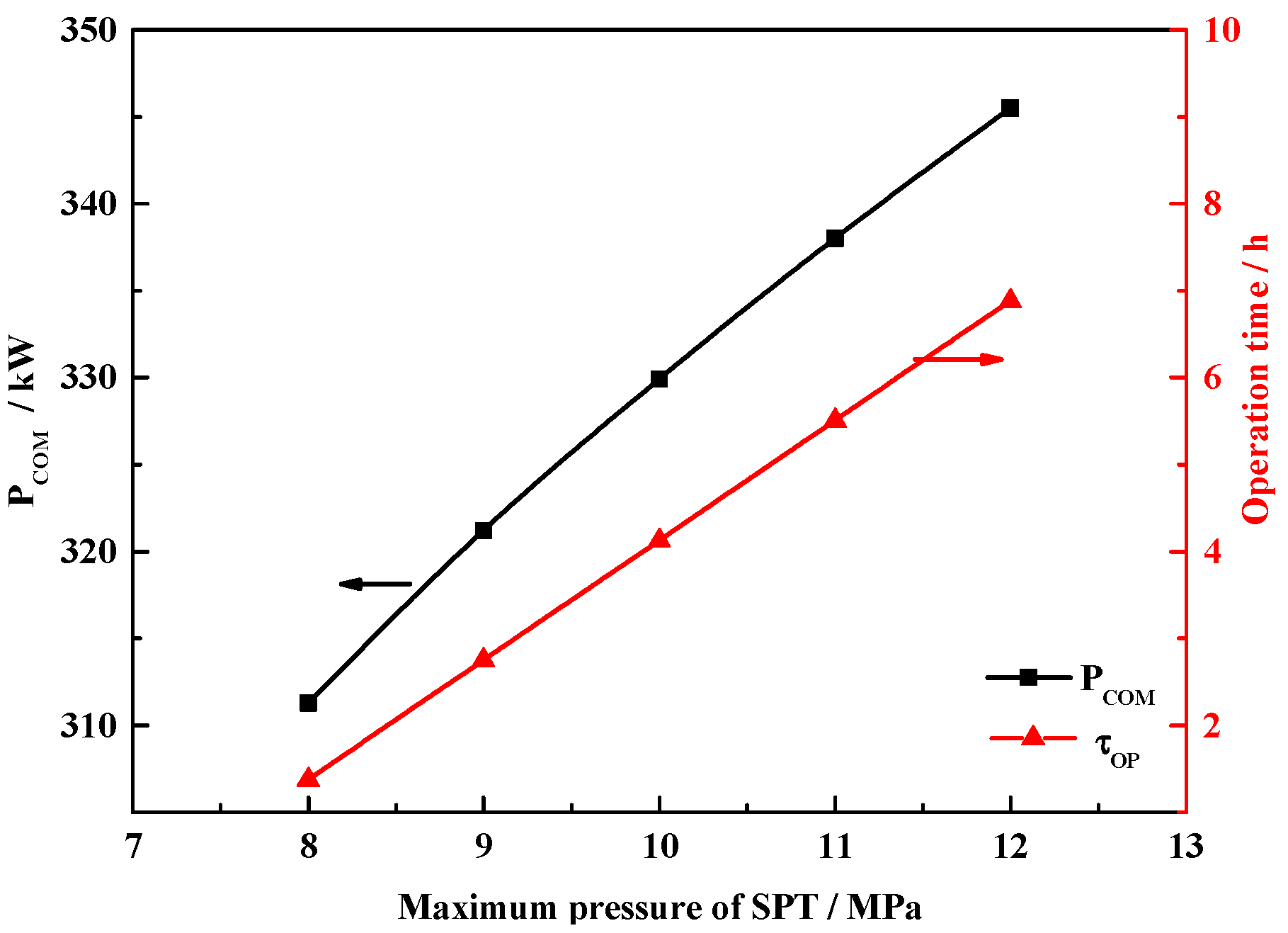
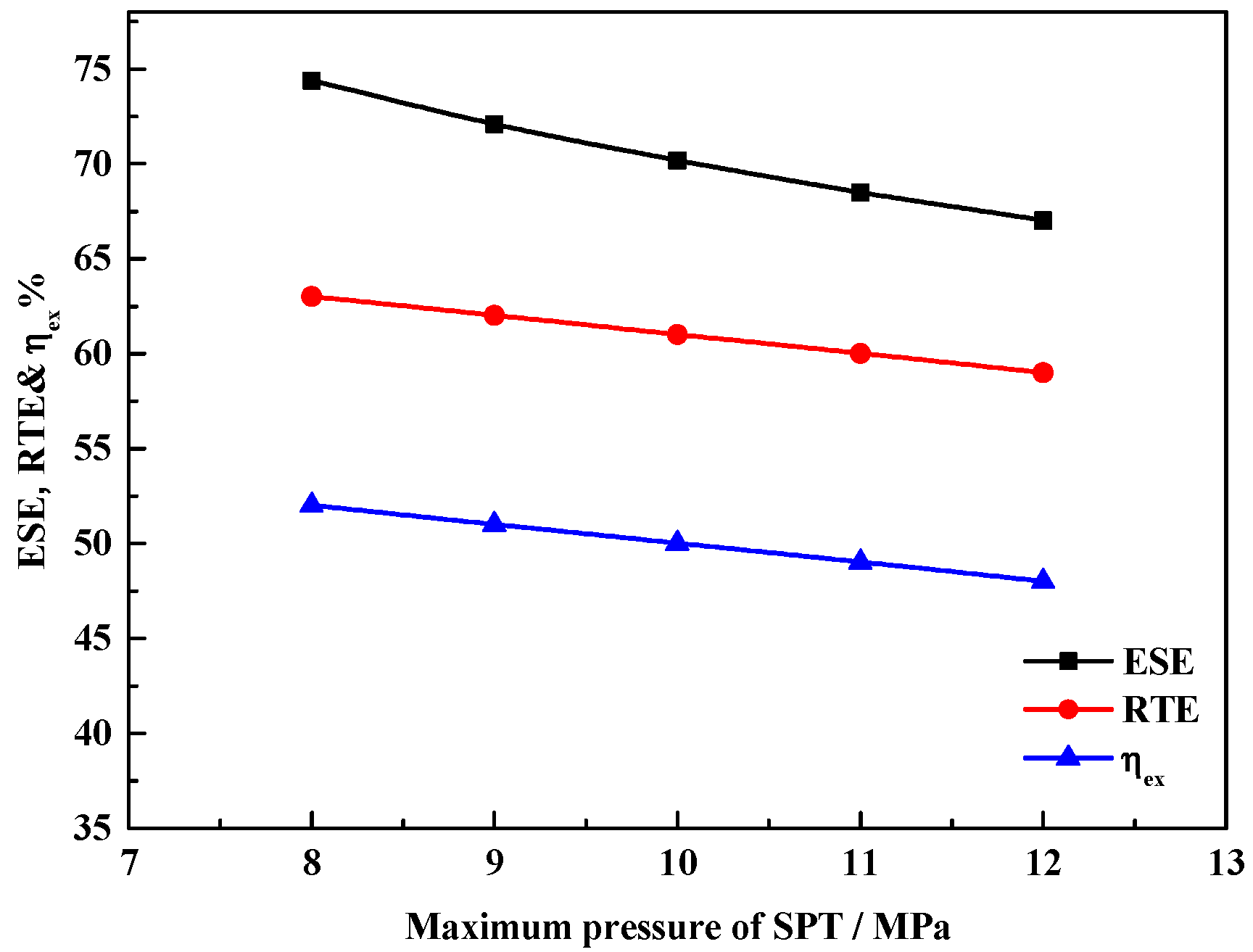
5. Conclusions
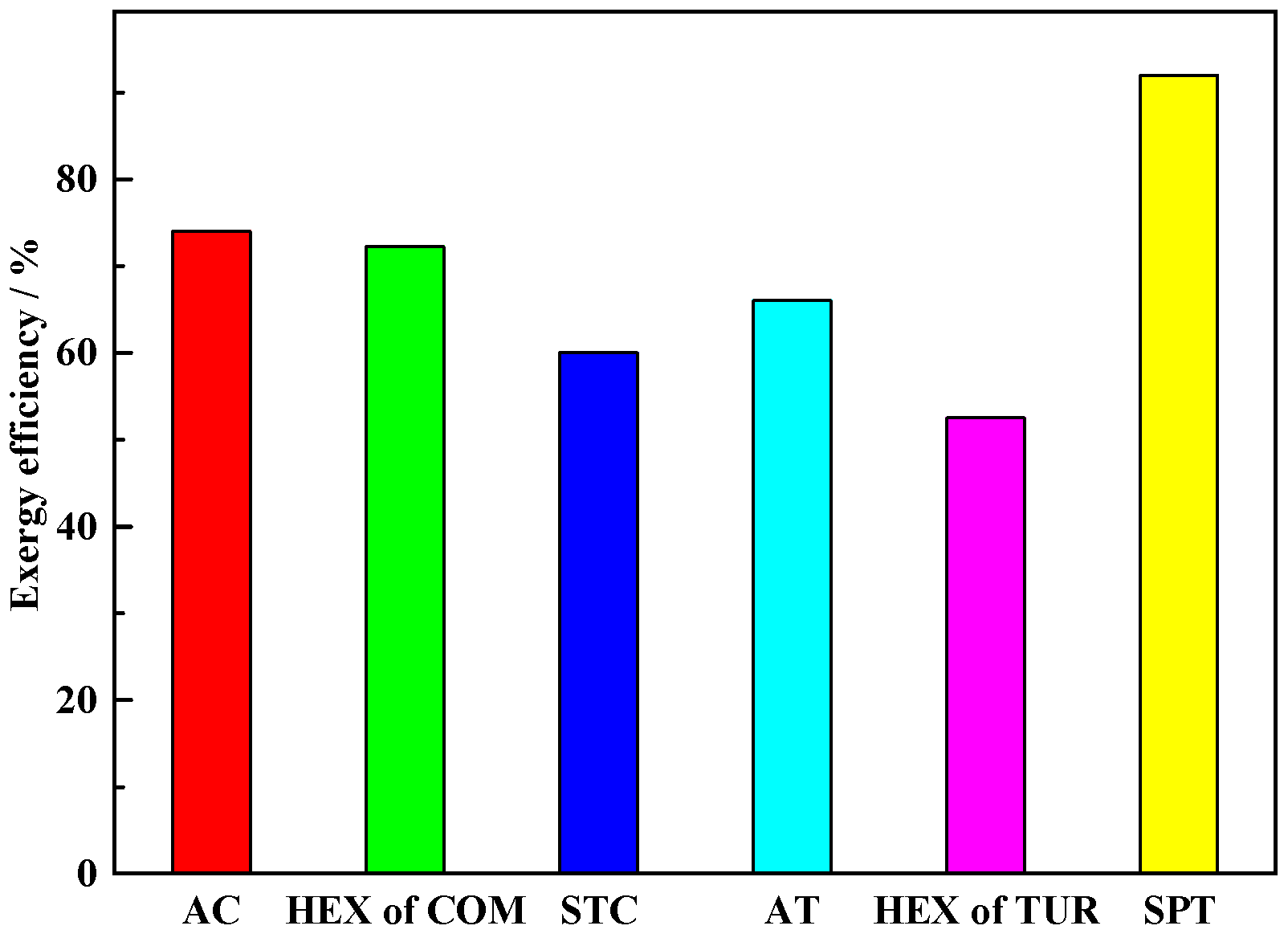
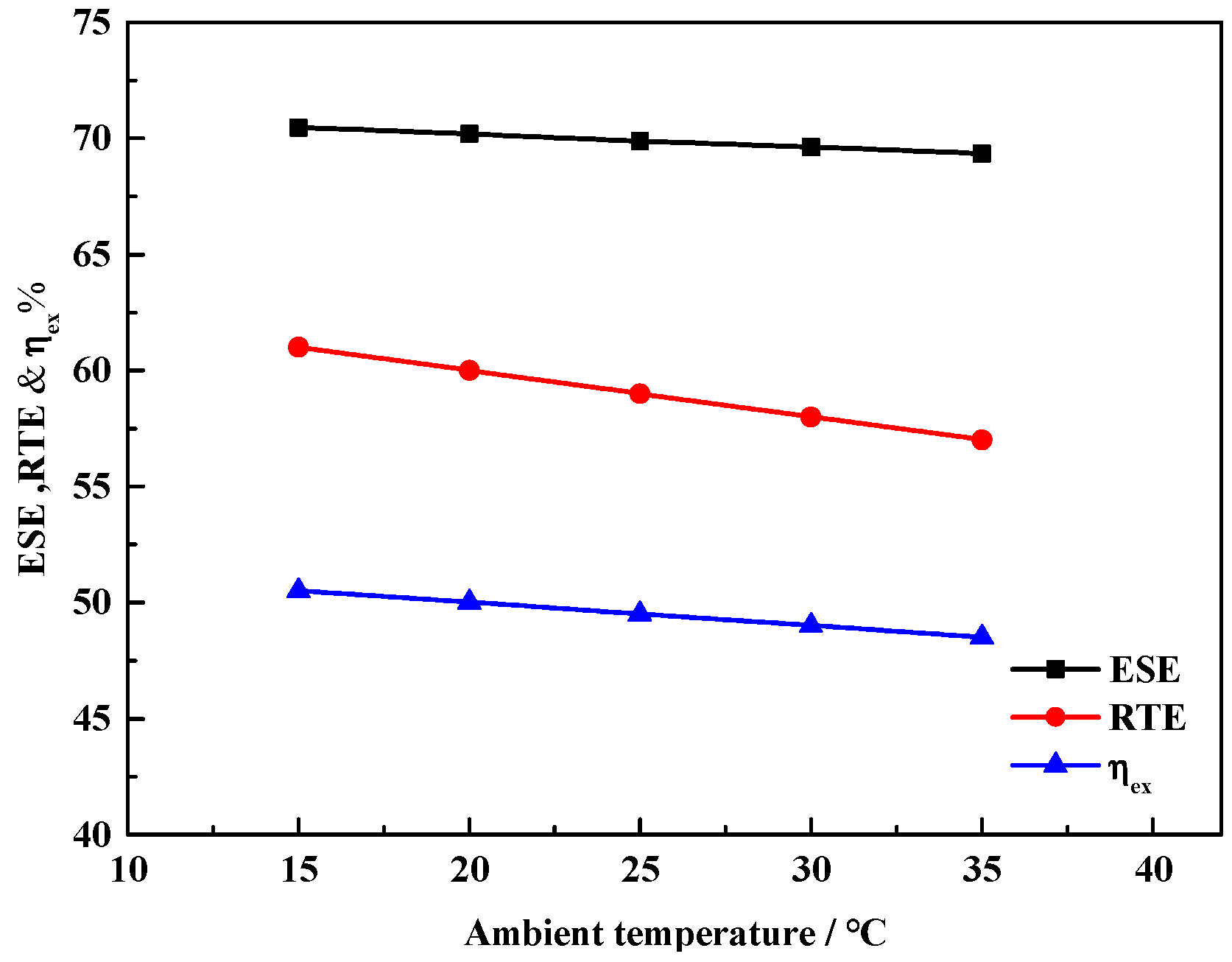
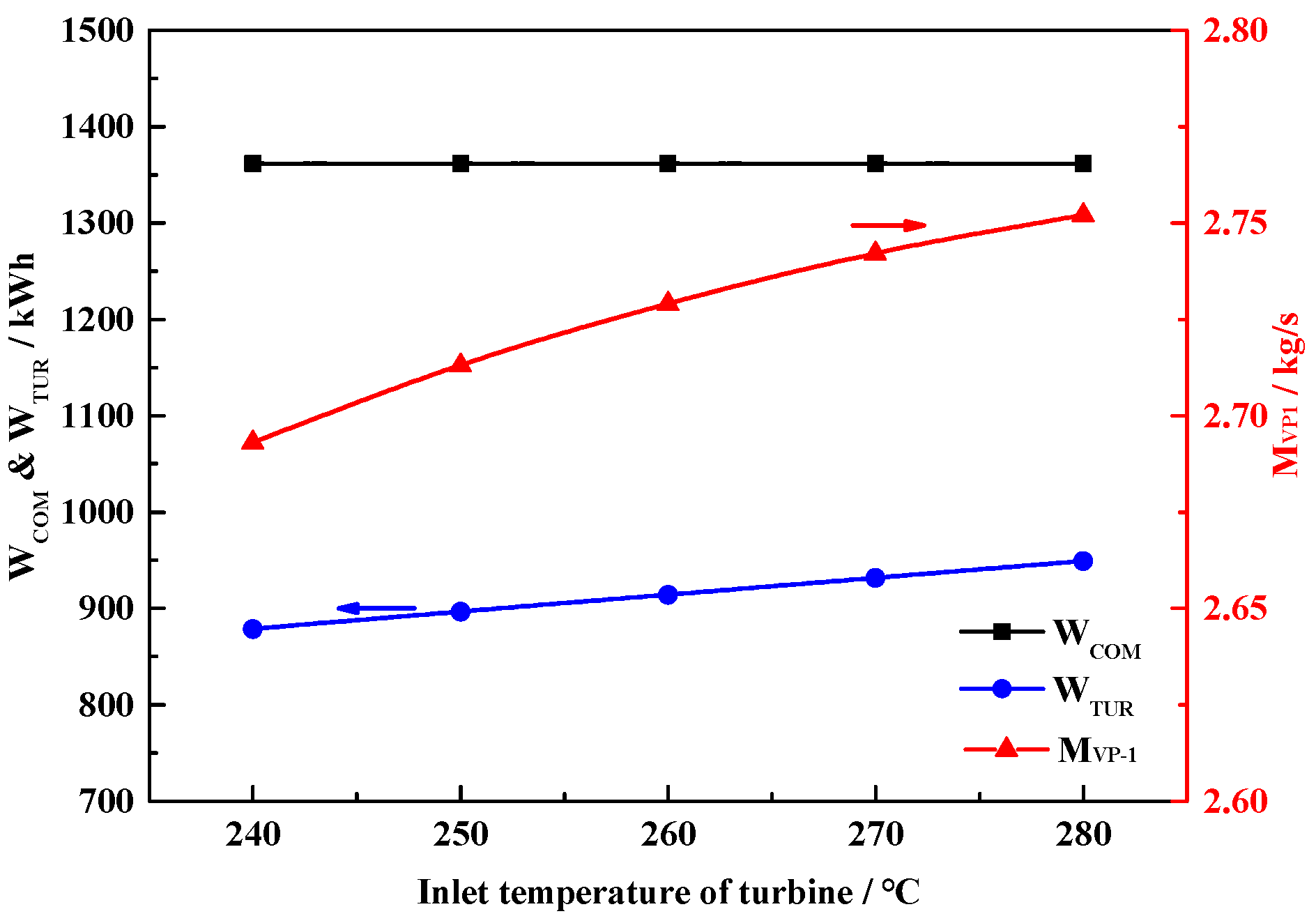
In this paper, we proposed a solar–thermal-assisted A-CAES, i.e., ST-CAES. Exhaust air preheats the compressed air, which is further heated by stable solar thermal energy, which greatly improves the performance of ST-CAES during the discharge process. In the charge process, water at ambient temperature was used to recover the compression heat and produce hot water, which provides heat for residents and reduces the power consumption of the compressor. Moreover, a mathematical model comprising energy and exergy analyses was developed. On an implementation of ST-CAES with a four-stage compression train and a three-stage expansion train, the ESE, RTE, and exergy efficiency were found to be 70.2%, 61%, and 50%, respectively. In addition, investigations of the system performance and the effects of key parameters have indicated that the turbine inlet temperature and pressure in the SPT are the critical parameters affecting the performance of the proposed ST-CAES system. Therefore, they can act as essential components in current smart grids and cities owing to the high efficiency and ability to accommodate renewables.