A Finite Difference Method on Non-Uniform Meshes for Time-Fractional Advection–Diffusion Equations with a Source Term
Abstract
:Featured Application
Abstract
1. Introduction
2. The Mathematical Model
3. Discretization in Time on a Non-Uniform Mesh
4. An Implicit Finite Difference Method
5. Consistency, Stability, and Convergence
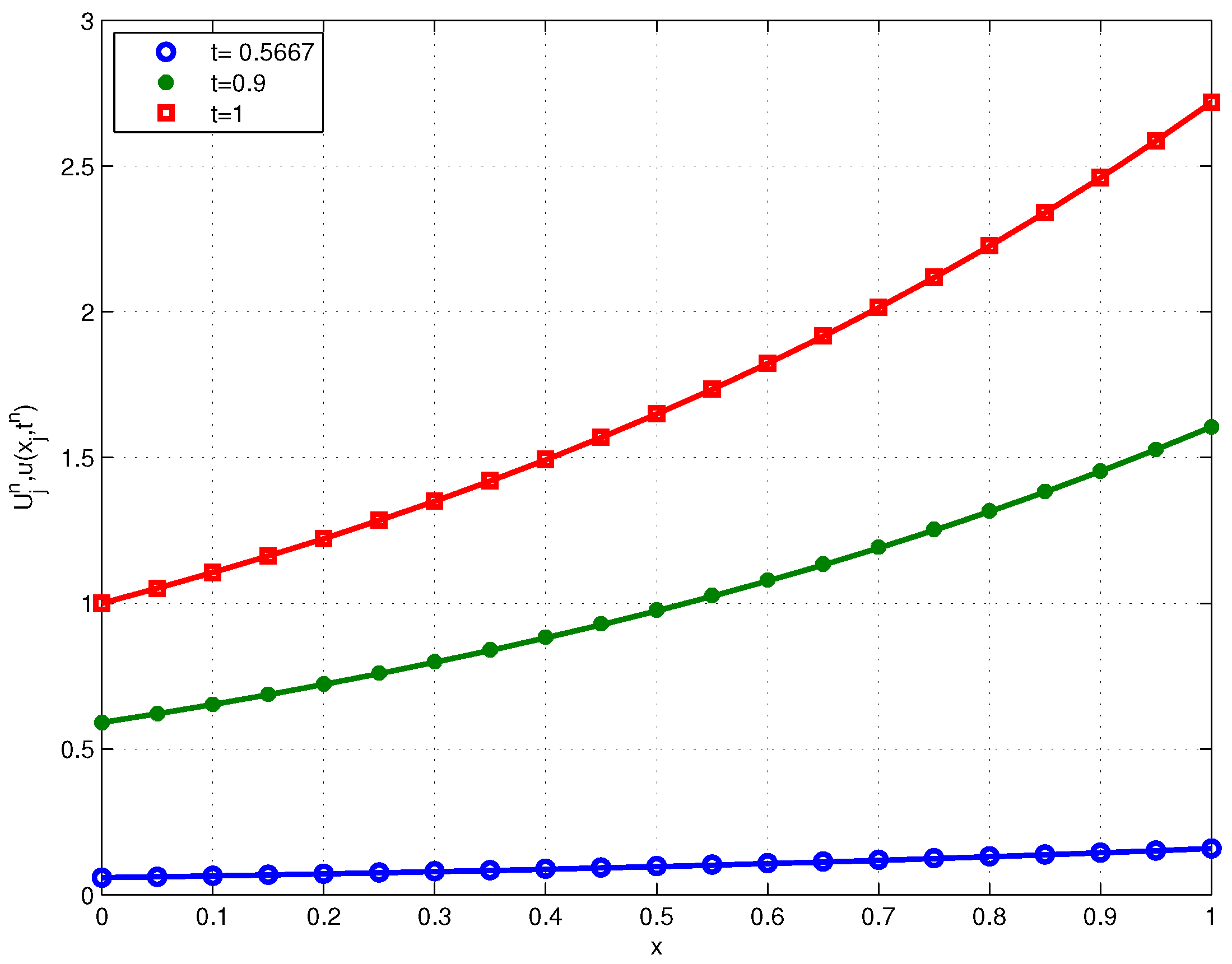
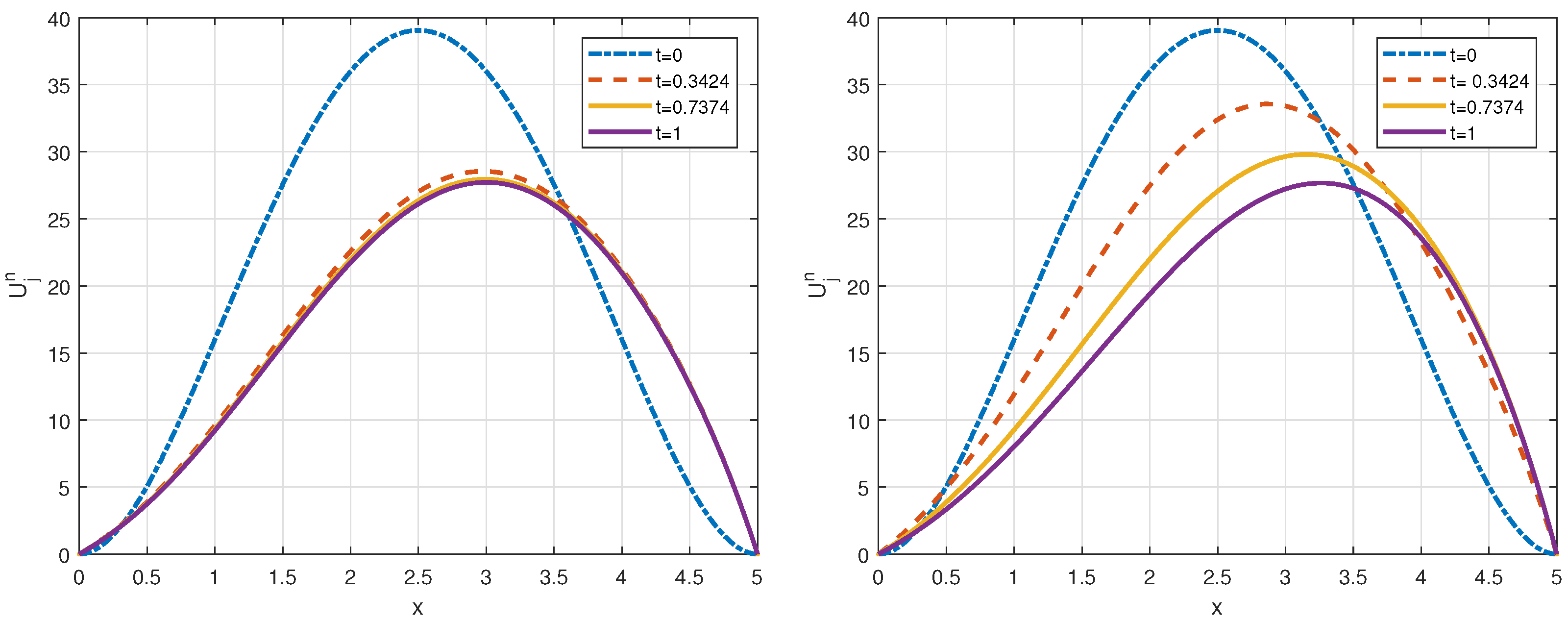
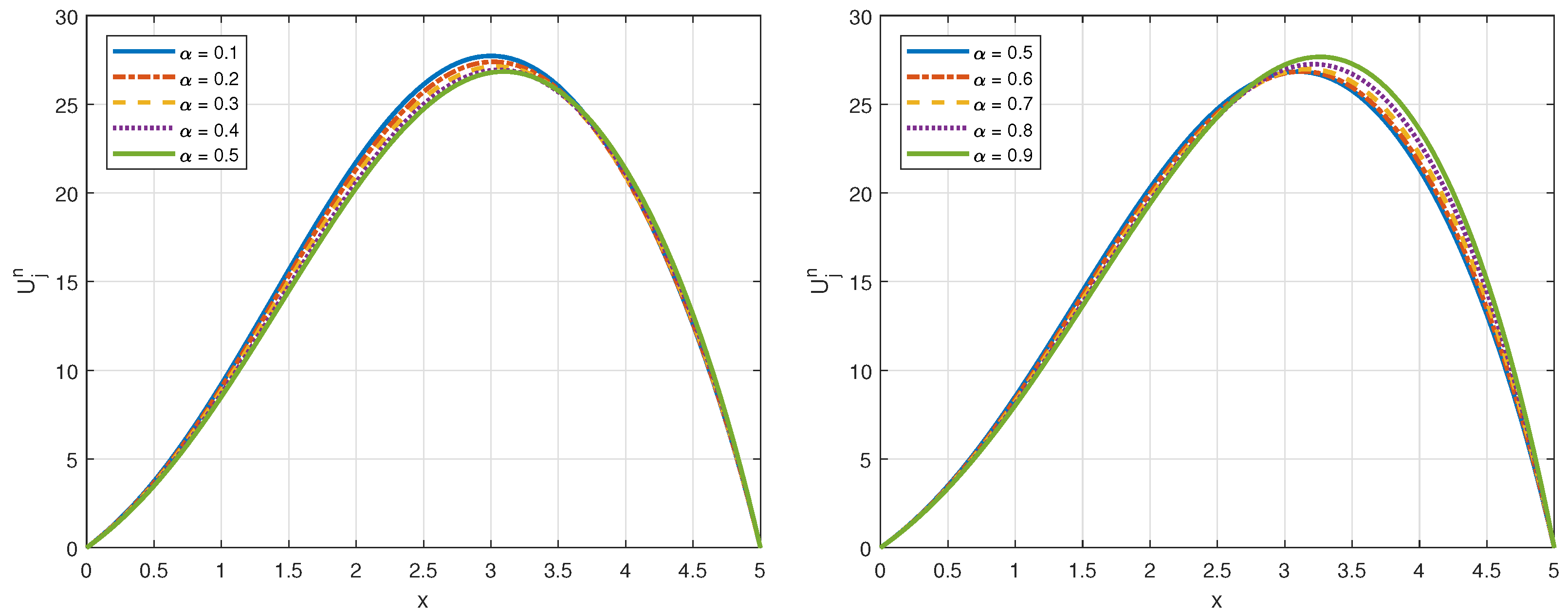
6. Numerical Experiments
7. Conclusions and Final Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies Series; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Samko, S.S.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Taylor and Francis: London, UK, 1993. [Google Scholar]
- Cheng, J.F.; Chu, Y.M. Solution to the linear fractional differential equation using Adomian decomposition method. Math. Probl. Eng. 2011. [Google Scholar] [CrossRef]
- Daftardar-Geji, V.; Jafari, H. Adomian decomposition: A tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 2005, 301, 508–518. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for nonlinear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Homotopy perturbation method for nonlinear partial differential equations of fractional order. Phys. Lett. A 2007, 365, 345–350. [Google Scholar] [CrossRef]
- Bucur, C. Local density of Caputo-stationary functions in the space of smooth functions. ESAIM Control Optim. Calc. Var. 2017, 23, 1361–1380. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, F.; Turner, I.; Anh, V. An implicit numerical method for the two-dimensional fractional percolation equation. Appl. Math. Comput. 2013, 219, 4322–4331. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Turner, I.; Burrage, K.; Anh, V. Numerical simulation for two-dimensional Riesz space fractional diffusion equations with a nonlinear reaction term. Open Phys. 2013, 11, 1221–1232. [Google Scholar] [CrossRef] [Green Version]
- Meerschaert, M.; Tadjeran, C. Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.; Scheffler, H. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 213, 205–213. [Google Scholar] [CrossRef]
- Ren, J.; Sun, Z.; Zhao, X. Compact difference scheme for the fractional sub-diffusion equation with Neumann boundary conditions. J. Comput. Phys. 2013, 232, 456–467. [Google Scholar] [CrossRef]
- Hejazi, H.; Moroney, T.; Liu, F. Stability and convergence of a finite volume method for the space fractional advection-dispersion equation. J. Comput. Appl. Math. 2014, 225, 684–697. [Google Scholar] [CrossRef] [Green Version]
- Ervin, V.; Heuer, N.; Roop, J. Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 2007, 45, 572–591. [Google Scholar] [CrossRef]
- Zhang, N.; Deng, W.; Wu, Y. Finite difference/element method for a two-dimensional modified fractional diffusion equation. Adv. Appl. Math. Mech. 2012, 4, 496–518. [Google Scholar] [CrossRef]
- Zeng, F.; Li, C.; Liu, F.; Turner, I. The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 2013, 35, A2976–A3000. [Google Scholar] [CrossRef]
- Doha, E.; Bhrawy, A.; Baleanu, D.; Ezz-Eldien, S. On shifted Jacobi spectral approximations for solving fractional differential equations. Appl. Math. Comput. 2013, 219, 8042–8056. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X.; Xu, C. Finite difference/spectral approximations for the fractional cable equation. Math. Comput. 2011, 80, 1369–1396. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation. Appl. Math. Comp. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Li, C.; Wu, R.; Ding, H. High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (I). Commun. Appl. Ind. Math. 2014, 6, e-536. [Google Scholar]
- Cao, J.; Li, C.; Chen, Y. High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (II). Fract. Calc. Appl. Anal. 2015, 18, 735–761. [Google Scholar] [CrossRef]
- Li, C.; Cao, J.; Li, H. High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (III). J. Comput. Appl. Math. 2016, 299, 159–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Liao, H. Finite difference methods for the time fractional advection diffusion equation on non-uniform meshes. J. Comput. Phys. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M. Analytical and numerical solutions of fractional type advection-diffusion equation. AIP Conf. Proc. 2017, 1863, 530005. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M. Exact and Numerical Solutions of Time-Fractional Advection-Diffusion Equation with a nonlinear source term by means of the Lie symmetries. Nonlinear Dyn. 2018, 92, 543–555. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M. Exact and Numerical Solutions of Space-Fractional Advection-Diffusion Equation with a nonlinear source term by means of the Lie symmetries. In In Proceedings of the Abstract of 10th Workshop Structural Dynamical Systems: Computational Aspects, Capitolo, Italy, 12–15 June 2018. [Google Scholar]
- Jannelli, A.; Ruggieri, M.; Speciale, M. Analytical and numerical solutions of time and space fractional advection–diffusion–reaction equation. Nonlinear Sci. Numer. Simul. 2018. preprint. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Benson, D.; Wheatcraft, S.; Meerschaert, M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef] [Green Version]
- Dipierro, S.; Valdinoci, E. A simple mathematical model inspired by the Purkinje cells: From delayed travelling waves to fractional diffusion. Bull. Math. Biol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Jannelli, A.; Fazio, R.; Ambrosi, D. A 3D mathematical model for the prediction of mucilage dynamics. Comput. Fluids 2003, 32, 47–57. [Google Scholar] [CrossRef]
- Conforto, F.; Groppi, M.; Jannelli, A. On shock solutions to balance equations for slow and fast chemical reaction. Appl. Math. Comput. 2008, 206, 892–905. [Google Scholar] [CrossRef]
- Fazio, R.; Jannelli, A. Second order numerical operator splitting for 3D advection-diffusion-reaction models. In Numerical Mathematics and Advanced Applications 2009; Springer: New York, NY, USA, 2010; pp. 317–324. [Google Scholar]
- Fazio, R.; Jannelli, A. Finite difference schemes on quasi-uniform grids for BVPs on infinite intervals. J. Comput. Appl. Math. 2014, 269, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Fazio, R.; Jannelli, A. Bvps on infinite intervals: A test problem, a non-standard finite difference scheme and a posteriori error estimator. Math. Meth. Appl. Sci. 2017, 40, 6285–6294. [Google Scholar] [CrossRef]
- Fazio, R.; Jannelli, A.; Rotondo, T. Numerical Study on Gas Flow Through a Micro-Nano Porous Medium based on Finite Difference Schemes on Quasi-Uniform Grids. Int. J. Non-Linear Mech. 2018, in press. [Google Scholar] [CrossRef]
- Fazio, R.; Jannelli, A. Finite Difference Methods for a Nonlinear BVP on Infinite Arising in Physical Oceanography. Atti della Accademia dei Pericolanti (AAPP) 2018. preprint. [Google Scholar]
- Gao, G.; Sun, Z. A compact finite difference scheme for the fractional sub-diffusion equations. J. Comput. Phys. 2011, 230, 586–595. [Google Scholar] [CrossRef]
- Langlands, T.A.; Henry, B.I. The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 2005, 205, 719–736. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Wu, H. Error estimates of Crank-Nicolson type difference schemes for the subdiffusion equation. SIAM J. Numer. Anal. 2011, 49, 2302–2322. [Google Scholar] [CrossRef]
- Du, R.; Cao, W.R.; Sun, Z.Z. A compact difference scheme for the fractional diffusion-wave equation. Appl. Math. Model. 2010, 34, 2998–3007. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Anh, V.; Turner, I. Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation. SIAM J. Sci. Comput. 2010, 32, 1740–1760. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Mustapha, K. An implicit finite-difference time-stepping method for a sub-diffusion equation, with spatial discretization by finite elements. IMA J. Numer. Anal. 2011, 31, 719–739. [Google Scholar] [CrossRef]
- Yuste, S.; Quintana-Murillo, J. A finite difference scheme with non-uniform time steps for fractional diffusion equations. Comput. Phys. Commun. 2012, 183, 2594–2600. [Google Scholar] [CrossRef]
- Yuste, S.; Quintana-Murillo, J. Fast, accurate and robust adaptive finite difference methods for fractional diffusion equations. Numer. Algorithms 2016, 71, 207–228. [Google Scholar] [CrossRef]
- Logan, J. Transport Modeling in Hydrogeochemical Systems; Springer: New York, NY, USA, 2001. [Google Scholar]
- Istas, J. Mathematical Modeling for the Life Sciences; Springer: Berlin, Germany, 2005. [Google Scholar]
- Chen-Charpentier, B.M.; Kojouharov, H.V. An unconditionally positivity preserving scheme for advection-diffusion reaction equations. Math. Comput. Model. 2013, 57, 2177–2185. [Google Scholar] [CrossRef]
- Stynes, M.; O’Riordan, E.; Gracia, J. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]


| N | |||||
|---|---|---|---|---|---|
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 | |||||
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 | |||||
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 |
| N | |||||
|---|---|---|---|---|---|
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 | |||||
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 | |||||
| 10 | |||||
| 20 | |||||
| 40 | |||||
| 80 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fazio, R.; Jannelli, A.; Agreste, S. A Finite Difference Method on Non-Uniform Meshes for Time-Fractional Advection–Diffusion Equations with a Source Term. Appl. Sci. 2018, 8, 960. https://doi.org/10.3390/app8060960
Fazio R, Jannelli A, Agreste S. A Finite Difference Method on Non-Uniform Meshes for Time-Fractional Advection–Diffusion Equations with a Source Term. Applied Sciences. 2018; 8(6):960. https://doi.org/10.3390/app8060960
Chicago/Turabian StyleFazio, Riccardo, Alessandra Jannelli, and Santa Agreste. 2018. "A Finite Difference Method on Non-Uniform Meshes for Time-Fractional Advection–Diffusion Equations with a Source Term" Applied Sciences 8, no. 6: 960. https://doi.org/10.3390/app8060960






