Unified Ciphertext-Policy Weighted Attribute-Based Encryption for Sharing Data in Cloud Computing

Abstract

With the rapid development of cloud computing, it is playing an increasingly important role in data sharing. Meanwhile, attribute-based encryption (ABE) has been an effective way to share data securely in cloud computing. In real circumstances, there is often a mutual access sub-policy in different providers’ access policies, and the significance of each attribute is usual diverse. In this paper, a secure and efficient data-sharing scheme in cloud computing, which is called unified ciphertext-policy weighted attribute-based encryption (UCP-WABE), is proposed. The weighted attribute authority assigns weights to attributes depending on their importance. The mutual information extractor extracts the mutual access sub-policy and generates the mutual information. Thus, UCP-WABE lowers the total encryption time cost of multiple providers. We prove that UCP-WABE is selectively secure on the basis of the security of ciphertext-policy weighted attribute-based encryption (CP-WABE). Additionally, the results of the implementation shows that UCP-WABE is efficient in terms of time.

1. Introduction

As one of the most promising applications, cloud computing [1,2,3] provides a more efficient way for data sharing. It enables data providers to store their data remotely in a cloud, and once data consumers can access the cloud, they can access the data any time and anywhere. Despite cloud computing supplying great convenience for data sharing, it also brings the serious challenge of information security [4]. Massive data are stored in the cloud storage platforms, and the data often contain sensitive information, such as personal health records in the medical cloud [5,6,7] and banking transactions in the financial cloud [8,9,10]. An untrustworthy entity named the cloud service provider (CSP) runs the cloud storage platforms, and it may steal the sensitive information to make a profit. Therefore, how to enforce a secure and efficient data sharing in the cloud has attracted many scholars’ attention [11,12,13,14].

Attribute-based encryption (ABE) [15] is a widespread cryptographic technology to protect the security of data in cloud computing. Different from traditional public key encryption, ABE does not encrypt plaintexts for an explicit consumer. Consumers’ secret keys and ciphertexts are associated with a set of attributes or an access policy, respectively. A consumer can decrypt a ciphertext if and only if his/her secret key has a match with the ciphertext. Weighted attribute-based encryption [16,17,18,19,20,21] is a variant of ABE. It assigns different weights to attributes according to their importance. For example, we can give full professor and distinguished professor with weights one and two, denoted as “professor(1)” and “professor(2)”, respectively. This can avoid a very complicated access structure and improve the efficiency of the encryption in certain scenarios.

1.1. Problem Statement

In practical applications [7,22], different data providers share their own data with weighted access policies, and these policies may have a mutual sub-policy. A simple instance is given to elucidate this issue.

As illustrated in Figure 1, the data providers have data $M_1$ and $M_2$ to share separately. The weighted access policy of $M_1$ is ${\Gamma }_1${Attr3(3) AND (Attr1(2) AND Attr2(3))}. The weighted access policy of $M_2$ is ${\Gamma }_2${Attr4(2) AND (Attr1(2) AND Attr2(3))}. We notice that there is a mutual sub-policy {Attr1(2) AND Attr2(3)} between ${\Gamma }_1$ and ${\Gamma }_2$, and this means that the encryptions of $M_1$ and $M_2$ have some processes of repetition. This provides the possibility of improving the efficiency of the data sharing.

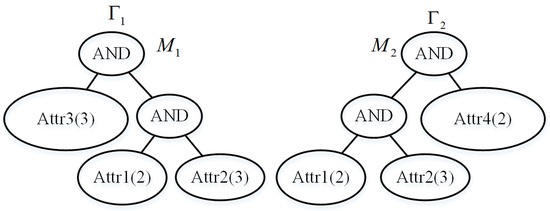
Figure 1. Two data providers have data $M_1$ and $M_2$ to share separately. ${\Gamma }_1$ and ${\Gamma }_2$ are the weighted access policies of $M_1$ and $M_2$.

1.2. Our Contributions

In this paper, we propose a new data-sharing scheme, which is called unified ciphertext-policy weighted attribute-based encryption (UCP-WABE), in cloud computing. UCP-WABE achieves both security and high performance. In this scheme, every attribute has its own weight depending on its importance defined in the system. The data providers share their data under their weighted access policies. When there is a mutual sub-policy among the weighted access policies, UCP-WABE optimizes the encryption of the data. UCP-WABE is proven to be selectively secure [23] on the basis of CP-WABE [16]. We carry out experiments for UCP-WABE, and the implementation results exhibit that UCP-WABE has better efficiency.

1.3. Organization

The rest of this paper is arranged as follows. Section 2 describes related work. Section 3 introduces preliminaries. In Section 4, we present the system model and security model of UCP-WABE. Section 5 proposes our data-sharing scheme. Section 6 represents the security analysis of UCP-WABE. The implementation results are presented in Section 7. Finally, the conclusions are stated in Section 8.

2. Related Work

As a popular cryptographic primitive used in cloud computing, ABE has two categories. One is ciphertext-policy ABE (CP-ABE) [24], and the other is key-policy ABE (KP-ABE) [25]. The major difference between CP-ABE and KP-ABE is the relationship of the ciphertext and secret key with the access policy and attributes. Specifically, for the former, a ciphertext is associated with an access policy that is expressed by threshold gates and attributes. A consumer’s secret key has attributes embedded. For the latter, a ciphertext is associated with attributes, and an access policy is embedded into a consumer’s secret key. CP-ABE enables data providers to construct its access policy freely; in other words, the providers describe who can get the shared data flexibly. Therefore, CP-ABE is more suitable for data sharing in the cloud.

In order to increase the efficiency and enlarge the use scope of ABE for data sharing, many researchers have made great efforts. Liu et al. [17] introduced the concept of weight into CP-ABE and proposed a ciphertext-policy weighted attribute-based encryption scheme. In this scheme, the authority transforms the attribute set into the weight attribute separation set, then the data provider encrypts the data with linear secret sharing methods [26]. Although the size of the ciphertext and private key increases, the scheme achieves fine-grained access control and reflects the significance of attributes. Therefore, the scheme is more suitable for the practical applications. However, the scheme only supports the linear secret sharing scheme (LSSS) [27] access structure. On the basis of [17], Liu et al. [18] proposed another ciphertext-policy weighted attribute-based encryption scheme that supports threshold access structure [28]. This structure can consist of a threshold and many attributes. Therefore, this scheme is more expressive and is more appropriate for the cloud computing environment. Meanwhile, the scheme is proven secure under the selective-weighted attribute model. Nevertheless, the scheme only supports the threshold access structure, which only contains one threshold gate in one structure, and this still limits the expression. Wang et al. [19] proposed a multi-authority-based weighted attribute encryption scheme, which introduced the concept of weight into multi-authority-based attribute encryption [29]. In this scheme, a central authority assigns a unique user identifier (UID) to each consumer. The UID is the global identity of a consumer in the system, and it is used to generate the attribute secret keys issued by multiple authorities. The attribute authorities assign different weights to attributes depending on their importance; whereas, the scheme only supports the threshold access structure. Liu et al. [16] proposed an improved ciphertext-policy weighted attribute-based encryption (CP-WABE) to improve the efficiency over the traditional CP-ABE scheme. In this scheme, every attribute has its own weight according to its importance. The data provider encrypts its data under a weighted access policy. The data consumer can decrypt the ciphertext only if his/her attributes satisfy the weighted access policy. The scheme supports the tree access structure, so it can encrypt data under a more complex access policy. The scheme is proven to be secure under the decision ℓ-Expanded bilinear Diffie–Hellmann exponent (ℓ-Expanded BDHE) assumption [30]. Ghosh et al. [21] proposed a secure and efficient data collaboration scheme, which is called blowfish hybridized weighted attribute-based encryption. In this scheme, The weight is assigned to each attribute based on its importance, and data are encrypted using access control policies. The consumers can access the data corresponding to their weight in order to reduce the computational overload. Nevertheless, when there is a mutual sub-policy among the access policies of providers, all above-mentioned schemes do not consider further optimization.

3. Preliminaries

In this section, we introduce the basic concepts of bilinear mapping [31] and the weighted access tree [16].

3.1. Bilinear Mapping

Let ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ be two cyclic groups of prime order p with the multiplication. Let g be a generator of ${\mathcal{G}}_1$ and $\widehat{e}$ be a bilinear mapping. Let $\widehat{e}$: ${\mathcal{G}}_1\times {\mathcal{G}}_1\to {\mathcal{G}}_2$ be a bilinear mapping having the following properties:

• Bilinearity: For any $u,v\in {\mathcal{G}}_1$ and $a,b\in {\mathbb{Z}}_p$, ${\mathbb{Z}}_p$ is the set of integers $[0,p-1]$. It has $\widehat{e}(u^a,v^b)=\widehat{e}{(u,v)}^{ab}$.
• Non-degeneracy: $\widehat{e}(g,g)\ne 1$.
• Computability: For all $u,v\in {\mathcal{G}}_1$, there is an efficient computation $\widehat{e}(u,v)$.

Note that $\widehat{e}$ is symmetric since $\widehat{e}(u^a,v^b)=\widehat{e}{(u,v)}^{ab}=\widehat{e}(u^b,v^a)$.

3.2. Weighted Access Tree

A weighted access tree is an image representation of a weighted access policy. Let $\Gamma$ be a weighted access tree. Let $N_j$ be the nodes of $\Gamma$ and $N_1$ be the root of $\Gamma$. There are two kinds of nodes in $\Gamma$, non-leaf node and leaf node. The former represents a threshold gate, for example “AND”, “OR”, “a of b $(a<b)$”. $nu{m}_j$ and $V_j$ describe the threshold gate, where $nu{m}_j$ denotes the number of children of $N_j$ and $V_j$ denotes the threshold value, $0<V_j\le nu{m}_j$. When $V_j=nu{m}_j$, the threshold gate is an AND gate, and when $V_j=1$, it is an OR gate. A leaf node is described by a data consumer’s attribute with weight, and $V_j=1$. We denote the parent of $N_i$ by $parent(N_i)$ and denote the index for $N_i$ in its parent’s children by $index(N_i)$, where $1\le index(N_i)\le nu{m}_i$.

In $\Gamma$, every non-leaf node $N_j$ corresponds to a function $V_j/nu{m}_j$. $V_j/nu{m}_j$ is a Boolean function, and it is TRUE if $N_j$ has at least $V_j$ child nodes whose Boolean functions are evaluated to be TRUE. We say that a data consumer’s attribute set $\mathbb{S}$ satisfies $\Gamma$ if $\Gamma (\mathbb{S})=$ TRUE, which is defined as described below.

For any leaf node $N_j$ that is associated with an attribute $a_i\in \mathbb{S}$, if its Boolean value is TRUE, the weight of $a_i$ from $\mathbb{S}$ must be greater than or equal to the weight of $N_j$. For any non-leaf node, its Boolean value is the value of its Boolean function. If and only if the tree’s root node’s Boolean value is TRUE, then $\Gamma (\mathbb{S})$ = TRUE.

For instance, as shown in Figure 1, two weighted access trees correspond to two weighted access policies. ${\Gamma }_1$: {Attr3(3) AND (Attr1(2) AND Attr2(3))}, ${\Gamma }_2$: {Attr4(2) AND (Attr1(2) AND Attr2(3))}. Considering a data consumer whose attribute set $\mathbb{S}$ is {Attr1(3), Attr2(3), Attr3(4), Attr4(1)}. We could calculate that ${\Gamma }_1(\mathbb{S})$ = TRUE, ${\Gamma }_2(\mathbb{S})$ = FALSE. Table 1 gives several outcomes of $\Gamma (\mathbb{S})$ with different attribute sets $\mathbb{S}$.

Table 1. Valuation of the weighted access trees in Figure 1.

$\mathbb{S}$	${\Gamma }_1(\mathbb{S})$	${\Gamma }_2(\mathbb{S})$
Attr1(3), Attr2(2), Attr3(4), Attr4(2)	FALSE	FALSE
Attr1(3), Attr2(3), Attr3(2), Attr4(2)	FALSE	TRUE
Attr1(3), Attr2(3), Attr3(4), Attr4(1)	TRUE	FALSE
Attr1(3), Attr2(3), Attr3(4), Attr4(2)	TRUE	TRUE

4. System Model and Security Model of UCP-WABE

In this section, we describe the system model and security model of UCP-WABE. The system model shows how UCP-WABE enforces data sharing in cloud computing. The security model makes a foundation for the security analysis in Section 6.

4.1. System Model of UCP-WABE

Figure 2 displays the data-sharing system using UCP-WABE in the cloud environment. This system model is improved from the system model of CP-WABE [16]. The system model consists of five types of entities: a weighted attribute authority (WAA), a mutual information extractor (MIE), a cloud storage platform, numerous data providers, and data consumers. The cloud storage platform is managed by CSP and offers data storage service due to its massive storage ability. The provider’s data are encrypted with its weighted access policy and uploaded to the cloud. The data consumer downloads the ciphertexts and decrypts them with his/her secret key to recover the data. All providers and consumers are supervised by WAA. WAA is responsible for authenticating the attributes of every data consumer. WAA also assigns different weights to attributes according to their importance. The MIE assists the providers in encrypting their data. For illustration, we consider two providers in the system.

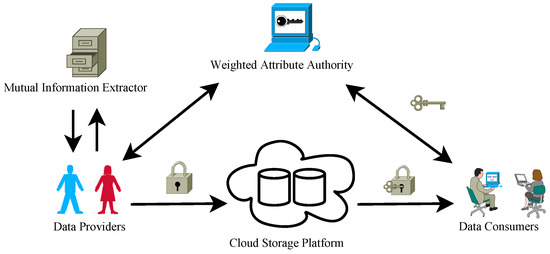
Figure 2. System model of UCP-WABE.

In Figure 2, WAA is a trustworthy entity that is in charge of producing the data consumers’ secret keys. CSP is honest but curious. This means that the cloud implements the manipulations dutifully and gives true outcomes; whereas, it also tries its best to get sensitive information. A data consumer could be compromised by an adversary; thus, this consumer could make attempts at obtaining data beyond his/her access range. The communication channels among the providers, the consumers, as well as the cloud are unsafe. In other words, the data in these channels could be eavesdropped by the adversary.

4.2. Security Model of UCP-WABE

The security model of UCP-WABE is described by a selective security game between a challenger and an adversary. This game is borrowed from CP-WABE [16]. The phases of the game are the following:

Init: The adversary declares the challenge weighted access policy ${\Gamma }^{*}$ that he/she will try to attack and sends ${\Gamma }^{*}$ to the challenger.

Setup: Here, the challenger calls the Setup algorithm to generate and send the public parameters to the adversary.

Phase 1: In this phase, the adversary can adaptively query for secret keys for the weighted attribute sets ${\mathbb{S}}_{q1},{\mathbb{S}}_{q2},\cdots$ to the challenger. The challenge weighted access policy ${\Gamma }^{*}$ must not be satisfied by any one of the queried attribute sets. The challenger responds by running the KeyGen algorithm to generate the corresponding secret keys $S{K}_{q1},S{K}_{q2},\cdots$.

Challenge: The adversary submits two messages of the same length $m_0,m_1$. Then, the adversary makes a weighted access policy ${\Gamma }^{\prime }$ that there is a mutual access sub-policy between ${\Gamma }^{*}$ and ${\Gamma }^{\prime }$. ${\Gamma }^{\prime }$ is sent to the challenger, as well. The challenger flips a random coin $b\stackrel{R}{⟵}\{0,1\}$ and encrypts $m_b$ under ${\Gamma }^{*}$. The ciphertext $C{T}^{*}$ is given to the adversary.

Phase 2: This phase is the same as Phase 1. The adversary asks for more secret keys, and the same restriction is that ${\Gamma }^{*}$ must not be satisfied by any one of the queried attribute sets.

Guess: The adversary outputs his/her guess $b^{\prime }$ on b.

Definition 1.

A UCP-WABE scheme is selectively secure if all polynomial time adversaries have at most a negligible advantage in the above security game, where the advantage of an adversary is defined as $Adv=Pr[b^{\prime }=b]-(1/2)$ [32].

According to this definition, if we prove that there is no such polynomial time adversary who has a non-negligible advantage in the above security game, we can prove that UCP-WABE is selectively secure. The details of the proof will be described in Section 6.1.

5. Proposed Unified Ciphertext-Policy Weighted Attribute-Based Encryption

This section first gives an overview of our scheme. Then, we articulate the proposed UCP-WABE data-sharing scheme, which consists of five algorithms.

5.1. Overview of UCP-WABE

In UCP-WABE, different providers’ weighted access trees can be merged into one if and only if the trees meet two conditions. One is that there is a mutual sub-policy between the weighted access trees. The other is that the sub-trees’ roots of every weighted access tree locate in a trunk. A merging process is displayed in Figure 3. The two weighted access policies belong to different providers and have a mutual sub-policy: {Attr3(3) AND (Attr1(2) OR Attr2(3))}. All roots of the left weighted access tree are in the trunk: “AND”–“AND”–“OR”. All roots of the right weighted access tree are in the trunk: “OR”–“AND”–“OR”. Therefore, the two conditions are met, and the weighted access trees can be merged. The structure of the new weighted access tree is a multi-root tree.

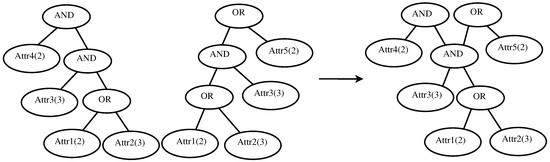
Figure 3. The merging process of two weighted access trees.

5.2. The Design of UCP-WABE

UCP-WABE can be described as a collection of the following five algorithms:

Setup($1^{\lambda },\mathcal{U}$). This algorithm generates the public parameters ($PP$) and the master secret key ($MSK$). WAA runs Setup, which takes a security parameter $\lambda$ and the set of all attributes $\mathcal{U}$ in the system as input. Each attribute has a weight depending on its importance in the system, and let $l_i$ be the maximum weight of attribute $u_i$, where $u_i\in \mathcal{U}$.

WAA chooses a group ${\mathcal{G}}_1$ of prime order p with generator g and random group elements ${\{h_{i,end},h_{i,j}\}}_{\forall u_i\in \mathcal{U},j=0,\cdots ,l_i}$. WAA also chooses a random exponent $\alpha \in {\mathbb{Z}}_p$ and computes $PP$ as:

$$PP=\left\{{\mathcal{G}}_1,g,\widehat{e}{(g,g)}^{\alpha },{\{h_{i,end},h_{i,j}\}}_{\forall u_i\in \mathcal{U},j=0,\cdots ,l_i}\right\}.$$

(1)

The master key of the system MSK can be calculated as:

$$MSK=g^{-\alpha }.$$

(2)

PP is released to all the data providers and data consumers.

MutualInfoGen($PP,{\Gamma }_1,{\Gamma }_2$). In [24], the cpabe toolkit [33] can transform an access policy into a stylized expression. Therefore, MIE is able to extract the mutual sub-policy when providers’ access policies meet the two conditions. Then, MIE creates an access tree ${\Gamma }_{ϵ}$ according to the mutual sub-policy. Let $Y_{ϵ}$ denote the set of the leaf nodes in ${\Gamma }_{ϵ}$. Each element of $Y_{ϵ}$ represents an attribute (denoted by $a_i$) with a weight (denoted by ${\omega }_i$). The number of leaf nodes is denoted by $k_{ϵ}$. $\forall a_i\in Y_{ϵ}$. Let $(i,j)$ denote the jth part of $a_i$, where $j=1,\cdots ,{\omega }_i$. MIE chooses a polynomial $f_c(x)$ for every node of ${\Gamma }_{ϵ}$. Let the polynomial degree $d_c=V_c-1$, as follows:

$$f_c(x)={\displaystyle \sum _{i=0}^{d_c}}{b}_i{x}^i,$$

(3)

where $b_i$ denotes the polynomial coefficient. Moreover, let $N_{ϵ}$ denote the root of ${\Gamma }_{ϵ}$. MIE picks a random quantity $s=f_{ϵ}(0)\in {\mathbb{Z}}_p$ and randomly chooses other $d_{ϵ}$ points of $f_{ϵ}(x)$ to determine $f_{ϵ}(x)$. MIE selects $f_q(x)$ for the non-root node $N_q$ of ${\Gamma }_{ϵ}$, where:

$$f_q(0)=f_{parent(N_q)}(index(N_q)).$$

(4)

MIE randomly picks the other $d_q$ points to determine $f_q(x)$. Therefore, it can get the polynomials $f_c(·)$ for any $N_c\in {\Gamma }_{ϵ}$.

MIE chooses random values $s_{1,0},\cdots ,s_{1,{\omega }_1-1},\cdots ,s_{k_{ϵ},0},\cdots ,$ $s_{k_{ϵ},{\omega }_{k_{ϵ}}-1}\in {\mathbb{Z}}_p$, and creates the mutual information $MI$ as follows:

$\forall a_i\in Y_{ϵ},i=1,\cdots ,k_{ϵ}$, MIE first calculates:

$$C_{(i,0),1}=g^{s_{i,0}},C_{(i,0),2}={(h_{i,0})}^{s_{i,0}}.$$

(5)

Then, for $j=1$ to ${\omega }_i-1$, MIE calculates:

$$C_{(i,j),1}=g^{s_{i,j}},C_{(i,j),2}={(h_{i,j})}^{s_{i,j}}·\mathcal{H}{(a_i)}^{s_{i,j-1}}.$$

(6)

When $j={\omega }_i$, let $s_{i,j}=f_{a_i}(0)$, where $f_{a_i}(·)$ is the polynomial of the node whose attribute is $a_i$. MIE calculates:

$$C_{(i,j),1}=g^{f_{a_i}(0)},C_{(i,j),2}={(h_{i,j})}^{f_{a_i}(0)}·\mathcal{H}{(a_i)}^{s_{i,j-1}}.$$

(7)

Then, MIE calculates:

$$C_{(i,end),1}=g^{f_{a_i}(0)},C_{(i,end),2}={(h_{i,end})}^{f_{a_i}(0)}.$$

(8)

Finally, MIE creates the mutual information $MI$:

$$MI=\left\{{\Gamma }_{ϵ},{\{C_{(i,j),1},C_{(i,j),2}\}}_{\forall a_i\in Y_{ϵ},j=1,\cdots ,{\omega }_i},{\{C_{(i,end),1},C_{(i,end),2}\}}_{\forall a_i\in Y_{ϵ}}\right\}.$$

(9)

Algorithm 1 shows the pseudocode of the MutualInfoGen algorithm.

Algorithm 1 The mutual information generation algorithm (MutualInfoGen).

Input:$PP$: The public parameter. ${\Gamma }_1$: The weighted access tree of Provider A. ${\Gamma }_2$: The weighted access tree of Provider B. Output:$MI$: The mutual information.  1: Create ${\Gamma }_{ϵ}$ according to the mutual sub-policy of ${\Gamma }_1$ and ${\Gamma }_2$  2: Select a random $s\in {\mathbb{Z}}_p$; set $f_{ϵ}(0)=s$; and randomly choose other $d_{ϵ}$ points to determine $f_{ϵ}(x)$  3: for ∀ non-root node $N_q$ do  4: Calculate $f_q(0)$, and randomly choose other $d_q$ points to determine $f_q(x)$  5: if $a_i\in Y_{ϵ}$ then  6:  Calculate $C_{(i,0),1},C_{(i,0),2}$  7:  for $j=1$ to ${\omega }_i$ do  8:   if $j\ne {\omega }_i$ then  9:    Calculate $C_{(i,j),1},C_{(i,j),2}$ 10:   else 11:    Set $s_{i,j}=f_{a_i}(0)$, and calculate $C_{(i,j),1},C_{(i,j),2}$ 12:   end if 13:  end for 14:  Calculate $C_{(i,end),1},C_{(i,end),2}$ 15: end if 16: end for 17: $MI=\left\{{\Gamma }_{ϵ},{\{C_{(i,j),1},C_{(i,j),2}\}}_{\forall a_i\in Y_{ϵ},j=1,\cdots ,{\omega }_i},{\{C_{(i,end),1},C_{(i,end),2}\}}_{\forall a_i\in Y_{ϵ}}\right\}$

Encrypt($PP,M_1,{\Gamma }_1,MI$). MIE sends $MI$ to the providers. Then, they encrypt the messages $M_1,M_2$, respectively. Consider Provider A as an instance. It runs Encrypt as follows. Provider A creates the access tree ${\Gamma }_1$ based on ${\Gamma }_{ϵ}$, which is a sub-tree of ${\Gamma }_1$. For any trunk node $N_c$ above $N_{ϵ}$ in ${\Gamma }_1$, the polynomial $f_c(x)$ is determined as follows.

$$f_c(index(trunkchild(N_c)))=f_{trunkchild(N_c)}(0),$$

(10)

where $trunkchild(N_c)$ denotes the child node of $N_c$ along the trunk and $index(N_c)$ is the index value of $N_c$ to its parent node. In order to calculate conveniently, when providers construct the access policies, it sets $index(trunkchild(N_c))=1$ for each trunk node. For $d_c$ non-constant coefficients of (3), Provider A selects them randomly. Then, the constant term $f_c(0)$ can be computed by (10). Taking a simple instance, let $N_{\delta }$ be the parent of $N_{ϵ}$. Provider A needs to determine:

$$f_{\delta }(x)={\displaystyle \sum _{i=0}^{d_{\delta }}}{b}_i{x}^i.$$

(11)

Provider A selects $d_{\delta }$ coefficients $\{b_1,b_2,\cdots ,b_{d_{\delta }}\}$ randomly, and $index(trunkchild(N_{\delta }))=1$. Due to (10), Provider A knows that:

$$f_{\delta }(1)=f_{ϵ}(0),$$

(12)

then it calculates the constant term $b_0$ with (3), as:

$$b_0=f_{ϵ}(0)-{\displaystyle \sum _{i=1}^{d_{\delta }}}{b}_i.$$

(13)

Similarly, MIE determines every trunk node’s polynomial. For any other node $N_q$ of ${\Gamma }_1$, the method of determining $f_q(x)$ is identical to the method of MIE creating ${\Gamma }_{ϵ}$.

Provider A obtains every polynomial of node in ${\Gamma }_1$ with (4) and (10), and ${\Gamma }_1$ is created completely. Provider B creates ${\Gamma }_2$ based on ${\Gamma }_{ϵ}$ likewise.

Let $Y_1$ denote the set of the leaf nodes in ${\Gamma }_1$. The number of leaf nodes is denoted by $k_1$. Provider A produces the ciphertext $C{T}_1$ of message $M_1$ as follows:

Provider A first calculates $C_M=M_1·\widehat{e}{(g,g)}^{\alpha f_{N_1}(0)}$, where $f_{N_1}(·)$ is the polynomial of access tree ${\Gamma }_1$’s root node $N_1$. For $\forall a_i\in Y_1\backslash Y_{ϵ},i=k_{ϵ}+1,\cdots ,k_1$, Provider A chooses random values $s_{k_{ϵ}+1,0},\cdots ,$ $s_{k_{ϵ}+1,{\omega }_{k_{ϵ}+1}-1},\cdots ,s_{k_1,0},\cdots ,s_{k_1,{\omega }_{k_1}-1}\in {\mathbb{Z}}_p$, and calculates:

$$C_{(i,0),1}=g^{s_{i,0}},C_{(i,0),2}={(h_{i,0})}^{s_{i,0}}.$$

(14)

Then, for $j=1$ to ${\omega }_i-1$, MIE calculates:

$$C_{(i,j),1}=g^{s_{i,j}},C_{(i,j),2}={(h_{i,j})}^{s_{i,j}}·\mathcal{H}{(a_i)}^{s_{i,j-1}}.$$

(15)

When $j={\omega }_i$, let $s_{i,j}=f_{a_i}(0)$, where $f_{a_i}(·)$ is the polynomial of the node whose attribute is $a_i$. MIE calculates:

$$C_{(i,j),1}=g^{f_{a_i}(0)},C_{(i,j),2}={(h_{i,j})}^{f_{a_i}(0)}·\mathcal{H}{(a_i)}^{s_{i,j-1}}.$$

(16)

Then, MIE calculates:

$$C_{(i,end),1}=g^{f_{a_i}(0)},C_{(i,end),2}={(h_{i,end})}^{f_{a_i}(0)}.$$

(17)

Finally, Provider A creates the ciphertext $C{T}_1$:

$$C{T}_1=\left\{{\Gamma }_1,C_M,{\{C_{(i,j),1},C_{(i,j),2}\}}_{\forall a_i\in Y_1,j=1,\cdots ,{\omega }_i},{\{C_{(i,end),1},C_{(i,end),2}\}}_{\forall a_i\in Y_1}\right\}.$$

(18)

Algorithm 2 represents the pseudocode of Encrypt algorithm.

KeyGen($PP,MSK,\mathbb{S}$). WAA calls this algorithm to produce $SK$ on the basis of $MSK$ and the data consumer’s attributes. Particularly, $\forall a_i\in \mathbb{S}$, let ${\omega }_i^{\prime }$ denote the weight of $a_i$, and let $(i,j)$ denote the jth part of $a_i$, where $j=1,\cdots ,{\omega }_i^{\prime }$. For each $(i,j)$, WAA chooses $D_{i,j}\in {\mathcal{G}}_1$ and $r_{i,j}\in {\mathbb{Z}}_p$ randomly. WAA also chooses random values $r_{i,en{d}_j}\in {\mathbb{Z}}_p$. WAA generates $SK$ components as follows:

$$K_{(i,0),1}=D_{(i,0)}{(h_{i,0})}^{r_{i,0}},K_{(i,0),2}=g^{r_{i,0}},K_{(i,j),1}=D_{(i,j-1)}^{-1}·\mathcal{H}{(a_i)}^{r_{i,j}},K_{(i,j),2}=g^{r_{i,j}},$$

(19)

$$K_{(i,j),3}=D_{(i,j)}{(h_{i,j})}^{r_{i,j}},K_{(i,en{d}_j),1}=g^{-\alpha }·D_{(i,j)}{(h_{i,end})}^{r_{i,en{d}_j}},K_{(i,en{d}_j),2}=g^{r_{i,en{d}_j}}.$$

(20)

Algorithm 2 The encryption algorithm (Encrypt).

Input:$PP$: The public parameter. $M_1$: The data that Provider A wants to share. ${\Gamma }_1$: The weighted access tree of Provider A. $MI$: The mutual information. Output:$C{T}_1$: The ciphertext of $M_1$.  1: Create ${\Gamma }_1$ based on ${\Gamma }_{ϵ}$  2: for ∀ trunk node $N_c$ above $N_{ϵ}$$\in {\Gamma }_1$ do  3: Calculate $f_c(1)$; select $d_c$ non-constant coefficients randomly; and calculate $f_c(0)$  4: if $N_c=N_1$ then  5:  Calculate $C_M$  6: end if  7: end for  8: for ∀ non-trunk node $N_q\in {\Gamma }_1$ do  9: Determine $f_q(x)$ the same as MutualInfoGen 10: if $a_i\in Y_1\setminus Y_{ϵ}$ then 11:  Calculate $C_{(i,0),1},C_{(i,0),2}$ 12:  for $j=1$ to ${\omega }_i$ do 13:   if $j\ne {\omega }_i$ then 14:    Calculate $C_{(i,j),1},C_{(i,j),2}$ 15:   else 16:    Set $s_{i,j}=f_{a_i}(0)$, and calculate $C_{(i,j),1},C_{(i,j),2}$ 17:   end if 18:  end for 19:  Calculate $C_{(i,end),1},C_{(i,end),2}$ 20: end if 21: end for 22: $C{T}_1=\left\{{\Gamma }_1,C_M,{\{C_{(i,j),1},C_{(i,j),2}\}}_{\forall a_i\in Y_1,j=1,\cdots ,{\omega }_i},{\{C_{(i,end),1},C_{(i,end),2}\}}_{\forall a_i\in Y_1}\right\}$

Then, WAA outputs:

$$SK=\left\{{\{K_{(i,0),1},K_{(i,0),2},K_{(i,j),1},K_{(i,j),2},K_{(i,j),3},K_{(i,en{d}_j),1},K_{(i,en{d}_j),2}\}}_{\forall a_i\in \mathbb{S},j=1,\cdots ,{\omega }_i^{\prime }}\right\}.$$

(21)

Decrypt($PP,SK,C{T}_1$). Consider that the aforementioned consumer gets $C{T}_1$, and he/she wants to recover $M_1$. The decryption process is defined as follows.

If $N_x$ is a leaf node of ${\Gamma }_1$ and is associated with attribute $a_i\in \mathbb{S}$ and ${\omega }_i\le {\omega }_i^{\prime }$, let $N_x$’s Boolean value be TRUE, and calculate:

$$\begin{array}{cc}\hfill F_{(x,0)}=& \frac{\widehat{e}(C_{(i,0),1},K_{(i,0),1})}{\widehat{e}(C_{(i,0),2},K_{(i,0),2})}\hfill \\ \hfill =& \frac{\widehat{e}(g^{s_{i,0}},D_{(i,0)}{(h_{i,0})}^{r_{i,0}})}{\widehat{e}({(h_{i,0})}^{s_{i,0}},g^{r_{i,0}})}\hfill \\ \hfill =& \frac{\widehat{e}{(g,D_{(i,0)})}^{s_{i,0}}·\widehat{e}{(g,h_{i,0})}^{s_{i,0}·r_{i,0}}}{\widehat{e}{(g,h_{i,0})}^{s_{i,0}·r_{i,0}}}\hfill \\ \hfill =& \widehat{e}{(g,D_{(i,0)})}^{s_{i,0}}\hfill \end{array}$$

(22)

Then, for $j=1$ to ${\omega }_i$:

$$F_{(x,j)}=F_{(x,j-1)}\frac{\widehat{e}(C_{(i,j-1),1},K_{(i,j),1})·\widehat{e}(C_{(i,j),1},K_{(i,j),3})}{\widehat{e}(C_{(i,j),2},K_{(i,j),2})}$$

(23)

When $j=1$ to ${\omega }_i-1$,

$$F_{(x,j)}=\widehat{e}{(g,D_{(i,j)})}^{s_{i,j}}.$$

(24)

When $j={\omega }_i$,

$$F_{(x,j)}=\widehat{e}{(g,D_{(i,{\omega }_i)})}^{f_{a_i}(0)}.$$

(25)

Finally, the consumer computes:

$$\begin{array}{cc}\hfill F_x=& F_{(x,{\omega }_i)}\frac{\widehat{e}(C_{(i,end),2},K_{(i,en{d}_{{\omega }_i}),2})}{\widehat{e}(C_{(i,end),1},K_{(i,en{d}_{{\omega }_i}),1})}\hfill \\ \hfill =& \frac{\widehat{e}{(g,D_{(i,{\omega }_i)})}^{f_{a_i}(0)}·\widehat{e}({(h_{i,end})}^{f_{a_i}(0)},g^{r_{i,en{d}_{{\omega }_i}}})}{\widehat{e}(g^{f_{a_i}(0)},g^{-\alpha }·D_{(i,{\omega }_i)}{(h_{i,end})}^{r_{i,en{d}_{{\omega }_i}}}}\hfill \\ \hfill =& \widehat{e}{(g,g)}^{\alpha f_{a_i}(0)}.\hfill \end{array}$$

(26)

$a_i$ is the attribute of leaf node $N_x$, so $f_{a_i}(·)=f_x(·)$, and:

$$F_x=\widehat{e}{(g,g)}^{\alpha f_{a_i}(0)}=\widehat{e}{(g,g)}^{\alpha f_x(0)}.$$

(27)

Equations (22) and (24)–(26) are on the basis of bilinear mapping properties, which were introduced in Section 3.1. If $a_i\in \mathbb{S},{\omega }_i>{\omega }_i^{\prime }$ or $a_i\notin \mathbb{S}$, then $F_x=\perp$, and ⊥ is a termination signal.

For a non-leaf node $N_x$ of ${\Gamma }_1$, let $N_z$ be the children of $N_x$ and $S_x$ be an arbitrary $V_x$-size set of $N_z$, where $F_z\ne \perp$. If $S_x$ does not exist, set $F_x=\perp$, or else, $N_x$’s Boolean value is TRUE, then compute:

$$\begin{array}{cc}\hfill F_x=& \prod _{z\in S_x}{F}_z^{{\Delta }_{z,S_x}(0)}\hfill \\ \hfill =& \prod _{z\in S_x}\widehat{e}{(g,g)}^{\alpha f_z(0){\Delta }_{z,S_x}(0)}\hfill \\ \hfill =& \prod _{z\in S_x}\widehat{e}{(g,g)}^{\alpha f_x(z){\Delta }_{z,S_x}(0)}\hfill \\ \hfill =& \widehat{e}{(g,g)}^{\alpha {\Sigma }_{z\in S_x}{f}_x(z){\Delta }_{z,S_x}(0)}\hfill \\ \hfill =& \widehat{e}{(g,g)}^{\alpha f_x(0)}.\hfill \end{array}$$

(28)

where ${\Delta }_{z,S_x}(y)={\Pi }_{i\in S_x,i\ne j}\frac{y-i}{j-i}$ is the Lagrange coefficient polynomial.

Therefore, if the access tree ${\Gamma }_1$ is satisfied by $\mathbb{S}$, the decryption algorithm begins from the root node $N_1$, and the consumer calculates:

$$\frac{C_M}{F_{N_1}}=\frac{M_1·\widehat{e}{(g,g)}^{\alpha f_{N_1}(0)}}{\widehat{e}{(g,g)}^{\alpha f_{N_1}(0)}}=M_1.$$

(29)

Algorithm 3 displays the pseudocode of Decrypt algorithm.

Figure 4 shows the working process of UCP-WABE for unified encryption. Figure 5 displays the process flow of a consumer for decryption.

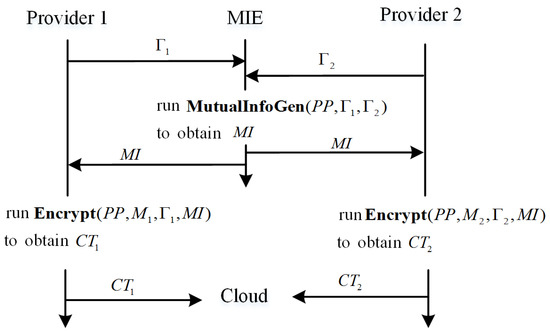
Figure 4. The process flow of unified encryption.

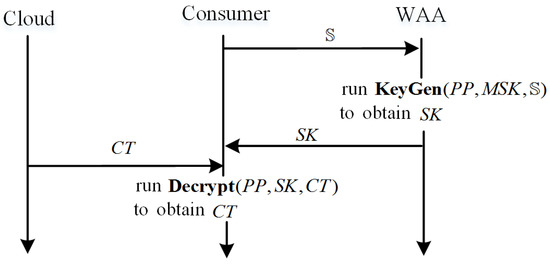
Figure 5. The process flow of decryption.

Algorithm 3 The decryption algorithm (Decrypt).

Input:$PP$: The public parameter. $SK$: The secret key of the consumer. $C{T}_1$: The ciphertext of $M_1$. Output:$M_1$: The plaintext of $C{T}_1$.  1: for ∀ leaf node $N_x\in {\Gamma }_1$ do  2: if attribute of $N_x\in \mathbb{S}$, and ${\omega }_i\le {\omega }_i^{\prime }$ then  3:  Set $N_x$’s Boolean value to be TRUE, and calculate $F_{(x,0)}$  4:  for $j=1$ to ${\omega }_i$ do  5:   if $j\le {\omega }_i-1$ then  6:    Calculate $F_{(x,j)}=\widehat{e}{(g,D_{(i,j)})}^{s_{i,j}}$  7:   else  8:    Calculate $F_{(x,j)}=\widehat{e}{(g,D_{(i,{\omega }_i)})}^{f_{a_i}(0)}$  9:   end if 10:  end for 11:  Calculate $F_x$ 12: else 13:  Set $F_x=\perp$ 14: end if 15: end for 16: for ∀ non-leaf node $N_x\in {\Gamma }_1$ do 17: Set $N_z$ as the children of $N_x$ and $S_x$ as an arbitrary $V_x$-size set of $N_z$, where $F_z\ne \perp$. 18: if $\nexists S_x$ then 19:  Set $F_x=\perp$ 20: else 21:  Set $N_x$’s Boolean value to be TRUE, and calculate $F_x$ 22: end if 23: end for 24: if $F_{N_1}$’s Boolean value is TRUE then 25: Calculate $\frac{C_M}{F_{N_1}}$ 26: end if 27: $M_1=\frac{C_M}{F_{N_1}}$

6. Security Analysis

6.1. Security Proof

Extended from CP-WABE, UCP-WABE is expected to have the same security property as CP-WABE, which has been proven to be selectively secure under a variant of the decision ℓ-bilinear Diffie-Hellmann exponent (BDHE) assumption [16]. Based on the selective security of CP-WABE, we prove UCP-WABE is selectively secure.

Theorem 1.

If no polynomial time adversary can selectively break CP-WABE with a weighted challenge access policy ${\Gamma }^{*}$, no polynomial time adversary can selectively break UCP-WABE with ${\Gamma }^{*}$.

Proof. 

To prove the theorem, we assume that there exists a polynomial time adversary $\mathcal{A}$, which has a non-negligible advantage $Ad{v}_{\mathcal{A}}$ in selectively breaking UCP-WABE. Using $\mathcal{A}$, we will build a polynomial time adversary $\mathcal{B}$, which selectively breaks CP-WABE with a non-negligible advantage $Ad{v}_{\mathcal{B}}$.

Init:$\mathcal{A}$ declares a challenge weighted access policy ${\Gamma }^{*}$ and sends it to $\mathcal{B}$. $\mathcal{B}$ sends ${\Gamma }^{*}$ to the CP-WABE challenger.

Setup: The public parameter of CP-WABE $PP$ = $\{{\mathcal{G}}_1,g,\widehat{e}{(g,g)}^{\alpha },{\{h_{i,end},h_{i,j}\}}_{\forall u_i\in \mathcal{U},j=0,\cdots ,l_i}\}$ is sent to $\mathcal{B}$, then $\mathcal{B}$ sends $P{P}^{\prime }=PP$ to $\mathcal{A}$.

Phase 1:$\mathcal{A}$ makes secret key queries to $\mathcal{B}$ for attribute sets, and none of these sets satisfy the challenge access policy ${\Gamma }^{*}$. Suppose $\mathcal{A}$ asks for attribute set ${\mathbb{S}}_{q1}$. $\mathcal{B}$ gives ${\mathbb{S}}_{q1}$ to the CP-WABE challenger and gets $S{K}_{q1}=\{\{K_{(i,0),1},K_{(i,0),2},K_{(i,j),1},K_{(i,j),2},K_{(i,j),3},K_{(i,en{d}_j),1},K_{(i,en{d}_j),2}{\}}_{\forall a_i\in {\mathbb{S}}_{q1},j=1,\cdots ,{\omega }_i^{\prime }}\}$. $\mathcal{B}$ returns $S{K}_{q1}^{\prime }=S{K}_{q1}$ to $\mathcal{A}$ to answer the query. This process would repeat until $\mathcal{A}$ no longer queries.

Challenge:$\mathcal{A}$ submits two messages of the same length $m_0,m_1$. Then, $\mathcal{A}$ constructs a weighted access policy ${\Gamma }^{\prime }$ that there is a mutual access sub-policy between ${\Gamma }^{*}$ and ${\Gamma }^{\prime }$. ${\Gamma }^{\prime }$ is also sent to $\mathcal{B}$. $\mathcal{B}$ sends $m_0,m_1$ to the CP-WABE challenger. The CP-WABE challenger flips a random coin $b\stackrel{R}{⟵}\{0,1\}$ and encrypts $m_b$ with ${\Gamma }^{*}$. The ciphertext is $CT=\{{\Gamma }^{*},C_{m_b},\{C_{(i,j),1},C_{(i,j),2}{\}}_{\forall a_i\in Y_1,j=1,\cdots ,{\omega }_i},{\{C_{(i,end),1},C_{(i,end),2}\}}_{\forall a_i\in Y_1}\}$, and the CP-WABE challenger sends it to $\mathcal{B}$. $\mathcal{B}$ constructs challenge ciphertext $C{T}^{*}$ as $C{T}^{*}=CT$ and returns it to $\mathcal{A}$.

Phase 2:$\mathcal{A}$ asks for more secret keys, and the same restriction is that ${\Gamma }^{*}$ must not be satisfied by any one of the queried attribute sets. $\mathcal{B}$ answers as in Phase 1.

Guess:$\mathcal{A}$ outputs its guess $b^{\prime }\in \{0,1\}$, and $\mathcal{B}$ outputs $b^{\prime }$ in its own game. $\mathcal{B}$ has an advantage in breaking CP-WABE as

$Ad{v}_{\mathcal{B}}=|Pr[b=b^{\prime }]-1/2|=Ad{v}_{\mathcal{A}}$

Thus, $\mathcal{B}$ has a non-negligible advantage in selectively breaking CP-WABE, so the proof of the theorem is completed. □

6.2. Discussion

In UCP-WABE, CSP cannot know the details of the data because the data are stored in an encrypted form. The data are encrypted under a weighted access policy, so only the consumers who possess a set of weighted attributes satisfying the policy can decrypt the ciphertext. Hence, UCP-WABE achieves a fine-grained access control, and the confidentiality of the data can be guaranteed against unauthorized consumers. A data provider constructs the weighted access policy according to the data consumers’ attributes instead of the data consumers’ detailed information. The threshold gates are also used to construct the weighted access policy. Therefore, the providers are able to construct sophisticated weighted access policies, and there is no limit to the number of threshold gates and attributes. Thus, UCP-WABE can support an extremely large number of weighted access policies, and UCP-WABE can implement flexible access control.

7. Evaluation of the Encryption Efficiency

The theoretical efficiency analysis of UCP-WABE is first given, then we carry out the experiments, and the results show that UCP-WABE has better efficiency than other schemes.

7.1. Efficiency Analysis Based on Encryption Methodologies

$C({\mathcal{G}}_i)$ denotes the operation in group ${\mathcal{G}}_i(i=0,1)$. $C_{\widehat{e}}$ denotes the operation in $\widehat{e}(·)$. In order to analyse the efficiency conveniently, suppose the number of levels of ${\Gamma }_1$ is equal to ${\Gamma }_2$’s and each level has the same number of attributes. Thus, ${\Gamma }_1,{\Gamma }_2$ have the same number of attributes, i.e., $k_1=k_2$. Let $B(\ast )$ be the bit size of an element of ∗ and $|\ast |$ be the number of elements of ∗. Let $\mathbb{S}({\Gamma }_1)$ denote the least node set that satisfies ${\Gamma }_1$. The comprehensive comparison among CP-ABE [24], CP-WABE [16], and our proposed UCP-WABE is summarized in Table 2. Moreover, the hash computation cost does not have to be included because it is very small.

Table 2. Comprehensive analysis.

Component	CP-ABE	CP-WABE	UCP-WABE
Public key size	$3B({\mathcal{G}}_1)+B({\mathcal{G}}_2)$	$({\displaystyle \sum _{i=1}^{\left|\mathcal{U}\right|}}{l}_i+2\left|\mathcal{U}\right|+1)B({\mathcal{G}}_1)+B({\mathcal{G}}_2)$	$({\displaystyle \sum _{i=1}^{\left|\mathcal{U}\right|}}{l}_i+2\left|\mathcal{U}\right|+1)B({\mathcal{G}}_1)+B({\mathcal{G}}_2)$
Master key size	$B({\mathbb{Z}}_p)+B({\mathcal{G}}_1)$	$B({\mathcal{G}}_1)$	$B({\mathcal{G}}_1)$
Secret key size	$(2|\mathbb{S}|+1)B({\mathcal{G}}_1)$	$(5{\displaystyle \sum _{i=1}^{k_1}}{\omega }_i^{\prime }+2{\displaystyle \sum _{i=1}^{k_1}})B({\mathcal{G}}_1)$	$(5{\displaystyle \sum _{i=1}^{k_1}}{\omega }_i^{\prime }+2{\displaystyle \sum _{i=1}^{k_1}})B({\mathcal{G}}_1)$
Ciphertext size	${\displaystyle \prod _{i=1}^{k_1}}(l_i-{\omega }_i+1)·$ $[(4k_1+2)B({\mathcal{G}}_1)+2B({\mathcal{G}}_2)]$	$4{\displaystyle \sum _{i=1}^{k_1}}({\omega }_i+1)B({\mathcal{G}}_1)+2B({\mathcal{G}}_2)$	$4{\displaystyle \sum _{i=1}^{k_1}}({\omega }_i+1)B({\mathcal{G}}_1)+2B({\mathcal{G}}_2)$
Encryption Time	${\displaystyle \prod _{i=1}^{k_1}}(l_i-{\omega }_i+1)·$ $[(4k_1+2)C({\mathcal{G}}_1)+4C({\mathcal{G}}_2)]$	$(8{\displaystyle \sum _{i=1}^{k_1}}{\omega }_i+8k_1)C({\mathcal{G}}_1)+4C({\mathcal{G}}_2)$	$[8{\displaystyle \sum _{i=1}^{k_1}}{\omega }_i+8k_1-(4{\displaystyle \sum _{i=1}^{k_{ϵ}}}{\omega }_i+$ $4k_{ϵ})]C({\mathcal{G}}_1)+4C({\mathcal{G}}_2)$
Decryption Time	$2(|\mathbb{S}|+1)C_{\widehat{e}}+$ $(2|\mathbb{S}({\Gamma }_1)|+2)C({\mathcal{G}}_2)$	$(3{\displaystyle \sum _{i=1}^{\left|\mathbb{S}\right|}}{\omega }_i+2\left|\mathbb{S}\right|)C_{\widehat{e}}+$ $(3{\displaystyle \sum _{i=1}^{\left|\mathbb{S}\right|}}{\omega }_i+3|\mathbb{S}({\Gamma }_1)|+1)C({\mathcal{G}}_2)$	$(3{\displaystyle \sum _{i=1}^{\left|\mathbb{S}\right|}}{\omega }_i+2\left|\mathbb{S}\right|)C_{\widehat{e}}+$ $(3{\displaystyle \sum _{i=1}^{\left|\mathbb{S}\right|}}{\omega }_i+3|\mathbb{S}({\Gamma }_1)|+1)C({\mathcal{G}}_2)$
Weighted Attributes	NO	YES	YES
Unified Encryption	NO	NO	YES

As shown in Table 2, suppose the values of $l_i$ are given. When $k_1$ and ${\omega }_i$ are fixed, the encryption time cost declines with $k_{ϵ}$ in UCP-WABE. In order to display the results more intuitively, we suppose all the attributes have the same weight in the access trees ${\Gamma }_1,{\Gamma }_2$ and all the maximum weights are the same in $\mathcal{U}$. Therefore, the time cost of encryption linearly declines with $k_{ϵ}$, and the rate of descent is $4({\omega }_i+1)C({\mathcal{G}}_1)$ in UCP-WABE. In CP-ABE and CP-WABE, the encryption time cost remains unchanged. When $k_{ϵ}$ and ${\omega }_i$ are fixed, the encryption time cost linearly rises with $k_1$, and the growth rate is $8({\omega }_i+1)C({\mathcal{G}}_1)$ in UCP-WABE. Although the growth rate of encryption time cost is also equal to $8({\omega }_i+1)C({\mathcal{G}}_1)$ in CP-WABE, it is always higher than that in UCP-WABE. The encryption time cost increases with $k_1$ exponentially in CP-ABE. When $k_1$ and $k_{ϵ}$ are fixed, the encryption time cost linearly rises with ${\omega }_i$, and the growth rate is $(8k_1-4k_{ϵ})C({\mathcal{G}}_1)$ in UCP-WABE. The encryption time cost also linearly rises with ${\omega }_i$, and the growth rate is $8k_{1}C({\mathcal{G}}_1)$ in CP-WABE. In spite of the encryption time cost declining with ${\omega }_i$ in CP-ABE, it still remains far higher than UCP-WABE. In Table 2, one noteworthy fact is that the encryption time cost is a summation of the two data providers’ encryption time.

7.2. Efficiency Analysis Based on Implementation

The implementation of UCP-WABE is on the basis of the cpabe toolkit [33] and the Pairing-Based Cryptography library [34]. The implementation uses a 160-bit elliptic curve group based on the supersingular curve $y^2=x^3+x$ over a 512-bit finite field. The experiments are conducted on a PC, in Intel Core2 Duo with 3.00-GHz CPU and 2GB RAM, running Ubuntu15.04. We compare UCP-WABE with CP-WABE and CP-ABE in the field of encryption time cost. For all experiments, we make all the weighted access policies’ threshold gates “AND” gates. This ensures that all of the ciphertext components could be calculated in Decrypt.

Figure 6 shows the encryption time cost with given experimental conditions $k_1=27,{\omega }_i=3$, and $l_i=4(i=1,\cdots ,7),l_i=3(i=8,\cdots ,27)$. We do not suppose all the attributes have the same maximum weight in this case for the reason that the result of CP-ABE is too high. The number of mutual attributes used in the experiments is $k_{ϵ}=\{2,5,8,11,14,17,20,23,26\}$. As shown in Figure 6, the encryption time cost of UCP-WABE follows a linear decline with the number of the mutual access tree attributes. For CP-WABE and CP-ABE, the encryption time cost almost keeps unchanged.

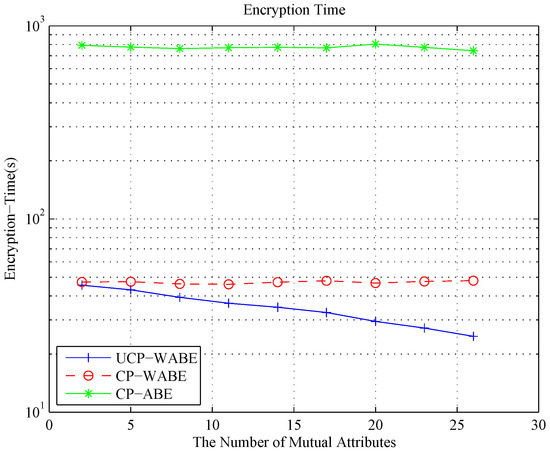
Figure 6. Encryption time cost for the changed number of mutual access tree attributes.

Figure 7 displays the encryption time with $k_{ϵ}=3,{\omega }_i=3$ and $l_i=4$. In the experiments, the number of ${\Gamma }_1$’s attributes is $k_1=\{4,5,6,7,8,9,10\}$. As shown in Figure 7, the encryption time cost follows a linear growth with the number of the access tree attributes in UCP-WABE and CP-WABE. Meanwhile, the former is lower than the latter. The result of CP-ABE increases exponentially with the number of access tree attributes.

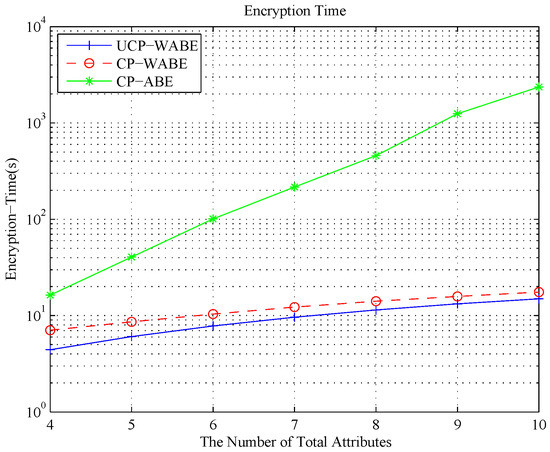
Figure 7. Encryption time cost for the changed number of access tree attributes.

Figure 8 shows the encryption time cost with given experimental conditions $k_1=3,k_{ϵ}=2$, and $l_i=9$. The weight of attributes in ${\Gamma }_1$ used in the experiments is ${\omega }_i=\{1,2,3,4,5,6,7\}$. Figure 8 shows that the encryption time cost of UCP-WABE and CP-WABE is following a linear growth in the weight of attributes, and the former is lower than the latter. The result of CP-ABE is decreasing with the weight of attributes; however, it is still higher than UCP-WABE. Therefore, UCP-WABE improves the efficiency of encryption.

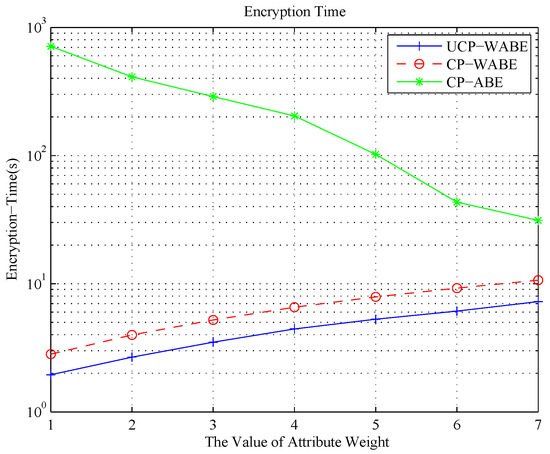
Figure 8. Encryption time cost for the changed weight of attributes in the access tree.

8. Conclusions

In this paper, we have proposed a novel UCP-WABE scheme for sharing data in cloud computing environments. The scheme optimizes the encryption of data that are encrypted under the multi-providers’ access policies where these policies have a mutual sub-policy. UCP-WABE utilizes a mutual information extractor to extract the mutual sub-policy and produce mutual information, which assists in optimizing the encryption. UCP-WABE also takes advantage of weighted attribute-based encryption to avoid too complex of an access structure. We analyse the computational complexity of UCP-WABE theoretically and experimentally. The analyses indicate that UCP-WABE has a better efficiency of encryption. The security analysis shows that UCP-WABE is selectively secure. It should be noted that we only consider the case of two data providers. In practice, UCP-WABE will have a more efficient data sharing if the more providers’ access policies have a mutual sub-policy. In our future work, we will optimize the system implementation and conduct comprehensive experiments with real-life cases in cloud computing.