Secure Multiple-Input Multiple-Output Communications Based on F–M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders
Abstract
:1. Introduction
2. Problem Formulation
- (i)
- Complete synchronization for .
- (ii)
- Anti–synchronization for .
- (iii)
- Matrix projective synchronization for .
- (iv)
- Inverse generalized synchronization for .
3. – Synchronization
3.1. Case 1:
3.2. Case 2:
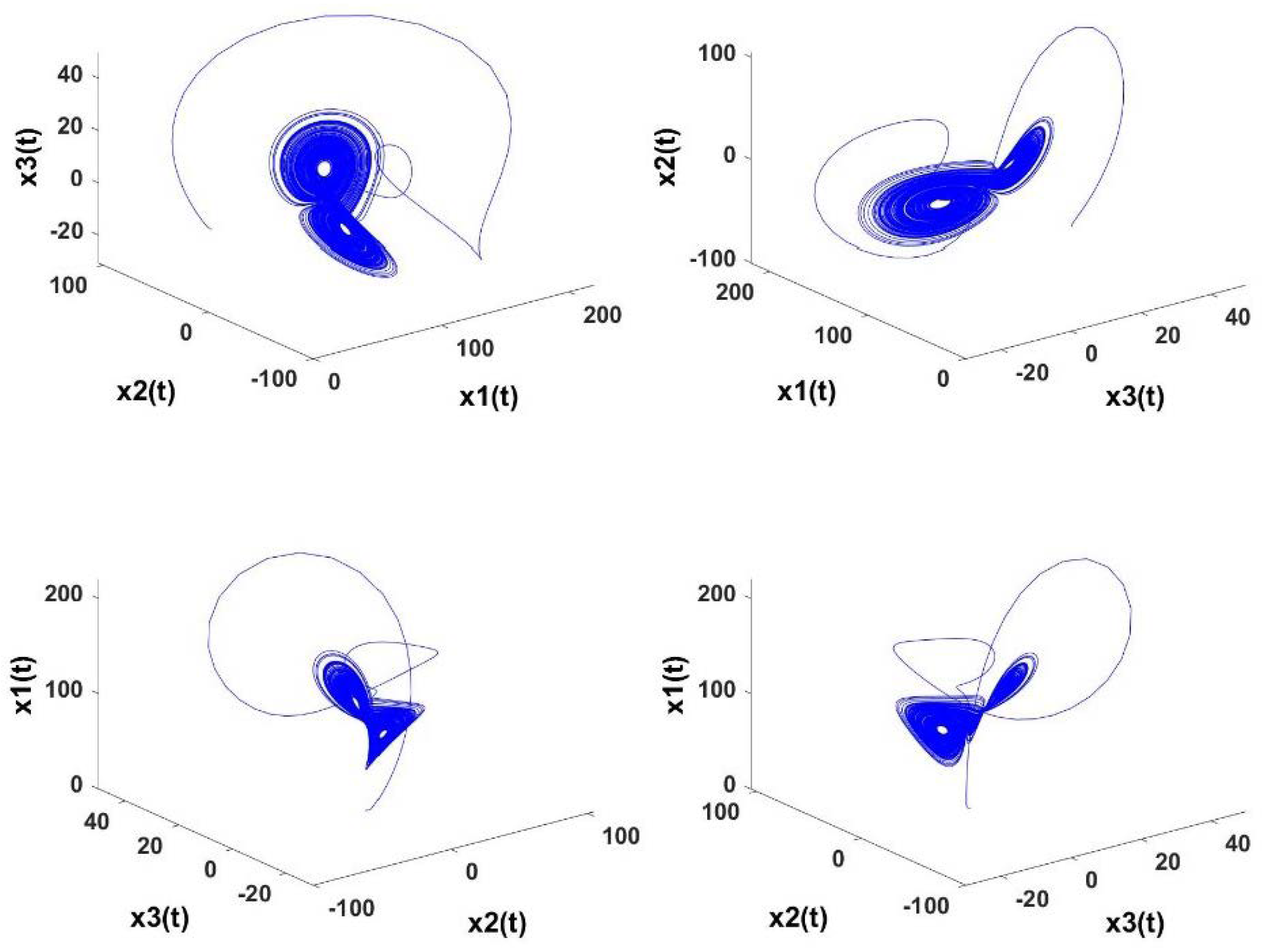
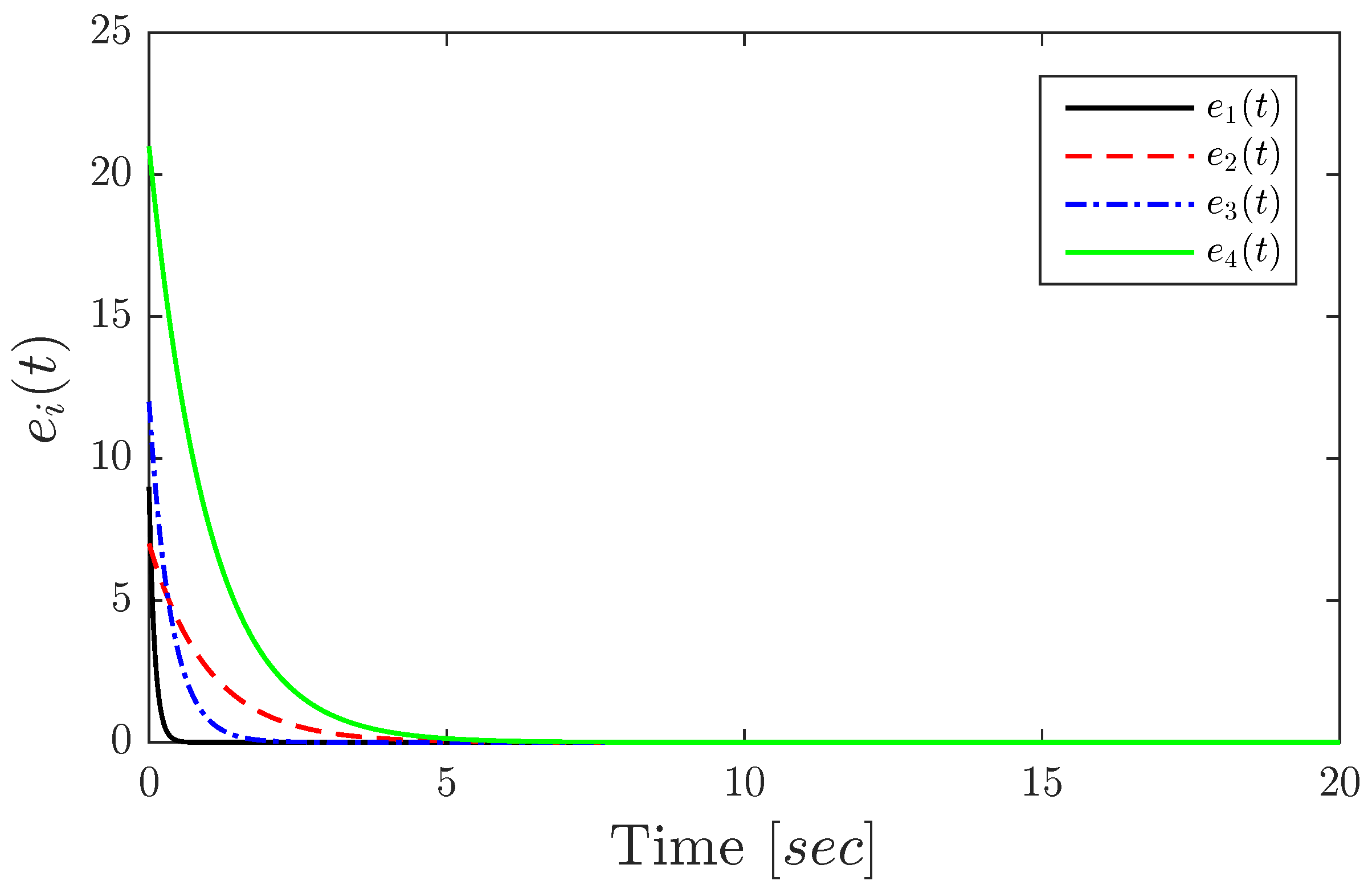
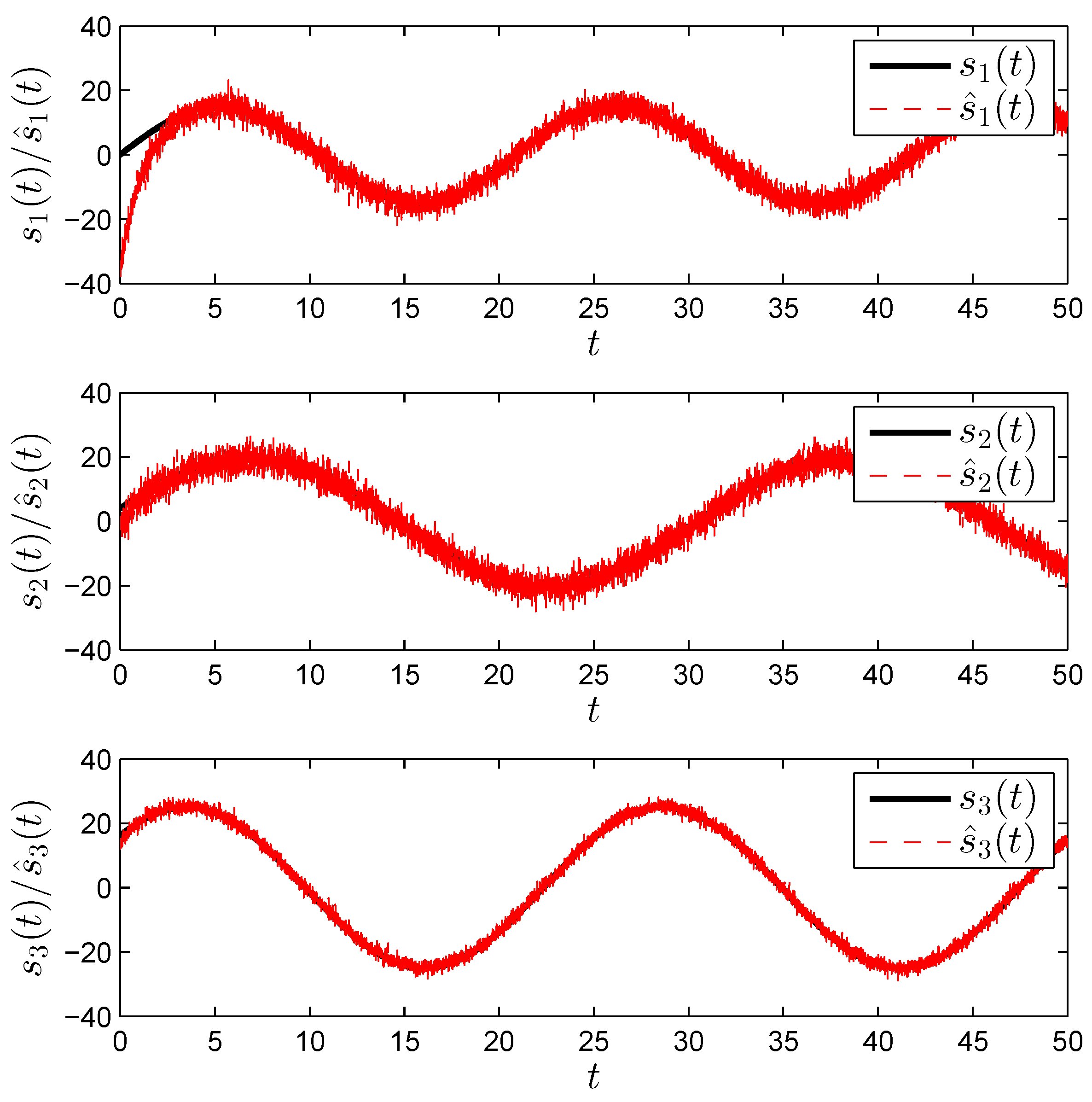
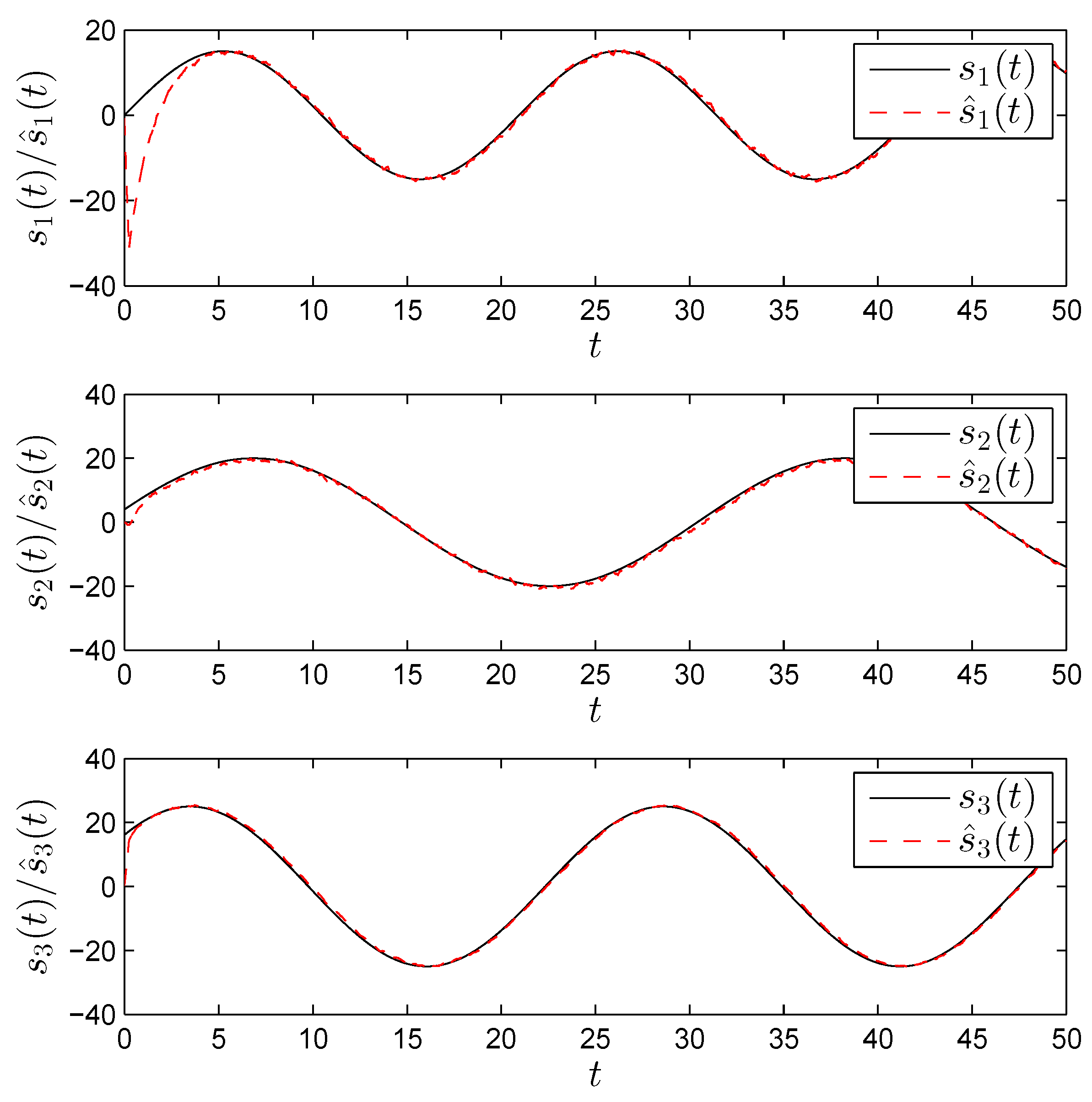
4. Numerical Example
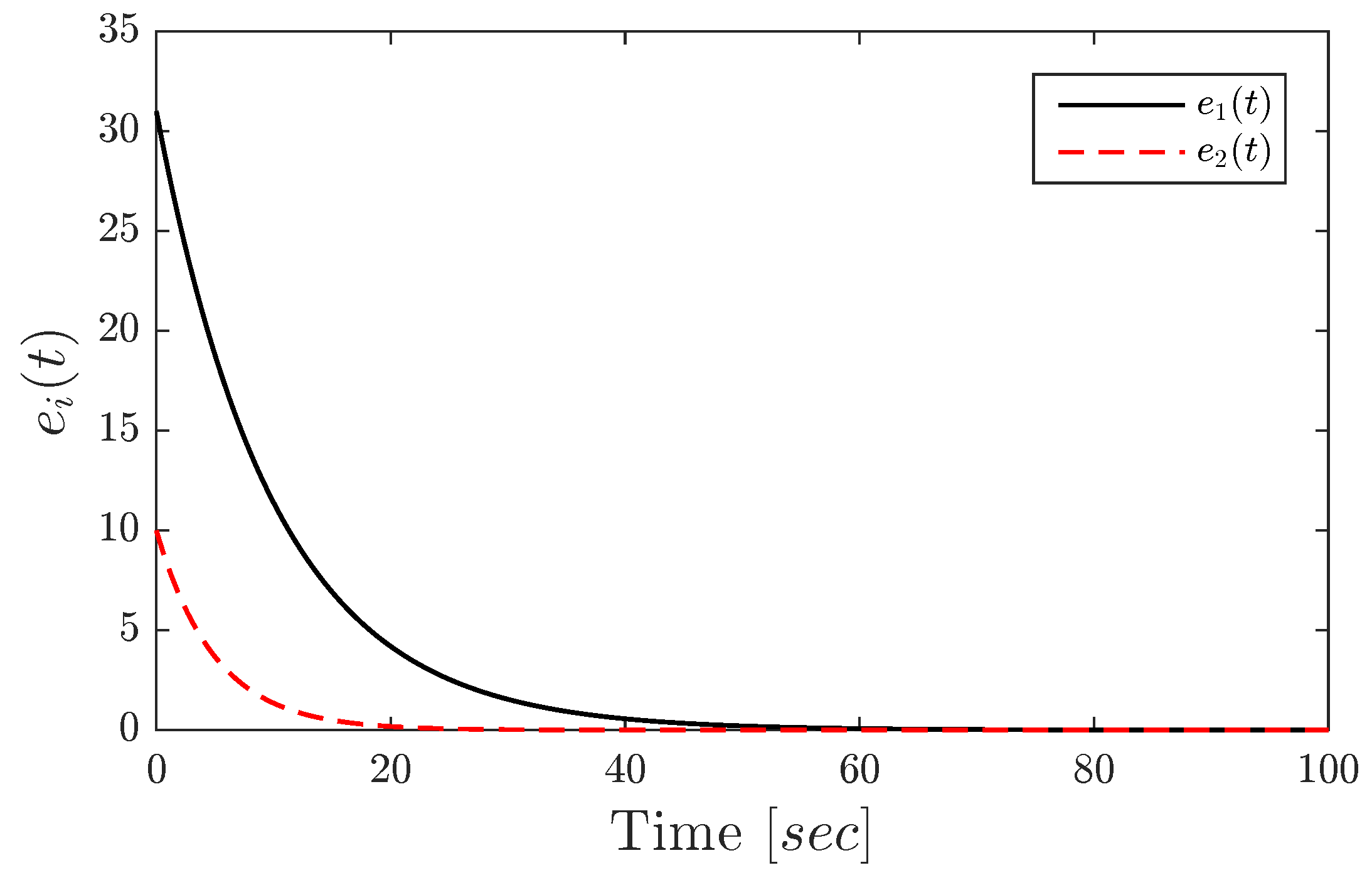
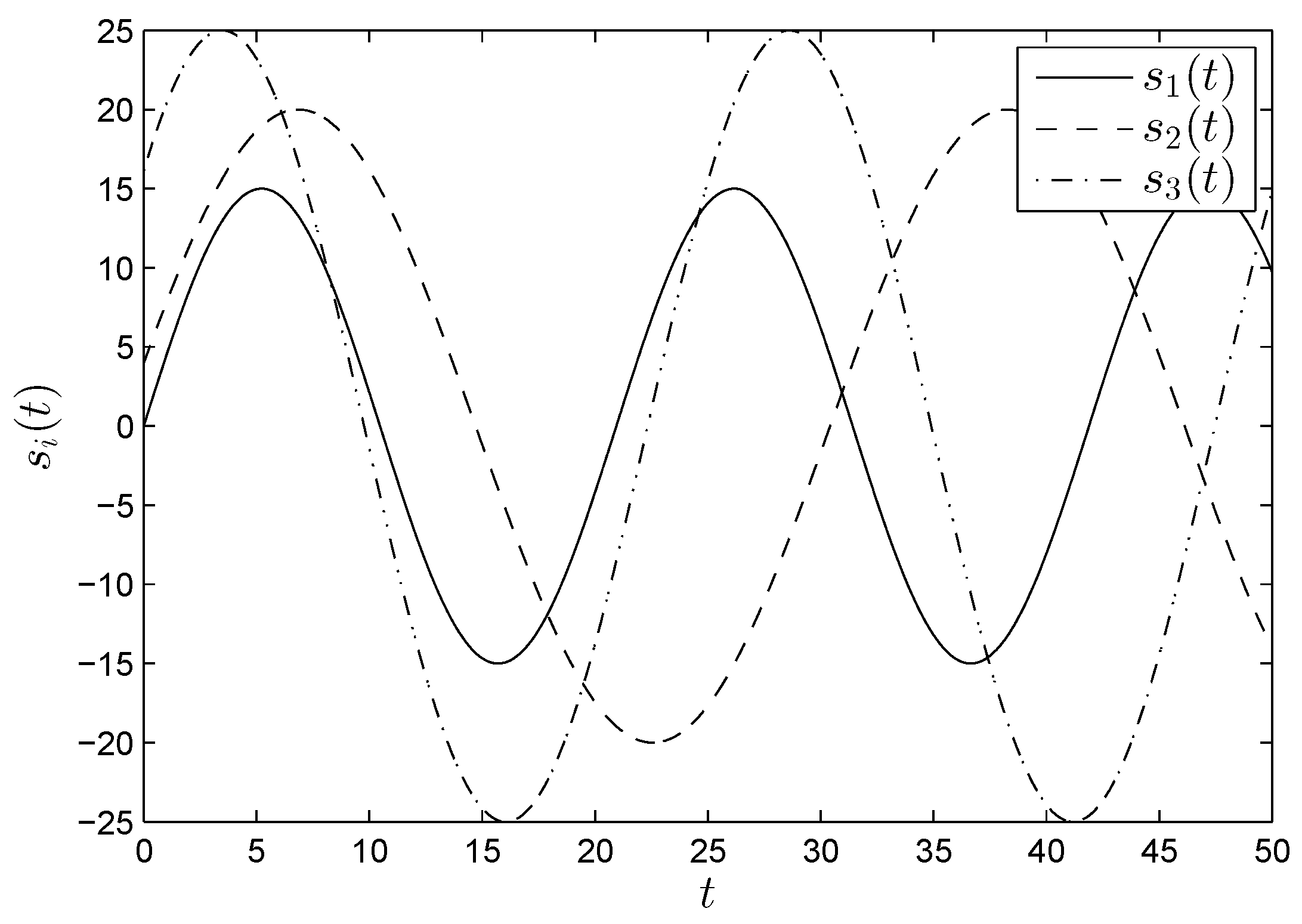
5. Application to MIMO Secure Communications
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, A.C. A theory for synchronization of dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1901–1951. [Google Scholar] [CrossRef]
- Martinez-Guerra, R.; Pérez-Pinacho, C.A.; Gómez-Cortés, G.C. Synchronization of Integral and Fractional Order Chaotic Systems; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Ouannas, A.; Grassi, G. Inverse full state hybrid projective synchronization for chaotic maps with different dimensions. Chinese Phys. B 2016, 25, 090503. [Google Scholar] [CrossRef]
- Ouannas, A.; Abu-Saris, R. On matrix projective synchronization and inverse matrix projective synchronization for different and identical dimensional discrete-time chaotic systems. J. Chaos 2015, 2016, 4912520. [Google Scholar] [CrossRef]
- Ouannas, A.; Odibat, Z. Generalized synchronization of different dimensional chaotic dynamical systems in discrete-time. Int. J. Nonlinear Dyn. Chaos Eng. Sys. 2015, 81, 765–771. [Google Scholar] [CrossRef]
- Ouannas, A.; Odibat, Z. On inverse generalized synchronization of continuous chaotic dynamical systems. Int. J. Appl. Comput. Math. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G. A new approach to study the coexistence of some synchronization types between chaotic maps with different dimensions. Int. J. Nonlinear Dyn. Chaos. Eng. Sys. 2016, 86, 1319–1328. [Google Scholar] [CrossRef]
- Ouannas, A.; Al-Sawalha, M.M. A new approach to synchronize different dimensional chaotic maps using two scaling matrices. Nonlinear Dyn. Sys. Theory 2015, 15, 400–408. [Google Scholar]
- Ouannas, A.; Abu-Saris, R. A robust control method for Q-S synchronization between different dimensional integer-order and fractional-order chaotic systems. J. Control Sci. Eng. 2015, 2015, 703753. [Google Scholar] [CrossRef]
- Ogunjo, S. Increased and reduced order synchronization of 2D and 3D dynamical systems. Int. J. Nonlinear Sci. 2013, 16, 105–112. [Google Scholar]
- Ojo, K.S.; Ogunjo, S.T.; Njah, A.N.; Fuwape, I.A. Increased-order generalized synchronization of chaotic and hyperchaotic systems. Pramana 2014, 84, 33–45. [Google Scholar] [CrossRef]
- Azar, A.T.; Vaidyanathan, S.; Ouannas, A. Fractional Order Control and Synchronization of Chaotic Systems; Studies in Computational Intelligence; Springer: Berlin, Germany, 2017; Volume 688, ISBN 978-3-319-50248-9. [Google Scholar]
- Zhang, F.; Chen, G.; Li, C.; Kurths, J. Chaos synchronization in fractional differential systems. Philos. Trans. R. Soc. A 2013, 371, 1990. [Google Scholar] [CrossRef] [PubMed]
- Ouannas, A.; Al-sawalha, M.M.; Ziar, T. Fractional chaos synchronization schemes for different dimensional systems with non-identical fractional-orders via two scaling matrices. Optik 2016, 127, 8410–8418. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G.; Ziar, T.; Odibat, Z. On a function projective synchronization scheme for non-identical Fractional-order chaotic (hyperchaotic) systems with different dimensions and orders. Optik 2017, 136, 513–523. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Paar, C.; Pelzl, J. Understanding Cryptography; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kocarev, L.; Lian, S. Chaos-Based Cryptography: Theory, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Podlubny, I.; Samko, S.G. Fractional Differential Equations; Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Dabiri, A.; Butcher, E.A. Efficient modified Chebyshev differentiation matrices for fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 284–310. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A. Comments on “Fractional order Lyapunov stability theorem and its applications in synchronization of complex dynamical networks”. Commun. Nonlinear Sci. Numer. Simul. 2015, 25, 145–148. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Xue, W.; Li, Y.; Cang, S.; Jia, H.; Wang, Z. Chaotic behavior and circuit implementation of a fractional-order permanent magnet synchronous motor model. J. Frankl. Inst. 2015, 352, 2887–2898. [Google Scholar] [CrossRef]
- Wu, X.; Wang, H.; Lu, H. Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application to secure communication. Nonlinear Anal. Real World Appl. 2012, 13, 1441–1450. [Google Scholar] [CrossRef]
- Gao, T.; Chen, G.; Chen, Z.; Cang, S. The generation and circuit implementation of a new hyper-chaos based upon Lorenz system. Phys. Lett. A 2007, 361, 78–86. [Google Scholar] [CrossRef]
- Sushchik, M.; Tsimring, L.S.; Volkovskii, A.R. Performance analysis of correlation-based communication schemes utilizing chaos. IEEE Trans. Circuits Syst. I 2000, 47, 1684–1691. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Xu, J.; Wang, L.; Chen, G. Performance of MIMO relay DCSK-CD systems over Nakagami fading channels. IEEE Trans. Circuits Syst. I 2013, 60, 757–767. [Google Scholar] [CrossRef]



| Synchronization Schemes |
|---|
| Inverse full state hybrid projective synchronization [3] |
| Matrix projective synchronization [4]. |
| Generalized synchronization [5]. |
| Inverse generalized synchronization [6]. |
| Hybrid synchronization [7]. |
| – synchronization [8]. |
| Q–S synchronization [9]. |
| Reduced order synchronization [10]. |
| Increased order generalized synchronization [11]. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouannas, A.; Debbouche, N.; Wang, X.; Pham, V.-T.; Zehrour, O. Secure Multiple-Input Multiple-Output Communications Based on F–M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders. Appl. Sci. 2018, 8, 1746. https://doi.org/10.3390/app8101746
Ouannas A, Debbouche N, Wang X, Pham V-T, Zehrour O. Secure Multiple-Input Multiple-Output Communications Based on F–M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders. Applied Sciences. 2018; 8(10):1746. https://doi.org/10.3390/app8101746
Chicago/Turabian StyleOuannas, Adel, Nadjette Debbouche, Xiong Wang, Viet-Thanh Pham, and Okba Zehrour. 2018. "Secure Multiple-Input Multiple-Output Communications Based on F–M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders" Applied Sciences 8, no. 10: 1746. https://doi.org/10.3390/app8101746





