Fast Method of Recovering Reference-Wave Intensity in Two-Step-Only Quadrature Phase-Shifting Holography
Abstract
:1. Introduction
2. Proposed Fast Method for Recovering Reference-Wave Intensity
3. Results and Discussion
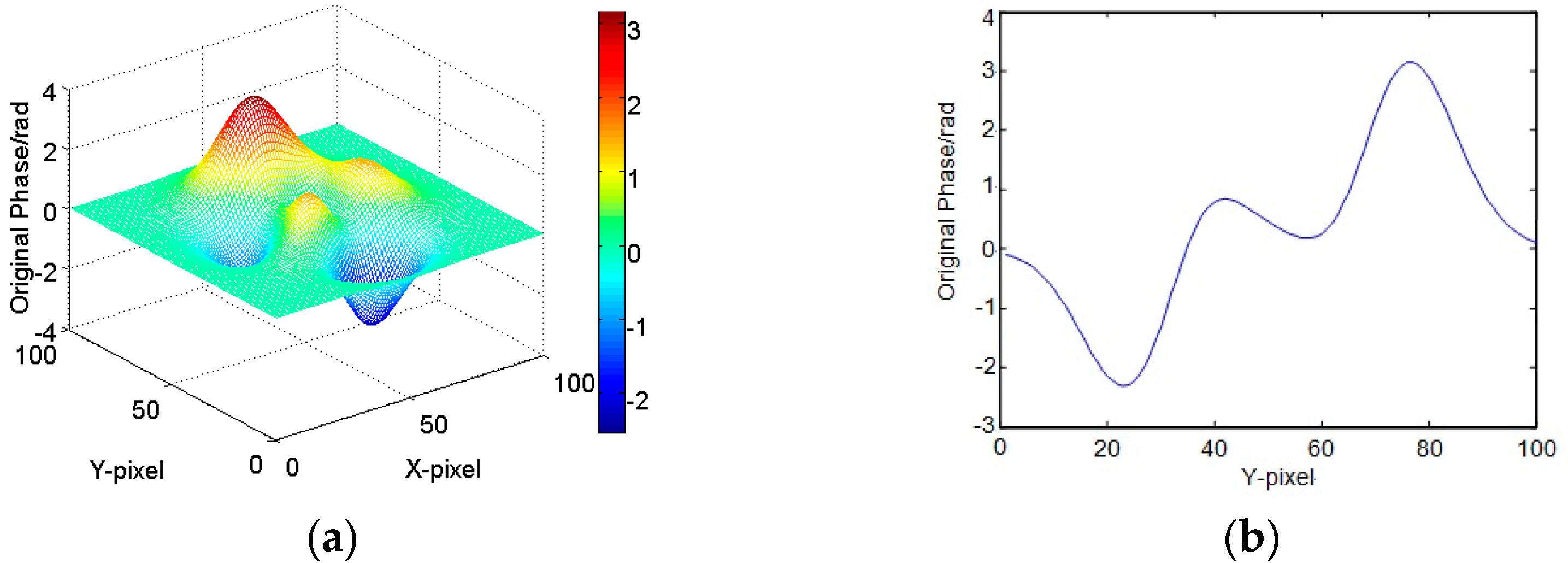
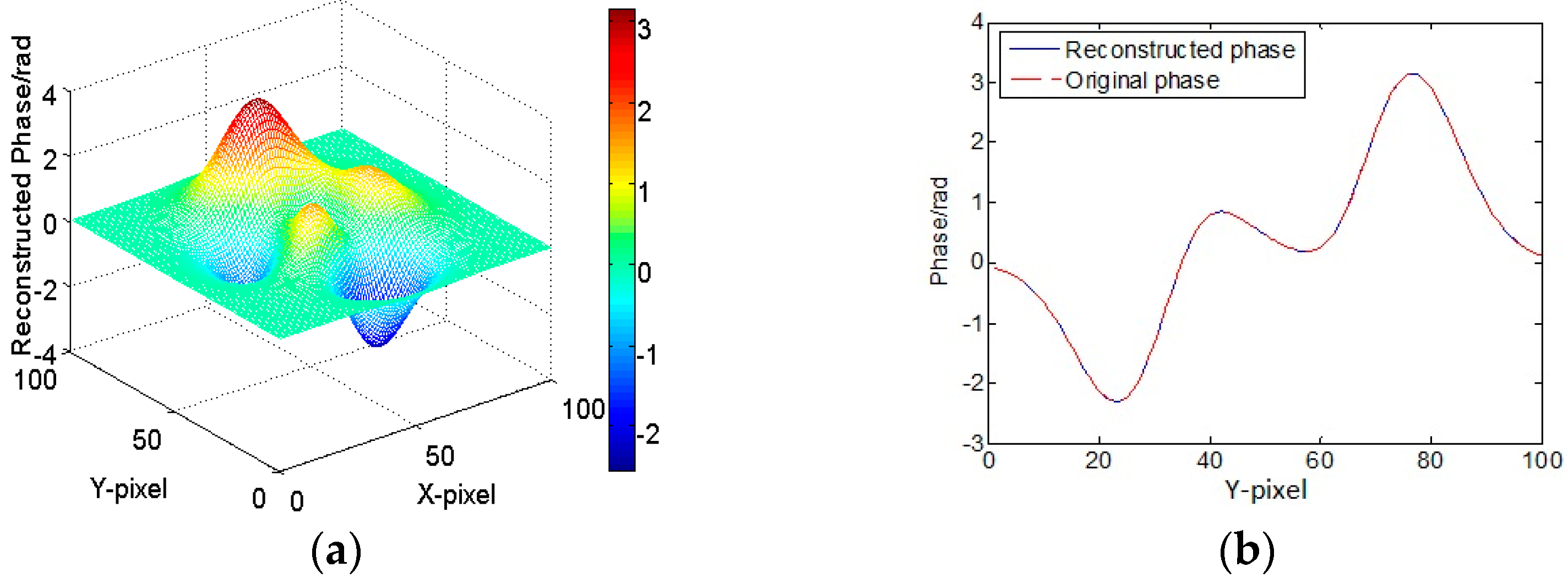
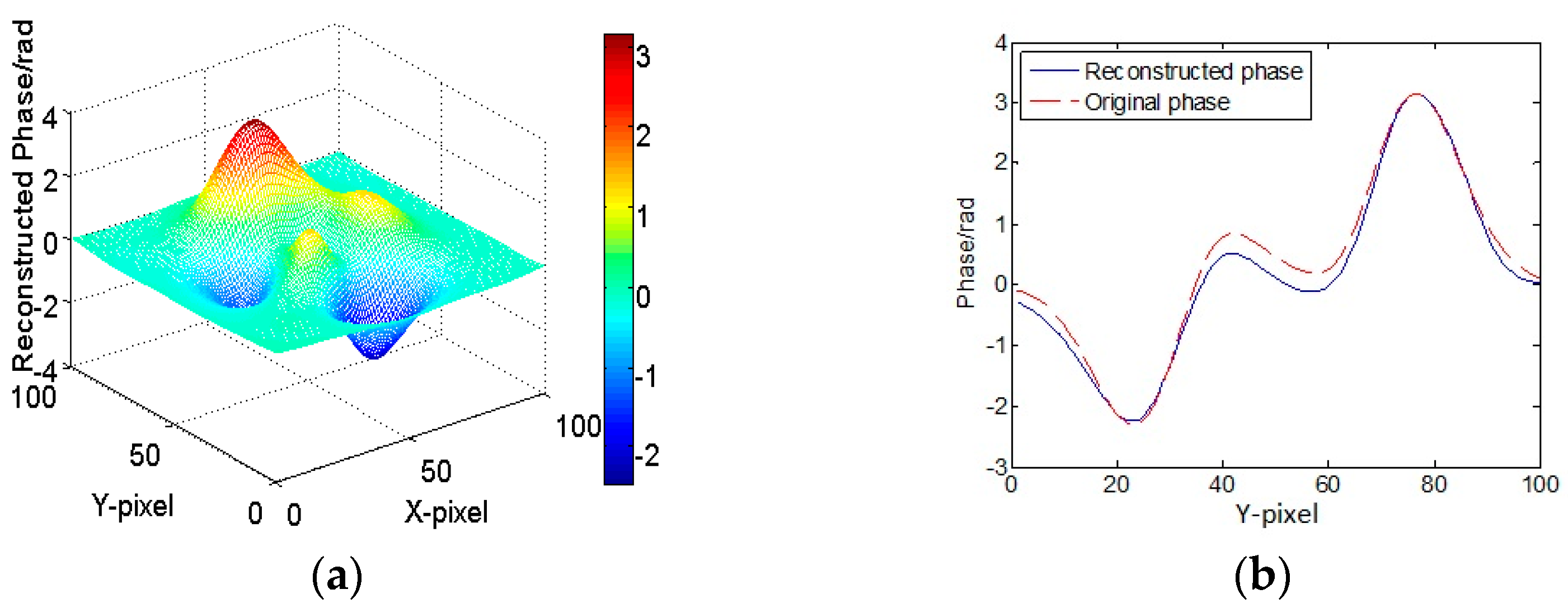
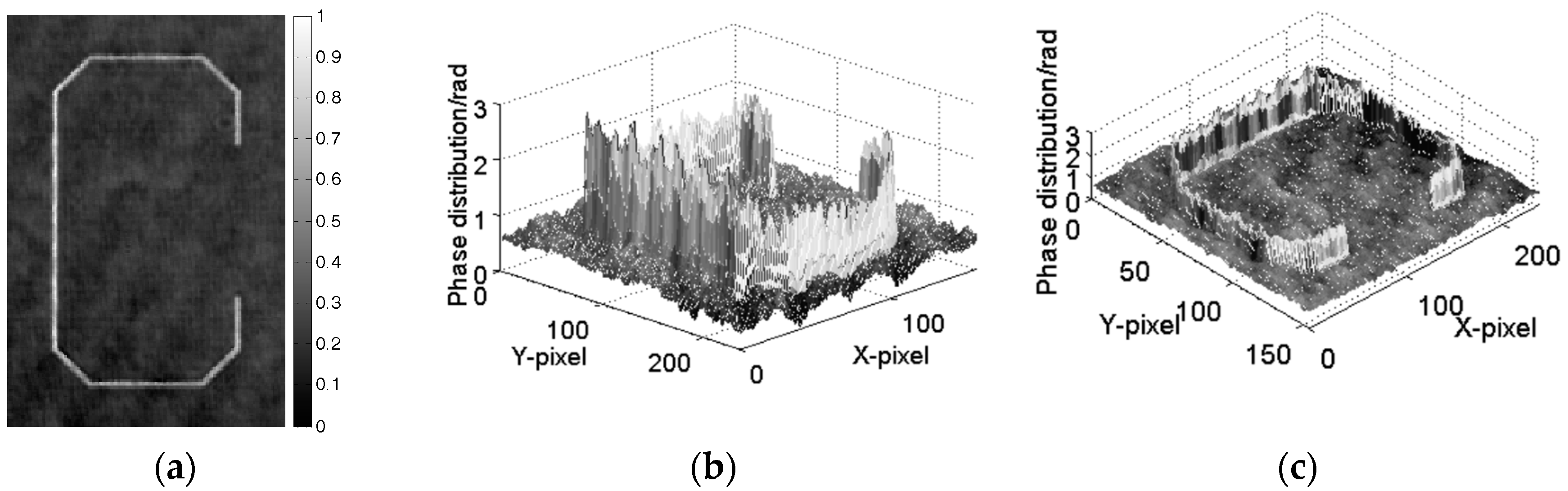
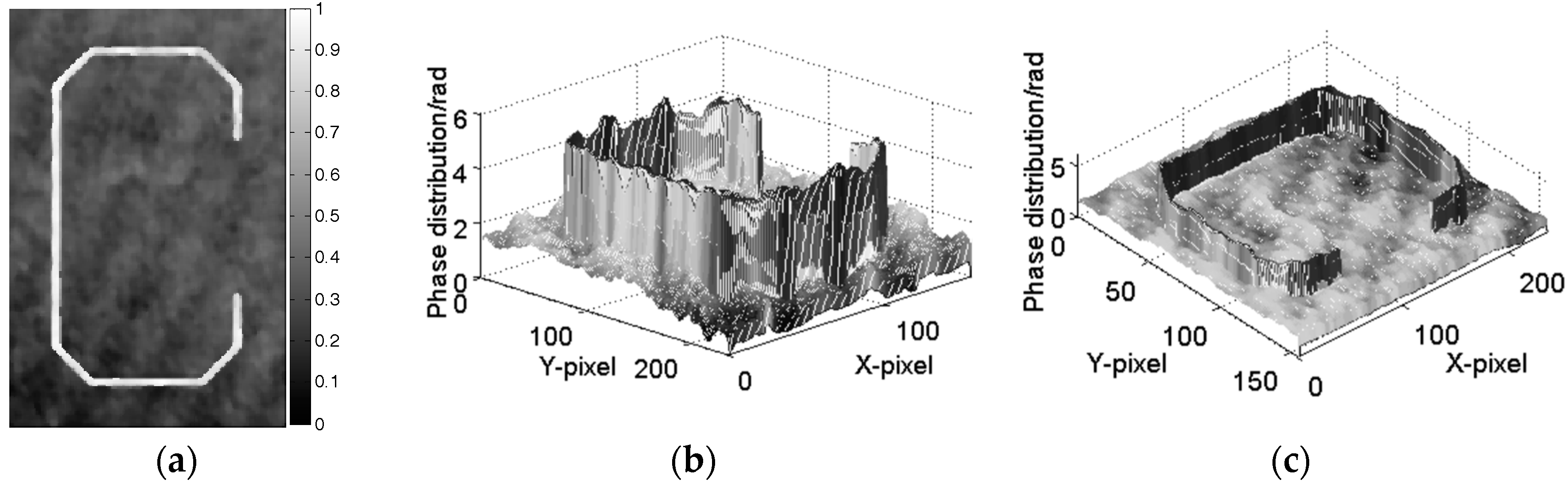
3.1. Computer Simulation Results
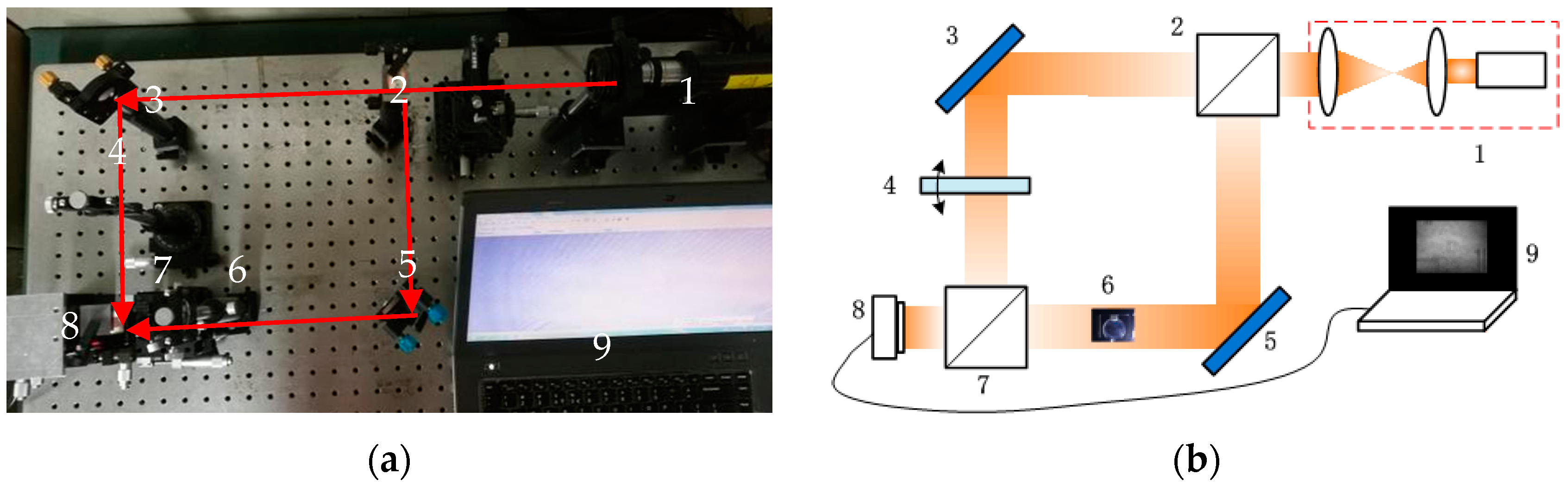
3.2. Optical Experimental Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schnars, U.; Jüptner, W. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, 85–101. [Google Scholar] [CrossRef]
- Poon, T.-C.; Liu, J.-P. Introduction to Modern Digital Holography with MATLAB; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Seebacher, S.; Osten, W.; Baumbach, T.; Jüptner, W. The determination of material parameters of microcomponents using digital holography. Opt. Lasers Eng. 2001, 36, 103–126. [Google Scholar] [CrossRef]
- Katz, J.; Sheng, J. Applications of holography in fluid mechanics and particle dynamics. Annu. Rev. Fluid Mech. 2010, 42, 531–555. [Google Scholar] [CrossRef]
- Wahba, H.H. Reconstruction of 3D refractive index profiles of PM PANDA optical fiber using digital holographic method. Opt. Fiber Technol. 2014, 20, 520–526. [Google Scholar] [CrossRef]
- Osten, W.; Faridian, A.; Gao, P.; Korner, K.; Naik, D.; Pedrini, G.; Singh, A.K.; Takeda, M.; Wilke, M. Recent advances in digital holography. Appl. Opt. 2014, 53, 44–63. [Google Scholar] [CrossRef] [PubMed]
- Leith, E.N.; Upatnieks, J. Reconstructed wavefronts and communication theory. J. Opt. Soc. Am. 1962, 52, 1123–1130. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Kato, J.-I.; Ohta, S.; Mizuno, J. Image formation in phase-shifting digital holography and applications to microscopy. Appl. Opt. 2001, 40, 6177–6186. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Poon, T.-C.; Jhou, G.S.; Chen, P.J. Comparison of two-, three-, and four-exposure quadrature phase-shifting holography. Appl. Opt. 2011, 50, 2443–2450. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Devaney, A.J. Digital microscopy using phase-shifting digital holography with two reference waves. Opt. Lett. 2004, 29, 857–859. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.F.; Cai, L.Z.; Wang, Y.R.; Yan, R.S. Direct phase shift extraction and wavefront reconstruction in two-step generalized phase-shifting interferometry. J. Opt. 2010, 12, 74–77. [Google Scholar] [CrossRef]
- Meng, X.F.; Cai, L.Z.; Xu, X.F.; Yang, X.L.; Shen, X.X.; Dong, G.Y.; Wang, Y.R. Two-step phase-shifting interferometry and its application in image encryption. Opt. Lett. 2006, 31, 1414–1416. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-P.; Poon, T.-C. Two-step-only quadrature phase-shifting digital holography. Opt. Lett. 2009, 34, 250–252. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.Q.; Zhou, J.Y. A new estimation method for two-step-only quadrature phase-shifting digital holography. Opt. Commun. 2015, 335, 183–188. [Google Scholar] [CrossRef]
- Chen, B.X.; Tian, Y.Z.; Zhao, N.N.; Wang, L.; Chen, D.X.; Liang, E.J. Optimization of two-step phase-shifting digital hologram algorithm and experimental verification. Laser Optoelectron. Prog. 2015, 52, 138–142. (In Chinese) [Google Scholar]
- Zhou, W.-J.; Yang, X.; Poon, T.-C. Reconstructing of two combined on-axis holograms with π/2-phase difference. In Proceedings of the IEEE 13th International Conference on Industrial Informatics, Cambridge, UK, 22–24 July 2015; IEEE: Cambridge, UK, 2015; pp. 746–749. [Google Scholar]
- Zhou, W.-J.; Zhang, H.B.; Yu, Y.J.; Poon, T.-C. Experiments on a simple setup for two-step quadrature phase shifting holography. IEEE Trans. Ind. Inform. 2016, 12, 1564–1570. [Google Scholar] [CrossRef]
- Zhou, W.-J.; Zheng, C.F.; Zhang, H.B.; Yu, Y.J.; Poon, T.-C. Phase retrieval in two-step quadrature phase-shifting holography. Proc. SPIE 2017, 10255, 1025501. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.-J.; Zheng, C.; Poon, T.-C. Fast Method of Recovering Reference-Wave Intensity in Two-Step-Only Quadrature Phase-Shifting Holography. Appl. Sci. 2017, 7, 1084. https://doi.org/10.3390/app7101084
Zhou W-J, Zheng C, Poon T-C. Fast Method of Recovering Reference-Wave Intensity in Two-Step-Only Quadrature Phase-Shifting Holography. Applied Sciences. 2017; 7(10):1084. https://doi.org/10.3390/app7101084
Chicago/Turabian StyleZhou, Wen-Jing, Caifu Zheng, and Ting-Chung Poon. 2017. "Fast Method of Recovering Reference-Wave Intensity in Two-Step-Only Quadrature Phase-Shifting Holography" Applied Sciences 7, no. 10: 1084. https://doi.org/10.3390/app7101084
APA StyleZhou, W.-J., Zheng, C., & Poon, T.-C. (2017). Fast Method of Recovering Reference-Wave Intensity in Two-Step-Only Quadrature Phase-Shifting Holography. Applied Sciences, 7(10), 1084. https://doi.org/10.3390/app7101084




