1. Introduction
Friction between two objects can produce a wide variety of sounds like squealing brakes, creaking doors, squeaking dishes or beautiful sounds from bowed strings in musical conditions. The understanding of such acoustical phenomena constitutes a historical challenge of physics that was subjected to early researches already from the 18th century [
1]. Today friction phenomena are still debated and several mechanisms are under investigation, such as the conversion process from kinetic to thermal energy provoked by friction at the atomic scale [
2]. In spite of the physical complexity of friction phenomena, physically inspired friction models have been developed within various domains [
3,
4]. Such models have for instance been used for musical purposes in the case of simulations of sounds from bowed string instruments intended for electronic cellos or violins [
5] or unusual friction driven instruments based on both physical and signal models [
6]. In the specific case of violin sounds, more elaborated models also considered the thermal effects that appear at the contact area between the bow and the string [
7,
8]. All these models strongly depend on physical considerations and require the control of specific physical parameters. For example in the model proposed by Avanzini et al. [
3] seven physical parameters must be defined to synthesize a friction sound. Although these parameters well characterize the physical behavior of the friction phenomenon, they are not at all intuitive for naive users. In fact, to facilitate the control of such models, a better understanding of the perceptual impact of its parameters would be needed. Other approaches based on holistic observations have been proposed. Rather than simulating the physical behavior of the phenomena, these models generally focus on the perceptual relevance of the elements that contribute to the generated sound and whether they contribute to the evocation of a particular event. For example, Van den Doel et al. [
9] considered that the noisy character of friction sounds was perceptually salient and proposed to synthesize noisy friction sounds by modeling the sound as band-pass filtered noise which central frequency varies with respect to the relative velocity of the two interacting objects. In addition to be computationally efficient, this model offers numerous control possibilities and provides a wide variety of controls of the friction sound that can be easily handled by naive users. In addition to the velocity control, the roughness of the surface can easily be modified by shaping the spectral content of the noise in filtering pre-processing step. Another advantage of using signal models that are unconstrained by mechanics is that physically impossible situations can be generated. Hence, unlimited sound generation possibilities are available, such as continuous morphing between sounding objects or perceptual cross-synthesis between sound properties.
In this article we therefore propose to synthesize nonlinear friction sounds from signal models using a paradigm based on perceptually relevant acoustic morphologies. This approach enables to elude the physical constraints and to separately control the nature of the interaction and the resonating object from a perceptual point of view. It should be noted that the underpinning terminology may therefore differ from the one used to describe the physics behind the friction phenomena. In particular, friction is generally modeled as an interaction between two objects while we here consider that a friction sound can be perceptually described as the consequence of an action of a moving, non-resonant exciter on a resonating object. Hence, the proposed approach makes it possible to freely combine actions and objects to simulate both real and physically non-plausible situations and to explore the ductility of synthesis in terms of control possibilities for various applications. For instance, from a perceptual point of view, squeaking or squealing sounds may convey the sense of “effort” or “annoyance” while tonal sounds may convey the sense of “success” or “wellness”. Based on these evocative auditory percepts, new sonic devices aiming at guiding or learning specific gestures can then be developed with such flexible sound synthesis models. In particular, transitions between perceptually different acoustical behaviors can be defined according to arbitrary mapping specifications related to the used devices. Depending on the mapping, such models also enable to choose different levels of difficulty in a learning process. In the present article, we focus on a general model that simulates different acoustical behaviors from spectral considerations. Finally, several applications linked to gesture guidance and video game applications are presented.
2. Perceptually Informed Friction Sound Synthesis
To design a ductile synthesis tool simulating non-linear acoustical phenomena, we used a paradigm describing the auditory perception of sound events. This paradigm can be illustrated by the following example: when hearing the sound of a metal plate hitting the floor, the material of the plate can easily be recognized. Likewise, if the plate is dragged on the floor, the recognition of its metallic nature remains possible, but the continuous sound-producing dragging action can also be recognized. This example points out a general principle of auditory perception consisting in decomposing sounds into two main contributions: one that characterizes the resonating object properties and another linked to the action generating the vibrating energy. In other words, the produced sound can be defined as the consequence of an action on an object. It must be noted that this is not true from a physical point of view, since friction between two objects induces mutual energetic exchanges between interacting objects. Nevertheless from a perceptual point of view, the action/object approach is still relevant as long as the action part simulates the acoustic morphologies that characterize the nonlinear behavior provoked by the interaction.
Such descriptions of an auditory event have been highlighted in various psychological studies, pointing out that our auditory perception uses information from invariant structures included in the auditory signal to recognize the auditory events. Inspired from the ecological theory of visual perception and the taxonomy of invariant features of visual flow proposed by Gibson [
10], McAdams [
11] and Gaver [
12,
13] adapted this theory to auditory perception. It has since then been successfully used for sound synthesis purposes. Concerning the object, it has been shown that the damping behavior of each partial characterizes the perceived material of an impacted object [
14]. In line with this result, a damping law defined by a global and a relative damping behavior was proposed to control the perceived material in an impact sound synthesizer [
15]. Concerning the action, recent studies focused on the synthesis of continuous interaction sounds such as rubbing, scratching and rolling [
16,
17,
18]. They revealed that the statistics of the series of impacts that model the continuous interaction between two objects characterize the nature of the perceived interaction. Additionally this enables to intuitively control the synthesis of such sounds. This ecological approach then provides a powerful framework to extract the acoustic information that makes sense when listening to a sound [
19].
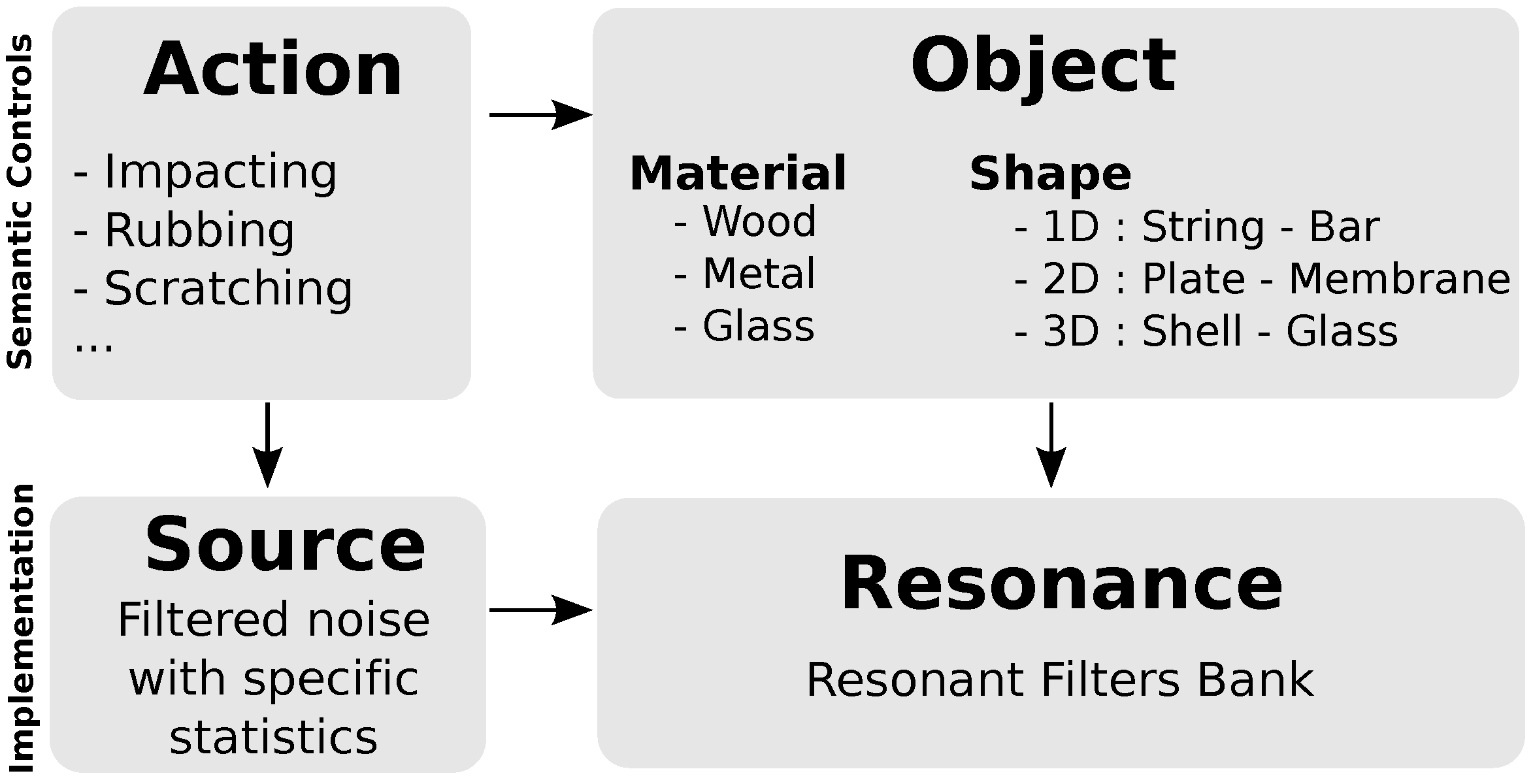
The framework of the action/object paradigm previously described supposes that actions and objects are perceived independently and can therefore be simulated separately. Practically, an implementation with a linear source-resonance filtering is well adapted to the present perceptual paradigm, see
Figure 1. The output sound indeed results from a convolution between a source signal
and the impulse response
of a vibrating object. The resonator part
is implemented with a resonant filter bank, which central frequencies correspond to the eigen frequencies of the object. A control strategy of the perceptual attributes of the object by semantic descriptions for example the perceived material, size and shape is proposed in [
20].
2.1. Source Modeling
In this section, the modeling of the source signal related to the perception of actions such as squeaking or creaking is examined. For that purpose, basics physical considerations and empirical observations made on recorded signals are firstly presented. A signal model is finally proposed according to invariant morphologies revealed by these observations.
2.1.1. The Coulomb Friction Model
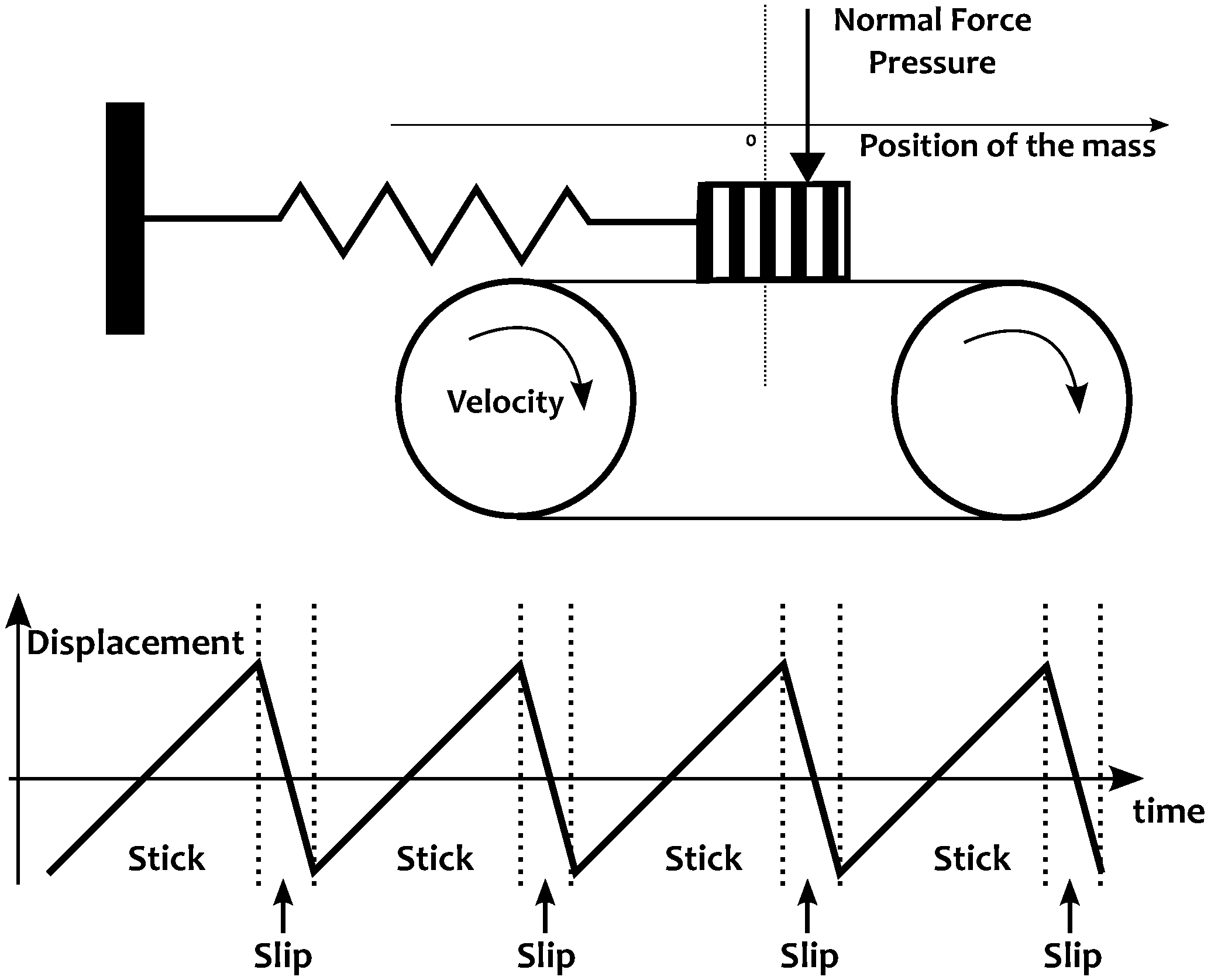
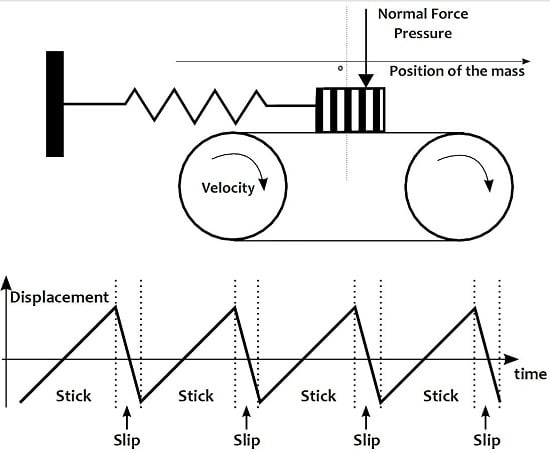
The Coulomb friction can be described in its first approximation by a simple phenomenological model sketched in
Figure 2. When an object is rubbing another one, and when the contact force between the objects is large enough, the friction behavior can be described by the displacement of a mass held by a spring, and gradually moved from its equilibrium position by a conveyer belt moving at a velocity
v. The object is then said to be in the sticking phase. When the friction force
becomes smaller than the restoring force
, the mass slides in the opposite direction until
becomes larger than
. The object is then said to be in the slipping phase. This model describes the so-called stick-slip motion, or the Helmoltz motion.
If we neglect the slipping phase, the resulting displacement
of the exciter on the conveyer belt surface corresponds to a sawtooth signal whose Fourier decomposition is:
Several models that take into account a non-zero sliding duration can be found, see
Figure 2. The Fourier decomposition of such a signal is a harmonic spectrum with decreasing amplitude according to the harmonic order.
This model provides a first a priori about the behavior of the source signal to be simulated: the excitation should have a harmonic spectrum. This model allows us to determine a physically informed signal morphology associated to the nonlinear friction phenomenon, even if we are aware that it cannot be generalized to any friction situation.
2.1.2. Empirical Observations on Recorded Sounds
In this section, empirical observations of various nonlinear friction sounds are presented. Five situations are analyzed: a creaky door, a squeaking and singing wet wineglass, a squeaking wet plate, and a bowed cello string. These five situations were chosen as they are the consequence of a human movement and are therefore good candidates to be used in gesture guidance device. Except for the door creak and the cello, the recordings were made in an anechoic room using a cardioid Neumann-KM84i microphone positioned about 30 cm above the rubbed object. The recorded sounds are available online [
21] from [
22]. An inharmonicity analysis was performed for each sound. A partial tracking routine developed by Dan Ellis [
23] was used to detect the set of peaks of the spectrum in each frame of the excerpt. A linear regression was applied to the inharmonicity value,
, where
is the n-th peak detected, and
the fundamental. If the spectrum is harmonic the inharmonicity
is 0. The analysis of the three recordings revealed that they all had harmonic spectra.
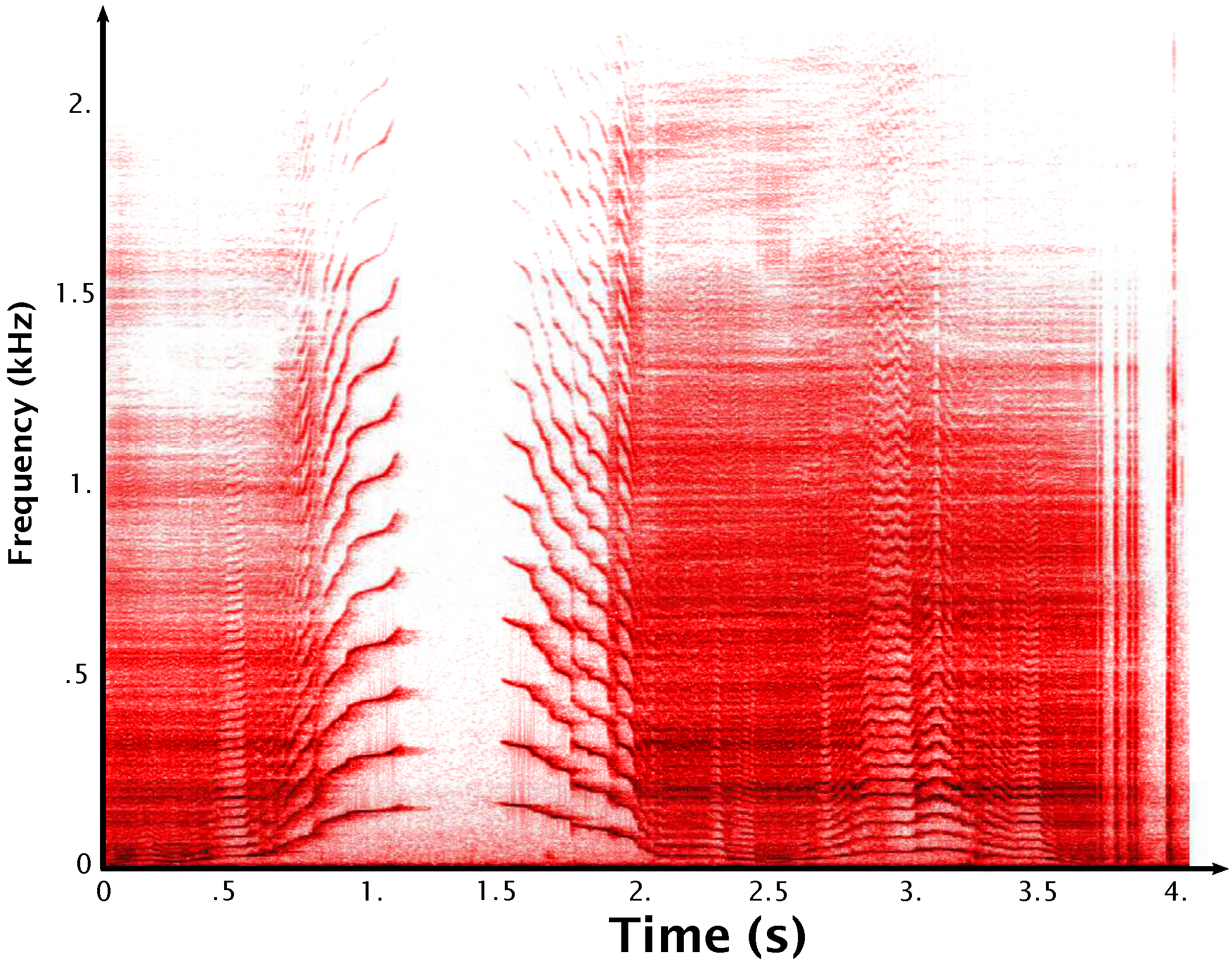
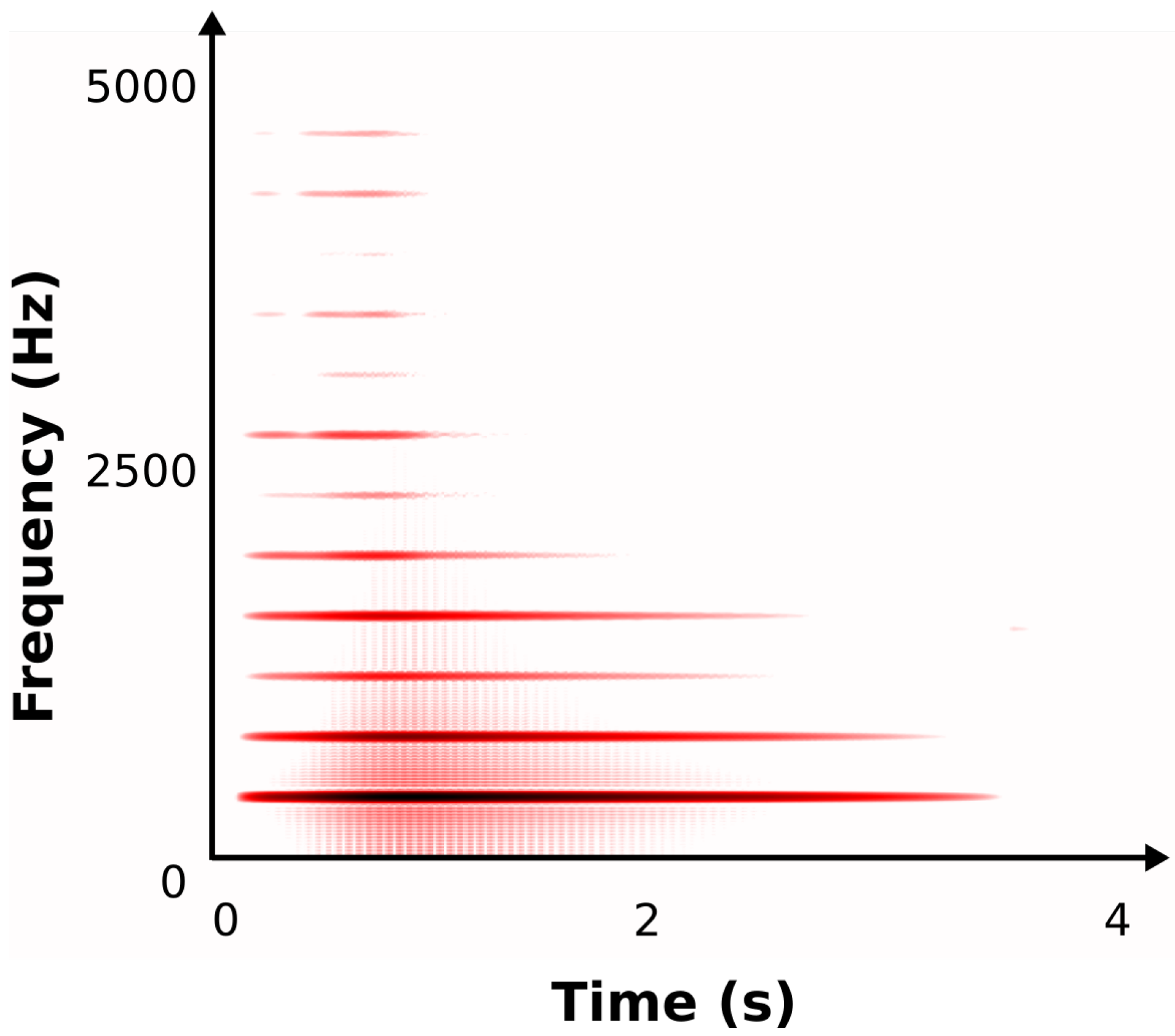
Creaky Door. The time-frequency representation of the sound is presented in
Figure 3. The sound has a harmonic spectrum whose fundamental frequency varies over time. The fundamental frequency is related to the rotation speed and the pressure at the rotation axis of the door. The large range of variations of the fundamental frequency is also a noticeable characteristic of this signal morphology that varies from a very noisy like sound when
is low, to a “singing” harmonic one for higher values.
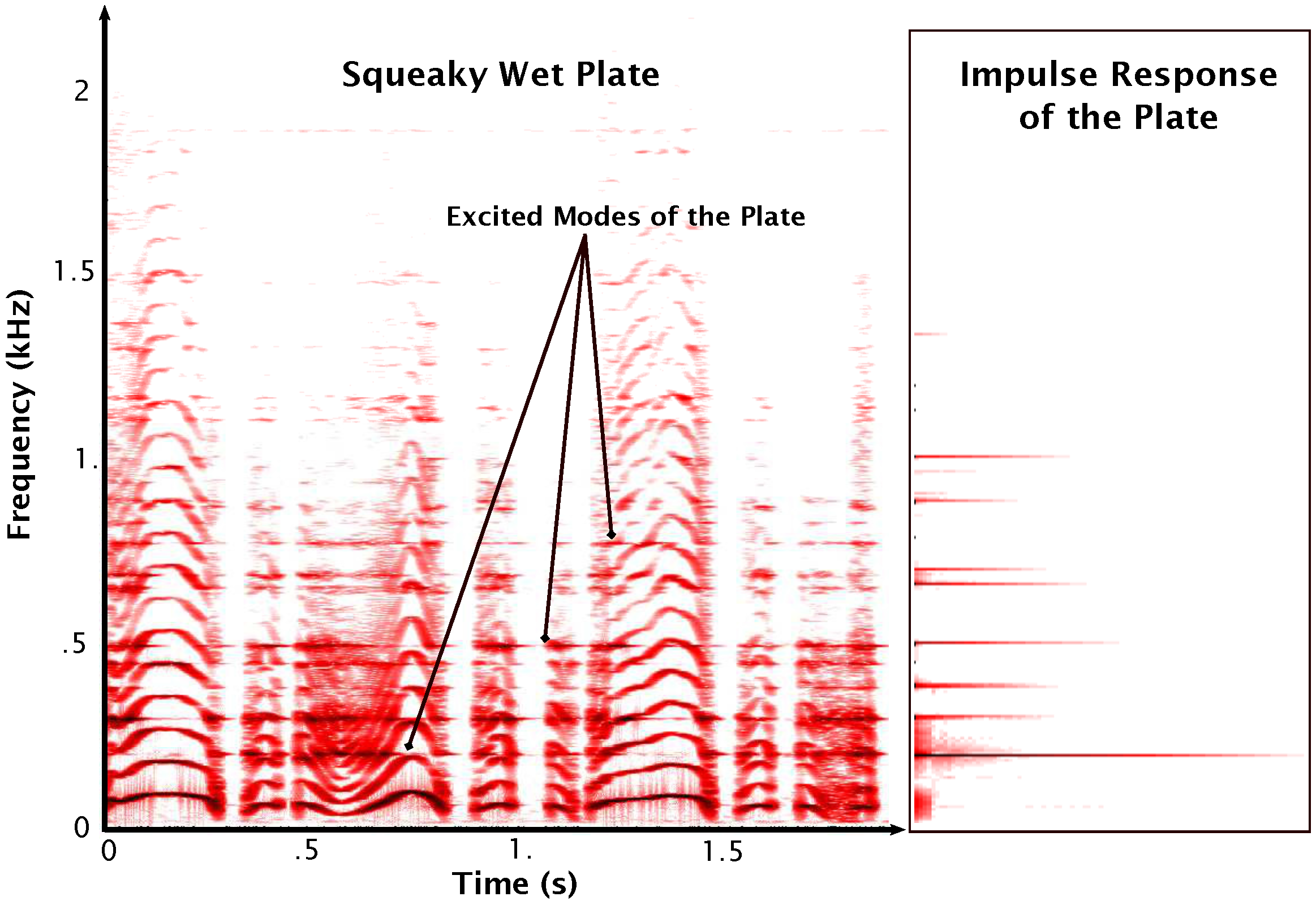
Squeaking Wet Plate. The spectrograms of the squeaking sound and the impulse response of the plate are shown in
Figure 4. This sound is also harmonic but provides less variations of the fundamental frequency than the creaky door. In addition, the fundamental frequency
slowly varies around a central value. The vibrating modes of the plate are clearly visible on the impulse response and are excited when
gets close to the excitation frequency. This observation consolidates the stance to use the perceptual action/object paradigm based on a separate control of the exciter and the resonator.
Squeaking and Singing Glass. When a glass is rubbed, the associated sound may reveal several behaviors qualified as squeaking and singing, see
Figure 5. The squeaking phase provides a similar behavior as the squeaking wet plate:
varies chaotically around a central value. The singing phase appears when
falls on a wineglass mode. The transitions between the squeaking and singing situations are almost instantaneous and hardly predictable.
Bowed Cello String. The sound of a bowed string shows behaviors similar to those of the singing wineglass, see
Figure 6. The fundamental frequency is locked to a vibrating mode of the string according to the bow velocity and force. The main difference resides in the attack which is smoother than in the singing wineglass sound.
These empirical observations lead us to hypothesize that the acoustical morphology that mainly characterizes such auditory events relies on the temporal evolution of the fundamental frequency of a harmonic spectrum. As it is well known for sustained musical instruments most of these acoustical behaviors can indeed be modeled by a harmonic spectrum whose fundamental frequency varies over time. The analyses of the previously recorded sounds confirmed that these assumptions also hold for other friction cases. Nevertheless, even if each spectrum locally is perfectly harmonic, each individual harmonic is not perfectly localized in frequency and should be considered as a band-pass filtered noise with a very thin bandwidth.
2.1.3. Signal Model
From the empirical signal observations presented in previous sections, the following general synthesis model of the source
is proposed:
where
and
the sample frequency. The instantaneous frequency is given by
, and
the amplitude modulation law for the
k-th harmonic. From a signal point of view, the sound morphologies for squeaking, creaking and singing objects differ by the temporal evolution of the fundamental frequency
and the amplitudes
.
Fundamental frequency behavior. The following general expression for
is proposed:
Φ represents the fundamental frequency defined from a given mapping
.
is a low pass filtered noise with cutoff frequency defined below 20 Hz. This stochastic part models the chaotic variations of the fundamental frequency observed in the case of squeaking or creaking sounds. In the case of self-sustained oscillations,
ϵ is null. For a more physically informed mapping, the fundamental frequency can be defined from the dynamical parameters of the two bodies in contact, in particular
, by assuming that the friction sounds mainly depend on the dynamic pressure
and the relative velocity
between objects. The mapping can be defined with other descriptors according to the desired applications as mentioned in the introduction and developed below in the applications section.
Amplitude Modulation Behavior. In the specific case of the singing wineglass low frequency beats are observed in the generated sounds. The frequency of the amplitude modulation is directly linked to the velocity
of the wet finger which is rubbing the glass rim and the diameter of the glass
D. An explicit expression of
as been proposed [
24,
25]:
In other words, the smaller the diameter, the higher the velocity and the amplitude modulation, and vice versa. For other situation than the singing wineglass we proposed an amplitude modulation law defined by
.
The parameters of the model related to different friction phenomena are summarized in
Table 1.
2.2. Implementation
The signal model previously described proposes to reach the expected flexibility through a source-filter approach that enables to separate the perceptual control of the action from that of the object. The action properties are thus characterized by the source signal which corresponds to a harmonic spectrum whose temporal evolution of fundamental frequency and amplitude characterize the evoked nonlinear behavior. In this section, we propose two different ways to implement such a source.
2.2.1. Additive Synthesis
Additive synthesis is certainly the most natural way to simulate the harmonic spectrum. This approach consists in summing the outputs of sinusoidal oscillators whose frequencies are driven by the different behaviors previously described.
The main flaw is that the synthesized sounds are sometimes perceived to be non natural. This is probably due to the fact that the harmonics are indeed not perfectly localized in frequency in the previously recorded sounds. They should therefore be considered as bandpass filtered noises with very thin bandwidths. Replacing the sinusoids by band-pass filtered noises could provide additional acoustic cues that are important for the perceived realism of the sound. Another possibility would be to expand the bandwidth around each harmonic by adding spectral components around each harmonic in an additive way. Nevertheless, this method drastically increases the complexity of the algorithm and makes it almost impossible to propose an intuitive control. In order to increase the realism of the synthesized sounds without loosing too much computational efficiency the following section proposes another way to implement the generation of a harmonic spectrum, and thus facilitating the shaping of the bandwidths around each harmonic.
2.2.2. Subtractive Synthesis
Subtractive synthesis emanated from the digital filtering theory [
27] and has been extensively used for speech analysis and synthesis [
28,
29]. It consists in shaping a sound with a rich harmonic content such as a noise by a filtering process. It is thus possible to generate a harmonic spectrum by creating a resonant filter bank whose central frequencies are defined to construct the desired harmonic spectrum. When the source is a noise and the damping of each filter is set to zero, the spectrum is perfectly tonal and corresponds to the one obtained by additive synthesis. Contrary to the additive synthesis, the bandwidth around each harmonic can globally be expanded by increasing the damping values to make the sound more noisy, without increasing the computational cost. Practically, we implemented such a subtractive method by designing a filter bank composed of 2nd-order resonant filters [
30] whose central frequencies are tuned to the frequencies of the harmonic spectrum. Their damping is then left as a control of the sound synthesis process. The source is finally generated by filtering a white noise with this resonant filter bank. The frequencies and amplitude modulation laws of the different friction behaviors described previously can then be applied in the same way as for the additive synthesis process.
3. Applications
The synthesis process and the control described above led to several applications. Three of them are presented here and constitute firstly the creation of a tool for motor disease rehabilitation and gesture learning, secondly the possibility to create flexible bowed string synthesizers enabling to choose their playability a priori, and finally the conception of an event-driven interactive sound synthesis tool in virtual audiovisual environments.
3.1. Auditory Guidance Tools for Motor Learning
The main goal behind the development of the flexible synthesis model described above was to create new devices based on sounds to guide gestures. In particular, this problem was motivated by the rehabilitation of a specific motor disease called dysgraphia which affects some children that aren’t able to write fluidly. The idea was thus to provide an auditory feedback based on a metaphoric “singing wineglass” as a correct target. Such a feedback would continuously inform them on the correctness of their gesture and would influence them to intuitively modify their graphical movement to reach the required fluidity.
In order to evaluate the relevance of real-time auditory feedback to improve handwriting gestures, a study was performed on adults who were asked to write new characters with their non-dominant hand [
31]. Thirty two French natives who were right-handed adults who had normal vision and hearing and presented no neurological or attentional deficits participated in this experiment. The task consisted in writing four new characters of Tamil script with their non-dominant hand on a sheet of paper that was affixed to a graphic tablet. A movie showing an example of the learning task is available online [
32]. The writing was accompanied by synthetic sounds simulating a natural action on an object, which varied as a function of the handwriting quality. A rubbing sound evoking a chalk on a blackboard was associated to a correct handwriting. When the handwriting was too slow, the rubbing was transformed into a more unpleasant sound evoking a squeaking door, which urged the writers to increase the speed of their movements to obtain a more pleasant sound. The handwriting was considered too slow when the instantaneous tangential velocity was below 1.5 cm·s
. Consequently, the transition between the friction sound and the rubbing sound was made at this threshold.
In addition to the continuous guidance, impact sounds evoking cracking sounds were added whenever the handwriting was jerky. These additional discrete sounds, which were obtained from a synthesizer developed for intuitive control of impact sounds [
15,
26], evoked a lack of fluency of the handwriting action and could in a metaphorical way be associated with a chalk that breaks while writing or a cracking vinyl record. These sounds were generated when the difference between two velocity peaks was less than 40 ms and when the velocity difference between these two peaks was less than 1.0 cm·s
. These thresholds were determined empirically and validated from previous experiments on movement fluency [
33].
The results were analyzed through two different types of variables: (1) kinematic variables on handwriting movement (2) spatial variables on the written trace. The kinematic variables were obtained from the mean tangential velocity on the tablet and the number of velocity peaks within a certain frequency range (5–10 Hz). The spatial variables corresponding to the trace length of the total trajectory was calculated in terms of a Euclidian distance between the subject’s trace and a reference trace obtained from the recordings of a trained proficient adult using his dominant hand. The better the character matched with the reference, the higher the score.
The subjects were divided in two groups and were told to learn the four unknown characters with their non-dominant hand with or without real-time auditory feedback. Half of the participants first learned the two characters without the auditory feedback and the following two characters with the auditory feedback, while the second half first learned the two characters with the auditory feedback and the following without the auditory feedback.
Results revealed that sonifying handwriting during the learning process of unknown characters improved the fluency and speed of their production, despite a slight reduction of their short-term accuracy, hereby validating the use of sounds to inform about handwriting kinematics. By transforming kinematic variables into sounds, proprioceptive signals are translated into exteroceptive signals, thus revealing hidden characteristics of the handwriting movement to the writer. Although this study focused on adult participants, the encouraging results incited the authors to propose a similar approach for learning and rehabilitation of dysgraphic children which also appeared to be efficient [
34]. In this study the difficulty of the task could be adjusted according to the degree of fluidity for each child. Results revealed that dysgraphic children increase their writing fluidity across training sessions by using this sonification tool. Current experiments are conducted to evaluate whether this sonification method is more efficient than existing ones based on visual and proprioceptive feedbacks.
3.2. Pedagogical Bowed String Instrument
The process of learning to play an instrument is generally long and cumbersome since specific and accurate gestures are involved. Instrument makers cannot easily simplify this learning process even if they can increase the playability to some extent by acting on the material of the instrument. However, they are always constrained by the physics and cannot ensure for example that a specific Shelleng diagram that is linked to the playability of a bowed string is associated to a given instrument. As the models proposed here enabled the generation of bowed string sounds that are not constrained by physics as traditional instruments, it is possible to imagine a new evolving pedagogical tool. We may indeed create a virtual instrument whose playability can be defined a priori in order to adapt the playability of the instrument to the progress of the performer. The violin string would be simulated by a metal string with controllable modal properties.
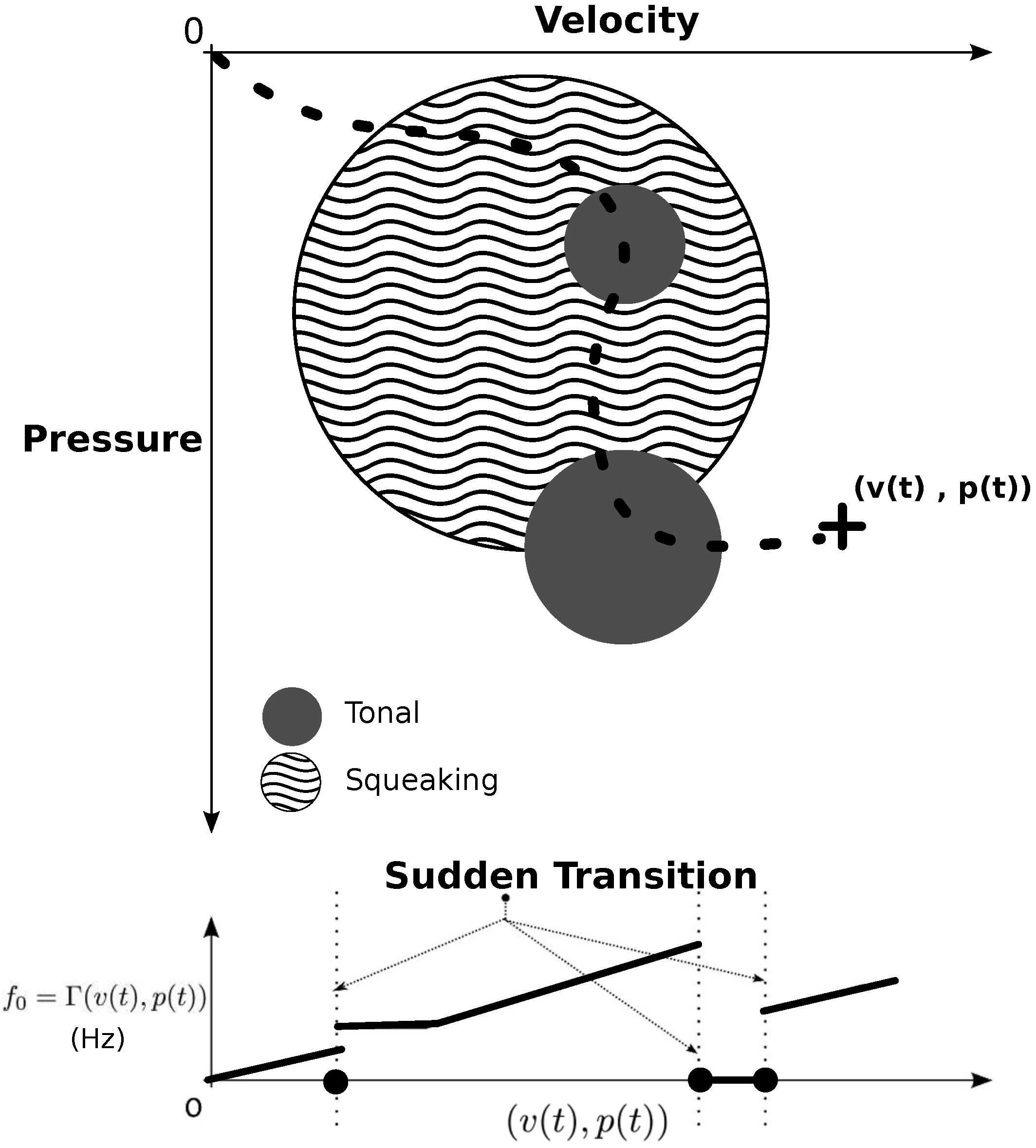
For instance, we defined the mapping function Γ between the dynamic descriptors
and the fundamental frequency
of the harmonic spectrum. The evolution of
with respect to Γ is freely tunable and enables the simulation of sudden transitions occurring in bowed string instruments. An example of the proposed space is presented in
Figure 7. This strategy fulfills the wanted requirements of flexibility. It enables to define behaviors which are theoretically not allowed by physics but that may be useful in the learning process. This mapping can further be adjusted with respect to the learning progress of a student.
3.3. Computer Animation
Most of the techniques used by current Foley artists are based on recorded samples which are triggered with the sound events occurring in the visual scene. Nevertheless, due to the use of pre-defined sound samples such techniques often lack of intrinsic timbre control and do not offer the possibility to precisely shape the sound continuously with respect to the user’s actions. For video games, the sample storage moreover occupies a lot of storage space and the graphical data often takes up most available resources. Our model offers the possibility to synthesize such sounds in real-time, to freely modify their timbre independently of physical constraints, and to directly link the dynamic parameters of visual events to the sound generating parameters. Above all, sound synthesis doesn’t use any data storage as sounds are directly generated on the fly. An example of such a control is available online [
22,
35].
In this context, a novel framework for interactive synthesis of solid sounds driven by a game engine has been developed in [
36]. This work highlights the possibilities offered by the so-called “procedural audio” generation aiming at replacing the use of pre-recorded samples for sound effects. Such a tool is particularly adapted to handle evolutive and interactive situations like morphing or continuous transitions between objects and/or actions. Practically, a game engine in which the virtual scene is designed drives the sound synthesizer. The mapping between the visual and the sound parameters is defined so that the audio-visual coherency of the global scene is respected. Friction sounds like squeaking vessels or singing glasses constitute relevant cases to highlight interactive situations for which the user’s actions have to be taken into account in a continuous way. An example of such an application to computer animation is available online [
37].
The implemented sound model is able to smoothly transform rubbing sounds into squeaking or tonal sounds. The different regimes are reached with respect to the velocity value of the user’s gesture. The squeaky effect is obtained by setting the filters so as to obtain a harmonic comb filter whose frequencies fluctuate with time. These random fluctuations happen around mean values which can be subject to sudden jumps depending on physical parameters of the interaction for example the relative speed and the normal force. Tonal source signals are obtained using a stationary and possibly inharmonic filter bank whose frequencies correspond to natural frequencies of the vibrating solid. An amplitude modulation is also added to the source signal. The transformation between rubbing and squeaking is achieved by a continuous increase of the filters’ gain. A smooth transformation from squeaking to tonal is obtained by progressively moving the filters’ frequencies from the frequencies of squeaking to natural frequencies of the solid. Simultaneously, the amplitude of the filter bank’s frequency jitter is progressively brought to zero while the depth of the amplitude modulation is smoothly increased from zero to its maximal value.
4. Conclusions and Perspectives
In this article, a sound synthesis model of nonlinear friction sounds is proposed. Based on perceptual considerations, this model enables to elude physical considerations and to intuitively control and morph between the different friction behaviors. In particular, it enables to separately simulate actions and objects, in order to generate sounds that perceptually evoke different interactions, e.g., squeaking and singing combined with different objects. Various applications of these tools are proposed such as the auditory guidance of gestures for the rehabilitation of motor diseases, learning processes of expert musical gestures and sounds for video games.
The proposed model achieves the initial goal of control flexibility for the desired applications. Some improvements can nevertheless be envisaged. Concerning the synthesis models, it would be interesting to make further signal analyses on recorded sounds in order to define specific amplitude and frequency modulation laws for the different nonlinear behaviors. Moreover, in the case of bowing sounds, this model only takes into account the string vibrations and doesn’t encompass the modeling of the body resonances of the instrument. These latter could be modeled by adding a filter bank to the output of the actual model and set up the filter parameters according to the modes and resonances of the instrument. It might also be of interest to provide a vibrato control. This could easily be achieved by defining a specific frequency modulation law of the fundamental frequency corresponding to such specific behaviors.
One other improvement of the synthesis model would be to give the possibility to simulate spectral behaviors such as multi-harmonic behaviors involved for instance in brake squeal sounds [
38]. As implemented here, the synthesis model only enables to synthesize purely harmonic spectra. Nevertheless it is still possible to synthesize multi-harmonic spectral contents by changing the general definition of the additive model (cf. Equation (
2)). For example, by considering two fundamental frequencies
and
, a multi-harmonic set of partials can be defined by the following instantaneous frequencies:
, with
m and
k integers greater than or equal 0 [
38]. More generally, the additive synthesis method offers the possibility to define any kind of spectral behaviors involving a sum of sinusoidal partials as those involved in many physical situations such as brake squeals [
38,
39]. The main difficulty resides in the high level of understanding of these phenomena, which may involve deterministic chaotic variations, in order to define intuitive controls of these behaviors for naive users.
The architecture based on a source-filter implementation is interesting as it is computationally efficient and also provides a modularity between the source and the resonance contributions. In the situations presented in this paper the source signal was a white noise but nothing prevents the user from employing other textures to create metaphoric situations such as a flow of water to which the same filtering process is applied. This enables to create physically impossible combinations between actions and objects such as squeaking on a liquid surface. This way of crossing the excitation with a resonating material could be seen as a kind of perceptual cross-synthesis [
18,
40]. Here, the crossing is not made between signal parameters of the two sounds like amplitudes and phases, but by crossing acoustical invariants that are separately related to different evocations. Such unheard-of sounds may be used to develop new worlds of sounds controlled by musical interfaces based on semantic descriptions.
Finally, in order to completely validate the perceptual relevance of the synthesized sounds, perceptual evaluations are planned. Such evaluations will necessitate several steps of investigations that are not only related to the sound quality, but also to the control issues and in particular the mapping strategies that determine how the gestural control of the synthesizer should be adapted to human gestures for a given application and how multimodal issues should be taken into account.
Acknowledgments
The first author is thankful to Simon Conan for the wide discussions and advices concerning the model implementation. The authors are also thankful to Jocelyn Rozé and Thierry Voinier for providing the cello recording. This work was funded by the French National Research Agency (ANR) under the MetaSon project (ANR-10-CORD-0003) in the CONTINT 2010 framework, the Physis project (ANR-12-CORD-0006) in the CONTINT 2012 framework, and the SoniMove project (ANR-14-CE24-0018).
Author Contributions
The authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coulomb, C. The theory of simple machines. Mem. Math. Phys. Acad. 1785, 10, 4, ark:/12148/bpt6k1095299. [Google Scholar]
- Akay, A. Acoustics of friction. J. Acoust. Soc. Am. 2002, 111, 1525–1548. [Google Scholar] [CrossRef] [PubMed]
- Avanzini, F.; Serafin, S.; Rocchesso, D. Interactive simulation of rigid body interaction with friction-induced sound generation. IEEE Trans. Speech Audio Process. 2005, 13, 1073–1081. [Google Scholar] [CrossRef]
- Rath, M.; Rocchesso, D. Informative sonic feedback for continuous human-machine interaction—Controlling a sound model of a rolling ball. IEEE Multimed. Spec. Interac. Sonification 2004, 12, 60–69. [Google Scholar] [CrossRef]
- Serafin, S. The Sound of Friction: Real-Time Models, Playability and Musical Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, June 2004. [Google Scholar]
- Serafin, S.; Huang, P.; Ystad, S.; Chafe, C.; Smith, J.O. Analysis and synthesis unusual friction-driven musical instruments. In Proceedings of the International Computer Music Conference, Gothenburg, Sweden, 16–21 September 2002.
- Woodhouse, J.; Galluzzo, P.M. The bowed string as we know it today. Acta Acust. United Acust. 2004, 90, 579–589. [Google Scholar]
- Maestre, E.; Spa, C.; Smith, J.O. A bowed string physical model including finite-width thermal friction and hair dynamics. In Proceedings of the Joint International Computer Music Conference and Sound and Music Computing, Athens, Greece, 14–20 September 2014.
- Van Den Doel, K.; Kry, P.G.; Pai, D.K. FoleyAutomatic: Physically-based sound effects for interactive simulation and animation. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2008; pp. 537–544.
- Gibson, J.J. The Senses Considered as Perceptual Systems; Houghton Mifflin: Oxford, UK, 1966. [Google Scholar]
- McAdams, S.E.; Bigand, E.E. Thinking in Sound: The Cognitive Psychology of Human Audition; Clarendon Press/Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Gaver, W.W. How do we hear in the world? Explorations in ecological acoustics. Ecol. Psychol. 1993, 5, 285–313. [Google Scholar] [CrossRef]
- Gaver, W.W. What in the world do we hear?: An ecological approach to auditory event perception. Ecol. Psychol. 1993, 5, 1–29. [Google Scholar] [CrossRef]
- Wildes, R.P.; Richards, W.A. Recovering material properties from sound. In Natural Computation; Richards, W.A., Ed.; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Aramaki, M.; Besson, M.; Kronland-Martinet, R.; Ystad, S. Controlling the perceived material in an impact sound synthesizer. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 301–314. [Google Scholar] [CrossRef]
- Conan, S.; Derrien, O.; Aramaki, M.; Ystad, S.; Kronland-Martinet, R. A synthesis model with intuitive control capabilities for rolling sounds. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1260–1273. [Google Scholar] [CrossRef]
- Conan, S.; Thoret, E.; Aramaki, M.; Derrien, O.; Gondre, C.; Ystad, S.; Kronland-Martinet, R. An Intuitive Synthesizer of Continuous-Interaction Sounds: Rubbing, Scratching, and Rolling. Comput. Music J. 2014, 38, 24–37. [Google Scholar] [CrossRef]
- Conan, S. Contrôle Intuitif de la Synthèse Sonore d’Interactions Solidiennes: Vers les Métaphores Sonores. Ph.D. Thesis, Ecole Centrale de Marseille, Marseille, France, December 2014. [Google Scholar]
- Thoret, E.; Aramaki, M.; Kronland-Martinet, R.; Velay, J.L.; Ystad, S. From sound to shape: Auditory perception of drawing movements. J. Exp. Psychol. Hum. Percept. Perform. 2014, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aramaki, M.; Kronland-Martinet, R. Analysis-synthesis of impact sounds by real-time dynamic filtering. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 695–705. [Google Scholar] [CrossRef]
- Thoret, E.; Aramaki, M.; Gondre, C.; Kronland-Martinet, R.; Ystad, S. Recorded Sounds. Available online: http://www.lma.cnrs-mrs.fr/%7ekronland/thoretDAFx2013/ (accessed on 22 June 2016).
- Thoret, E.; Aramaki, M.; Gondre, C.; Kronland-Martinet, R.; Ystad, S. Controlling a non linear friction model for evocative sound synthesis applications. In Proceedings of the 16th International Conference on Digital Audio Effects (DAFx), Maynooth, Ireland, 2–5 September 2013.
- Ellis, D.P.W. Sinewave and Sinusoid + Noise Analysis/Synthesis in Matlab. Available online: http://www.ee.columbia.edu/%7edpwe/resources/matlab/sinemodel/ (accessed on 13 March 2015).
- Rossing, T.D. Acoustics of the glass harmonica. J. Acoust. Soc. Am. 1994, 95, 1106–1111. [Google Scholar] [CrossRef]
- Inácio, O.; Henrique, L.L.; Antunes, J. The dynamics of tibetan singing bowls. Acta Acust. United Acust. 2006, 92, 637–653. [Google Scholar]
- Aramaki, M.; Gondre, C.; Kronland-Martinet, R.; Voinier, T.; Ystad, S. Imagine the sounds: An intuitive control of an impact sound synthesizer. In Auditory Display; Ystad, S., Aramaki, M., Kronland-Martinet, R., Jensen, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rabiner, L.R.; Gold, B. Theory and Application of Digital Signal Processing; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Atal, B.S.; Hanauer, S.L. Speech analysis and synthesis by linear prediction of the speech wave. J. Acoust. Soc. Am. 1971, 50, 637–655. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, J.L.; Coker, C.; Rabiner, L.; Schafer, R.W.; Umeda, N. Synthetic voices for computers. IEEE Spectr. 1970, 7, 22–45. [Google Scholar] [CrossRef]
- Mathews, M.; Smith, J.O. Methods for synthesizing very high Q parametrically well behaved two pole filters. In Proceedings of the Stockholm Musical Acoustic Conference (SMAC), Stockholm, Sweden, 6–9 August 2003.
- Danna, J.; Fontaine, M.; Paz-Villagrán, V.; Gondre, C.; Thoret, E.; Aramaki, M.; Kronland-Martinet, R.; Ystad, S.; Velay, J.L. The effect of real-time auditory feedback on learning new characters. Hum. Mov. Sci. 2015, 43, 216–228. [Google Scholar] [CrossRef] [PubMed]
- Danna, J.; Fontaine, M.; Paz-Villagrán, V.; Gondre, C.; Thoret, E.; Aramaki, M.; Kronland-Martinet, R.; Ystad, S.; Velay, J.L. Example of Learning Session. Available online: http://www.lma.cnrs-mrs.fr/%7ekronland/TheseEThoret/content/flv/chap5/newCharacters.mp4 (accessed on 22 June 2016).
- Danna, J.; Paz-Villagrán, V.; Velay, J.L. Signal-to-Noise velocity peaks difference: A new method for evaluating the handwriting movement fluency in children with dysgraphia. Res. Dev. Disabil. 2013, 34, 4375–4384. [Google Scholar] [CrossRef] [PubMed]
- Danna, J.; Paz-Villagrán, V.; Capel, A.; Pétroz, C.; Gondre, C.; Pinto, S.; Thoret, E.; Aramaki, M.; Ystad, S.; Kronland-Martinet, R.; et al. Movement Sonification for the Diagnosis and the Rehabilitation of Graphomotor Disorders. In Sound, Music, and Motion; Aramaki, M., Derrien, O., Kronland-Martinet, R., Ystad, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Thoret, E.; Aramaki, M.; Gondre, C.; Kronland-Martinet, R.; Ystad, S. Example of Intuitive Control of Non Linear Friction Sounds. Available online: http://www.lma.cnrs-mrs.fr/%7ekronland/thoretDAFx2013/content/video/Thoretdafx2013.mp4 (accessed on 22 June 2016).
- Pruvost, L.; Scherrer, B.; Aramaki, M.; Ystad, S.; Kronland-Martinet, R. Perception-based interactive sound synthesis of morphing solids’ interactions. In Proceedings of the SIGGRAPH Asia 2015 Technical Briefs, Kobe, Japan, 2–5 November 2015; p. 17.
- Pruvost, L.; Scherrer, B.; Aramaki, M.; Ystad, S.; Kronland-Martinet, R. Example of Application to Computer Animation. Available online: http://www.lma.cnrs-mrs.fr/%7ekronland/siggraph2015/index.html (accessed on 22 June 2016).
- Sinou, J.J. Transient non-linear dynamic analysis of automotive disc brake squeal—On the need to consider both stability and non-linear analysis. Mech. Res. Commun. 2010, 37, 96–105. [Google Scholar] [CrossRef]
- Oberst, S.; Lai, J. Statistical analysis of brake squeal noise. J. Sound Vib. 2011, 330, 2978–2994. [Google Scholar] [CrossRef]
- Smith, J. Cross-Synthesis—CCRMA. Available online: https://ccrma.stanford.edu/%7ejos/sasp/Cross_Synthesis.html (accessed on 13 March 2015).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).