Coupling Motion and Energy Harvesting of Two Side-by-Side Flexible Plates in a 3D Uniform Flow
Abstract
:1. Introduction
2. Physical Problem and Numerical Methods
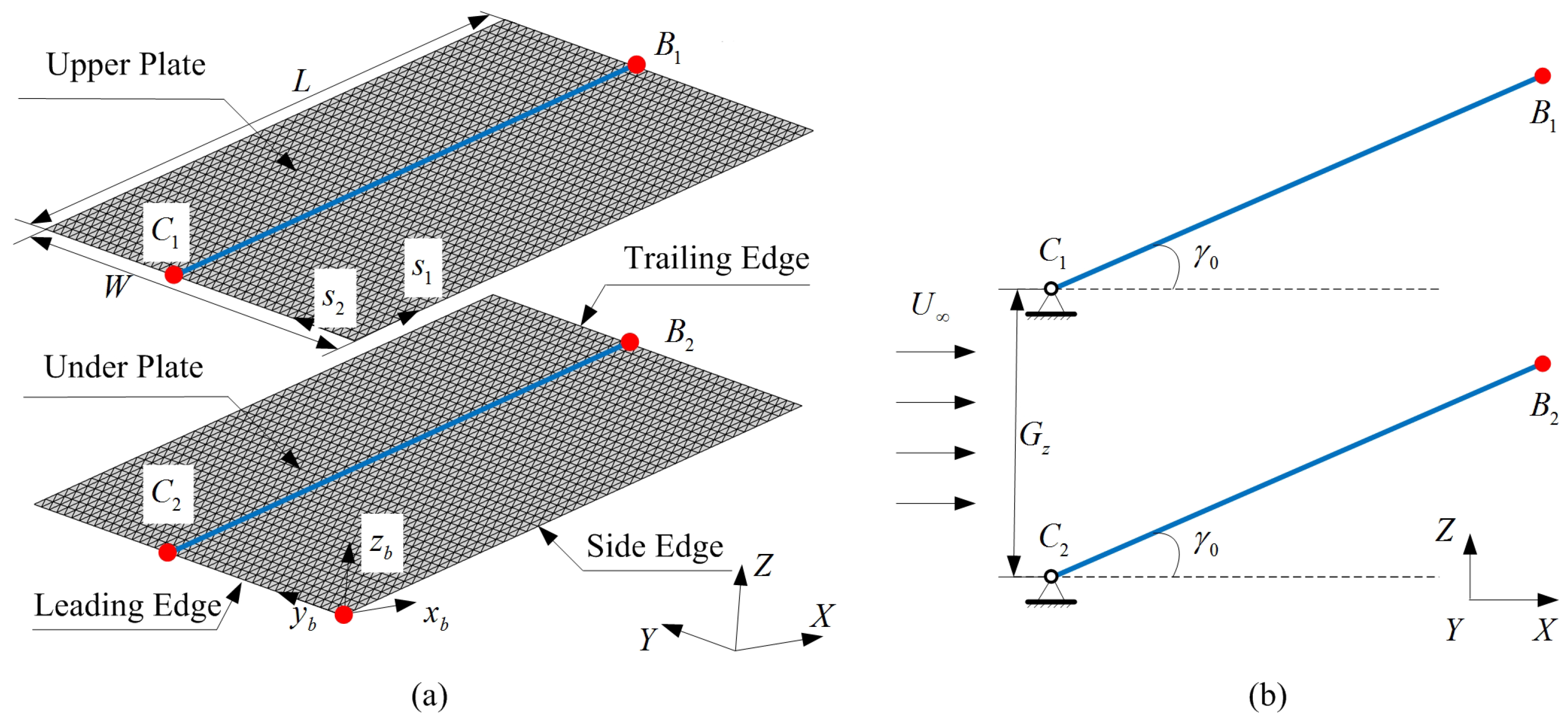
2.1. Physical Problem
2.2. Numerical Methods
2.2.1. Mathematical Formulation
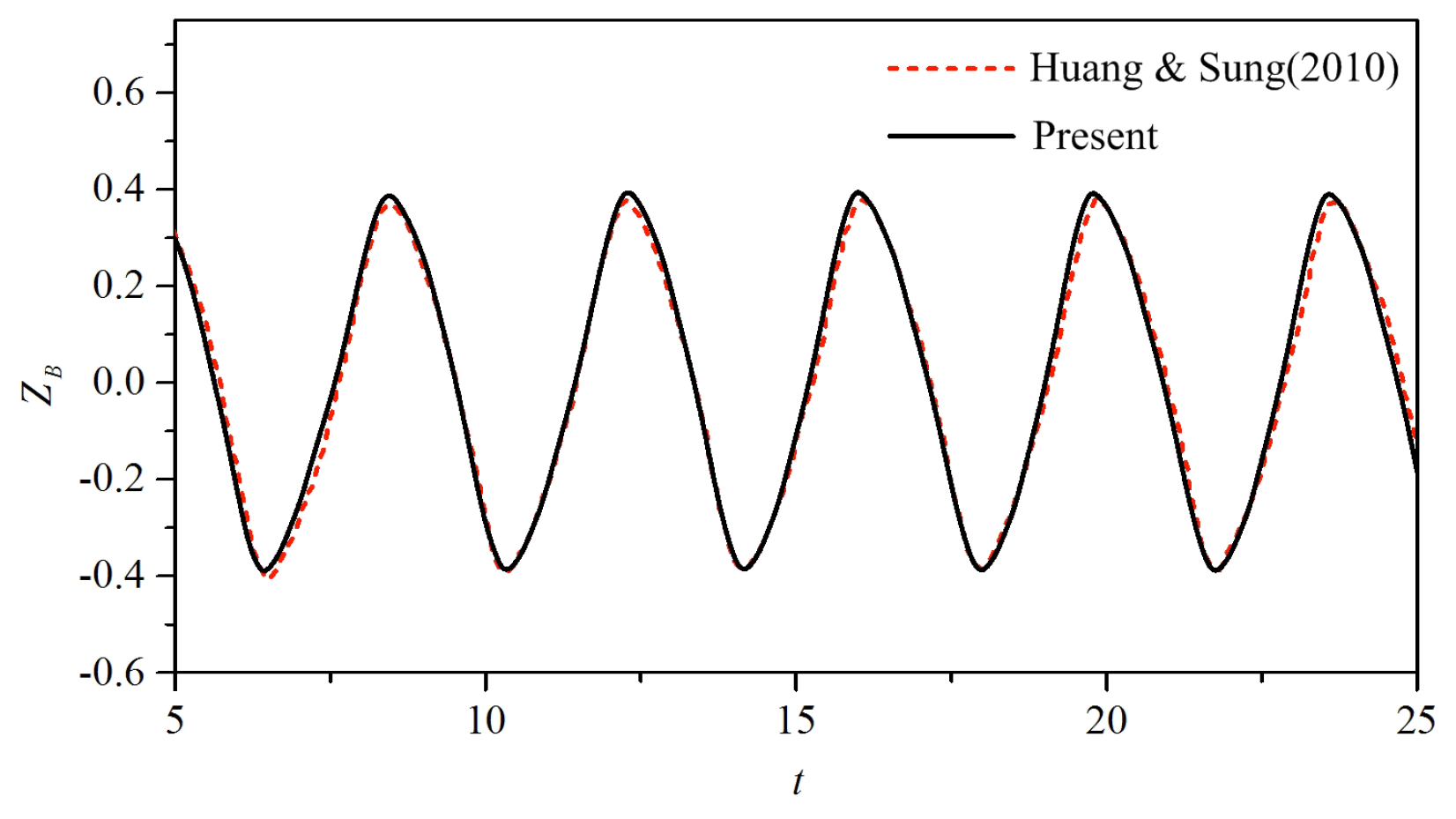
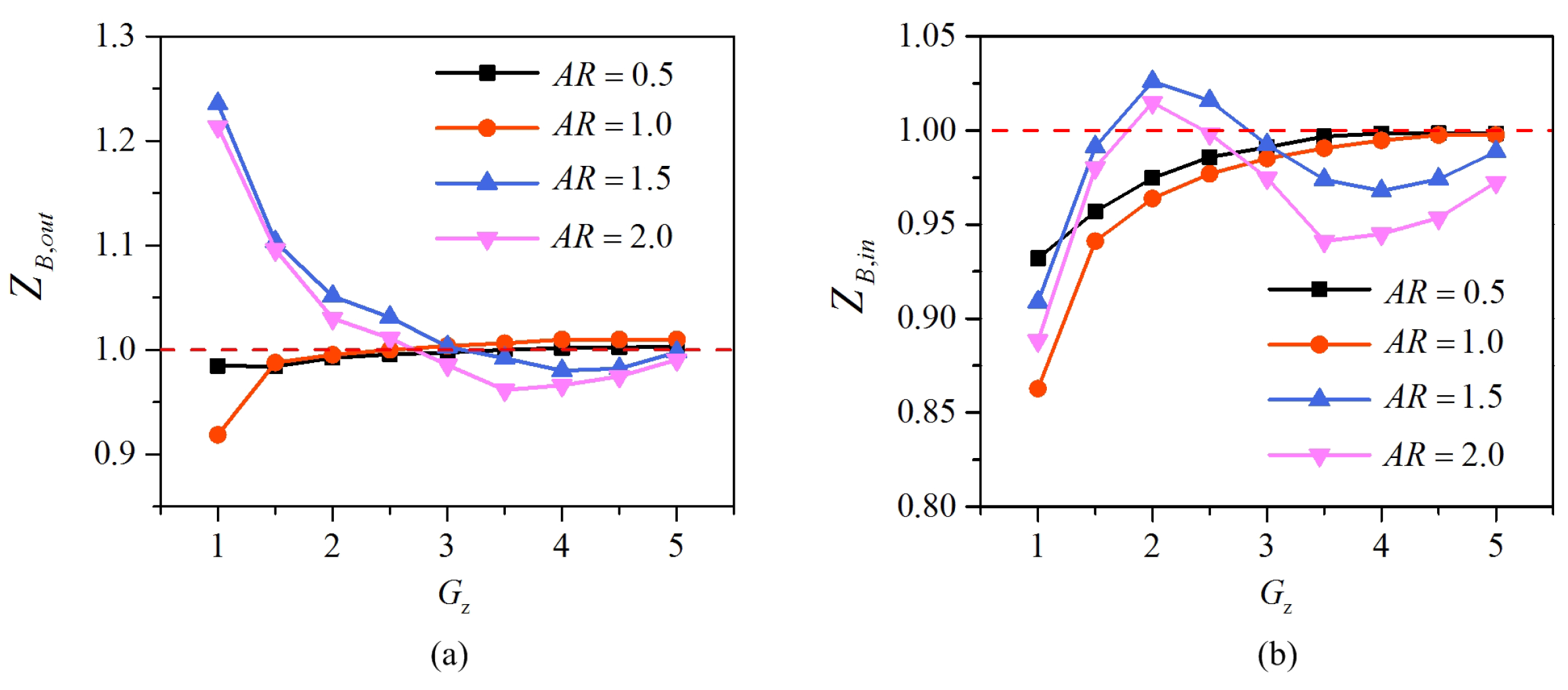
2.2.2. Validation
3. Results and Discussion
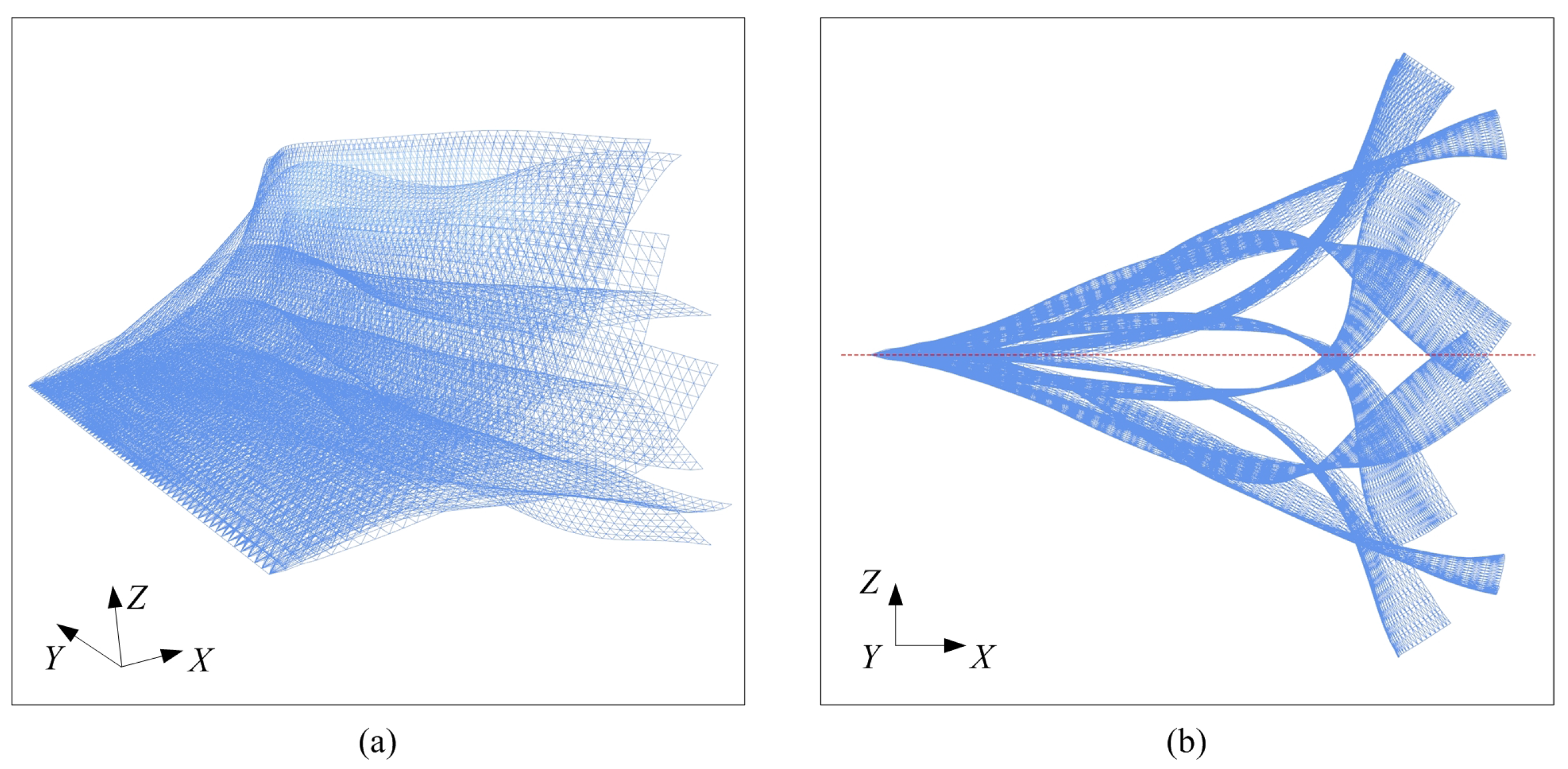
3.1. Flow around an Isolated Flexible Plate
3.2. Flow around Two Flexible Plates in Side-by-Side Arrangement
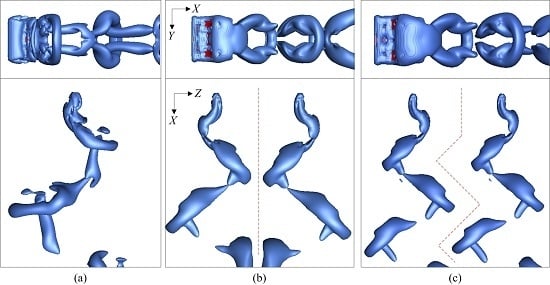
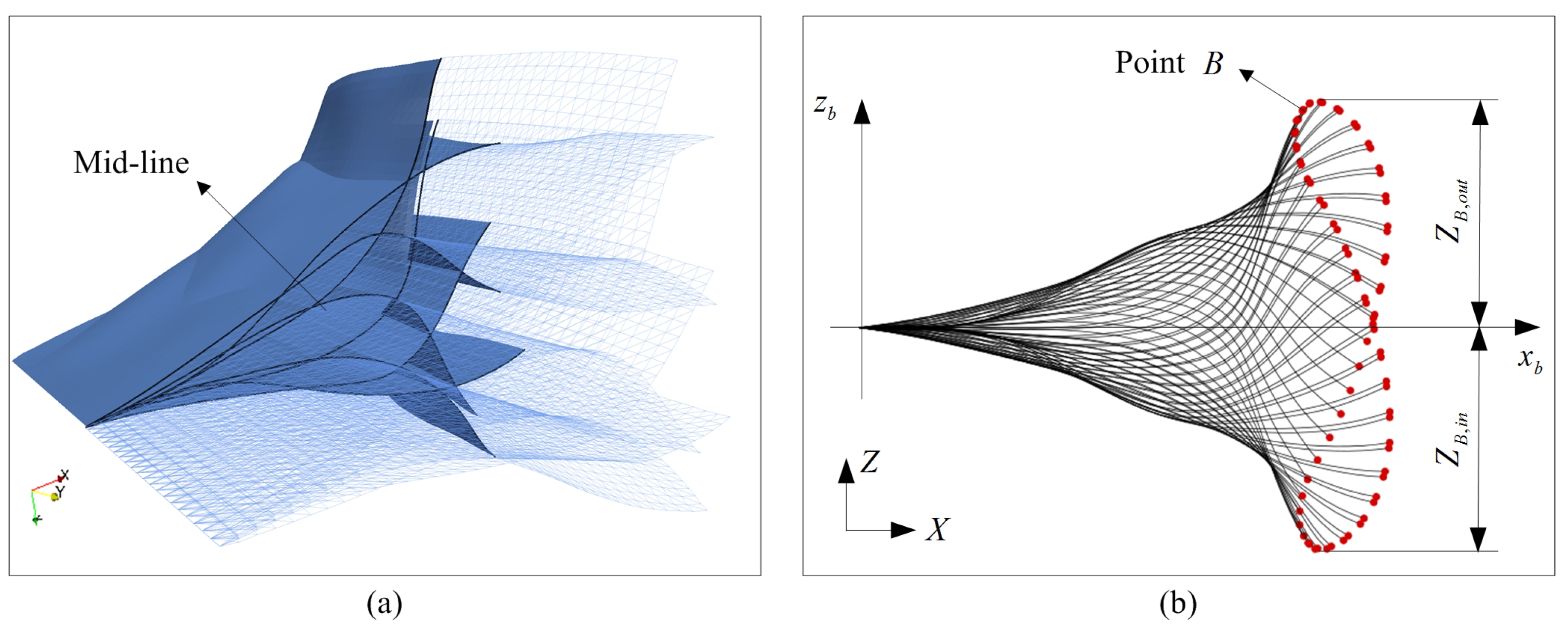
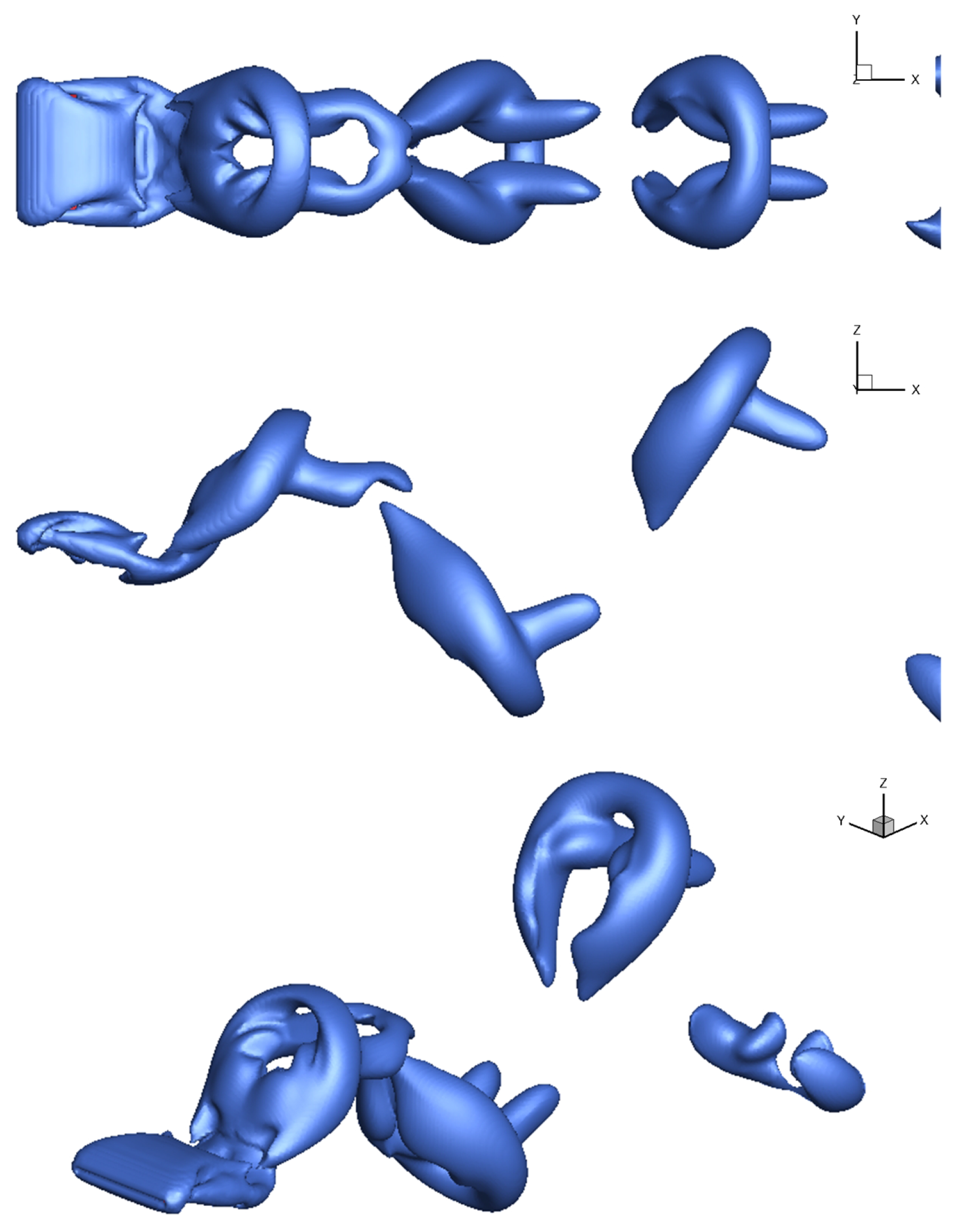
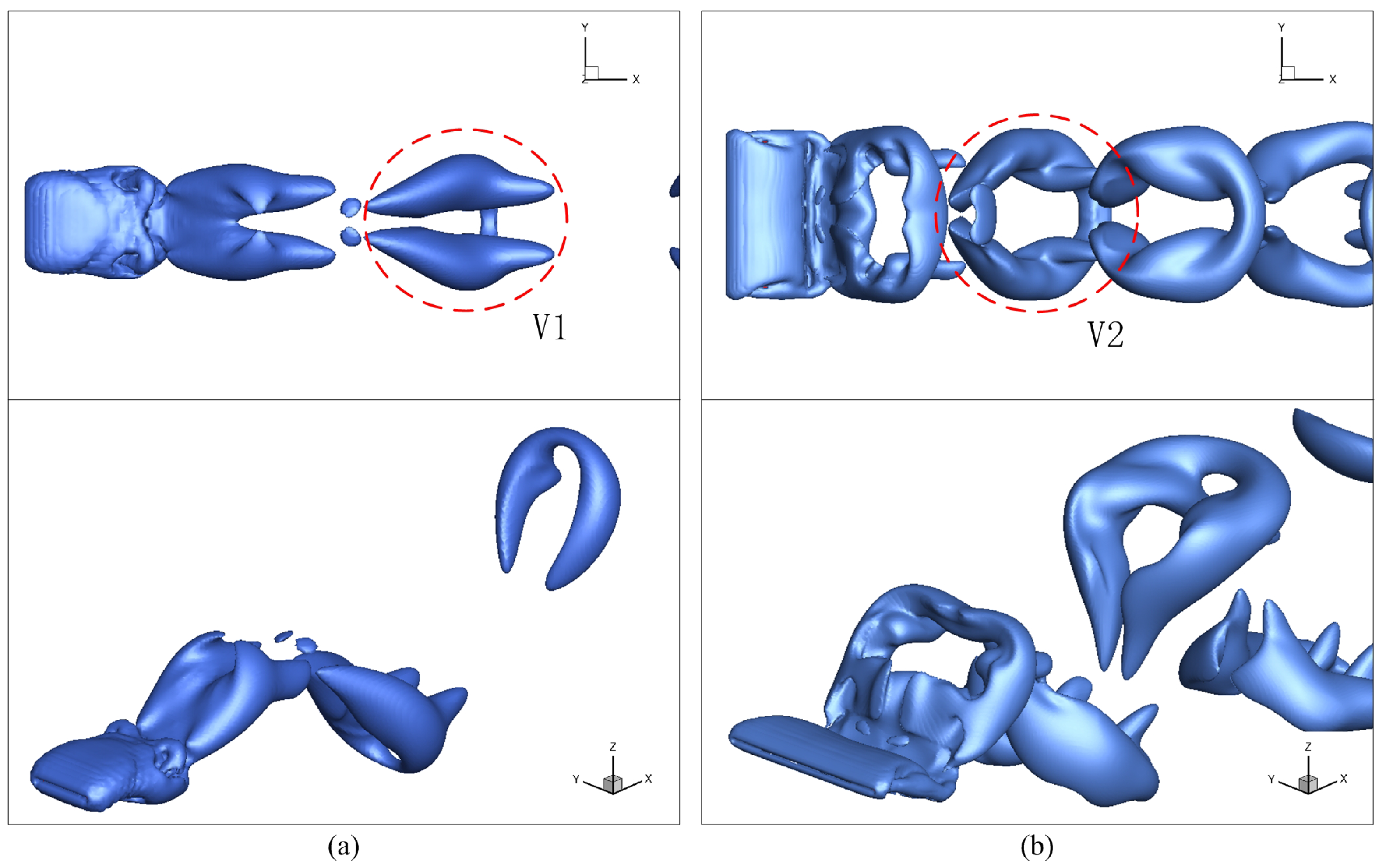
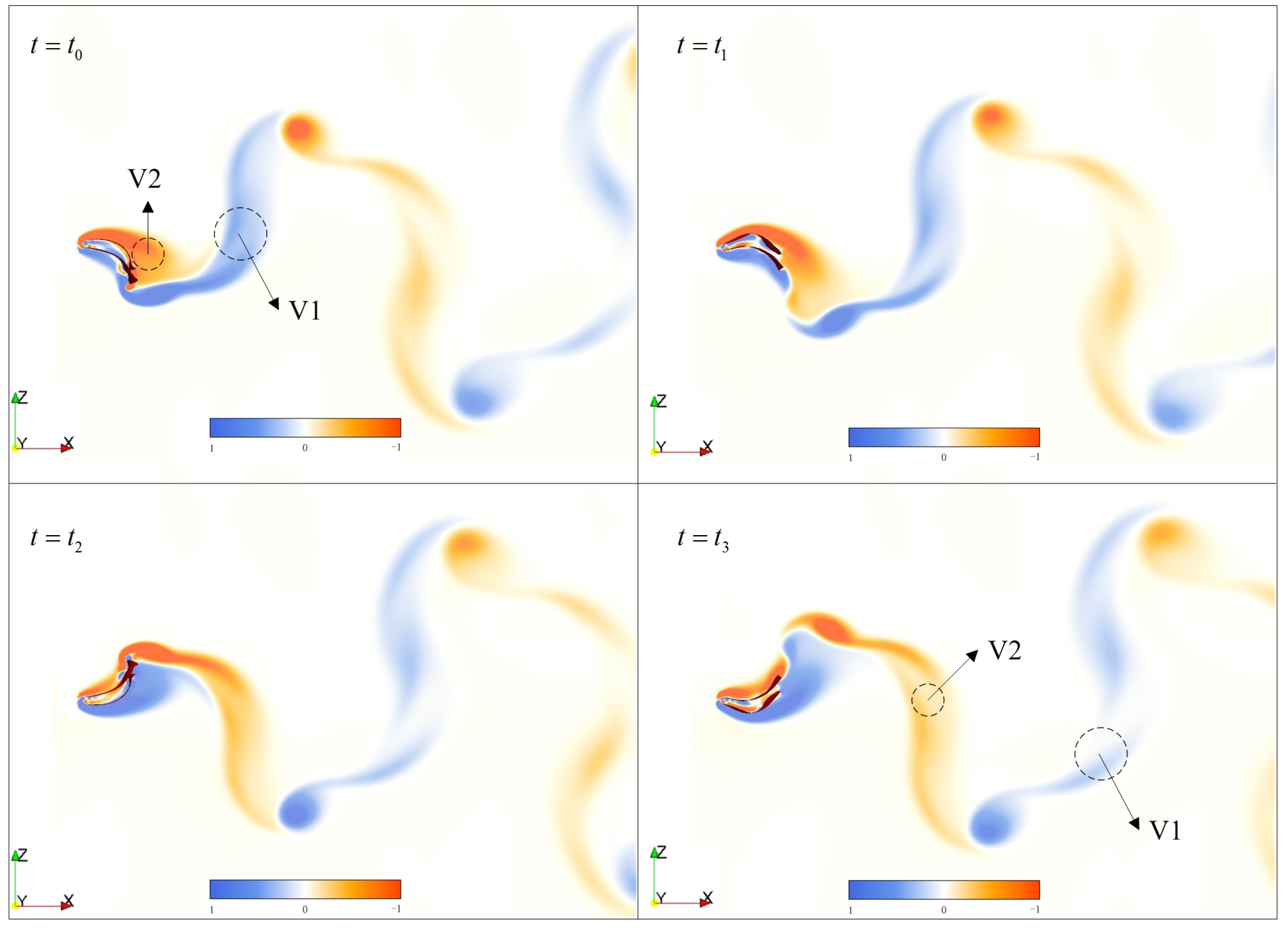
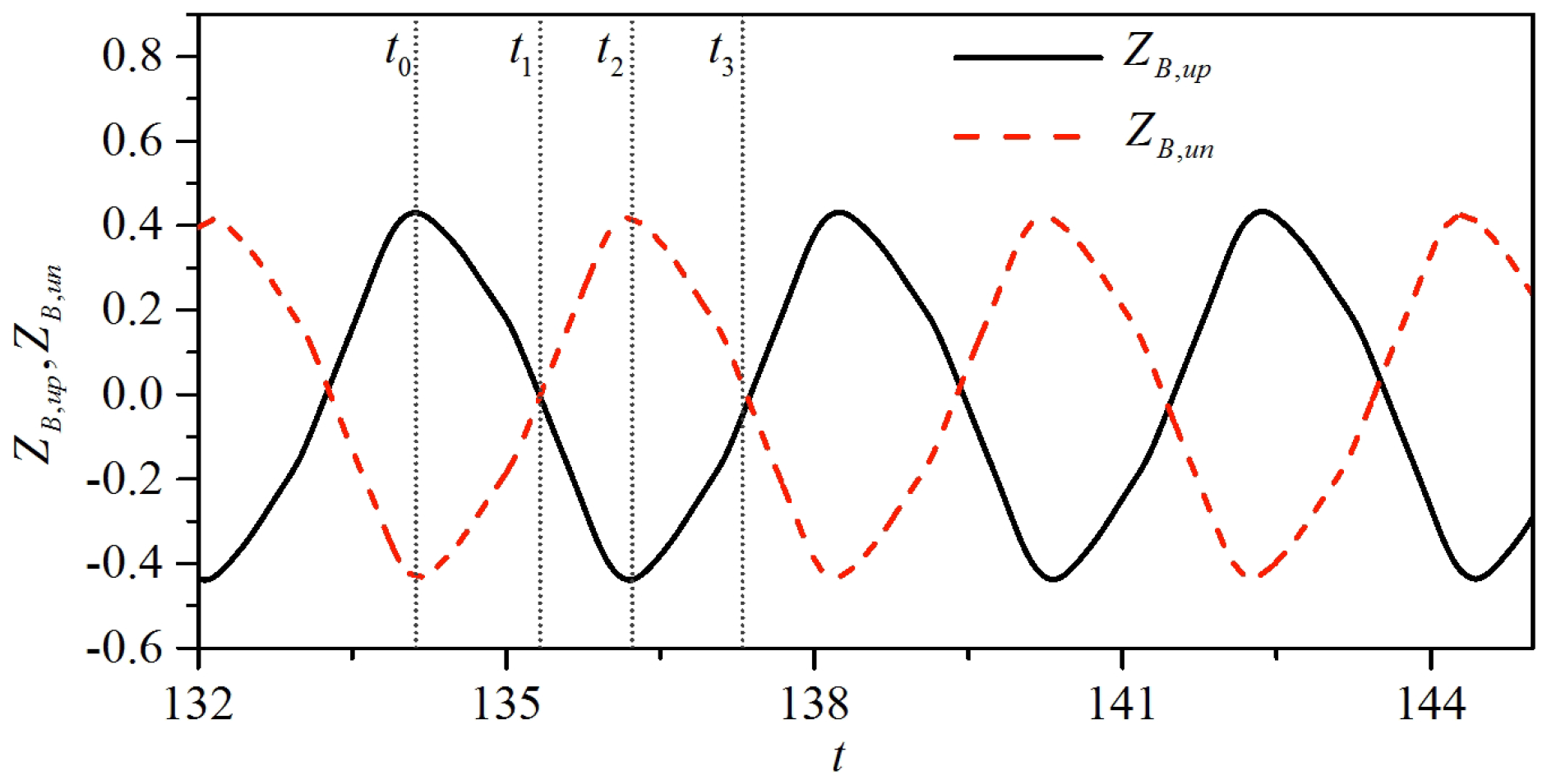
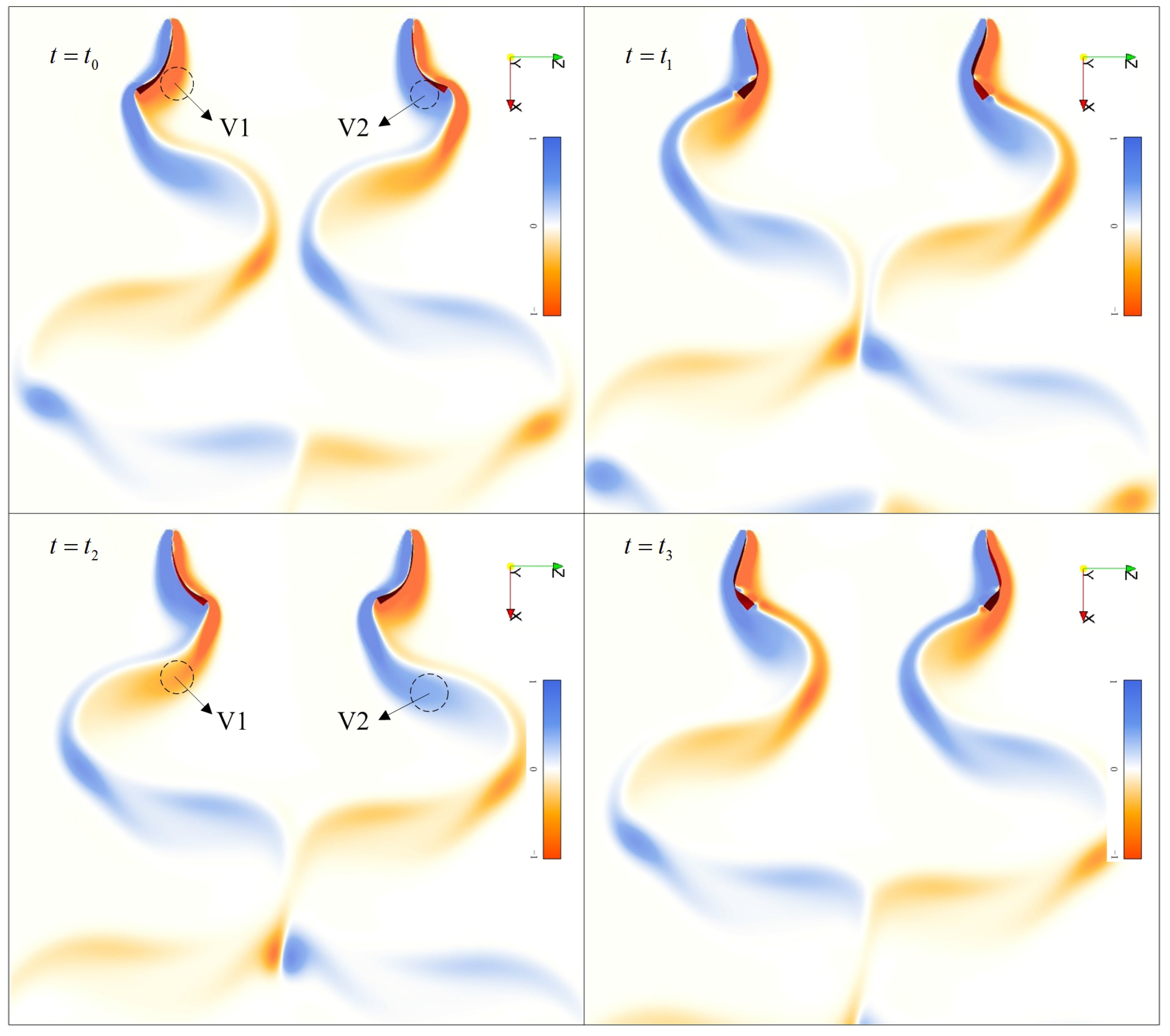
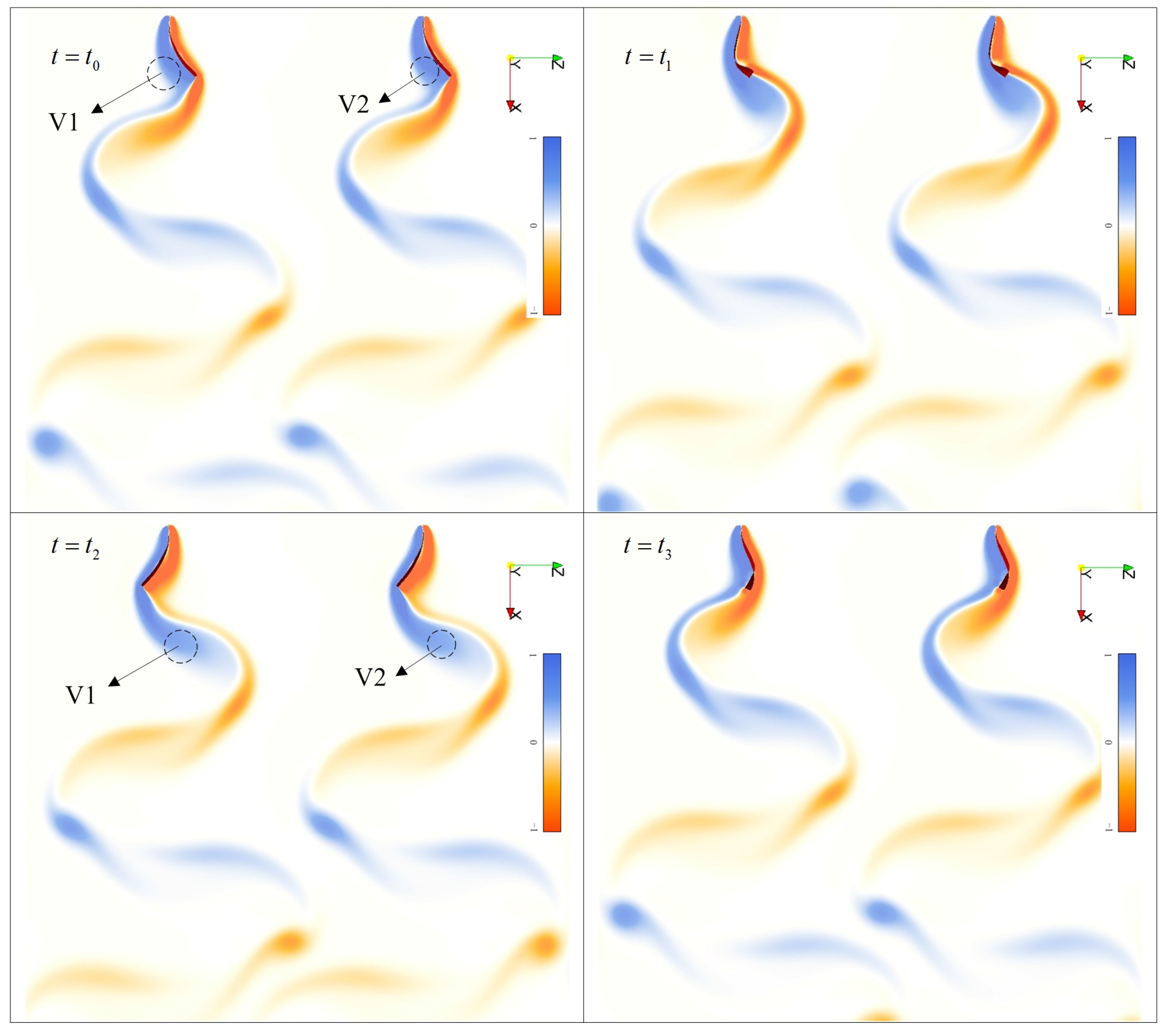
3.2.1. Coupling Motions and Vortical Structures
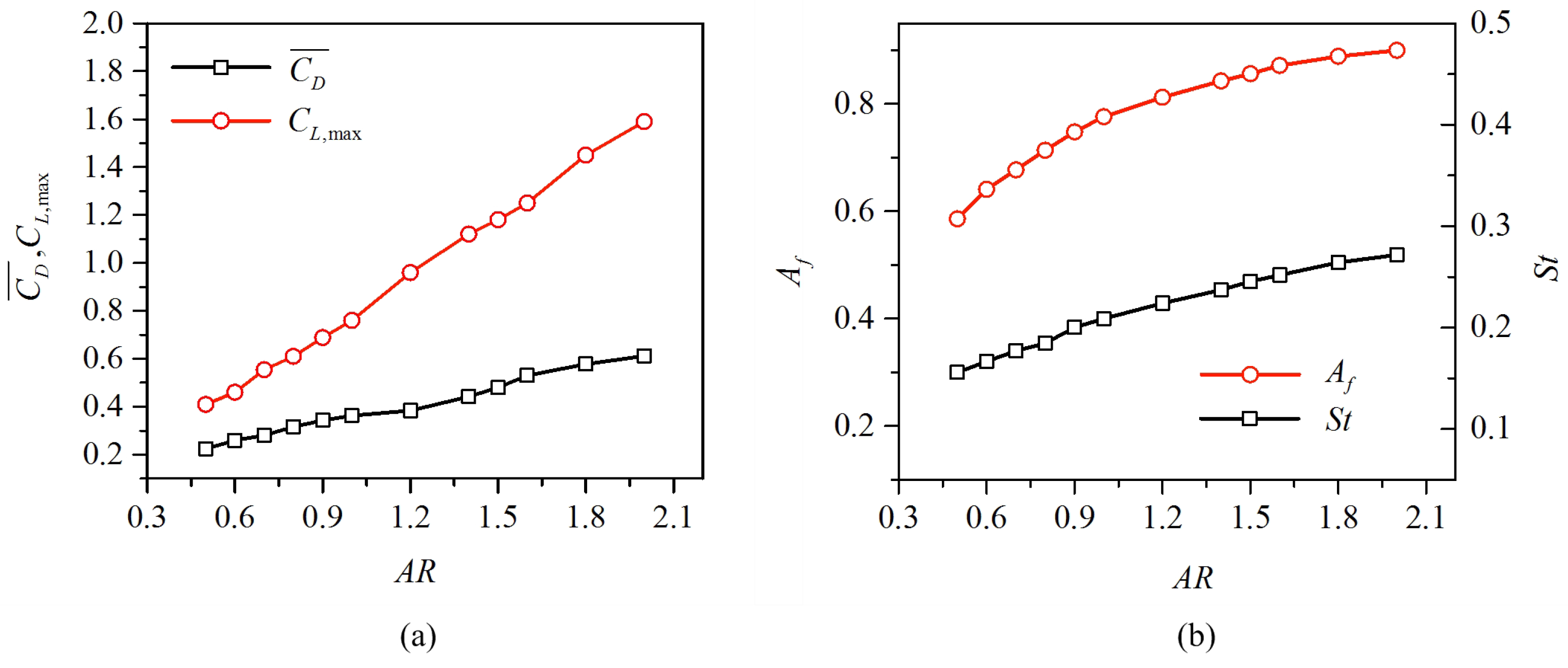
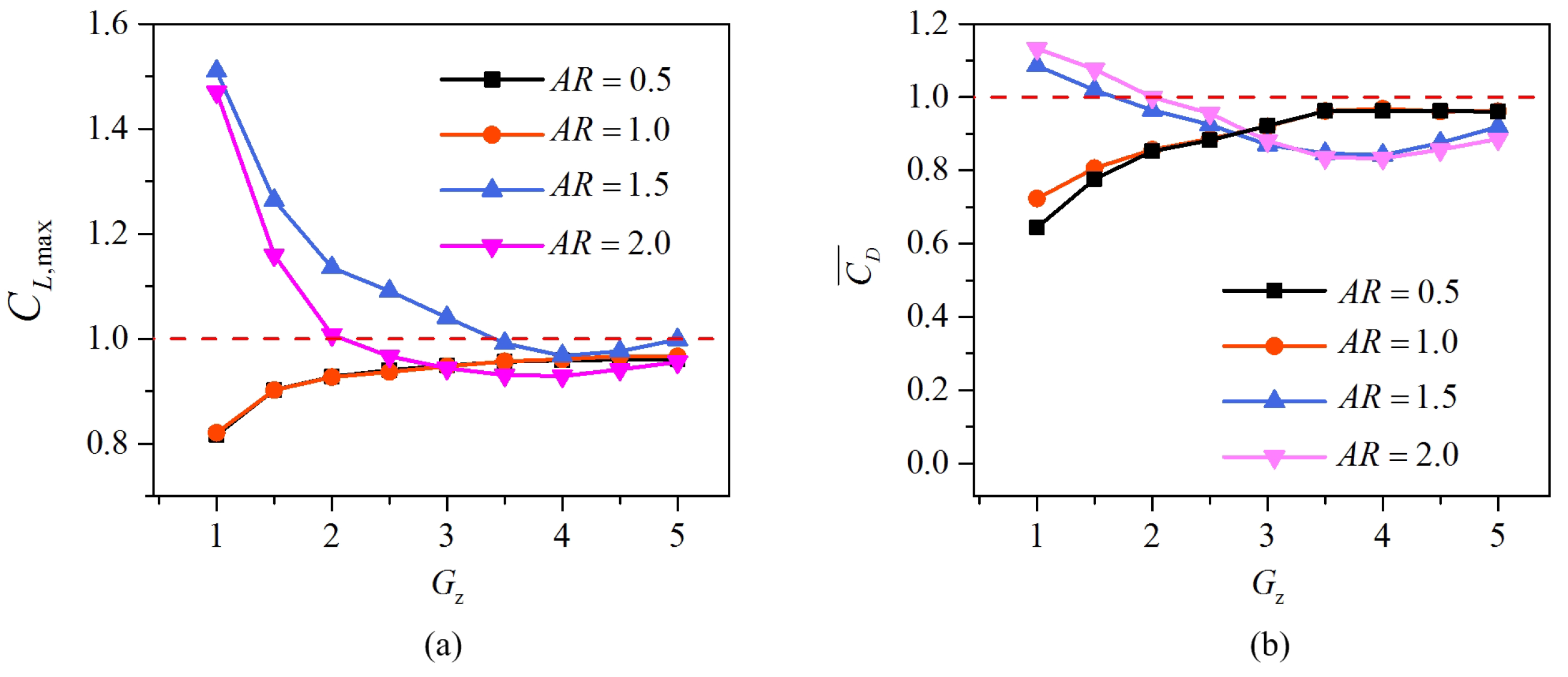
3.2.2. Force and Energy Conversion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vogel, S. Drag and reconfiguration of broad leaves in high winds. J. Exp. Bot. 1989, 40, 941–948. [Google Scholar] [CrossRef]
- Tadrist, L.; Julio, K.; Saudreau, M.; de Langre, E. Leaf flutter by torsional galloping: Experiments and model. J. Fluids Struct. 2015, 56, 1–10. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Triantafyllou, G.; Yue, D. Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Gazzola, M.; Argentina, M.; Mahadevan, L. Scaling macroscopic aquatic locomotion. Nat. Phys. 2014, 10, 758–761. [Google Scholar] [CrossRef]
- Lauder, G.V. Fish locomotion: Recent advances and new directions. Annu. Rev. Mar. Sci. 2015, 7, 521–545. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish exploiting vortices decrease muscle activity. Science 2003, 302, 1566–1569. [Google Scholar] [CrossRef] [PubMed]
- Beal, D.; Hover, F.; Triantafyllou, M.; Liao, J.; Lauder, G. Passive propulsion in vortex wakes. J. Fluid Mech. 2006, 549, 385–402. [Google Scholar] [CrossRef]
- Eldredge, J.D.; Pisani, D. Passive locomotion of a simple articulated fish-like system in the wake of an obstacle. J. Fluid Mech. 2008, 607, 279–288. [Google Scholar] [CrossRef]
- Lauder, G.V.; Anderson, E.J.; Tangorra, J.; Madden, P.G. Fish biorobotics: Kinematics and hydrodynamics of self-propulsion. J. Exp. Biol. 2007, 210, 2767–2780. [Google Scholar] [CrossRef] [PubMed]
- Kopman, V.; Laut, J.; Acquaviva, F.; Rizzo, A.; Porfiri, M. Dynamic modeling of a robotic fish propelled by a compliant tail. IEEE J. Ocean. Eng. 2015, 40, 209–221. [Google Scholar] [CrossRef]
- Giorgio-Serchi, F.; Arienti, A.; Laschi, C. Underwater soft-bodied pulsed-jet thrusters: Actuator modeling and performance profiling. Int. J. Robot. Res. 2016. [Google Scholar] [CrossRef]
- Ornes, S. Inner Workings: A soft robot that swims like a fish. Proc. Natl. Acad. Sci. 2014, 111. [Google Scholar] [CrossRef] [PubMed]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Bi, S.; Zheng, L. Design and experiments of a robotic fish imitating cow-nosed ray. J. Bionic Eng. 2010, 7, 120–126. [Google Scholar] [CrossRef]
- Moored, K.; Dewey, P.; Smits, A.; Haj-Hariri, H. Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J. Fluid Mech. 2012, 708, 329–348. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, J.; Zhao, D. Design and Experiment on a Biomimetic Robotic Fish Inspired by Freshwater Stingray. J. Bionic Eng. 2015, 12, 204–216. [Google Scholar] [CrossRef]
- Allen, J.; Smits, A. Energy harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Purohit, A.; Darpe, A.K.; Singh, S. Experimental investigations on flow induced vibration of an externally excited flexible plate. J. Sound Vib. 2016, 371, 237–251. [Google Scholar] [CrossRef]
- McCarthy, J.; Watkins, S.; Deivasigamani, A.; John, S. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Taneda, S. Waving motions of flags. J. Phys. Soc. Jpn. 1968, 24, 392–401. [Google Scholar] [CrossRef]
- Turek, S.; Hron, J.; Razzaq, M. Numerical benchmarking of fluid-structure interaction between elastic object and laminar incompressible flow. Available online: http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/TurekHron2006b.pdf (accessed on 10 May 2016).
- Zhu, L.; Peskin, C.S. Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 2002, 179, 452–468. [Google Scholar] [CrossRef]
- Connell, B.S.; Yue, D.K. Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 2007, 581, 33–67. [Google Scholar] [CrossRef]
- Alben, S.; Shelley, M.J. Flapping states of a flag in an inviscid fluid: Bistability and the transition to chaos. Phys. Rev. Lett. 2008, 100, 074301. [Google Scholar] [CrossRef] [PubMed]
- Favier, J.; Revell, A.; Pinelli, A. Numerical study of flapping filaments in a uniform fluid flow. J. Fluids Struct. 2015, 53, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Farnell, D.J.; David, T.; Barton, D. Coupled states of flapping flags. J. Fluids Struct. 2004, 19, 29–36. [Google Scholar] [CrossRef]
- Alben, S. Wake-mediated synchronization and drafting in coupled flags. J. Fluid Mech. 2009, 641, 489–496. [Google Scholar] [CrossRef]
- Sun, C.; Wang, S.; Jia, L.; Yin, X. Force measurement on coupled flapping flags in uniform flow. J. Fluids Struct. 2016, 61, 339–346. [Google Scholar] [CrossRef]
- Daghooghi, M.; Borazjani, I. The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 2015, 10, 056018. [Google Scholar] [CrossRef] [PubMed]
- Hemelrijk, C.; Reid, D.; Hildenbrandt, H.; Padding, J. The increased efficiency of fish swimming in a school. Fish Fish. 2015, 16, 511–521. [Google Scholar] [CrossRef]
- Huang, W.X.; Sung, H.J. Three-dimensional simulation of a flapping flag in a uniform flow. J. Fluid Mech. 2010, 653, 301–336. [Google Scholar] [CrossRef]
- Lee, I.; Choi, H. A discrete-forcing immersed boundary method for the fluid–structure interaction of an elastic slender body. J. Comput. Phys. 2015, 280, 529–546. [Google Scholar] [CrossRef]
- Zhu, X.; He, G.; Zhang, X. An improved direct-forcing immersed boundary method for fluid-structure interaction simulations. J. Fluids Eng. 2014, 136, 040903. [Google Scholar] [CrossRef]
- Kim, Y.; Peskin, C.S. Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 2007, 19, 053103. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Doyle, J.F. Static and Dynamic Analysis of Structures: With an Emphasis on Mechanics and Computer Matrix Methods; Springer Science & Business Media: Berlin, Germany, 2012; Volume 6. [Google Scholar]
- Doyle, J.F. Nonlinear Analysis of Thin-Walled Structures: Statics, Dynamics, and Stability; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Hua, R.N.; Zhu, L.; Lu, X.Y. Dynamics of fluid flow over a circular flexible plate. J. Fluid Mech. 2014, 759, 56–72. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL (Europhys. Lett.) 1992, 17. [Google Scholar] [CrossRef]
- Trizila, P.; Kang, C.K.; Aono, H.; Shyy, W.; Visbal, M. Low-Reynolds-number aerodynamics of a flapping rigid flat plate. AIAA J. 2011, 49, 806–823. [Google Scholar] [CrossRef]
- Suryadi, A.; Ishii, T.; Obi, S. Stereo PIV measurement of a finite, flapping rigid plate in hovering condition. Exp. Fluids 2010, 49, 447–460. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, J.; Chen, W. Numerical Study on Hydrodynamic Performance of Bionic Caudal Fin. Appl. Sci. 2016, 6. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Izraelevitz, J.S.; Triantafyllou, M.S. Adding in-line motion and model-based optimization offers exceptional force control authority in flapping foils. J. Fluid Mech. 2014, 742, 5–34. [Google Scholar] [CrossRef]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Dabiri, J.O.; Gharib, M. The role of optimal vortex formation in biological fluid transport. Proc. R. Soc. Lond. B Biol. Sci. 2005, 272, 1557–1560. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Cossé, J.; Cerdeira, C.H.; Gharib, M. Flapping dynamics of an inverted flag. J. Fluid Mech. 2013, 736. [Google Scholar] [CrossRef]






© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, D.; Chen, W.; Shi, S. Coupling Motion and Energy Harvesting of Two Side-by-Side Flexible Plates in a 3D Uniform Flow. Appl. Sci. 2016, 6, 141. https://doi.org/10.3390/app6050141
Dong D, Chen W, Shi S. Coupling Motion and Energy Harvesting of Two Side-by-Side Flexible Plates in a 3D Uniform Flow. Applied Sciences. 2016; 6(5):141. https://doi.org/10.3390/app6050141
Chicago/Turabian StyleDong, Dibo, Weishan Chen, and Shengjun Shi. 2016. "Coupling Motion and Energy Harvesting of Two Side-by-Side Flexible Plates in a 3D Uniform Flow" Applied Sciences 6, no. 5: 141. https://doi.org/10.3390/app6050141