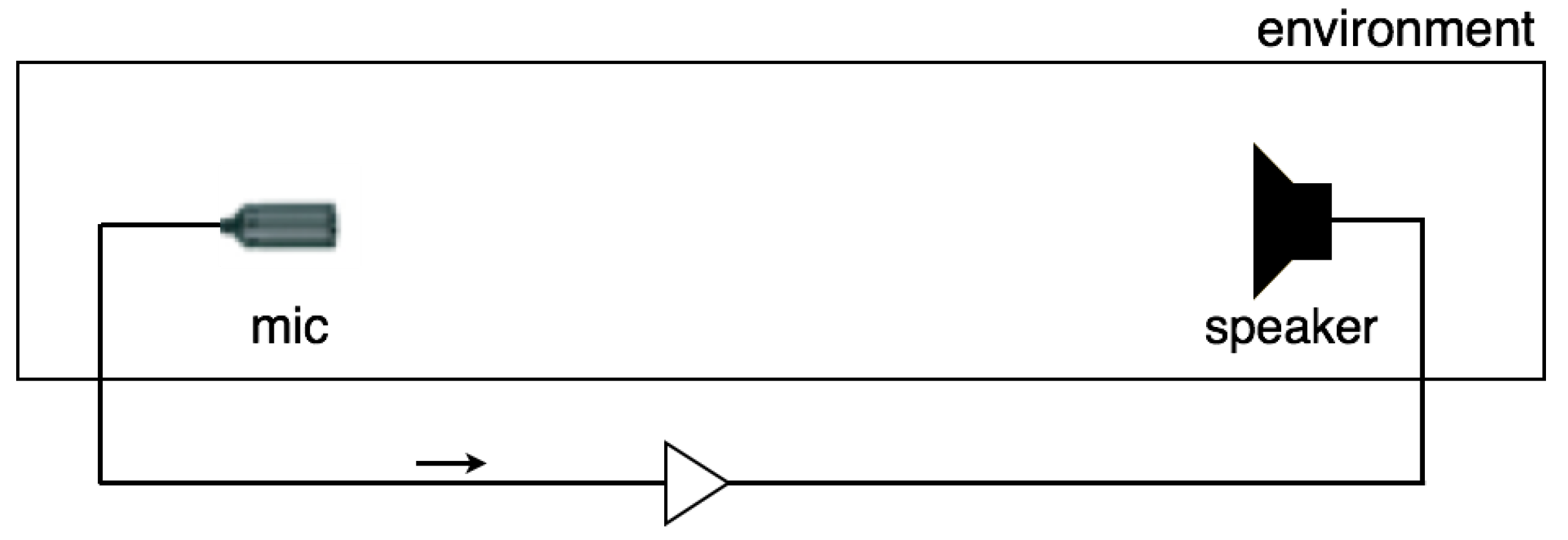
Figure 1.
Basic structure for audio feedback. Signals from a microphone are amplified, emitted by a loudspeaker, then received by the microphone again to be endlessly re-amplified.
Figure 1.
Basic structure for audio feedback. Signals from a microphone are amplified, emitted by a loudspeaker, then received by the microphone again to be endlessly re-amplified.
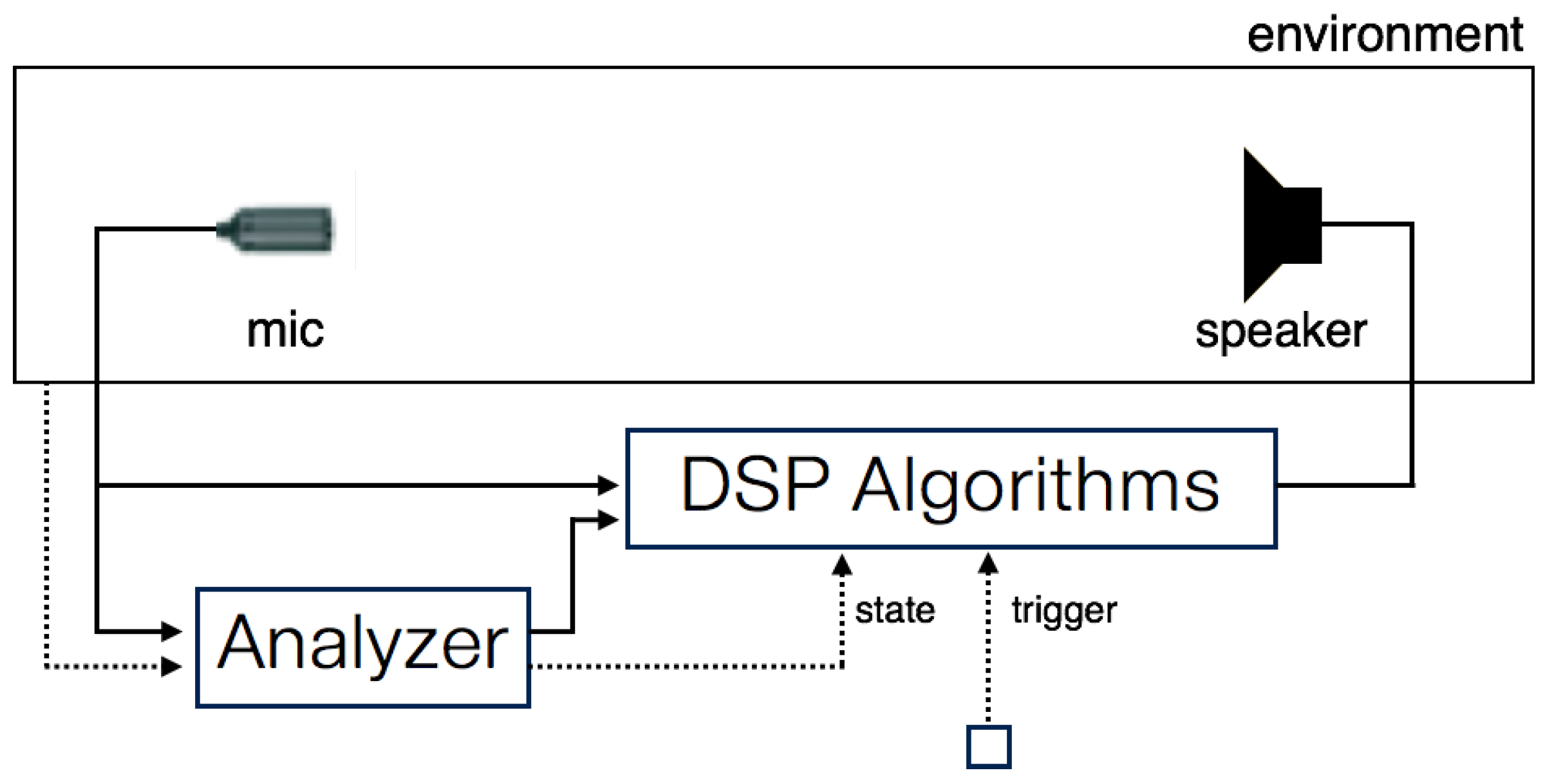
Figure 2.
Structure of feedback-based audio/music systems (redesigned diagram of
Figure 2 in [
2]). The analyzer extracts the environmental information from the audio signal and controls the state in digital signal processing (DSP) algorithms. Other agents may exist to trigger the audio feedback.
Figure 2.
Structure of feedback-based audio/music systems (redesigned diagram of
Figure 2 in [
2]). The analyzer extracts the environmental information from the audio signal and controls the state in digital signal processing (DSP) algorithms. Other agents may exist to trigger the audio feedback.
Figure 3.
Overview of the system for simulating (
a) tempo control by delay line length depending on room reverberation (
Section 3.1), (
b) volume control by gain threshold depending on volume of ambient noise (
Section 3.2), (
c) timbre control by cutoff frequency of a low-pass filter depending on a prominent resonance (
Section 3.3) and (
d) timbre control by gain of a one-pole high-pass filter according to the distribution of room modes (
Section 3.4).
Figure 3.
Overview of the system for simulating (
a) tempo control by delay line length depending on room reverberation (
Section 3.1), (
b) volume control by gain threshold depending on volume of ambient noise (
Section 3.2), (
c) timbre control by cutoff frequency of a low-pass filter depending on a prominent resonance (
Section 3.3) and (
d) timbre control by gain of a one-pole high-pass filter according to the distribution of room modes (
Section 3.4).
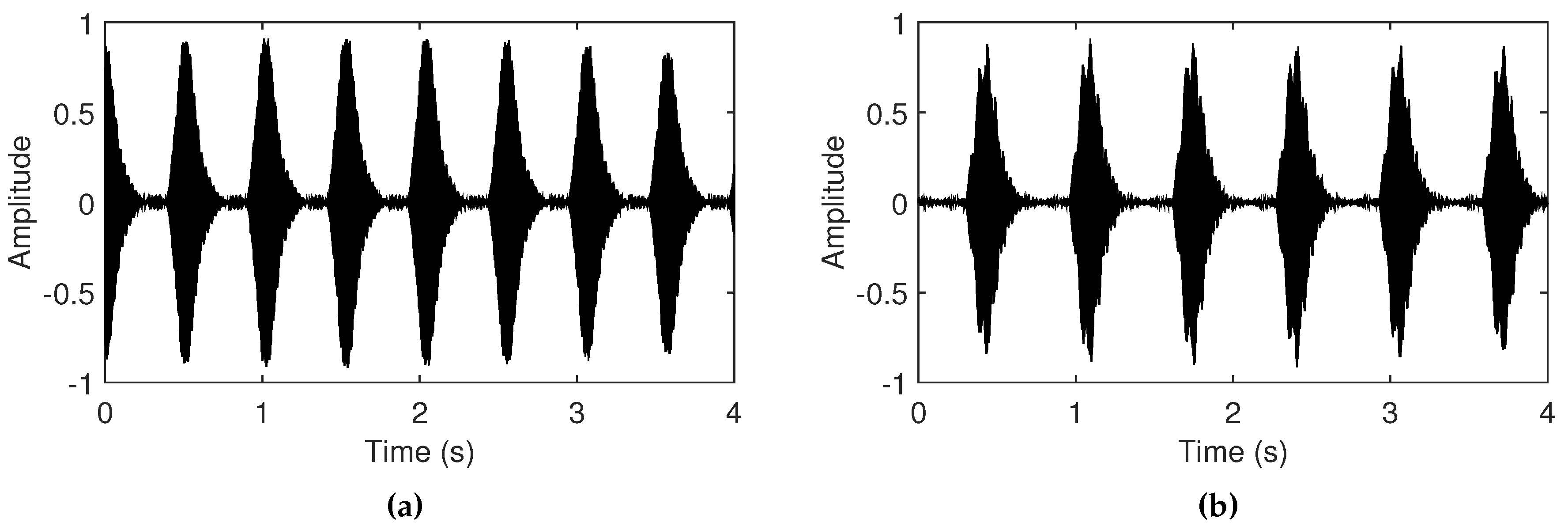
Figure 4.
Simulated tempo-scale effects of feedback sounds when length of the delay line is (a) 22,000 samples (2 Hz) and (b) 28,500 samples (1.55 Hz). The signals are normalized to compare the tempo-scale periodic occurrences of the Larsen tones, depending on delay line length.
Figure 4.
Simulated tempo-scale effects of feedback sounds when length of the delay line is (a) 22,000 samples (2 Hz) and (b) 28,500 samples (1.55 Hz). The signals are normalized to compare the tempo-scale periodic occurrences of the Larsen tones, depending on delay line length.
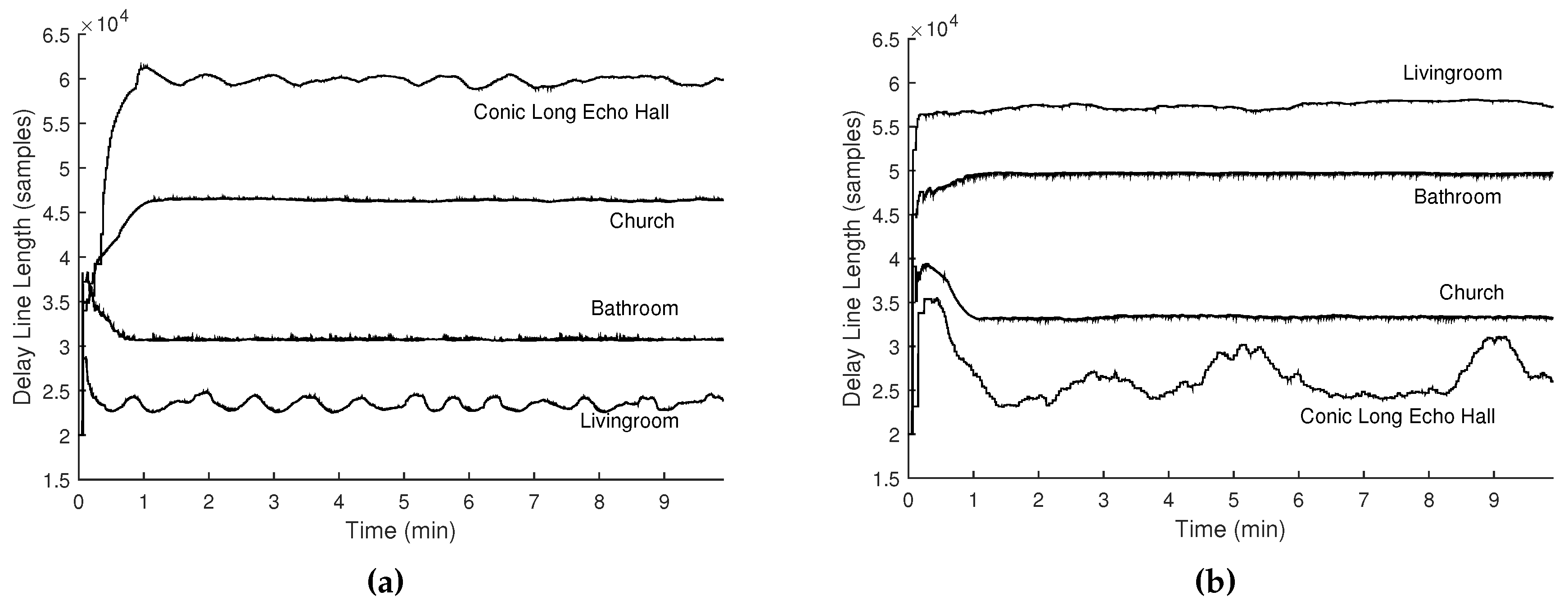
Figure 5.
Delay line length curves simulated using impulse response data of several locations with different reverberant characteristics (measured in
Table 2), using the (
a) proportional (
) and (
b) reflected (
) mappings.
Figure 5.
Delay line length curves simulated using impulse response data of several locations with different reverberant characteristics (measured in
Table 2), using the (
a) proportional (
) and (
b) reflected (
) mappings.
Figure 6.
Simulated amplitude control of feedback sounds when the low and high threshold values are (a) small (0.3 and 0.6) and (b) large (0.5 and 1.0). The length of the delay line is set to 30,000 samples (1.47 Hz).
Figure 6.
Simulated amplitude control of feedback sounds when the low and high threshold values are (a) small (0.3 and 0.6) and (b) large (0.5 and 1.0). The length of the delay line is set to 30,000 samples (1.47 Hz).
Figure 7.
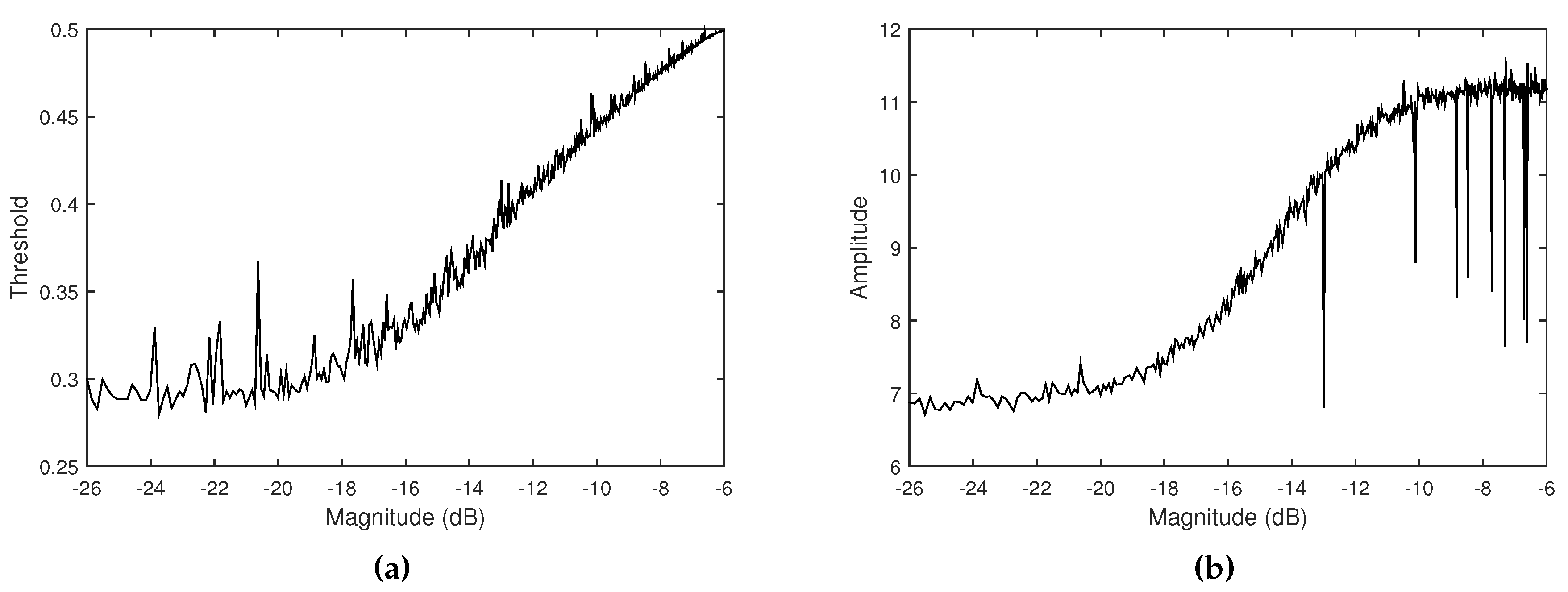
(a) Low threshold and (b) average peak amplitude curves of the feedback signals according to volume level of ambient noise. Ambient noise is simulated using different volumes of white noises.
Figure 7.
(a) Low threshold and (b) average peak amplitude curves of the feedback signals according to volume level of ambient noise. Ambient noise is simulated using different volumes of white noises.
Figure 8.
Resonant frequency approximations by the position of maximum energy in the spectra of the simulated feedback signals. Distance is simulated as the length of a silence appended to the beginning of the impulse response.
Figure 8.
Resonant frequency approximations by the position of maximum energy in the spectra of the simulated feedback signals. Distance is simulated as the length of a silence appended to the beginning of the impulse response.
Figure 9.
Plots of the magnitude spectrum of the normalized feedback signals when the cutoff frequency of the low-pass filter is (a) 300 Hz and (b) 6000 Hz. Spectral centroids are 3327 Hz and 3965 Hz respectively. The distance is set to 4 meters.
Figure 9.
Plots of the magnitude spectrum of the normalized feedback signals when the cutoff frequency of the low-pass filter is (a) 300 Hz and (b) 6000 Hz. Spectral centroids are 3327 Hz and 3965 Hz respectively. The distance is set to 4 meters.
Figure 10.
Approximations of spectral centroids and resonant frequencies from the simulated feedback signals when the cutoff frequency of the low-pass filter is (a,d) constant and (b,e) controlled with the proportional mapping and (c,f) reflected mappings. Vertical dot lines in the upper figures represent the positions where the approximated resonant frequencies deviate from the thresholds. These thresholds are depicted as the horizontal dot lines in the lower figures.
Figure 10.
Approximations of spectral centroids and resonant frequencies from the simulated feedback signals when the cutoff frequency of the low-pass filter is (a,d) constant and (b,e) controlled with the proportional mapping and (c,f) reflected mappings. Vertical dot lines in the upper figures represent the positions where the approximated resonant frequencies deviate from the thresholds. These thresholds are depicted as the horizontal dot lines in the lower figures.
Figure 11.
Variances of magnitudes of transfer functions simulated using impulse response data of several locations with different distributions of room modes (measured in
Table 3).
Figure 11.
Variances of magnitudes of transfer functions simulated using impulse response data of several locations with different distributions of room modes (measured in
Table 3).
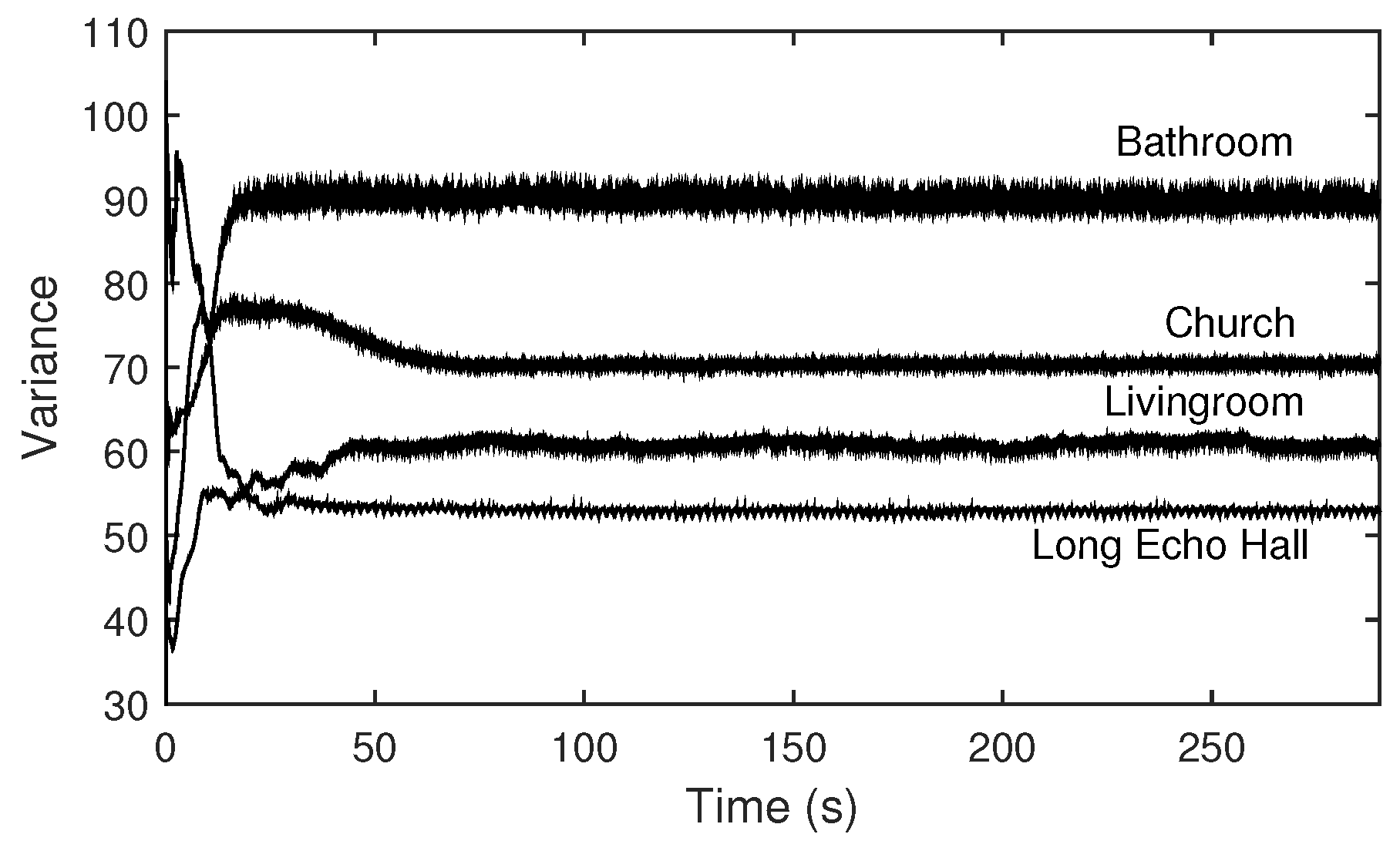
Figure 12.
Spectral centroids measured using the impulse response data of (a) long echo hall, (b) living room, (c) church, and (d) bathroom. Solid curves represent unmodified signals, and dot curves represent output signals mixed with the output of the one-pole high-pass filter, where the mix ratio between the two signals is controlled depending on the estimated variances.
Figure 12.
Spectral centroids measured using the impulse response data of (a) long echo hall, (b) living room, (c) church, and (d) bathroom. Solid curves represent unmodified signals, and dot curves represent output signals mixed with the output of the one-pole high-pass filter, where the mix ratio between the two signals is controlled depending on the estimated variances.
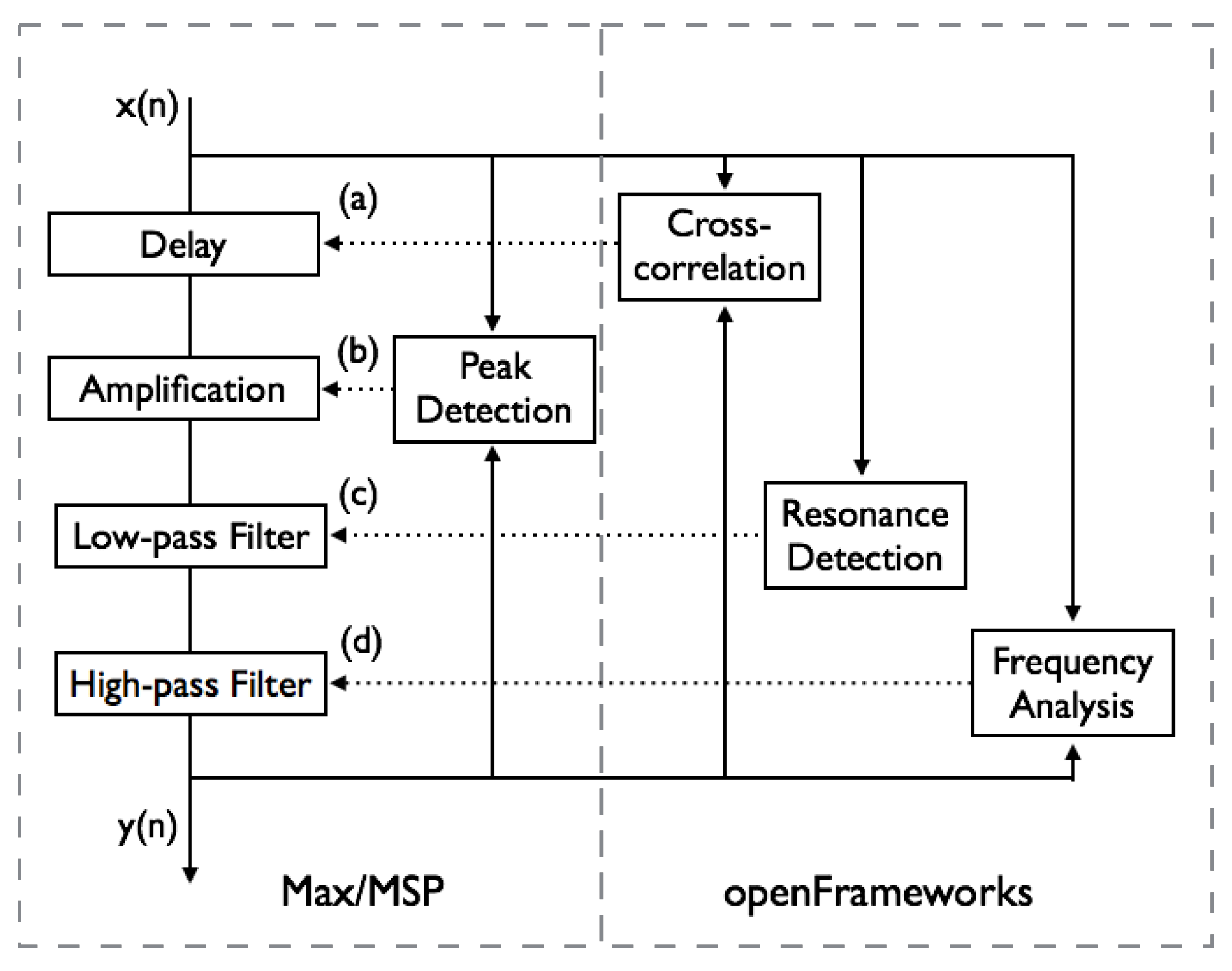
Figure 13.
Overview of the system implemented as software (Max/MSP and openFrameworks), for (
a) tempo control depending on room reverberation (
Section 4.1), (
b) volume control depending on ambient noise volume (
Section 4.2) and (
c) timbre control depending on frequency response of the acoustic environment (
Section 4.3) and (
d) timbre control depending on distribution of room modes (
Section 4.4).
Figure 13.
Overview of the system implemented as software (Max/MSP and openFrameworks), for (
a) tempo control depending on room reverberation (
Section 4.1), (
b) volume control depending on ambient noise volume (
Section 4.2) and (
c) timbre control depending on frequency response of the acoustic environment (
Section 4.3) and (
d) timbre control depending on distribution of room modes (
Section 4.4).
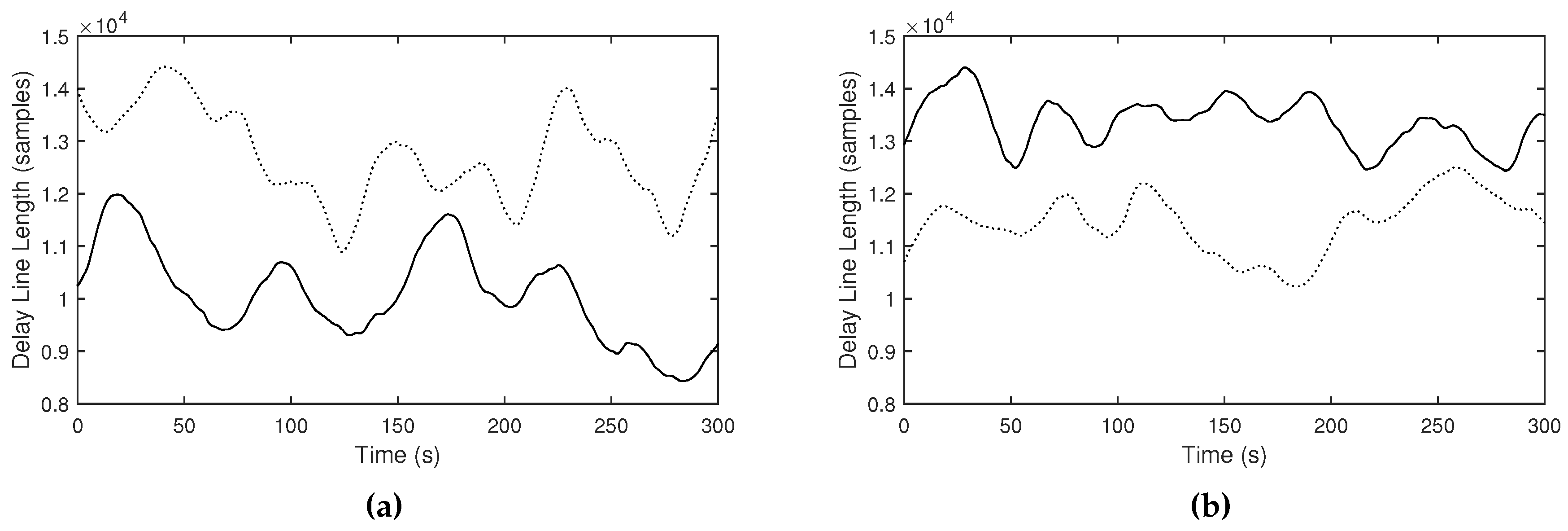
Figure 14.
Delay line length curves measured in the strongly reverberant (RT30 of 8.50 seconds, solid curves) and weakly reverberant environment (RT30 of 0.65 seconds, dot curves), using the (a) proportional () and (b) reflected () mappings.
Figure 14.
Delay line length curves measured in the strongly reverberant (RT30 of 8.50 seconds, solid curves) and weakly reverberant environment (RT30 of 0.65 seconds, dot curves), using the (a) proportional () and (b) reflected () mappings.
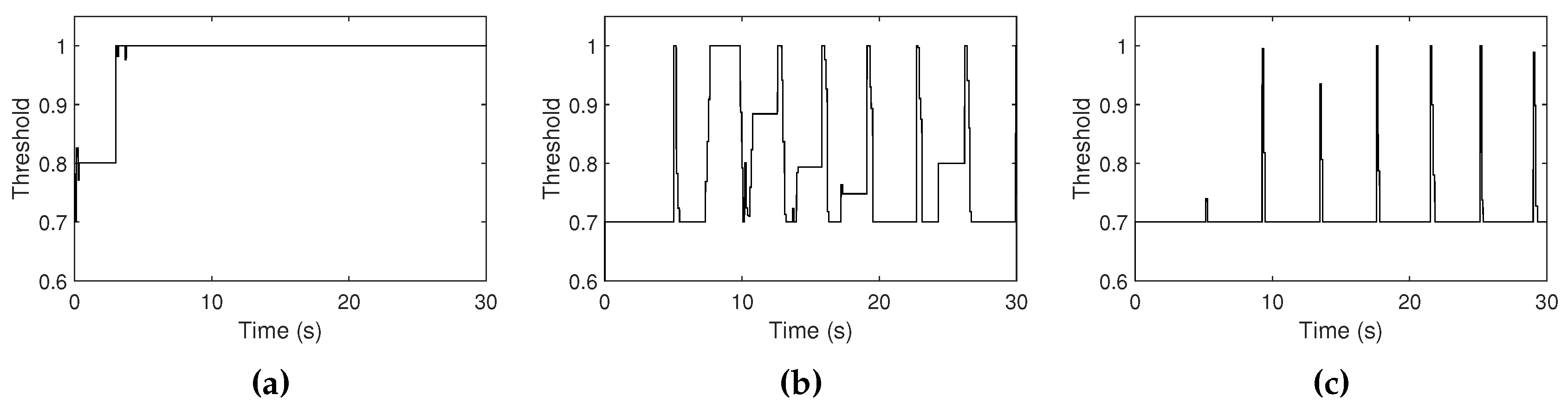
Figure 15.
High threshold curves measured when the volume level of ambient noise is measured as (a) −25 dB, (b) −30 dB, and (c) −47 dB. The range of the high threshold is constrained between 0.7 and 1.0.
Figure 15.
High threshold curves measured when the volume level of ambient noise is measured as (a) −25 dB, (b) −30 dB, and (c) −47 dB. The range of the high threshold is constrained between 0.7 and 1.0.
Figure 16.
Approximated (a) resonant frequencies and (b) spectral centroids according to the distance between the loudspeaker and the microphone, with different cutoff frequency settings of the low-pass filter: constant (straight lines), determined by the measured resonant frequency, using the proportional (, dash lines) and reflected mappings (, dash-dot lines). The threshold was set to 140 Hz (dot line in (a)).
Figure 16.
Approximated (a) resonant frequencies and (b) spectral centroids according to the distance between the loudspeaker and the microphone, with different cutoff frequency settings of the low-pass filter: constant (straight lines), determined by the measured resonant frequency, using the proportional (, dash lines) and reflected mappings (, dash-dot lines). The threshold was set to 140 Hz (dot line in (a)).
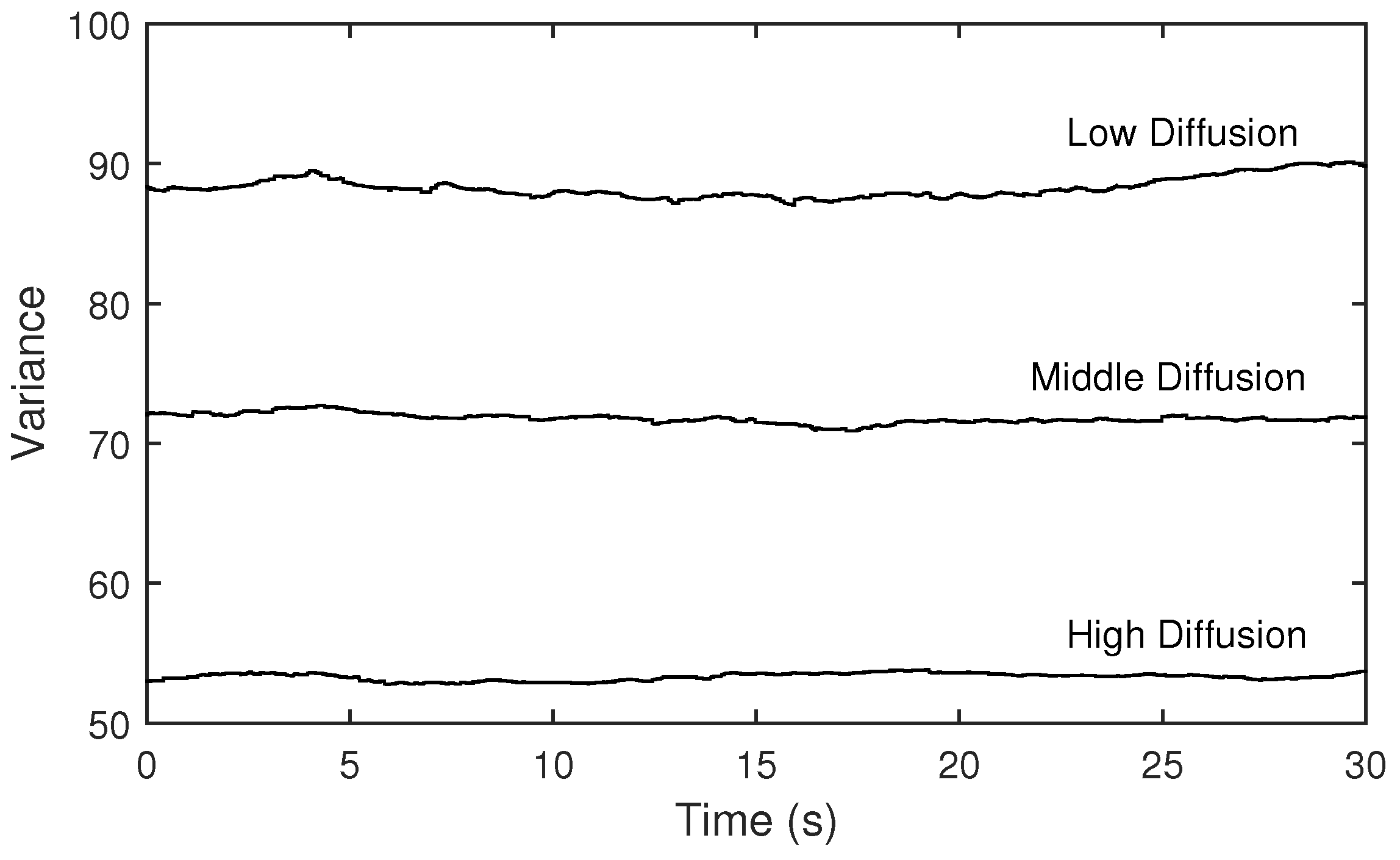
Figure 17.
Variances of magnitudes of the measured transfer functions when the diffusion parameter is set to low, middle and high.
Figure 17.
Variances of magnitudes of the measured transfer functions when the diffusion parameter is set to low, middle and high.
Figure 18.
Spectral centroids measured when the diffusion parameter is set to (a) low, (b) middle and (c) high. Solid curves represent unmodified signals, and dot curves represent output signals mixed with the output of the one-pole high-pass filter, where the mix ratio between the two signals is controlled depending on the estimated variances.
Figure 18.
Spectral centroids measured when the diffusion parameter is set to (a) low, (b) middle and (c) high. Solid curves represent unmodified signals, and dot curves represent output signals mixed with the output of the one-pole high-pass filter, where the mix ratio between the two signals is controlled depending on the estimated variances.
Table 1.
Comparison of input information, approximation methods, control targets and methods for composition of musical tendencies depending on information carried in the feedback signals regarding the acoustic environment.
Table 1.
Comparison of input information, approximation methods, control targets and methods for composition of musical tendencies depending on information carried in the feedback signals regarding the acoustic environment.
| Input Information | Approximation Methods | Control Targets | Control Methods |
|---|
| Reverberation | Cross-correlation of input/output | Tempo | Delay line length |
| Ambient noise volume | Peak amplitude | Output level | Gain threshold |
| Acoustic resonance | Freq. of maximum energy | Timbre | LPF cutoff freq. |
| Distribution of room modes | Variance of magnitudes | Timbre | HPF gain |
| | from the transfer function | | |
Table 2.
Comparison of the reverberant characteristics measured by RT60 (the reverberation time over a 60 dB decay range), the cross-correlation values when the delay line is set to 28,000 samples, and average delay line lengths (in sample) using the proportional () and reflected () mappings.
Table 2.
Comparison of the reverberant characteristics measured by RT60 (the reverberation time over a 60 dB decay range), the cross-correlation values when the delay line is set to 28,000 samples, and average delay line lengths (in sample) using the proportional () and reflected () mappings.
| Room Types | RT60 (s) | Xcorr | | |
|---|
| Livingroom | 0.28 | 0.0407 | 23496 | 46991 |
| Bathroom | 0.58 | 0.1365 | 30674 | 42633 |
| Church | 0.97 | 0.4205 | 46311 | 30691 |
| Long Echo Hall | 3.07 | 0.4904 | 59604 | 25302 |
Table 3.
Comparison of the distributions of room modes measured by spectral flatness and variance of the magnitudes of the impulse response data (), average variance of the frequency magnitudes of the estimated transfer function (), and average gain values mapped by (g).
Table 3.
Comparison of the distributions of room modes measured by spectral flatness and variance of the magnitudes of the impulse response data (), average variance of the frequency magnitudes of the estimated transfer function (), and average gain values mapped by (g).
| Room Types | Spectral Flatness | Var(||) | Var(||) | g |
|---|
| Long Echo Hall | 0.85 | 29.71 | 52.90 | 0.56 |
| Livingroom | 0.83 | 31.52 | 61.08 | 0.74 |
| Church | 0.73 | 52.68 | 70.37 | 0.95 |
| Bathroom | 0.64 | 79.15 | 90.00 | 1.0 |
Table 4.
Comparison of the reverberant characteristics (RT30) and the average delay line lengths during the first 5 minutes, using the proportional () and reflected () mappings.
Table 4.
Comparison of the reverberant characteristics (RT30) and the average delay line lengths during the first 5 minutes, using the proportional () and reflected () mappings.
| RT30 (s) | | |
|---|
| 0.65 | 12720 | 11450 |
| 1.33 | 11690 | 11940 |
| 8.50 | 10070 | 13360 |