Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures
Abstract
:1. Introduction
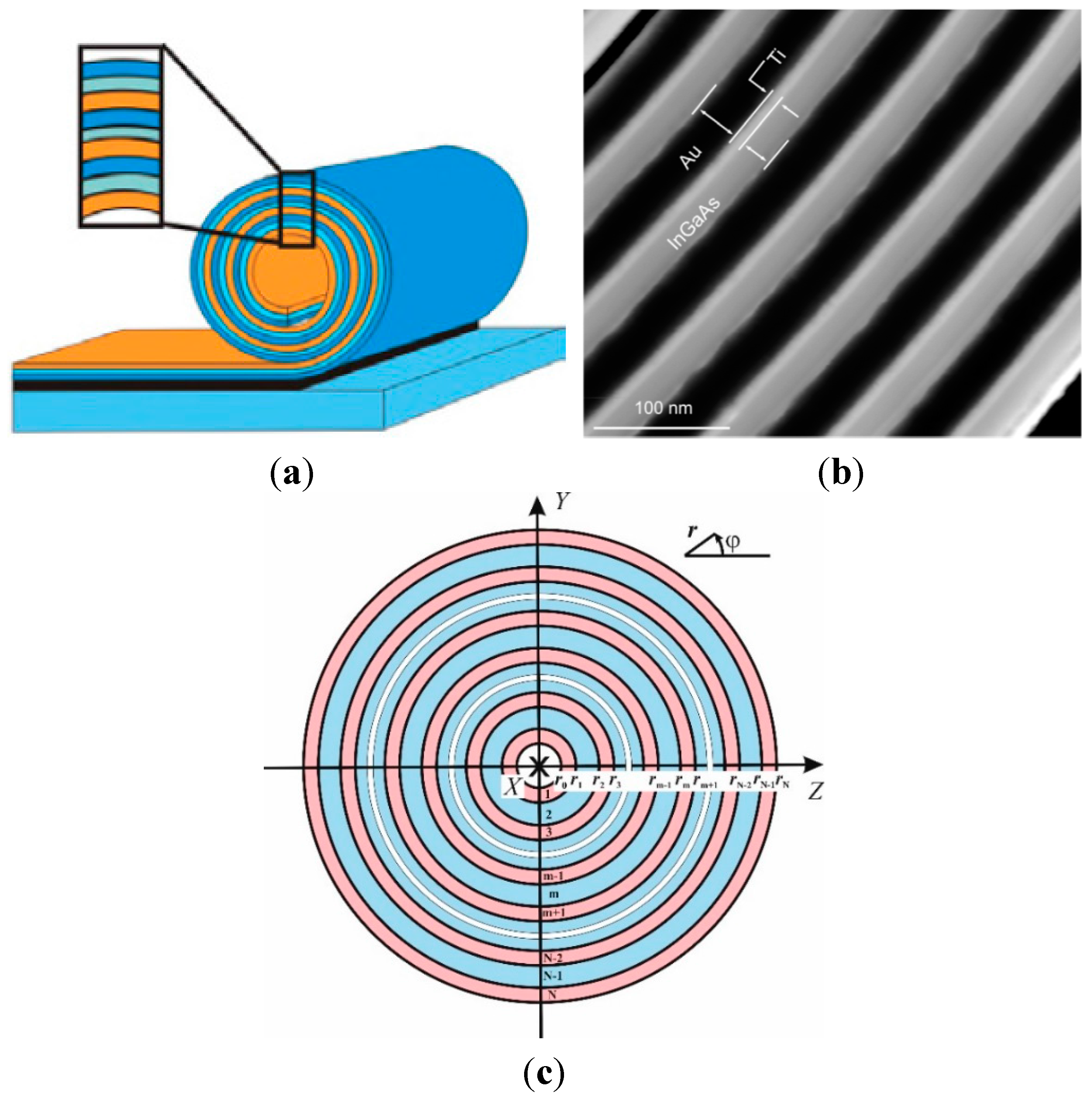
2. Theoretical Model
| Parity i of the layer number m | 1 | 2 |
|---|---|---|
| Material | InAs | GaAs |
| λi, dyn/cm2 | 4.54 × 1011 | 5.34 × 1011 |
| μi, dyn/cm2 | 1.90 × 1011 | 3.285 × 1011 |
| ρi, g/cm3 | 5.68 | 5.317 |
| Δri, nm | 5 | 5 |
| Characteristic of the layer with parity i of the number m | Denotation |
|---|---|
| Velocity of a dilatational wave | v1i = [(λi + 2μi)/ ρi]1/2 |
| Velocity of a shear wave | v2i = [μi/ ρi]1/2 |
| Squared radial wave number for a dilatational wave | αi2 = ω2/v1i2 − ζ2 |
| Squared radial wave number for a shear wave | βi2 = ω2/v2i2 − ζ 2 |
| Dispersion of the Rayleigh waves αi2 = 0 | ω = v1iζ |
| Dispersion of the Rayleigh waves βi2 = 0 | ω = v2iζ |
| Physical quantity | Unit |
|---|---|
| Longitudinal wave vector ζ | 1/Δr2 |
| Frequency ω | πv22/Δr2 |
| Group velocity dω/dζ | πv22 |
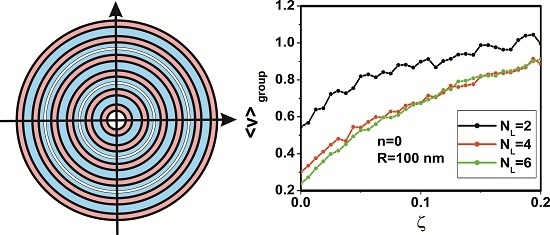
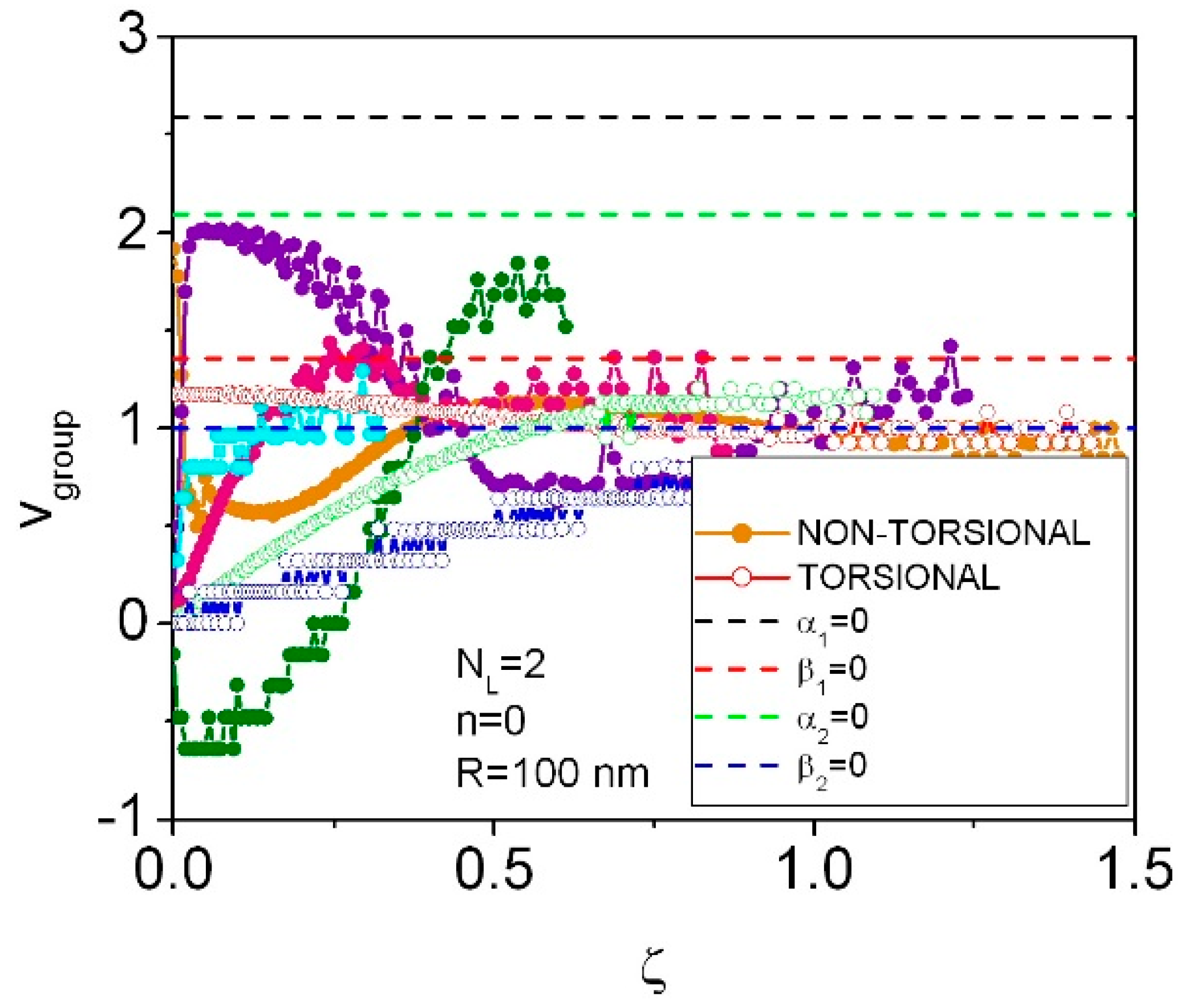
3. Results for NL = 2

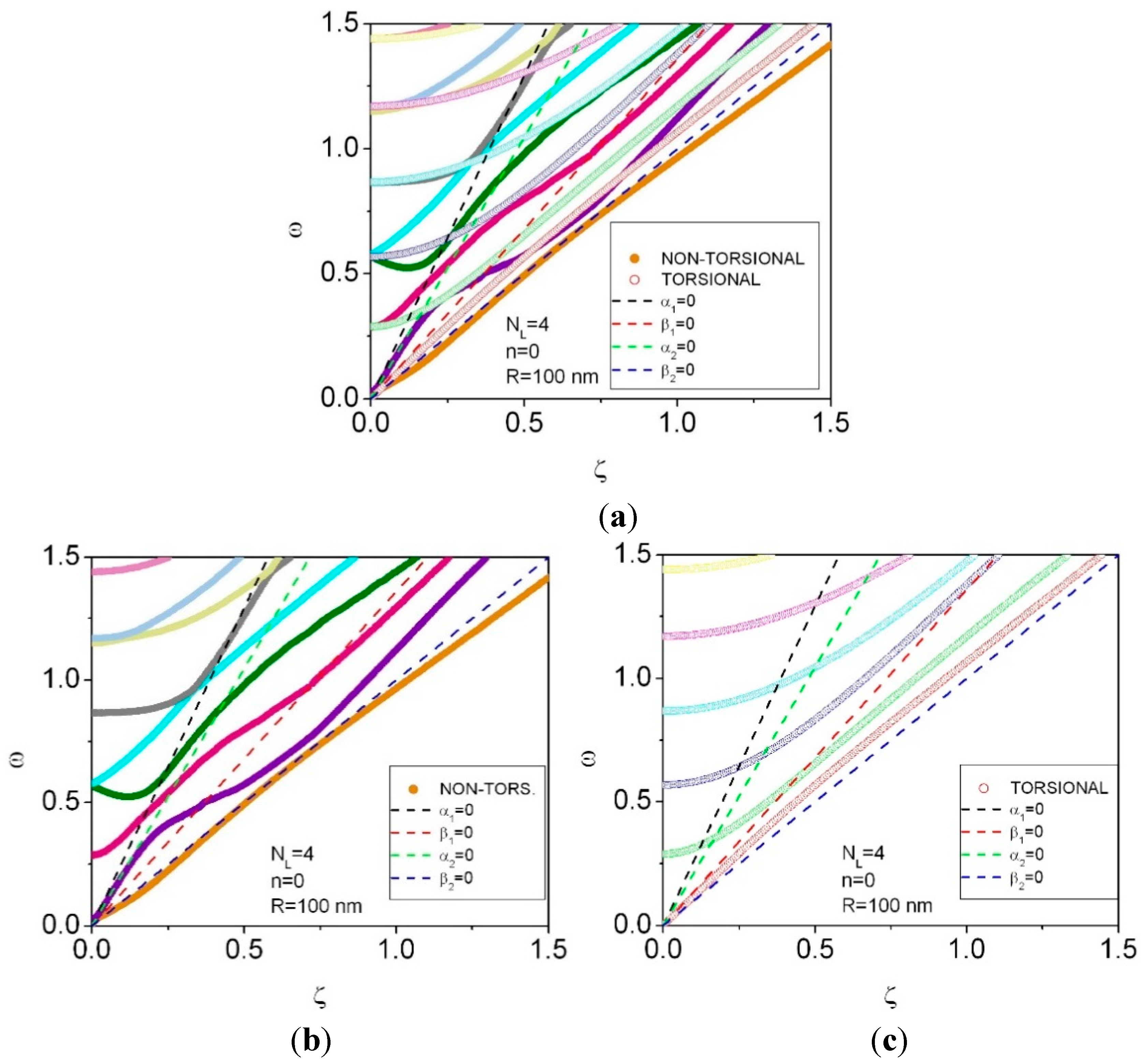
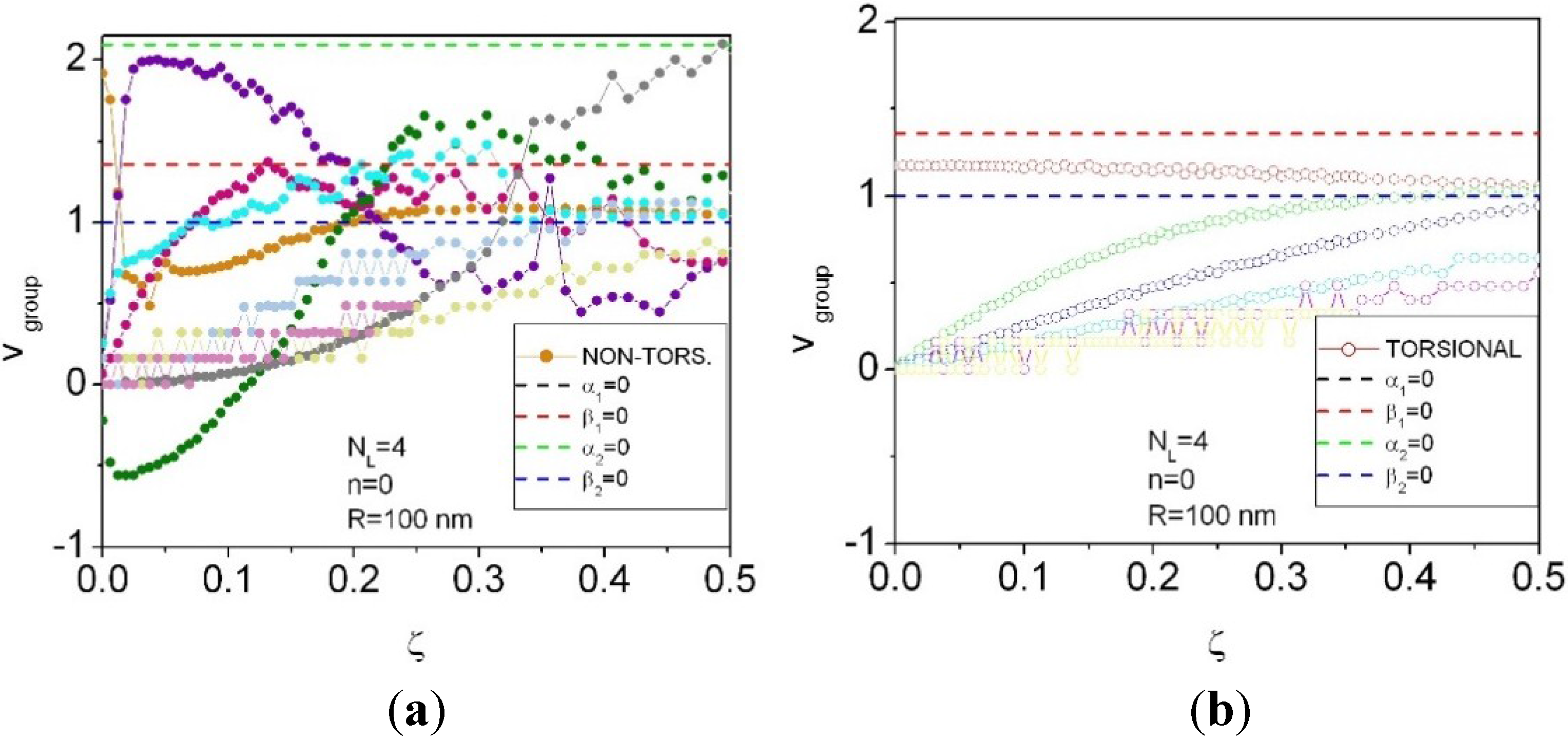
4. Results for NL = 4 and NL =6


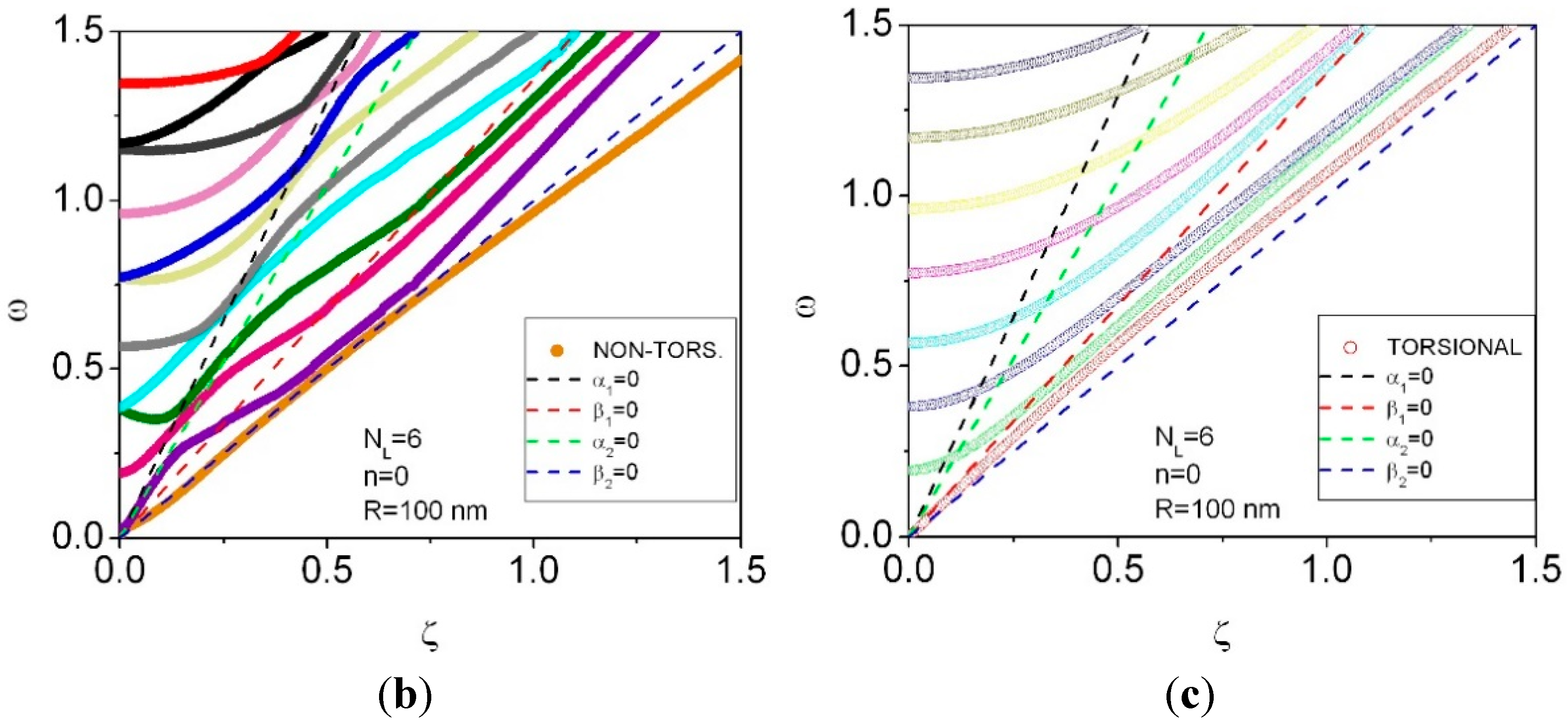

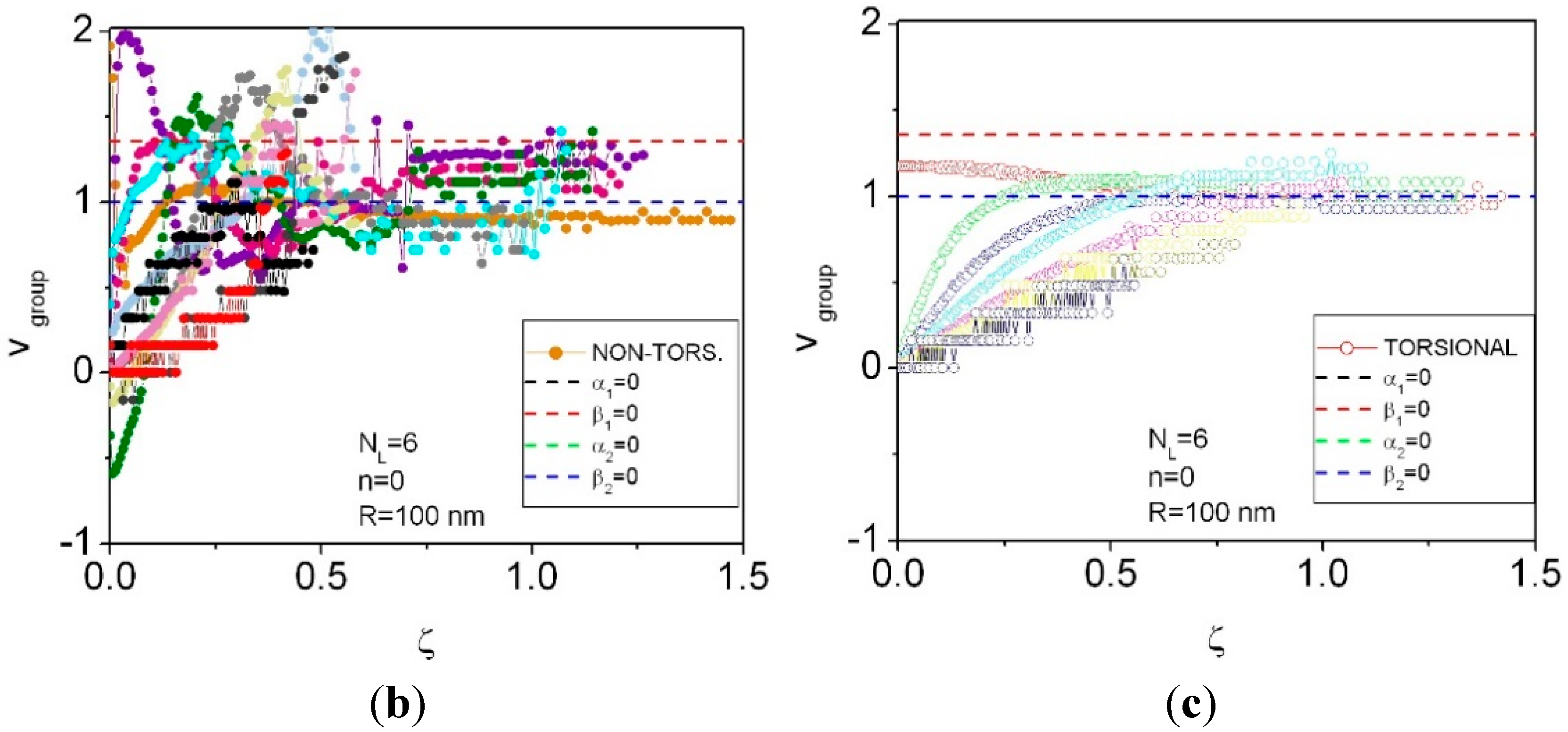
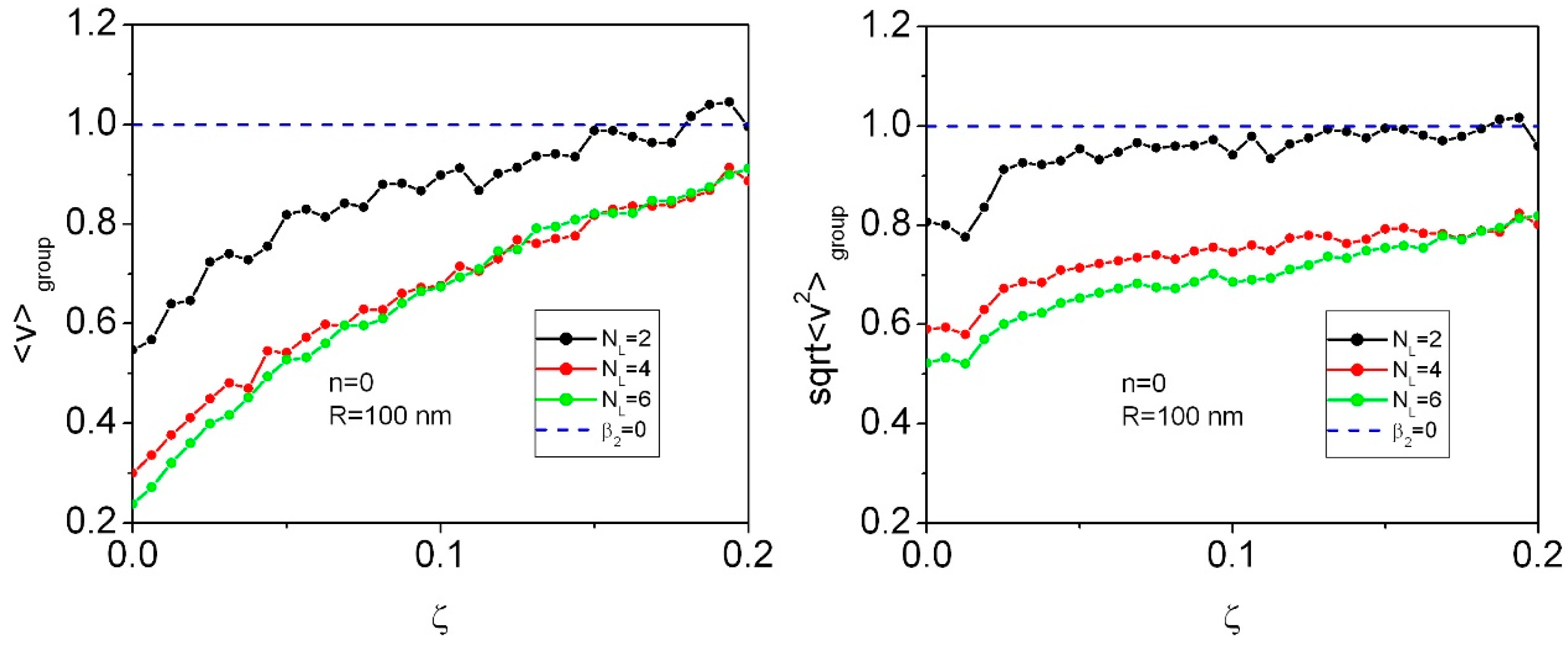
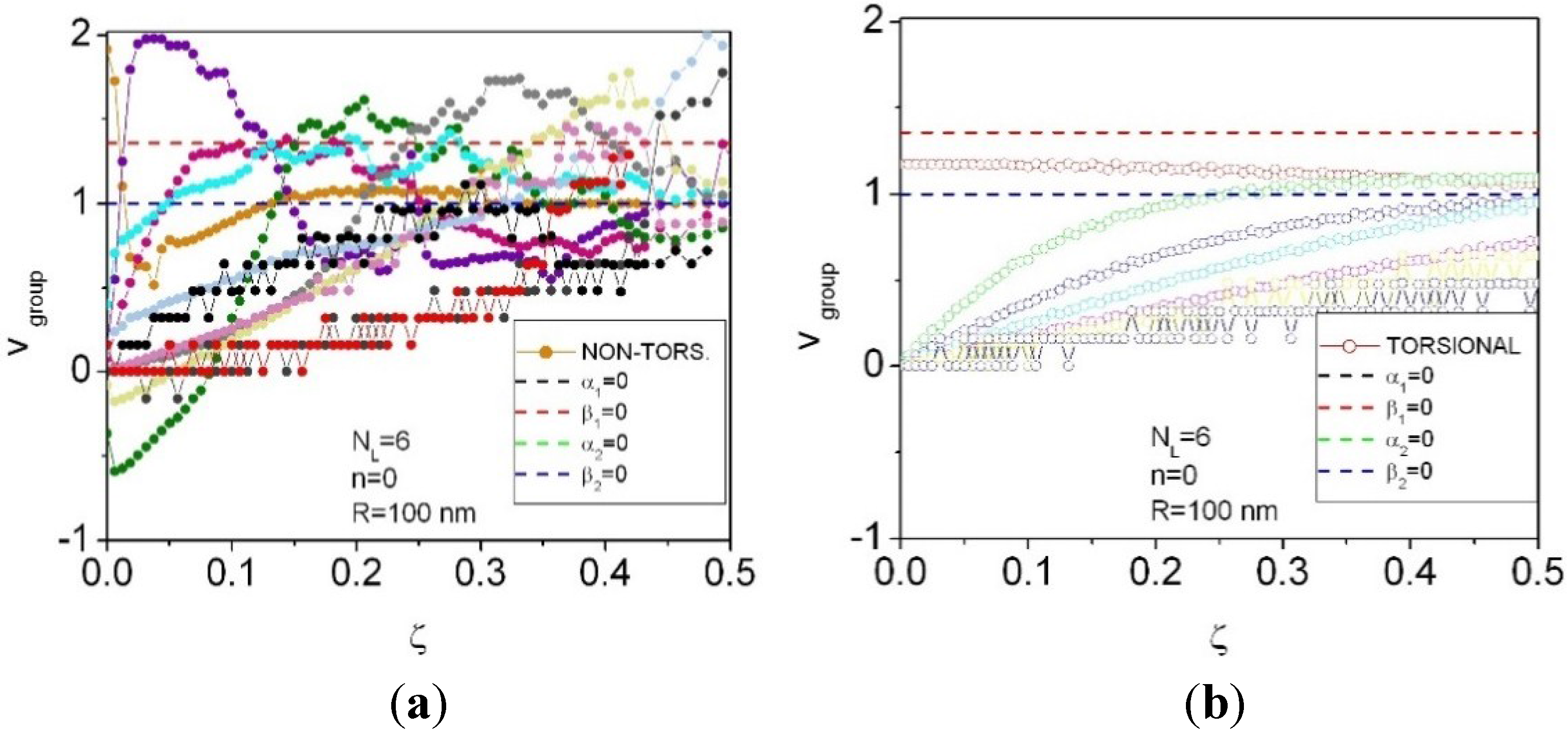
5. Geometric Effects in the Phonon Dispersion and Group Velocities for Different Numbers of Layers
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix

References
- Fomin, V.M.; Pokatilov, E.P. Phonons and the electron-phonon interaction in multi-layer systems. Phys. Stat. Sol. 1985, 132, 69–82. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Fomin, V.M.; Beril, S.I. Vibrational excitations, polarons and excitons in multi-layer structures and superlattices; Shtiintsa: Kishinev, USSR, 1990; pp. 1–280. [Google Scholar]
- Pokatilov, E.P.; Fomin, V.M.; Semenovskaya, N.N.; Beril, S.I. Interaction Hamiltonian between an electron and polar surface vibrations in a symmetrical three-layer structure. Phys. Rev. B 1993, 47, 16597–16600. [Google Scholar] [CrossRef]
- Klimin, S.N.; Pokatilov, E.P.; Fomin, V.M. Bulk and interface polarons in quantum wires and dots. Phys. Stat. Sol. 1994, 184, 373–383. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Fomin, V.M.; Klimin, S.N.; Balaban, S.N. Characterization of nanostructures by virtue of the phenomena due to the electron-phonon interaction. Appl. Surf. Sci. 1996, 104–105, 546–551. [Google Scholar] [CrossRef]
- Stroscio, M.A.; Dutta, M. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2001; pp. 1–282. [Google Scholar]
- Balandin, A.A. Nanophononics: Phonon engineering in nanostructures and nanodevices. J. Nanosci. Nanotechnol. 2005, 5, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Pokatilov, E.P.; Nika, D.L. Phonon engineering in hetero- and nanostructures. J. Nanoelectron. Optoelectron. 2007, 2, 140–170. [Google Scholar] [CrossRef]
- Balandin, A.A.; Nika, D.L. Phononics in low-dimensional materials. Mater. Today 2012, 15, 266–275. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Significant decrease of the lattice thermal conductivity due to phonon confinement in a free-standing semiconductor quantum well. Phys. Rev. B 1998, 58, 1544–1549. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Phonon spectrum and group velocities in AlN/GaN/AlN and related heterostructures. Superlatt. Microstruct. 2003, 33, 155–171. [Google Scholar] [CrossRef]
- Mingo, N.; Yang, L.; Li, D.; Majumdar, A. Predicting the thermal conductivity of Si and Ge nanowires. Nano Lett. 2003, 3, 1713–1716. [Google Scholar] [CrossRef]
- Mingo, N. Calculation of Si nanowire thermal conductivity using complete phonon dispersion relations. Phys. Rev. B 2003, 68, 113308. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Acoustic-phonon propagation in rectangular semiconductor nanowires with elastically dissimilar barriers. Phys. Rev. B 2005, 72, 113311. [Google Scholar] [CrossRef]
- Bannov, N.; Aristov, V.; Mitin, V.; Stroscio, M.A. Electron relaxation times due to the deformation-potential interaction of electrons with confined acoustic phonons in a free-standing quantum well. Phys. Rev. B 1995, 51, 9930–9942. [Google Scholar] [CrossRef]
- Stroscio, M.A. Interaction between longitudinal-optical-phonon modes of a rectangular quantum wire and charge carriers of a one-dimensional electron gas. Phys. Rev. B 1989, 40, 6428–6431. [Google Scholar] [CrossRef]
- Mickevičius, R.; Mitin, V. Acoustic-phonon scattering in a rectangular quantum wire. Phys. Rev. B 1993, 48, 17194–17201. [Google Scholar] [CrossRef]
- Mickevičius, R.; Mitin, V.; Harithsa, U.K.; Jovanovic, D.; Leburton, J.P. Superlinear electron transport and noise in quantum wires. J. Appl. Phys. 1994, 75, 973–978. [Google Scholar] [CrossRef]
- Svizhenko, A.; Balandin, A.; Bandyopadhyay, S.; Stroscio, M.A. Electron interaction with confined acoustic phonons in quantum wires subjected to a magnetic field. Phys. Rev. B 1998, 57, 4687–4693. [Google Scholar] [CrossRef]
- Svizhenko, A.; Bandyopadhyay, S.; Stroscio, M.A. The effect of acoustic phonon confinement on the momentum and energy relaxation of hot carriers in quantum wires. J. Phys. Cond. Matter 1998, 10, 6091–6094. [Google Scholar] [CrossRef]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. Confined electron-confined phonon scattering rates in wurtzite AlN/GaN/AlN heterostructures. J. Appl. Phys. 2004, 95, 5626–5632. [Google Scholar] [CrossRef]
- Fomin, V.M.; Pokatilov, E.P.; Devreese, J.T.; Klimin, S.N.; Gladilin, V.N.; Balaban, S.N. Multiquantum optical processes in semiconductor quantum dots. Phys. Stat. Sol. 1997, 164, 417–420. [Google Scholar] [CrossRef]
- Fomin, V.M.; Gladilin, V.N.; Devreese, J.T.; Pokatilov, E.P.; Balaban, S.N.; Klimin, S.N. Photoluminescence of spherical quantum dots. Phys. Rev. B 1998, 57, 2415–2425. [Google Scholar] [CrossRef]
- Fomin, V.M.; Klimin, S.N.; Gladilin, V.N.; Devreese, J.T. Characterization of self-assembled quantum dots using the phonon-induced features of PL spectra. J. Lumin. 2000, 87–89, 330–332. [Google Scholar] [CrossRef]
- Fomin, V.M.; Devreese, J.T. Theory of excitons in semiconductor quantum dots. Nonlinear Opt. 2002, 29, 321–327. [Google Scholar]
- Fonoberov, V.A.; Pokatilov, E.P.; Fomin, V.M.; Devreese, J.T. Photoluminescence of tetrahedral quantum-dot quantum wells. Phys. Rev. Lett. 2004, 92, 127402. [Google Scholar] [CrossRef] [PubMed]
- Klimin, S.N.; Fomin, V.M.; Devreese, J.T.; Bimberg, D. Model of Raman scattering in self-assembled InAs/GaAs quantum dots. Phys. Rev. B 2008, 77, 045307. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Sun, G. Enhancement of light absorption in a quantum well by surface plasmon polariton. Appl. Phys. Lett. 2009, 94, 191106. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Effect of phonon confinement on the thermoelectric figure of merit of quantum wells. J. Appl. Phys. 1998, 84, 6149–6153. [Google Scholar] [CrossRef]
- Khitun, A.; Balandin, A.; Wang, K.L. Modification of the lattice thermal conductivity in silicon quantum wires due to spatial confinement of acoustic phonons. Superlatt. Microstruct. 1999, 26, 181–193. [Google Scholar] [CrossRef]
- Zou, J.; Balandin, A. Phonon heat conduction in a semiconductor nanowire. J. Appl. Phys. 2001, 89, 2932–2938. [Google Scholar] [CrossRef]
- Fonoberov, V.A.; Balandin, A.A. Giant enhancement of the carrier mobility in Silicon nanowires with diamond coating. Nano Lett. 2006, 6, 2442–2446. [Google Scholar] [CrossRef] [PubMed]
- Nika, D.L.; Pokatilov, E.P.; Balandin, A.A. Phonon-engineered mobility enhancement in the acoustically mismatched silicon/diamond transistor channels. Appl. Phys. Lett. 2009, 93, 173111. [Google Scholar] [CrossRef]
- Zincenco, N.D.; Nika, D.L.; Pokatilov, E.P.; Balandin, A.A. Acoustic phonon engineering of thermal properties of silicon-based nanostructures. J. Phys. Conf. Ser. 2007. [Google Scholar] [CrossRef]
- Wingert, M.C.; Chen, Z.C.Y.; Dechaumphai, E.; Moon, J.; Kim, J.-H.; Xiang, J.; Chen, R. Thermal conductivity of Ge and Ge-Si core-shell nanowires in the phonon confinement regime. Nano Lett. 2011, 11, 5507–5513. [Google Scholar] [CrossRef] [PubMed]
- Cuffe, J.; Chávez, E.; Shchepetov, A.; Chapuis, P.-O.; El Boudouti, E.H.; Alzina, F.; Kehoe, T.; Gomis-Bresco, J.; Dudek, D.; Pennec, Y.; et al. Phonons in slow motion: Dispersion relations in ultrathin Si membranes. Nano Lett. 2012, 12, 3569–3573. [Google Scholar] [PubMed]
- Johnson, W.L.; Kim, S.A.; Geiss, R.; Flannery, C.M.; Bertness, K.A.; Heyliger, P.R. Vibrational modes of GaN nanowires in the gigahertz range. Nanotechnology 2012, 23, 495709. [Google Scholar] [CrossRef] [PubMed]
- Pokatilov, E.P.; Nika, D.L.; Balandin, A.A. A phonon depletion effect in ultrathin heterostructures with acoustically mismatched layers. Appl. Phys. Lett. 2004, 85, 825–827. [Google Scholar] [CrossRef]
- Nika, D.L.; Zincenco, N.D.; Pokatilov, E.P. Engineering of thermal fluxes in phonon mismatched heterostructures. J. Nanoelect. Optoelect. 2009, 4, 180–185. [Google Scholar] [CrossRef]
- Hu, M.; Giapis, K.P.; Goicochea, J.V.; Zhang, X.; Poulikakos, D. Significant reduction of thermal conductivity in Si/Ge core-shell nanowires. Nano Lett. 2011, 11, 618–623. [Google Scholar] [CrossRef] [PubMed]
- Bi, K.; Wang, J.; Wang, Y.; Sha, J.; Wang, Z.; Chen, M.; Chen, Y. The thermal conductivity of SiGe heterostructure nanowires with different cores and shells. Phys. Lett. A 2012, 376, 2668–2671. [Google Scholar] [CrossRef]
- He, Y.; Galli, G. Microscopic origin of the reduced thermal conductivity of Silicon nanowires. Phys. Rev. Lett. 2012, 108, 215901. [Google Scholar] [CrossRef] [PubMed]
- Wave Propagation in Materials for Modern Applications; Petrin, A. (Ed.) InTech: Rijeka, Croatia, 2010; pp. 1–552.
- Acoustic Metamaterials and Phononic Crystals; Deymier, P.A. (Ed.) Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–378.
- Narayana, S.; Sato, Y. Heat flux manipulation by engineered thermal materials. Phys. Rev. Lett. 2012, 108, 214303. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Yang, S.; Gan, C.; Lei, H. A new procedure for exploring the dispersion characteristics of longitudinal guided waves in a multi-layered tube with a weak interface. J. Nondestruct. Eval. 2013, 32, 263–276. [Google Scholar] [CrossRef]
- Wang, L.; Hu, H.; Guo, W. Wave Propagation in Carbon Nanotubes. In Wave Propagation in Materials for Modern Applications; Petrin, A., Ed.; InTech: Rijeka, Croatia, 2010; pp. 225–252. [Google Scholar]
- Sigalas, M.M.; Economou, M.N. Elastic and acoustic wave band structure. J. Sound Vibr. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Economou, M.N. Band structure of elastic waves in two dimensional systems. Solid State Communs. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Movchan, A.B.; Guenneau, S. Split-ring resonators and localized modes. Phys. Rev. B 2004, 70, 125116. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602(R). [Google Scholar] [CrossRef]
- Prinz, V.Y.; Seleznev, V.A.; Gutakovsky, A.K.; Chehovskiy, A.V.; Preobrazhenskii, V.V.; Putyato, M.A.; Gavrilova, T.A. Free-standing and overgrown InGaAs/GaAs nanotubes, nanohelices and their arrays. Physica E: Low-dimension. Syst. Nanostruct. 2000, 6, 828–831. [Google Scholar] [CrossRef]
- Schmidt, O.G.; Eberl, K. Nanotechnology—Thin solid films roll up into nanotubes. Nature 2001, 410, 168. [Google Scholar] [CrossRef] [PubMed]
- Krause, B.; Mocuta, C.; Metzger, T.H.; Deneke, C.; Schmidt, O.G. Local structure of a rolled-up single crystal: An X-ray microdiffraction study of individual semiconductor nanotubes. Phys. Rev. Lett. 2006, 96, 165502. [Google Scholar] [CrossRef] [PubMed]
- Deneke, C.; Jin-Phillipp, N.-Y.; Loa, I.; Schmidt, O.G. Radial superlattices and single nanoreactors. Appl. Phys. Lett. 2004, 84, 4475–4477. [Google Scholar] [CrossRef]
- Deneke, C.; Songmuang, R.; Jin-Phillipp, N.Y.; Schmidt, O.G. The structure of hybrid radial superlattices. J. Phys. D Appl. Phys. 2009, 42, 103001. [Google Scholar] [CrossRef]
- Grimm, D.; Wilson, R.B.; Teshome, B.; Gorantla, S.; Rümmeli, M.H.; Bublat, T.; Zallo, E.; Li, G.; Cahill, D.G.; Schmidt, O.G. Thermal conductivity of mechanically joined semiconducting/metal nanomembrane superlattices. Nano Lett. 2014, 14, 2387–2393. [Google Scholar] [CrossRef] [PubMed]
- Pokatilov, E.P.; Fomin, V.M.; Devreese, J.T.; Balaban, S.N.; Klimin, S.N. Bipolaron binding in quantum wires. Phys. Rev. B 2000, 61, 2721–2728. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, H.-J. Fröhlich electron-interface and -surface optical phonon interaction Hamiltonian in multilayer coaxial cylindrical AlxGa1−xAs/GaAs quantum cables. J. Phys. Condens. Matter 2003, 15, 5871–5879. [Google Scholar]
- Kanyinda-Malu, C.; Clares, F.J.; de la Cruz, R.M. Axial interface optical phonon modes in a double-nanoshell system. Nanotechnology 2008, 19, 285713. [Google Scholar] [CrossRef] [PubMed]
- Deneke, C.; Sigle, W.; Eigenthaler, U.; van Aken, P.A.; Schütz, G.; Schmidt, O.G. Interfaces in semiconductor/metal radial superlattices. Appl. Phys. Lett. 2007, 90, 263107. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Dover: New York, NY, USA, 1991; pp. 1–688. [Google Scholar]
- Armenàkas, A.E. Propagation of Harmonic Waves in Composite Circular Cylindrical Shells. I: Theoretical investigation. Am. Inst. Aeronaut. Astronautics (AIAA) J. 1966, 5, 740–744. [Google Scholar] [CrossRef]
- Armenàkas, A.E. Propagation of Harmonic Waves in Composite Circular Cylindrical Shells. Part II: Numerical Analysis. Am. Inst. Aeronaut. Astronautics (AIAA) J. 1971, 9, 599–605. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.National Bureau of Standards: Washington, DC, USA, 1972; pp. 1–1046.
- Intel® Visual Fortran with Microsoft Visual Studio 2008. Available online: https://www.visualstudio.com/ (accessed on 29 September 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fomin, V.M.; Balandin, A.A. Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures. Appl. Sci. 2015, 5, 728-746. https://doi.org/10.3390/app5040728
Fomin VM, Balandin AA. Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures. Applied Sciences. 2015; 5(4):728-746. https://doi.org/10.3390/app5040728
Chicago/Turabian StyleFomin, Vladimir M., and Alexander A. Balandin. 2015. "Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures" Applied Sciences 5, no. 4: 728-746. https://doi.org/10.3390/app5040728
APA StyleFomin, V. M., & Balandin, A. A. (2015). Phonon Spectrum Engineering in Rolled-up Micro- and Nano-Architectures. Applied Sciences, 5(4), 728-746. https://doi.org/10.3390/app5040728