Thermal Lattice Boltzmann Simulation of Entropy Generation within a Square Enclosure for Sensible and Latent Heat Transfers
Abstract
:1. Introduction
2. Problem Description and Formulation
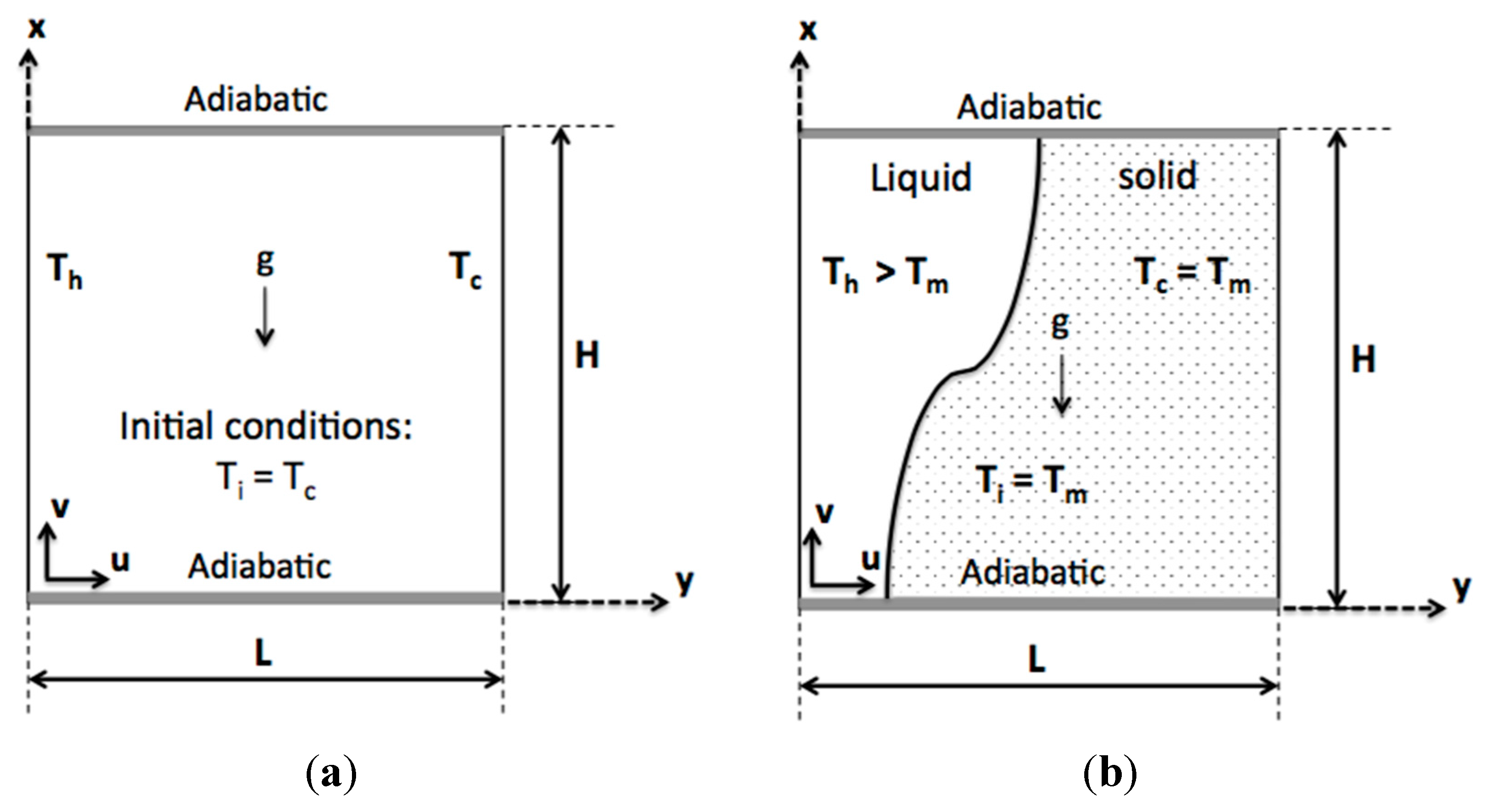
2.1. Mathematical Model
2.2. Entropy Generation
3. Numerical Model
3.1. Thermal Lattice Boltzmann Equations
3.2. Boundary Conditions
3.3. Macroscopic Quantities
4. Model Validation
4.1. Melting with Convection
4.1.1. Comparison with Similar LBM Schemes
| Parameter | Pr | Ra | Ste | Grid |
|---|---|---|---|---|
| Value | 1 | 1.7 × 105 | 10 | 150 × 150 |

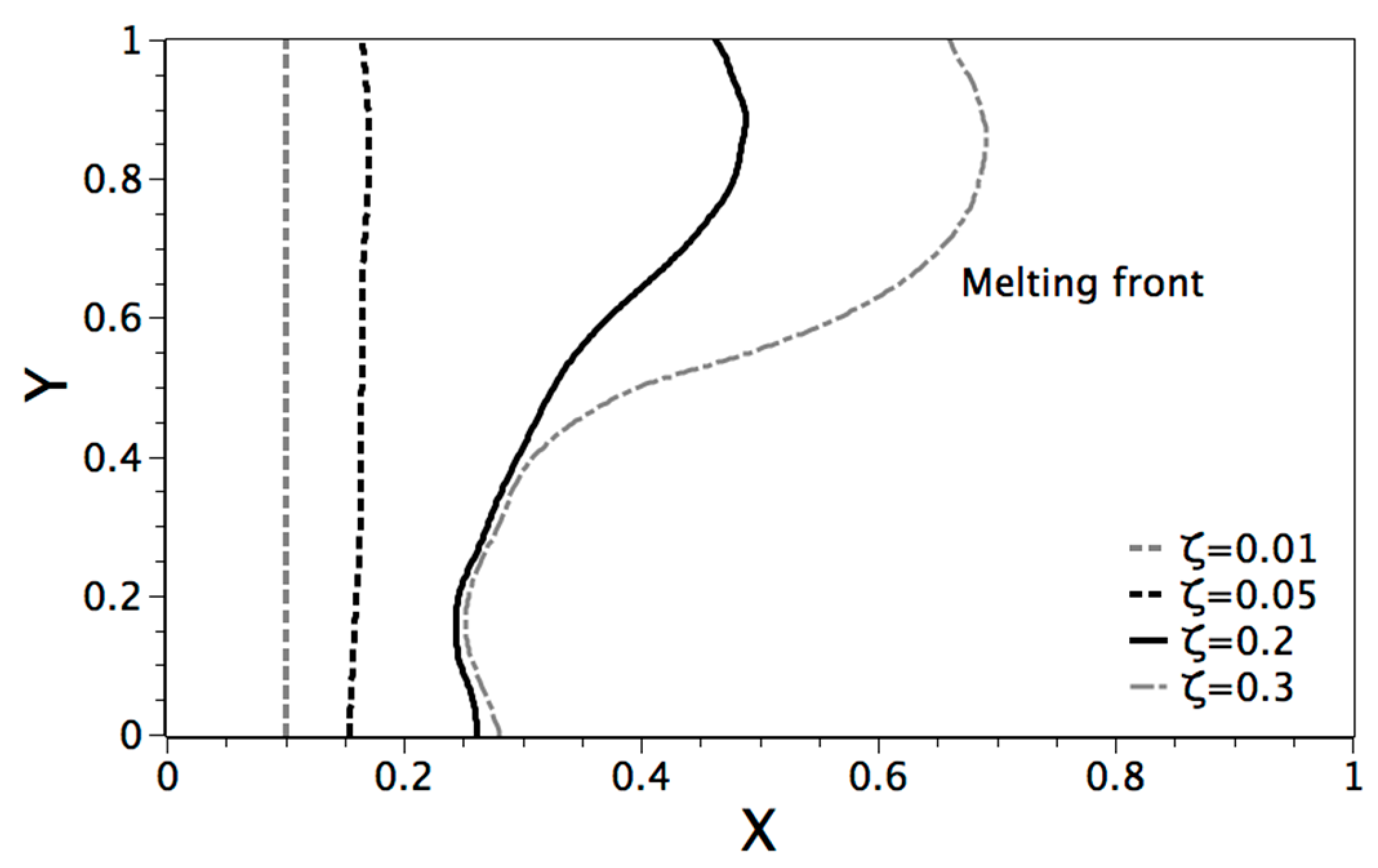
4.1.2. Comparison with Experimental Results and the Finite Volume Method
| Parameter | Pr | Ra | Ste | Aspect Ratio |
|---|---|---|---|---|
| Value | 0.021 | 6 × 105 | 0.039 | H/L = 1.4 |
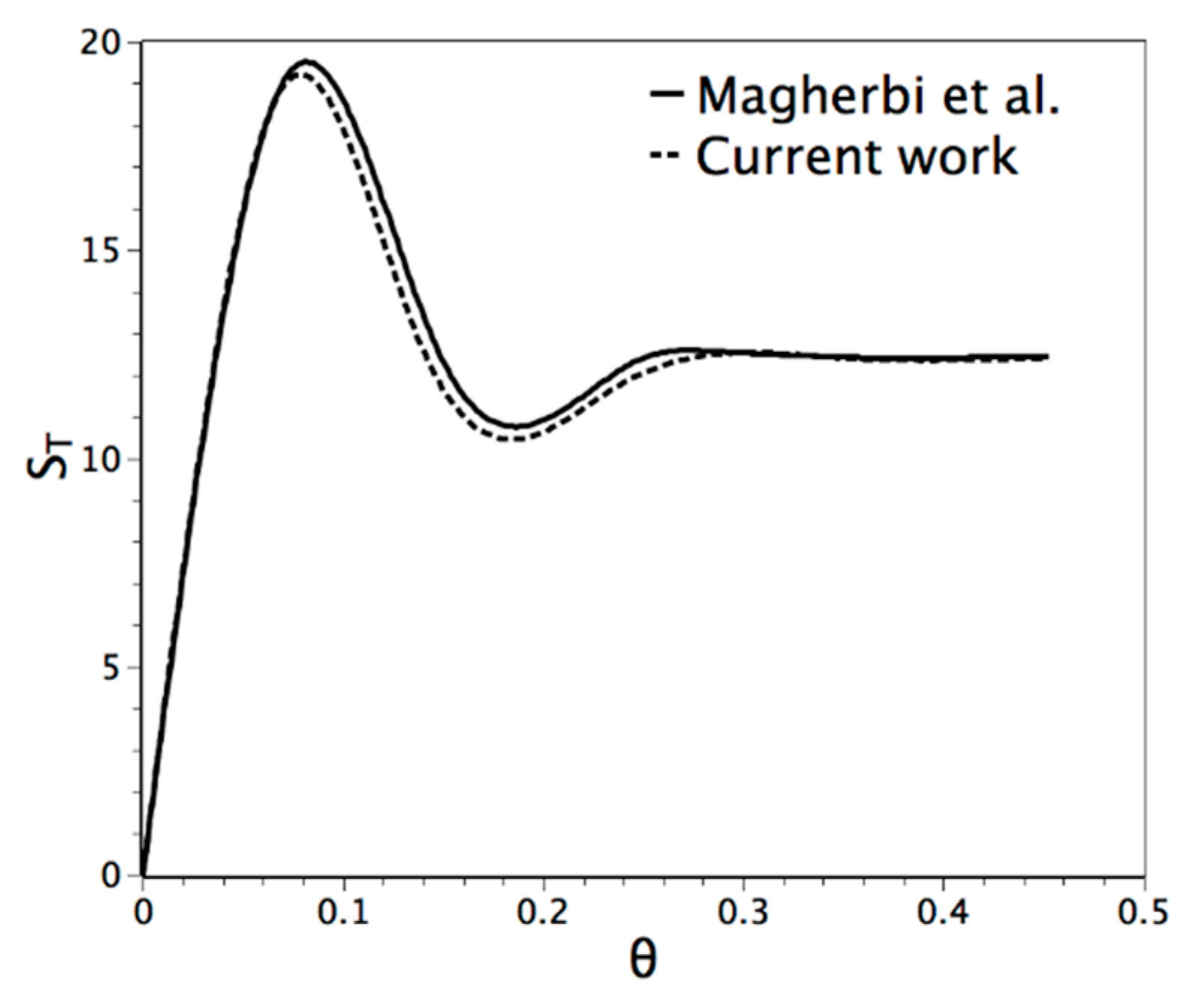
4.2. Entropy Generation
| Parameter | Pr | Ra | φ | ΔT |
|---|---|---|---|---|
| Value | 0.7 | 104 | 10−3 | 1.0 |

5. Results and Analysis
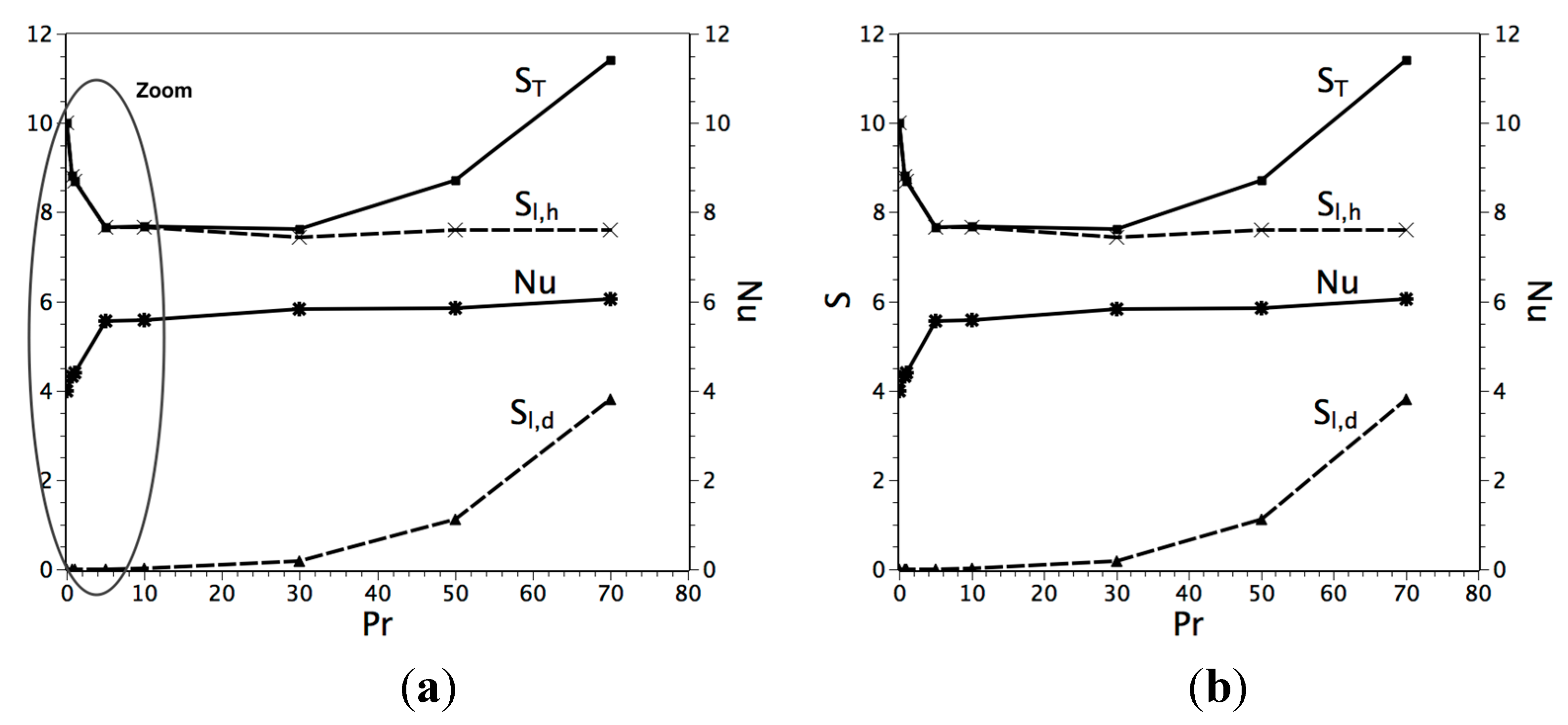
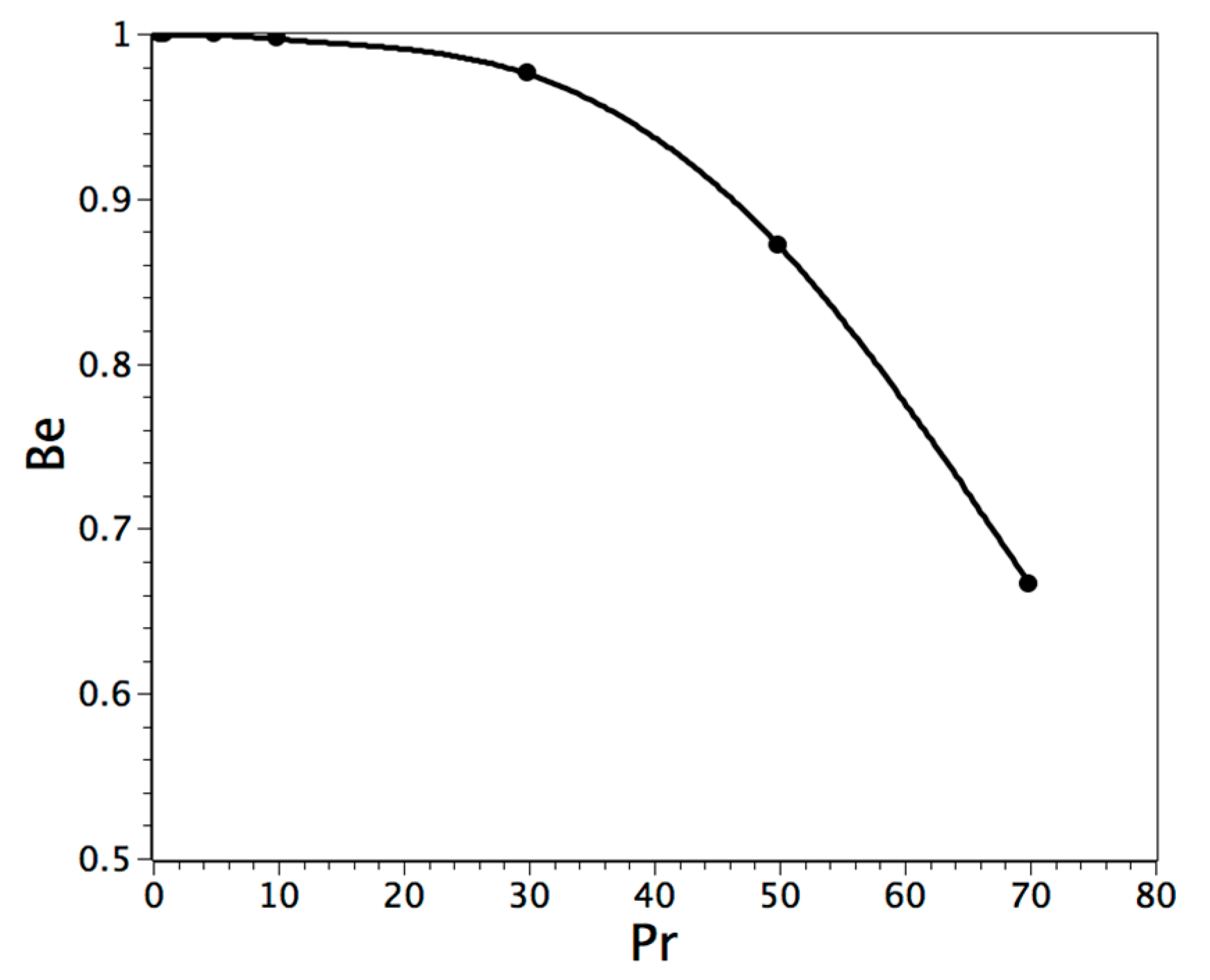
Single-Phase and Solid-Liquid Phase Change with High Prandtl Number
| Parameter | Pr | Ra | φ | Ste (Figure 1b) |
|---|---|---|---|---|
| Value | 50 | 104 − 105 | 10−5 | 1.0 |
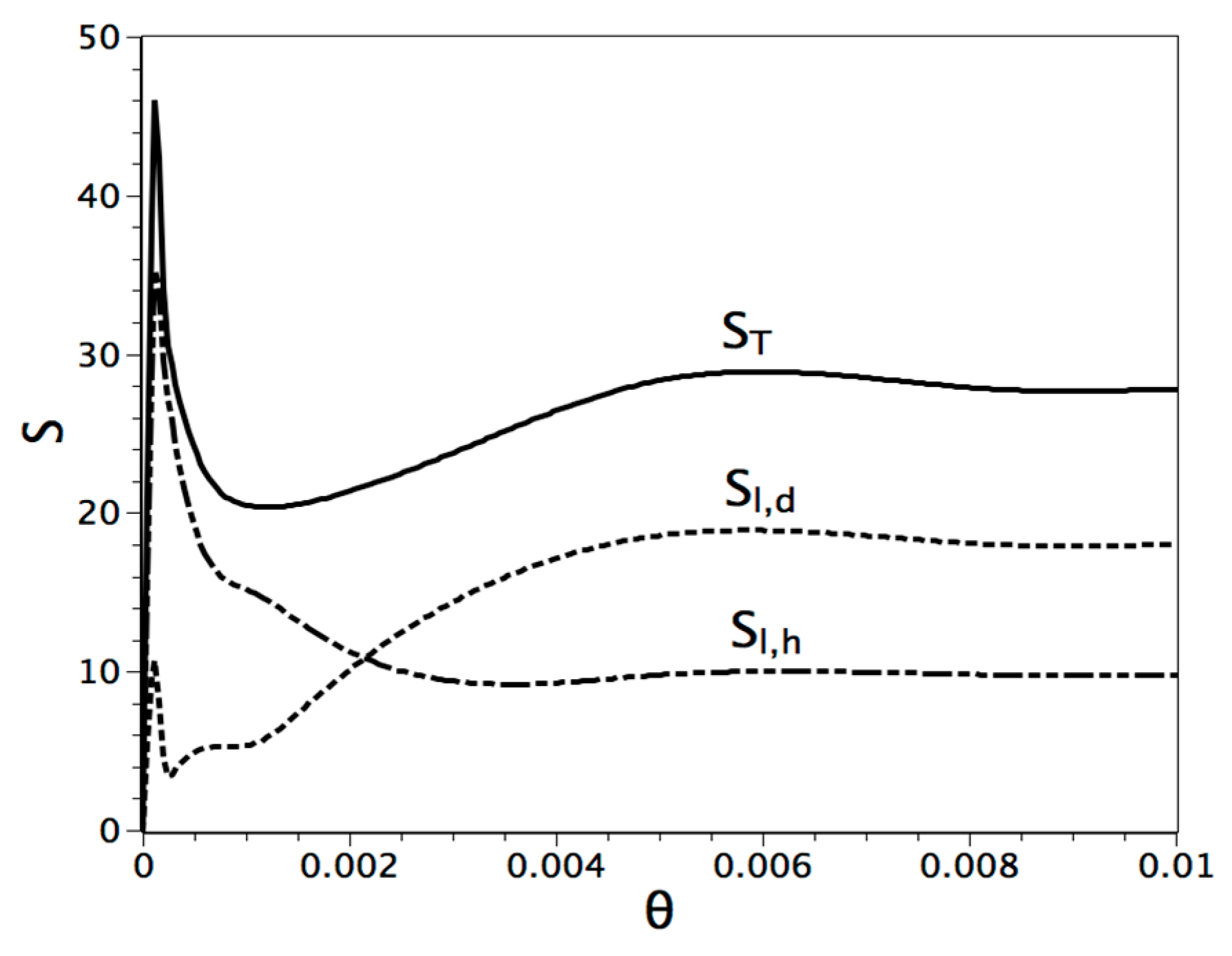
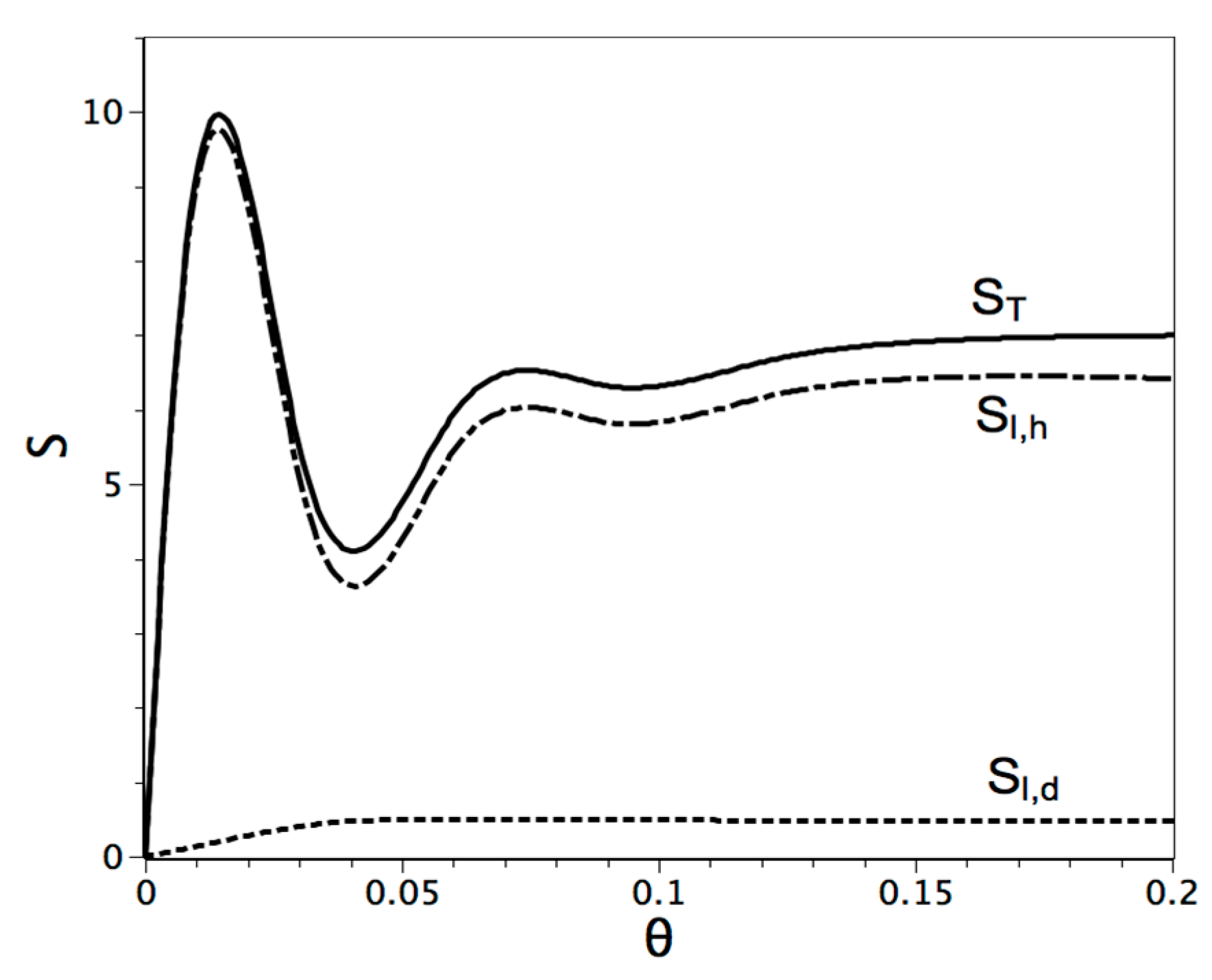
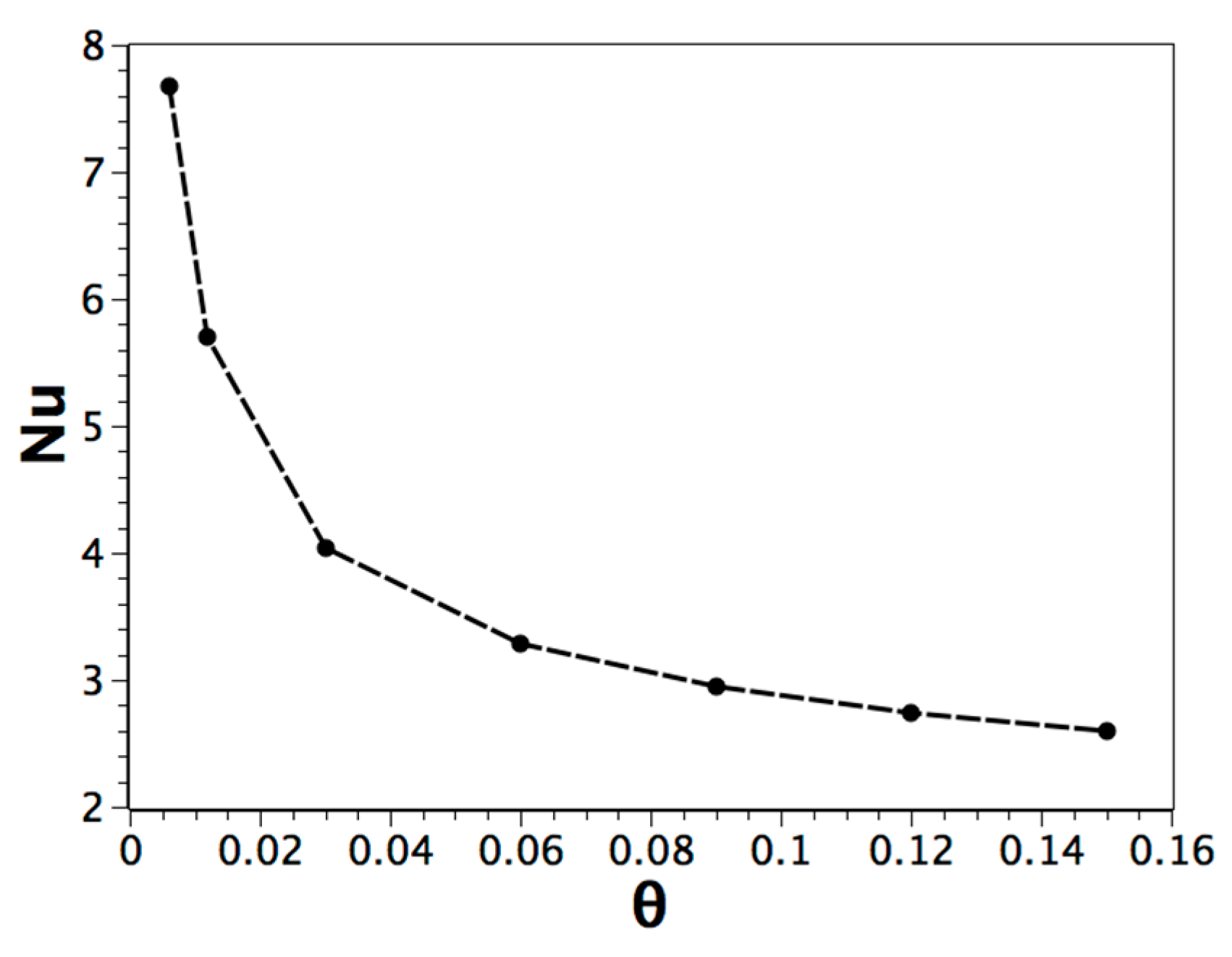

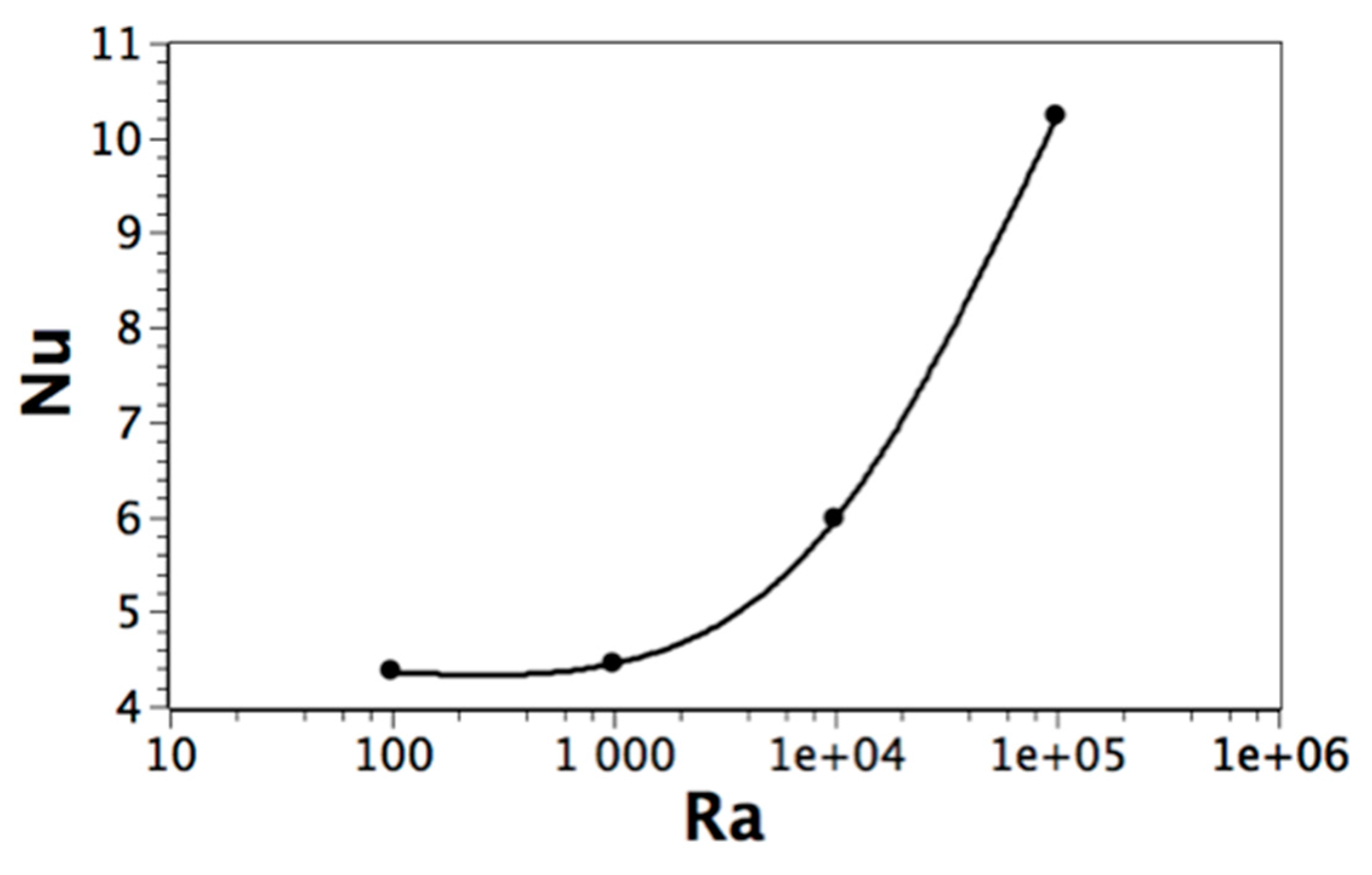
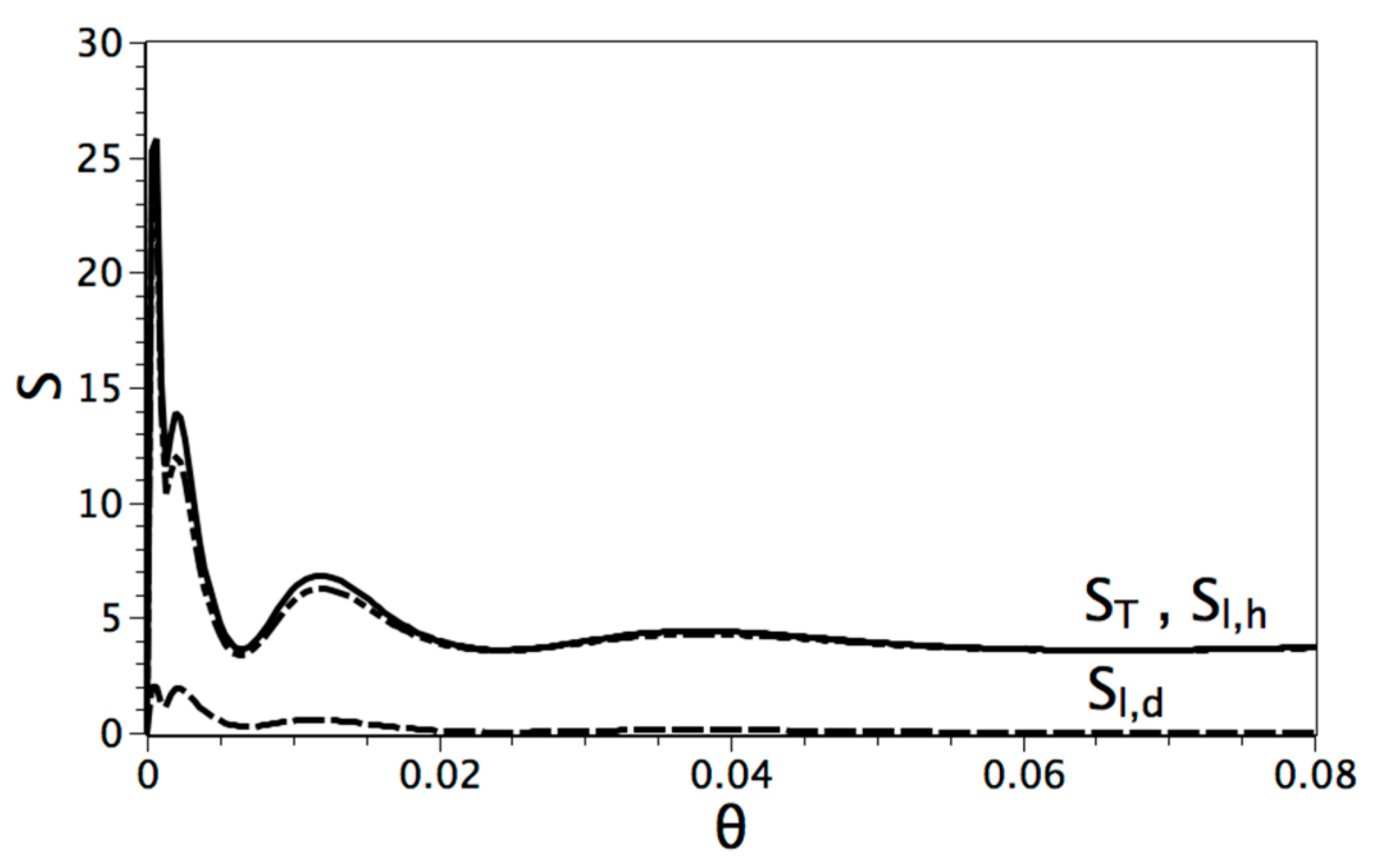
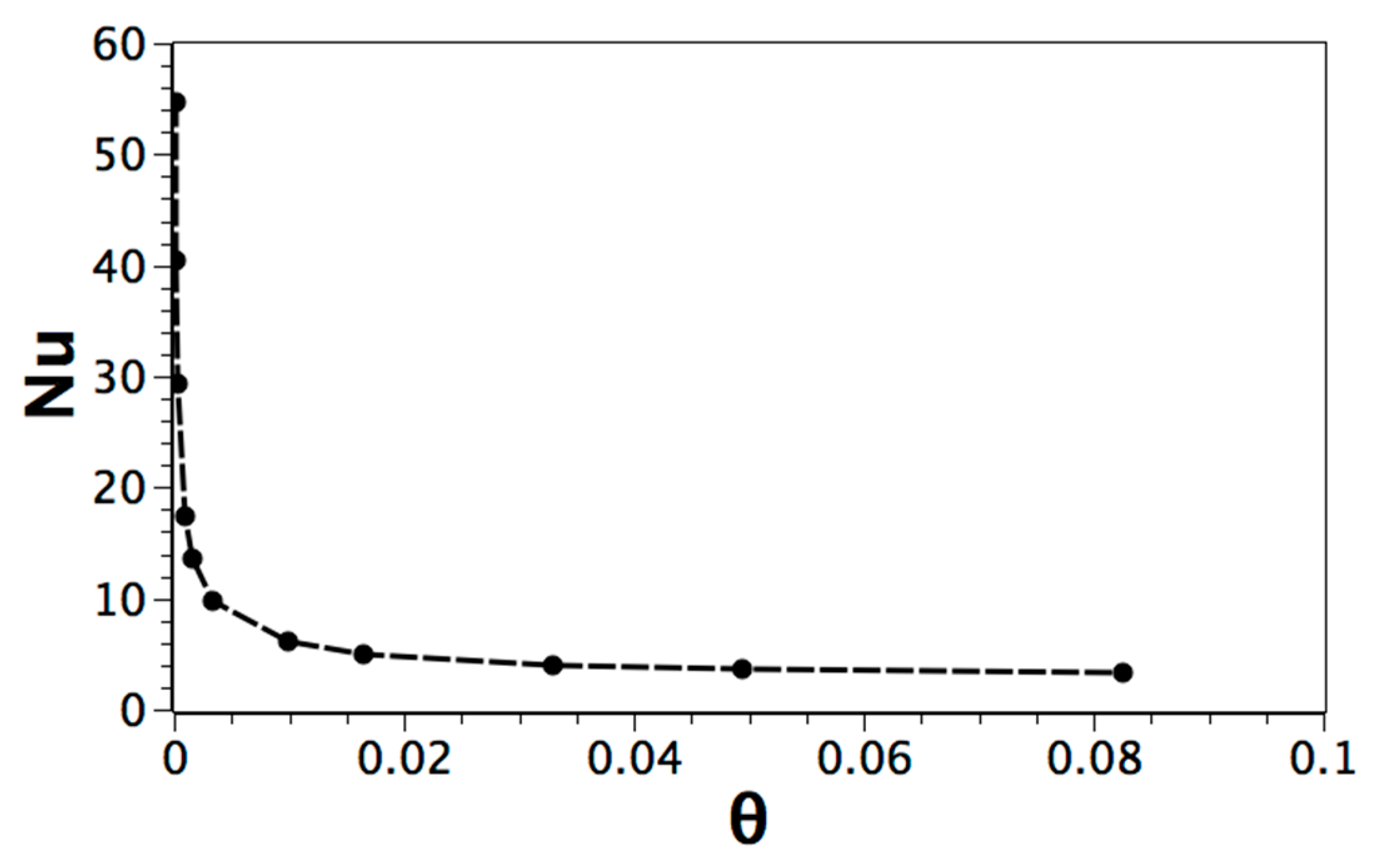
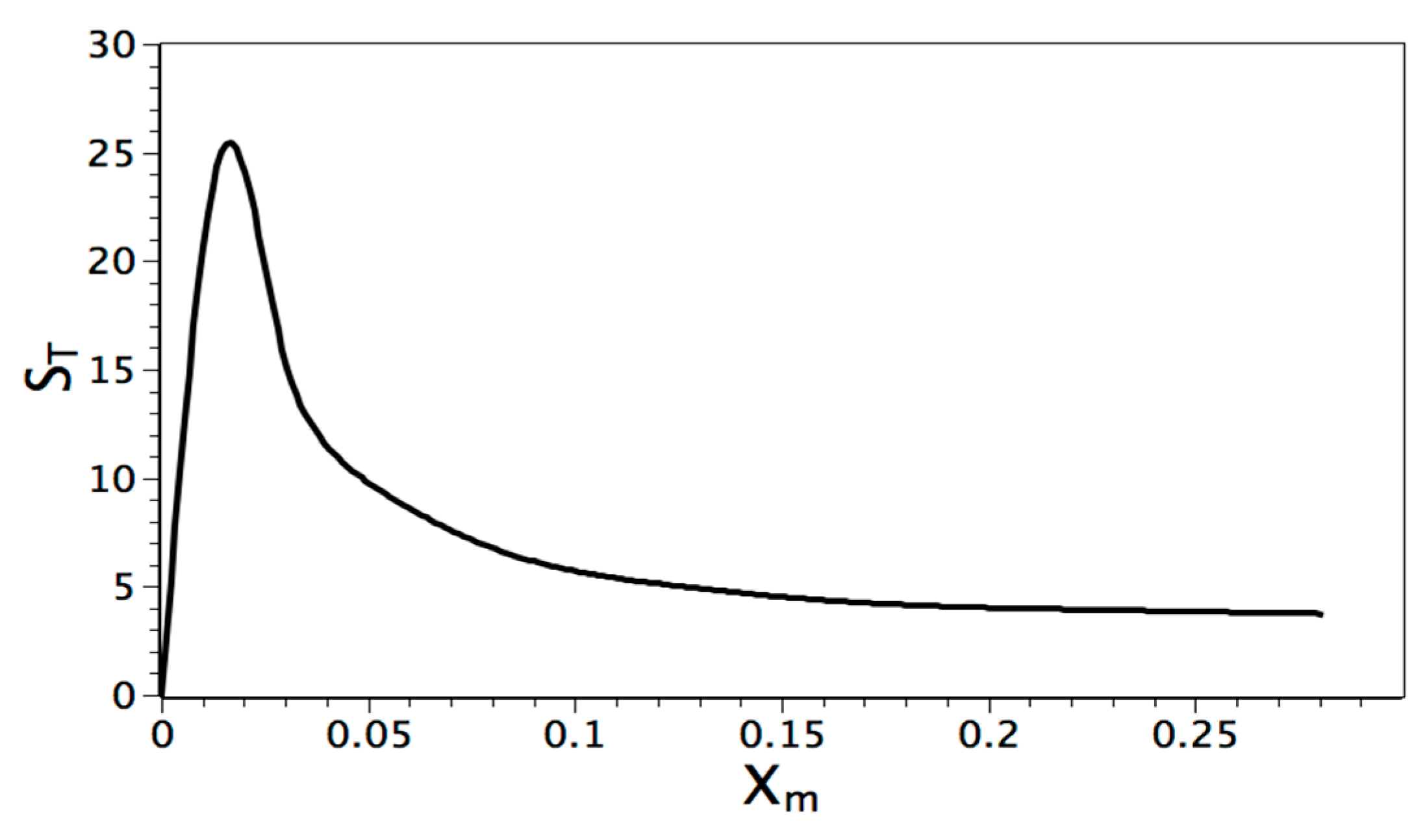
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ellahi, R.; Hassan, M. Magnetohydrodynamic flow of water/ethylene glycol based nanofluids with natural convection through porous medium. Eur. Phys. J. Plus 2014. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R.; Mohsan, H.; Soleimani, S. A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1906–1927. [Google Scholar] [CrossRef]
- Qi, C.; He, Y.; Yan, S.; Tian, F.; Hu, Y. Numerical simulation of natural convection in a square enclosure filled wih nanofluid using the two-phase lattice Boltzmann method. Nanoscale Res. Lett. 2013, 8, 1–56. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Aute, V.; Radermacher, R. Usefulness of entropy generation minimization through a heat exchanger modeling tool. In Proceedings of the International Refrigeration and Air Conditioning Conference, Poznan, Poland, 15–17 October 2008; p. 958.
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA; New York, NY, USA, 1996. [Google Scholar]
- Maghrebi, M.; Abbassi, H.; Brahim, A.B. Entropy generation at the onset of natural convection. Int. J. Heat Mass Transf. 2003, 46, 3441–3450. [Google Scholar] [CrossRef]
- Abu-Hijleh, B.A.K.; Abu-Qudais, M.; Abu-Nada, E. Numerical prediction of entropy generation due to natural convection from a horizontal cylinder. Energy 1999, 24, 327–333. [Google Scholar] [CrossRef]
- Mahmud, S.; Island, A.K.S. Laminar free convection and entropy generation inside an inclined wavy enclosure. Int. J. Therm. Sci. 2003, 42, 1003–1012. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in CuH2O nanofluid on entropy generation. Int. J. Heat Mass Trans. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, T.S.; Guo, Z.L. Thermal lattice Bhatnagar-Gross-Krook model for flows with viscous heat dissipation in the incompressible limit. Phys. Rev. E 2004, 70, 0663101–06631010. [Google Scholar]
- Li, Q.; He, Y.L.; Wang, Y.; Tang, G.H. An improved thermal lattice Boltzmann model for flows without viscous heat dissipation and compression work. Int. J. Mod. Phys. C 2008, 19, 125–150. [Google Scholar] [CrossRef]
- Sheikholelasmi, M.; Bandpy, M.G.; Ellahi, R.; Zeeshan, A. Simulation of MHD CuOwater nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mater. 2014, 369, 69–80. [Google Scholar] [CrossRef]
- Huber, C.; Parmigiani, A.; Chopard, B.; Manga, M.; Bachmann, O. Lattice Boltzmann model for melting with natural convection. Int. J. Heat Fluid Flow 2008, 29, 1469–1480. [Google Scholar] [CrossRef]
- Jourabian, M.; Farhadi, M.; Darzi, A.A.R. Convection-dominated melting of phase change material in partially heated cavity: Lattice Boltzmann study. Heat Mass Transf. 2013, 49, 555–565. [Google Scholar] [CrossRef]
- Bejan, A. Fundamentals of exergy analysis, entropy-generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26, 545–565. [Google Scholar] [CrossRef]
- Mohamad, A.A.; Bennacer, R.; El-Ganaoui, M. Double dispersion, natural convection in an open end cavity simulation via lattice Boltzmann method. Int. J. Therm. Sci. 2010, 49, 1944–1953. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Razali, S.A. Lattice Boltzmann method for convective heat transfer of nanofluids–A review. Renew. Sustain. Energy Rev. 2014, 38, 864–875. [Google Scholar] [CrossRef]
- Chen, H.; Shan, X. Simulation of nonideal gases and gas-liquid phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941–2948. [Google Scholar]
- Luo, L.-S. Lattice-Gas Automata and Lattice Boltzmann Equations for Two-Dimensional Hydrodynamics. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1993. [Google Scholar]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling: An introduction for Geoscientists and Engineers; Springer: Berlin, Germany, 2006. [Google Scholar]
- Yehya, A.; Naji, H.; Sukop, M.C. Simulating flows in multi-layered and spatially-variable permeability media via a new Gray Lattice Boltzmann model. Comp. Geotech. 2015, 70, 150–158. [Google Scholar] [CrossRef]
- Inamuro, T.; Yoshino, M.; Inoue, H.; Mizuno, R.; Ogino, F. A lattice Boltzmann method for a binary miscible fluid mixture and its application to a heat-transfer problem. J. Comput. Phys. 2002, 179, 201–215. [Google Scholar] [CrossRef]
- Jany, P.; Bejan, A. Scaling theory of melting with natural convection in an enclosure. Int. J. Heat Mass Transf. 1988, 31, 1221–1235. [Google Scholar] [CrossRef]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delanno, Y.; Gobin, D.; Lacroix, M.; Quéré, P.L.; Médale, M.; Mencinger, J.; et al. Melting driven by natural convection. A comparison exercise: First results. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]
- Miller, W.; Succi, S. A lattice Boltzmann model for anisotropic crystal growth from melt. J. Stat. Phys. 2002, 112, 173–186. [Google Scholar] [CrossRef]
- Semma, E.A.; Ganaoui, M.E.; Bennacer, R. Lattice Boltzmann method for melting/solidification problems. Comptes Rendus Méc. 2007, 335, 295–303. [Google Scholar] [CrossRef]
- Su, Y.; Davidson, J.H. A new mesoscopic scale timestep adjustable non-dimensional lattice Boltzmann method for melting and solidification heat transfer. Int. J. Heat Mass Transf. 2016, 92, 1106–1119. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a metal system in a rectangular cavity. Int. J. Heat Mass Transf. 1984, 27, 113–123. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transfer A 1988, 13, 297–318. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yehya, A.; Naji, H. Thermal Lattice Boltzmann Simulation of Entropy Generation within a Square Enclosure for Sensible and Latent Heat Transfers. Appl. Sci. 2015, 5, 1904-1921. https://doi.org/10.3390/app5041904
Yehya A, Naji H. Thermal Lattice Boltzmann Simulation of Entropy Generation within a Square Enclosure for Sensible and Latent Heat Transfers. Applied Sciences. 2015; 5(4):1904-1921. https://doi.org/10.3390/app5041904
Chicago/Turabian StyleYehya, Alissar, and Hassane Naji. 2015. "Thermal Lattice Boltzmann Simulation of Entropy Generation within a Square Enclosure for Sensible and Latent Heat Transfers" Applied Sciences 5, no. 4: 1904-1921. https://doi.org/10.3390/app5041904








