Electrical Properties of Graphene for Interconnect Applications

Abstract

A semi-classical electrodynamical model is derived to describe the electrical transport along graphene, based on the modified Boltzmann transport equation. The model is derived in the typical operating conditions predicted for future integrated circuits nano-interconnects, i.e., a low bias condition and an operating frequency up to 1 THz. A generalized non-local dispersive Ohm’s law is derived, which can be regarded as the constitutive equation for the material. The behavior of the electrical conductivity is studied with reference to a 2D case (the infinite graphene layer) and a 1D case (the graphene nanoribbons). The modulation effects of the nanoribbons’ size and chirality are highlighted, as well as the spatial dispersion introduced in the 2D case by the dyadic nature of the conductivity.

1. Introduction

Due to their outstanding physical properties, graphene and its allotropes (carbon nanotubes (CNTs) and graphene nanoribbons (GNRs)) are the major candidates to become the silicon of the 21st century and open the era of so-called carbon electronics [1,2].

Amongst all such applications, the low electrical resistivity, high thermal conductivity, high current carrying capability, besides other excellent mechanical properties, make graphene a serious candidate to replace conventional materials in realizing VLSI nano-interconnects [3,4]. A carbon-based VLSI technology is not yet a pure theoretical wish, since in the last few years, the rapid progress in graphene fabrication made possible the first examples of real-world applications. The works [5,6] present high frequency CMOS oscillators integrating CNT or GNR interconnects, whereas [7] shows the first example of a computer with PMOS transistors entirely made of CNTs. Carbon nanotubes or graphene interconnects are also successfully integrated into innovative organic transistors for flexible plastic electronics [8].

The increasing interest in carbon nano-interconnects leads to the quest for more and more accurate and reliable models, able to include all the quantum effects arising at the nanoscale. This topic has been given great attention by the recent literature, which presented several modeling approaches, like phenomenological [9] and semi-classical ones [10]. Based on such models, many papers predicted that carbon materials could outperform copper for IC on-chip interconnects and vias [11,12,13,14,15,16].

In the typical working conditions of nano-interconnects, namely a frequency up to THz and low bias conditions, such nano-structures do not exhibit tunneling transport. Thus, the electrodynamics may be studied by using a semi-classical description of the electron transport. This leads to the derivation of a constitutive relation between the electrical field and the density of the current in the form of a generalization of the classical Ohm’s law, introducing non-local interactions and dispersion. By coupling such a relation to Maxwell equations, it is possible to derive a generalized transmission line model for such nano-interconnects. This approach has been followed by the authors to model isolated metallic CNTs in [16], CNTs with arbitrary radius and chirality in [17,18], multi-walled CNTs [19] and GNRs [20]. The semi-classical model gives results consistent with those provided by an alternative hydrodynamic model [21].

In this paper, a comprehensive and self-consistent analysis of the electrical properties of graphene is presented, with special emphasis on its application as an innovative material for nano-interconnects. The self-consistency is guaranteed by the fact that the used transport model is derived from an electrodynamical model described in terms of physically meaningful parameters. This differs from what can be obtained by means of heuristics approaches. In particular, a self-consistent model provides a clear analytical relation between the model parameters and the physical and geometrical properties of the investigated structure. The considered frequency range of applications is limited to values up to 1 THz, and the operational conditions fall into the low bias regime (the longitudinal electric field along the interconnect should be E_z < 0.54 V/μm). For such cases, interband transitions are absent and non-linear effects are negligible, and thus, a simple linear transport of the conducting electrons (π-electrons) may be derived based on the tight-binding model and the semi-classical Boltzmann equation.

Section 2 is devoted to a brief résumé of the main properties of the band structure for a graphene sheet and for a graphene nanoribbon. In Section 3, the transport model is presented, derived from a semi-classical model based on the linearized Boltzmann transport equation. The model leads to the constitutive relation for the graphene, written in terms of a generalized non-local Ohm’s law in the frequency and wave-number domain. Section 4 presents a detailed discussion about the properties of the electrical conductivity, which, in general, results in being a dyad.

2. Band Structure

In this chapter, we briefly summarize the main features of the band structure, first for an infinite graphene layer (a 2D structure) and, then, for the graphene nanoribbon (a 1D structure).

2.1. Graphene Layer

Figure 1a shows the Bravais lattice of the graphene. The unit cell, S_g, is spanned by the two vectors, a₁ and a₂, and contains two carbon atoms. The basis vectors (a₁,a₂) have the same length, |a₁| = |a₂| = a = b, and form an angle of π/3, where b = 1.42 Å is the interatomic distance. The components of the vectors, a₁ and a₂, with respect to the rectangular coordinate system, (0,x,y) are, respectively, ( a₀/ 2,a₀/ 2) and ( a₀/ 2,−a₀/ 2). The area of the unit cell, S_g, is A_g = / 2.

Figure 1. The structure of graphene. (a) Bravais lattice; (b) reciprocal lattice.

Figure 1. The structure of graphene. (a) Bravais lattice; (b) reciprocal lattice.

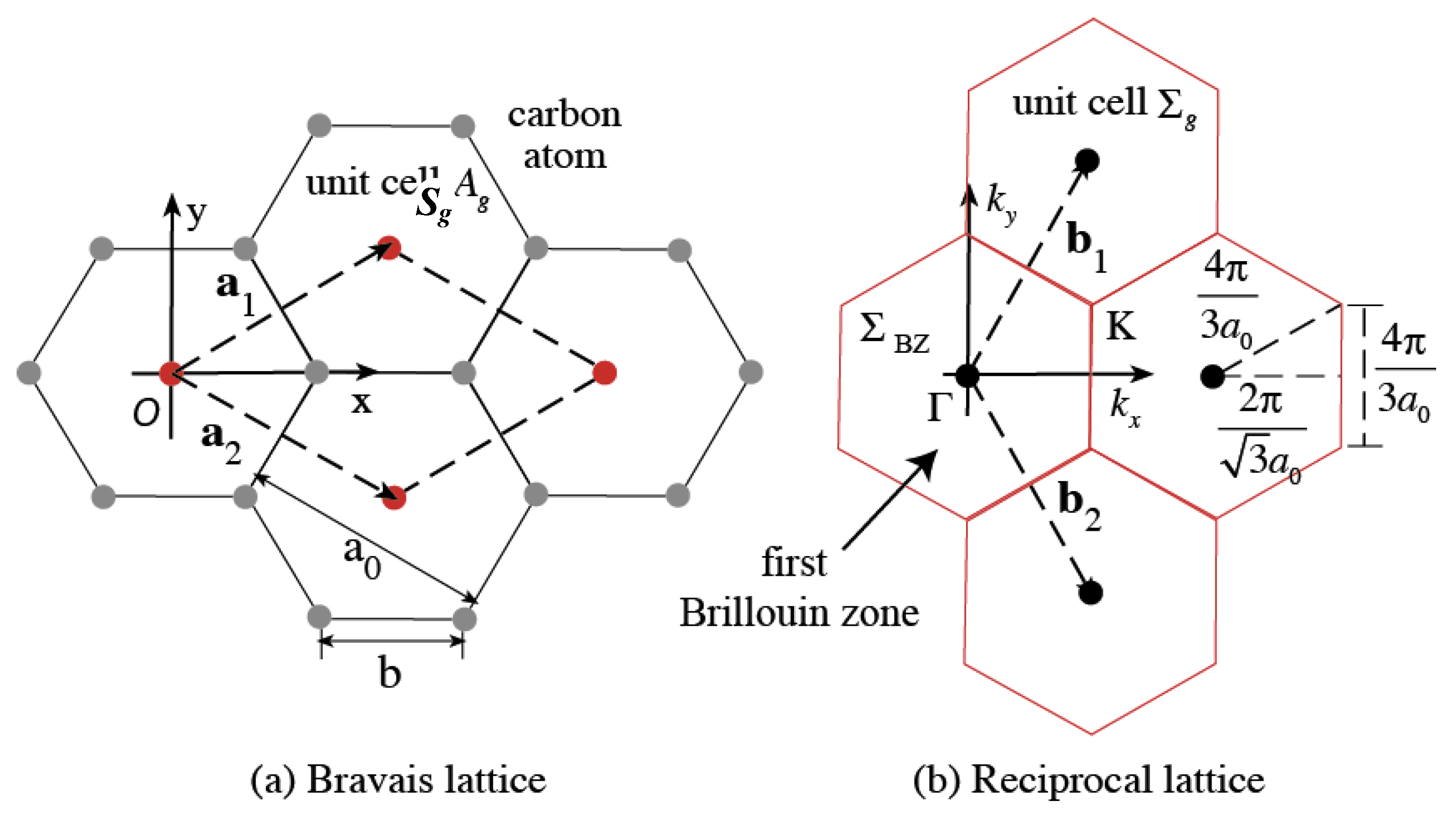
In the reciprocal k-space depicted in Figure 1b, the graphene is characterized by the unit cell, ∑_g, spanned by the two vectors, b₁ and b₂, which have the same length |b₁| = |b₂| = b₀ = 4π a₀ and form an angle of 2π/3. The components of the vectors, b₁ and b₂, with respect to the rectangular coordinate system (Q,K_x, k_y) are, respectively, (2π / a₀,2π/ a₀) and (2π / a₀,−2π/ a₀). The area of the unit cell, ∑_g, is The basis vectors of the direct space (a₁,a₂) and the basis vectors of the reciprocal space (b₁,b₂) are related by a_i∙b_j = 2πδ_ij with i,j = 1,2 and the areas, A_g and B_g, are related by A_gB_g = (2π)².

The graphene possesses four valence electrons for each carbon atom. Three of these (the so-called σ-electrons) form tight bonds with the neighboring atoms in the plane and do not play a part in the conduction phenomenon. The fourth electron (the so-called π-electron), instead, may move freely between the positive ions of the lattice.

In the nearest-neighbors tight-binding approximation, the π-electrons energy dispersion relation is

(1)

where E^(±) denotes the energy, the + sign denotes the conduction band, the − sign denotes the valence band and γ = 2.7 eV is the carbon-carbon interaction energy. The electronic band structure is depicted in Figure 2: the valence and conduction bands touch each other at the six vertices of each unit cell, the so-called Fermi points. In the neighborhood of each Fermi point, the energy dispersion relation may be approximated as:

(2)

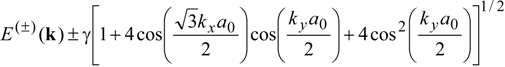
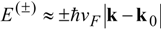
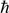where k₀ is the wavenumber at a Fermi point, ν_F ≈ 0.87 × 10⁶ m/s is the Fermi velocity of the π-electrons and is the Planck constant.

Figure 2. Graphene electronic band structure. Inset: the neighborhood of a Fermi point.

Figure 2. Graphene electronic band structure. Inset: the neighborhood of a Fermi point.

In the ground state, the valence band of the graphene is completely filled by the π-electrons. In general, at equilibrium, the energy distribution function of π-electrons is given by the Dirac–Fermi function:

(3)

where k_B is the Boltzmann constant and T₀ is the graphene absolute temperature, the electrochemical potential of the graphene being null valued. The distribution function differs from the ideal distribution function F[E^(±)] = u[−E^(±)], where u = u(x) is the Heaviside function, only in a region of order k_BT₀ around the point E^(±) = 0; at room temperature, it results k_BT₀ ≅ 0.02eV.

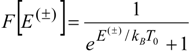
2.2. Graphene Nanoribbons

Let us now discuss the so-called graphene nanoribbons (GNRs), i.e., ribbons obtained by cutting a graphene layer, characterized by a high aspect-ratio, namely a transverse width, w, much smaller than the longitudinal ribbon length. Figure 3 shows the two basic shapes for GNRs, namely nanoribbons with armchair edges and nanoribbons with zigzag edges (e.g., [20]). These edges have a 30° difference in their orientation within the graphene sheet. We assume that all dangling bonds at graphene edges are terminated by hydrogen atoms and, thus, do not contribute to the electronic states near the Fermi level. In the following, we will assume the Fermi energy to be zero. However, this level may move to values such as 0.2–0.4 eV, considering the interactions at the GNR/substrate interface.

Figure 3. The structure of graphene nanoribbons. (a) Armchair edges; (b) zigzag edges.

Figure 3. The structure of graphene nanoribbons. (a) Armchair edges; (b) zigzag edges.

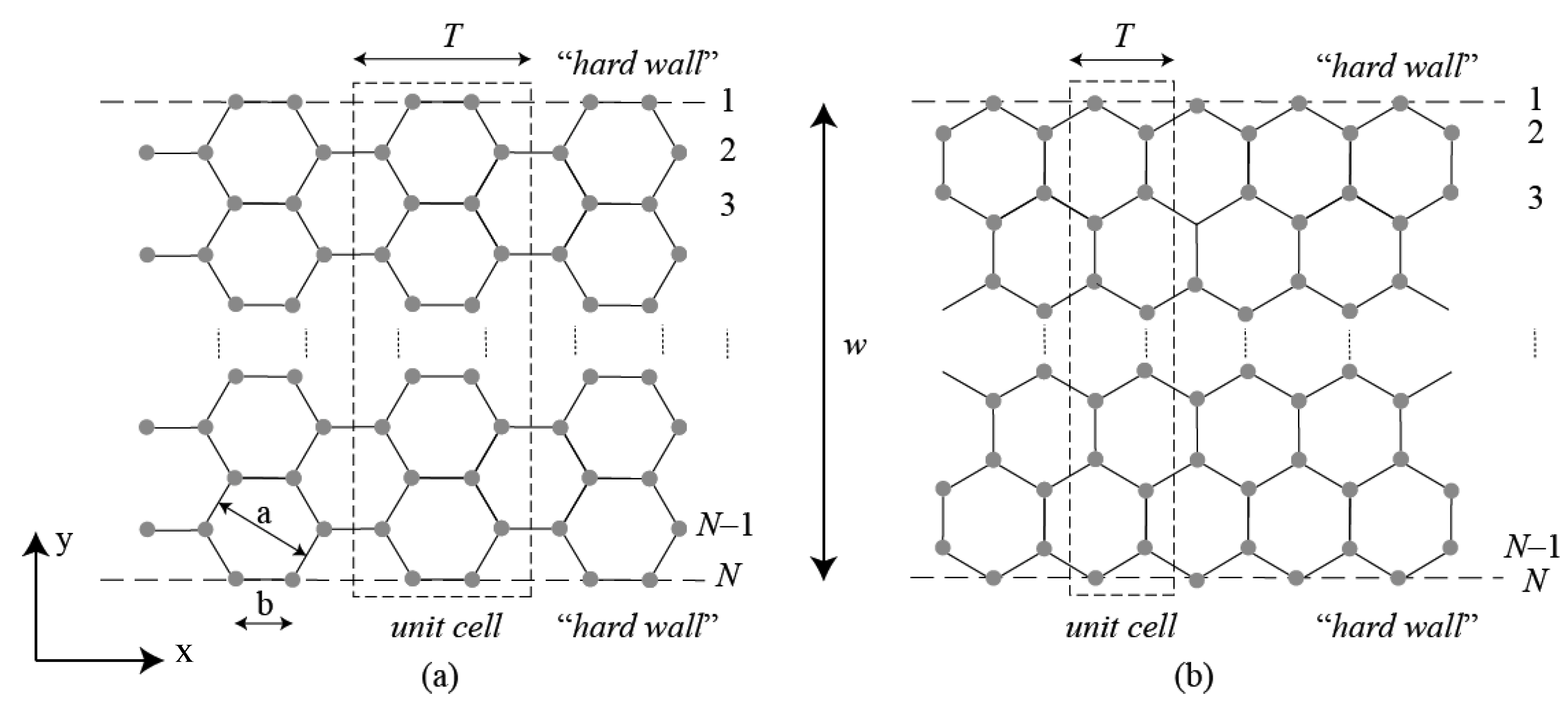
As shown in Figure 3, the width, w, of a graphene nanoribbon is directly related to the integer, N, indicating the number of dimers (two carbon sites) for the armchair nanoribbons and the number of zigzag lines for the zigzag nanoribbons. For armchair GNRs, the unit cell has a length T = a and a width w = Na/2, whereas for zigzag ones, it is T = a and w = Na/2.

Given the number N and, thus, the GNR width, w, the energy spectrum of the π-electrons can be obtained by slicing the band structure of graphene in Figure 2 (e.g., [20,22,23]). Figure 4 shows the band structure for an armchair GNR, assuming N = 5 and N = 6. For N =3q – 1 (q = 1,2,…), there exists a sub-band, µ, for which the direct bandgap is zero; hence, the GNR behaves as a metal. For other values, the armchair GNRs is semiconducting. However, the direct bandgap decreases with w increasing and approaches zero in the limit of very large w, consistent with the behavior of the graphene layer reported in Section 2.1. Therefore, the value of the width (hence, the number, N) determines whether the nanoribbon is metallic or semiconducting.

Figure 4. Energy band structure of an armchair nanoribbon versus the normalized wavenumber k' = kl/π. (a) N = 5; (b) N = 6.

Figure 4. Energy band structure of an armchair nanoribbon versus the normalized wavenumber k' = kl/π. (a) N = 5; (b) N = 6.

Figure 5 refers to a zigzag GNR, assuming N = 5 and N = 20: such nanoribbons have partially flat bands owing to the edge states; hence, their bandgap is always zero, and their behavior is always metallic.

Figure 5. The energy band structure of a zigzag nanoribbon versus the normalized wavenumber k' = kl/π. (a) N = 5; (b) N = 20.

Figure 5. The energy band structure of a zigzag nanoribbon versus the normalized wavenumber k' = kl/π. (a) N = 5; (b) N = 20.

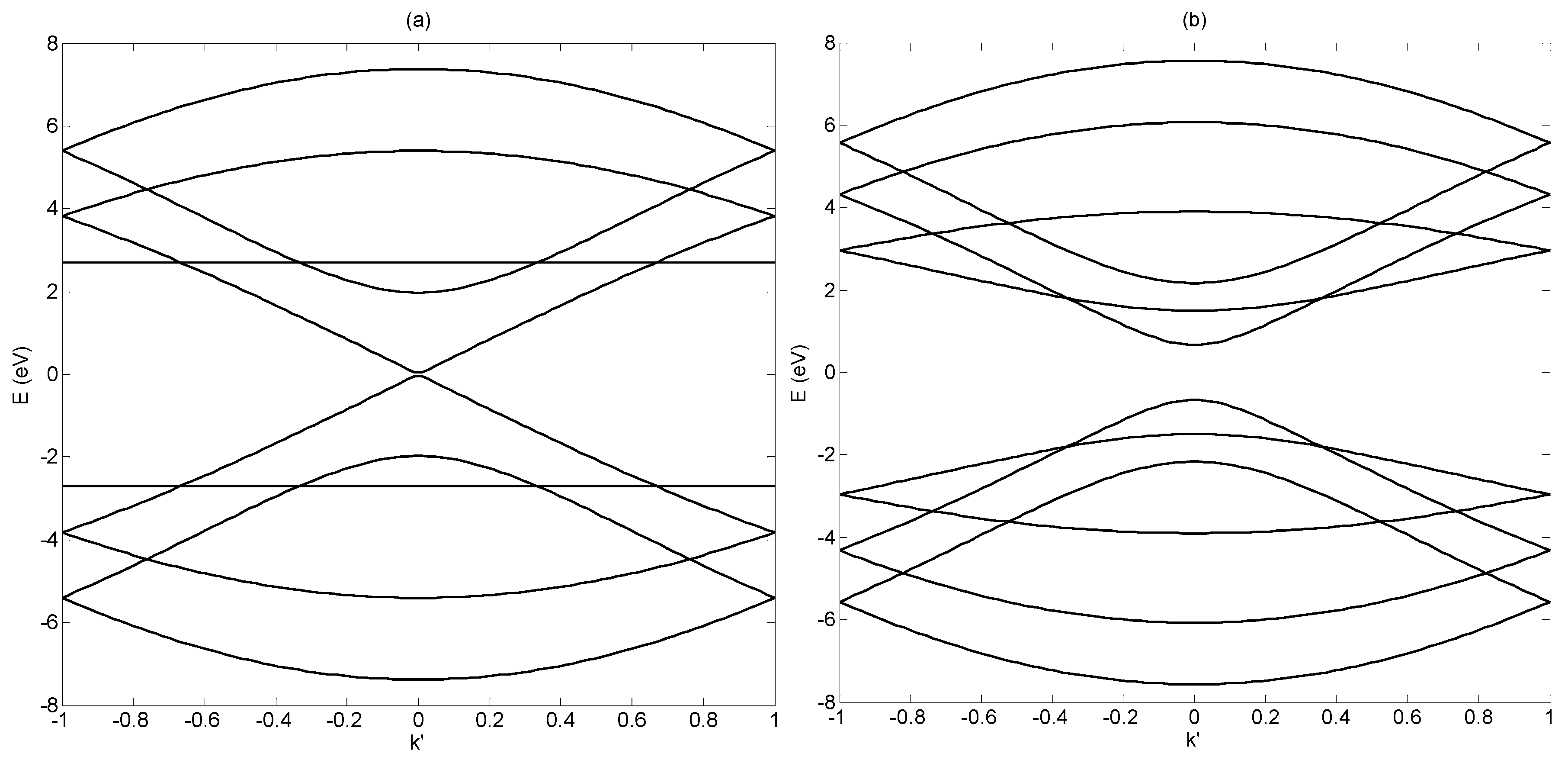
3. Transport Model

We model the propagation of an electromagnetic wave along a graphene nanoribbon in the low frequency regime, where only intraband transitions of π-electrons with unchanged transverse quasi momentum are allowed. These transitions contribute to the axial conductivity, but not to the transverse conductivity. For typical dimensions of the nano-interconnects for the 14 nm technology node and below, this assumption limits the model to a frequency up to some THz. Following the stream of what is done in [18,19,24], in such a condition, the electrodynamics of the π-electrons may be described by the quasi-classical Boltzmann equation. In the following, we start from the 2D case (graphene infinite layer) and then particularize the results to the 1D case (GNRs).

3.1. Transport Model for the Graphene Layer

The π-electrons in an infinite graphene layer behave as a two-dimensional electron gas moving on the surface under the action of the electric field. We disregard the Lorentz force term due to the magnetic field, because it does not contribute to the linear response of the electron gas.

The electron gases are described by the distribution functions f^(±) = f^(±)(r,k,t), where r is the vector position in the direct space with the origin at O, k is the electron wave-vector restricted to the first Brillouin zone and ∑_BZ and t represents the time variable. Here, the + sign denotes the conduction band, the − sign denotes the valence band.

Each of these distribution functions satisfies the quasi-classic Boltzmann kinetic equation,

(4)

where e is the electron charge, E_t = E_t(r,t) represents the tangential component of the electric field at the graphene surface, ν is the relaxation frequency (v ≅ 5·10 s⁻¹) and v^(±) = v^(±)(k) is the velocity of the π-electrons in the conduction/valence band given by:

(5)

The symbols, ∂/∂_r and ∂/∂_k, denote the gradients with respect to the variables, r and k, respectively. The distribution functions of the π-electrons at equilibrium are:

(6)

Let us consider a time-harmonic field, in the form E_t(r,t) = Re{Ê_texp[i(ωt−β·r)]}), where β is the wave-vector defined in the two-dimensional space. Let us set f^(±) = f₀^(±)(k) + δf^(±)(r, k, t) and consider a time-harmonic perturbation δf^(±)(r, k, t) = Re{δf₁^(±)(k, ω, β)exp[i(ωt − β·r)]}, where δf₁^(±) is a small quantity to be found: using Equation (4) and retaining only the first order terms, we obtain:

(7)

Let us now introduce the time harmonic surface current density j(r,t) = Re{Ĵ(ω, β)exp[i(ωt−β·r)]}): its amplitude, Ĵ(ω, β), can be computed by summing the contributions from all the sub-bands in the first Brillouin zone:

(8)

Here, the first term is related to the valence bands and the second one to the conduction bands. By combining Equations (7) and (8) we get the constitutive relation of the medium:

(9)

This can be regarded as a generalized Ohm’s law, for which the conductivity is a symmetric dyad, given by:

(10)

The function:

(11)

is an even function. As a consequence of this property and of the right-left symmetry of the energy dispersion curves with respect to the point k = 0, the sum in the r.h.s. of Equation (10) is twice the contribution of the conduction bands, hence:

(12)

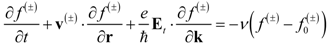
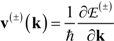
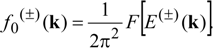
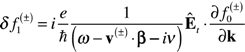
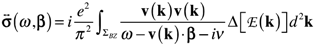
Note that the function, Δ, behaves as an impulsive function centered at ; hence, only the neighbors of the Fermi points with radius and belonging to the first Brillouin zone give a meaningful contribution: let us indicate with C_F the circumference of radius k_eff centered at the Fermi point with electron wave vector K. In addition, assuming , , we get the final expression:

(13)

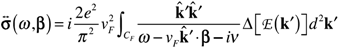
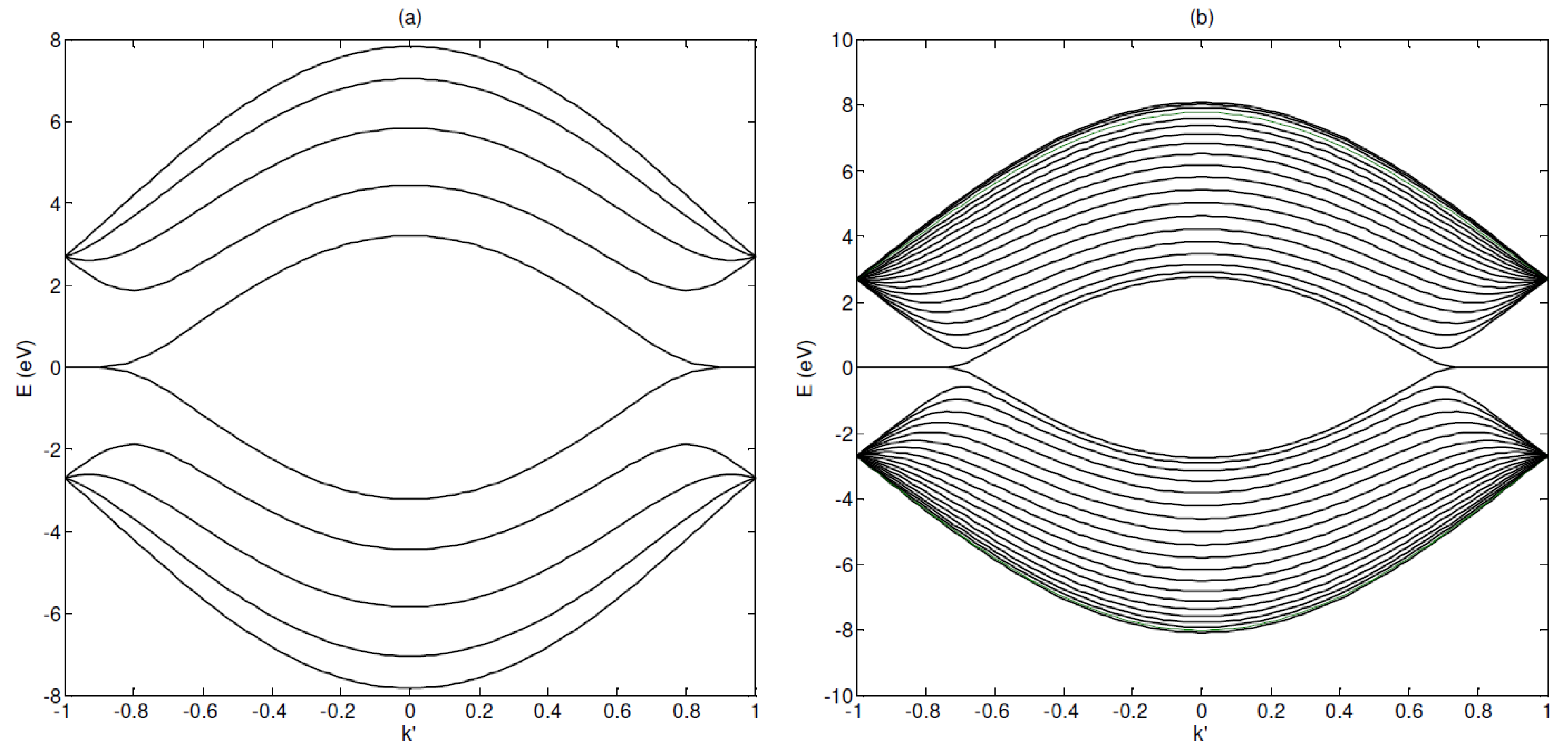
3.2. Transport Model for a Graphene Nanoribbon

Along a graphene nanoribbon, in the operating conditions assumed here, the π-electrons mainly move along the longitudinal axis, i.e., the transverse components may be neglected. Therefore, the transport model is derived from that exposed in Section 3.1, assuming a 1D case: the electrons are quantum confined laterally and, thus, occupy quantized energy levels, whereas along the longitudinal axis, the wave-vector, k, is assumed to be almost continuous.

If T is the translational length of the unit cell (see Figure 3), the first Brillouin zone is given by the interval (−π/T,π/T) and the longitudinal conductivity in the spatial and wavenumber domain obtained from Equation (13) is given by the sum of the contribution of the N conduction sub-bands in the circumference C_F:

(14)

where:

(15)

Using the above results, the generalized Ohm’s law Equation (9) may be expressed for a GNR as follows:

(16)

where we have introduced the following functions:

(17)

R₀ = 12.9 kΩ being the quantum resistance, and:

(18)

(19)

The quantity M in Equation (19) is the equivalent number of conducting channels, a measure of the number of sub-bands that effectively contribute to the electric conduction, i.e., those that cross or are closer to the Fermi level. A detailed discussion on the behavior of such a number M for CNTs and GNRs may be found in [18,19,20], where it is clearly shown how such a quantity strongly depends on the chirality, size and temperature of such carbon nanostructures.

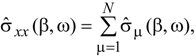
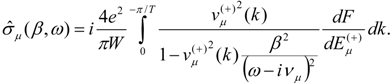
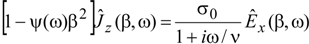
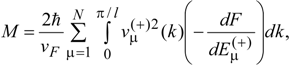
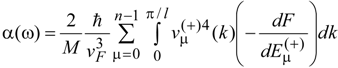
4. Discussion

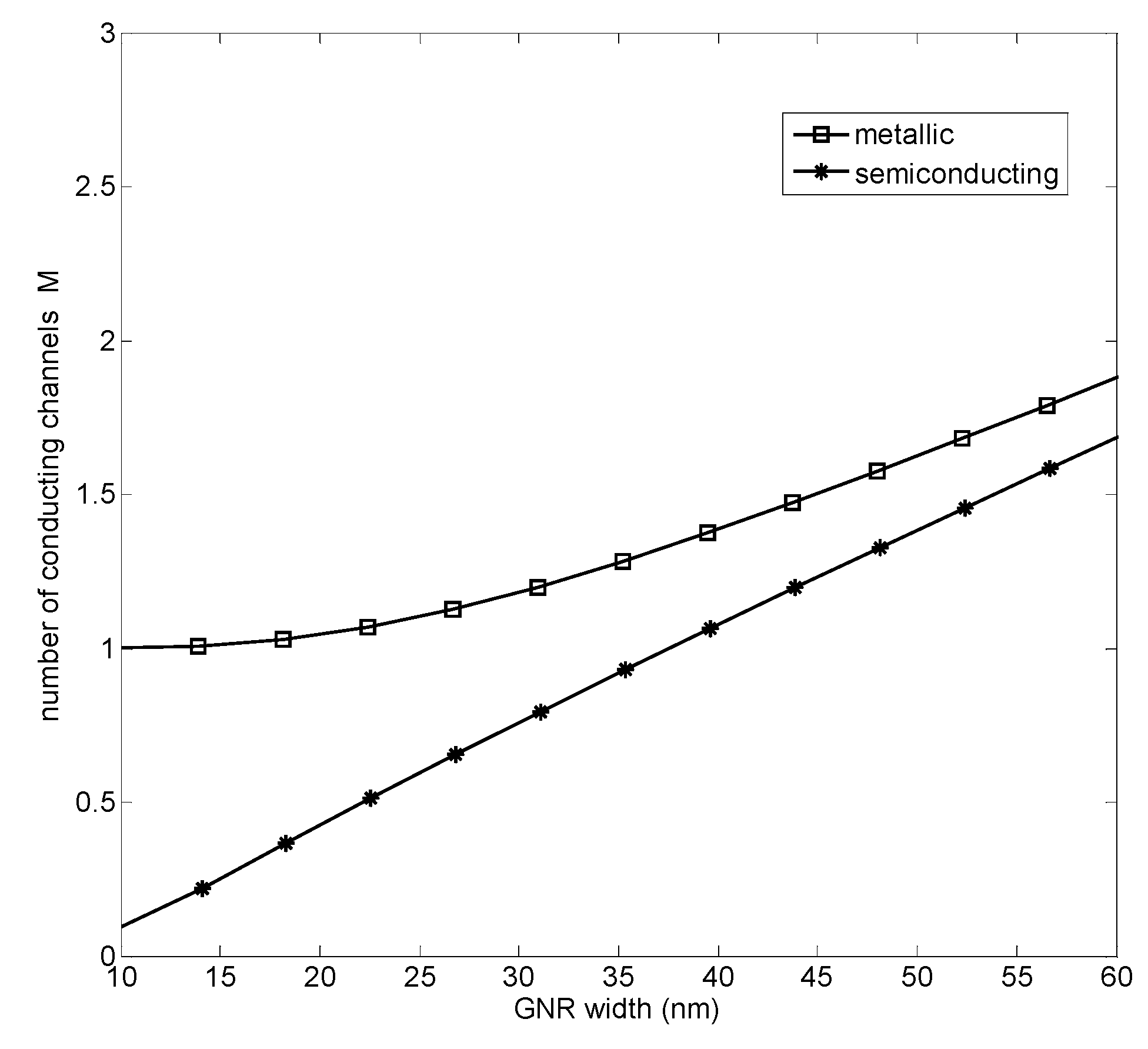
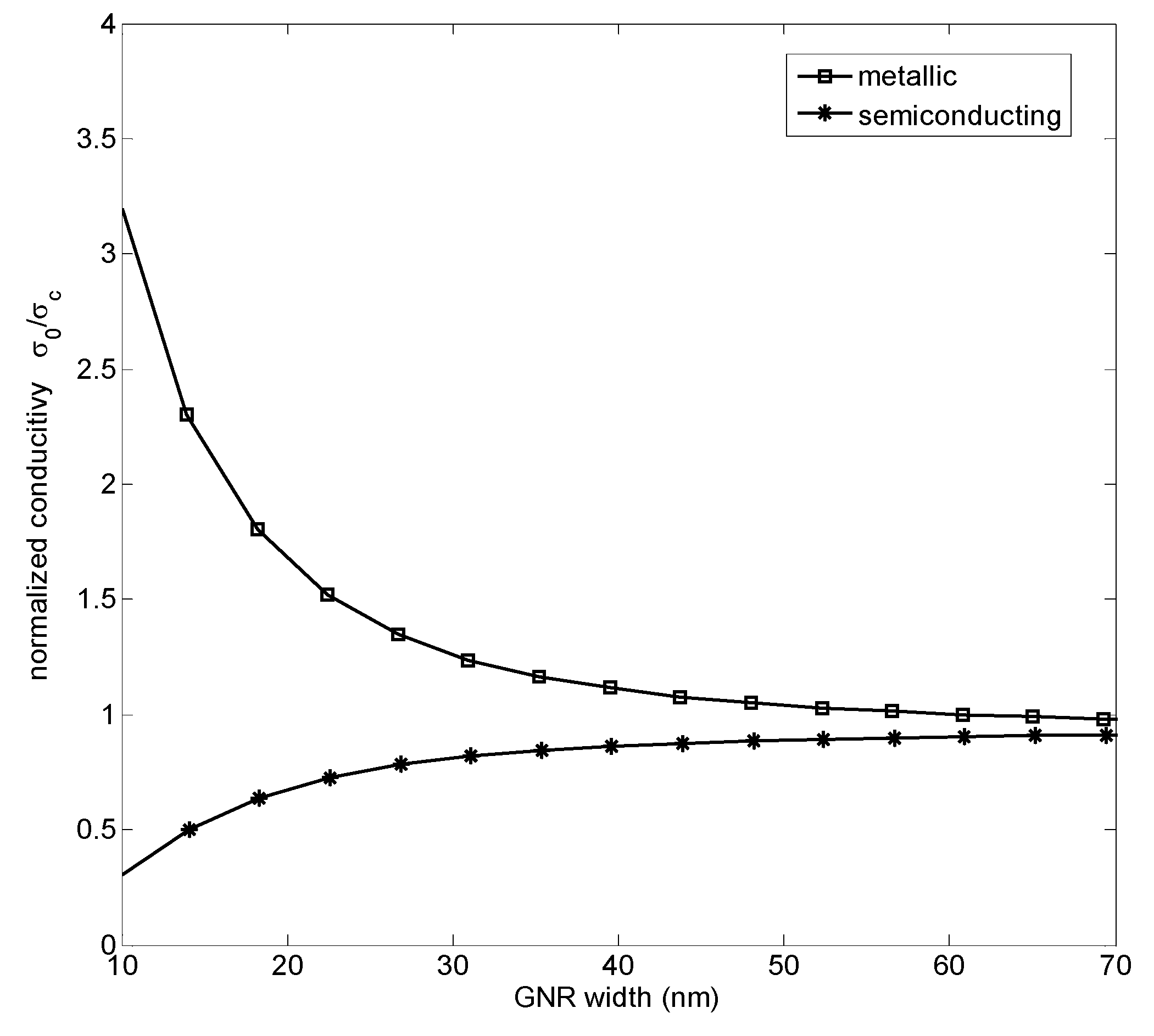
4.1. Electrical Conductivity in the Long Wavelength Limit

Let us first assume the case of a graphene layer in the long wavelength limit β = 0, for which Equation (13) reduces to:

(20)

In the reference system indicated in Figure 1, the four components, σ_xx(ω,0), σ_yy(ω,0), σ_xy(ω,0) and σ_yx(ω,0) of the dyad, σ(ω,0), reduce to the following expressions:

(21)

where:

(22)

In the same condition, the generalized Ohm’s law for a graphene nanoribbon Equation (16) would reduce to:

(23)

Figure 6. Equivalent number of conducting channels for metallic and semiconducting armchair graphene nanoribbons (GNRs) at 300 K.

Figure 6. Equivalent number of conducting channels for metallic and semiconducting armchair graphene nanoribbons (GNRs) at 300 K.

The conductivity, σ_c, in Expression (22) is consistent with σ₀ in Equation (23): σ_c may be obtained from σ₀ by taking the limit W → ∞, i.e., when the transverse size of the GNR tends to infinity. To explain this behavior, Figure 6 shows the computed value of the number of conducting channels, M, in Equation (18), for a metallic and semiconducting armchair GNR vs. the GNR width. For smaller values of W, the contribution to the conductivity given from the semiconducting GNRs is negligible, but it becomes non-negligible as W increases. Figure 7, instead, shows the behavior of the ratio, σ₀/σ_c, as a function of W, which proves the consistency stated above.

Figure 7. The ratio, σ₀/σ_c, for metallic and semiconducting armchair GNRs at 300 K.

Figure 7. The ratio, σ₀/σ_c, for metallic and semiconducting armchair GNRs at 300 K.

As a conclusion, in the case of a long wavelength limit, the conductivity of graphene does not show spatial dispersion, but only frequency dispersion, according to Equation (22). For a GNR (as in Figure 3), the conductivity may be assumed to have only the longitudinal component σ_xx(ω,0) = σ(ω).

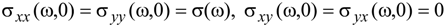
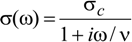
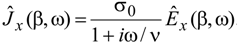
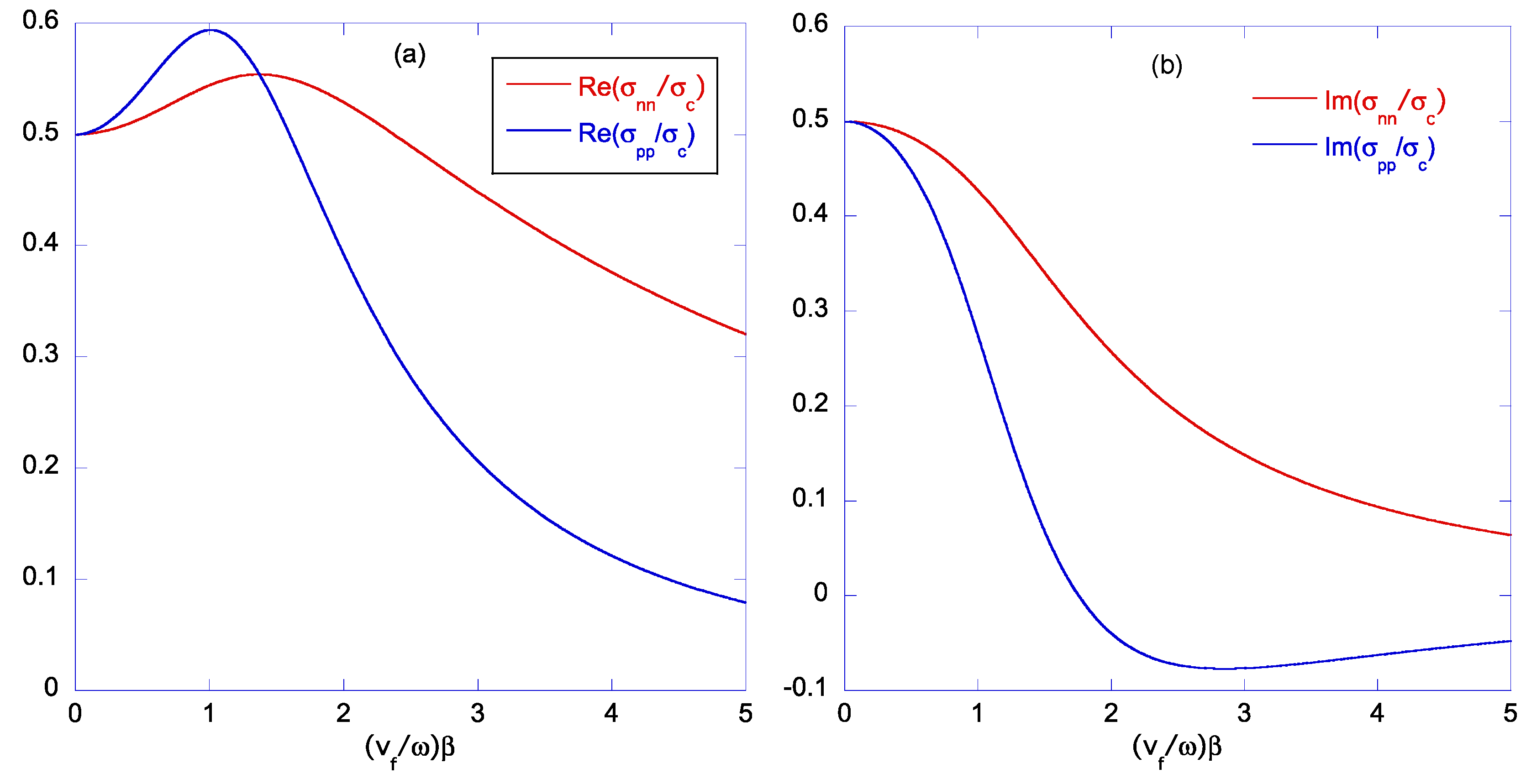
4.2. Electrical Conductivity in the General Case: Spatial Dispersion

In the general case, we must take into account the dyadic nature of the conductivity. For the sake of simplicity, let us refer to the components of any vector to the parallel and orthogonal directions with respect to the vector, β, denoting them with the symbols “||” and “⊥”, respectively. In this system, the four components, σ_||||(ω,β), σ_⊥⊥(ω,β), σ_||⊥(ω,β) and σ_⊥||(ω,β), of the dyad, σ(ω,β), reduce to the following expressions:

(24)

σ_||⊥(ω,β) = σ_⊥||(ω,β) = 0

(25)

where:

(26)

From such components, it is possible to derive the x-y components, by the simple transformation:

(27)

Figure 8. Real (a) and imaginary (b) parts of σ_||||(ω,β) and σ_⊥⊥(ω,β), normalized to σ_c, vs. (ν_F/ω)β for ν/ω = 0.1.

Figure 8. Real (a) and imaginary (b) parts of σ_||||(ω,β) and σ_⊥⊥(ω,β), normalized to σ_c, vs. (ν_F/ω)β for ν/ω = 0.1.

By using Equation (27), it is easy to show that there are off-diagonal terms of the dyad; hence, in general, σ_xy(ω,β) = σ_yx(ω,β) ≠ 0. The dyadic nature of the conductivity introduces a spatial dispersion, which may be easily observed from Figure 8 and Figure 9, which show the real and imaginary parts of σ_||||(ω,β) and σ_⊥⊥(ω,β), normalized to σ_c, versus (ν_F/ω)β for ν/ω = 0.1 and ν/ω = 1, respectively. It is evident that a resonance still arises at ω ≅ βv_F in both cases.

Figure 9. Real (a) and imaginary (b) parts of σ_||||(ω,β) and σ_⊥⊥(ω,β), normalized to σ_c, vs. (ν_F/ω)β for ν/ω = 1.

Figure 9. Real (a) and imaginary (b) parts of σ_||||(ω,β) and σ_⊥⊥(ω,β), normalized to σ_c, vs. (ν_F/ω)β for ν/ω = 1.

The relation between the dyadic nature of the conductivity and the spatial dispersion is consistent with the result obtained in [25], where the graphene conductivity dyad is derived from the Kubo formula and numerically evaluated with an integral formulation.

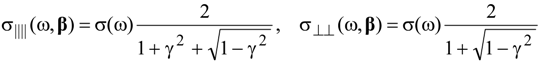
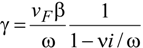
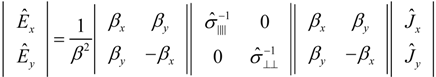
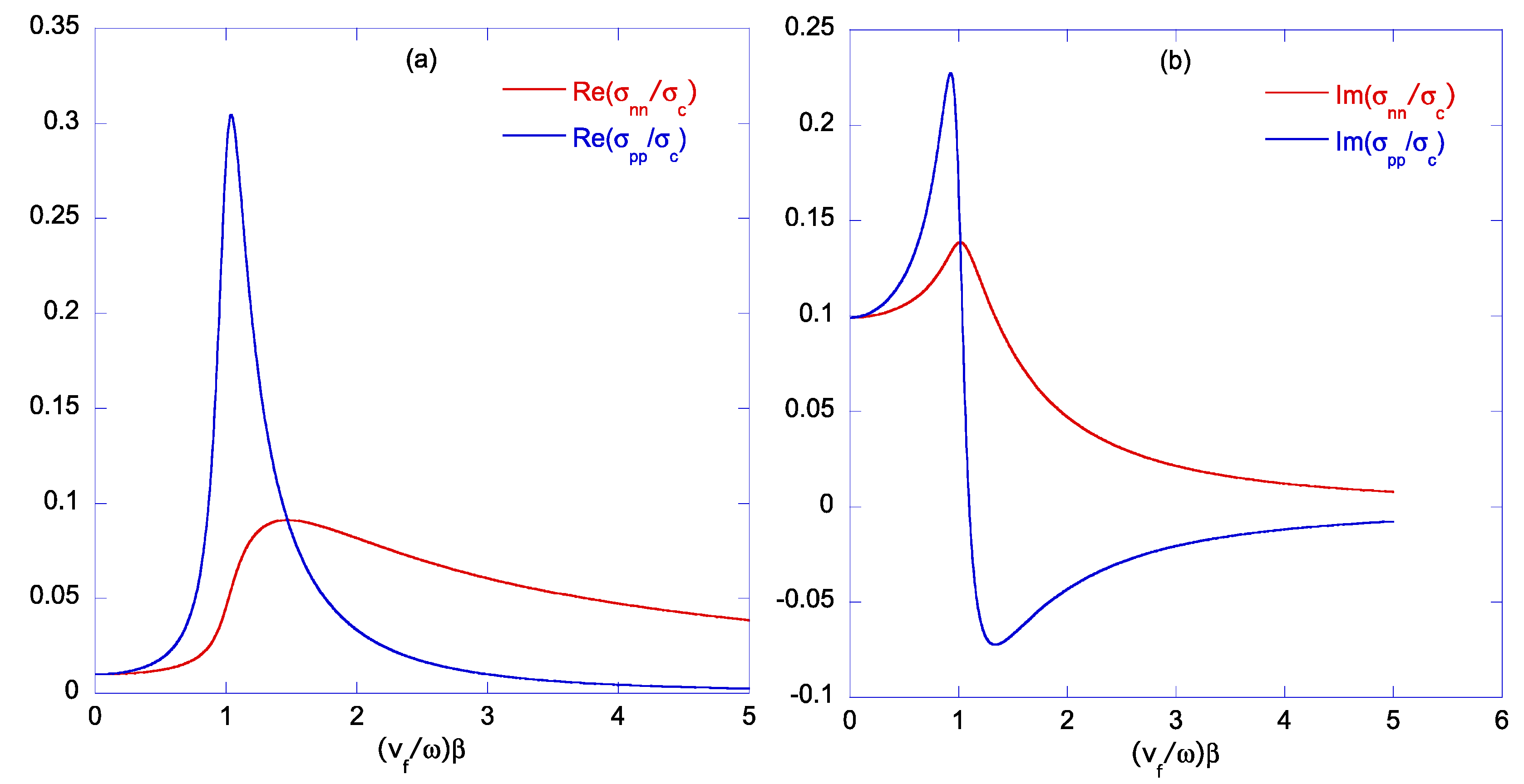
5. Conclusions

In the operating conditions predicted for future electronic nano-interconnects, the low bias and the low frequency allows the modeling of the electrical transport with a linearized semi-classical electrodynamical model, which does not include interband transitions. This leads to a generalized non-local dispersive Ohm’s law, which is regarded as the constitutive equation for the material. In the 2D case (graphene layer), the conductivity is dyadic and shows a spatial dispersion as an effect of the coupling between the components. This coupling is absent in the long-wavelength limit. In the 1D case (graphene nanoribbon), the transverse components of the currents are negligible, and the conductivity reduces to a scalar quantity, modulated by the size and chirality, which strongly affect the number of conducting channels.