1. Introduction
Synchrotron light sources have shown remarkable scientific capabilities and quite successfully reveal various scientific and technological phenomena in a wide range of materials, including semiconductors, polymers, ceramics and biological molecules. However, the current third-generation synchrotron light sources (3G SLSs) generate X-ray pulses in the picosecond time domain, which does not allow the study and the manipulation of ultrafast dynamics in atoms, molecules and nanoscopic systems. An X-ray free electron laser (XFEL), which is brighter by approximately 10 orders of magnitude and 100–1000-times shorter in pulse duration than 3G SLSs, can be a boon for paradigm-shifting science, such as the study of ultrafast phenomena in atomic, molecular and nanoscopic systems under intense light fields. With the advent of XFEL, a new era of X-ray science has arrived; yet, the current XFEL is to be further developed to deliver attosecond pulse, with which real-time studies of electron-electron correlations, unexplored up to now, can be fully investigated.
In this vein, this paper concerns the generation of attosecond hard X-ray pulses, including also a review of current XFEL technologies. The structure of this paper is as follows. In
Section 2, the advances in FEL developments are reviewed, including elaborate innovative schemes based on self-amplified spontaneous emission (SASE)-FEL for radiation pulses in the attosecond domain. In
Section 3, we provide our simulation results for the generation of an isolated attosecond pulse using the Pohang Accelerator Laboratory (PAL)-XFEL parameters. A summary and conclusions are presented in
Section 4.
2. Review of Efforts toward Attosecond Hard X-ray FEL
Hard X-ray FEL machines are either in operation or under construction [
1,
2,
3,
4]. In the early 1980s, the basic concept of the current SASE-FELs was developed [
5]. Even though SASE-FEL has been always a favorite choice as a potential source for sub-femtosecond X-ray pulses, its inherent problem limits the temporal coherence of the output radiation of a SASE-FEL. Moreover, this radiation consists of many sub-femtosecond peaks, whose arrival time varies randomly from shot to shot. This makes the use of SASE-FEL in pump probe experiments in the attosecond time scale very difficult.
Exploiting the SASE scheme, several experiments and simulation work have been done for the generation of picosecond, femtosecond and attosecond X-ray pulses. SASE-FEL radiations in the vacuum ultraviolet (VUV), extreme ultraviolet (EUV) and soft X-ray regions have been demonstrated successfully [
6,
7,
8,
9,
10,
11,
12,
13].The efforts towards the generation of hard X-ray pulses in a femtosecond time domain have been made. In the hard X-ray region, the linac coherent light source (LCLS) at the Stanford Linear Accelerator (SLAC) [
14] is the first hard X-ray FEL machine, which has been in operation since 2009. This facility has tunable radiation wavelengths from 2.2 to 0.12 nm by varying the electron energy from 3.5 to 15 GeV. Since March 2012, scientists have also an access to the second hard X-ray FEL: The Spring-8 Angstrom Compact Free Electron Laser (SACLA). The shortest wavelength attained is 0.06 nm, with a maximum power of 10 GW, with a pulse duration of 10 fs [
15].
Many applications, including spectroscopic studies of correlated electron materials and imaging studies, demand an excellent temporal coherence. Such a demand has resulted in various high gain seeded FEL schemes, including external seeding [
16,
17,
18,
19,
20,
21,
22,
23] or self-seeding [
24,
25,
26]. The Free Electron Laser for Multidisciplinary Investigations (FERMI) at Elettra is a seeded FEL, which has been designed for producing high quality photon pulses in the EUV and soft X-ray spectral range [
22]. The first undulator line, named FEL-1, was successfully operated to produce coherent radiation in the spectral range from 65 nm to 20 nm [
23]. The second undulator line FEL-2, currently under commissioning, will cover the spectral range between 20 nm and 4 nm.
Among these schemes, echo-enabled harmonic generation (EEHG) shows a great promise for producing a fully coherent short wavelength FEL. A classic high gain harmonic generation (HGHG) scheme [
16] has suffered from the low up-frequency conversion efficiency. Consequently, this led naturally to a multistage approach for X-ray production seeded at an ultraviolet wavelength [
27]. The beam echo effect has remarkable frequency up-conversion efficiency and allows for the generation of high harmonics with a relatively small energy modulation [
20]. Using an EEHG scheme, coherent soft X-rays at 5 nm with GW peak power was calculated, starting from a 240 nm seeding laser [
28]. Later, the EEHG scheme with an additional electron bunch compression has been proposed [
29]. The calculation showed that X-ray pulses at 1 nm with a peak power of a few hundred megawatts and a pulse duration of 20 attoseconds full width at half maximum (FWHM) is expected. For the radiation at an even shorter wavelength, a four-stage HGHG-FEL scheme has been proposed, for which a train of attosecond pulses at 0.1 nm wavelength was expected in simulation [
30]. This concept was realized by the generation of the eighth harmonic of SASE radiation using a single electron bunch and a four-stage HGHG configuration, as shown in
Figure 1. The electron bunch passes through a sequence of four relatively short undulators.
Figure 1.
(Color online). High gain harmonic generation (HGHG) attosecond free electron laser (FEL). Ultrafast X-ray pulses are produced through a sequence of undulators, which are resonant at different wavelengths [
30].
Figure 1.
(Color online). High gain harmonic generation (HGHG) attosecond free electron laser (FEL). Ultrafast X-ray pulses are produced through a sequence of undulators, which are resonant at different wavelengths [
30].
The first undulator is a SASE FEL undulator tuned at 0.8 nm, which operates in the high gain linear regime. The 0.1 nm wavelength radiation is achieved by a successive division of 0.8 nm to 0.4 nm to 0.2 nm and to 0.1 nm in a sequence. The duration of the spikes is expected to be in the range of 400 to 600 attoseconds. SLAC has recently tested out a self-seeding scheme by using the first half of the undulator to seed the second half through a diamond-based monochromator and has demonstrated self-seeding at angstrom wavelengths [
31]. They noticed the reduction of a bandwidth by a factor of 40–50 with respect to SASE.
Later, with the advent of a carrier-envelope-phase (CEP)-stabilized few-cycle laser, the interaction of such a laser with an electron bunch in a wiggler magnet of single or double period prior to an X-ray undulator in SASE FEL was considered. This interaction plays a vital role for the eventual generation of isolated attosecond X-ray pulses with FEL. The use of a few-cycle optical pulse laser in FEL was first recognized in 2004 [
32], where an ultra-relativistic electron beam, a few-cycle optical laser pulse and a coherent X-ray radiation from harmonic cascade was used. The simulation showed the generation of a 100 attoseconds FWHM X-ray pulse with multi-megawatt power. In another simulation using a simpler layout, as shown in
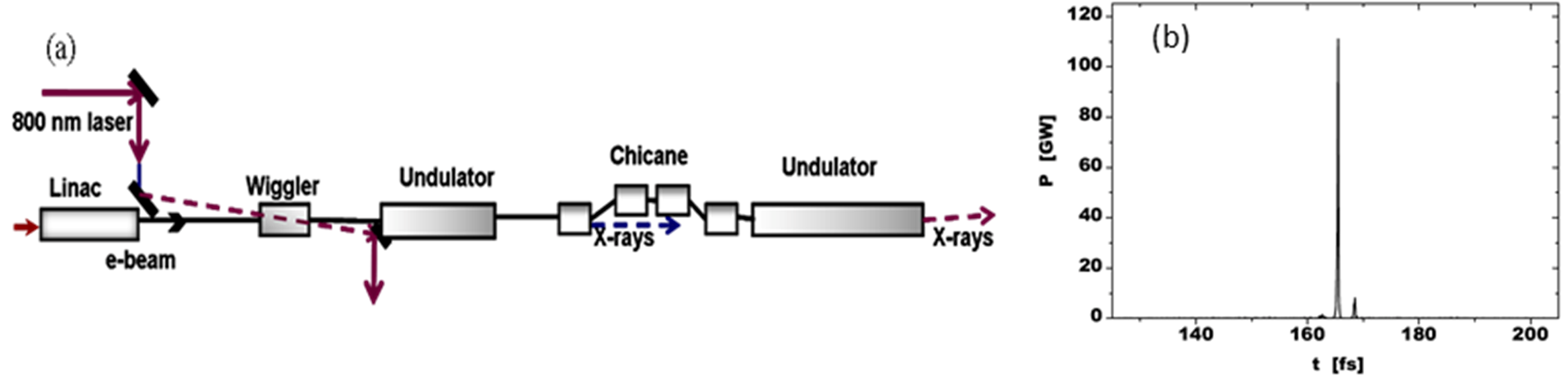
Figure 2 [
33], a femtosecond CEP laser and a wiggler magnet were used for energy modulation prior to entering into the SASE FEL to produce a train of 300 attoseconds X-ray pulses at 0.1 nm with GW power. The laser modulates the energy profile of an electron beam in a two-period wiggler resonant to the laser wavelength. This energy-modulated electron beam enters an X-ray undulator, which produces SASE radiation. A train of attosecond pulses was obtained in simulation (see
Figure 2b). A crystal monochromator after the X-ray undulator was suggested for the selection of the single peak pulse. The scheme is supposed to produce 300 attoseconds-long single pulses with GW-level output power (a few hundred nJ) at a 0.1 nm wavelength.
Figure 2.
(Color online). Attosecond enhanced self-amplified spontaneous emission (SASE) (ESASE) scheme. (
a) The layout of the scheme. (
b) The single shot temporal structure of the central part of the radiation pulse. Dotted line represents the energy modulation of electron bunch [
33].
Figure 2.
(Color online). Attosecond enhanced self-amplified spontaneous emission (SASE) (ESASE) scheme. (
a) The layout of the scheme. (
b) The single shot temporal structure of the central part of the radiation pulse. Dotted line represents the energy modulation of electron bunch [
33].
In a later proposal [
34], instead of the monochromator, two undulators of different lengths were suggested, as shown in
Figure 3. There is no monochromator between an X-ray undulator and a sample. The undulator is divided in two uneven parts, with the first part being a source for a seed signal, which is fed into the second part. Using an offset frequency resonance in the second undulator, the simulation showed the generation of a 300 attoseconds pulse with 100-GW output power. A magnetic chicane is used to allow the interaction between the seed signal and virgin electrons of the same electron bunch. The second undulator is tuned to an offset frequency of the radiation produced in the first undulator. Hence, a seed radiation at the offset frequency is exponentially amplified, while a seed radiation at reference-frequency remains the same. This scheme expects to deliver a 300 attosecond FWHM pulse with a peak power of 10 GW, which can be further increased to 100 GW using a tapered undulator.
Figure 3.
(Color online). Double undulator ESASE scheme. (
a) The layout of the scheme. (
b) Temporal structure of the radiation pulse after monochromator [
34].
Figure 3.
(Color online). Double undulator ESASE scheme. (
a) The layout of the scheme. (
b) Temporal structure of the radiation pulse after monochromator [
34].
The energy modulation of an electron beam at a low energy is more convenient than at a high energy, because a longer wiggler is required at a higher energy. Another advantage of the energy modulation at a lower energy is the small energy spread induced in an electron beam by a wiggler magnet itself. This energy modulation at low energy was studied in combination with another successive accelerator, prior to entering into a long SASE FEL undulator [
35].The simulation resulted in the generation of X-ray pulses with a pulse width of ~200 attoseconds with a perfect synchronization to a modulating laser pulse. The inherent problem in the current enhancement scheme by a CEP-stabilized few-cycle laser is the possibility of the generation of a train of attosecond pulses. When a few-cycle laser interacts with an electron beam, the energy of the electron bunch is modulated to follow the oscillation of the electric field of the laser. When such a modulated electron bunch passes through a wiggler, the microbunching happens every cycle, leading to several sizable current spikes. These spikes strongly radiate in an undulator, resulting in several attosecond pulses or a train of attosecond pulses. The contrast between a major peak and secondary peaks is also poor. To avoid this problem and to obtain a dominant (or isolated) spike, special attention is demanded, either in the selection of the wavelength of laser or in the energy profile of the electron bunch interacting with a laser.
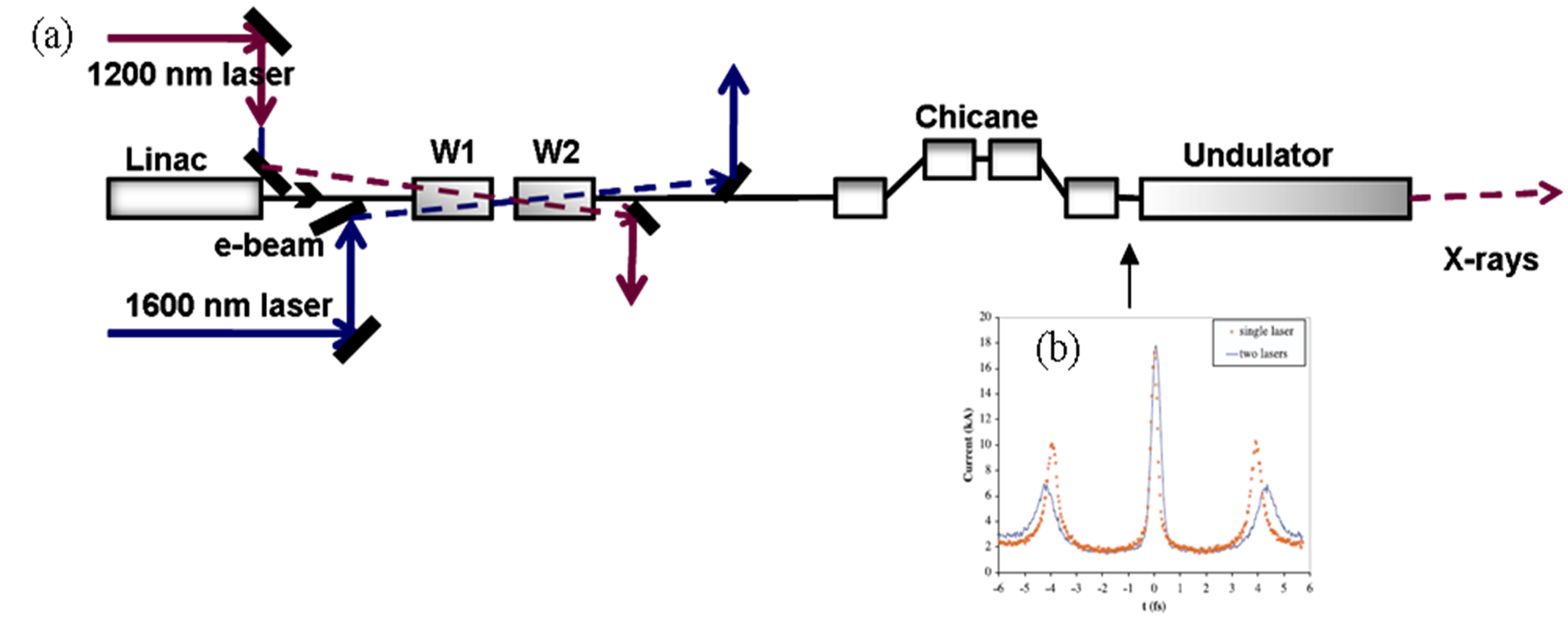
As one way to improve this contrast, a two-color approach was proposed, as shown in
Figure 4 [
36]. The electron beam enters two adjacent wiggler magnets, W1 and W2. Each magnet has just one wiggler period. Two co-propagating laser pulses (1200 nm, 0.2 nJ pulse energy and 7.5 fs FWHM; 1600 nm, 0.07 mJ and 10 fs FWHM) enter the wigglers at a small angle. The first laser is focused at the center of the first wiggler, and the second laser is focused at the center of the second wiggler. The phase of the carrier wave of the first laser pulse is adjusted so that when the peak of the envelope of the laser pulse reaches the center of the first wiggler, the electric field is zero. The phase of the carrier wave of the second laser pulse is also adjusted in a similar way. After passing through two consecutive modulation sections, the electron beam enters into a dispersive section for microbunching of the electrons and enhancement of the current peak. The enhancement produced in the central cycle of the two laser pulses is about two-times stronger than that produced during other laser cycles. However, after propagation through a long undulator, this current still emits a train of attosecond X-ray pulses of 250 attoseconds FWHM.
Figure 4.
(Color online). Two-color ESASE scheme. (
a) The layout of the scheme. (
b) Current profiles of electron bunch after interaction with lasers; for two lasers (blue-line) and single laser (red-cross) [
36].
Figure 4.
(Color online). Two-color ESASE scheme. (
a) The layout of the scheme. (
b) Current profiles of electron bunch after interaction with lasers; for two lasers (blue-line) and single laser (red-cross) [
36].
The effect of a linear energy chirp on FEL amplification has been studied and a new proposal of using a tapered undulator was made, showing the generation of 200 attoseconds X-ray pulses with a power of 100 GW [
37].
The angular modulation of electron’s trajectories can also contribute towards an attosecond pulse generation. The modulation of electron’s angles by a CEP laser was utilized for the creation of a115 attoseconds X-ray pulse with a peak power of 100 GW [
38]. Moreover, the angular modulation was combined with the energy modulation for the shortening and the improved selection of an attosecond pulse. The manipulation of the energy profile of an electron beam may lead to the generation of an isolated attosecond pulse of ~100 attoseconds FWHM at 0.1 nm wavelength [
39].
A Compton backscattering scheme can be utilized for the generation of an attosecond γ-ray pulse. Using Compton backscattering with an energy-modulated electron beam, it was shown in simulation that an isolated attosecond gamma-ray pulse at 64 keV with a pulse width of 550 attoseconds and a contrast ratio of 5.1:1 can be generated [
40]. The spectral filtering (such as a crystal spectrometer) allows one to obtain an isolated attosecond gamma ray.
3. Toward the Generation of Isolated Attosecond Hard X-ray Pulse
All the efforts described in the above have made remarkable contributions to the progress toward the generation of attosecond pulses in the hard X-ray region. Most of the proposals cited above shows the generation of a train of attosecond pulses. For a real, meaningful pump-probe experiment with attosecond temporal resolution, however, an isolated attosecond pulse is demanded.
This section deals with our study about the generation of an isolated attosecond hard X-ray pulse. We employ the enhanced SASE scheme for the PAL-XFEL parameters. Comparative simulations for different laser wavelengths, laser pulse duration, laser power and wiggler field, the bending angle of a chicane and the length between the dipole magnets have been performed to control and minimize side current peaks and to achieve an isolated attosecond X-ray pulse. We demonstrate that an isolated attosecond X-ray pulse can be indeed produced by manipulating electron beam energy distributions together with density modulation in an enhanced SASE scheme for a given laser wavelength. These will be discussed in this section in detail.
3.1. Current Scheme
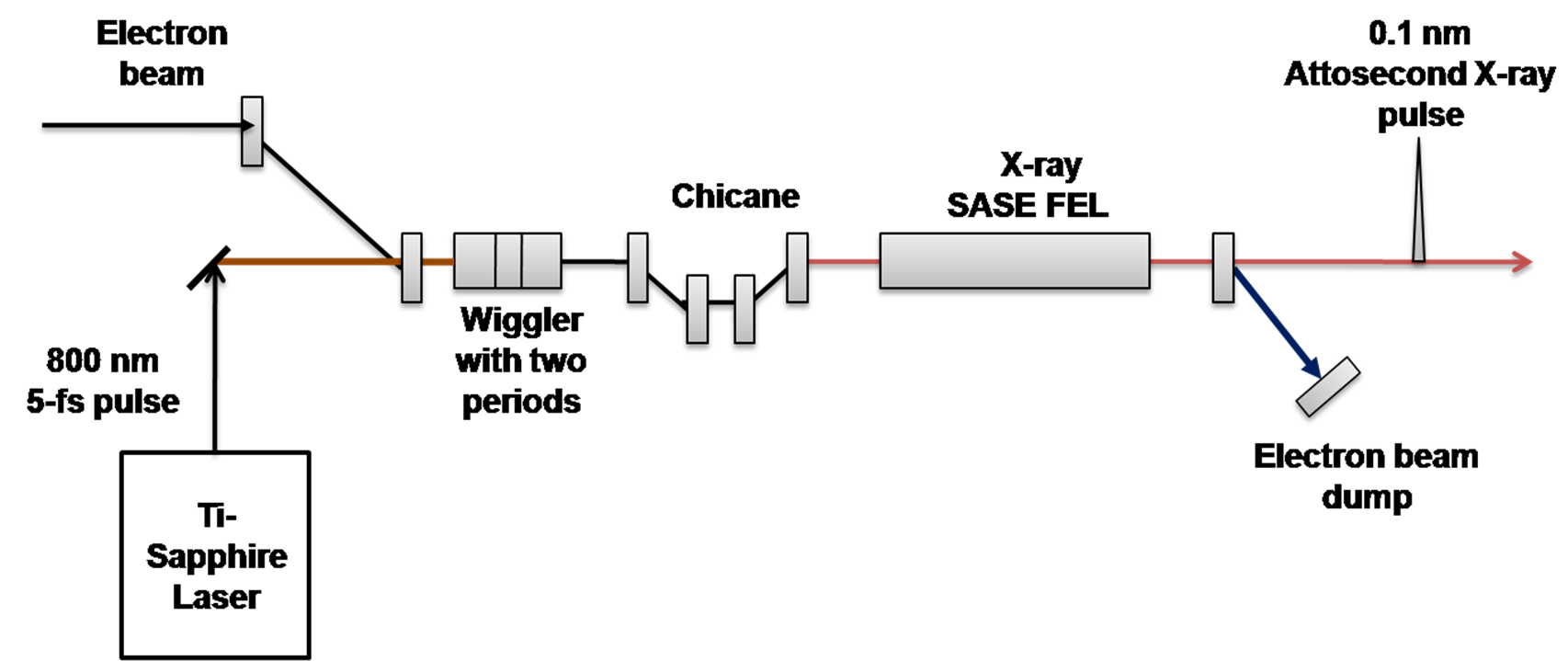
We consider a simpler enhanced SASE (ESASE) scheme, as shown in
Figure 5. An electron bunch from a linear accelerator is sent to a double-period wiggler magnet. The energy modulation in the electron bunch inside the wiggler is produced by co-propagating a few-cycle CEP stabilized laser. Only a small longitudinal section of the electron bunch interacts with the laser. The peak power of the laser is selected in such a way that the amplitude of energy modulation is significantly larger than the magnitude of random noise in electron energy. The electron beam now enters into a chicane, which introduces dispersion: the higher the electron energy is, the shorter it travels. In general, this leads to the density modulation, producing the microbunching of electrons at a laser wavelength spacing and the periodic current peaks. The increase in the peak current results from a corresponding increase in the energy spread of electrons. Finally, the electron bunch enters into a long undulator so that the microbunching is improved and the current spikes strongly radiate at a resonant wavelength via standard SASE process.
Figure 5.
(Color online). ESASE scheme for attosecond pulse generation.
Figure 5.
(Color online). ESASE scheme for attosecond pulse generation.
In our study, the laser wavelengths, FWHM pulse duration and electron bunch energy distributions were optimized to control the side current peaks and to obtain a single isolated attosecond pulse.
3.2. Optimization of Current Profile by the Selection of Laser Wavelengths (Single Peak Current Profile)
The effect of laser wavelength on the current profile has been studied for the generation of an attosecond hard X-ray pulse, using the parameters of the electron bunch of PAL-XFEL [
4]: A beam energy of 10 GeV, a total electron bunch charge of 0.2 nC, a beam normalized emittance of 0.5 μm-rad and an electron bunch average-current of 3 kA or higher. A CEP-stabilized few-cycle (800 nm, ~0.13 mJ) laser modulates the electron beam energy. The beam waist at focus is 250 μm. The wiggler magnet is a two-period magnet with B
0 = 1.1459 Tesla and λ
w = 55 cm. ELEGANT [
41], the six-dimensional particle tracking code, is used to calculate electron bunch properties.
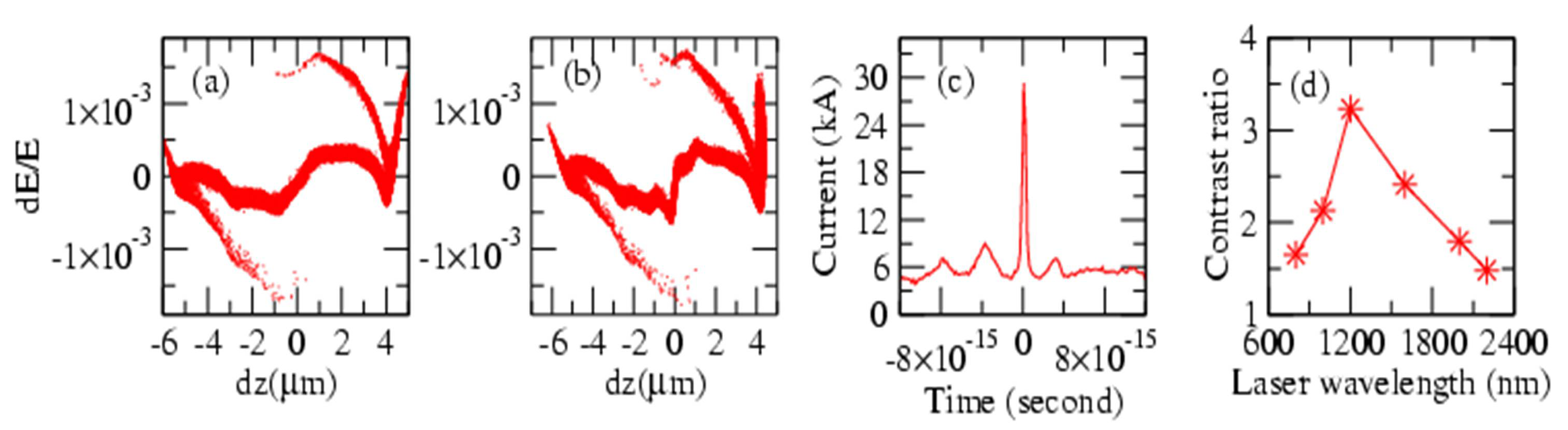
First, an electron bunch with a total length of ~12 μm (~40 fs) and an average current of 6 kA is considered. The longitudinal energy distribution of this electron bunch before wiggler and after chicane, respectively, is shown in
Figure 6a,b. The simulations for different laser wavelengths and pulse durations have been done. The laser wavelength is scanned from 800 nm (5 fs FWHM) to 2400 nm (14 fs FWHM), maintaining the number of laser cycles around 1.85 It is found that the current peaks vary in number and magnitude, depending on the laser wavelength and pulse duration. It is found that a 1200 nm, 7.5 fs FWHM laser produces the maximum main-peak current in the current profile of the electron bunch after chicane with the highest contrast ratio (the contrast ratio is defined by the ratio of the current of the strongest peak to that of the second strongest peak), as shown in
Figure 6c.
Figure 6d shows the variation of the contrast ratio with respect to laser wavelengths, 800 nm to 2400 nm. A 1200 nm and 7.5 fs laser gives the best contrast ratio with a maximum current of the main peak.
Figure 6.
(Color online). (
a) The longitudinal energy distribution of the electron bunch before the wiggler. (
b) The longitudinal energy distribution after chicane. (
c) The electron bunch current profile after chicane for λ
L = 1,200 nm and τ (FWHM) = 7.5 fs. (
d) The change of contrast ratio with respect to laser wavelength [
42].
Figure 6.
(Color online). (
a) The longitudinal energy distribution of the electron bunch before the wiggler. (
b) The longitudinal energy distribution after chicane. (
c) The electron bunch current profile after chicane for λ
L = 1,200 nm and τ (FWHM) = 7.5 fs. (
d) The change of contrast ratio with respect to laser wavelength [
42].
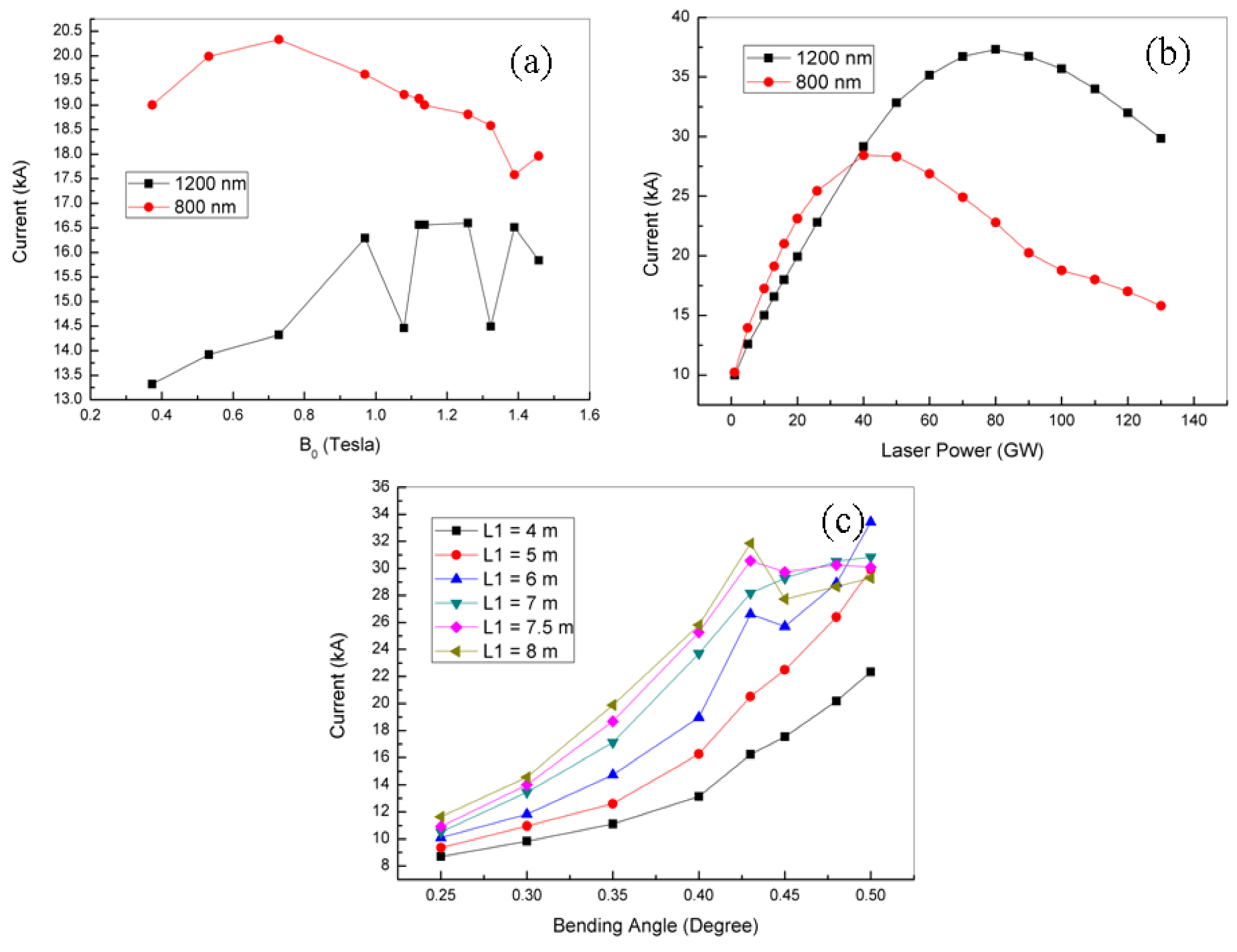
3.3. Effect of Wiggler Field, Laser Power and Chicane Bending Angle on Main Peak Current
The effect of the wiggler field strength, B
0, on the main peak current in the electron bunch current profile after chicane has been studied for fixed laser parameters. The simulation has been done for two laser wavelengths, 800 nm and 1200 nm, with corresponding pulse durations of 5 fs and 7.5 fs FWHM, respectively. The results are shown in
Figure 7a. One can see that the wiggler field has no significant effect (less than 20%) on the main peak current. We also studied the effect of a laser power on the main peak current. As shown in
Figure 7b, note that the effect of laser power on the main peak current of the electron bunch is significant (by a factor of 3–4). The main peak current increases linearly with a laser power up to a certain value, and after that, it starts to decrease. We optimize the chicane parameters to enhance the main peak current of the electron bunch. In
Figure 7c, we present the results for different lengths between dipole magnets and for different bending angles. The length between dipole magnets and the bending angle of the dipole are chosen such that the momentum compaction factor, R
56, always remains less than 0.06 cm.
Figure 7.
(Color online). The variation of the main peak current after chicane. (a) The effect of the wiggler field, B0, for two different laser wavelengths, 800 nm and 1200 nm. (b) The effect of laser power for two different laser wavelengths, 800 nm and 1200 nm. (c) The effect of the bending angle and the length between dipole magnets (L1).
Figure 7.
(Color online). The variation of the main peak current after chicane. (a) The effect of the wiggler field, B0, for two different laser wavelengths, 800 nm and 1200 nm. (b) The effect of laser power for two different laser wavelengths, 800 nm and 1200 nm. (c) The effect of the bending angle and the length between dipole magnets (L1).
3.4. Optimization of Current Profile by Manipulation of Energy Profile of Electron Bunch
Another method to control the side peaks in an electron bunch current profile is to manipulate the electron bunch energy distribution. Three different energy distributions are generated by changing radio frequency (RF) phases in a photo-injector section, as well as in the accelerator part, and by adjusting the parameters of a bunch compressor in the acceleration section. These three different energy distributions are as follows: (1) ~20 μm (~66 fs)-long electron bunch with an average current of 3 kA (
Figure 8a), (2) ~16 μm (~53 fs)-long electron bunch with an average current of 4 kA (
Figure 9a) and (3) ~12 μm (~40 fs)-long electron bunch with an average current 6 kA (
Figure 10a). The rest of the electron beam parameters are chosen to be the same as in the beginning of
Section 3.2. These energy distributions are generated by using the ELEGANT code. The parameters of the laser under consideration for this study are as follows: laser power is 13 GW, laser wavelength 1200 nm and pulse duration 7.5 fs FWHM. The momentum compaction factor, R
56, is selected between the quality of electron beam and the size of chicane.
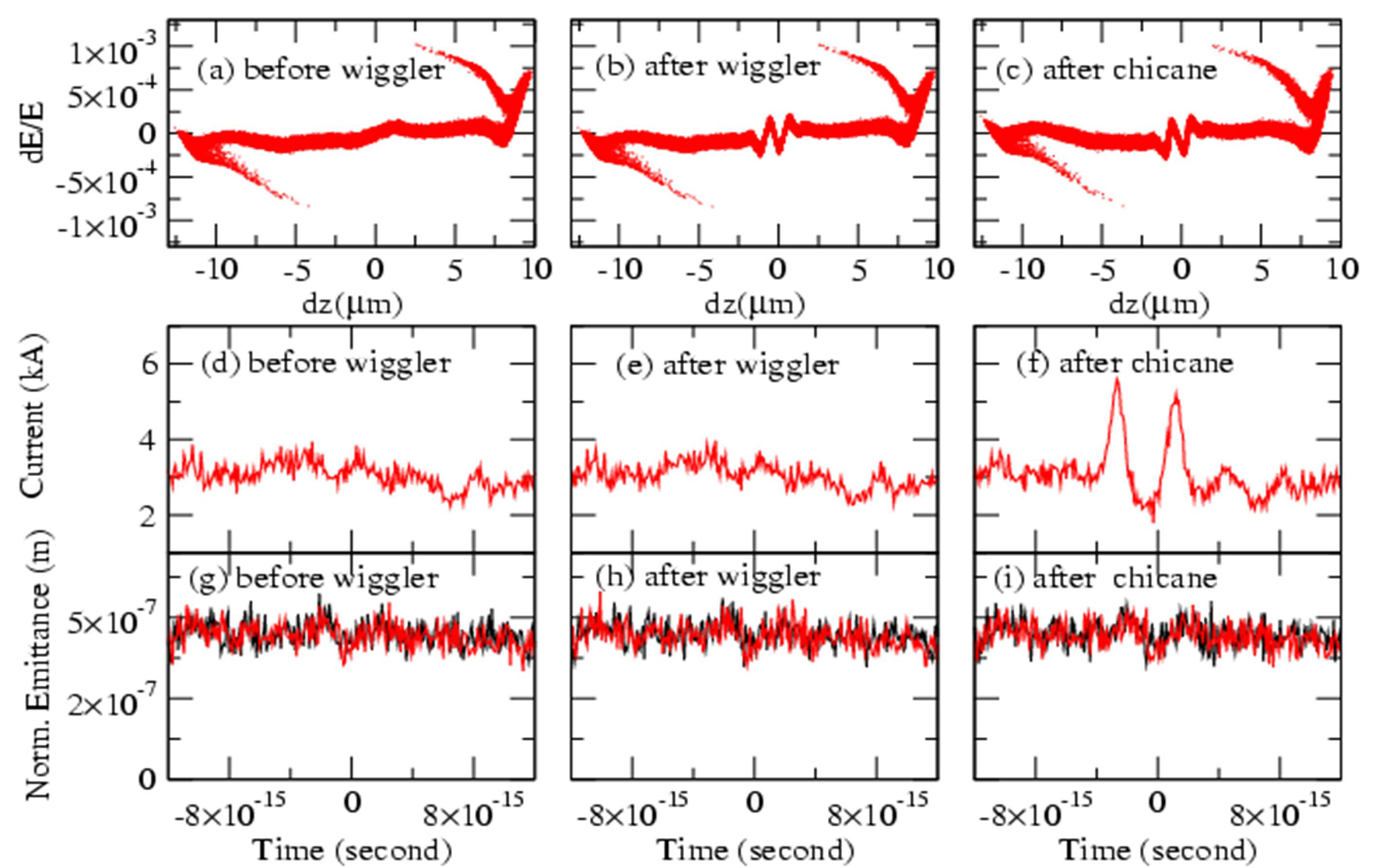
Figure 8 shows the simulation results for a ~20 μm (average current 3 kA)-long electron bunch.
Figure 8a–c shows the longitudinal energy distribution before wiggler, after wiggler and after chicane, respectively. In
Figure 8a, the electron bunch has a slight uphill in the central part of the electron bunch. The interaction of the electron bunch with the co-propagating laser (7.5 fs FWHM, 800 nm) duplicates the laser field oscillation in the energy distribution of the electron bunch, as shown in
Figure 8b. In
Figure 8c, the electron bunch is further compressed by the chicane, so that its profile becomes steeper. The energy spread is (Δ
E/E) always less than the FEL parameter (ρ = 5.4 × 10
−4).
Figure 8d–f shows the current profile; before wiggler, after wiggler and after chicane, respectively. The current profiles before wiggler and after wiggler are similar in shape and magnitude. As seen in
Figure 8f, after chicane, the current profile contains two major current peaks of 5.6 kA and 5 kA in the central part, due to the density modulation in the chicane. This current enhancement in the central part of electron bunch is caused by the steepening of the Δ
E/E profile in the energy spread of electrons (
Figure 8c).
Figure 8g–i shows normalized emittances (both longitudinal and transverse) of the electron bunches. No significant change is observed in emittance due to these interactions.
Figure 8.
(Color online). The change of the characteristics of the 3 kA, 20 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line) on time scale [
42].
Figure 8.
(Color online). The change of the characteristics of the 3 kA, 20 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line) on time scale [
42].
Figure 9 shows the results for the case of the 4 kA, 16 μm (~53 fs) electron bunch. Before a wiggler, the energy distribution looks as shown in
Figure 9a. When this electron bunch goes through a wiggler, it interacts with the laser and consequently suffers from the change in the electron beam energy distribution (
Figure 9b). After passing through a chicane, the energy distributions becomes steeper (
Figure 9c).
Figure 9d,e and f show corresponding current profiles of this electron bunch. One can notice that after chicane, the current profile contains two major peaks of 7 kA and 7.39 kA. Corresponding normalized emittance is also shown in
Figure 9g–i, indicating no difference in magnitude and shape between these locations.
Figure 9.
(Color online). The change of the characteristics of the 4 kA, 16 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line) [
42].
Figure 9.
(Color online). The change of the characteristics of the 4 kA, 16 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line) [
42].
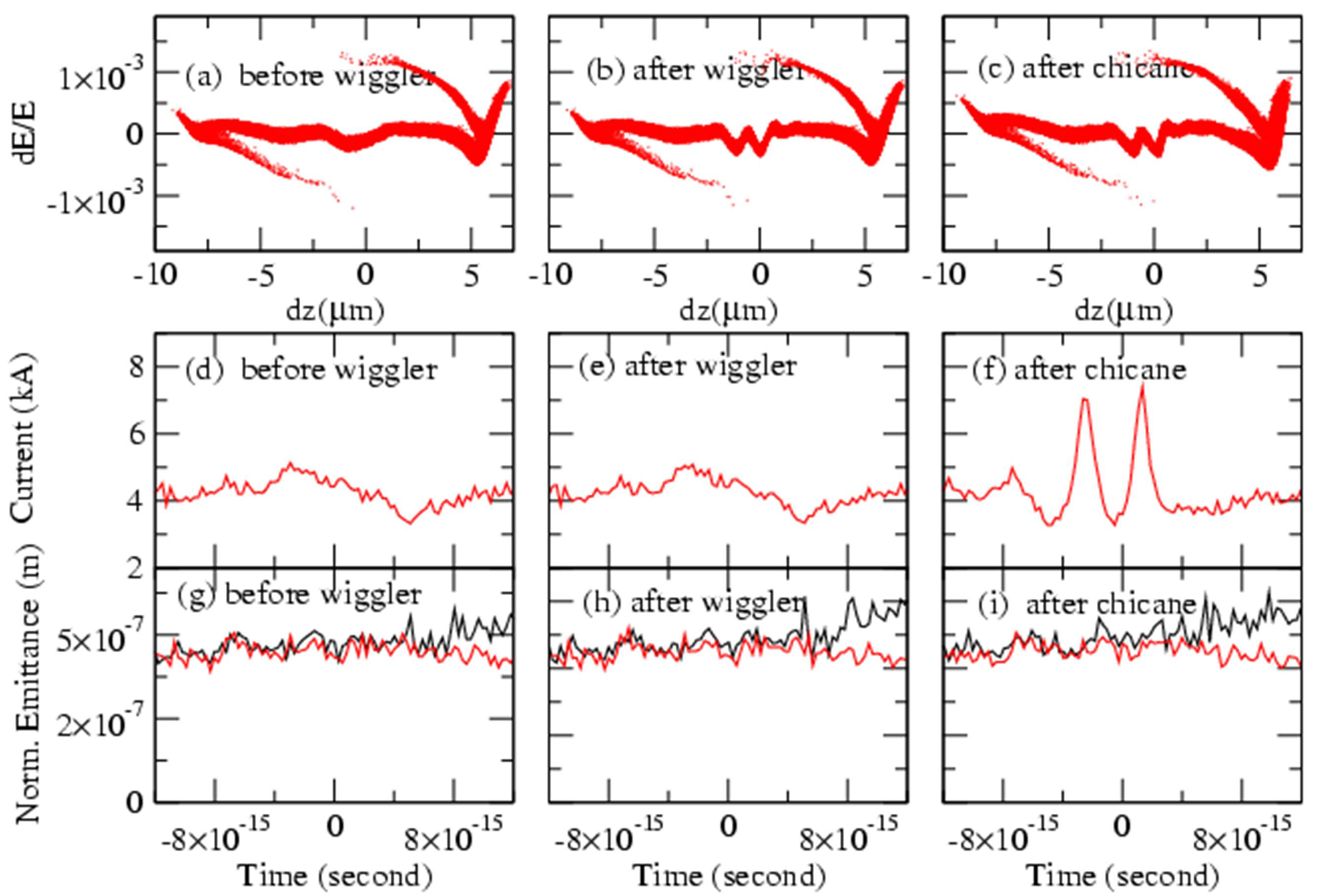
Figure 10.
(Color online). The change of the characteristics of the 6 kA, 12 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line)[
42].
Figure 10.
(Color online). The change of the characteristics of the 6 kA, 12 μm-long electron bunch. (
a)–(
c): the longitudinal energy distribution. (
d)–(
f): current profile. (
g)–(
i): horizontal (black line) and transverse normalized-emittance (red line)[
42].
We display the simulation results for the case of 6 kA, 12 μm long (~40 fs)-electron bunch in
Figure 10. The longitudinal energy distributions of this electron bunch before wiggler, after wiggler and after chicane, respectively, are shown in
Figure 10a–c. Note that the current profile (
Figure 10a) differs from those in
Figure 8a,
Figure 9b.
Figure 10d–f shows corresponding current profiles. Note that there is only one major current peak of 17 kA current in the central part and side peaks almost disappear (
Figure 10f) compared to the cases of the 3 kA and 4 kA electron beam. The rise in the peak current in the central part is due to the steepening of the energy spread. This demonstrates that by the manipulation of the energy distribution of electron bunch, the side peaks can be suppressed, resulting in a single isolated current peak. The time length of this current-peak is around one fs FWHM, getting even shorter in the undulator.
3.5. An Isolated Attosecond Hard X-ray Pulse Generation
Ultimately, the electron bunch shown in
Figure 10 is sent to an undulator, where the electrons residing in the central peak part radiate most strongly (enhanced SASE), because of its high current. The electrons outside the central peak part also contribute to radiation, but the magnitude is relatively small due to the weak current. To calculate the radiation from this electron bunch, we use the three-dimensional time-dependent undulator radiation code, GENESIS [
43]. This whole calculation has been done at 0.1 nm. In a simulation, one electron bunch is divided into many slices. The radiations from each electron are averaged over many slices. What is presented below is the result of this average.
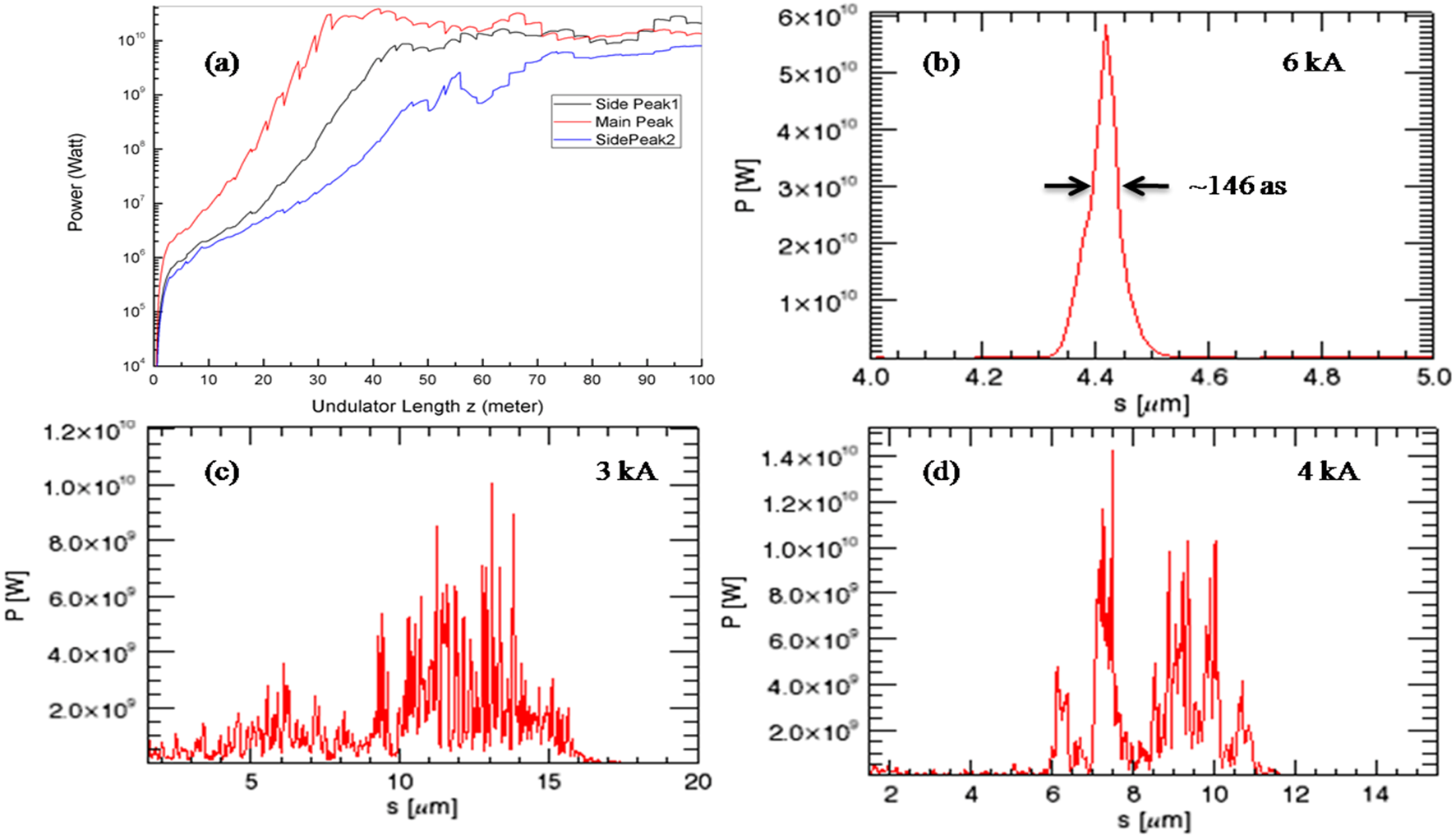
Figure 11a shows the logarithmic plot of x-ray output power from the 6 kA electron bunch with a strong current peak and two very weak side peaks (
Figure 10f) as a function of distance along an undulator. The saturation occurs around z = 34 meters, and the radiation power at z = 34 meters’ distance is around 58 GW. The saturation position is the point where the exponential growth of the radiation power stops. After this point, the radiation power produced by the main current peak does not grow, because the slippage lengthens the pulse width. As we note, the radiation power produced by the main peak is two orders of magnitude greater than the power produced by side peaks.
Figure 11b shows the radiation pulse at z = 34 meters for the 6 kA electron bunch. The radiation pulse width is around ~146 attoseconds with a total power of 58 GW.
We have also calculated the saturation point for the cases of the 3 kA (
Figure 8) and 4 kA (
Figure 9) electron bunch. We find that the saturation length is larger for the low current cases. For the 3 kA electron bunch, the saturation point is around 73 meters and 55 meters for the 4 kA electron bunch.
Figure 11c represents the radiation pulse at the saturation point,
i.e., z = 73 meters, for the 3 kA electron bunch. The saturation power is ~10 GW.
Figure 11d shows the radiation pulse for the 4 kA electron bunch at a saturation point of z = 55 meters. Here, the saturation power is ~14 GW.
We have neglected the space-charge effects in our simulation. Our electron beam energy for the ESASE scheme is 10 GeV, which is quite a high energy, so that the space charge effects are not so important. Some simulations including space charge effects were done. The results indeed indicated that there is no difference in SASE radiation between the with- and without-space charge effects.
Figure 11.
(Color online). The GENESIS simulation for radiation power at 0.1 nm, using the three electron bunches shown in
Figure 8,
Figure 9,
Figure 10. (
a) The radiation power from the main peak and two side peaks along the undulator for 6 kA case. (
b) The radiation pulse at z = 34 meters for the 6 kA, 12 μm-long bunch. (
c) The radiation pulse at z = 73 meters for the 3 kA, 20 μm-long bunch. (
d) The radiation pulse at z = 55 meters for the 4 kA, 16 μm-long bunch (here, 1 μm ≈ 3.3 fs in time scale) [
42].
Figure 11.
(Color online). The GENESIS simulation for radiation power at 0.1 nm, using the three electron bunches shown in
Figure 8,
Figure 9,
Figure 10. (
a) The radiation power from the main peak and two side peaks along the undulator for 6 kA case. (
b) The radiation pulse at z = 34 meters for the 6 kA, 12 μm-long bunch. (
c) The radiation pulse at z = 73 meters for the 3 kA, 20 μm-long bunch. (
d) The radiation pulse at z = 55 meters for the 4 kA, 16 μm-long bunch (here, 1 μm ≈ 3.3 fs in time scale) [
42].