2. Experimental Section
The control technique basically includes a variable intensity attenuator, a variable delay line and a spectrum analyzer, which are managed by a computer. The experimental realization is limited by the existence of the optical elements at the different bandwidths and photon energies that are of interest. In this respect, the present work attempts to demonstrate the feasibility of the control method by analyzing different significant examples, since the observed effect cannot be addressed in general due to the intrinsic characteristics of a coherent control tool based on feedback loop schemes. Otherwise, the observed results are based on a conceptually clear physical mechanism. The manipulation of the spectral amplitude/phase of the harmonics is based on the coherent combination of several harmonic generation zones with appropriate delays in between and with optimal intensities, such that the resulting spectral amplitude/phase is modified in a broad spectral region, or equivalently, the addition of a weak filtered region of the emitted spectrum to the IR intense driving pulse produces a small reshape of the IR field that conveniently modifies the amplitude and phase of the electron quantum trajectories generating the different photon energies in the HHG process.
As schematically illustrated in
Figure 1, a 5 fs laser pulse with Gaussian temporal profile, carrier-envelope phase CEP = 0
°, central wavelength of 800 nm and peak intensity of 2 × 10
14 W/cm
2 interacts with a gas medium–helium in the present simulations (ionization potential 24.59 eV), producing high-order harmonics with a photon energy cutoff at
≈ 70 eV. In the present study, the considered feedback loop scheme evolves as follows: a first spectral filter selects the desired bandwidth of the generated radiation in the XUV region that is to be optimized. The energy of this XUV
1 pulse is modified by a variable light attenuator (A
1) that scans for optimal intensities, and then it passes through a variable delay line (D
1) that scans for the position with respect to the IR pulse where the XUV
1 pulse is to be added. Coherently combined, the resulting IR + XUV
1 pulse is then sent to a second helium gas target that produces a second high-order harmonics signal. The output from the second gas target is filtered to select the same bandwidth as in the first interaction region, and the spectral amplitude of this last generated XUV pulse is reconstructed by using a spectrum analyzer. The information of the spectrum is then examined by a numerical algorithm that performs a linear regression from the data of the spectral amplitude versus photon energy and calculates its normalized chi-square (
χ2) function, such that the
flattest spectral amplitude can be selected.
Hence, the problem of fitting a set of
N data points (
xi,
yi) to a straight-line model
y =
a +
bx is considered, and the
χ2 function is used to measure how well the model agrees with the data. The
χ2 function is defined here as
The distance from each data point to the straight-line model is minimized by varying the parameters
a and
b in the sum of the squared distances between the data points and the estimate obtained from the function
y(
x), which is often called a least squares fit [
28]. If the straight-line passes through all the data points, the
χ2 function will obviously be zero and the fit is perfect. Due to the evident deviations of the spectral amplitude shape from the straight line this will not happen, and the numerical algorithm will thus find the parameters
a and
b that minimize
χ2. A linear regression and a value of
χ2 is computed for each intensity and position of the XUV
1 pulse, and after normalizing
χ2 with
![Applsci 02 00816 i002]()
in each case, where
![Applsci 02 00816 i003]()
, the minimum normalized
χ2 value provides the combination of IR andXUV
1 pulses that produce the flattest spectral amplitude,
i.e., the closest to a straight-line. The methodcan readily be iterated by splitting the XUV pulse from the first gas target (XUV
1, XUV
2, ..., XUV
n, see
Figure 1), so that an optimal driving pulse can be obtained iteratively resulting in some cases in an improved result, as it will be detailed below.
Figure 1.
(Color online) Schematic illustration of the numerical experiment. An intense IR laser pulse interacts with a first gas target—helium in this case. The output is filtered in a particular spectral region—and occasionally split in several pulses, in order to modify the XUV intensity, which is achieved by using variable light attenuators Ai. The attenuated XUVi pulses are combined with the original IR pulse with a given delay provided by variable delay lines Di. The combination of the IR+XUVi pulses generates harmonics in a second gas target. The output from the second interaction region is analyzed by a spectrum analyzer for optimization of the spectral amplitude in an iterative loop procedure managed by a computer.
Figure 1.
(Color online) Schematic illustration of the numerical experiment. An intense IR laser pulse interacts with a first gas target—helium in this case. The output is filtered in a particular spectral region—and occasionally split in several pulses, in order to modify the XUV intensity, which is achieved by using variable light attenuators Ai. The attenuated XUVi pulses are combined with the original IR pulse with a given delay provided by variable delay lines Di. The combination of the IR+XUVi pulses generates harmonics in a second gas target. The output from the second interaction region is analyzed by a spectrum analyzer for optimization of the spectral amplitude in an iterative loop procedure managed by a computer.
The simulations have been performed by numerically solving the atomic response in the single-atom non-adiabatic strong-field approximation [
29] in order to demonstrate the control mechanism in the simplest case. Propagation effects can be important and their influence will be studied in a future extension of the work. Therefore, the present results apply for low-pressure HHG processes and for short propagation lengths.
3. Results and Discussion
In
Figure 2 the optimization has been obtained by filtering the harmonics in a spectral region centered at 36 eV and considering a bandwidth of 30 eV, using a single loop iteration. The XUV
1 pulse resulting from the first gas target is combined with the IR intense pulse and sent to the second interaction region by scanning its intensity from
α = 10
6 to
α = 10
7, in steps of ∆
α = 10
6, where
α is an attenuation coefficient that has been defined with respect to the peak intensity of the IR pulse as
IXUV =
IIR/α, with
IXUV and
IIR being the peak intensities of the XUV and the IR pulses, respectively. The position at which the XUV1 pulse is combined with the IR pulse has been scanned from
θ =
−720
° to
θ = 720
°, in steps of ∆
θ = 2
°, where
θ is the angular location defined with respect to the IR cycle. From
Figure 2a, we can observe that the obtained optimal spectral amplitude (red dotted line) is substantially enhanced with respect to the original spectrum (black line), although the optimal XUV
1 pulse corresponds to an attenuation parameter as high as
α = 10
7. As commented above, the fitness function considered for the spectral amplitude control is the normalized
χ2 function obtained from a linear regression of the spectral amplitude versus photon energy in the second interaction region. The normalized
χ2 parameter is minimized by the numerical algorithm in order to find the values of the attenuation
α and delay
θ fitness parameters that produce a spectral amplitude shape the closest to a straight-line. The present results demonstrate that the fitness function
χ2 is indeed extremely efficient to achieve optimal isolated attosecond pulses by spectral amplitude shaping. As it can be observed from
Figure 2c,d, the energy from the original HHG process is strongly compressed in time by the effect of the optimization process, which results in an almost single attosecond pulse, as shown in
Figure 2d.
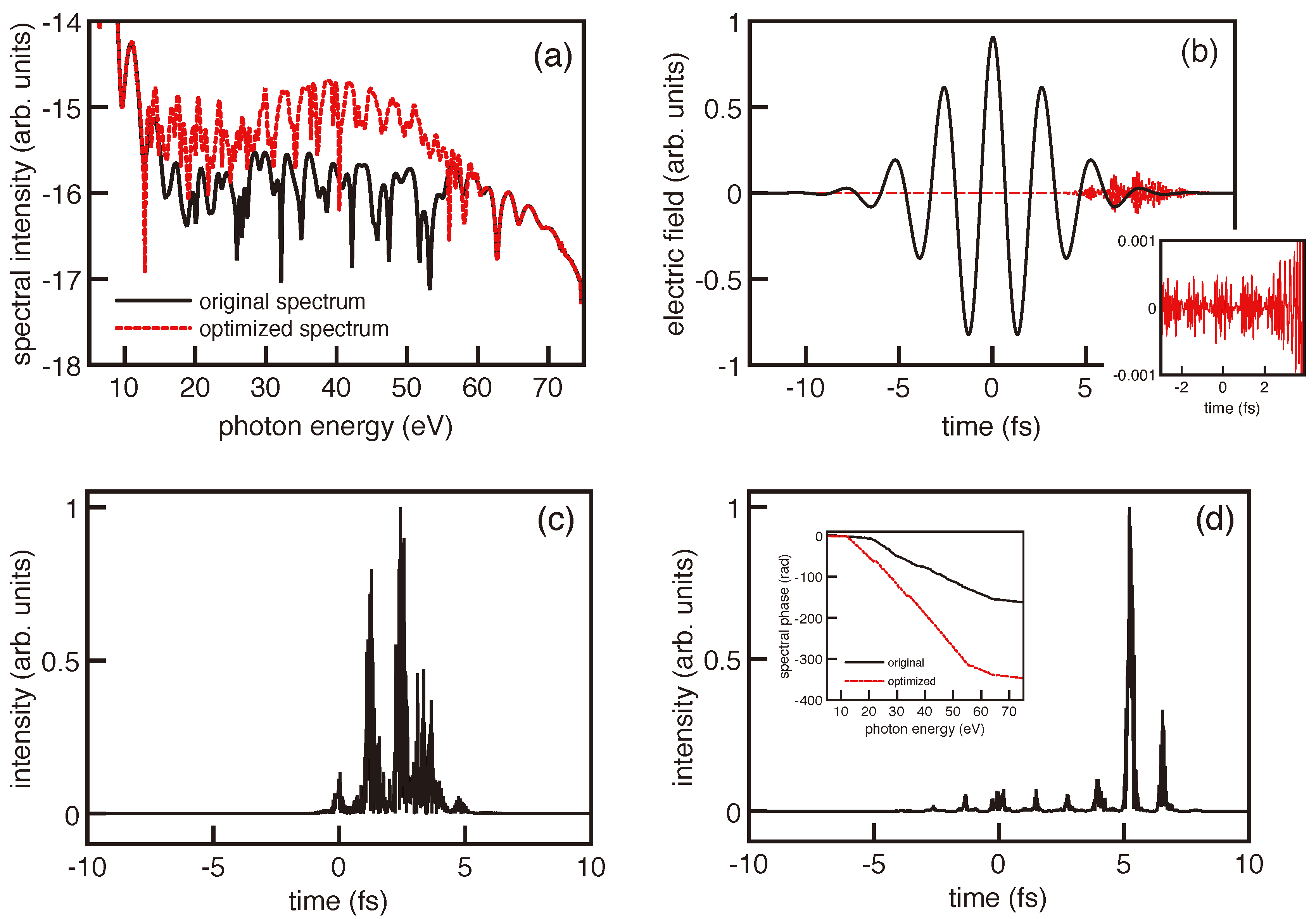
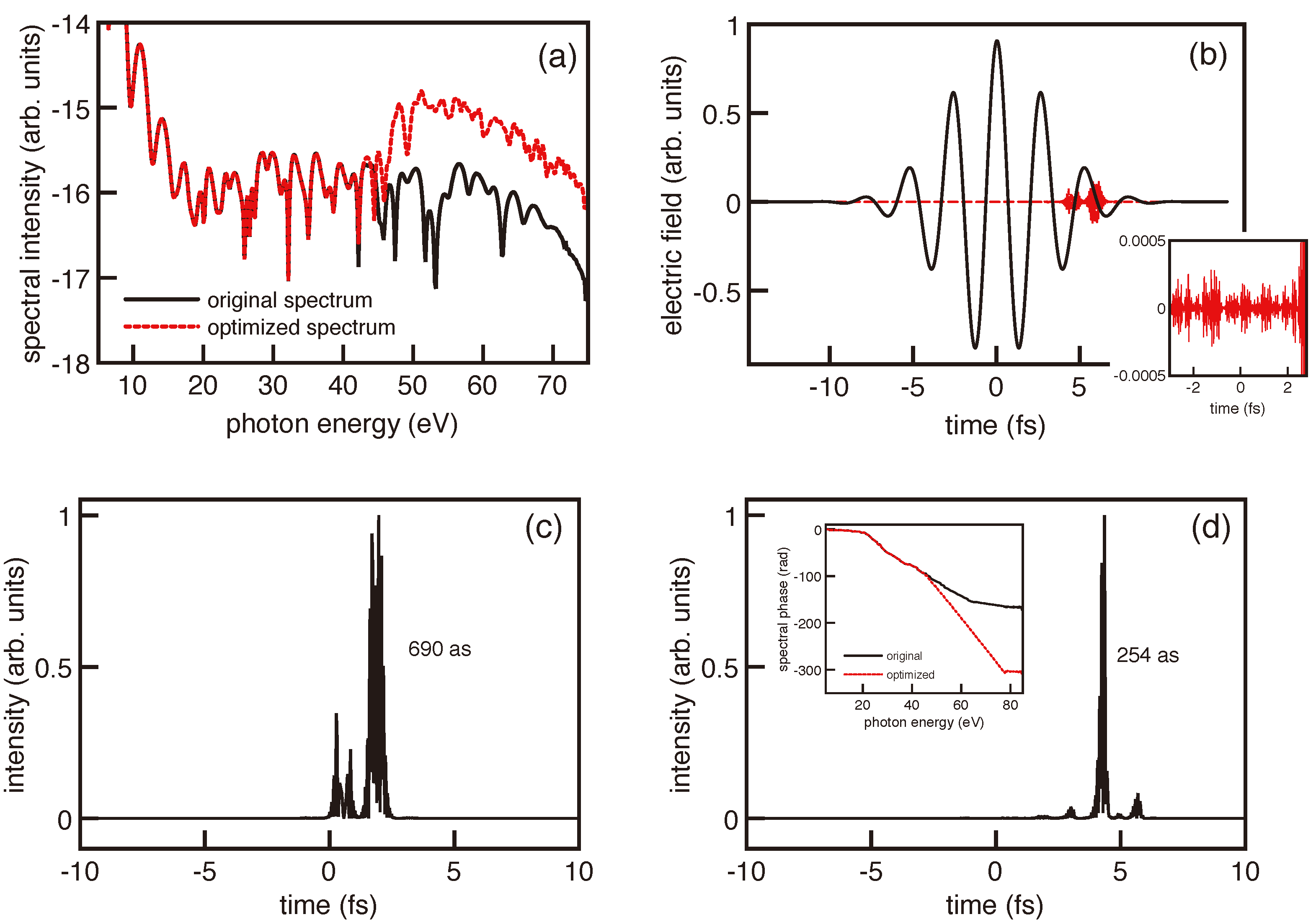
Figure 2.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering a single feedback loop. The scan in θ is from θ = −720° to θ = 720°, and α is scanned from α = 106 to α = 107. The value of the normalized χ2 function is 0.9998 for the original spectrum and 0.8929 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV1 pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV1 pulse has been rescaled to allow its visualization. In this case the optimal values of the fitness parameters are α = 107 and θ = 718°. (c) and (d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 36 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
Figure 2.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering a single feedback loop. The scan in θ is from θ = −720° to θ = 720°, and α is scanned from α = 106 to α = 107. The value of the normalized χ2 function is 0.9998 for the original spectrum and 0.8929 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV1 pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV1 pulse has been rescaled to allow its visualization. In this case the optimal values of the fitness parameters are α = 107 and θ = 718°. (c) and (d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 36 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
![Applsci 02 00816 g002]()
The physical mechanism by which the optimal pulse is achieved, and in particular how much of the ionization in the process is due to tunneling, considering a tiny change in the electric field of the IR pulse, how much is due to ionization caused by the XUV
1 field, or by the effect of time modulation of the atomic potential and bound wave function is difficult to elucidate. However, some insight of the physics behind the described process can be obtained.
Figure 2b shows how the optimal position at which the XUV
1 pulse is added lies in the temporal late wing of the IR pulse, which in this case corresponds to
θ = 718
°. Also, the inset in
Figure 2b shows the amplitude of the XUV
1 pulse nea the center of the IR pulse. Observing the reduction of the intensity generated in the HHG process from the central part of the IR pulse (
Figure 2d), we can conclude that the small perturbations in the center of the IR pulse caused by the early wing of the XUV
1 pulse induce a phase reshaping in the HHG quantum trajectories that result in a strong cancellation of the HHG signal. This conjecture is supported by the fact that small variations on the amplitude of the IR field can produce a substantial change on the phase of the quantum trajectories, as it is described in detail in [
20], and also by an analysis of the mostly contributing trajectories that will be shown below. In the present case we hence observe that a flattening of the spectral amplitude involves a synchronization of the phases in the quantum trajectories participating in the HHG process, so that the overall spectral phase results optimally changed. As it is shown in the inset of
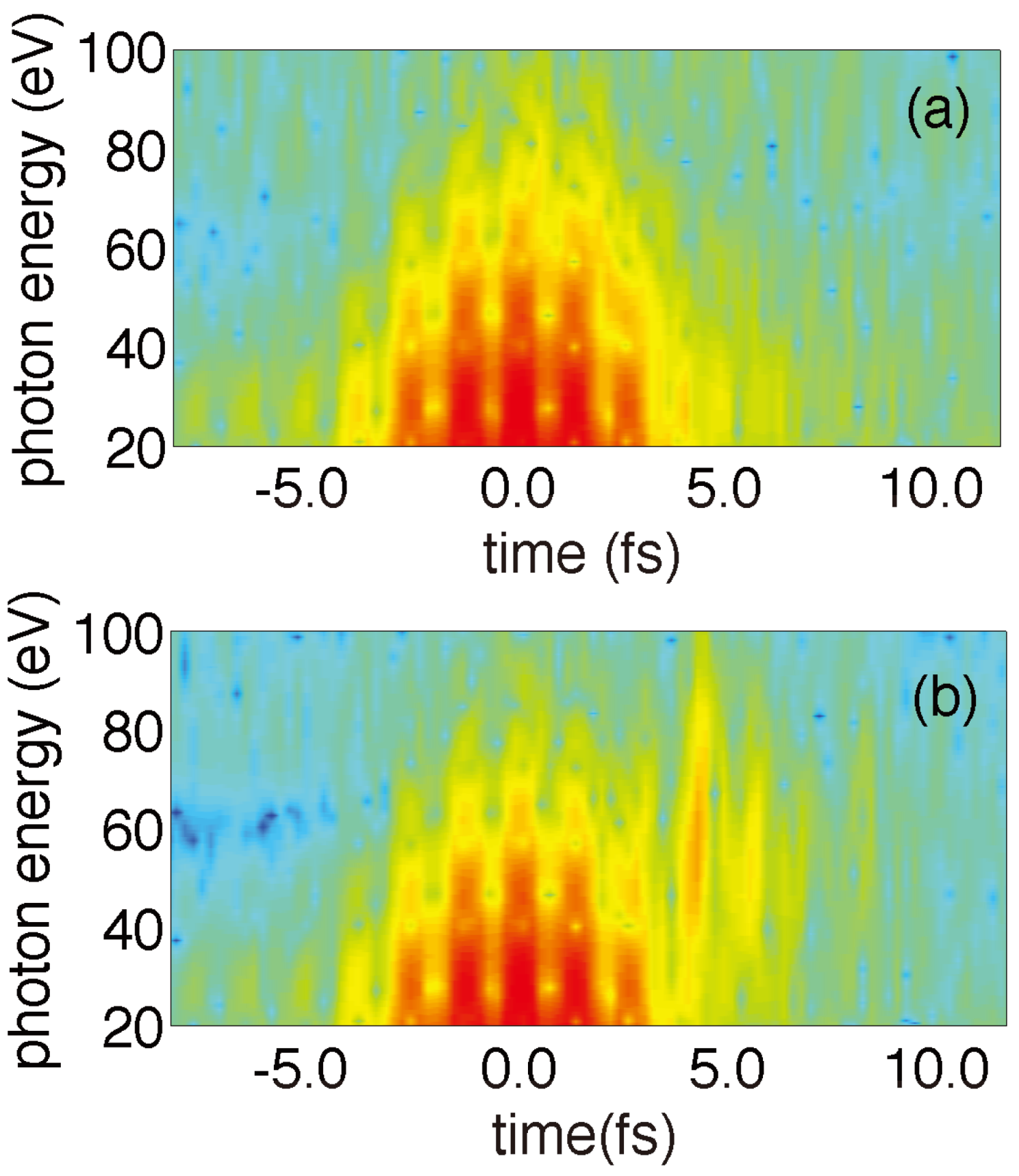
Figure 2d, the spectral phase of the spectrum is indeed substantially modified by the optimization process. As commented above, an additional insight on the contribution of the two main electron trajectories involved in the HHG generation process can be obtained by an study of the time distribution of the energy in the spectrum, which is shown in
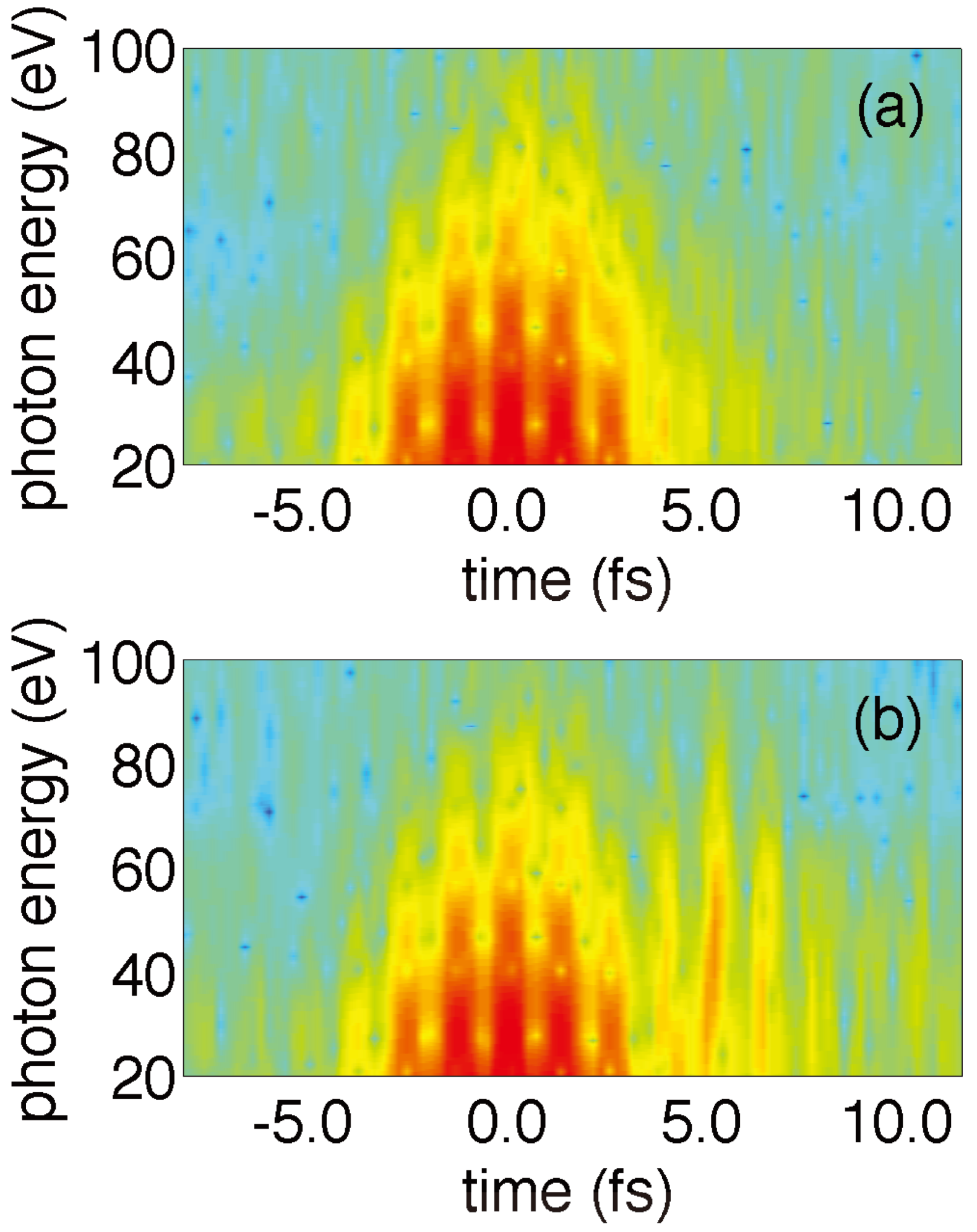
Figure 3. Although the resolution of the figure is not optimal due to limitations from the numerical simulations, the cycles in the photon energy versus time plane, which correspond to the time-dependent intensity profile of the IR pulse, can still be well recognized. Indeed, each cycle accords to half period of the driving IR pulse, with the earlier half of each cycle showing the first occurring recollisions (short trajectories) and the second half showing the contribution of the long trajectories. The duration of the two trajectories coincides in the cutoff, where the highest photon energies are generated. Only qualitative results are shown in
Figure 3 for clarity, with a more intense red color indicating a higher harmonics yield. In
Figure 3a the original unperturbed spectrum shows an obvious symmetry. The spectrum in
Figure 3b, which corresponds to the optimized case, shows two important features: first, there is not a selection of a particular trajectory in the central part of the IR pulse, which supports that a destructive interference between the short and long trajectories is produced in this region due to variations in their relative phase. Second, the perturbation produced by the XUV
1 pulse in the late wing of the IR pulse induces an enhancement of the signal in the spectral region that is optimized (21–51 eV) together with a suppression of the contribution of the long trajectories in that region, which is a relevant consequence of the optimization procedure. The overall effect is a confinement of the HHG signal at
≈ 5 fs ahead from the peak of the IR pulse, which results in an almost isolated attosecond pulse (see
Figure 2d).
Figure 3.
(Color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 2.
Figure 3.
(Color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 2.
In order to investigate the influence of the position at which the attosecond XUV
1 pulse is added with respect to the IR driving field on the optimization procedure, the previous simulations have been repeated by allowing the scan of the position angle
θ to run only from
θ =
−180
° to
θ = 180
°, and by keeping the attenuation parameter fixed to
α = 10
7. As shown in
Figure 4, an optimal angular position is found in this case at
θ =
−22
°, which results in a perturbation of the IR driving pulse around the end of its first cycle (see
Figure 4b). By comparing Figures 2a and 4a, it can be observed that the effect of the shift of the position of the XUV
1 pulse to the higher values of the IR electric field results in a higher enhancement of the optimal spectral amplitude with respect to the original spectrum. Also, since the value of the normalized fitness function
χ2 for the optimal spectrum is not as low in this case (
χ2= 0.9893) as it was in the previous simulations (
χ2= 08929),
i.e., the achieved spectrum is not as optimal, since the results in
Figure 2 have been obtained by using a scan in
θ that includes the region of the scan considered in
Figure 4, the resulting compression in time of the output pulse is not as efficient as in the previous case, as it is clear by comparing
Figure 2d with
Figure 4d. The time-frequency analysis from this case is shown in
Figure 5. We can observe again that the perturbation by the XUV
1 pulse in the optimal configuration induces a considerable suppression of the long trajectories in the enhanced region. Note that the suppression of the long trajectories is however not as complete in this case as it was in the case of
Figure 3, but it can still be observed in the photon energy region between 21 and 51 eV, in the 3 last mostly IR contributing cycles.
Figure 4.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering a single feedback loop. The scan in θ is from θ = −180° to θ = 180°, and α is fixed to 107. The value of the normalized χ2 function is 0.9998 for the original spectrum and 0.9893 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV pulse has been rescaled to allow its visualization. The optimal value for the angular position results in θ = −22°. (c) and (d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 36 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
Figure 4.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering a single feedback loop. The scan in θ is from θ = −180° to θ = 180°, and α is fixed to 107. The value of the normalized χ2 function is 0.9998 for the original spectrum and 0.9893 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV pulse has been rescaled to allow its visualization. The optimal value for the angular position results in θ = −22°. (c) and (d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 36 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
![Applsci 02 00816 g004]()
The results shown in
Figure 2 and
Figure 4 consider one iteration of the optimization procedure (see
Figure 1). For a scan of the attenuation parameter such as the one that has been used (10
6< α < 10
7), no further optimization is observed in this case by considering additional iteration loops. In order to investigate the capabilities of the multiple iteration procedure, simulations have been performed by considering weak perturbations of the IR driving pulse and by allowing the iteration procedure to run until a convergence of the fitness function is obtained. In the simulations shown in
Figure 6, the first iteration has been performed by scanning the attenuation parameter from
α = 10
9 to
α = 10
10 in steps of ∆
α = 5×10
8, and the angular position has been scanned from
θ =
−720
° to
θ = 720
° in steps of ∆
θ = 2
°. The optimal values of the fitness parameters from the first iteration in this case are
α = 10
9 and
θ = 466
°, and
χ2= 0.6789. Once the optimal values have been determined from the first iteration, further iterations are performed by scanning only near the first iteration optimal region, which substantially improves the performance of the iterative method. In the present simulation the value of the fitness function converges at approximately the 5
th iteration. The optimal values of the fitness parameters from the 5
th iteration are
α = 10
10 and
θ = 496
°, and the value of the fitness function is
χ2 = 0.4927. In
Figure 6a the spectral amplitudes that result from the first and 5
th iterations are shown. As it can be observed, the effect of the XUV pulses on the spectral amplitude is readily small, which is expected since the perturbation of the IR pulse is weak (
α = 10
9− 10
10). The intensity of the optimal XUV pulse after the 5
th iteration is shown in
Figure 6b, and the inset shows the evolution of the value of the normalized
χ2 function for the increasing iterations. Clearly, as the iteration procedure evolves, the value of the fitness function improves such that at the 5
th iteration an optimal compressed pulse is achieved. As shown in the inset of
Figure 6b, the value of the normalized
χ2 function becomes basically constant after the 5
th iteration, and therefore no substantial improvements are achieved by considering further iterations. This simulation therefore shows the robustness of the control method, which is able to achieve optimal fitness targets both by using relatively weak perturbations of the IR driving pulse with a single iteration and by considering very weak perturbations in a multiple iteration procedure.
Figure 5.
(color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 4.
Figure 5.
(color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 4.
Figure 6.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering several iterations of the feedback loop for α scanned from α = 109 to α = 1010(a,b) and from α = 1011 to α = 1012 (c,d). (a,b): The scan in the first iteration in θ is from θ = −720° to θ = 720°. In the subsequent iterations, θ is scanned from θ = 200° to θ = 700°. In (a) the spectral intensity of the original and optimized spectra are shown for the first and 5th iterations, as indicated. The optimal values of the fitness parameters for the 5th iteration are in this case α = 1010 and θ = 496°. In (b) the temporal evolution of the intensity of the XUV pulse resulting from the second interaction region after the 5th iteration (loop) is shown. The inset in (b) shows the value of the normalized χ2 parameter as a function of the iteration number. From approximately the 5th iteration the value of χ2 and the intensity profile of the resulting XUV pulse do not change substantially. (c) and (d): The scan in the all the iterations in θ is from θ = −720° to θ = 720°. In (c) the spectral intensity of the original and optimized spectra are shown for the first and 8th iterations, as indicated. The optimal values of the fitness parameters for the 8th iteration are in this case α = 1012 and θ = 365°. In (d) the temporal evolution of the intensity of the XUV pulse resulting from the second interaction region after the 8th iteration is shown, which is an isolated single cycle pulse centered at 36 eV. The inset in (d) shows the value of the normalized χ2 parameter as a function of the iteration number. From approximately the 8th iteration, the duration of the intensity profile of the resulting central XUV pulse does not change substantially. Note that the labels in the vertical axis of (a) and (c) indicate a logarithmic scale.
Figure 6.
(Color online) Optimization of the HHG spectral region 21–51 eV obtained by considering several iterations of the feedback loop for α scanned from α = 109 to α = 1010(a,b) and from α = 1011 to α = 1012 (c,d). (a,b): The scan in the first iteration in θ is from θ = −720° to θ = 720°. In the subsequent iterations, θ is scanned from θ = 200° to θ = 700°. In (a) the spectral intensity of the original and optimized spectra are shown for the first and 5th iterations, as indicated. The optimal values of the fitness parameters for the 5th iteration are in this case α = 1010 and θ = 496°. In (b) the temporal evolution of the intensity of the XUV pulse resulting from the second interaction region after the 5th iteration (loop) is shown. The inset in (b) shows the value of the normalized χ2 parameter as a function of the iteration number. From approximately the 5th iteration the value of χ2 and the intensity profile of the resulting XUV pulse do not change substantially. (c) and (d): The scan in the all the iterations in θ is from θ = −720° to θ = 720°. In (c) the spectral intensity of the original and optimized spectra are shown for the first and 8th iterations, as indicated. The optimal values of the fitness parameters for the 8th iteration are in this case α = 1012 and θ = 365°. In (d) the temporal evolution of the intensity of the XUV pulse resulting from the second interaction region after the 8th iteration is shown, which is an isolated single cycle pulse centered at 36 eV. The inset in (d) shows the value of the normalized χ2 parameter as a function of the iteration number. From approximately the 8th iteration, the duration of the intensity profile of the resulting central XUV pulse does not change substantially. Note that the labels in the vertical axis of (a) and (c) indicate a logarithmic scale.
![Applsci 02 00816 g006]()
From the simulations that have been carried out, it can in general be concluded that the optimized configuration is not critically sensitive to the value of the intensity of the XUV
1 pulse, and also that weak perturbations of the IR pulse seem to be generally more effective. This supports the fact that the short trajectories contribute most on the optimal configuration, since they are more robust against changes in the intensity compared with the long trajectories [
2]. In order to compare the effect of a weaker XUV field on the iterative procedure, the previous simulations have been repeated by scanning the attenuation parameter from
α = 10
11 to
α = 10
12 in steps of ∆
α = 5
× 10
11. The corresponding results are shown in
Figure 6c,d. Clearly, the iterative procedure is more effective by
gently perturbing the IR field, achieving in this case an isolated single cycle pulse of 120 as at a central photon energy of 36 eV. Weaker XUV intensities have been computed with no further improvements of the optimization in this case.
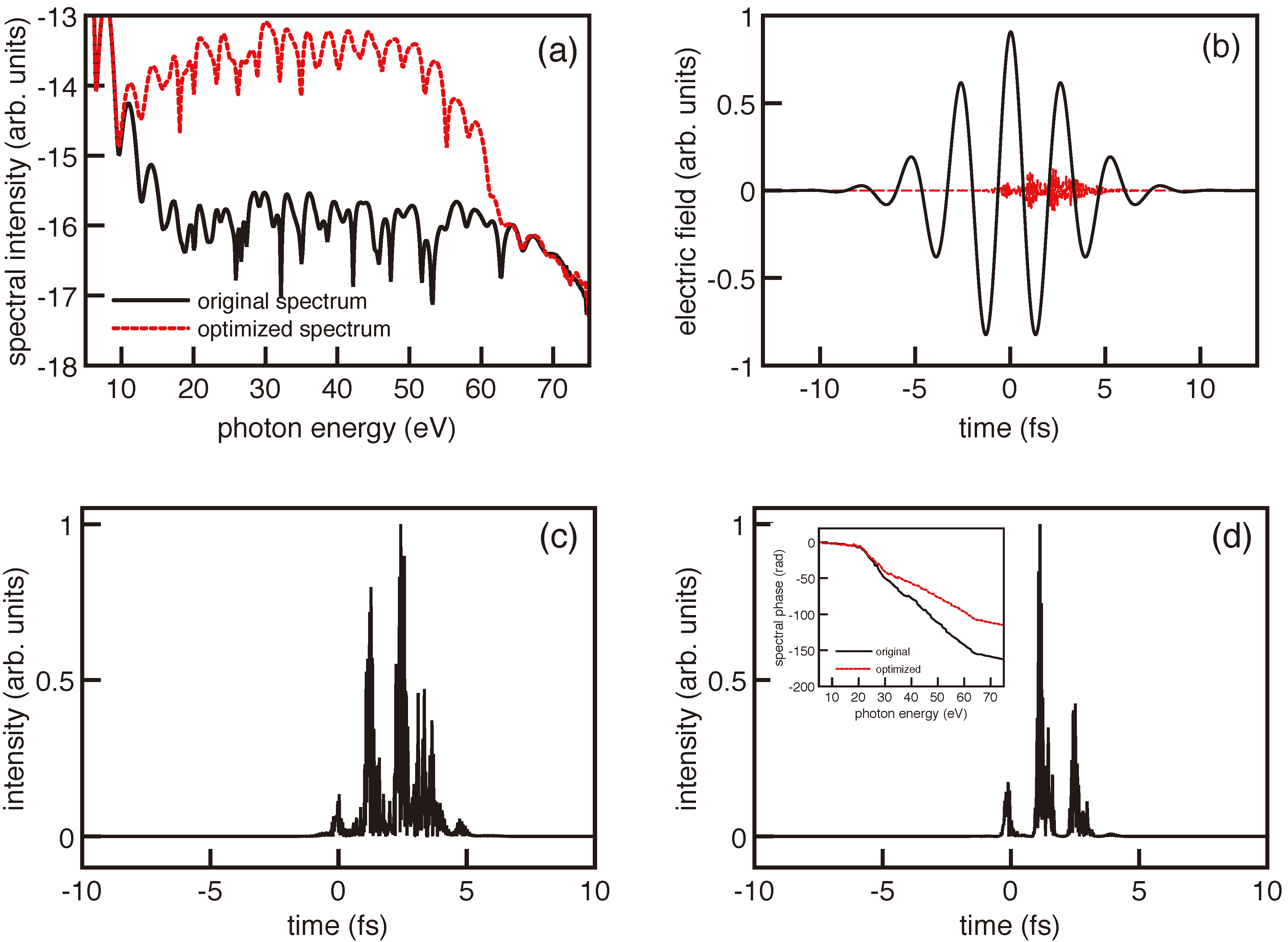
Figure 7.
(Color online) Optimization of the HHG spectral region 50–70 eV obtained by considering a single feedback loop. The scan in θ is from θ = −720° to θ = 720°, and α is scanned from α = 107 to α = 108. The value of the normalized χ2 function is 0.8771 for the original spectrum and 0.2309 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV pulse has been rescaled to allow its visualization. In this case the optimal values of the fitness parameters are α = 108 and θ = 550°. (c,d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 60 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
Figure 7.
(Color online) Optimization of the HHG spectral region 50–70 eV obtained by considering a single feedback loop. The scan in θ is from θ = −720° to θ = 720°, and α is scanned from α = 107 to α = 108. The value of the normalized χ2 function is 0.8771 for the original spectrum and 0.2309 for the optimized one. In (a) the spectral intensity of the original and optimized spectra are shown, as indicated. The IR driving pulse together with the optimal XUV pulse are shown in (b). The amplitude of the IR pulse is normalized, and the one corresponding to the XUV pulse has been rescaled to allow its visualization. In this case the optimal values of the fitness parameters are α = 108 and θ = 550°. (c,d) show the temporal evolution of the intensities of the XUV pulses resulting from the second interaction region, before and after optimization, respectively, which are centered at a photon energy of 60 eV. The inset in (d) shows the spectral phase for the original and optimized spectra. Note that the labels in the vertical axis of (a) indicate a logarithmic scale.
![Applsci 02 00816 g007]()
Finally, the optimization of the spectral amplitude has also been considered in a spectral region near the cutoff, as a second significative example, which shows the generality of the control technique. The filtered spectral region in this case is centered at 60 eV with a bandwidth of 20 eV, and the results are shown in
Figure 7. The numerical algorithm considers only a single feedback loop and scans from
α = 10
7 to
α = 10
8, in steps of ∆
α = 10
7, and from
θ =
−720
° to
θ = 720
°, in steps of ∆
θ = 10
°. The optimal values obtained in this case are
α = 10
8 and
θ = 550
°.
Figure 7a shows how the spectral intensity is modified basically near the cutoff,
i.e., in the spectral region that is to be optimized. As in the case analyzed in
Figure 2, where the optimization was considered for a region well in the plateau, the optimal position of the XUV
1 pulse with respect to the IR driving pulse lies near the late temporal wing, as shown in
Figure 7b. As a result of this optimization procedure, the XUV original radiation from the second gas target, which includes a central pulse of
≈ 690 as (
Figure 7c), is compressed to an isolated attosecond pulse of only 254 as, as shown in
Figure 7d. The inset in
Figure 7d shows how the phase of the spectrum is strongly modified due to the early wing of the XUV
1 pulse–the corresponding field amplitude is shown in the inset of
Figure 7b, which induce a suppression of the yield generated around the central part of the IR pulse, as it was also observed in the case of
Figure 2 and
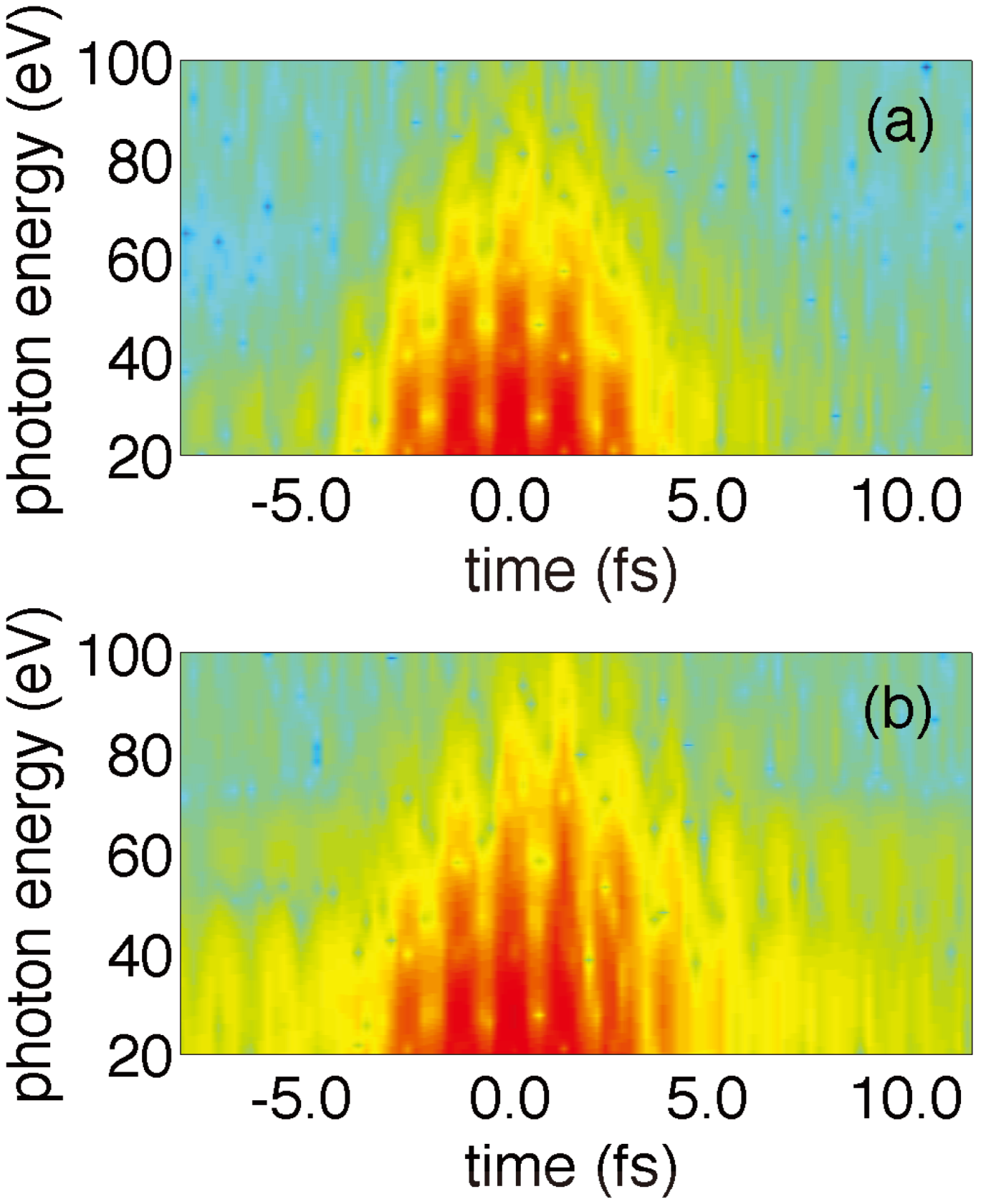
Figure 3. Finally, the time-frequency analysis for the case near the cutoff is shown in
Figure 8. As in the simulations commented previously, a yield enhancement can be observed in the late wing region of the IR field where the XUV
1 optimal pulse is centered, clearly showing again a selection of the short trajectories around the HHG region that is being optimized (50–70 eV).
Figure 8.
(Color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 7.
Figure 8.
(Color online) Time-frequency analysis of the original (
a) and optimized (
b) spectra, for the case shown in
Figure 7.
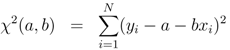
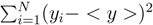 in each case, where
in each case, where 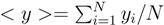 , the minimum normalized χ2 value provides the combination of IR andXUV1 pulses that produce the flattest spectral amplitude, i.e., the closest to a straight-line. The methodcan readily be iterated by splitting the XUV pulse from the first gas target (XUV1, XUV2, ..., XUVn, see Figure 1), so that an optimal driving pulse can be obtained iteratively resulting in some cases in an improved result, as it will be detailed below.
, the minimum normalized χ2 value provides the combination of IR andXUV1 pulses that produce the flattest spectral amplitude, i.e., the closest to a straight-line. The methodcan readily be iterated by splitting the XUV pulse from the first gas target (XUV1, XUV2, ..., XUVn, see Figure 1), so that an optimal driving pulse can be obtained iteratively resulting in some cases in an improved result, as it will be detailed below.