The Noise Blowing-Up Strategy Creates High Quality High Resolution Adversarial Images against Convolutional Neural Networks
Abstract
1. Introduction
1.1. Standart Adversarial Attacks
1.2. Challenges and Related Works
1.3. Our Contribution
1.4. Organisation of the Paper
2. CNNs and Attack Scenarios
2.1. Assessment of the Human Perception of Distinct Images
- ,
- ,
- ,
- FID(, )
2.2. Attack Scenarios in the Domain
2.3. Attack Scenarios Expressed in the Domain


- For the target scenario: , , and with dominant among all categories, and, furthermore, if one additionally requires the adversarial image to be -strong adversarial.
- For the untarget scenario: , , and with c such that .
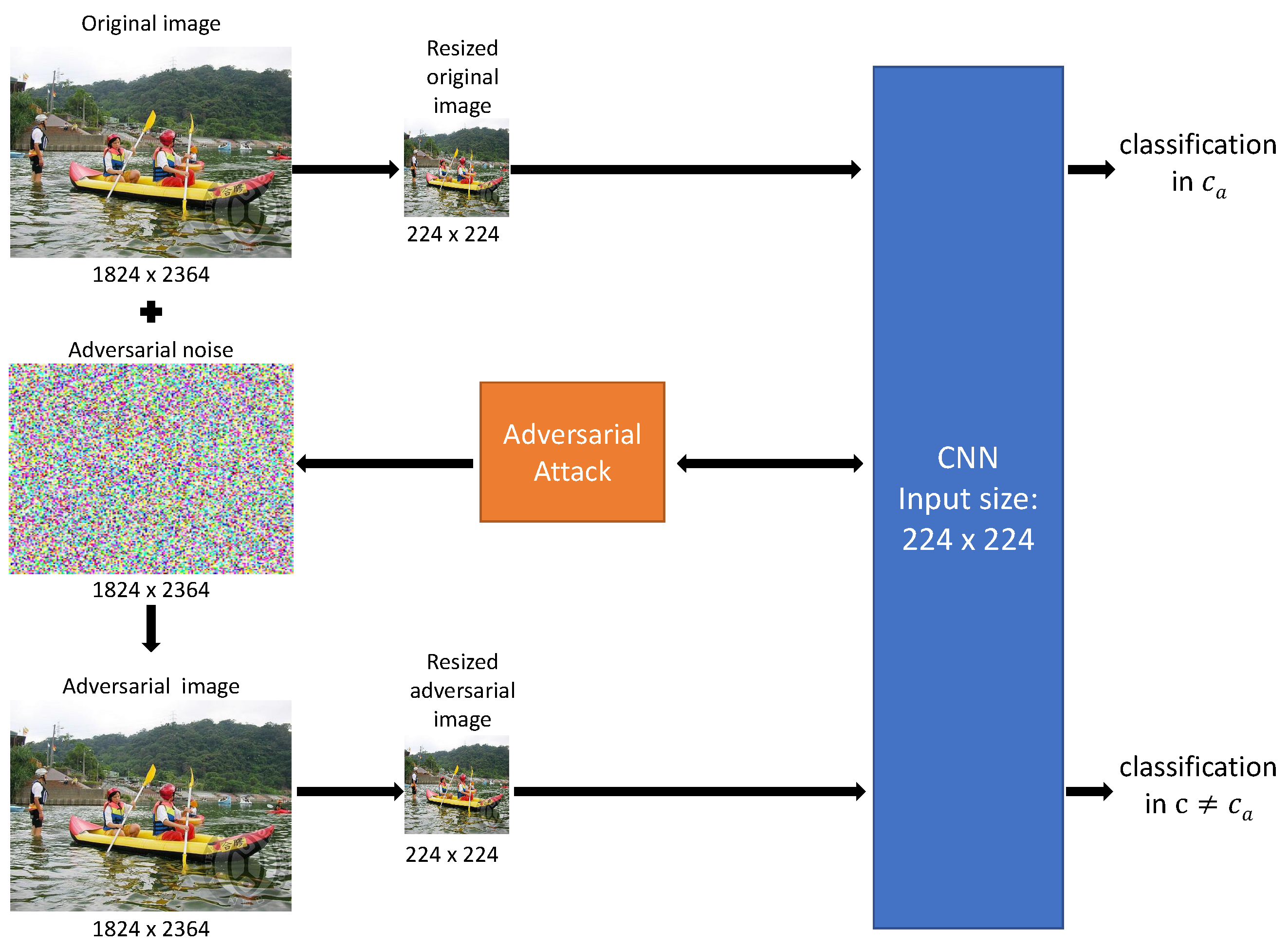
3. The Noise Blowing-Up Strategy
3.1. Constructing Images Adversarial in out of Those Adversarial in

3.2. Indicators
- and in the domain. One writes () and the corresponding values.
- and in the domain. One writes () and the corresponding values.
- and in the domain. One writes () and the corresponding values.
- , in the domain. One writes the corresponding values.
- and in the domain. One writes the corresponding values.
4. Ingredients of the Experimental Study
4.1. The Selection of and of
4.2. The CNNs
4.3. The HR Clean Images
4.4. The Attacks
5. Experimental Results of the Noise Blowing-Up Method
5.1. Phase 1: Running
5.2. Interpretation of the Results of Phase 1
5.3. Phase 2: Running
5.4. Interpretation of the Results of Phase 2
6. Revisiting the Failed Cases with
6.1. Revisiting the Failed Cases in Both Scenarios
6.2. Outcome of Revisiting the Failed Cases
7. Comparison of the Lifting Method and of the Noise Blowing-Up Method
7.1. The Three HR Images, the CNN, the Attack, the Scenario
7.2. Implementation and Outcomes
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Clean Images

| Ancestor Images and Their Original Size | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| abacus | 1 | 2448 × 3264 | 960 × 1280 | 262 × 275 | 598 × 300 | 377 × 500 | 501 × 344 | 375 × 500 | 448 × 500 | 500 × 500 | 2448 × 3264 | |
| acorn | 2 | 374 × 500 | 500 × 469 | 375 × 500 | 500 × 375 | 500 × 500 | 500 × 500 | 375 × 500 | 374 × 500 | 461 × 500 | 333 × 500 | |
| baseball | 3 | 398 × 543 | 240 × 239 | 2336 × 3504 | 333 × 500 | 262 × 350 | 310 × 310 | 404 × 500 | 344 × 500 | 375 × 500 | 285 × 380 | |
| broom | 4 | 500 × 333 | 286 × 490 | 360 × 480 | 298 × 298 | 413 × 550 | 366 × 500 | 400 × 400 | 348 × 500 | 346 × 500 | 640 × 480 | |
| brown bear | 5 | 700 × 467 | 903 × 1365 | 333 × 500 | 500 × 333 | 497 × 750 | 336 × 500 | 480 × 599 | 375 × 500 | 334 × 500 | 419 × 640 | |
| canoe | 6 | 500 × 332 | 450 × 600 | 500 × 375 | 375 × 500 | 406 × 613 | 600 × 400 | 1067 × 1600 | 333 × 500 | 1536 × 2048 | 375 × 500 | |
| hippopotamus | 7 | 375 × 500 | 1200 × 1600 | 333 × 500 | 450 × 291 | 525 × 525 | 375 × 500 | 500 × 457 | 424 × 475 | 500 × 449 | 339 × 500 | |
| llama | 8 | 500 × 333 | 618 × 468 | 500 × 447 | 253 × 380 | 500 × 333 | 333 × 500 | 375 × 1024 | 375 × 500 | 290 × 345 | 375 × 500 | |
| maraca | 9 | 375 × 500 | 375 × 500 | 470 × 627 | 1328 × 1989 | 250 × 510 | 375 × 500 | 768 × 104 | 375 × 500 | 375 × 500 | 500 × 375 | |
| mountain bike | 10 | 375 × 500 | 500 × 375 | 375 × 500 | 333 × 500 | 500 × 375 | 300 × 402 | 375 × 500 | 446 × 500 | 375 × 500 | 500 × 333 | |
| CNNs | p | Abacus | Acorn | Baseball | Broom | Brown Bear | Canoe | Hippopotamus | Llama | Maraca | Mountain Bike |
|---|---|---|---|---|---|---|---|---|---|---|---|
DenseNet-121 | 1 | 1.000 | 0.994 | 0.997 | 0.982 | 0.996 | 0.987 | 0.999 | 0.998 | 0.481 | 0.941 |
| 2 | 1.000 | 0.997 | 0.993 | 0.999 | 0.575 | 0.921 | 0.999 | 0.974 | 0.987 | 0.992 | |
| 3 | 0.999 | 0.954 | 1.000 | 0.999 | 0.999 | 0.675 | 0.993 | 0.996 | 1.000 | 0.814 | |
| 4 | 0.998 | 0.998 | 1.000 | 1.000 | 0.998 | 0.552 | 0.684 | 0.966 | 0.742 | 0.255 | |
| 5 | 1.000 | 0.999 | 1.000 | 0.999 | 0.993 | 0.827 | 1.000 | 0.999 | 0.153 | 0.637 | |
| 6 | 1.000 | 0.998 | 0.946 | 0.997 | 1.000 | 0.975 | 0.991 | 0.961 | 0.684 | 0.995 | |
| 7 | 0.999 | 0.999 | 0.997 | 0.945 | 0.949 | 0.524 | 0.973 | 0.987 | 0.960 | 0.835 | |
| 8 | 1.000 | 0.999 | 0.985 | 0.940 | 0.999 | 0.893 | 1.000 | 0.999 | 0.997 | 0.968 | |
| 9 | 1.000 | 0.996 | 0.967 | 1.000 | 0.998 | 0.710 | 1.000 | 1.000 | 0.991 | 0.969 | |
| 10 | 0.997 | 1.000 | 0.999 | 0.997 | 0.992 | 0.790 | 1.000 | 0.935 | 0.929 | 0.907 | |
DenseNet-169 | 1 | 1.000 | 0.998 | 0.999 | 0.973 | 0.999 | 0.995 | 0.995 | 0.999 | 0.991 | 0.799 |
| 2 | 0.999 | 1.000 | 0.998 | 0.991 | 0.343 | 0.683 | 0.999 | 0.999 | 0.991 | 0.862 | |
| 3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.929 | 1.000 | 0.997 | 1.000 | 0.922 | |
| 4 | 0.990 | 0.999 | 1.000 | 1.000 | 1.000 | 0.479 | 0.927 | 0.960 | 0.665 | 0.885 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.999 | 0.998 | 0.941 | 1.000 | 0.993 | 0.681 | 0.969 | |
| 6 | 1.000 | 1.000 | 0.999 | 0.999 | 1.000 | 0.997 | 0.997 | 0.991 | 0.829 | 0.952 | |
| 7 | 1.000 | 1.000 | 0.999 | 1.000 | 0.990 | 0.796 | 0.990 | 0.999 | 0.727 | 0.856 | |
| 8 | 1.000 | 1.000 | 0.998 | 0.985 | 1.000 | 0.944 | 0.998 | 1.000 | 1.000 | 0.942 | |
| 9 | 1.000 | 1.000 | 0.886 | 1.000 | 1.000 | 0.949 | 1.000 | 1.000 | 0.908 | 0.941 | |
| 10 | 0.948 | 1.000 | 0.998 | 0.999 | 0.999 | 0.897 | 0.999 | 0.999 | 0.720 | 0.502 | |
DenseNet-201 | 1 | 1.000 | 0.999 | 0.994 | 1.000 | 0.994 | 0.990 | 0.999 | 0.999 | 0.565 | 0.986 |
| 2 | 1.000 | 1.000 | 0.985 | 1.000 | 0.928 | 0.949 | 0.999 | 0.978 | 0.999 | 0.995 | |
| 3 | 0.983 | 0.957 | 0.999 | 1.000 | 0.999 | 0.719 | 1.000 | 0.995 | 1.000 | 0.829 | |
| 4 | 0.937 | 0.987 | 1.000 | 1.000 | 0.999 | 0.846 | 0.919 | 1.000 | 0.732 | 0.752 | |
| 5 | 1.000 | 1.000 | 0.999 | 0.995 | 0.995 | 0.786 | 1.000 | 0.993 | 0.316 | 0.936 | |
| 6 | 1.000 | 1.000 | 0.996 | 1.000 | 1.000 | 0.990 | 1.000 | 0.790 | 0.733 | 0.994 | |
| 7 | 1.000 | 1.000 | 1.000 | 0.998 | 0.997 | 0.817 | 0.997 | 0.984 | 0.959 | 0.682 | |
| 8 | 1.000 | 1.000 | 0.965 | 0.999 | 0.966 | 0.925 | 0.992 | 1.000 | 0.998 | 0.992 | |
| 9 | 1.000 | 0.998 | 0.818 | 1.000 | 0.980 | 0.980 | 1.000 | 0.999 | 0.971 | 0.964 | |
| 10 | 1.000 | 1.000 | 0.995 | 0.998 | 0.979 | 0.976 | 0.964 | 0.990 | 0.604 | 0.966 | |
MobileNet | 1 | 0.944 | 0.216 | 0.609 | 0.646 | 0.966 | 0.287 | 0.876 | 0.621 | 0.324 | 0.736 |
| 2 | 0.867 | 0.984 | 0.966 | 0.957 | 0.506 | 0.751 | 0.613 | 0.838 | 0.972 | 0.937 | |
| 3 | 0.967 | 0.905 | 0.937 | 0.982 | 0.969 | 0.778 | 0.970 | 0.933 | 0.999 | 0.939 | |
| 4 | 0.984 | 0.978 | 0.966 | 0.940 | 0.961 | 0.621 | 0.758 | 0.968 | 0.472 | 0.576 | |
| 5 | 0.915 | 0.984 | 0.917 | 0.829 | 0.971 | 0.836 | 0.9311 | 0.873 | 0.383 | 0.708 | |
| 6 | 0.989 | 0.950 | 0.942 | 0.932 | 0.970 | 0.854 | 0.971 | 0.808 | 0.573 | 0.863 | |
| 7 | 0.970 | 0.962 | 0.929 | 0.903 | 0.895 | 0.524 | 0.683 | 0.989 | 0.740 | 0.671 | |
| 8 | 0.970 | 0.985 | 0.834 | 0.906 | 0.942 | 0.732 | 0.723 | 0.986 | 0.788 | 0.930 | |
| 9 | 0.998 | 0.965 | 0.755 | 0.986 | 0.940 | 0.767 | 0.873 | 0.967 | 0.921 | 0.855 | |
| 10 | 0.923 | 1.000 | 0.804 | 0.934 | 0.772 | 0.877 | 0.975 | 0.766 | 0.844 | 0.850 | |
NASNet Mobile | 1 | 0.948 | 0.930 | 0.888 | 0.880 | 0.887 | 0.904 | 0.911 | 0.945 | 0.699 | 0.867 |
| 2 | 0.972 | 0.917 | 0.882 | 0.901 | 0.426 | 0.897 | 0.941 | 0.954 | 0.976 | 0.915 | |
| 3 | 0.896 | 0.938 | 0.887 | 0.976 | 0.943 | 0.707 | 0.929 | 0.747 | 0.876 | 0.945 | |
| 4 | 0.859 | 0.940 | 0.893 | 0.961 | 0.920 | 0.549 | 0.517 | 0.889 | 0.991 | 0.310 | |
| 5 | 0.949 | 0.950 | 0.879 | 0.956 | 0.896 | 0.577 | 0.914 | 0.977 | 0.720 | 0.792 | |
| 6 | 0.975 | 0.945 | 0.953 | 0.970 | 0.921 | 0.698 | 0.903 | 0.926 | 0.307 | 0.859 | |
| 7 | 0.985 | 0.902 | 0.868 | 0.953 | 0.837 | 0.809 | 0.865 | 0.955 | 0.984 | 0.519 | |
| 8 | 0.969 | 0.955 | 0.879 | 0.922 | 0.881 | 0.870 | 0.800 | 0.969 | 0.498 | 0.912 | |
| 9 | 0.971 | 0.874 | 0.574 | 0.934 | 0.935 | 0.691 | 0.924 | 0.942 | 0.902 | 0.938 | |
| 10 | 0.847 | 0.979 | 0.842 | 0.945 | 0.811 | 0.782 | 0.946 | 0.917 | 0.410 | 0.605 | |
ResNet-50 | 1 | 0.999 | 0.998 | 0.996 | 0.883 | 0.996 | 0.997 | 0.999 | 1.000 | 0.597 | 0.959 |
| 2 | 0.980 | 0.999 | 0.999 | 0.999 | 0.529 | 0.990 | 1.000 | 0.998 | 0.997 | 0.984 | |
| 3 | 0.999 | 0.989 | 0.999 | 0.999 | 0.999 | 0.801 | 1.000 | 1.000 | 1.000 | 0.990 | |
| 4 | 0.999 | 0.999 | 0.999 | 0.999 | 0.998 | 0.831 | 0.970 | 0.994 | 0.350 | 0.444 | |
| 5 | 0.999 | 0.999 | 0.999 | 0.994 | 0.986 | 0.950 | 0.997 | 0.278 | 0.543 | 0.871 | |
| 6 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.985 | 1.000 | 0.920 | 0.725 | 0.685 | |
| 7 | 0.999 | 0.999 | 0.999 | 0.998 | 0.991 | 0.584 | 1.000 | 1.000 | 0.987 | 0.803 | |
| 8 | 1.000 | 0.999 | 0.926 | 0.990 | 0.997 | 0.981 | 0.970 | 1.000 | 0.999 | 0.963 | |
| 9 | 1.000 | 0.999 | 0.808 | 0.999 | 0.999 | 0.911 | 1.000 | 1.000 | 0.998 | 0.991 | |
| 10 | 0.999 | 0.999 | 0.999 | 0.999 | 0.982 | 0.987 | 0.996 | 0.984 | 0.775 | 0.939 | |
ResNet-101 | 1 | 1.000 | 1.000 | 0.997 | 0.999 | 1.000 | 0.999 | 0.999 | 1.000 | 0.665 | 0.973 |
| 2 | 1.000 | 1.000 | 0.972 | 1.000 | 0.836 | 0.984 | 1.000 | 0.868 | 0.995 | 0.992 | |
| 3 | 1.000 | 0.898 | 1.000 | 1.000 | 1.000 | 0.940 | 1.000 | 1.000 | 1.000 | 0.778 | |
| 4 | 0.744 | 1.000 | 1.000 | 1.000 | 0.997 | 0.556 | 0.941 | 0.999 | 0.447 | 0.835 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.999 | 0.968 | 0.939 | 0.999 | 0.894 | 0.325 | 0.694 | |
| 6 | 1.000 | 1.000 | 0.996 | 1.000 | 1.000 | 0.983 | 1.000 | 0.837 | 0.719 | 0.996 | |
| 7 | 1.000 | 1.000 | 1.000 | 0.997 | 0.990 | 0.920 | 1.000 | 1.000 | 0.305 | 0.330 | |
| 8 | 1.000 | 1.000 | 0.999 | 0.997 | 0.978 | 0.993 | 0.943 | 1.000 | 0.997 | 0.988 | |
| 9 | 1.000 | 1.000 | 0.959 | 1.000 | 0.997 | 0.903 | 1.000 | 1.000 | 0.969 | 0.983 | |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | 0.965 | 0.999 | 0.995 | 0.927 | 0.961 | |
ResNet-152 | 1 | 1.000 | 1.000 | 1.000 | 0.998 | 0.999 | 0.994 | 1.000 | 0.999 | 0.597 | 0.992 |
| 2 | 0.578 | 1.000 | 0.999 | 1.000 | 0.356 | 0.979 | 1.000 | 0.999 | 0.997 | 0.998 | |
| 3 | 1.000 | 0.974 | 1.000 | 1.000 | 1.000 | 0.676 | 1.000 | 1.000 | 1.000 | 0.919 | |
| 4 | 0.996 | 1.000 | 1.000 | 1.000 | 1.000 | 0.610 | 0.961 | 0.985 | 0.597 | 0.896 | |
| 5 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.909 | 1.000 | 0.919 | 0.161 | 0.928 | |
| 6 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | 0.999 | 0.869 | 0.951 | 0.964 | |
| 7 | 0.997 | 1.000 | 1.000 | 1.000 | 0.960 | 0.500 | 1.000 | 1.000 | 0.962 | 0.721 | |
| 8 | 1.000 | 1.000 | 0.999 | 1.000 | 0.995 | 0.986 | 1.000 | 1.000 | 0.998 | 0.967 | |
| 9 | 1.000 | 1.000 | 0.918 | 1.000 | 0.993 | 0.941 | 1.000 | 0.999 | 0.749 | 0.999 | |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | 0.910 | 1.000 | 0.998 | 0.897 | 0.886 | |
VGG-16 | 1 | 0.996 | 0.430 | 1.000 | 0.973 | 0.996 | 0.991 | 0.999 | 0.855 | 0.586 | 0.832 |
| 2 | 0.540 | 0.976 | 1.000 | 0.913 | 0.925 | 0.896 | 0.999 | 0.964 | 0.693 | 0.963 | |
| 3 | 0.998 | 0.531 | 1.000 | 0.997 | 1.000 | 0.910 | 1.000 | 1.000 | 1.000 | 0.949 | |
| 4 | 0.987 | 0.997 | 1.000 | 0.983 | 0.998 | 0.802 | 0.212 | 0.998 | 0.389 | 0.485 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.959 | 0.999 | 0.819 | 0.999 | 0.854 | 0.226 | 0.652 | |
| 6 | 1.000 | 1.000 | 0.869 | 0.992 | 1.000 | 0.890 | 1.000 | 0.833 | 0.450 | 0.877 | |
| 7 | 0.987 | 0.996 | 0.999 | 1.000 | 0.968 | 0.605 | 0.944 | 1.000 | 0.371 | 0.617 | |
| 8 | 0.917 | 0.995 | 1.000 | 0.858 | 0.999 | 0.931 | 0.997 | 1.000 | 0.954 | 0.941 | |
| 9 | 1.000 | 0.989 | 0.861 | 0.989 | 0.899 | 0.301 | 1.000 | 1.000 | 0.901 | 0.922 | |
| 10 | 0.977 | 1.000 | 1.000 | 0.994 | 0.992 | 0.974 | 1.000 | 0.998 | 0.840 | 0.564 | |
VGG-19 | 1 | 1.000 | 0.959 | 1.000 | 0.669 | 1.000 | 0.740 | 1.000 | 0.989 | 0.466 | 0.879 |
| 2 | 0.993 | 0.996 | 0.999 | 0.947 | 0.939 | 0.756 | 0.999 | 0.970 | 0.785 | 0.818 | |
| 3 | 1.000 | 0.740 | 1.000 | 0.998 | 0.998 | 0.935 | 1.000 | 1.000 | 1.000 | 0.861 | |
| 4 | 0.996 | 0.952 | 1.000 | 0.890 | 0.997 | 0.684 | 0.468 | 0.992 | 0.828 | 0.291 | |
| 5 | 1.000 | 0.999 | 1.000 | 0.743 | 0.999 | 0.499 | 0.999 | 0.252 | 0.587 | 0.794 | |
| 6 | 1.000 | 1.000 | 0.999 | 0.993 | 1.000 | 0.735 | 0.999 | 0.952 | 0.693 | 0.846 | |
| 7 | 0.999 | 0.998 | 0.999 | 0.999 | 0.903 | 0.656 | 0.988 | 1.000 | 0.370 | 0.494 | |
| 8 | 1.000 | 0.999 | 1.000 | 0.987 | 0.998 | 0.744 | 0.994 | 1.000 | 0.996 | 0.795 | |
| 9 | 1.000 | 1.000 | 0.610 | 0.999 | 0.974 | 0.550 | 1.000 | 1.000 | 0.552 | 0.818 | |
| 10 | 0.998 | 1.000 | 1.000 | 0.999 | 0.995 | 0.791 | 1.000 | 0.994 | 0.758 | 0.761 |
| CNNs | p | Abacus | Acorn | Baseball | Broom | Brown Bear | Canoe | Hippopotamus | Llama | Maraca | Mountain Bike |
|---|---|---|---|---|---|---|---|---|---|---|---|
DenseNet-121 | 1 | 1.000 | 0.981 | 0.997 | 0.999 | 0.995 | 0.992 | 0.999 | 0.997 | 0.607 | 0.942 |
| 2 | 1.000 | 0.997 | 0.989 | 1.000 | 0.670 | 0.909 | 0.998 | 0.987 | 0.883 | 0.987 | |
| 3 | 0.998 | 0.845 | 1.000 | 1.000 | 0.996 | 0.836 | 0.987 | 0.997 | 1.000 | 0.891 | |
| 4 | 0.996 | 0.997 | 1.000 | 1.000 | 0.997 | 0.620 | 0.239 | 0.984 | 0.312 | 0.619 | |
| 5 | 1.000 | 0.999 | 1.000 | 0.998 | 0.955 | 0.811 | 1.000 | 1.000 | 0.145 | 0.986 | |
| 6 | 1.000 | 1.000 | 0.957 | 0.998 | 1.000 | 0.990 | 0.997 | 0.916 | 0.692 | 0.999 | |
| 7 | 0.998 | 0.999 | 0.999 | 0.973 | 0.937 | 0.525 | 0.985 | 0.974 | 0.902 | 0.940 | |
| 8 | 1.000 | 0.999 | 0.993 | 0.993 | 0.995 | 0.913 | 1.000 | 1.000 | 0.999 | 0.962 | |
| 9 | 1.000 | 0.998 | 0.981 | 1.000 | 0.997 | 0.820 | 0.999 | 1.000 | 0.999 | 0.992 | |
| 10 | 1.000 | 0.996 | 1.000 | 0.999 | 0.995 | 0.923 | 0.999 | 0.886 | 0.572 | 0.870 | |
DenseNet-169 | 1 | 0.999 | 0.978 | 1.000 | 0.999 | 0.999 | 0.997 | 0.997 | 0.999 | 0.952 | 0.873 |
| 2 | 1.000 | 0.999 | 0.998 | 0.992 | 0.535 | 0.764 | 0.998 | 0.999 | 0.995 | 0.861 | |
| 3 | 1.000 | 0.998 | 1.000 | 1.000 | 0.999 | 0.880 | 1.000 | 0.994 | 1.000 | 0.977 | |
| 4 | 0.990 | 0.996 | 1.000 | 1.000 | 1.000 | 0.549 | 0.553 | 0.981 | 0.583 | 0.973 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.994 | 1.000 | 0.915 | 1.000 | 0.994 | 0.530 | 0.997 | |
| 6 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 0.997 | 0.995 | 0.975 | 0.091 | 0.991 | |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 0.954 | 0.827 | 0.996 | 1.000 | 0.964 | 0.945 | |
| 8 | 1.000 | 1.000 | 0.998 | 0.998 | 0.999 | 0.951 | 0.999 | 1.000 | 1.000 | 0.975 | |
| 9 | 1.000 | 1.000 | 0.943 | 1.000 | 0.999 | 0.905 | 1.000 | 1.000 | 0.993 | 0.964 | |
| 10 | 0.970 | 1.000 | 0.999 | 1.000 | 0.997 | 0.952 | 0.999 | 0.998 | 0.608 | 0.507 | |
DenseNet-201 | 1 | 0.999 | 0.975 | 0.998 | 1.000 | 0.990 | 0.990 | 0.998 | 0.996 | 0.584 | 0.986 |
| 2 | 1.000 | 1.000 | 0.984 | 1.000 | 0.844 | 0.957 | 0.996 | 0.996 | 0.993 | 0.997 | |
| 3 | 0.987 | 0.950 | 1.000 | 1.000 | 0.998 | 0.669 | 0.999 | 0.994 | 1.000 | 0.886 | |
| 4 | 0.886 | 0.994 | 1.000 | 1.000 | 0.998 | 0.822 | 0.870 | 1.000 | 0.541 | 0.947 | |
| 5 | 1.000 | 1.000 | 0.999 | 0.983 | 0.980 | 0.586 | 1.000 | 0.998 | 0.141 | 0.980 | |
| 6 | 1.000 | 1.000 | 0.995 | 1.000 | 1.000 | 0.994 | 0.999 | 0.724 | 0.693 | 0.996 | |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | 0.865 | 0.997 | 0.970 | 0.973 | 0.917 | |
| 8 | 1.000 | 1.000 | 0.993 | 1.000 | 0.874 | 0.978 | 0.990 | 0.999 | 0.997 | 0.993 | |
| 9 | 1.000 | 0.999 | 0.877 | 1.000 | 0.984 | 0.995 | 1.000 | 0.999 | 0.987 | 0.988 | |
| 10 | 1.000 | 1.000 | 0.998 | 0.999 | 0.978 | 0.984 | 0.987 | 0.963 | 0.365 | 0.983 | |
MobileNet | 1 | 0.945 | 0.589 | 0.770 | 0.829 | 0.966 | 0.560 | 0.933 | 0.480 | 0.556 | 0.854 |
| 2 | 0.903 | 0.948 | 0.981 | 0.955 | 0.669 | 0.903 | 0.707 | 0.725 | 0.932 | 0.967 | |
| 3 | 0.922 | 0.850 | 0.935 | 0.971 | 0.985 | 0.830 | 0.958 | 0.938 | 0.999 | 0.985 | |
| 4 | 0.934 | 0.971 | 0.977 | 0.972 | 0.924 | 0.820 | 0.711 | 0.975 | 0.586 | 0.851 | |
| 5 | 0.896 | 0.981 | 0.905 | 0.653 | 0.982 | 0.787 | 0.953 | 0.846 | 0.498 | 0.910 | |
| 6 | 0.990 | 0.976 | 0.881 | 0.973 | 0.913 | 0.818 | 0.989 | 0.774 | 0.355 | 0.935 | |
| 7 | 0.982 | 0.979 | 0.838 | 0.923 | 0.791 | 0.750 | 0.748 | 0.978 | 0.884 | 0.379 | |
| 8 | 0.964 | 0.919 | 0.860 | 0.798 | 0.941 | 0.823 | 0.806 | 0.995 | 0.962 | 0.928 | |
| 9 | 0.997 | 0.851 | 0.730 | 0.996 | 0.943 | 0.692 | 0.970 | 0.988 | 0.848 | 0.758 | |
| 10 | 0.968 | 0.994 | 0.835 | 0.780 | 0.886 | 0.948 | 0.992 | 0.568 | 0.416 | 0.883 | |
NASNet Mobile | 1 | 0.940 | 0.945 | 0.885 | 0.948 | 0.892 | 0.925 | 0.914 | 0.945 | 0.288 | 0.869 |
| 2 | 0.947 | 0.946 | 0.905 | 0.892 | 0.454 | 0.932 | 0.829 | 0.951 | 0.957 | 0.902 | |
| 3 | 0.903 | 0.884 | 0.889 | 0.978 | 0.948 | 0.702 | 0.926 | 0.754 | 0.911 | 0.923 | |
| 4 | 0.844 | 0.929 | 0.895 | 0.961 | 0.910 | 0.513 | 0.656 | 0.928 | 0.993 | 0.667 | |
| 5 | 0.943 | 0.930 | 0.886 | 0.914 | 0.936 | 0.586 | 0.921 | 0.976 | 0.734 | 0.972 | |
| 6 | 0.973 | 0.945 | 0.949 | 0.972 | 0.925 | 0.792 | 0.846 | 0.936 | 0.085 | 0.854 | |
| 7 | 0.983 | 0.897 | 0.842 | 0.944 | 0.872 | 0.869 | 0.893 | 0.941 | 0.885 | 0.781 | |
| 8 | 0.962 | 0.950 | 0.870 | 0.908 | 0.887 | 0.864 | 0.824 | 0.965 | 0.930 | 0.904 | |
| 9 | 0.975 | 0.904 | 0.691 | 0.949 | 0.925 | 0.783 | 0.925 | 0.949 | 0.965 | 0.957 | |
| 10 | 0.861 | 0.957 | 0.851 | 0.955 | 0.809 | 0.860 | 0.941 | 0.929 | 0.397 | 0.495 | |
ResNet-50 | 1 | 1.000 | 0.795 | 0.998 | 0.841 | 0.999 | 0.998 | 0.999 | 0.999 | 0.801 | 0.986 |
| 2 | 0.411 | 1.000 | 1.000 | 1.000 | 0.931 | 0.991 | 1.000 | 0.998 | 0.850 | 0.995 | |
| 3 | 1.000 | 0.901 | 1.000 | 1.000 | 1.000 | 0.778 | 1.000 | 1.000 | 1.000 | 0.993 | |
| 4 | 1.000 | 0.993 | 1.000 | 1.000 | 0.999 | 0.897 | 0.881 | 0.999 | 0.424 | 0.929 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.969 | 0.996 | 0.945 | 1.000 | 0.381 | 0.253 | 0.995 | |
| 6 | 0.999 | 1.000 | 1.000 | 0.999 | 0.999 | 0.995 | 1.000 | 0.771 | 0.211 | 0.941 | |
| 7 | 1.000 | 1.000 | 1.000 | 0.988 | 0.992 | 0.743 | 1.000 | 1.000 | 0.969 | 0.892 | |
| 8 | 1.000 | 0.998 | 0.998 | 0.999 | 0.997 | 0.993 | 0.962 | 1.000 | 0.999 | 0.987 | |
| 9 | 1.000 | 1.000 | 0.695 | 1.000 | 0.999 | 0.971 | 1.000 | 1.000 | 0.998 | 0.999 | |
| 10 | 1.000 | 0.999 | 1.000 | 0.999 | 0.959 | 0.994 | 0.970 | 0.723 | 0.385 | 0.965 | |
ResNet-101 | 1 | 1.000 | 0.982 | 0.999 | 0.995 | 0.999 | 0.999 | 1.000 | 1.000 | 0.984 | 0.969 |
| 2 | 1.000 | 1.000 | 0.973 | 1.000 | 0.941 | 0.986 | 1.000 | 0.988 | 0.975 | 0.997 | |
| 3 | 1.000 | 0.929 | 1.000 | 1.000 | 1.000 | 0.882 | 1.000 | 1.000 | 1.000 | 0.895 | |
| 4 | 0.778 | 0.999 | 1.000 | 1.000 | 0.993 | 0.525 | 0.680 | 0.999 | 0.894 | 0.970 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.991 | 0.945 | 0.835 | 1.000 | 0.940 | 0.557 | 0.990 | |
| 6 | 1.000 | 1.000 | 0.994 | 0.998 | 0.999 | 0.996 | 1.000 | 0.722 | 0.599 | 0.998 | |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 0.911 | 0.961 | 1.000 | 1.000 | 0.772 | 0.756 | |
| 8 | 1.000 | 1.000 | 1.000 | 0.996 | 0.910 | 0.994 | 0.976 | 1.000 | 0.995 | 0.990 | |
| 9 | 1.000 | 1.000 | 0.979 | 1.000 | 0.997 | 0.848 | 1.000 | 1.000 | 0.959 | 0.980 | |
| 10 | 1.000 | 0.993 | 1.000 | 1.000 | 0.927 | 0.975 | 0.996 | 0.917 | 0.537 | 0.984 | |
ResNet-152 | 1 | 1.000 | 0.998 | 1.000 | 0.996 | 0.992 | 0.987 | 0.999 | 0.999 | 0.954 | 0.991 |
| 2 | 0.713 | 1.000 | 0.997 | 1.000 | 0.513 | 0.983 | 1.000 | 1.000 | 0.956 | 0.998 | |
| 3 | 1.000 | 0.665 | 1.000 | 1.000 | 1.000 | 0.794 | 0.999 | 1.000 | 1.000 | 0.969 | |
| 4 | 0.998 | 0.997 | 1.000 | 1.000 | 1.000 | 0.626 | 0.872 | 0.972 | 0.885 | 0.960 | |
| 5 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 | 0.841 | 1.000 | 0.927 | 0.219 | 0.993 | |
| 6 | 1.000 | 1.000 | 1.000 | 0.994 | 1.000 | 0.997 | 0.999 | 0.805 | 0.436 | 0.986 | |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 0.996 | 0.557 | 0.995 | 1.000 | 0.959 | 0.860 | |
| 8 | 1.000 | 1.000 | 1.000 | 1.000 | 0.951 | 0.965 | 0.999 | 1.000 | 1.000 | 0.991 | |
| 9 | 1.000 | 1.000 | 0.857 | 1.000 | 0.978 | 0.979 | 0.992 | 1.000 | 0.949 | 0.999 | |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 0.861 | 0.871 | 1.000 | 0.872 | 0.818 | 0.961 | |
VGG-16 | 1 | 0.999 | 0.392 | 1.000 | 0.725 | 0.997 | 0.990 | 0.999 | 0.940 | 0.592 | 0.862 |
| 2 | 0.952 | 0.997 | 1.000 | 0.918 | 0.922 | 0.918 | 1.000 | 0.968 | 0.683 | 0.979 | |
| 3 | 0.998 | 0.688 | 1.000 | 1.000 | 1.000 | 0.896 | 1.000 | 1.000 | 1.000 | 0.952 | |
| 4 | 0.996 | 0.999 | 1.000 | 0.993 | 0.998 | 0.764 | 0.214 | 0.999 | 0.703 | 0.740 | |
| 5 | 1.000 | 0.999 | 1.000 | 0.913 | 0.997 | 0.678 | 1.000 | 0.918 | 0.175 | 0.936 | |
| 6 | 1.000 | 1.000 | 0.674 | 0.972 | 0.999 | 0.883 | 1.000 | 0.828 | 0.470 | 0.952 | |
| 7 | 0.999 | 0.998 | 0.999 | 0.999 | 0.947 | 0.595 | 0.935 | 1.000 | 0.358 | 0.640 | |
| 8 | 0.987 | 0.995 | 1.000 | 0.844 | 0.999 | 0.952 | 0.999 | 1.000 | 0.979 | 0.973 | |
| 9 | 1.000 | 0.999 | 0.896 | 0.992 | 0.915 | 0.382 | 1.000 | 1.000 | 0.918 | 0.895 | |
| 10 | 0.998 | 1.000 | 1.000 | 0.998 | 0.964 | 0.981 | 1.000 | 0.998 | 0.745 | 0.614 | |
VGG-19 | 1 | 1.000 | 0.959 | 1.000 | 0.503 | 1.000 | 0.547 | 1.000 | 0.977 | 0.507 | 0.909 |
| 2 | 0.990 | 0.998 | 0.999 | 0.957 | 0.984 | 0.812 | 1.000 | 0.983 | 0.514 | 0.903 | |
| 3 | 1.000 | 0.767 | 1.000 | 0.996 | 1.000 | 0.946 | 1.000 | 1.000 | 1.000 | 0.912 | |
| 4 | 0.995 | 0.980 | 1.000 | 0.994 | 0.996 | 0.663 | 0.241 | 0.995 | 0.821 | 0.270 | |
| 5 | 1.000 | 0.999 | 1.000 | 0.617 | 0.997 | 0.716 | 1.000 | 0.463 | 0.436 | 0.934 | |
| 6 | 1.000 | 1.000 | 0.998 | 0.975 | 0.999 | 0.779 | 0.999 | 0.932 | 0.713 | 0.957 | |
| 7 | 1.000 | 0.999 | 1.000 | 0.999 | 0.881 | 0.586 | 0.995 | 1.000 | 0.336 | 0.422 | |
| 8 | 1.000 | 1.000 | 1.000 | 0.956 | 0.997 | 0.846 | 0.997 | 1.000 | 0.994 | 0.930 | |
| 9 | 1.000 | 1.000 | 0.575 | 0.991 | 0.988 | 0.441 | 1.000 | 1.000 | 0.660 | 0.752 | |
| 10 | 0.999 | 1.000 | 1.000 | 1.000 | 0.993 | 0.859 | 0.999 | 0.966 | 0.731 | 0.862 |
Appendix B. Choice of (ρ, λ, ρ) Based on a Case Study
| Step 1–3 | Step 4–8 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LLL | Avg | 0.548 | 0.504 | 0.955 | 0.94 | 0.99 | 0.03 | 0.02 | 0.02 | 1.77 | 9.9 | 4.5 | 5.3 | 46.6 | 46.2 | 125 | 0.043 |
| Min | 0.294 | 0.273 | 0.910 | 0.88 | 0.90 | 0.01 | 0.01 | 0.00 | 0.25 | 4.7 | 7.0 | 5.4 | 21 | 22 | 18 | 0.007 | |
| Max | 0.554 | 0.543 | 0.974 | 0.97 | 1.00 | 0.04 | 0.04 | 0.11 | 13.5 | 1.6 | 9.7 | 2.0 | 77 | 74 | 200 | 0.116 | |
| LLN | Avg | 0.548 | 0.456 | 0.955 | 0.95 | 0.85 | 0.03 | 0.02 | 0.03 | 0.98 | 9.9 | 4.5 | 7.9 | 46.6 | 46.2 | 196 | 0.499 |
| Min | 0.294 | 0.073 | 0.910 | 0.88 | 0.35 | 0.01 | 0.01 | 0.00 | 0.23 | 4.7 | 7.0 | 7.8 | 21 | 22 | 113 | 0.256 | |
| Max | 0.554 | 0.999 | 0.974 | 0.97 | 0.97 | 0.04 | 0.04 | 0.12 | 3.86 | 1.6 | 9.7 | 2.3 | 77 | 74 | 255 | 0.554 | |
| LNL | Avg | 0.548 | 0.290 | 0.955 | 0.95 | 0.85 | 0.03 | 0.03 | 0.03 | 1.06 | 9.9 | 4.9 | 7.9 | 46.6 | 46.6 | 196 | 0.349 |
| Min | 0.294 | 0.080 | 0.910 | 0.89 | 0.35 | 0.01 | 0.01 | 0.00 | 0.25 | 4.7 | 7.7 | 7.8 | 21 | 21 | 113 | 0.100 | |
| Max | 0.554 | 0.862 | 0.974 | 0.97 | 0.97 | 0.04 | 0.04 | 0.12 | 4.22 | 1.6 | 1.0 | 2.3 | 77 | 77 | 255 | 0.551 | |
| NLL | Avg | 0.548 | 0.423 | 0.956 | 0.95 | 0.99 | 0.03 | 0.02 | 0.03 | 1.25 | 1.0 | 4.6 | 7.3 | 46.8 | 46.7 | 196 | 0.478 |
| Min | 0.350 | 0.053 | 0.928 | 0.92 | 0.90 | 0.01 | 0.01 | 0.00 | 0.29 | 5.5 | 7.0 | 6.9 | 25 | 25 | 56 | 0.129 | |
| Max | 0.553 | 0.997 | 0.974 | 0.97 | 1.00 | 0.04 | 0.04 | 0.13 | 4.61 | 1.5 | 9.5 | 2.7 | 74 | 69 | 320 | 0.553 | |
| LNN | Avg | 0.548 | 0.536 | 0.955 | 0.95 | 0.85 | 0.03 | 0.03 | 0.03 | 1.06 | 9.9 | 4.9 | 7.9 | 46.6 | 46.6 | 196 | 0.526 |
| Min | 0.294 | 0.076 | 0.910 | 0.89 | 0.35 | 0.01 | 0.01 | 0.00 | 0.25 | 4.7 | 7.7 | 7.8 | 21 | 21 | 113 | 0.294 | |
| Max | 0.554 | 0.999 | 0.974 | 0.97 | 0.97 | 0.04 | 0.04 | 0.12 | 4.22 | 1.6 | 1.0 | 2.3 | 77 | 77 | 255 | 0.554 | |
| NLN | Avg | 0.548 | 0.416 | 0.956 | 0.95 | 0.99 | 0.03 | 0.02 | 0.03 | 1.25 | 1.0 | 4.6 | 7.3 | 46.8 | 46.7 | 196 | 0.138 |
| Min | 0.350 | 0.155 | 0.928 | 0.92 | 0.90 | 0.01 | 0.01 | 0.00 | 0.29 | 5.5 | 7.0 | 6.9 | 25 | 25 | 56 | 0.0002 | |
| Max | 0.553 | 0.550 | 0.974 | 0.97 | 1.00 | 0.04 | 0.04 | 0.13 | 4.61 | 1.5 | 9.5 | 2.7 | 74 | 69 | 320 | 0.395 | |
| NNL | Avg | 0.548 | 0.531 | 0.956 | 0.95 | 0.69 | 0.03 | 0.03 | 0.03 | 1.03 | 1.0 | 5.0 | 9.5 | 46.8 | 46.8 | 224 | 0.532 |
| Min | 0.350 | 0.057 | 0.928 | 0.92 | 0.25 | 0.01 | 0.01 | 0.00 | 0.30 | 5.5 | 7.6 | 9.0 | 25 | 25 | 127 | 0.350 | |
| Max | 0.553 | 0.999 | 0.974 | 0.97 | 0.92 | 0.04 | 0.04 | 0.14 | 3.80 | 1.5 | 1.0 | 2.9 | 74 | 74 | 255 | 0.553 | |
| NNN | Avg | 0.548 | 0.402 | 0.955 | 0.95 | 0.69 | 0.03 | 0.03 | 0.03 | 1.01 | 9.9 | 4.9 | 9.5 | 46.6 | 46.6 | 225 | 0.262 |
| Min | 0.350 | 0.098 | 0.928 | 0.92 | 0.25 | 0.01 | 0.01 | 0.00 | 0.30 | 5.5 | 7.6 | 9.0 | 25 | 25 | 127 | 9.5 | |
| Max | 0.556 | 0.979 | 0.974 | 0.97 | 0.92 | 0.04 | 0.04 | 0.14 | 3.80 | 1.5 | 1.0 | 2.9 | 74 | 74 | 255 | 0.552 | |
| Number of | Number of | Average Loss | |||
|---|---|---|---|---|---|
| L-L-L | 92 | 92 | 0 | 0 | 0.0439 |
| L-L-N | 92 | 10 | 25 | 57 | 0.5019 |
| L-N-L | 92 | 59 | 11 | 22 | 0.3501 |
| N-L-L | 92 | 16 | 21 | 55 | 0.4802 |
| L-N-N | 92 | 6 | 23 | 63 | 0.5295 |
| N-L-N | 92 | 89 | 0 | 3 | 0.1384 |
| N-N-L | 92 | 1 | 21 | 70 | 0.5345 |
| N-N-N | 92 | 62 | 10 | 20 | 0.2615 |
Appendix C. Enhancing the Noise Blowing-Up Method: Exploring its Performance with Varied Strength Levels of Adversarial Images
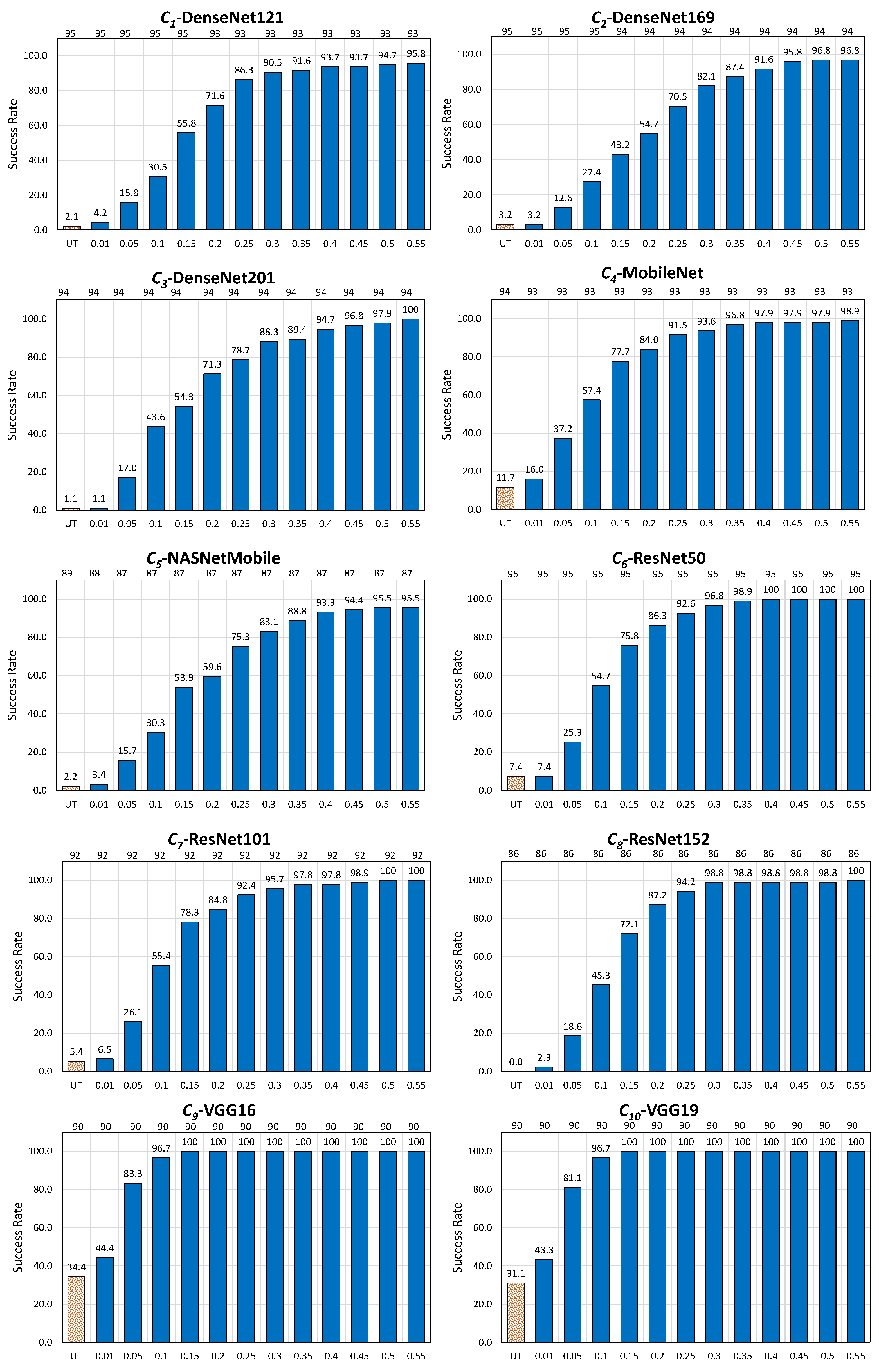


Appendix D. Overall FID Results
| Targeted | EA | BIM | PGD Inf | PGD L2 |
|---|---|---|---|---|
| 12.586 | 4.605 | 11.873 | 5.439 | |
| 12.043 | 4.654 | 12.146 | 6.527 | |
| 14.038 | 4.944 | 13.574 | 6.917 | |
| 13.873 | 3.438 | 9.345 | 5.037 | |
| 17.848 | 3.065 | 6.437 | 5.006 | |
| 14.572 | 3.671 | 6.617 | 5.434 | |
| 16.277 | 3.867 | 7.494 | 5.970 | |
| 15.926 | 4.133 | 7.801 | 6.137 | |
| 27.902 | 9.705 | 29.225 | 15.025 | |
| 31.200 | 10.933 | 32.713 | 15.681 | |
| Avg | 17.627 | 5.302 | 13.723 | 7.717 |
| Untargeted | EA | AdvGAN | SimBA | FGSM | BIM | PGD Inf | PGD L2 |
|---|---|---|---|---|---|---|---|
| 3.677 | 17.974 | 3.857 | 41.697 | 4.435 | 23.385 | 6.64 | |
| 2.110 | 14.886 | 2.624 | 42.452 | 4.212 | 16.749 | 6.283 | |
| 3.568 | 14.915 | 13.548 | 44.555 | 4.436 | 21.838 | 7.141 | |
| 2.614 | 15.823 | 5.117 | 37.838 | 4.006 | 11.463 | 5.240 | |
| 2.142 | 10.517 | 13.879 | 42.274 | 3.244 | 7.250 | 4.996 | |
| 2.222 | 11.638 | 12.871 | 47.503 | 4.862 | 13.424 | 7.522 | |
| 3.575 | 20.894 | 7.233 | 48.869 | 5.138 | 14.150 | 7.407 | |
| NA | 14.588 | 7.956 | 45.522 | 4.834 | 13.513 | 7.453 | |
| 6.313 | 15.235 | 9.191 | 71.849 | 10.231 | 56.493 | 16.181 | |
| 3.754 | 14.172 | 8.221 | 72.283 | 11.515 | 61.131 | 19.001 | |
| Avg | 3.754 | 15.064 | 8.450 | 49.484 | 5.691 | 23.940 | 8.786 |
References
- Taye, M.M. Theoretical Understanding of Convolutional Neural Network: Concepts, Architectures, Applications, Future Directions. Computation 2023, 11, 52. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving deep convolutional neural networks for image classification. IEEE Trans. Evol. Comput. 2019, 24, 394–407. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.J.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Gao, H.; Cheng, B.; Wang, J.; Li, K.; Zhao, J.; Li, D. Object classification using CNN-based fusion of vision and LIDAR in autonomous vehicle environment. IEEE Trans. Ind. Inform. 2018, 14, 4224–4231. [Google Scholar] [CrossRef]
- Coşkun, M.; Uçar, A.; Yildirim, Ö.; Demir, Y. Face recognition based on convolutional neural network. In Proceedings of the 2017 International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; pp. 376–379. [Google Scholar]
- Yang, S.; Wang, W.; Liu, C.; Deng, W. Scene understanding in deep learning-based end-to-end controllers for autonomous vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 53–63. [Google Scholar] [CrossRef]
- Ghosh, A.; Jana, N.D.; Das, S.; Mallipeddi, R. Two-Phase Evolutionary Convolutional Neural Network Architecture Search for Medical Image Classification. IEEE Access 2023, 11, 115280–115305. [Google Scholar] [CrossRef]
- Abdou, M.A. Literature review: Efficient deep neural networks techniques for medical image analysis. Neural Comput. Appl. 2022, 34, 5791–5812. [Google Scholar] [CrossRef]
- Chugh, A.; Sharma, V.K.; Kumar, S.; Nayyar, A.; Qureshi, B.; Bhatia, M.K.; Jain, C. Spider monkey crow optimization algorithm with deep learning for sentiment classification and information retrieval. IEEE Access 2021, 9, 24249–24262. [Google Scholar] [CrossRef]
- Fahfouh, A.; Riffi, J.; Mahraz, M.A.; Yahyaouy, A.; Tairi, H. PV-DAE: A hybrid model for deceptive opinion spam based on neural network architectures. Expert Syst. Appl. 2020, 157, 113517. [Google Scholar] [CrossRef]
- Cao, J.; Lam, K.Y.; Lee, L.H.; Liu, X.; Hui, P.; Su, X. Mobile augmented reality: User interfaces, frameworks, and intelligence. ACM Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Coskun, H.; Yiğit, T.; Üncü, İ.S. Integration of digital quality control for intelligent manufacturing of industrial ceramic tiles. Ceram. Int. 2022, 48, 34210–34233. [Google Scholar] [CrossRef]
- Khan, M.J.; Singh, P.P. Advanced road extraction using CNN-based U-Net model and satellite imagery. E-Prime Electr. Eng. Electron. Energy 2023, 5, 100244. [Google Scholar] [CrossRef]
- Saralioglu, E.; Gungor, O. Semantic segmentation of land cover from high resolution multispectral satellite images by spectral-spatial convolutional neural network. Geocarto Int. 2022, 37, 657–677. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Liu, J.; Miao, J.; Argyriou, A.; Wang, L.; Xu, Z. 360-attack: Distortion-aware perturbations from perspective-views. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 15035–15044. [Google Scholar]
- Meng, W.; Xing, X.; Sheth, A.; Weinsberg, U.; Lee, W. Your online interests: Pwned! a pollution attack against targeted advertising. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 129–140. [Google Scholar]
- Hardt, M.; Nath, S. Privacy-aware personalization for mobile advertising. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; pp. 662–673. [Google Scholar]
- Biggio, B.; Corona, I.; Maiorca, D.; Nelson, B.; Šrndić, N.; Laskov, P.; Giacinto, G.; Roli, F. Evasion attacks against machine learning at test time. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Prague, Czech Republic, 23–27 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 387–402. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Wang, Y.; Liu, J.; Chang, X.; Misic, J.V.; Misic, V.B. IWA: Integrated Gradient based White-box Attacks for Fooling Deep Neural Networks. arXiv 2021, arXiv:2102.02128. [Google Scholar] [CrossRef]
- Mohammadian, H.; Ghorbani, A.A.; Lashkari, A.H. A gradient-based approach for adversarial attack on deep learning-based network intrusion detection systems. Appl. Soft Comput. 2023, 137, 110173. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–7 April 2017; pp. 506–519. [Google Scholar]
- Andriushchenko, M.; Croce, F.; Flammarion, N.; Hein, M. Square attack: A query-efficient black-box adversarial attack via random search. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 484–501. [Google Scholar]
- Chitic, R.; Bernard, N.; Leprévost, F. A proof of concept to deceive humans and machines at image classification with evolutionary algorithms. In Proceedings of the Intelligent Information and Database Systems, 12th Asian Conference, ACIIDS 2020, Phuket, Thailand, 23–26 March 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 467–480. [Google Scholar]
- Chitic, R.; Leprévost, F.; Bernard, N. Evolutionary algorithms deceive humans and machines at image classification: An extended proof of concept on two scenarios. J. Inf. Telecommun. 2020, 5, 121–143. [Google Scholar] [CrossRef]
- Al-Ahmadi, S.; Al-Eyead, S. GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier. In Proceedings of the 19th International Conference on Security and Cryptography—Volume 1: SECRYPT, INSTICC, Lisbon, Portugal, 11–13 July 2022; SciTePress: Setúbal, Portugal, 2022; pp. 451–460. [Google Scholar] [CrossRef]
- Topal, A.O.; Chitic, R.; Leprévost, F. One evolutionary algorithm deceives humans and ten convolutional neural networks trained on ImageNet at image recognition. Appl. Soft Comput. 2023, 143, 110397. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. The ImageNet Image Database. 2009. Available online: http://image-net.org (accessed on 14 April 2024).
- Leprévost, F.; Topal, A.O.; Avdusinovic, E.; Chitic, R. A Strategy Creating High-Resolution Adversarial Images against Convolutional Neural Networks and a Feasibility Study on 10 CNNs. J. Inf. Telecommun. 2022, 7, 89–119. [Google Scholar] [CrossRef]
- Leprévost, F.; Topal, A.O.; Avdusinovic, E.; Chitic, R. Strategy and Feasibility Study for the Construction of High Resolution Images Adversarial against Convolutional Neural Networks. In Proceedings of the Intelligent Information and Database Systems, 13th Asian Conference, ACIIDS 2022, Ho-Chi-Minh-City, Vietnam, 28–30 November 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 467–480. [Google Scholar]
- Leprévost, F.; Topal, A.O.; Mancellari, E. Creating High-Resolution Adversarial Images Against Convolutional Neural Networks with the Noise Blowing-Up Method. In Intelligent Information and Database Systems; Nguyen, N.T., Boonsang, S., Fujita, H., Hnatkowska, B., Hong, T.P., Pasupa, K., Selamat, A., Eds.; Springer: Singapore, 2023; pp. 121–134. [Google Scholar]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Oliphant, T.E. Guide to NumPy; Trelgol, 2006; Available online: https://web.mit.edu/dvp/Public/numpybook.pdf (accessed on 14 April 2024).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org (accessed on 14 April 2024).
- Keras. 2015. Available online: https://keras.io (accessed on 14 April 2024).
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; The Scikit-Image Contributors. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Luo, C.; Lin, Q.; Xie, W.; Wu, B.; Xie, J.; Shen, L. Frequency-driven imperceptible adversarial attack on semantic similarity. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 15315–15324. [Google Scholar]
- Chen, F.; Wang, J.; Liu, H.; Kong, W.; Zhao, Z.; Ma, L.; Liao, H.; Zhang, D. Frequency constraint-based adversarial attack on deep neural networks for medical image classification. Comput. Biol. Med. 2023, 164, 107248. [Google Scholar] [CrossRef]
- Liu, J.; Lu, B.; Xiong, M.; Zhang, T.; Xiong, H. Adversarial Attack with Raindrops. arXiv 2023, arXiv:2302.14267. [Google Scholar]
- Zhao, Z.; Liu, Z.; Larson, M. Towards large yet imperceptible adversarial image perturbations with perceptual color distance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1039–1048. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- Patel, V.; Mistree, K. A review on different image interpolation techniques for image enhancement. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 129–133. [Google Scholar]
- Agrafiotis, D. Chapter 9—Video Error Concealment. In Academic Press Library in signal Processing; Theodoridis, S., Chellappa, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 5, pp. 295–321. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. Climatol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Parsania, P.S.; Virparia, P.V. A comparative analysis of image interpolation algorithms. Int. J. Adv. Res. Comput. Commun. Eng. 2016, 5, 29–34. [Google Scholar] [CrossRef]
- Chitic, R.; Topal, A.O.; Leprévost, F. ShuffleDetect: Detecting Adversarial Images against Convolutional Neural Networks. Appl. Sci. 2023, 13, 4068. [Google Scholar] [CrossRef]
- Nicolae, M.I.; Sinn, M.; Tran, M.N.; Buesser, B.; Rawat, A.; Wistuba, M.; Zantedeschi, V.; Baracaldo, N.; Chen, B.; Ludwig, H.; et al. Adversarial Robustness Toolbox v1.2.0. arXiv 2018, arXiv:1807.01069. [Google Scholar]
- Xiao, C.; Li, B.; Zhu, J.Y.; He, W.; Liu, M.; Song, D. Generating Adversarial Examples with Adversarial Networks. arXiv 2019, arXiv:1801.02610. [Google Scholar]
- Guo, C.; Gardner, J.; You, Y.; Wilson, A.G.; Weinberger, K. Simple black-box adversarial attacks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2484–2493. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2015, arXiv:1810.00069. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. arXiv 2016, arXiv:1607.02533. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2019, arXiv:1706.06083. [Google Scholar]
- SpeedyGraphito. Mes 400 Coups; Panoramart: France, 2020. [Google Scholar]






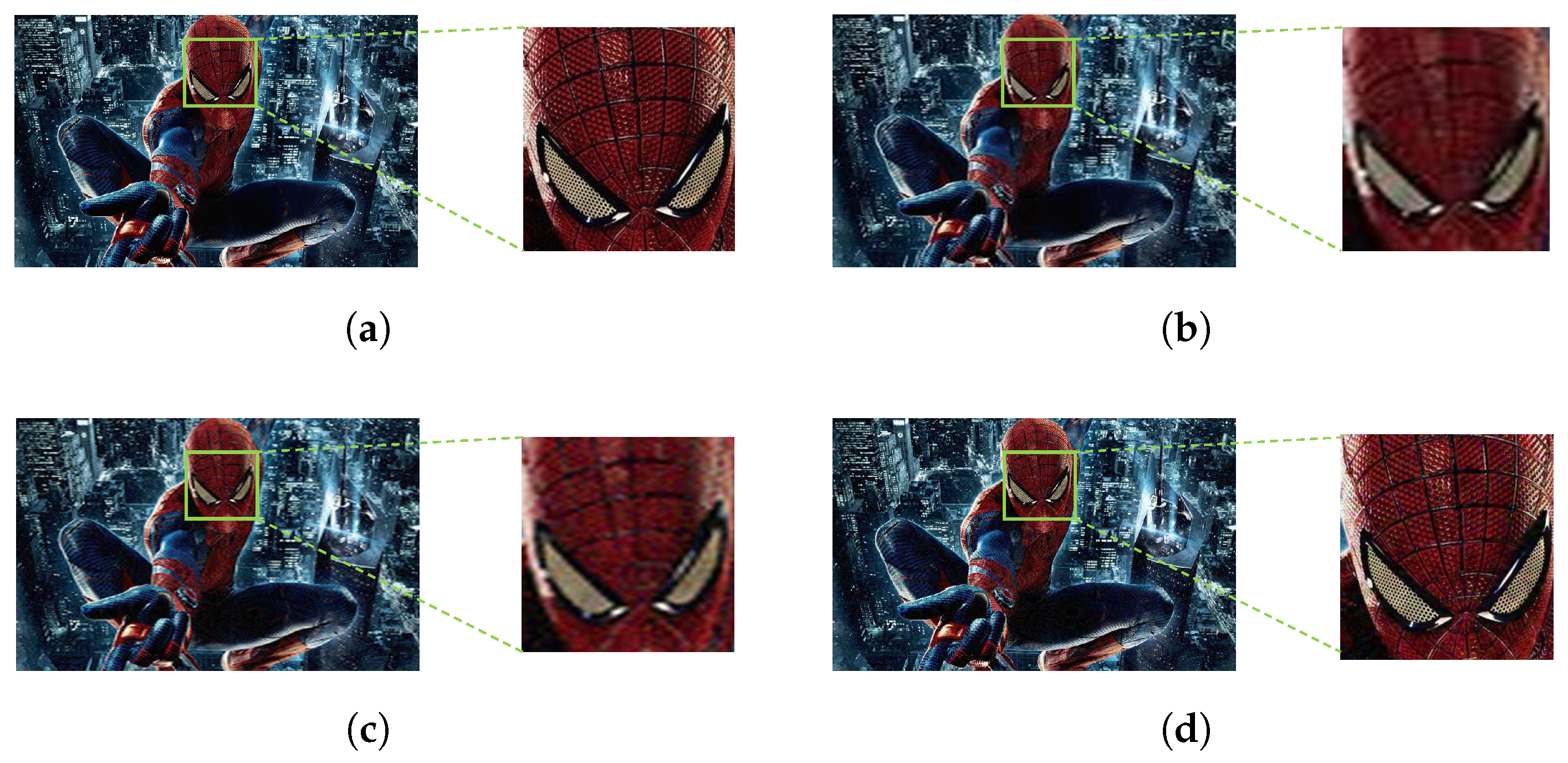


| Name of the CNN | Parameters | Top-1 Accuracy | Top-5 Accuracy | |
|---|---|---|---|---|
| DenseNet121 | 8M | 0.750 | 0.923 | |
| DenseNet169 | 14M | 0.762 | 0.932 | |
| DenseNet201 | 20M | 0.773 | 0.936 | |
| MobileNet | 4M | 0.704 | 0.895 | |
| NASNetMobile | 4M | 0.744 | 0.919 | |
| ResNet50 | 26M | 0.749 | 0.921 | |
| ResNet101 | 45M | 0.764 | 0.928 | |
| ResNet152 | 60M | 0.766 | 0.931 | |
| VGG16 | 138M | 0.713 | 0.901 | |
| VGG19 | 144M | 0.713 | 0.900 |
| p | ||
|---|---|---|
| 1 | (abacus, 398) | (bannister, 421) |
| 2 | (acorn, 988) | (rhinoceros beetle, 306) |
| 3 | (baseball, 429) | (ladle, 618) |
| 4 | (broom, 462) | (dingo, 273) |
| 5 | (brown bear, 294) | (pirate, 724) |
| 6 | (canoe, 472) | (saluki, 176) |
| 7 | (hippopotamus, 344) | (trifle, 927) |
| 8 | (llama, 355) | (agama, 42) |
| 9 | (maraca, 641) | (conch, 112) |
| 10 | (mountain bike, 671) | (strainer, 828) |
| 97 | 99 | 98 | 97 | 95 | 98 | 95 | 95 | 93 | 94 | |
| 99 | 97 | 97 | 95 | 94 | 97 | 95 | 94 | 93 | 94 |
| Attacks | White Box | Black Box | Targeted | Untargeted |
|---|---|---|---|---|
| EA | x | x | x | |
| advGAN | x | x | x | |
| SimBA | x | x | ||
| FGSM | x | x | ||
| BIM | x | x | x | |
| PGD Inf | x | x | x | |
| PGD | x | x | x |
| Attacks | EA | AdvGAN | SimBA | FGSM | BIM | PGD Inf | PGD L2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| untarg | targ | untarg | targ | untarg | targ | untarg | targ | untarg | targ | untarg | targ | untarg | targ | |
| 95 | 89 | 96 | 81 | 91 | 0 | 78 | 0 | 96 | 68 | 97 | 96 | 97 | 82 | |
| 95 | 92 | 94 | 85 | 94 | 0 | 63 | 2 | 98 | 78 | 99 | 98 | 99 | 90 | |
| 94 | 90 | 93 | 82 | 92 | 0 | 67 | 1 | 96 | 71 | 98 | 98 | 97 | 85 | |
| 94 | 90 | 81 | 88 | 91 | 0 | 64 | 0 | 96 | 84 | 97 | 97 | 97 | 94 | |
| 89 | 77 | 89 | 74 | 85 | 0 | 50 | 0 | 88 | 56 | 93 | 83 | 94 | 71 | |
| 95 | 94 | 92 | 79 | 90 | 0 | 84 | 1 | 96 | 96 | 97 | 98 | 96 | 98 | |
| 92 | 87 | 86 | 78 | 92 | 0 | 80 | 1 | 93 | 93 | 95 | 95 | 93 | 93 | |
| 86 | 93 | 88 | 74 | 78 | 0 | 75 | 0 | 94 | 94 | 95 | 95 | 89 | 94 | |
| 90 | 92 | 78 | 58 | 87 | 0 | 86 | 3 | 92 | 76 | 92 | 93 | 91 | 83 | |
| 90 | 94 | 79 | 59 | 87 | 1 | 87 | 1 | 92 | 77 | 93 | 94 | 92 | 84 | |
| 0.546 | 0.555 | 0.762 | 0.481 | 0.508 | 0.041 | 0.993 | 0.457 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | |
| 0.007 | 0.550 | 0.003 | 0.031 | 0.038 | 0.041 | 0.050 | 0.257 | 0.258 | 0.289 | 0.524 | 0.721 | 0.277 | 0.221 | |
| avg | 0.359 | 0.551 | 0.150 | 0.255 | 0.352 | 0.041 | 0.522 | 0.340 | 0.958 | 0.901 | 0.987 | 0.986 | 0.966 | 0.943 |
| Attacks | Targeted | Untargeted |
|---|---|---|
| EA, FGSM, BIM, PGD Inf, PGD L2 | FGSM, BIM, PGD Inf, PGD L2 | |
| images () | () | () |
| () | () |
| Targeted Attacks | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EA | 81 | 74 | 80 | 76 | 61 | 91 | 86 | 89 | 92 | 94 | 824 | |
| 8 | 18 | 10 | 14 | 16 | 3 | 1 | 4 | 0 | 0 | |||
| 8 | 18 | 10 | 14 | 3 | 3 | 1 | 4 | 0 | 0 | |||
| ↑ SR | 91.0 | 80.4 | 88.9 | 84.4 | 79.2 | 96.8 | 98.9 | 95.7 | 100 | 100 | 91.5 | |
| 0.202 | 0.213 | 0.189 | 0.249 | 0.243 | 0.139 | 0.129 | 0.120 | 0.044 | 0.036 | 0.156 | ||
| AdvGAN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | |
| 4 | 4 | 2 | 5 | 11 | 8 | 4 | 3 | 24 | 21 | |||
| 76 | 81 | 80 | 83 | 63 | 72 | 74 | 71 | 34 | 36 | |||
| ↑ SR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8.7 | 0.9 | |
| 0.113 | 0.218 | 0.211 | 0.160 | 0.162 | 0.176 | 0.221 | 0.186 | 0.034 | 0.040 | 0.152 | ||
| BIM | 50 | 64 | 53 | 69 | 47 | 96 | 92 | 92 | 75 | 72 | 710 | |
| 18 | 14 | 18 | 15 | 9 | 0 | 1 | 2 | 1 | 5 | |||
| 17 | 13 | 18 | 15 | 6 | 0 | 1 | 2 | 1 | 3 | |||
| ↑ SR | 73.5 | 83.1 | 74.6 | 82.1 | 83.9 | 100 | 98.9 | 97.9 | 98.6 | 93.5 | 88.6 | |
| 0.100 | 0.165 | 0.167 | 0.117 | 0.119 | 0.007 | 0.024 | 0.023 | 0.025 | 0.025 | 0.077 | ||
| PGD Inf | 96 | 98 | 97 | 96 | 78 | 98 | 95 | 95 | 93 | 94 | 940 | |
| 0 | 0 | 1 | 1 | 5 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | 1 | 4 | 0 | 0 | 0 | 0 | 0 | |||
| ↑ SR | 100 | 100 | 98.9 | 98.9 | 93.9 | 100 | 100 | 100 | 100 | 100 | 99.2 | |
| 0.013 | 0.010 | 0.011 | 0.017 | 0.046 | 3 | 7 | 6 | 2 | 1 | 0.009 | ||
| PGD L2 | 69 | 76 | 75 | 89 | 64 | 96 | 92 | 93 | 82 | 81 | 817 | |
| 13 | 14 | 10 | 5 | 7 | 2 | 1 | 1 | 1 | 3 | |||
| 13 | 14 | 10 | 5 | 4 | 2 | 1 | 1 | 1 | 2 | |||
| ↑ SR | 84.1 | 84.4 | 88.2 | 94.7 | 90.1 | 97.9 | 98.9 | 98.9 | 98.8 | 96.4 | 93.2 | |
| 0.013 | 0.126 | 0.114 | 0.081 | 0.070 | 0.005 | 0.005 | 0.004 | 0.015 | 0.020 | 0.058 | ||
| ↑ Average SR | 69.7 | 69.6 | 70.1 | 72.0 | 69.4 | 78.9 | 79.3 | 78.5 | 79.5 | 79.7 | 74.7 | |
| ↓ Average | 0.114 | 0.146 | 0.138 | 0.125 | 0.128 | 0.065 | 0.076 | 0.067 | 0.024 | 0.024 | 0.091 | |
| Untargeted Attacks | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EA | 2 | 3 | 1 | 11 | 2 | 7 | 5 | 0 | 31 | 28 | 90 | |
| 2 | 3 | 1 | 11 | 2 | 7 | 5 | 0 | 31 | 28 | |||
| 93 | 92 | 93 | 83 | 87 | 88 | 87 | 86 | 59 | 62 | |||
| ↑ SR | 2.2 | 3.2 | 1.1 | 11.7 | 2.2 | 7.4 | 5.4 | 0.0 | 34.4 | 31.1 | 9.9 | |
| AdvGAN | 4 | 8 | 4 | 4 | 8 | 7 | 2 | 6 | 18 | 22 | 83 | |
| 4 | 8 | 4 | 4 | 8 | 7 | 2 | 6 | 18 | 22 | |||
| 92 | 86 | 89 | 77 | 81 | 85 | 84 | 82 | 60 | 57 | |||
| ↑ SR | 4.2 | 8.5 | 4.3 | 4.9 | 9.0 | 7.6 | 2.3 | 6.8 | 23.1 | 27.8 | 9.9 | |
| SimBA | 25 | 23 | 22 | 24 | 18 | 25 | 32 | 30 | 31 | 36 | 266 | |
| 25 | 23 | 22 | 24 | 18 | 25 | 32 | 30 | 31 | 36 | |||
| 66 | 71 | 70 | 67 | 67 | 65 | 60 | 48 | 56 | 51 | |||
| ↑ SR | 27.5 | 24.5 | 23.9 | 26.4 | 21.2 | 27.8 | 34.8 | 38.5 | 35.6 | 41.4 | 30.1 | |
| FGSM | 77 | 60 | 64 | 63 | 49 | 84 | 79 | 75 | 86 | 87 | 724 | |
| 77 | 59 | 62 | 59 | 49 | 83 | 74 | 75 | 86 | 86 | |||
| 1 | 3 | 3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |||
| ↑ SR | 98.7 | 95.2 | 95.5 | 98.4 | 98.0 | 100.0 | 98.8 | 100.0 | 100.0 | 100.0 | 98.5 | |
| BIM | 95 | 97 | 96 | 95 | 88 | 96 | 93 | 93 | 92 | 92 | 937 | |
| 95 | 96 | 96 | 92 | 87 | 96 | 93 | 93 | 92 | 92 | |||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |||
| ↑ SR | 99.0 | 99.0 | 100.0 | 99.0 | 100.0 | 100.0 | 100.0 | 98.9 | 100.0 | 100.0 | 99.6 | |
| PGD Inf | 97 | 99 | 98 | 97 | 93 | 97 | 95 | 95 | 92 | 93 | 956 | |
| 97 | 99 | 98 | 97 | 92 | 97 | 95 | 95 | 92 | 93 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| SR | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100.0 | |
| PGD L2 | 96 | 98 | 97 | 96 | 92 | 96 | 93 | 89 | 91 | 92 | 940 | |
| 96 | 98 | 97 | 96 | 92 | 96 | 93 | 89 | 90 | 92 | |||
| 1 | 1 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | |||
| ↑ SR | 99.0 | 99.0 | 100.0 | 99.0 | 97.9 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.5 | |
| ↑ Average SR | 61.5 | 61.3 | 60.7 | 62.8 | 61.2 | 63.3 | 63.0 | 63.5 | 70.5 | 71.5 | 63.9 | |
| Targeted Attack/# of Adversarial Images Used | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EA/824 | BIM/710 | PGD Inf/940 | PGD L2/817 | Overall/3291 | |||||||
| Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | ||
| 0.945 | 0.014 | 0.979 | 0.013 | 0.971 | 0.010 | 0.995 | 0.009 | 0.829 | 0.009 | ||
| 0.939 | 0.015 | 0.833 | 0.036 | 0.858 | 0.043 | 0.645 | 0.023 | 0.744 | 0.024 | ||
| 0.998 | 0.009 | 0.997 | 0.012 | 0.996 | 0.014 | 0.996 | 0.014 | 0.996 | 0.010 | ||
| 0.047 | 0.078 | 0.009 | 0.035 | 0.010 | 0.003 | 0.003 | 3 | 0.014 | 0.023 | ||
| 0.023 | 0.006 | 0.005 | 0.001 | 0.009 | 0.003 | 0.003 | 3 | 0.009 | 0.002 | ||
| 0.027 | 0.017 | 0.022 | 0.014 | 0.025 | 0.016 | 0.023 | 0.015 | 0.021 | 0.014 | ||
| / | 1.271 | 1.112 | 0.362 | 0.338 | 0.562 | 0.480 | 0.214 | 0.202 | 0.543 | 0.467 | |
| 8 | 2 | 2 | 2 | 3 | 9 | 1 | 9 | 3 | 7 | ||
| 4 | 2 | 8 | 3 | 2 | 6 | 7 | 2 | 1 | 6 | ||
| 5 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 4 | 2 | ||
| 36 | 11 | 2 | 0 | 8 | 0 | 17 | 4 | 16 | 4 | ||
| 38 | 10 | 5 | 0 | 13 | 2 | 18 | 5 | 18 | 4 | ||
| 129 | 41 | 125 | 42 | 127 | 42 | 125 | 42 | 119 | 34 | ||
| FID | 17.6 | 6.6 | 5.3 | 2.7 | 13.7 | 9.4 | 7.7 | 4.1 | 11.1 | 5.7 | |
| 14.4 | 1.2 | 14.2 | 0.7 | 13.9 | 0.3 | 14.2 | 0.5 | 14.2 | 0.7 | ||
| Untargeted Attack/# of Adversarial Images | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EA/90 | AdvGAN/83 | SimBA/266 | FGSM/724 | BIM/937 | PGD Inf/956 | PGD L2/940 | Overall/3996 | ||||||||||
| Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | Avg | StDev | ||
| 0.822 | 0.150 | 0.838 | 0.088 | 0.994 | 0.050 | 0.990 | 0.017 | 0.980 | 0.013 | 0.974 | 0.011 | 0.993 | 0.010 | 0.942 | 0.048 | ||
| 0.825 | 0.107 | 0.851 | 0.064 | 0.809 | 0.091 | 0.966 | 0.010 | 0.844 | 0.031 | 0.879 | 0.039 | 0.654 | 0.018 | 0.832 | 0.051 | ||
| 0.996 | 0.015 | 0.998 | 0.011 | 0.995 | 0.016 | 0.998 | 0.006 | 0.996 | 0.014 | 0.996 | 0.014 | 0.996 | 0.014 | 0.997 | 0.013 | ||
| 0.011 | 0.005 | 0.021 | 0.011 | 0.008 | 0.003 | 0.031 | 0.001 | 0.006 | 0.001 | 0.012 | 0.003 | 0.004 | 2 | 0.013 | 0.003 | ||
| 0.010 | 0.005 | 0.019 | 0.009 | 0.007 | 0.003 | 0.026 | 0.001 | 0.005 | 0.001 | 0.011 | 0.003 | 0.003 | 3 | 0.012 | 0.003 | ||
| 0.020 | 0.012 | 0.025 | 0.012 | 0.023 | 0.015 | 0.027 | 0.017 | 0.025 | 0.017 | 0.025 | 0.018 | 0.025 | 0.018 | 0.025 | 0.015 | ||
| / | 0.808 | 1.055 | 0.761 | 0.055 | 0.606 | 0.931 | 1.461 | 1.284 | 0.343 | 0.327 | 0.680 | 0.608 | 0.205 | 0.197 | 0.695 | 0.637 | |
| 3 | 2 | 9 | 5 | 3 | 9 | 8 | 2 | 2 | 1 | 4 | 9 | 1 | 3 | 4 | 1 | ||
| 2 | 1 | 3 | 2 | 1 | 7 | 4 | 1 | 9 | 3 | 2 | 7 | 7 | 2 | 2 | 8 | ||
| 4 | 2 | 5 | 3 | 5 | 3 | 6 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | ||
| 17 | 8 | 103 | 33 | 13 | 6 | 8 | 0 | 2 | 0 | 8 | 0 | 16 | 4 | 24 | 7 | ||
| 16 | 8 | 103 | 39 | 13 | 6 | 20 | 1 | 5 | 0 | 14 | 1 | 17 | 4 | 27 | 8 | ||
| 119 | 46 | 139 | 41 | 121 | 43 | 132 | 40 | 127 | 42 | 127 | 42 | 126 | 42 | 127 | 42 | ||
| FID | 3.7 | 1.9 | 15.1 | 2.9 | 8.5 | 3.9 | 49.5 | 12.3 | 5.7 | 2.8 | 23.9 | 18.9 | 8.8 | 4.8 | 16.5 | 6.7 | |
| 14.5 | 4.6 | 24.4 | 7.6 | 15.5 | 2.5 | 16.1 | 1.6 | 14.1 | 0.5 | 14.0 | 0.3 | 13.5 | 2.1 | 16.0 | 2.7 | ||
| Images | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | Overhead | ‰ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EA | 0.144 | 0.047 | 848.7 | 3 | 0.053 | 0.101 | 0.363 | 0.048 | 0.757 | 0.89 | |
| 0.010 | 0.048 | 443.2 | 3 | 0.003 | 0.002 | 0.011 | 0.047 | 0.122 | 0.28 | ||
| FGSM | 0.148 | 0.050 | 59.2 | 2 | 0.045 | 0.103 | 0.360 | 0.049 | 0.755 | 12.75 | |
| 0.009 | 0.049 | 58.1 | 2 | 0.003 | 0.002 | 0.011 | 0.046 | 0.120 | 2.06 | ||
| BIM | 0.143 | 0.049 | 83.8 | 2 | 0.045 | 0.103 | 0.356 | 0.049 | 0.744 | 8.88 | |
| 0.009 | 0.047 | 97.5 | 2 | 0.003 | 0.002 | 0.010 | 0.046 | 0.118 | 1.22 | ||
| PGD Inf | 0.143 | 0.048 | 90.7 | 2 | 0.045 | 0.102 | 0.357 | 0.049 | 0.744 | 8.21 | |
| 0.009 | 0.051 | 88.3 | 2 | 0.003 | 0.002 | 0.010 | 0.046 | 0.122 | 1.38 | ||
| PGD L2 | 0.141 | 0.048 | 104.2 | 2 | 0.044 | 0.101 | 0.350 | 0.047 | 0.732 | 7.02 | |
| 0.009 | 0.048 | 106.3 | 2 | 0.003 | 0.002 | 0.010 | 0.046 | 0.118 | 1.11 | ||
| AVG | 0.144 | 0.048 | 2 | 0.047 | 0.102 | 0.357 | 0.048 | 0.746 | |||
| 0.009 | 0.049 | 2 | 0.003 | 0.002 | 0.010 | 0.046 | 0.120 |
| Images | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | Overhead | ‰ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FGSM | 0.056 | 0.042 | 66.3 | 2 | 0.021 | 0.037 | 0.136 | 0.042 | 0.334 | 5.04 | |
| 0.007 | 0.045 | 67.2 | 2 | 0.002 | 0.001 | 0.005 | 0.042 | 0.103 | 1.53 | ||
| BIM | 0.055 | 0.042 | 78.9 | 2 | 0.021 | 0.038 | 0.135 | 0.042 | 0.333 | 4.22 | |
| 0.007 | 0.043 | 79.1 | 2 | 0.002 | 0.001 | 0.005 | 0.042 | 0.101 | 1.27 | ||
| PGD Inf | 0.056 | 0.043 | 80.9 | 2 | 0.020 | 0.038 | 0.137 | 0.042 | 0.336 | 4.15 | |
| 0.007 | 0.043 | 81.8 | 2 | 0.002 | 0.001 | 0.005 | 0.042 | 0.100 | 1.23 | ||
| PGD L2 | 0.055 | 0.043 | 80.9 | 2 | 0.021 | 0.038 | 0.137 | 0.042 | 0.337 | 4.17 | |
| 0.007 | 0.045 | 81.5 | 2 | 0.002 | 0.001 | 0.005 | 0.040 | 0.101 | 1.24 | ||
| AVG | 0.055 | 0.043 | 2 | 0.021 | 0.038 | 0.136 | 0.042 | 0.335 | |||
| 0.007 | 0.044 | 2 | 0.002 | 0.001 | 0.005 | 0.041 | 0.101 |
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
|---|---|---|---|---|---|---|---|---|---|
| 0.587 | 0.779 | 0.723 | 0.575 | 0.731 | 0.636 | 0.588 | 0.770 | 0.690 | |
| 0.593 | 0.778 | 0.725 | 0.583 | 0.689 | 0.633 | 0.619 | 0.766 | 0.710 | |
| 0.597 | 0.777 | 0.720 | 0.613 | 0.757 | 0.662 | 0.594 | 0.772 | 0.701 | |
| 0.572 | 0.771 | 0.657 | 0.571 | 0.688 | 0.624 | 0.581 | 0.771 | 0.654 | |
| 0.564 | 0.775 | 0.653 | 0.572 | 0.739 | 0.633 | 0.582 | 0.748 | 0.646 | |
| 0.610 | 0.780 | 0.725 | 0.587 | 0.741 | 0.655 | 0.581 | 0.778 | 0.691 | |
| 0.587 | 0.778 | 0.725 | 0.604 | 0.749 | 0.655 | 0.610 | 0.767 | 0.691 | |
| 0.603 | 0.777 | 0.724 | 0.586 | 0.756 | 0.654 | 0.606 | 0.788 | 0.699 | |
| 0.593 | 0.778 | 0.709 | 0.584 | 0.733 | 0.633 | 0.594 | 0.775 | 0.674 | |
| 0.593 | 0.779 | 0.708 | 0.584 | 0.749 | 0.632 | 0.605 | 0.775 | 0.677 | |
| Avg | 0.590 | 0.777 | 0.707 | 0.586 | 0.733 | 0.641 | 0.596 | 0.771 | 0.683 |
| a | 1 | 2 | 3 |
|---|---|---|---|
 |  |  | |
| (Comic Book, 0.4916) | (Coffee Mug, 0.0844) | (Hippopotamus, 0.9993) | |
| altar | hamper | trifle |
| 0.963 | 0.938 | 0.999 | ||
| 0.973 | 0.970 | 0.969 | ||
| 0.920 | 0.960 | 0.961 | ||
| 0.071 | 0.037 | 0.029 | ||
| 0.075 | 0.049 | 0.049 | ||
| 0.021 | 0.028 | 0.032 | ||
| 6 | 2 | 2 | ||
| 6 | 2 | 3 | ||
| 2 | 1 | 2 | ||
| 244 | 174 | 191 | ||
| 245 | 163 | 198 | ||
| 27 | 30 | 58 | ||
| FID | 180.5 | 45.5 | 50.4 | |
| 221.9 | 44.1 | 64.1 | ||
| 55.3 | 34.9 | 21.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Topal, A.O.; Mancellari, E.; Leprévost, F.; Avdusinovic, E.; Gillet, T. The Noise Blowing-Up Strategy Creates High Quality High Resolution Adversarial Images against Convolutional Neural Networks. Appl. Sci. 2024, 14, 3493. https://doi.org/10.3390/app14083493
Topal AO, Mancellari E, Leprévost F, Avdusinovic E, Gillet T. The Noise Blowing-Up Strategy Creates High Quality High Resolution Adversarial Images against Convolutional Neural Networks. Applied Sciences. 2024; 14(8):3493. https://doi.org/10.3390/app14083493
Chicago/Turabian StyleTopal, Ali Osman, Enea Mancellari, Franck Leprévost, Elmir Avdusinovic, and Thomas Gillet. 2024. "The Noise Blowing-Up Strategy Creates High Quality High Resolution Adversarial Images against Convolutional Neural Networks" Applied Sciences 14, no. 8: 3493. https://doi.org/10.3390/app14083493
APA StyleTopal, A. O., Mancellari, E., Leprévost, F., Avdusinovic, E., & Gillet, T. (2024). The Noise Blowing-Up Strategy Creates High Quality High Resolution Adversarial Images against Convolutional Neural Networks. Applied Sciences, 14(8), 3493. https://doi.org/10.3390/app14083493







