Artificial Neural Network (ANN) Validation Research: Free Vibration Analysis of Functionally Graded Beam via Higher-Order Shear Deformation Theory and Artificial Neural Network Method
Abstract
:1. Introduction
2. Theory and Formulation
2.1. Material Properties
2.2. Constitutive Equations
2.3. Equations of Motion
3. Solution Procedure
3.1. Analytical Part of Solution
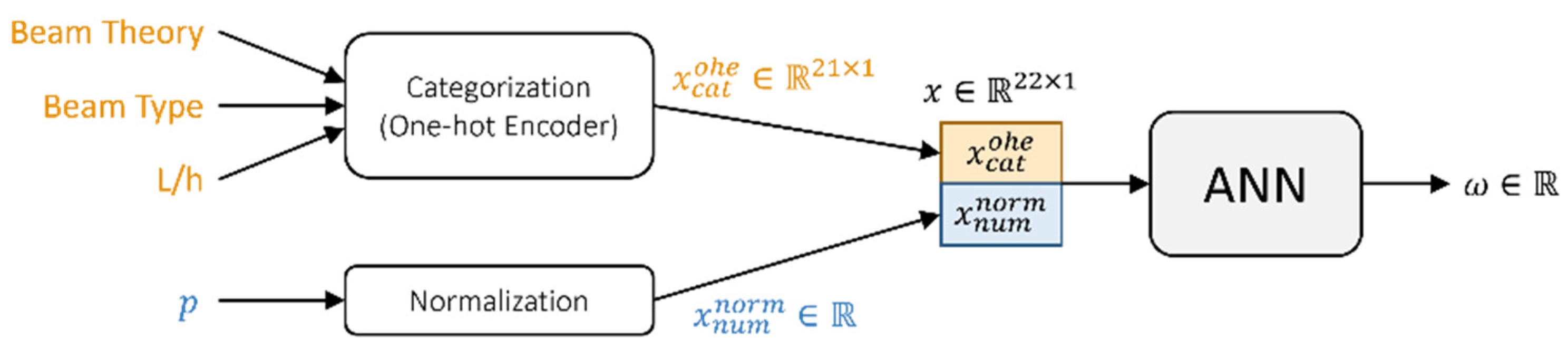
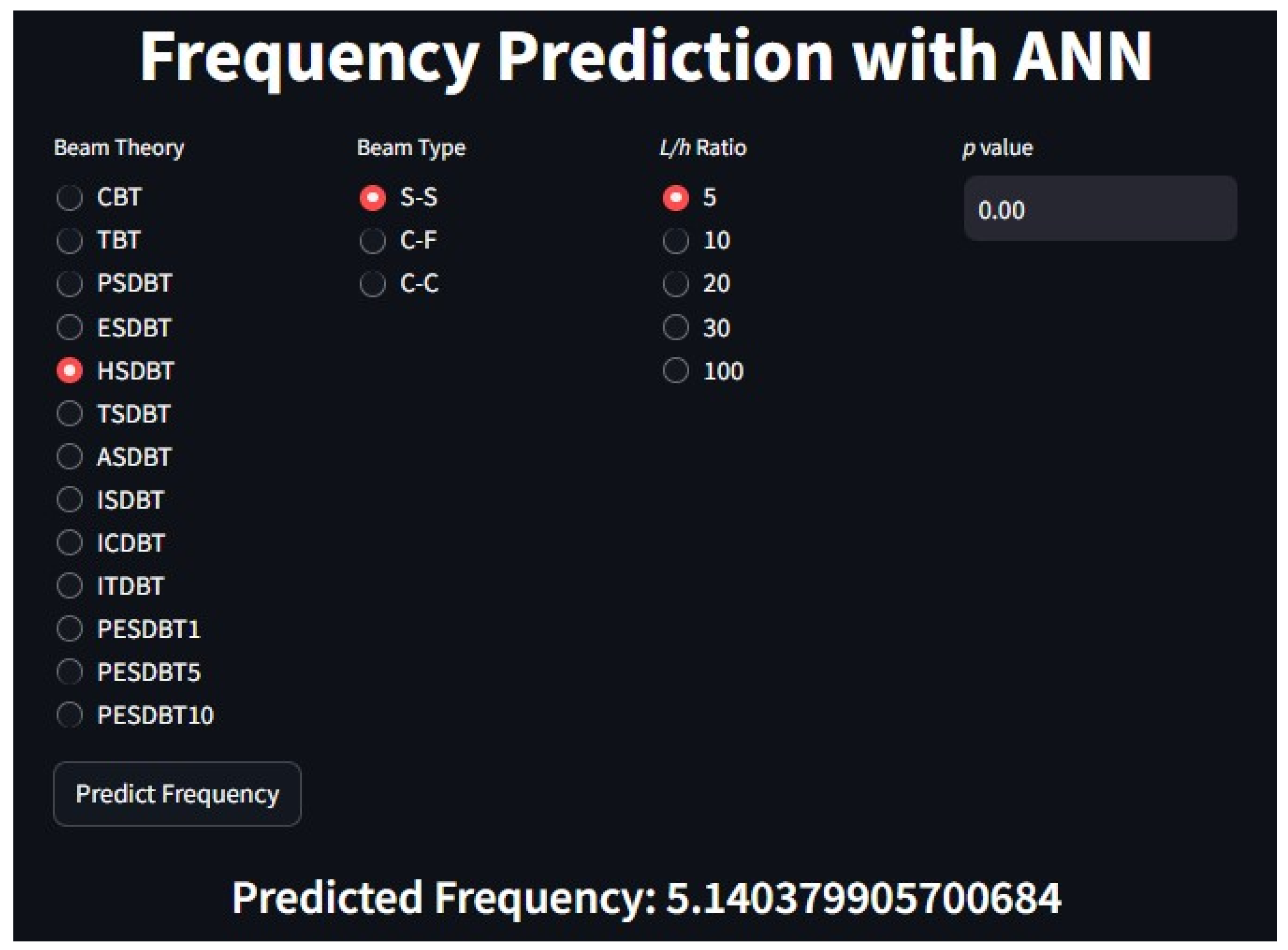
3.2. Artificial Neural Network (ANN) Method
4. Results and Discussion
5. Conclusions
- (a)
- It was observed that the results obtained with HSDT substantially overlap with other higher-order shear deformation theories used in the literature.
- (b)
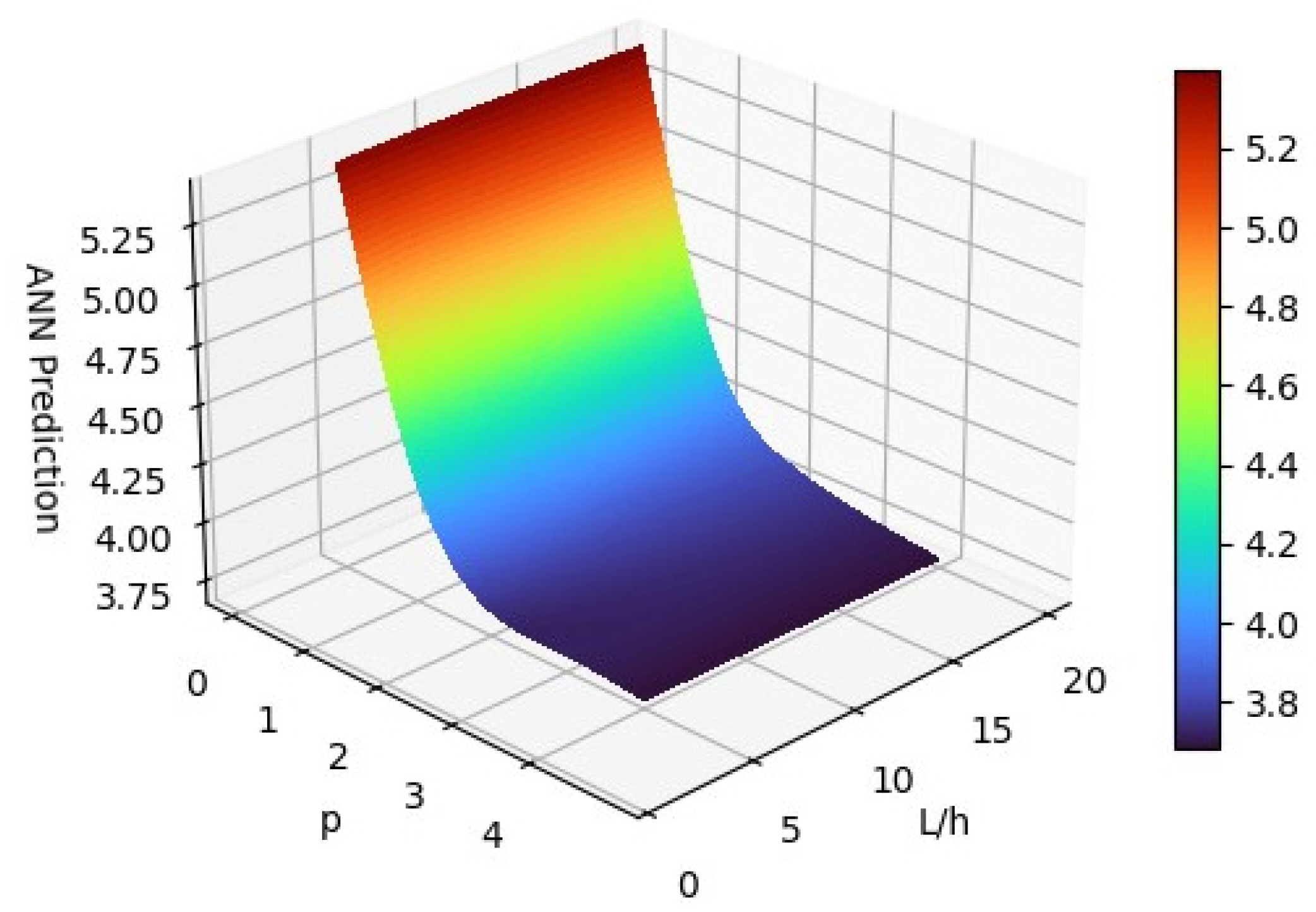
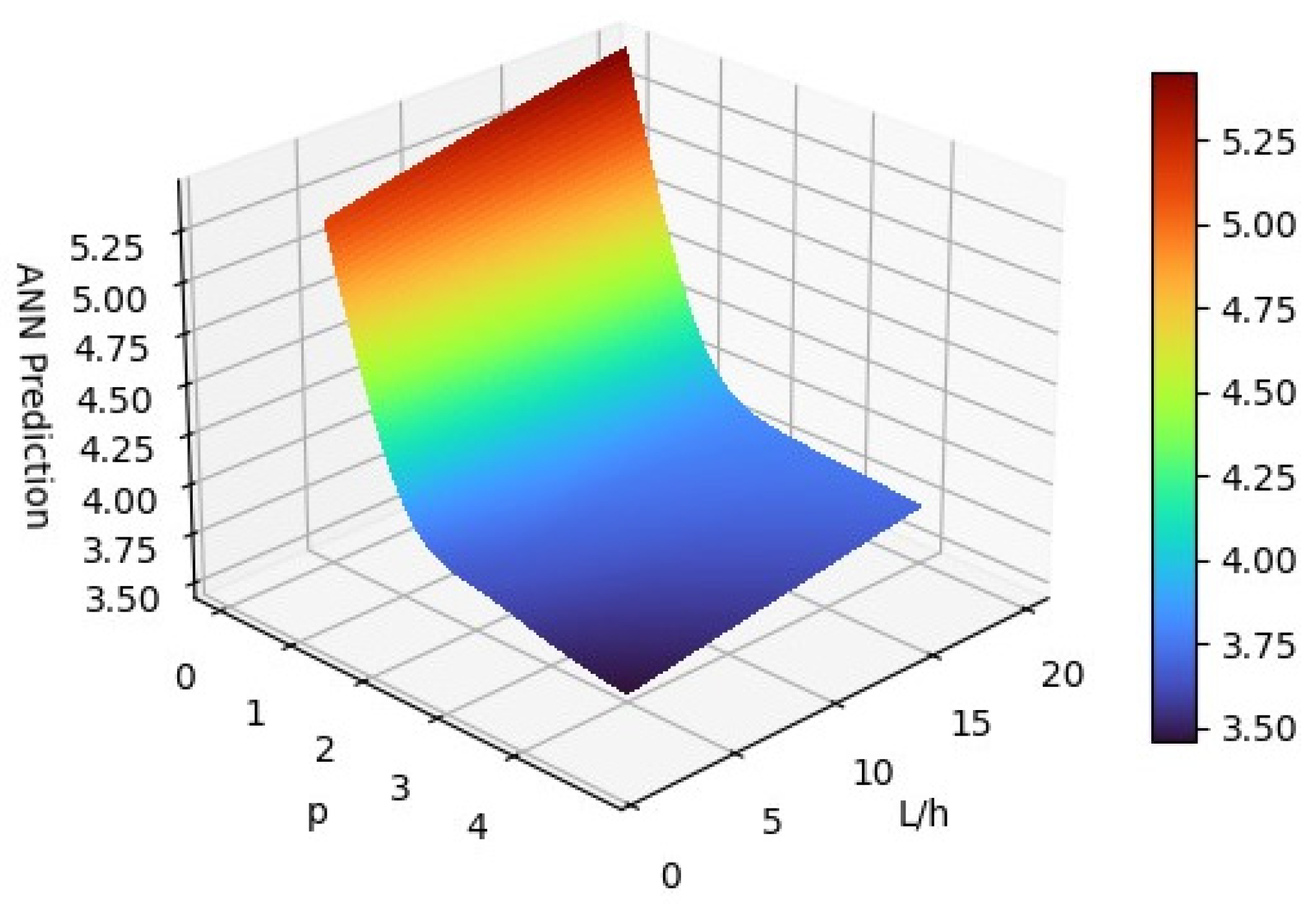
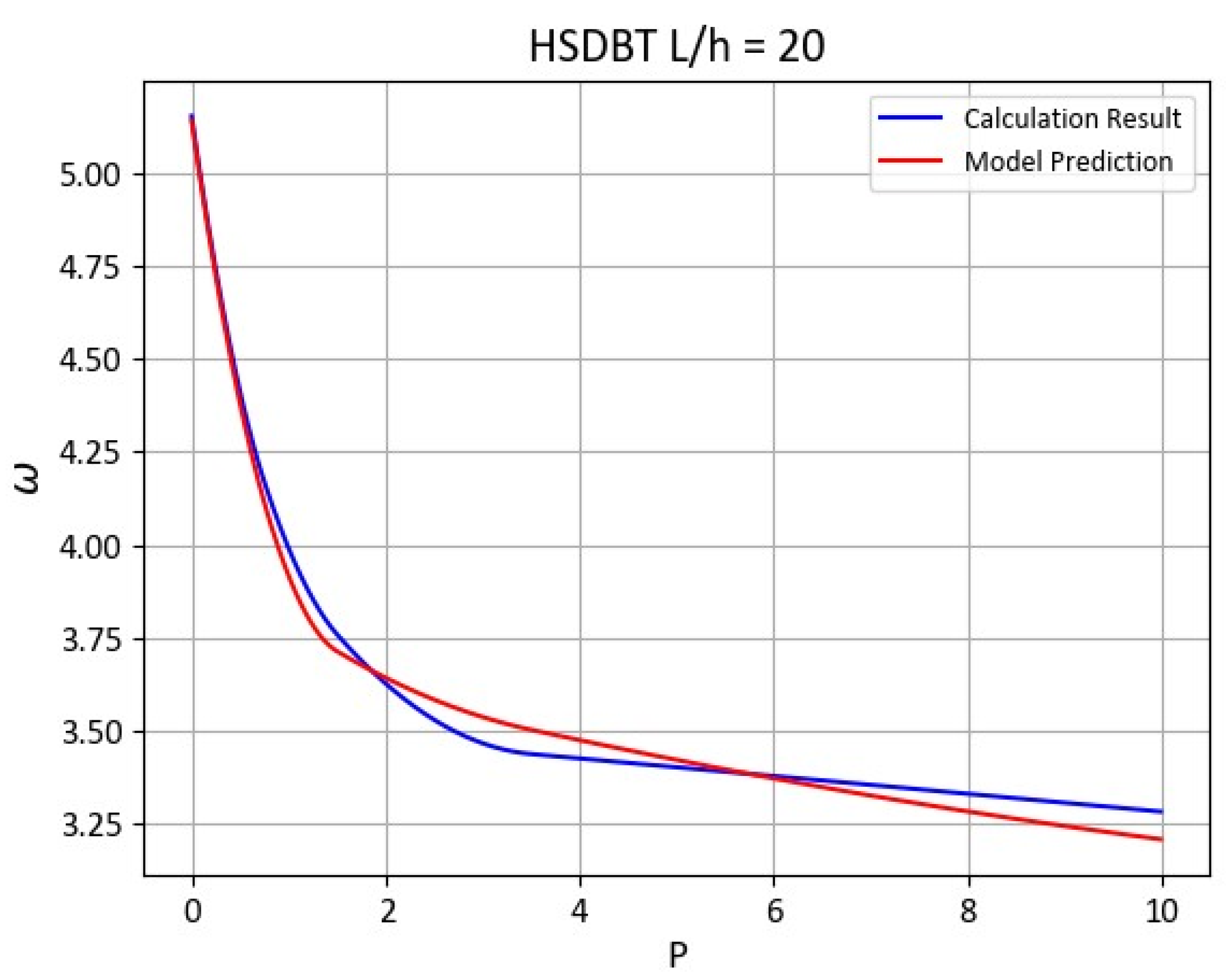
- Non-dimensional frequency values obtained from the ANN converged significantly to the results obtained with the analytical solution, with a very low margin of error.
- (c)
- The accurate natural frequency values can be attained by taking the shear effect into account (shear deformation effects lead to a decline in the natural frequencies).
- (d)
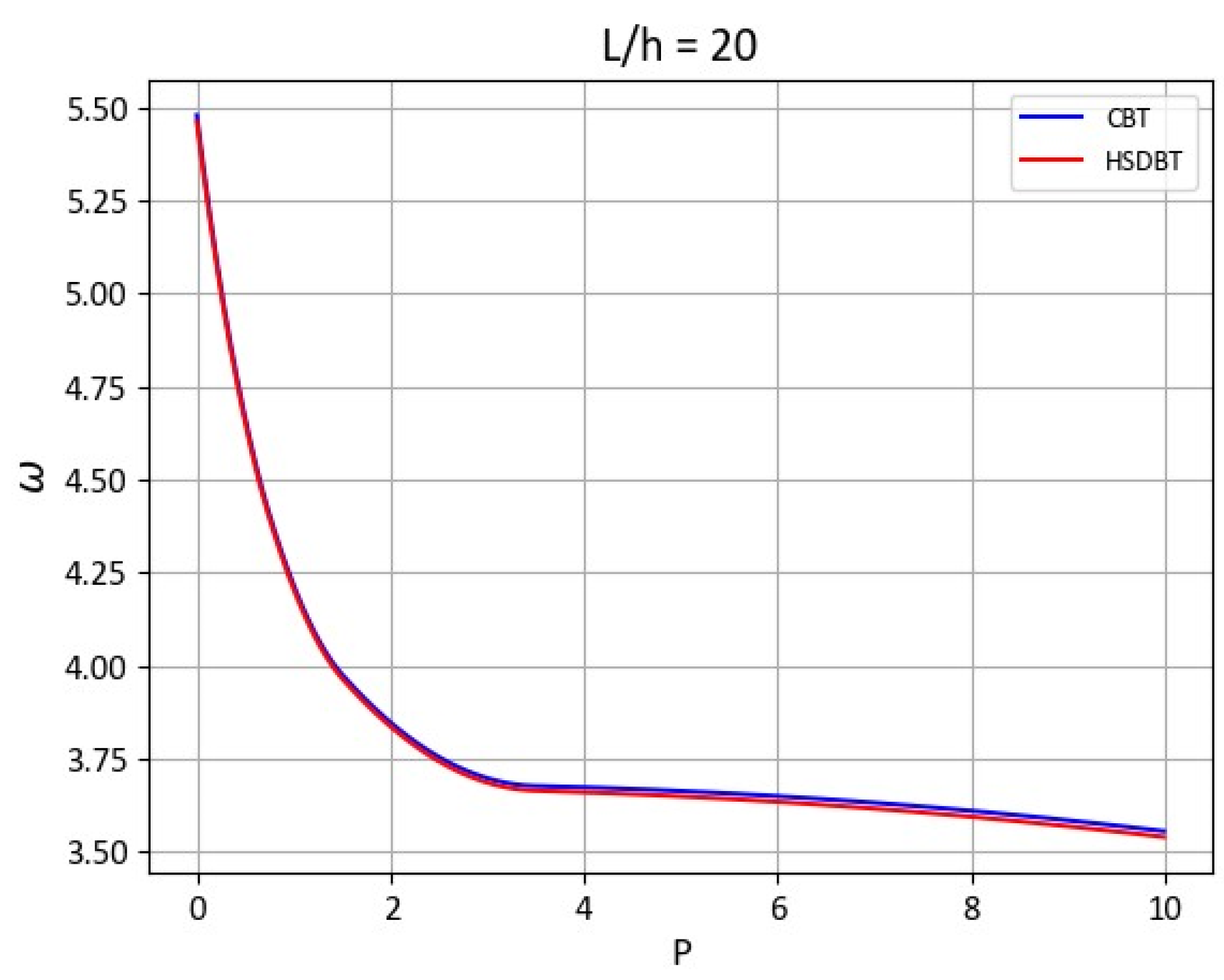
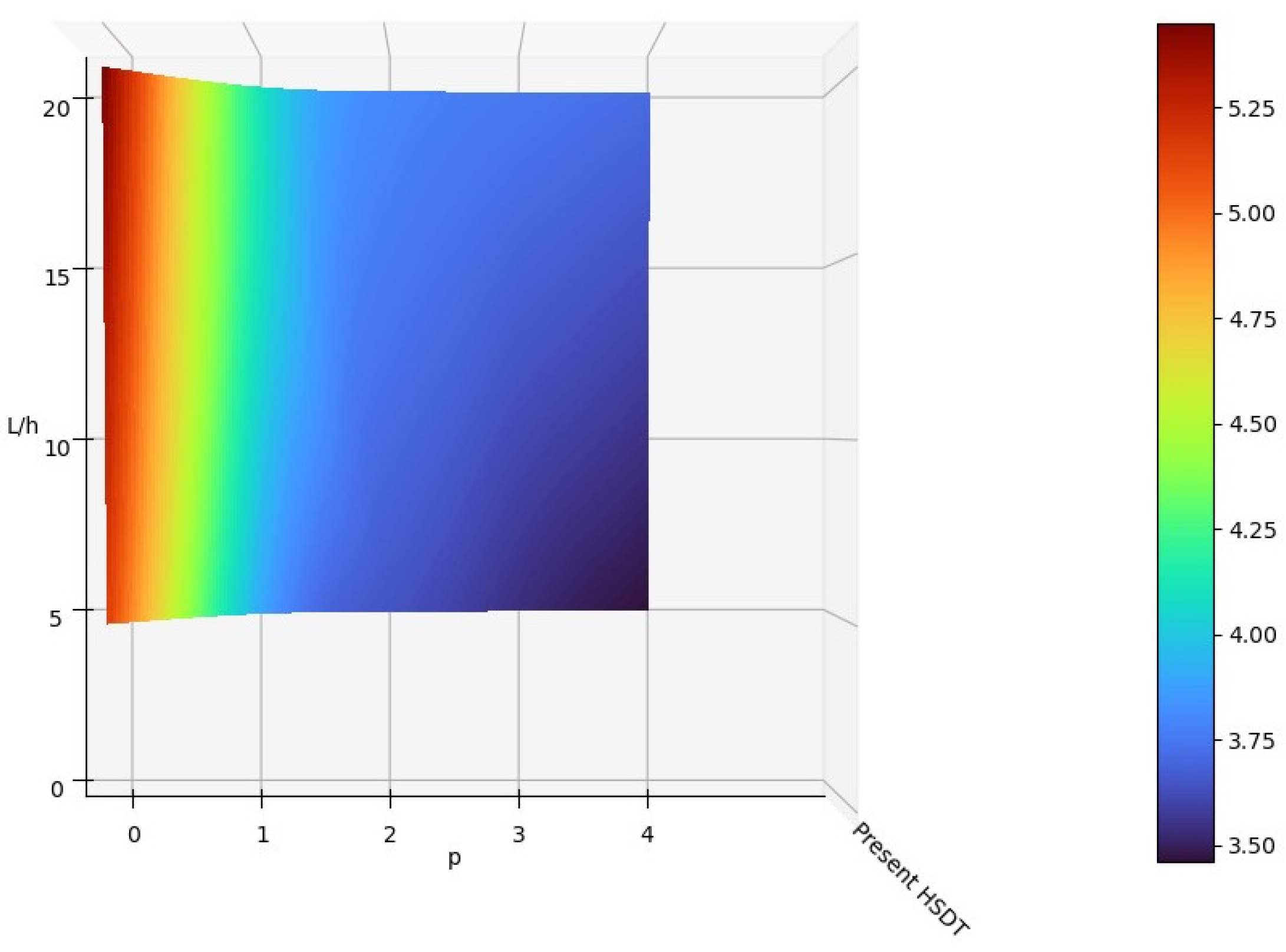
- It can be implied that the non-dimensional frequency values obtained by higher-order shear deformation theory and classical beam theory for the analytical and ANN solutions converge depending on an increase in the span-to-height ratio.
- (e)
- The ANN algorithm can be improved by providing more datasets to predict deformation parameters with smaller amounts of error.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Yesilce, Y.; Catal, H.H. Solution of free vibration equations of semi-rigid connected Reddy–Bickford beams resting on elastic soil using the differential transform method. Arch. Appl. Mech. 2011, 81, 199–213. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K. A transverse shear deformation theory for homogeneous mono-clinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 2012, 62, 57–66. [Google Scholar] [CrossRef]
- Pham, Q.H.; Tran, T.T.; Nguyen, P.C. Nonlocal free vibration of functionally graded porous nanoplates using higher-order isogeometric analysis and ANN prediction. Alex. Eng. J. 2023, 66, 651–667. [Google Scholar] [CrossRef]
- Reddy, J. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Exact solution for thermoelastic deformations of functionally graded thick rectangular plates. AIAA J. 2002, 40, 1421–1433. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Batra, R.C.; Roque, C.M.C.; Qian, L.F.; Martins, P.A.L.S. Static analysis of functionally graded plates using third-order shear deformation theory and a meshless method. Compos. Struct. 2005, 69, 449–457. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Roque, C.M.C.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M.M. A quasi-3D sinusoidal shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos. B. Eng. 2012, 43, 711–725. [Google Scholar] [CrossRef]
- Taj, M.G.; Chakrabarti, A.; Sheikh, A.H. Analysis of functionally graded plates using higher order shear deformation theory. Appl. Math. Model 2013, 37, 8484–8494. [Google Scholar]
- Li, X.F. A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams. J. Sound Vib. 2008, 318, 1210–1229. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.F.A. New approach for free vibration of axially functionally graded beams with non-uniform cross-section. J. Sound Vib. 2010, 329, 2291–2303. [Google Scholar] [CrossRef]
- Aydogdu, M.; Taskin, V. Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 2007, 28, 1651–1656. [Google Scholar] [CrossRef]
- Mahi, A.; Bedia, E.A.A.; Tounsi, A.; Mechab, I. An analytical method for temperature-dependent free vibration analysis of functionally graded beams with general boundary conditions. Compos. Struct. 2010, 92, 1877–1887. [Google Scholar] [CrossRef]
- Sankar, B.V. An elasticity solution for functionally graded beams. Compos. Sci. Technol. 2001, 61, 689–696. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, Y.H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Shahrjerdi, A.; Bayat, M.; Mustapha, F.; Sapuan, S.; Zahari, R. Second-order shear deformation theory to analyze stress distribution for solar functionally graded plates. Mech. Based Des. Struct. Mach. 2010, 38, 348–361. [Google Scholar] [CrossRef]
- Demirkan, E.; Artan, R. Buckling analysis of nanobeams based on nonlocal Timoshenko beam model by the method of initial values. Int. J. Struct. Stab. Dyn. 2018, 19, 1950036. [Google Scholar] [CrossRef]
- Çelik, M.; Artan, R. An investigation of static bending of a bi-directional strain-gradient Euler–Bernoulli nano-beams with the method of initial values. Microsyst. Technol. 2020, 26, 2921–2929. [Google Scholar] [CrossRef]
- Çelik, M.; Artan, R. Buckling Analysis of a Bi-Directional Strain-Gradient Euler–Bernoulli Nano-Beams. Int. J. Struct. Stab. Dyn. 2020, 20, 2050114. [Google Scholar] [CrossRef]
- Larbi, O.L.; Kaci, A.; Houari, M.S.A.; Tounsi, A. An Efficient Shear Deformation Beam Theory Based on Neutral Surface Position for Bending and Free Vibration of Functionally Graded Beams. Mech. Based Des. Struct. Mach. 2013, 41, 421–433. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Chintala, S. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2019; Volume 32. [Google Scholar]
- Zohra, Z.; Lemya, H.; Abderahman, Y.; Mustapha, M.; Abdelouahed, T.; Djamel, O. Free vibration analysis of functionally graded beams using a higher-order shear deformation theory. Math. Model. Eng. Probl. 2017, 4, 7–12. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. Free vibration response of functionally graded thick plates with shear and normal deformations effects. Compos. Struct. 2012, 96, 799–823. [Google Scholar] [CrossRef]





| Inputs | Ref. [5] | Present | ANN Prediction | Error (%) | |||
|---|---|---|---|---|---|---|---|
| Beam Type | Beam Theory | L/h | p | ||||
| S-S | HSDT | 5 | 0 | 5.1527 | 5.1527 | 5.1404 | 0.24 |
| 0.5 | 4.4107 | 4.4107 | 4.3784 | 0.73 | |||
| 1 | 3.9904 | 3.9903 | 3.9163 | 1.86 | |||
| 2 | 3.6265 | 3.6264 | 3.6419 | 0.42 | |||
| 5 | 3.4014 | 3.4014 | 3.4209 | 0.57 | |||
| 10 | 3.2817 | 3.2817 | 3.2072 | 2.27 | |||
| 20 | 0 | 5.4603 | 5.4603 | 5.4503 | 0.18 | ||
| 0.5 | 4.6511 | 4.6511 | 4.5956 | 1.19 | |||
| 1 | 4.2051 | 4.2049 | 4.1425 | 1.49 | |||
| 2 | 3.8361 | 3.8361 | 3.7991 | 0.96 | |||
| 5 | 3.6485 | 3.6485 | 3.6715 | 0.63 | |||
| 10 | 3.539 | 3.5390 | 3.4599 | 2.24 | |||
| CBT | 5 | 0 | 5.3953 | 5.3953 | 5.3703 | 0.46 | |
| 0.5 | 4.5931 | 4.5931 | 4.6144 | 0.46 | |||
| 1 | 4.1484 | 4.1484 | 4.1775 | 0.70 | |||
| 2 | 3.7793 | 3.7793 | 3.7545 | 0.66 | |||
| 5 | 3.5949 | 3.5949 | 3.6508 | 1.55 | |||
| 10 | 3.4921 | 3.4921 | 3.4816 | 0.30 | |||
| 20 | 0 | 5.4777 | 5.4777 | 5.3975 | 1.46 | ||
| 0.5 | 4.6641 | 4.6641 | 4.5927 | 1.53 | |||
| 1 | 4.2163 | 4.2163 | 4.1843 | 0.76 | |||
| 2 | 3.8472 | 3.8472 | 3.8234 | 0.62 | |||
| 5 | 3.6628 | 3.6628 | 3.6532 | 0.26 | |||
| 10 | 3.5547 | 3.5547 | 3.4890 | 1.85 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelik, M.; Gündoğdu, E.; Özdilek, E.E.; Demirkan, E.; Artan, R. Artificial Neural Network (ANN) Validation Research: Free Vibration Analysis of Functionally Graded Beam via Higher-Order Shear Deformation Theory and Artificial Neural Network Method. Appl. Sci. 2024, 14, 217. https://doi.org/10.3390/app14010217
Çelik M, Gündoğdu E, Özdilek EE, Demirkan E, Artan R. Artificial Neural Network (ANN) Validation Research: Free Vibration Analysis of Functionally Graded Beam via Higher-Order Shear Deformation Theory and Artificial Neural Network Method. Applied Sciences. 2024; 14(1):217. https://doi.org/10.3390/app14010217
Chicago/Turabian StyleÇelik, Murat, Emircan Gündoğdu, Emin Emre Özdilek, Erol Demirkan, and Reha Artan. 2024. "Artificial Neural Network (ANN) Validation Research: Free Vibration Analysis of Functionally Graded Beam via Higher-Order Shear Deformation Theory and Artificial Neural Network Method" Applied Sciences 14, no. 1: 217. https://doi.org/10.3390/app14010217





