Analytical Solution and Shaking Table Test on Tunnels through Soft-Hard Stratum with a Transition Tunnel and Flexible Joints
Abstract
:1. Introduction
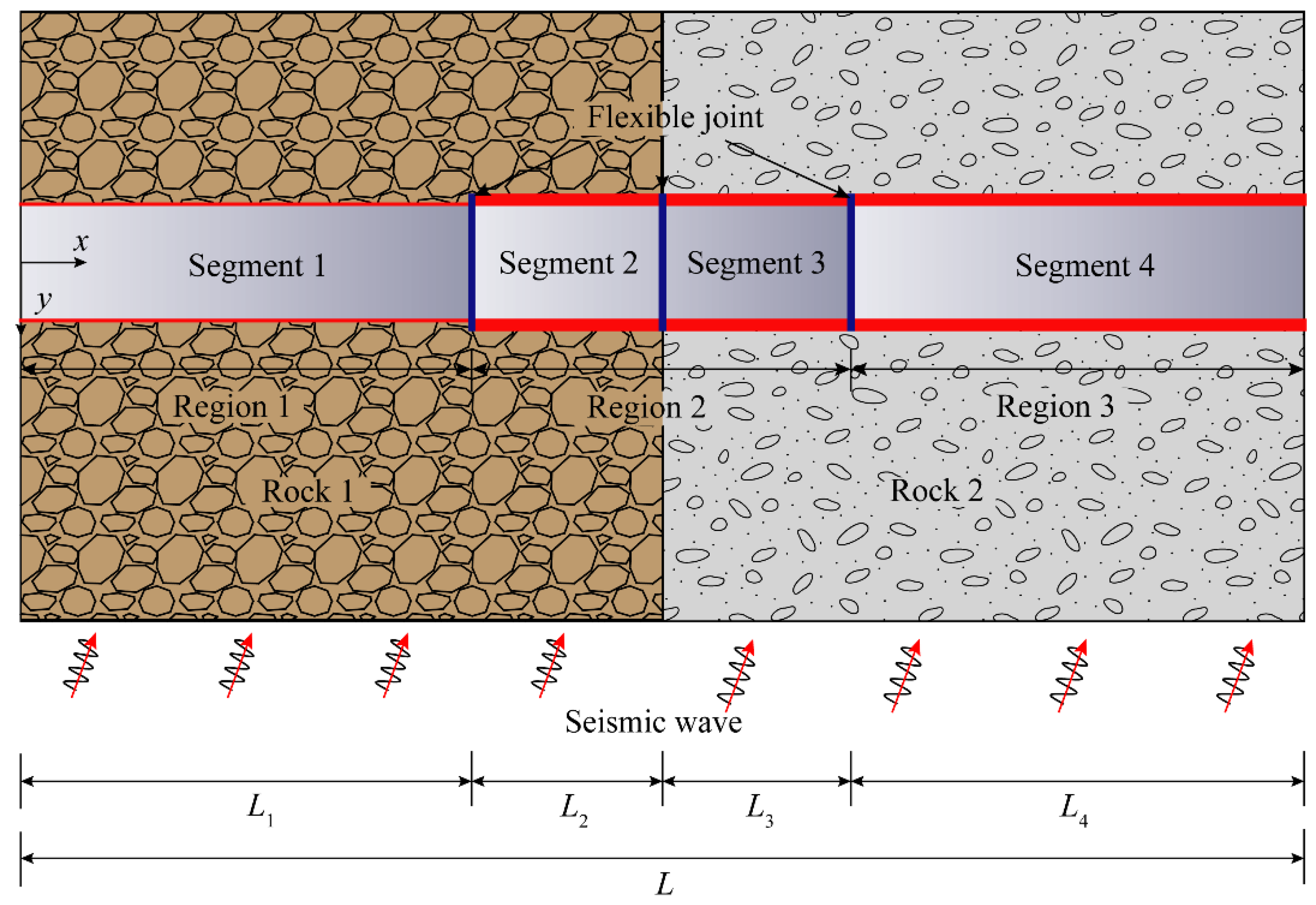
2. Simplified Analytical Solution
- Each lining segment has homogeneous isotropic linear elasticity and its sounding rock is viscoelastic.
- The axial deformation of the tunnel is not considered.
- The seismic input motion is assumed as an incident sinusoidal wave.
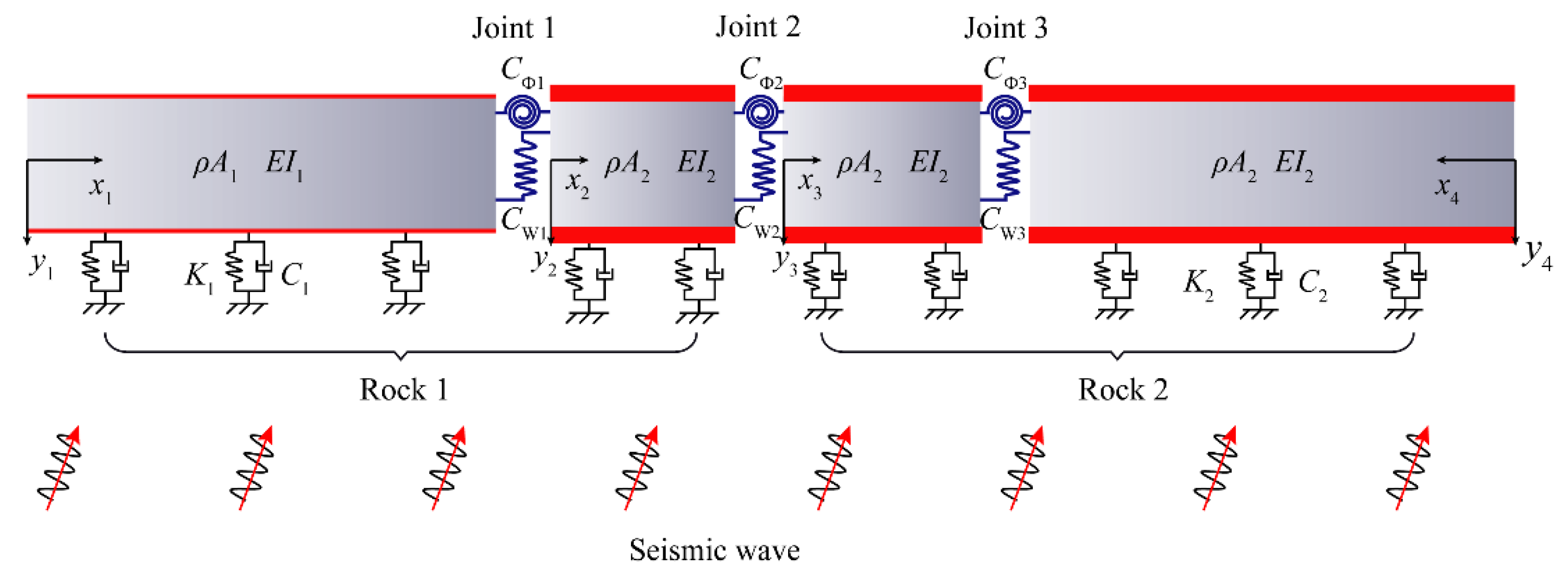
2.1. Closed-Form Solution for Responses of Tunnel Lining under Earthquake Wave
2.2. Closed-Form Solution of Tunnel through Soft-Hard Stratum Junction with Flexible Joints
3. Analytical Results
3.1. Project Introduction
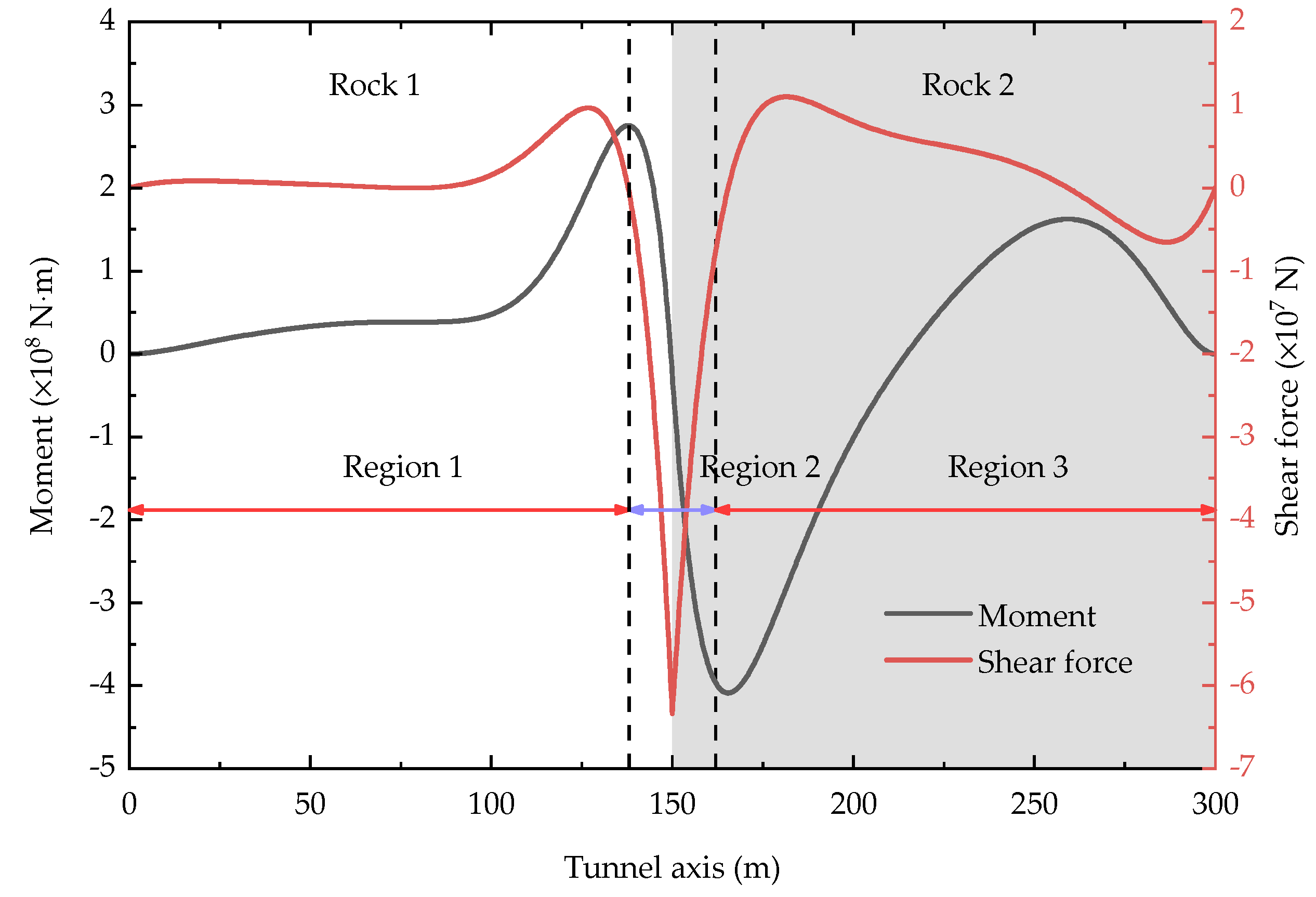
3.2. General Responses
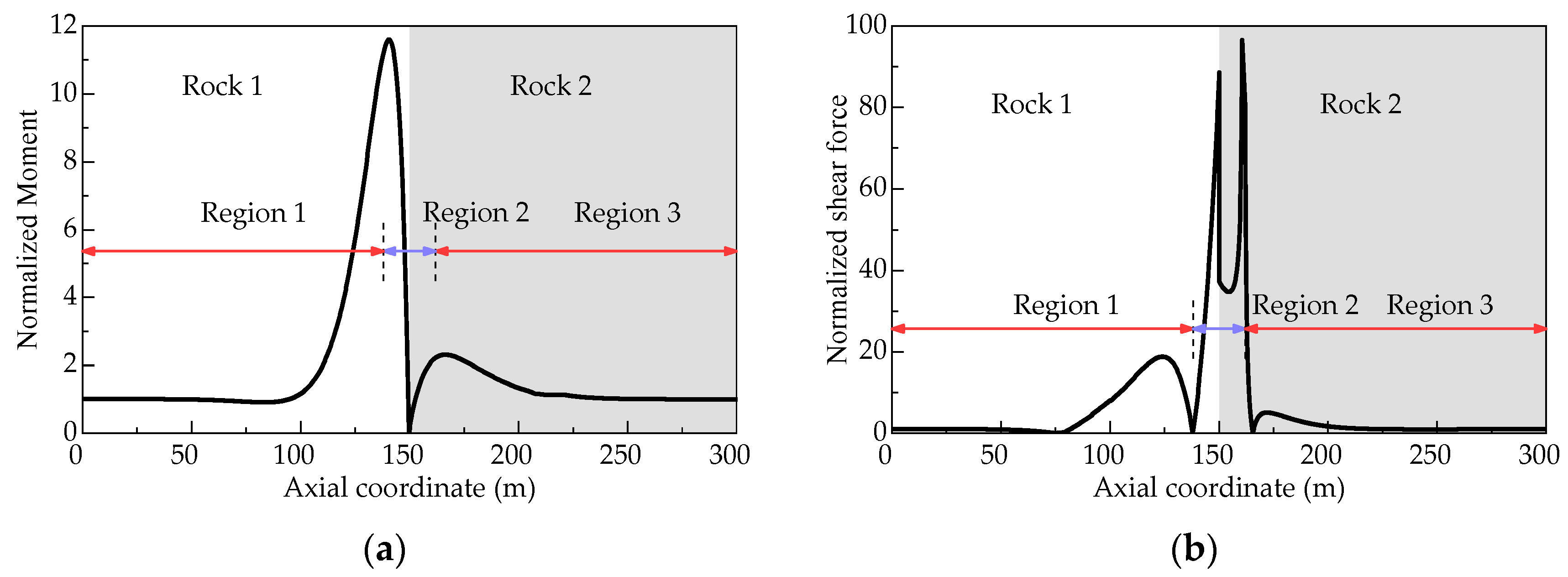
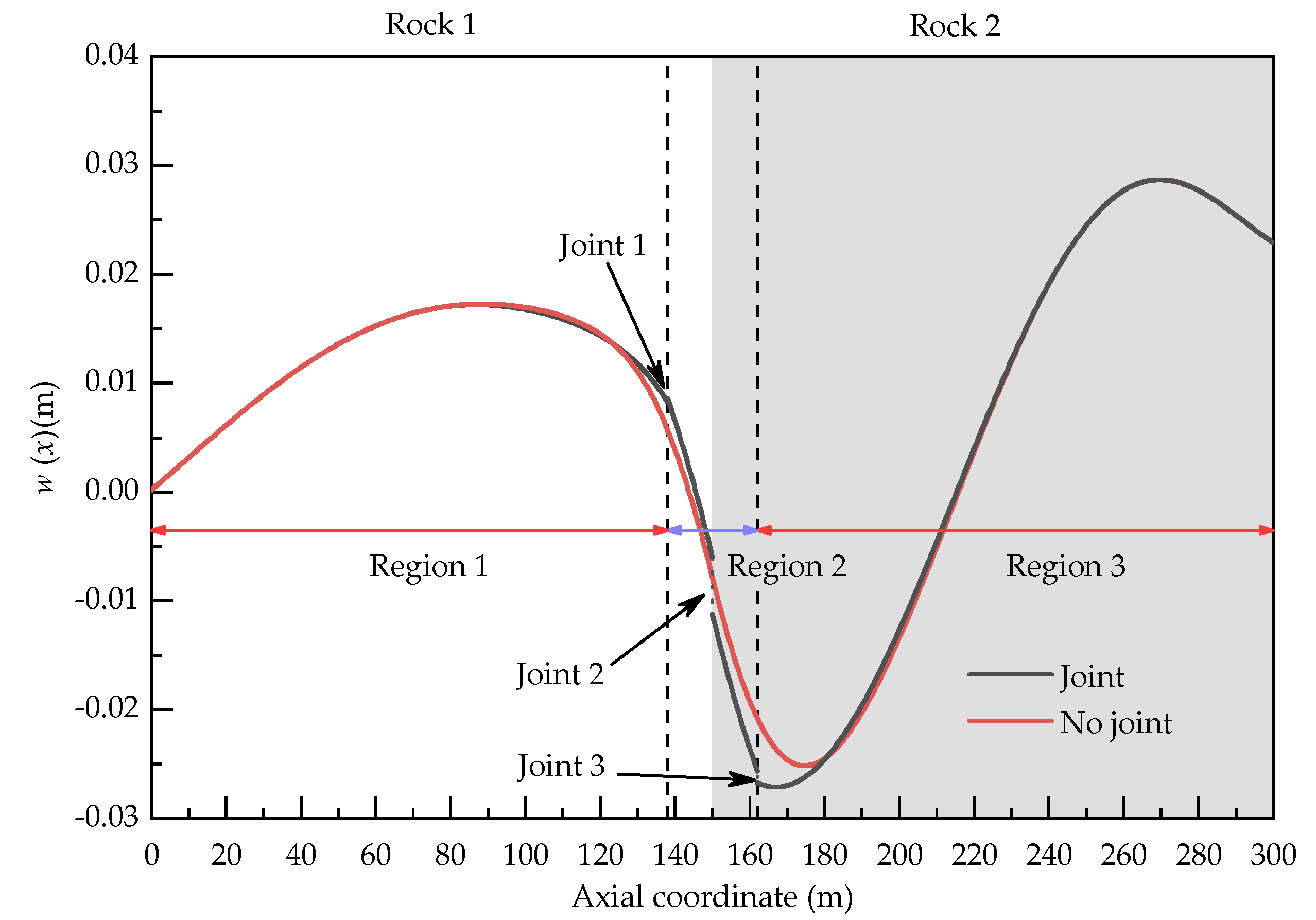
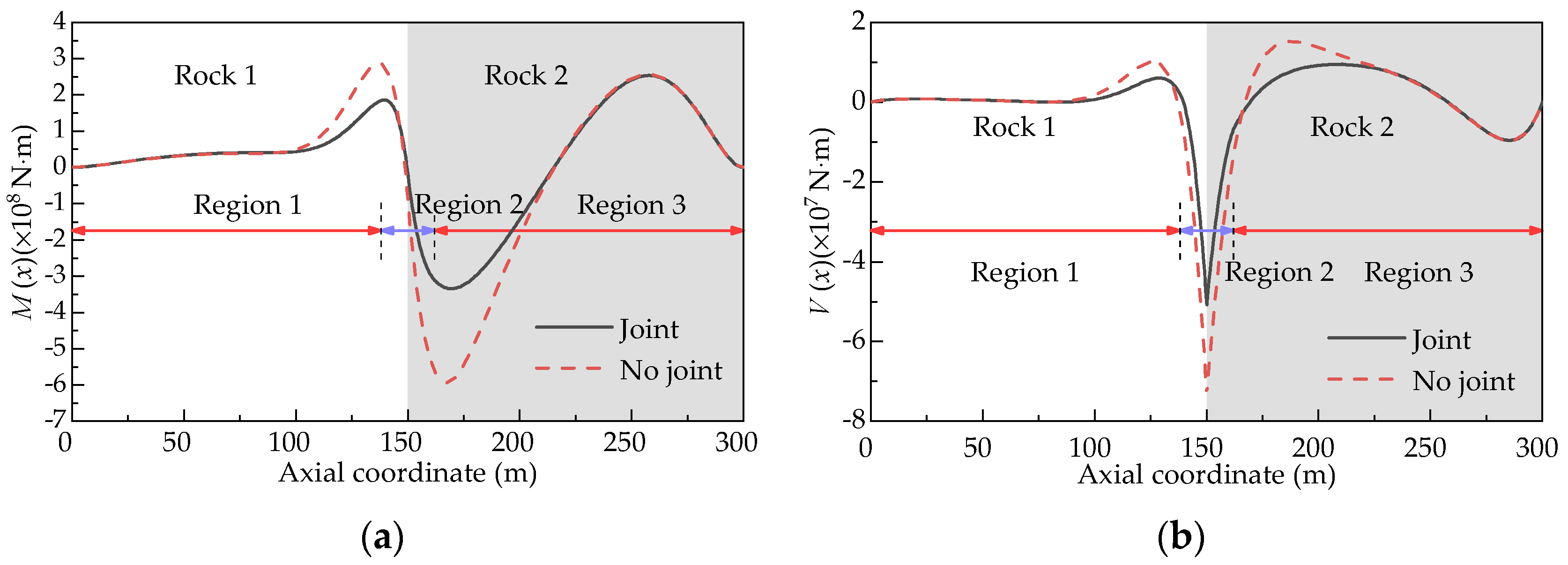
3.3. Influence of Joint on Responses of Tunnel
3.4. Influence of the Length of the Transition Zone
4. Shaking Table Test
4.1. Test Modelling and Apparatus
4.2. Law of Similarity and Model Materials
4.3. Sensor Layout
4.4. Test Cases
4.5. Test Results
4.5.1. Comparison with the Proposed Solution
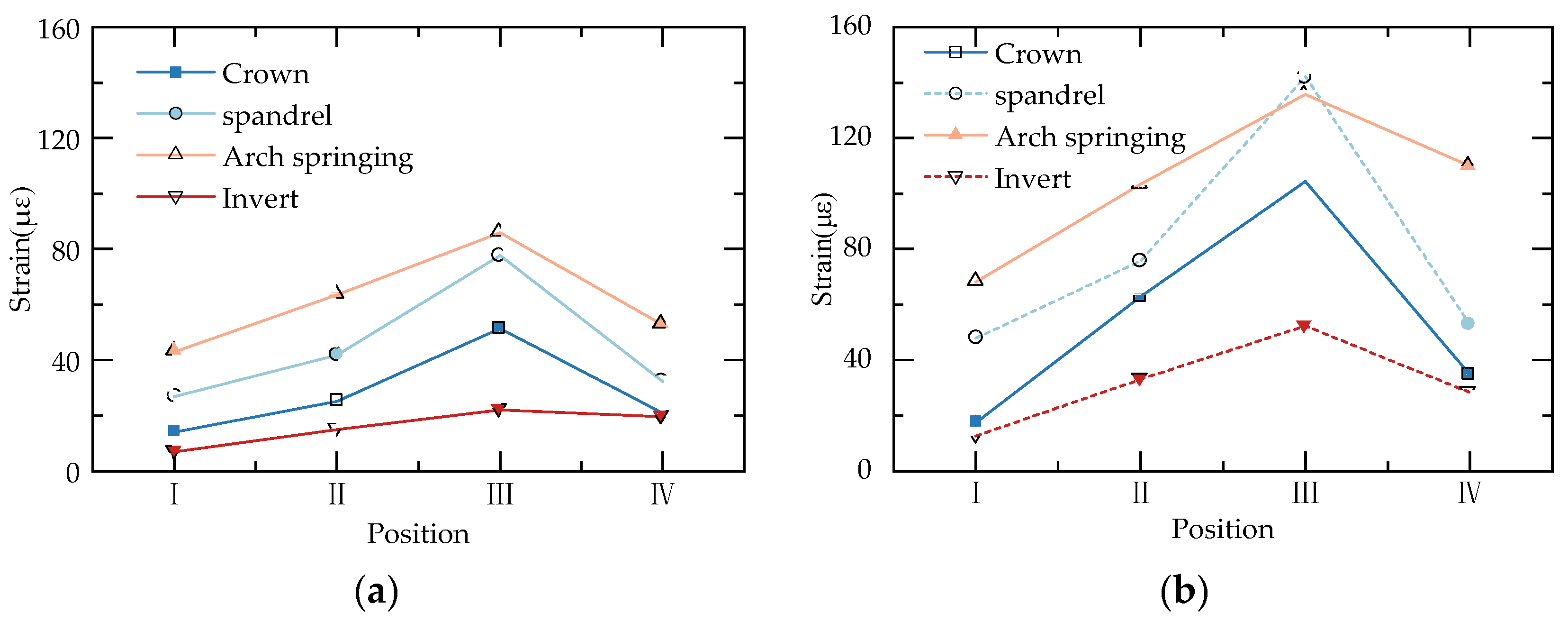
4.5.2. Strain Responses of Tests
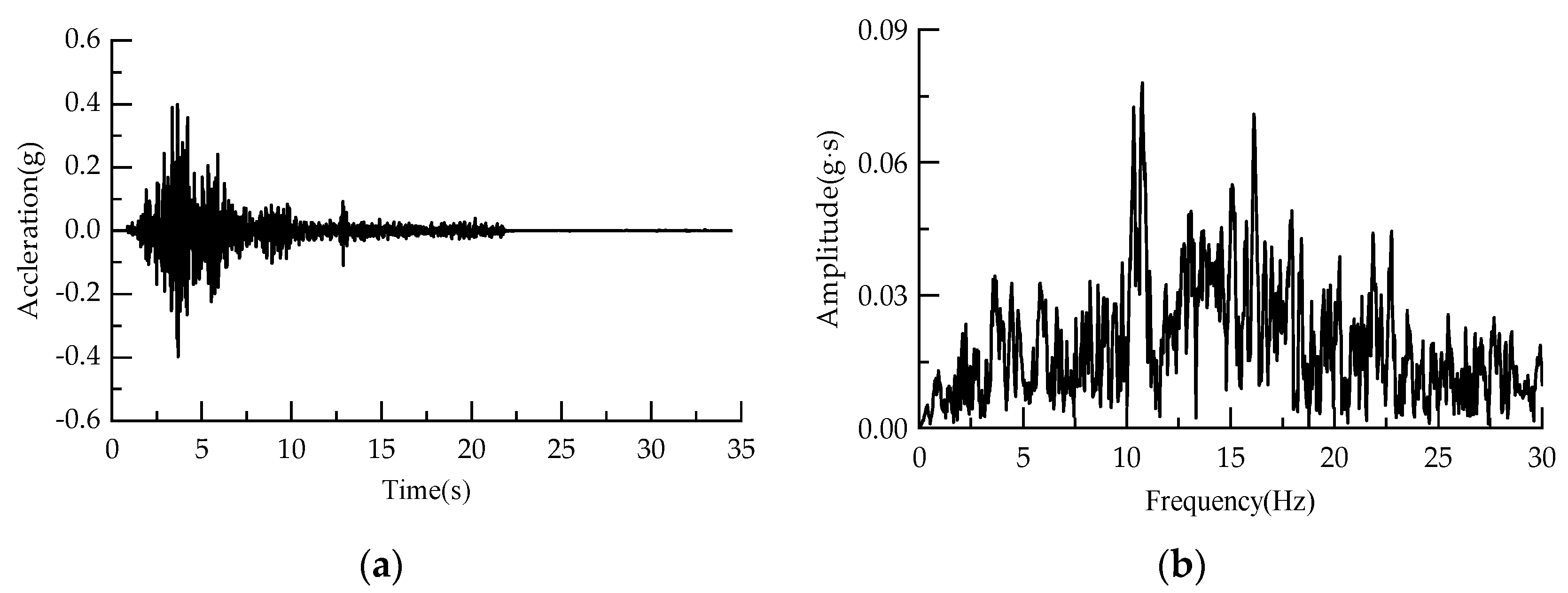
4.5.3. Acceleration Responses of Tests
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the taiwan chi-chi earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Li, T. Damage to mountain tunnels related to the wenchuan earthquake and some suggestions for aseismic tunnel construction. B. Eng. Geol. Environ. 2012, 71, 297–308. [Google Scholar] [CrossRef]
- Liang, J.; Xu, A.; Ba, Z.; Chen, R.; Zhang, W.; Liu, M. Shaking table test and numerical simulation on ultra-large diameter shield tunnel passing through soft-hard stratum. Soil Dyn. Earthq. Eng. 2021, 147, 106790. [Google Scholar] [CrossRef]
- Koizumi, A.; He, C. Dynamic behavior in longitudinal direction of shield tunnel located at irregular ground with considering effect of secondary lining. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Zhang, J.; He, C.; Geng, P.; He, Y.; Wang, W.; Meng, L. Shaking table tests on longitudinal seismic response of shield tunnel through soft-hard stratum junction. Chin. J. Rock Mech. Eng. 2017, 36, 68–77. [Google Scholar]
- Wang, D.; Yuan, J.; Cui, G.; Liu, J.; Wang, H. Experimental study on characteristics of seismic damage and damping technology of absorbing joint of tunnel crossing interface of soft and hard rock. Shock Vib. 2020, 2020, 2128045. [Google Scholar] [CrossRef]
- Tang, G.; Fang, Y.; Zhong, Y.; Yuan, J.; Ruan, B.; Fang, Y.; Wu, Q. Numerical study on the longitudinal response characteristics of utility tunnel under strong earthquake: A case study. Adv. Civ. Eng. 2020, 2020, 8813303. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; I-Chiang Yao, J. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Zhao, M.; Li, H.; Huang, J.; Du, X.; Wang, J.; Yu, H. Analytical solutions considering tangential contact conditions for circular lined tunnels under longitudinally propagating shear waves. Comput. Geotech. 2021, 137, 104301. [Google Scholar] [CrossRef]
- Newmark, N.M. Problems in wave propagation in soil and rock. In Proceedings of the International Symposium on Wave Propagation and Dynamic Properties of Earth Materials, Albuquerque, NM, USA, 23–25 August 1967. [Google Scholar]
- Bobet, A. Effect of pore water pressure on tunnel support during static and seismic loading. Tunn. Undergr. Space Technol. 2003, 18, 377–393. [Google Scholar] [CrossRef]
- Zhou, X.L.; Wang, J.H.; Lu, J.F. Transient foundation solution of saturated soil to impulsive concentrated loading. Soil Dyn. Earthq. Eng. (1984) 2002, 22, 273–281. [Google Scholar] [CrossRef]
- Kontoe, S.; Avgerinos, V.; Potts, D.M. Numerical validation of analytical solutions and their use for equivalent-linear seismic analysis of circular tunnels. Soil Dyn. Earthq. Eng. 2014, 66, 206–219. [Google Scholar] [CrossRef]
- St John, C.M.; Zahrah, T.F. Aseismic design of underground structures. Tunn. Undergr. Space Technol. 1987, 2, 165–197. [Google Scholar] [CrossRef]
- Tariverdilo, S.; Mirzapour, J.; Shahmardani, M.; Shabani, R.; Gheyretmand, C. Vibration of submerged floating tunnels due to moving loads. Appl. Math. Model. 2011, 35, 5413–5425. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, Y. Analytical solution for an infinite euler-bernoulli beam on a viscoelastic foundation subjected to arbitrary dynamic loads. J. Eng. Mech. 2014, 140, 542–551. [Google Scholar] [CrossRef]
- Yu, H.; Cai, C.; Yuan, Y.; Jia, M. Analytical solutions for euler-bernoulli beam on pasternak foundation subjected to arbitrary dynamic loads. Int. J. Numer. Anal. Geomech. 2017, 41, 1125–1137. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Z.; Chen, J.; Bobet, A.; Zhao, M.; Yuan, Y. Analytical solution for longitudinal seismic response of tunnel liners with sharp stiffness transition. Tunn. Undergr. Space Technol. 2018, 77, 103–114. [Google Scholar] [CrossRef]
- Shahidi, A.R.; Vafaeian, M. Analysis of longitudinal profile of the tunnels in the active faulted zone and designing the flexible lining (for koohrang-iii tunnel). Tunn. Undergr. Space Technol. 2005, 20, 213–221. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Musgrove, M.I.; Harmon, J.A.; Groholski, D.; Phillips, C.A.; Park, D. Deepsoil v6.1, User Manual; Board of Trustees of University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2016. [Google Scholar]
- Kim, S.; Cho, Y. Vibration and dynamic buckling of shear beam-columns on elastic foundation under moving harmonic loads. Int. J. Solids Struct. 2006, 43, 393–412. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Lin, B.; Zhao, X.; Zhu, W.; Yang, Y.; Li, Y. Closed-form solutions for forced vibrations of a cracked double-beam system interconnected by a viscoelastic layer resting on winkler–pasternak elastic foundation. Thin Wall. Struct. 2021, 163, 107688. [Google Scholar] [CrossRef]
- Chen, B.; Lin, B.; Li, Y.; Tang, H. Exact solutions of steady-state dynamic responses of a laminated composite double-beam system interconnected by a viscoelastic layer in hygrothermal environments. Compos. Struct. 2021, 268, 113939. [Google Scholar] [CrossRef]
- Yu, H.; Li, X.; Li, P. Analytical solution for vibrations of a curved tunnel on viscoelastic foundation excited by arbitrary dynamic loads. Tunn. Undergr. Space Technol. 2022, 120, 104307. [Google Scholar] [CrossRef]
- Zhao, K. Seismic Response and Anti-Dislocation Technology of Tunnel across Fault Subjected to Earthquake. Ph.D. Thesis, University of Chinese Academy of Sciences, Wuhan, China, 2018. (In Chinese). [Google Scholar]
- Yan, G.; Gao, B.; Shen, Y.; Zheng, Q.; Fan, K.; Huang, H. Shaking table test on seismic performances of newly designed joints for mountain tunnels crossing faults. Adv. Struct. Eng. 2020, 23, 248–262. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Jiang, Y.J.; Zhu, C.A.; Sun, T.C. Shaking table tests of tunnel linings in progressive states of damage. Tunn. Undergr. Space Technol. 2015, 50, 109–117. [Google Scholar] [CrossRef]
- Wen, Y.M.; Xin, C.L.; Shen, Y.S.; Huang, Z.M.; Gao, B. The seismic response mechanisms of segmental lining structures applied in fault-crossing mountain tunnel: The numerical investigation and experimental validation. Soil Dyn. Earthq. Eng. 2021, 151, 107001. [Google Scholar] [CrossRef]
- Tao, L.; Ding, P.; Shi, C.; Wu, X.; Wu, S.; Li, S. Shaking table test on seismic response characteristics of prefabricated subway station structure. Tunn. Undergr. Space Technol. 2019, 91, 102994. [Google Scholar] [CrossRef]







| Physical Quantity | Length | Density | Young’s Modulus | Cohesion | Friction Angle | Strain |
|---|---|---|---|---|---|---|
| Similarity relation | Cl | Cρ | CE | CC = CE | Cφ | Cε |
| Ratio of similarity ratio | 1/30 | 1/1.5 | 1/45 | 1/45 | 1 | 1 |
| Name | Young’s Modulus (GPa) | Density (kg/m3) | Cohesion (kPa) | Friction Angle (°) | Poisson’s Ratio | Compression Strength (MPa) |
|---|---|---|---|---|---|---|
| Rock model | 0.06 | 1467 | 16.5 | 32.3 | - | - |
| Fault model | 0.02 | 1200 | 4.0 | 25 | - | - |
| Lining model | 0.68 | 1600 | - | - | 0.25 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Zhao, B. Analytical Solution and Shaking Table Test on Tunnels through Soft-Hard Stratum with a Transition Tunnel and Flexible Joints. Appl. Sci. 2022, 12, 3151. https://doi.org/10.3390/app12063151
Yan G, Zhao B. Analytical Solution and Shaking Table Test on Tunnels through Soft-Hard Stratum with a Transition Tunnel and Flexible Joints. Applied Sciences. 2022; 12(6):3151. https://doi.org/10.3390/app12063151
Chicago/Turabian StyleYan, Gaoming, and Boming Zhao. 2022. "Analytical Solution and Shaking Table Test on Tunnels through Soft-Hard Stratum with a Transition Tunnel and Flexible Joints" Applied Sciences 12, no. 6: 3151. https://doi.org/10.3390/app12063151






