Detailed and Average Models of a Grid-Connected MMC-Controlled Permanent Magnet Wind Turbine Generator
Abstract
:1. Introduction
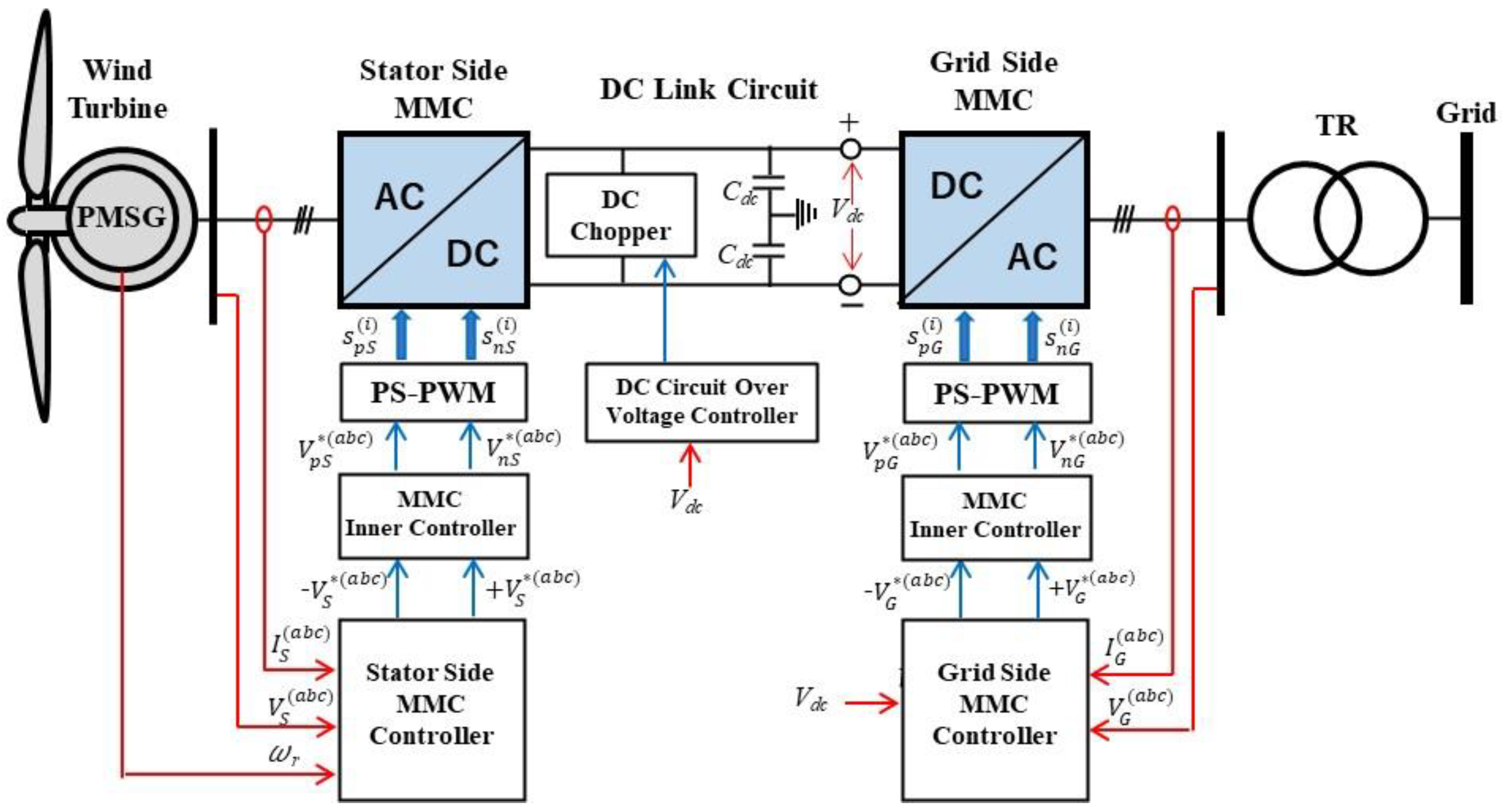
2. Detailed Model of MMC-Controlled Wind Turbine Generator
2.1. Wind Turbine Model
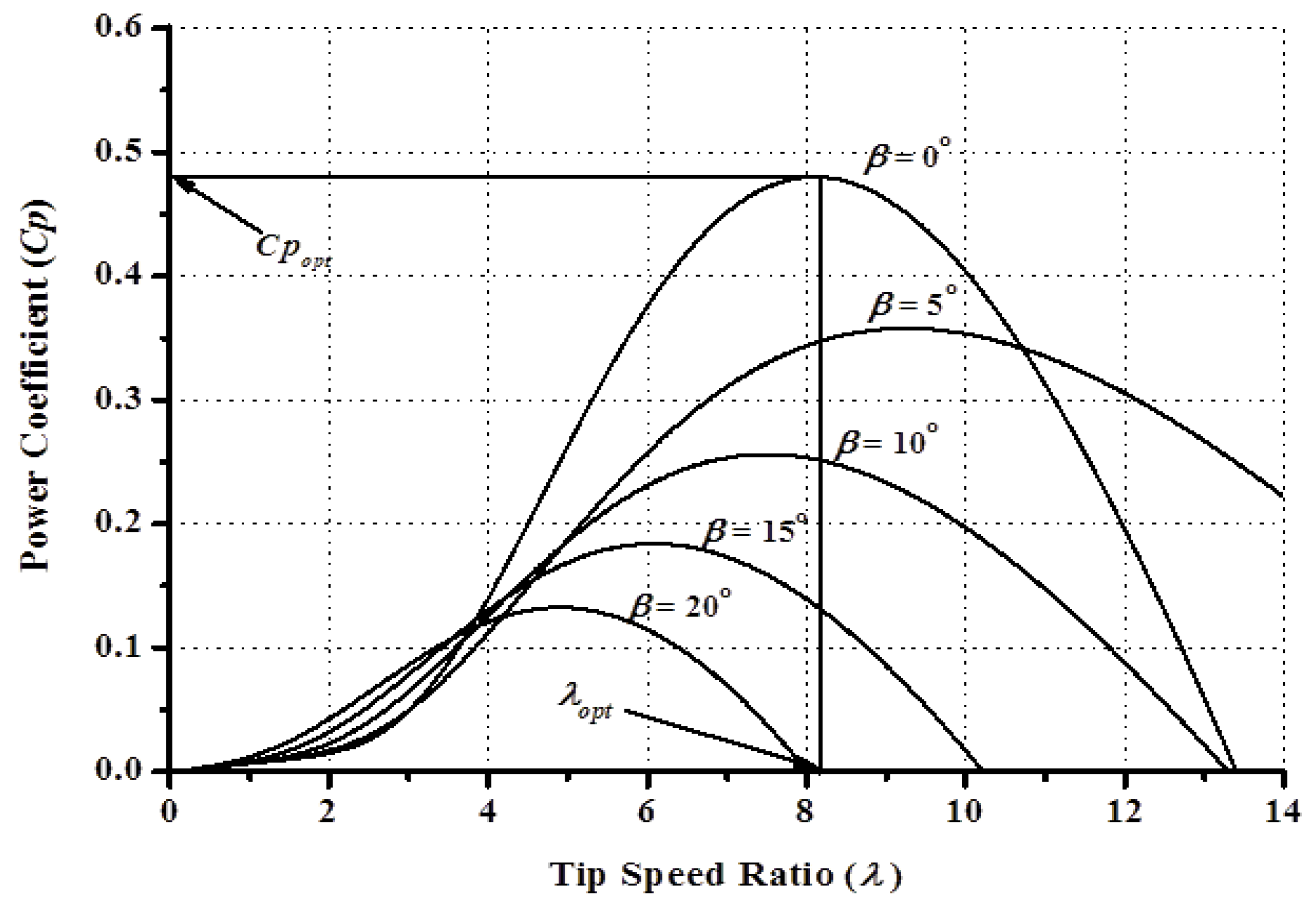
2.1.1. Power Conversion and Characteristics of Wind Turbine
2.1.2. Drive Train Model
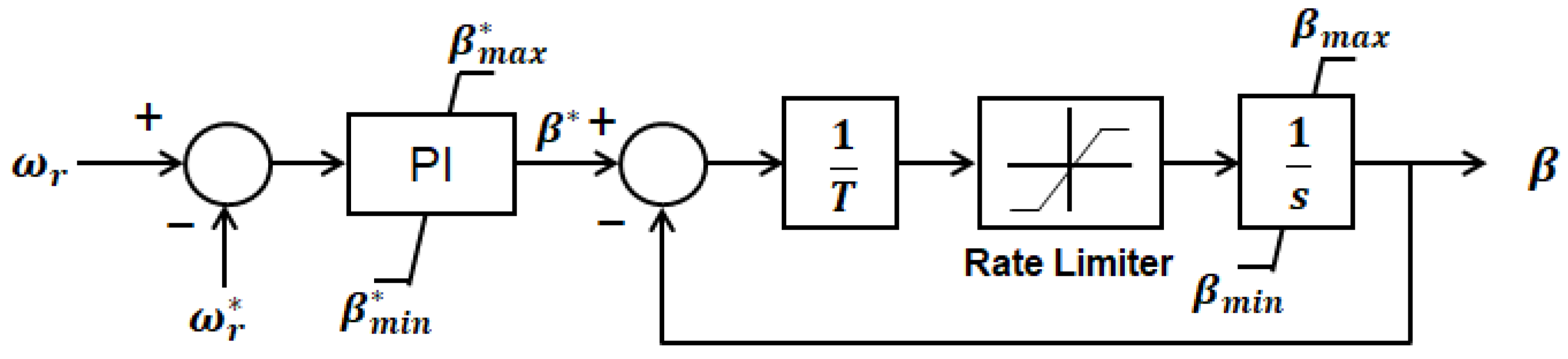
2.1.3. Pitch Blade Controller
2.2. Generator Model
2.3. MMC System
2.3.1. Configuration and Operation of MMC
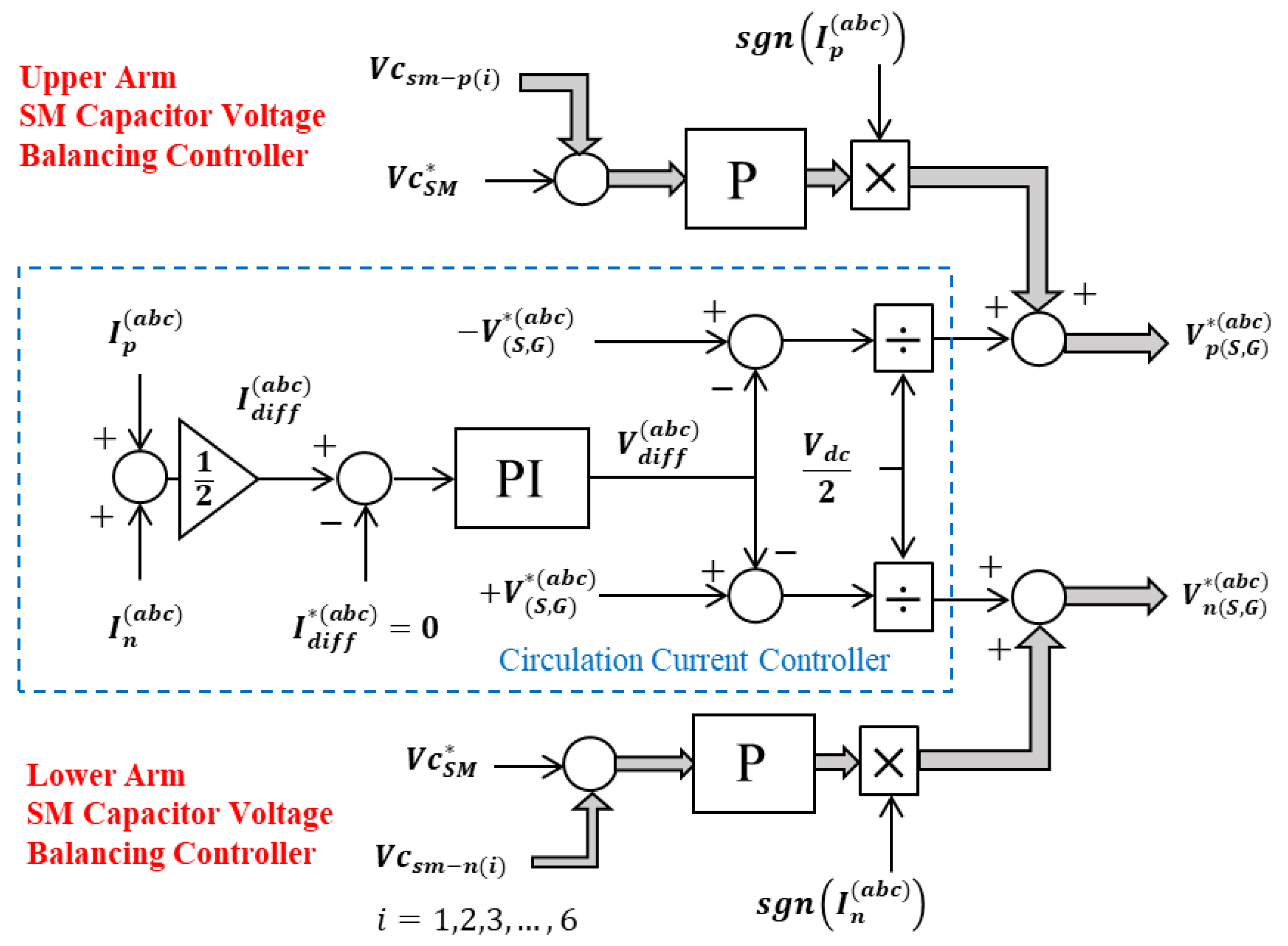
2.3.2. Stator-Side MMC Controller
2.3.3. Grid-Side MMC Controller
2.3.4. MMC Inner Control
2.3.5. Phase Shifted Pulse Width Modulation (PS-PWM)
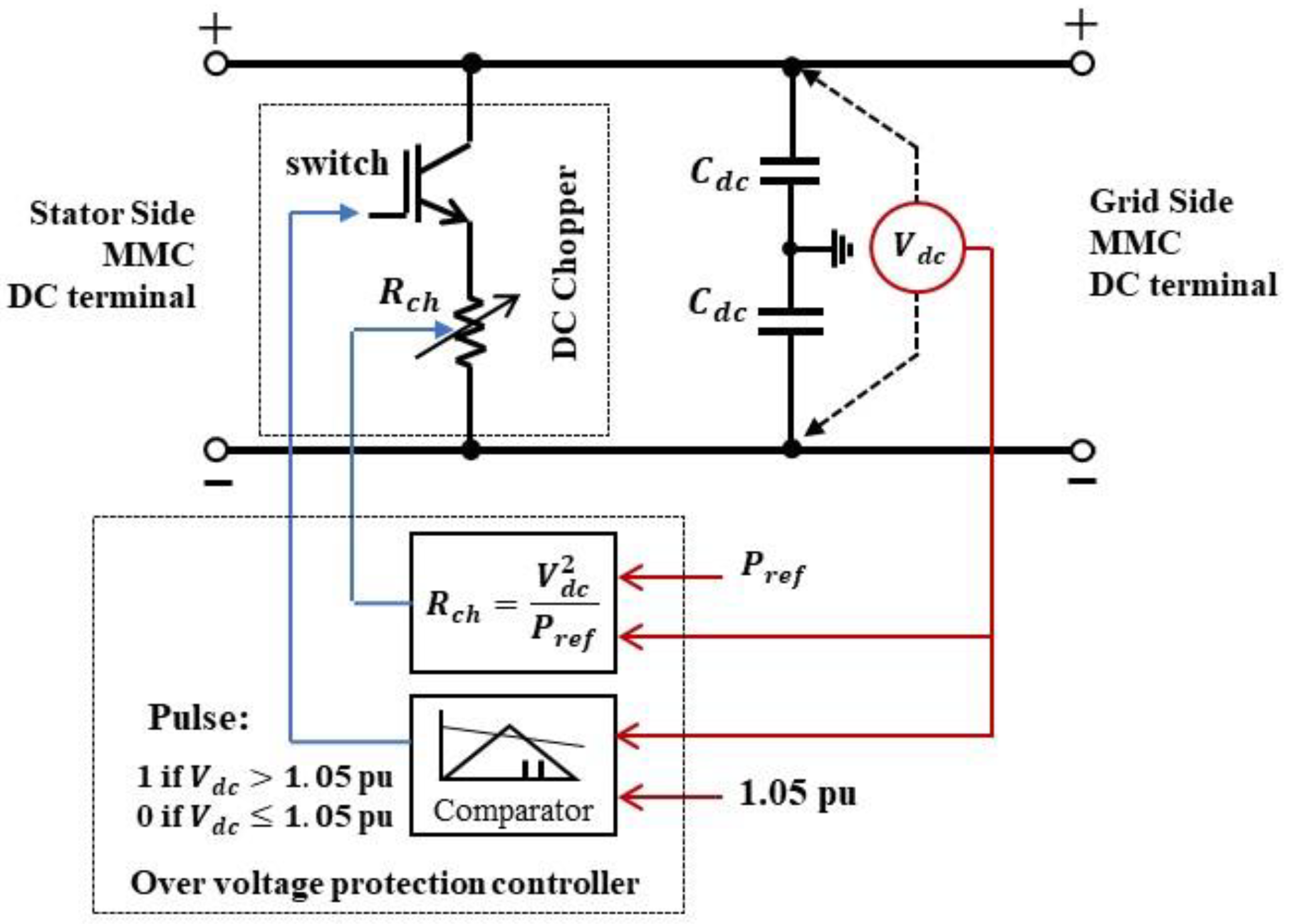
2.4. DC Link Circuit and Overvoltage Protection System
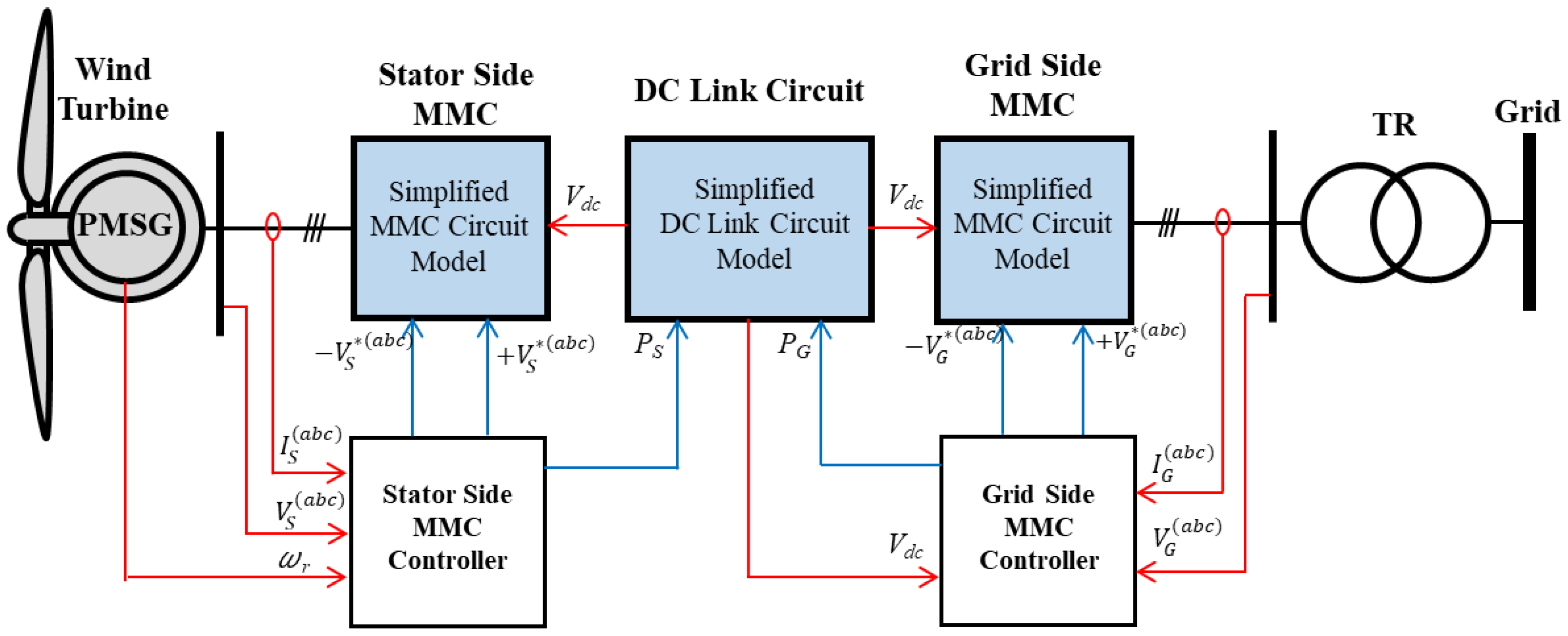
3. Average Model of MMC-Controlled Wind Turbine Generator
3.1. MMC Circuit Model
3.2. DC Link Circuit Model
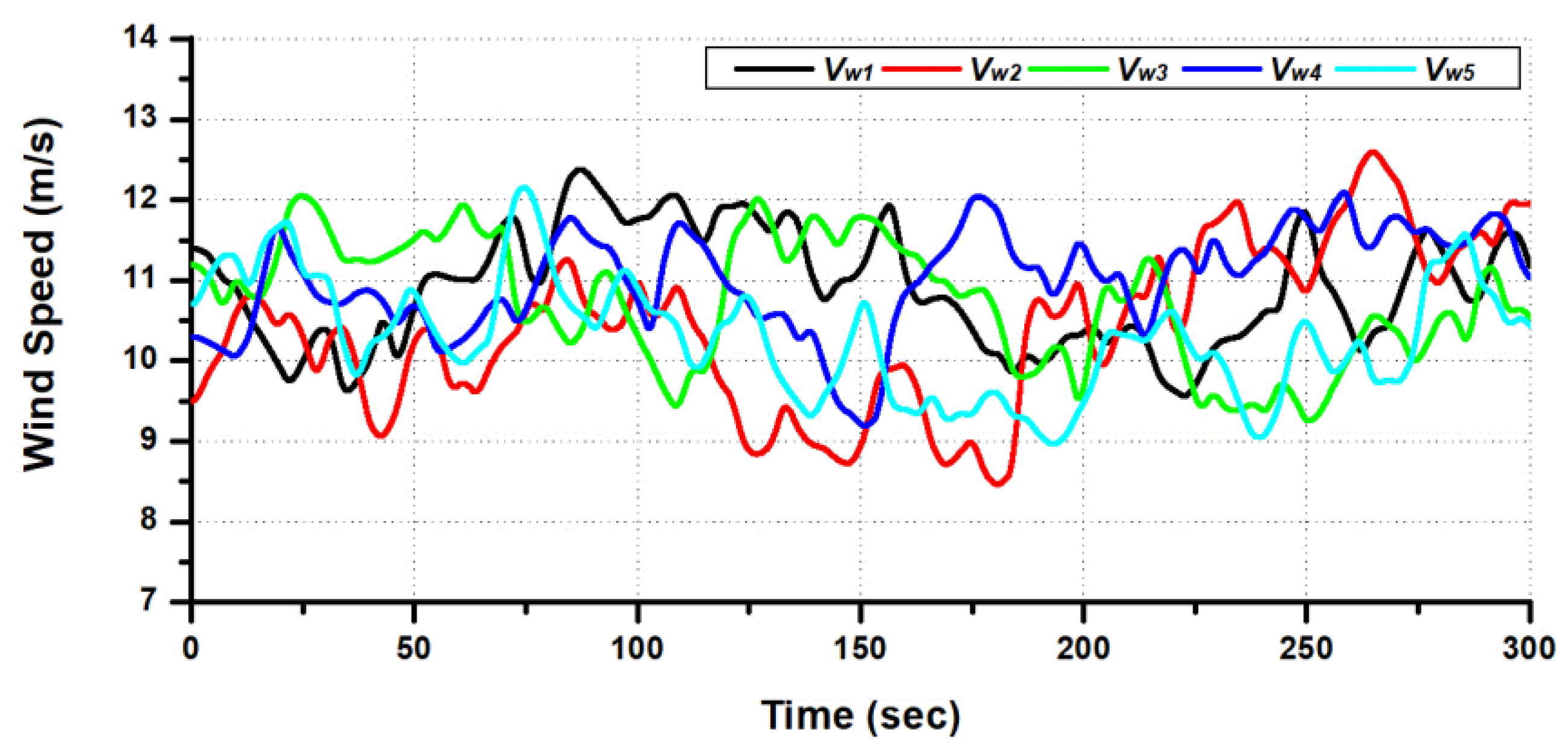
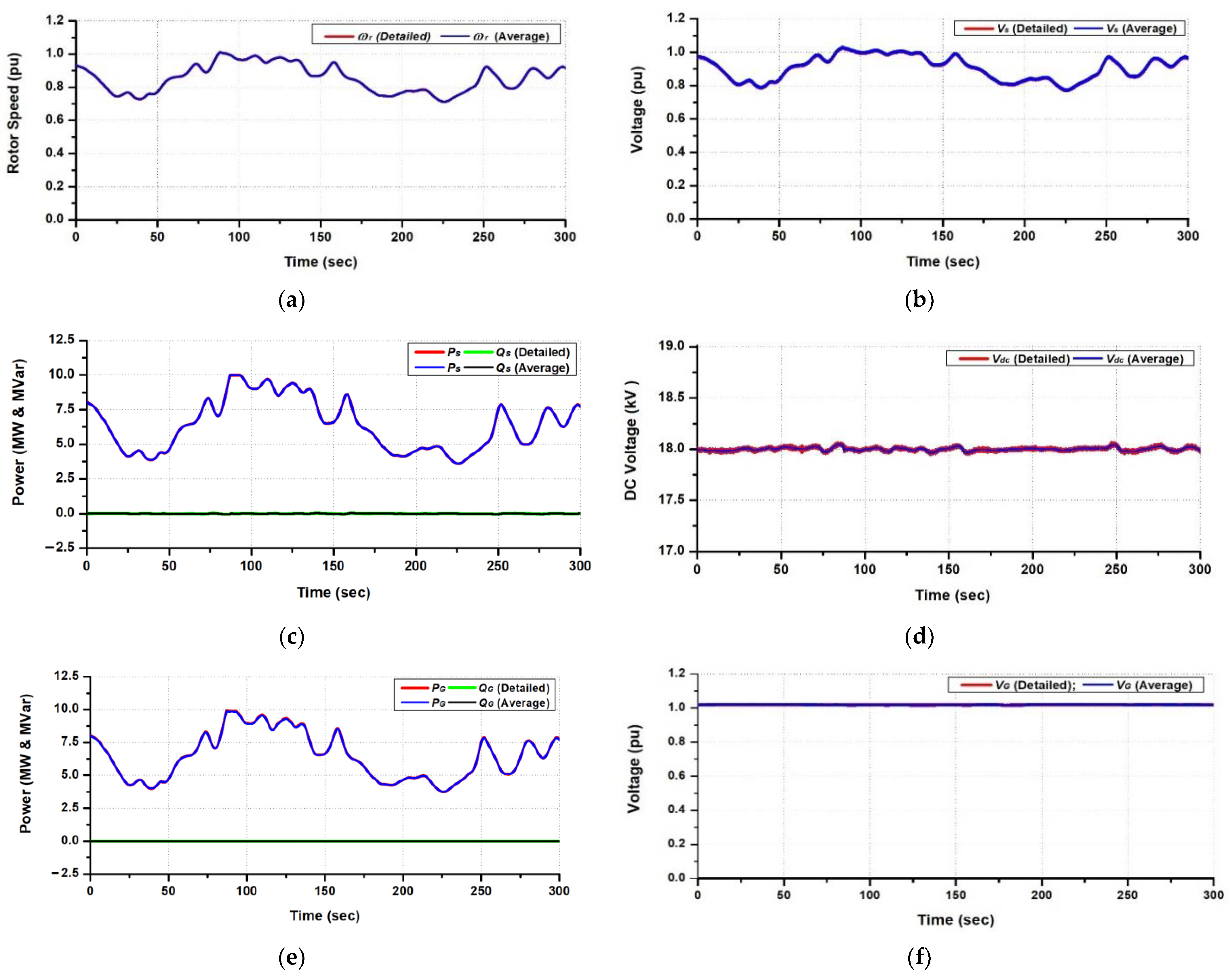
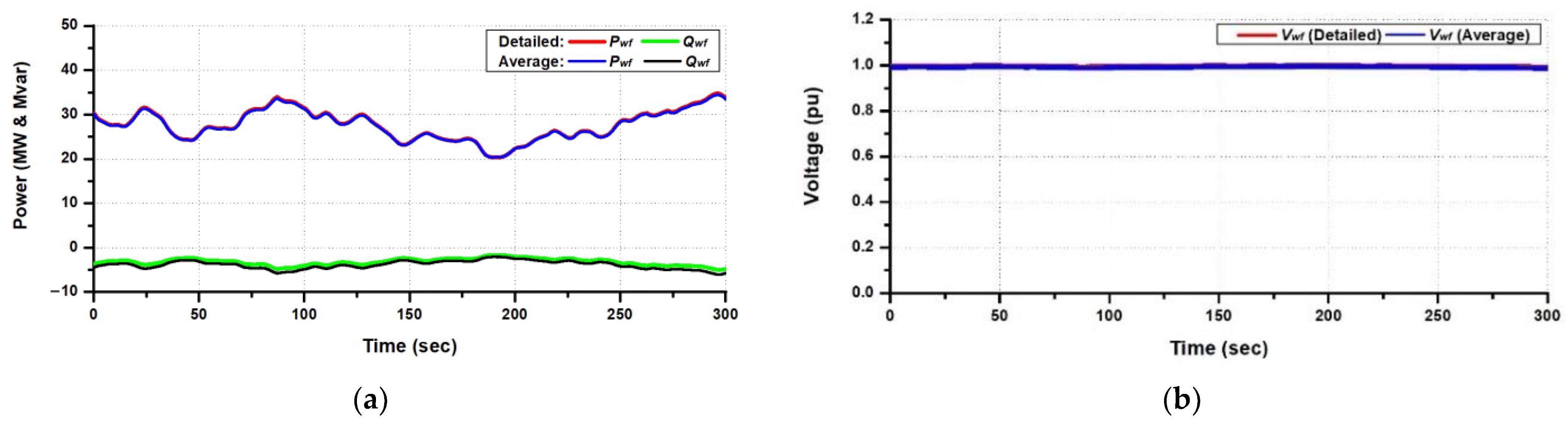
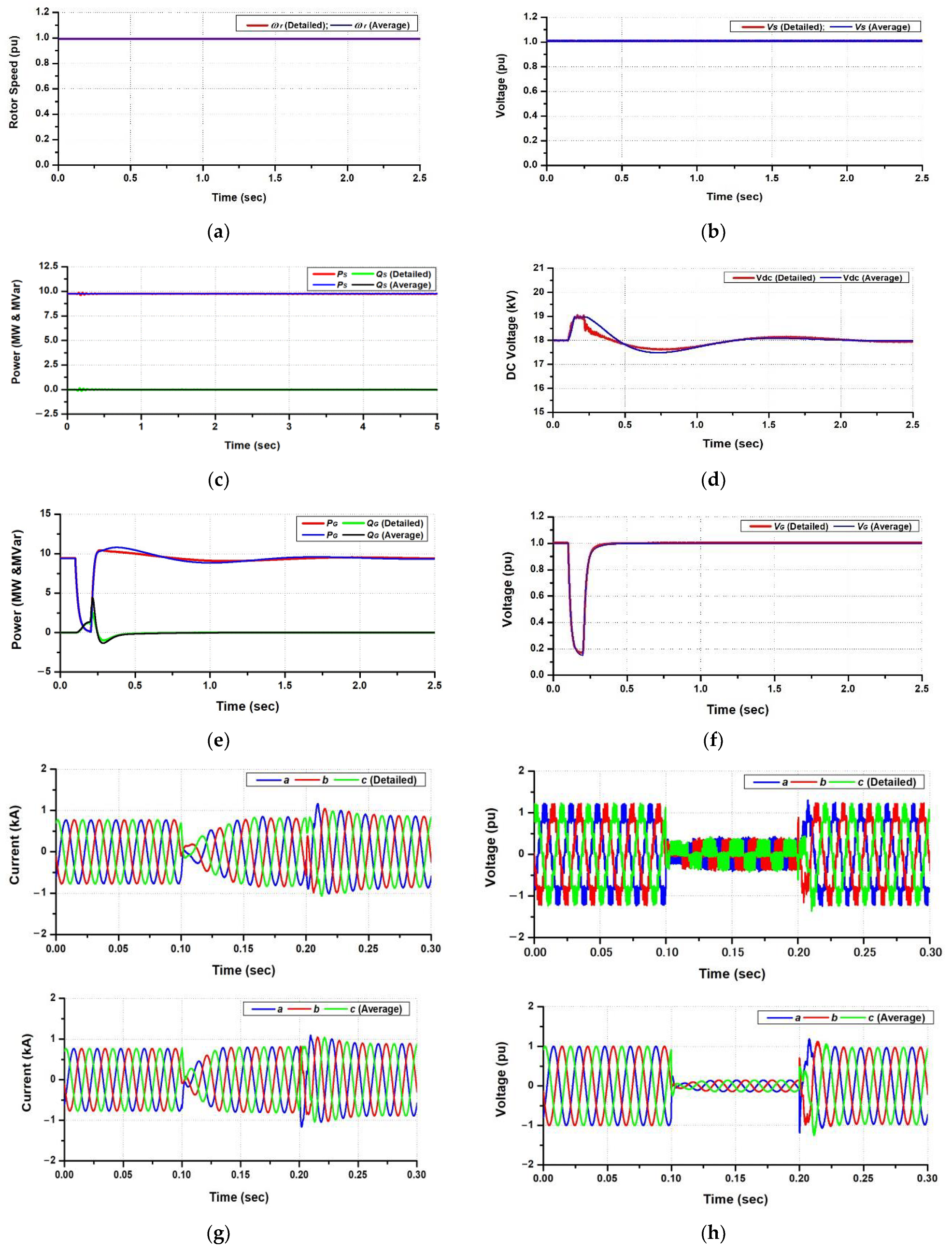
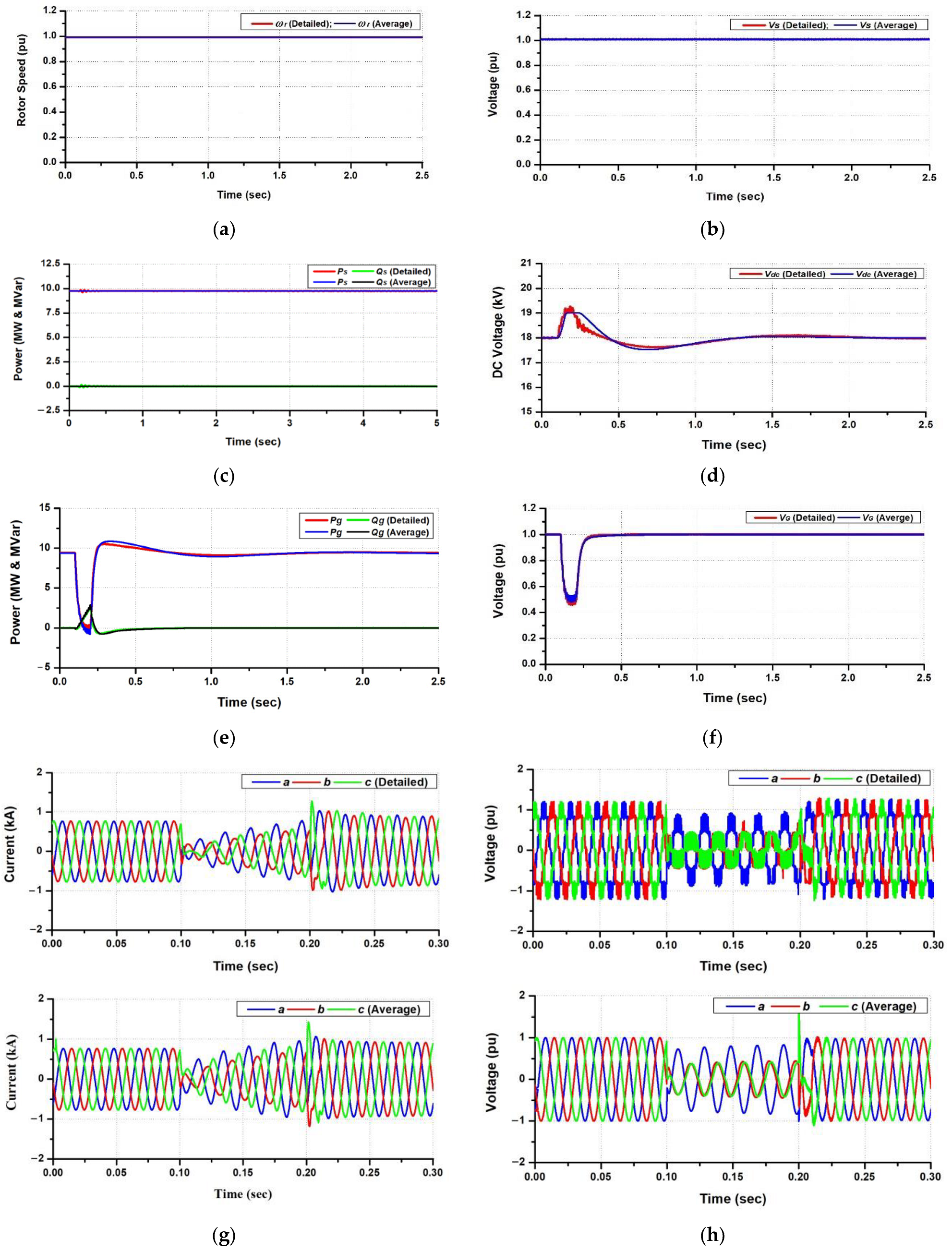
4. Simulation and Analysis
4.1. Steady-State Performance Analysis
4.2. Transient Performance Analysis
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Vestas to Launch Giant 15 MW Offshore Wind Turbine. Available online: https://www.oedigital.com/news/485191-vestas-to-launch-giant-15mw-offshore-wind-turbine (accessed on 10 February 2021).
- Wind Power Experts Expect Wind Eenergy Costs to Decline up to 35% by 2035. Available online: https://www.renewableenergyworld.com/wind-power/wind-power-experts-expect-wind-energy-costs-to-decline-up-to-35-by-2035/#gref (accessed on 15 April 2021).
- Qin, J.Q.; Saeedifard, M.; Rockhill, A.; Zhou, R. Hybrid design of modular multilevel converters for HVDC systems based on various submodule circuits. IEEE Trans. Power Deliv. 2015, 30, 385–394. [Google Scholar] [CrossRef]
- Shi, X.; Wang, Z.; Liu, B.; Liu, Y.; Tolbert, L.M.; Wang, F. Characteristic investigation and control of a modular multilevel converter-based HVDC system under single-line-to-ground fault conditions. IEEE Trans. Power Electron. 2015, 30, 408–421. [Google Scholar] [CrossRef]
- Lesnicar, A.; Maquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Zhang, Z.; Lee, J.; Jang, G. Improved control strategy of MMC-HVDC to improve frequency support of AC system. Appl. Sci. 2020, 10, 7282. [Google Scholar] [CrossRef]
- Husain, N.; Ali, S.M.U. On integration of wind power into existing grids via Modular Multilevel Converter based HVDC Systems. Int. J. Renew. Energy Res. 2020, 10, 1060–1070. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Lyu, J.; Zong, H.; Xue, T.; Fang, Z.; Cai, X. Stability analysis of wind farm connected to hybrid HVDC converter. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020. [Google Scholar]
- Hossain, M.I.; Abido, M.A. Positive-Negative Sequence Current Controller for LVRT Improvement of Wind Farms Integrated MMC-HVDC Network. IEEE Access 2020, 8, 193314–193339. [Google Scholar] [CrossRef]
- Li, Y.; Guo, J.; Zhang, X.; Wang, S.; Ma, S.; Zhao, B.; Wu, G.; Wang, T. Over-voltage suppression methods for the MMC-VSC-HVDC wind farm integration system. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 355–359. [Google Scholar] [CrossRef]
- Popova, L.; Ma, K.; Blaabjerg, F.; Pyrhonen, J. Device loading of a modular multilevel converter in wind power. IEEJ J. Ind. Appl. 2014, 4, 380–386. [Google Scholar] [CrossRef]
- Guan, W.; Huang, S.; Huang, X. Medium-voltage wind generation system based on MPMSG and MMC and its fault-tolerant. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019. [Google Scholar]
- Salman, S.K.; Teo, A.L. Windmill modeling consideration and factors influencing the stability of a grid-connected wind power-based embedded generator. IEEE Trans. Power Syst. 2003, 18, 793–802. [Google Scholar] [CrossRef]
- Dizdarevic, N.; Majstrovic, M.; Zutobradic, S. Power quality in a distribution network after wind power plant connection. In Proceedings of the IEEE PES Power System Conference and Exposition, New York, NY, USA, 10–13 October 2004. [Google Scholar]
- A New Era in Direct Drive Generator Design. Available online: https://www.lagerwey.com/technology/generator/ (accessed on 5 December 2021).
- Kiyoki, S.; Sakamoto, K.; Kakuya, H.; Saeki, M. 5-MW downwind wind turbine demonstration and work toward smart operation control. Hitachi Review 2017, 66. Available online: https://www.hitachi.com/rev/archive/2017/r2017_05/R5-02/index.html (accessed on 5 December 2021).
- E-160 EP5. Available online: https://www.enercon.de/en/products/ep-5/e-160-ep5/ (accessed on 5 December 2021).
- Heier, S. Grid Integration of Wind Energy Conversion System; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Muyeen, S.M.; Takahashi, R.; Murata, T.; Tamura, J. A variable speed wind turbine control strategy to meet wind farm grid code requirements. IEEE Trans. Power Syst. 2010, 25, 331–340. [Google Scholar] [CrossRef]
- Yin, M.; Zhao, C. Modeling of the wind turbine with a permanent magnet synchronous generator for integratin. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- González-Longatt, F.M.; Wall, P.; Terzija, V. A simplified model for dynamic behavior of permanent magnet synchronous generator for direct drive wind turbine. In Proceedings of the IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- PSCAD V5 Application Help. Available online: https://www.pscad.com/webhelp-v5-ol/ol-help.htm (accessed on 17 January 2021).
- Permanent Magnet Machine. Available online: https://www.pscad.com/knowledge-base/article/293 (accessed on 16 September 2018).
- Guide for Electromagnetic Transient Studies Involving VSC Converter; CIGRE Technical Brochure Reference 832; CIGRE: Paris, France, April 2021.
- Li, P.; Xiong, L.; Ma, M.; Huang, S.; Zhu, Z.; Wang, Z. Energy-shaping L2-gain controller for PMSG wind turbine to mitigate sub synchronous interaction. Int. J. Electr. Power Energy Syst. 2021, 135, 107571. [Google Scholar] [CrossRef]
- Li, P.; Xiong, L.; Wu, F.; Ma, M.; Wang, J. Sliding mode controller based on feedback linearization for damping of sub-synchronous control interaction in DFIG-based wind power plants. Int. J. Electr. Power Energy Syst. 2019, 107, 239–250. [Google Scholar] [CrossRef]
- Timofejevs, A.; Gamboa, D. Control of MMC in HVDC Applications. Master’s Thesis, Department of Energy Technology, Aalborg University, Aalborg, Denmark, 2013. [Google Scholar]
- Darus, R.; Konstantinou, G.; Pou, J.; Ceballos, S.; Agelidis, V.G. Comparison of phase-shifted and level-shifted PWM in the modular multilevel converter. In Proceedings of the IEEE the International Power Electronics Conference (IPEC—ECCE Asia), Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Marquardt, R. Modular Multilevel Converter: An universal concept for HVDC-networks and extended DC-Bus-applications. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA-, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Holtz, J. Pulse width modulation—A survey. In Proceedings of the 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992. [Google Scholar]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar]
- Stamatiou, G. Analysis of VSC-based HVDC systems. Ph.D. Thesis, Department of Energy and Environment, Division of Electric Power Engineering, Chalmers University of Technology, Gothenburg, Sweden, 2016. [Google Scholar]
- Rodrigues, R.; Li, J.; Ginn, H. A novel frequency domain control method for modular multilevel converters under non-sinusoidal supply conditions. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Fernandes, L.M.; Garcia, C.A.; Jurado, F. Operating capability as a PQ/PV node of a direct-drive wind turbine based on a permanent magnet synchronous generator. J. Renew. Energy 2010, 35, 1308–1318. [Google Scholar] [CrossRef]



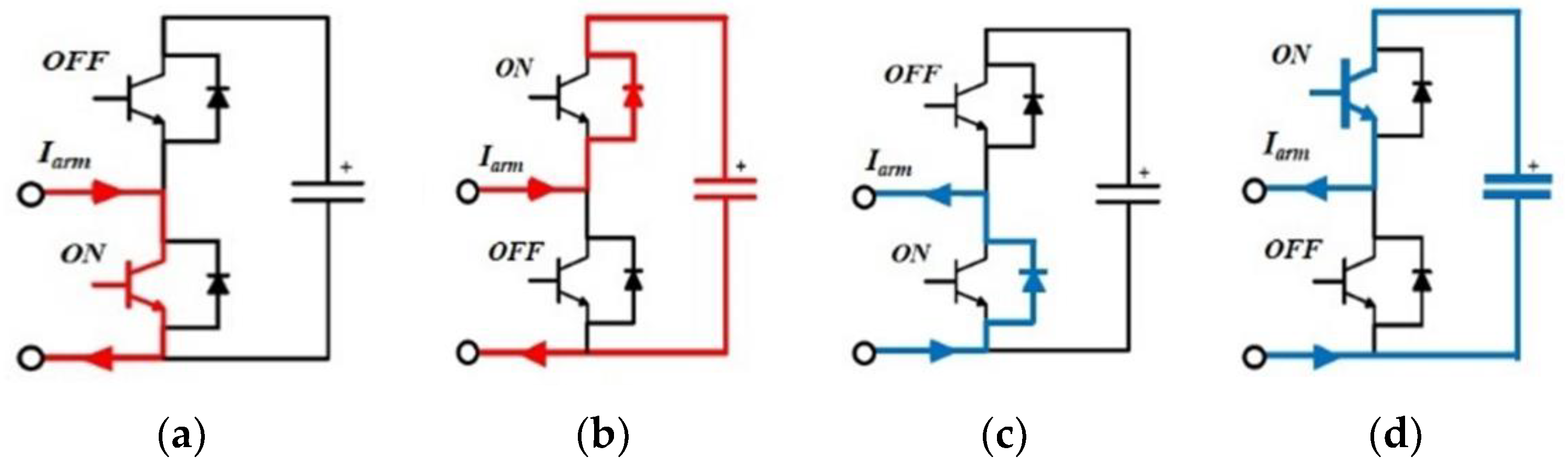









| Switching State | Terminal Voltage of SM (VSM) | Arm Current Polarity | Status of Capacitor | |
|---|---|---|---|---|
| S1 | S2 | |||
| OFF | ON | 0 | + | Bypass |
| ON | OFF | Vcsm | + | Charging |
| OFF | ON | 0 | − | Bypass |
| ON | OFF | Vcsm | − | Discharging |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated MVA | 10 MVA | Stator Winding Resistance | 0.017 pu |
| Rated Voltage (L-L) | 10 kV | Stator Leakage Reactance | 0.0364 |
| Rated Frequency | 50 Hz | d-axis Unsaturated Reactance [Xd] | 0.55 pu |
| Magnetic Strength | 1.1 pu | q-axis Unsaturated Reactance [Xq] | 1.11 pu |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated Power | 10 MVA | SM Capacitor | 9.2 mF |
| Rated AC Voltage | 10 kV | Arm Inductance | 3.8 mH |
| Rated DC Voltage | 18 kV | Arm Resistance | 0.097 Ω |
| Number of SMs per arm | 6 | Reactor Inductance | 0.773 mH |
| Carrier Frequency | 1000 Hz | Reactor Resistance | 0.019 Ω |
| DC link Capacitor | 7.4 mF |
| Simulation | Computation Time | |
|---|---|---|
| Detailed Model | Average Model | |
| Time step | 10 μs | 100 μs |
| Duration | 840 h | 11 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosyadi, M.; Umemura, A.; Takahashi, R.; Tamura, J. Detailed and Average Models of a Grid-Connected MMC-Controlled Permanent Magnet Wind Turbine Generator. Appl. Sci. 2022, 12, 1619. https://doi.org/10.3390/app12031619
Rosyadi M, Umemura A, Takahashi R, Tamura J. Detailed and Average Models of a Grid-Connected MMC-Controlled Permanent Magnet Wind Turbine Generator. Applied Sciences. 2022; 12(3):1619. https://doi.org/10.3390/app12031619
Chicago/Turabian StyleRosyadi, Marwan, Atsushi Umemura, Rion Takahashi, and Junji Tamura. 2022. "Detailed and Average Models of a Grid-Connected MMC-Controlled Permanent Magnet Wind Turbine Generator" Applied Sciences 12, no. 3: 1619. https://doi.org/10.3390/app12031619






