Evaluation of Cracks on the Welding of Austenitic Stainless Steel Using Experimental and Numerical Techniques
Abstract
:1. Introduction
2. Materials
3. Global Equations and Parameters
3.1. Random Numbers Generation
3.2. Electromagnetic Equation
3.3. Impedance Computation
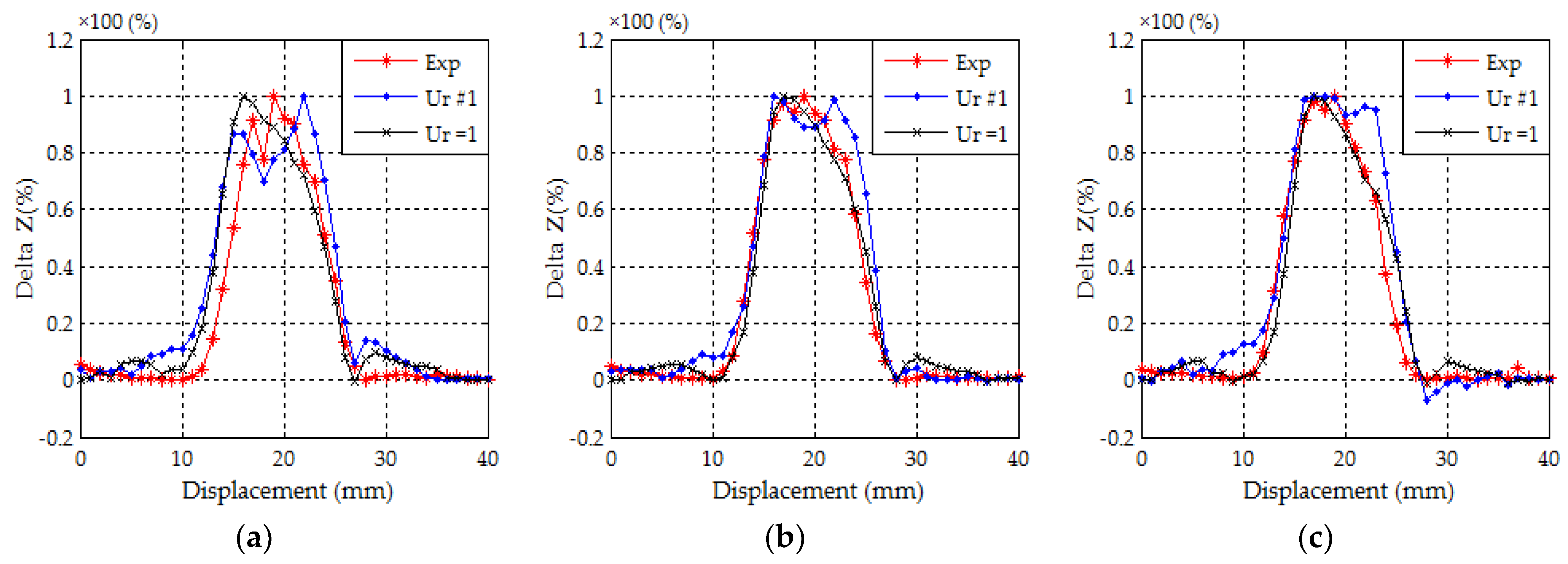
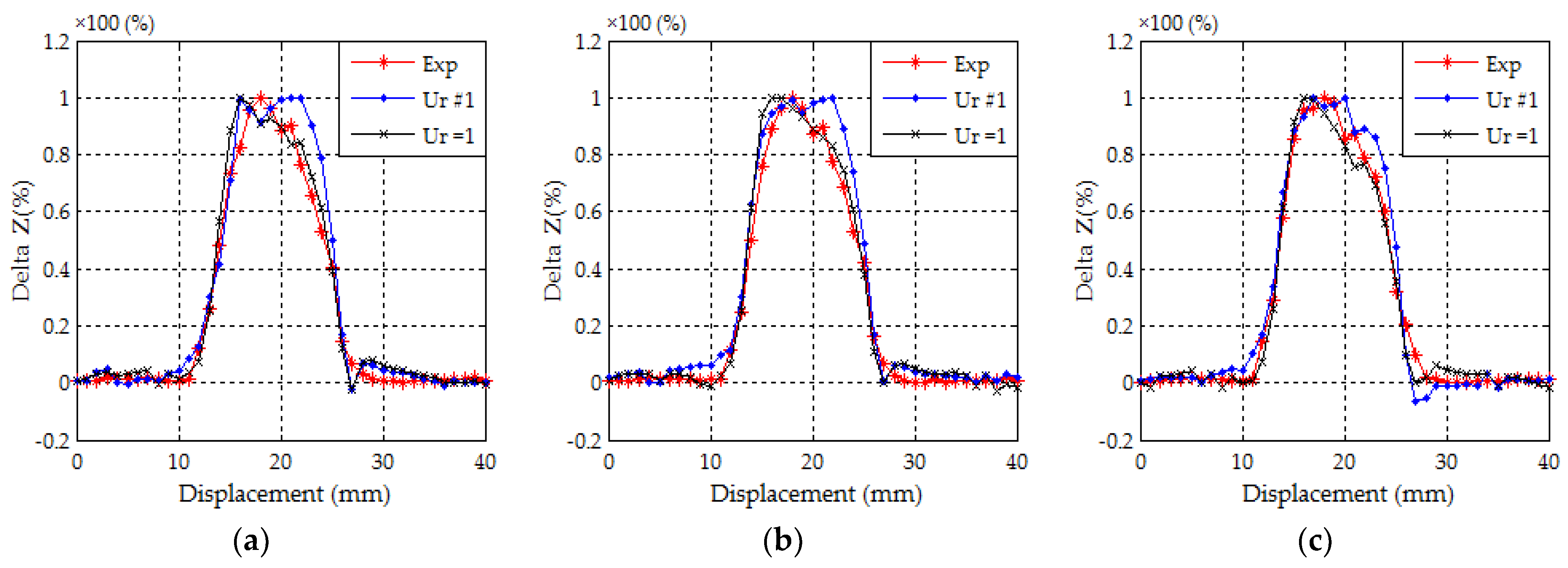
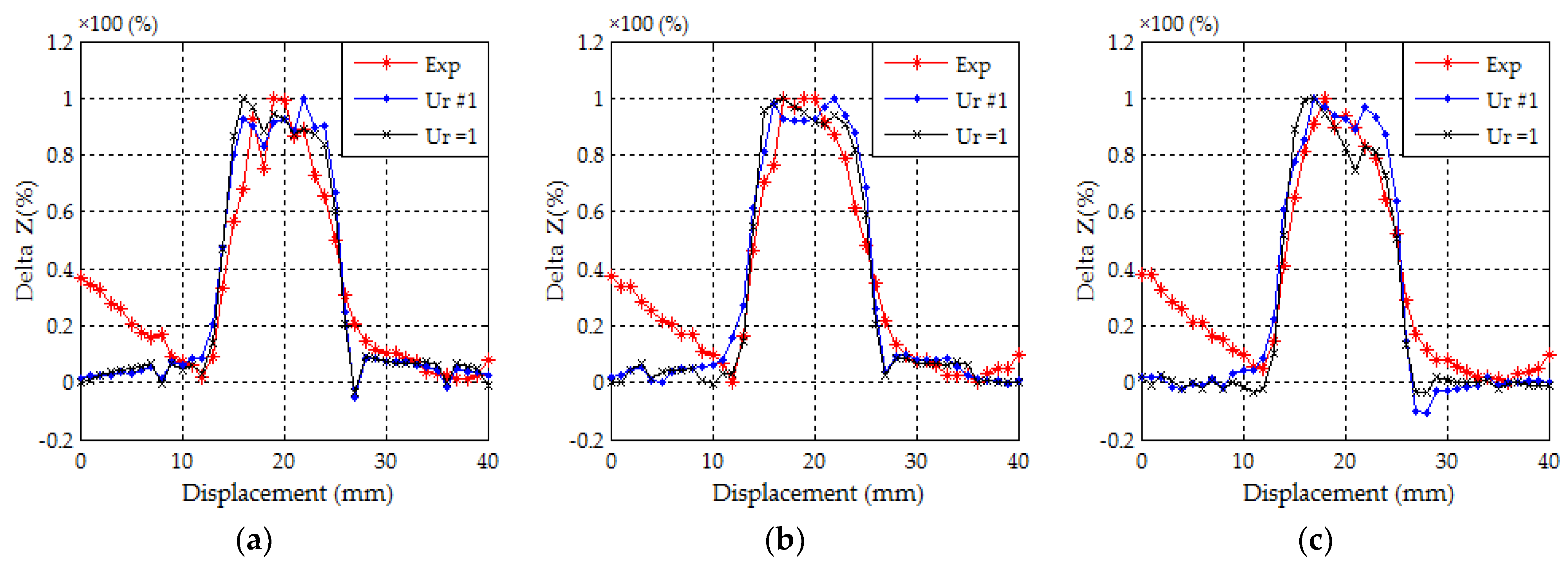
4. Results and Discussion
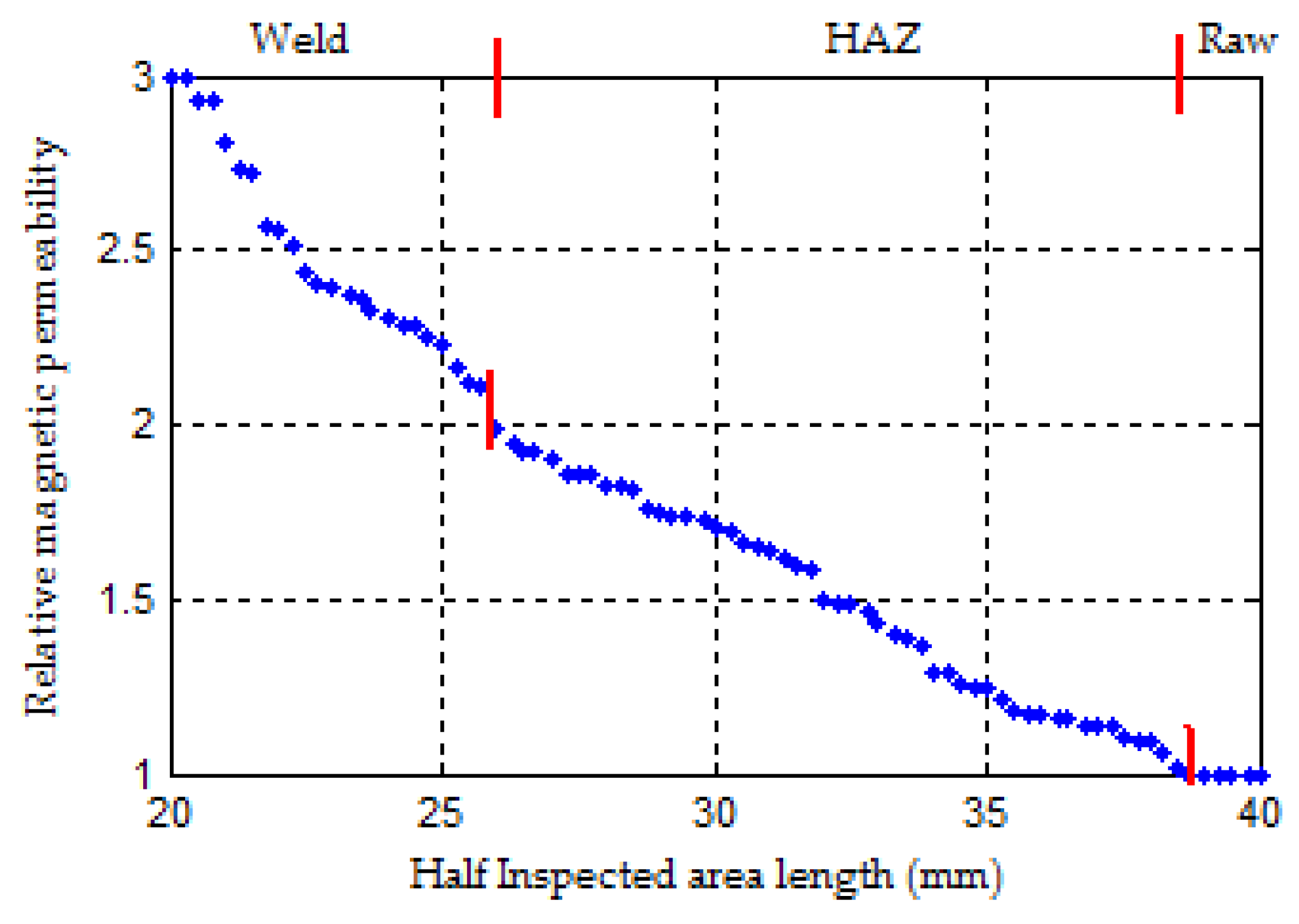
- Eddy currents are well adapted to the detection of thin surface cracks under the stress of the heat welding which affects the relative magnetic permeability locally.
- The validity of the modeling and the analysis approach.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nam, T.H.; An, E.; Kim, B.J.; Shin, S.; Ko, W.S.; Park, N.; Kang, N.; Jong, B.J. Effect of post weld heat treatment on the microstructure and mechanical properties of a submerged-arc-welded 304 stainless steel. Metals 2018, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Jang, D.; Kim, K.; Kim, H.C.; Jeon, J.B.; Nam, D.G.; Sohn, K.Y.; Kim, B.J. Evaluation of Mechanical property for welded austenitic stainless steel 304 by following post weld heat treatment. Korean J. Met. Mater. 2017, 55, 664–670. [Google Scholar] [CrossRef]
- Kawahara, Y. Application of high temperature corrosion-resistant materials and coatings under severe corrosive environment in waste-to-energy boilers. J. Therm. Spray Technol. 2007, 16, 202–213. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Fung, W.K.; Karnik, A. Recent advances in pipelines monitoring and oil leakage detection Technologies: Principles and approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Feng, H.; Wang, T.; Xuan, W.; Liang, Z.; Yang, X. Pipe crack recognition based on eddy current NDT and 2D impedance characteristics. Appl. Sci. 2019, 9, 689. [Google Scholar] [CrossRef] [Green Version]
- Mehaddene, H.; Mohellebi, H.; Berkache, A.; Berthiau, G. Experimental and numerical multi-defects analysis in ferromagnetic medium. Przegląd Elektrotechniczny 2020, 96, 57–61. [Google Scholar] [CrossRef]
- AbdAlla, A.N.; Faraj, M.A.; Samsuri, F.; Rifai, D.; Ali, K.; Al-Douri, Y. Challenges in improving the performance of eddy current testing: Review. Meas. Control 2019, 52, 46–64. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wei, Z.; Xie, F.; Sun, B. Assessment of the Properties of AISI 410 Martensitic Stainless Steel by an Eddy Current Method. Materials 2019, 12, 1290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ISO 12718. Non-Destructive Testing—Eddy Current Testing—Vocabulary, 2nd ed.; ISO: Geneva, Switzerland, 2019. [Google Scholar]
- Berkache, A.; Oudni, Z.; Mehaddene, H.; Mohellebi, H.; Lee, J. Inspection and characterization of random physical property defects by stochastic finite element method. PrzeglądElektrotechniczny 2019, 95, 96–101. [Google Scholar] [CrossRef]
- Kim, J.; Le, M.; Lee, J.; Hwang, Y.H. Eddy current testing and evaluation of far-side corrosion around rivet in jet-engine of aging supersonic aircraft. J. Nondestruct. Eval. 2014, 33, 471–480. [Google Scholar] [CrossRef]
- Tsuboi, H.; Ikeda, K.; Kurata, M.; Kainuma, K.; Nakamura, K. Eddy current analysis for the pipe welding. IEEE Trans. Magn. 1998, 34, 1234–1236. [Google Scholar] [CrossRef]
- Sim, S.; Le, M.; Kim, J.; Lee, J.; Kim, H.; Do, H.S. Nondestructive inspection of control rods in nuclear power plants using an encircling-type magnetic camera. Int. J. Appl. Electromagn. Mech. 2016, 52, 1561–1567. [Google Scholar] [CrossRef]
- Costanza, G.; Sili, A.; Tata, M.E. Weldability of austenitic stainless steel by metal arc welding with different shielding gas. Procedia Struct. Integr. 2016, 2, 3508–3514. [Google Scholar] [CrossRef] [Green Version]
- Cho, D.W.; Cho, W.I.; Na, S.J. Modeling and simulation of arc: Laser and hybrid welding process. J. Manuf. Process. 2013, 16, 26–55. [Google Scholar] [CrossRef]
- Kah, P.; Layus, P.; Hiltunen, E.; Martikainen, J. Real-time weld process monitoring. Adv. Mater. Res. 2014, 933, 117–124. [Google Scholar] [CrossRef]
- Wu, C.; Kim, J.W. Review on mitigation of welding-induced distortion based on FEM analysis. J. Weld. Join. 2020, 38, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Ma, W.; Qi, P.; Wen-jiao, D.; Yuan, X.; Yin, X. Detection and evaluation of weld defects in stainless steel using alternating current field measurement. In Proceedings of the 44th Annual Review of Progress in QNDE, Provo, Utah, USA, 16–21 July 2017; American Institute of Physics: College Park, MD, USA, 2018; Volume 1949, p. 230019. [Google Scholar] [CrossRef] [Green Version]
- Saito, T.; Ichiyama, Y. Weld defects and evaluation of weld quality: Welding phenomena and process control in flash welding of steel sheets. Weld. Int. 1996, 10, 117–123. [Google Scholar] [CrossRef]
- Park, I.; Kim, E.-Y.; Yang, W.-J. Microstructural Investigation of Stress Corrosion Cracking in Cold-Formed AISI 304 Reactor. Metals 2021, 11, 7. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, H.-Y.; Luo, Y.; Jin, Q.; Peng, W.; Yi, C.-M. A Study on Microstructure, Residual Stresses and Stress Corrosion Cracking of Repair Welding on 304 Stainless Steel: Part II-Effects of Reinforcement Height. Materials 2020, 13, 2434. [Google Scholar] [CrossRef] [PubMed]
- Oršulová, T.; Palček, P.; Kúdelčík, J. Effect of plastic deformation on the magnetic properties of selected austenitic stainless steels. Prod. Eng. Arch. 2017, 14, 15–18. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. ASME Boiler and Pressure Vessel Code, 2010 ed.; ASME: New York, NY, USA, 2010; p. 108. [Google Scholar]
- UGITECH. Magnetism and Stainless Steel. Available online: https://www.swisssteelinternational.us/fileadmin/user_upload/Ugitec/Documents_publics/AC/MARCHES/Magnetism/7512UGITECHMagnetGB.pdf (accessed on 1 January 2009).
- ISO 9712. Non-Destructive Testing—Qualification and Certification of NDT Personnel, 4th ed.; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Pasqualini, L.; Parton, M. Pseudo random number generation through reinforcement learning and recurrent neural networks. Algorithms 2020, 13, 307. [Google Scholar] [CrossRef]
- Irfan, M.; Ali, A.; Khan, M.A.; ul-Haq, M.E.; Shah, S.N.M.; Saboor, A.; Ahmad, W. Pseudorandom number generator (PRNG) design using hyper-chaotic modified robust logistic map (HC-MRLM). Electronics 2020, 9, 104. [Google Scholar] [CrossRef] [Green Version]
- L’Ecuyer, P. Pseudorandom number generators. In Encyclopedia of Quantitative Finance; Simulation Methods in Financial Engineering; Cont, R., Ed.; John Wiley: Chichester, UK, 2010; pp. 1431–1437. [Google Scholar]
- Bhattacharjee, K.; Maity, K.; Das, S. Search for good pseudo-random number generators: Survey and empirical studies. arXiv 2018, arXiv:1811.04035. [Google Scholar]
- Greenberger, M. Notes on a new pseudo-random number generator. JACM 1961, 8, 163–167. [Google Scholar] [CrossRef]
- Salmon, J.K.; Moraes, M.A.; Dror, R.O.; Shaw, D.E. Parallel Random Numbers: As Easy as 1,2,3. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, WA, USA, 12–18 November 2011. [Google Scholar] [CrossRef]
- Datcu, O.; Macovei, C.; Hobincu, R. Chaos based cryptographic pseudo-random number generator template with dynamic state change. Appl. Sci. 2020, 10, 451. [Google Scholar] [CrossRef] [Green Version]
- Silvester, P.; Chari, M.V.K. Finite element solution of saturable magnetic field problems. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 1642–1651. [Google Scholar] [CrossRef]
- Ida, N.; Betzold, K.; Lord, W. Finite element modeling of absolute eddy current probe signals. J. Nondestruct. Eval. 1982, 3, 147–154. [Google Scholar] [CrossRef]
- Thomas, J.L. Simplified Modeling of Eddy Current Control of Steam Generator Tubes Report of Internship ESA IGELEC; University of Nantes: Nantes, France, 1998. [Google Scholar]
- Oudni, Z.; Feliachi, M.; Mohellebi, H. Assessment of the probability of failure for EC nondestructive testing based on intrusive spectral stochastic finite element method. Eur. Phys. J. Appl. Phys. 2014, 66, 30904. [Google Scholar] [CrossRef]
- Chen, D.; Shao, K.R.; Lavers, J.D. Very fast numerical analysis of benchmark models of eddy-current testing for steam generator tube. IEEE Trans. Magn. 2002, 38, 2355–2357. [Google Scholar] [CrossRef]
- Takagi, T.; Hashimoto, M.; Fukutomi, H.; Kurohwa, M.; Miya, K.; Tsuboi, H.; Tanaka, M.; Tani, J.; Serizawa, T.; Harada, Y.; et al. Benchmark models of eddy current testing for steam generator tube: Experiment and numerical analysis. Int. J. Appl. Electromagn. Mater. 1994, 5, 149–162. [Google Scholar] [CrossRef]
- Takagi, T.; Hashimoto, M.; Sugiura, T.; Norimatsu, S.; Arita, S.; Miya, K. 3D Numerical Simulation of Eddy Current Testing of a Block with a Crack. Rev. Prog. Nondestr. Eval. 1990, 9, 327–334. [Google Scholar] [CrossRef] [Green Version]
- Korea Electric Association. MI in Service Inspection of N.P.P; MIA Special ed.; 2005 ed∼2009 add; Korea Electric Association: Seoul, Korea, 2009; p. 32. [Google Scholar]










| Probe | Test Specimen | ||
|---|---|---|---|
| Inner diameter Outer diameter Height Numbers of turns Lift-off | 3 mm | Thickness | 9 mm |
| 4 mm 4 mm | Conductivity Permeability1 | 1.38 Ms/m 1 | |
| N/A 0.1 mm | Permeability2 Permeability3 Weld width | Random Random 12 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berkache, A.; Lee, J.; Choe, E. Evaluation of Cracks on the Welding of Austenitic Stainless Steel Using Experimental and Numerical Techniques. Appl. Sci. 2021, 11, 2182. https://doi.org/10.3390/app11052182
Berkache A, Lee J, Choe E. Evaluation of Cracks on the Welding of Austenitic Stainless Steel Using Experimental and Numerical Techniques. Applied Sciences. 2021; 11(5):2182. https://doi.org/10.3390/app11052182
Chicago/Turabian StyleBerkache, Azouaou, Jinyi Lee, and Eunho Choe. 2021. "Evaluation of Cracks on the Welding of Austenitic Stainless Steel Using Experimental and Numerical Techniques" Applied Sciences 11, no. 5: 2182. https://doi.org/10.3390/app11052182








